Peptide- and proton-driven allosteric clamps catalyze anthrax toxin translocation across membranes

Significance

High-resolution structural information on anthrax toxin allows for elucidation of detailed molecular models of transmembrane translocation. The toxin’s translocase channel component, protective antigen (PA), utilizes a series of polypeptide clamp sites, which serve as binding sites. It is not known how these clamps catalyze the translocation of large proteins while avoiding kinetic traps in which the translocated protein would remain tightly bound inside the channel. Here the clamp sites in PA are revealed to operate allosterically, allowing for the coordination of their activities and the avoidance of kinetic traps that would impede translocation. The ability of the translocating peptide to form a helix correlates with the observed allostery and supports an allosteric helix-compression model for translocation.

Abstract

Anthrax toxin is an intracellularly acting toxin in which sufficient information is available regarding the structure of its transmembrane channel, allowing for detailed investigation of models of translocation. Anthrax toxin, comprising three proteins—protective antigen (PA), lethal factor (LF), and edema factor—translocates large proteins across membranes. Here we show that the PA translocase channel has a transport function in which its catalytic active sites operate allosterically. We find that the phenylalanine clamp (ϕ-clamp), the known conductance bottleneck in the PA translocase, gates as either a more closed state or a more dilated state. Thermodynamically, the two channel states have >300-fold different binding affinities for an LF-derived peptide. The change in clamp thermodynamics requires distant α-clamp and ϕ-clamp sites. Clamp allostery and translocation are more optimal for LF peptides with uniform stereochemistry, where the least allosteric and least efficiently translocated peptide had a mixed stereochemistry. Overall, the kinetic results are in less agreement with an extended-chain Brownian ratchet model but, instead, are more consistent with an allosteric helix-compression model that is dependent also on substrate peptide coil-to-helix/helix-to-coil cooperativity.

The molecular mechanisms of pore loops and peptide clamps are critical to understanding nanomachines involved in peptide transport, including extracellular matrix secretion machinery (1), housekeeping secretases (2, 3), pore-forming toxins (4, 5), binary toxins (6–10), and unfoldases (11, 12). These clamps or pore loops are catalytic active sites that promote translocation by binding, pushing, or pulling on the substrate chain as it enters the translocase/unfoldase. Here we describe an allosteric clamp mechanism that governs anthrax toxin translocation.

Anthrax toxin (13) intoxicates cells when oligomeric protective antigen (PA) forms a translocase channel that transports lethal factor (LF) and edema factor (EF) across the endosomal membrane into the host cytosol (8, 14). The channel functions via three nonspecific peptide clamp sites (15): α-clamp (9), ϕ-clamp (7), and charge clamp (10). The α-clamps are deep clefts located on the top surface of PA between the subunits that bind to helices nonspecifically (9). Each PA heptamer or octamer can bind three or four LF or EF via the α-clamp clefts. In the center of the channel is the functionally required ϕ-clamp—a narrow ring of Phe residues (7). The charge clamp, beneath the ϕ-clamp, rectifies proton-gradient (ΔpH)-driven peptide movement through the channel (10). It is unclear how distant clamp sites promote translocation while avoiding tight binding and related adventitious kinetic traps.

A high-resolution cryoelectron microscopy (cryoEM) structure of the heptameric PA channel to 2.9 Å shows the central ϕ-clamp site is a narrow 6-Å configuration of F427 residues (16) (Fig. 1A). This configuration could, at best, accommodate extended-chain but not α-helical structure. The narrow ϕ-clamp structure may, at first glance, support the model that LF/EF translocate as fully extended chain (17) via a ΔpH-driven Brownian ratchet mechanism (10, 18–23). However, a structure of octameric PA (PA₈) bound to four PA-binding domains from LF (LF_N) showed an α-helix unfolded from each LF_N and docked into an α-clamp cleft (9). This structural insight led to another possible hypothesis that LF/EF form and melt helices within the translocon, and thus helix formation itself may transduce force via a power-stroke-driven, helix-compression mechanism (8).

Fig. 1.

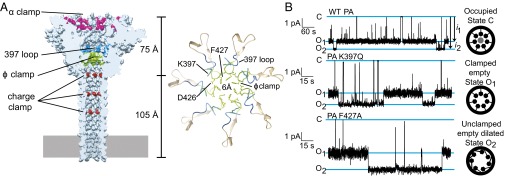
Alternate conductance states of the ϕ-clamp/397-loop network. (A) (Left) CryoEM structure of PA heptamer channel showing the locations of key clamps and loops. (Right) Detail of the ϕ-clamp and 397-loop sites showing the locations of key residues. (B) Single-channel planar lipid bilayer records at symmetric pH 7.6 and asymmetric KCl (100 mM [added KCl]_cis, 0 mM [added KCl]_trans) of (Top) WT PA, (Middle) PA K397Q, and (Bottom) PA F427A. The O₁ and O₂ open states and one closed state (C) are indicated. Unitary currents are designated as i₁ and i₂ (marked by arrows). Cartoons to right show how ϕ-clamp site is putatively configured in each state. Records are Gaussian-filtered to 50 Hz.

In the helix compression model, the translocating chain forms and melts α-helices cooperatively through the allosteric conversion of the clamp sites. Although a wider-diameter, helix-accepting ϕ-clamp has not been observed in a channel structure, a phylogenetic analysis suggested the ϕ-clamp makes a second conformation where the contact is made to an adjacent 397 loop in a neighboring monomer (24, 25) (Fig. 1A). Moreover, two alternate pore loop conformations have been also observed in the PA₈ prechannel oligomer structures (8, 9, 26). How two different pore loop configurations may promote proton-driven translocation is unclear, although their role in a putative allosteric mechanism is realistic given their dominant-negative phenotype (27, 28) and their phylogenetic requirement (25) for translocase function. Here we test two hypotheses. (i) The ϕ-clamp loop network is allosterically controlled by peptide binding to the distant α-clamp site. (ii) Substrate peptide helix-to-coil/coil-to-helix cooperativity is integral to the mechanism of translocation. Finally, these results are used to distinguish translocation models.

Clamped and Unclamped Conductance States

To determine if the central ϕ-clamp loops interconvert between two different configurations, single-channel currents were recorded. Three states of the channel were resolved: fully closed (C) and two open states (O₁ and O₂) (Fig. 1B and Fig. S1). The C state occurs when a contaminant small molecule, buffer ion, or peptide momentarily binds and occupies the ϕ-clamp (7, 29). Relative to the O₁ state, the O₂ state was the most conducting; therefore, O₂ represented a more dilated state of the channel (Fig. 1B). These two open states are better resolved at pH 7.6 than at pH 5.6 (Fig. 1B and Fig. S1). The O₁ and O₂ states logically interconverted, and hence they were not due to contaminating smaller/larger channels (Fig. 1B). These two open states were observed for multiple PA mutants in the ϕ-clamp (PA F427A) (7, 24, 27), the 397 loop (PA K397Q) (24, 25), and the α-clamp (PA R178A) (9, 30) at pH 5.6 and 7.6 (Fig. S1). Also, more importantly, the difference in single-channel current between O₂ and O₁ at pH 7.6 was greater for the PA F427A mutant relative to wild type (WT) [2.1 (±0.2) pA versus 0.7 (±0.2) pA, respectively] (Fig. 1B). This result supports the model that channel dilation specifically occurred at the ϕ-clamp, the conductivity (7), and structural (16) bottleneck. Thus, there are two open states of the ϕ-clamp network: (i) a clamped, empty state (O₁) and (ii) an unclamped, empty, dilated state (O₂).

Fig. S1.

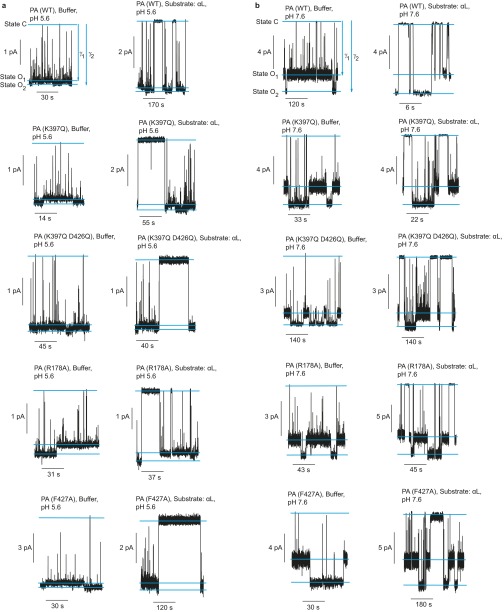
Single-channel records of alternate conductance states. Single-channel planar lipid bilayer records of WT PA and various indicated PA mutants in the presence or absence of peptide αl at asymmetric KCl (100 mM [added KCl]_cis, 0 mM [added KCl]_trans) and at symmetric (A) pH 5.6 or (B) pH 7.6. The O₁ and O₂ open states and the closed state (C) are indicated. Records are Gaussian-filtered to 50 Hz.

Allostery Thermodynamics

The two alternate states of the ϕ-clamp/397-loop network suggested the hypothesis that the clamp sites were part of a larger allosteric network. Indeed, at symmetric pH 5.6, the αl peptide (residues 1–50 of LF) bound cooperatively to WT PA in ensemble measurements (Fig. 2A and Table S1). The cooperativity, however, was not observed at pH 7.6 (Fig. 2A). This result indicated cooperativity was pH-dependent and was consistent with the fact that translocation is driven by a ΔpH. Mutation of the ϕ- or α-clamp sites also significantly diminished the cooperativity (Fig. 2B and Table S1). Together, these results suggested the affinity for peptide was under an allosteric control mechanism, where α-clamp binding allosterically modulated the peptide binding site found in the ϕ-clamp/397-loop network.

Fig. 2.

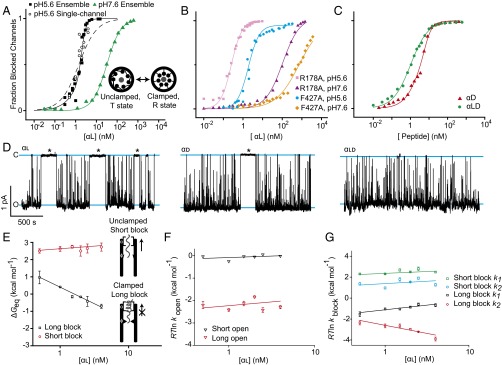
Single-channel and ensemble measurements of allosteric clamping. Binding of peptide αl to PA channels at symmetric pH 5.6 and asymmetric KCl (100 mM [added KCl]_cis, 0 mM [added KCl]_trans) for (A) ensemble measurements of WT PA at pH 5.6 (black square) and pH 7.6 (green triangle) and single-channel measurements at pH 5.6 (open black circle) where pH 5.6 data are fit to the MWC model (solid line) and a single-site binding model (dashed line) and (B) ensemble measurements of PA R178A at pH 5.6 (pink square) and pH 7.6 (purple triangle) and PA F427A at pH 5.6 (blue circle) and pH 7.6 (orange diamond). (C) Ensemble binding results for peptide αd (red triangle) and αld (green circle) peptides to WT PA at pH 5.6. Data for WT PA and peptide αl (pH 5.6) in A and for WT PA and peptide αd (pH 5.6) in C were fit to MWC allostery model. Fit parameters are given in Table S2. All other fits are to the Hill equation defined in Methods, where the parameters are given in Table S1. In A−C, SEs from the measurements of current values were propagated to fraction blocked and are less than a symbol width. (D) Single-channel records of WT PA at symmetric pH 5.6, asymmetric KCl (100 mM [added KCl]_cis, 0 mM [added KCl]_trans) in the presence of 1.5 nM peptides (Left) αl, (Middle) αd, and (Right) αld. Open (O) and closed (C) states are marked with blue lines, and long blocked states are marked with asterisks. Thermodynamic and kinetic parameters obtained from similar single-channel records for (E) thermodynamics (ΔG_eq) of long (black square) and short (red circle) dwell-time blockade events relative to opened-state dwell times; (F) kinetic rate constants for short-duration (black triangle) and long-duration (red triangle) open-dwell-time events, where rate constants are converted to a log scale by RT ln k; and (G) kinetics of long and short dwell-time blockade events for two-exponential fits, where rate constants are converted to a log scale by RT ln k, with rate-constant k₁ (green square) and k₂ (blue circle) for short-duration blocks and k₁ (black square) and k₂ (red circle) for long-duration blocks. Error bars (SD) are propagated from two to five membranes/measurements per point.

Table S1.

Hill equation estimate of cooperativity for peptide binding to PA channels

PA	Peptide	pH	Kd, nM*	n*
WT	αl	7.6	31.8 (±0.8)	1.28 (±0.04)
WT	αl	5.6	1.42 (±0.07)	3.1 (±0.3)
	αd	5.6	3.2 (±0.2)	1.6 (±0.1)
	αld	5.6	1.02 (±0.05)	0.99 (±0.04)
R178A	αl	5.6	0.26 (±0.01)	1.63 (±0.06)
	αd	5.6	0.35 (±0.03)	0.96 (±0.06)
	αld	5.6	0.62 (±0.04)	0.91 (±0.03)
F427A	αl	5.6	1.9 (±0.1)	1.6 (±0.1)
	αd	5.6	28 (±2)	0.64 (±0.02)
	αld	5.6	17.4 (±0.8)	0.78 (±0.02)

Cooperativity was estimated by using the Hill equation, f = 1/1 + (K_d/L)ⁿ, where f is fraction blocked channels as a function of peptide concentration, L. K_d is an apparent equilibrium dissociation constant, and n is the Hill coefficient.

^*Data shown are mean (±SE).

To further confirm the allosteric mechanism, we tested whether the cooperative dataset at pH 5.6 could be fit to a Monod, Wyman, and Changeux (MWC) allostery model (31). There were two limiting states of the clamps in the model. The successful fit determined that one state (R, relaxed) bound αl peptide >300-fold more tightly than the other state (T, taut) (Fig. 2A). The number of sites in the model, n, was fixed to seven, and the equilibrium constant, K_TR, was fixed to 10¹⁵ to allow for convergence in the fit. The allosteric mechanism also fit to single-channel binding results (Fig. 2A). However, the data did not fit well to a simple single-site binding model (Fig. 2A). In summary, there are two bound states of the PA channel, which we are terming the “clamped” state for the tightly bound R state and the “unclamped/dilated” state for the more weakly bound T state.

To gain structure/function insight on whether substrate-α-clamp interactions triggered changes in the ϕ-clamp, we designed some “conformational mutants” of the αl peptide. These mutants were made by varying the stereochemistry (32) of αl in a way that would alter its helical propensity and helix-to-coil cooperativity (33). Peptide αd was the same sequence as αl, but it was synthesized solely with d-amino acids; peptide αld similarly had αl sequence, but it was synthesized with alternating l- and d-amino acids. Sequence/stereochemistry information is in Fig. S2A. We confirmed the stereochemical modification of the peptides with circular dichroism (CD) spectroscopy. For αl, its spectra in aqueous buffer showed negative molar ellipticity consistent with right-handed helix and random coil (Fig. S2B). Peptide αd had positive molar ellipticity consistent with left-handed helix and random coil. Peptide αld had no molar ellipticity, consistent with it having a balance of left- and right-handed α-helical structure and random coil. Overall, the spectra in aqueous solvent were dominated by random coil. However, in 20% (vol/vol) 2,2,2-trifluoroethanol (TFE), the spectra for peptide αl and αd were consistent with fully right-handed and left-handed α-helix, respectively (Fig. S2C). Peptide αld had no CD signal in TFE, consistent with it having offsetting left- and right-handed helical structures.

Fig. S2.

LF_1–50 peptide sequence with stereochemical modifications. (A) (Top) Sequence of LF_1–50 (LF residues 1–50) with an amino-terminal six-histidine tag and a carboxyl-terminal tryptophan. The coding sequence of LF is underlined and numbered accordingly. Beneath (Upper Middle to Bottom) are the stereochemical compositions of the αl, αd, and αld peptides, where the l-isomers (white L) and d-isomers (black D) are indicated. The nonchiral glycines are indicated, in gray, by their amino acid symbol “G.” CD spectra of αl (black line), αd (red line), and αld (green line) peptides in the (B) absence and (C) presence of 20% TFE are plotted.

As judged by their Hill coefficients (n), peptides with altered stereochemistry bound less cooperatively than αl (Fig. 2C and Table S1). The ratio of the MWC equilibrium dissociation constants for the taut and relaxed states, K_dT and K_dR, was also used as a metric for degree of cooperativity (Table S2). For the most cooperative αl peptide, this K_dT/K_dR ratio was 330 (±40)-fold, and the Hill coefficient, n was 3.1 (±0.3). The αd peptide retained an intermediate level of cooperativity [n of 1.6 (±0.1) and K_dT/K_dR of 180 (±20)], and the αld peptide showed no cooperativity [n of 0.99 (±0.04)]. Thus, these data indicate that helix cooperativity is related to the allosteric mechanism.

Table S2.

MWC allostery model fit parameters

PA	Peptide	pH	KdT, nM*	KdR, nM*	KdT/KdR*
WTPA	αl	5.6	3.1 (±0.3)	0.009 (±0.0004)	330 (±40)
	αd	5.6	3.8 (±0.4)	0.021 (±0.001)	180 (±20)

The stoichiometry, n, and equilibrium constant, K_TR, were fixed to 7 and 10¹⁵, respectively.

^*Data shown are mean (±SE).

Clamped Peptides Avoid Retrotranslocation by Dissociating Slowly

A productive allosteric clamp should not release a peptide readily in the direction of unproductive retrotranslocation. To test this feature of the model, single PA channels were each exposed to natural and stereochemically altered peptides, and opened-state and closed-state dwell times were observed (Fig. 2D). The closed-state dwell times varied over a wide time range, with unusually long-lived dwell times lasting for >250 s. We divided the closed-state dwells into “short-lived,” which were less than 3 s, and “long-lived,” which were greater than 3 s. Long-lived closed-state dwells were most often observed with the isotactic, uniform stereochemistry αl peptide (Fig. 2D). The isotactic all-d-amino acid peptide, αd, also showed some instances of long-lived closed-state dwells; however, the syndiotactic, mixed stereochemistry αld peptide did not show appreciable long-lived closed-state dwells (Fig. 2D). These results indicated that clamping behavior, which corresponded to increasingly populated long-lived blocked states, was peptide-stereochemistry-dependent and apparently varied with the observed allostery.

To further investigate the long-lived blocking phenomenon, αl-induced single-channel blockades were analyzed thermodynamically and kinetically. Free energies (ΔG_eq) were computed for the long-lived and short-lived blockades. The equilibrium association ΔG_eq for the long-lived blockades (but not the short-lived blockades) became more favorable as the concentration of αl increased (Fig. 2E). The kinetic rate constants corresponding to peptide association (k_open) and dissociation (k_block) were also determined, and they were plotted on a log scale as RT ln k_open and RT ln k_block, respectively. (R is the gas constant, and T is the temperature in kelvins.) Interestingly, as αl increased over a 10-fold range in concentration, the change in association kinetics (given as RT ln k_open) did not correspondingly increase, as it only increased modestly by ∼0.5 kcal⋅mol⁻¹ (Fig. 2F). For a general binding phenomenon, binding is typically mediated through an increase in association kinetic rate constants. Surprisingly, however, the change in dissociation kinetics (given by RT ln k_block) decreased for the long-lived blockades by ∼1.5 kcal⋅mol⁻¹ over the same concentration range (Fig. 2G). This unusual kinetic behavior explained the MWC mechanism and suggested that the allostery within the translocase was mediated through dissociation rate constants. Thus, the allosteric site controlled the affinity for the peptide, ultimately clamping the peptide to slow its rate of unproductive release in the direction of retrotranslocation.

Clamp Allostery Governs Peptide Translocation Kinetics

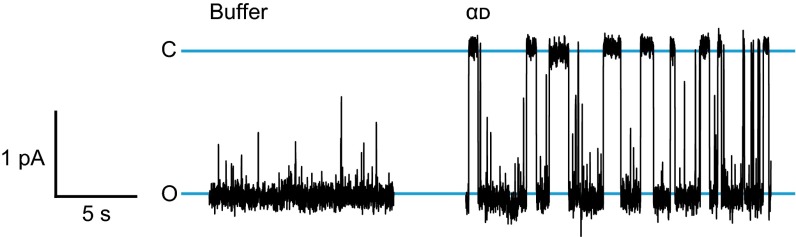
To kinetically function as a productive translocase, PA must vectorially release peptide to the other side of the membrane. To test this aspect of the translocation mechanism, single PA channels were examined under conditions that drove translocation. Single PA channels were inserted into a planar lipid bilayer under a +2-unit ΔpH driving force [membrane potential (Δψ) of 0 mV], a condition that strongly promotes translocation (18, 20). Upon addition of peptide, closures of the channels were observed. Closure times under these conditions corresponded to the time required to translocate. The αl peptide and the αd peptide exhibited 100-fold shorter closed dwell times (t_obs) than αld (Fig. 3A and Fig. S3). Control experiments with buffer alone distinguished peptide and buffer interactions (Fig. S3). On average, αd translocated slightly slower than αl [<t_obs> of 1.1 (±0.4) s versus 0.31 (±0.01) s, respectively]; however, these isotactic peptides were ∼40-fold to 130-fold faster than their syndiotactic counterpart, αld, which had a <t_obs> of 40 (±10) s (Fig. 3B). The resulting cumulative distribution functions (CDFs) for the closure events were not fit by single-exponential functions. Rather, they were S-shaped (on a linear time axis), indicative of a complex, multistep mechanism containing more than one intermediate (Fig. 3B). Compared with full-length LF and LF_N [with <t_obs> of 14 (±4) s and 7 (±1) s, respectively], it was found that αl and αd translocated faster than LF_N, but αld translocated slower than the 263-residue LF_N and the 776-residue LF (Fig. 3B). Thus, αld translocation was highly perturbed, indicating that peptide conformation played a key mechanistic role.

Fig. 3.

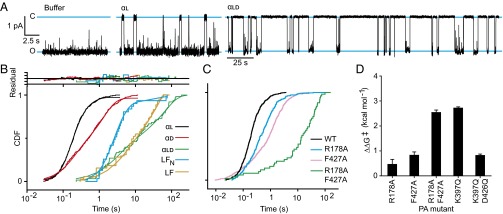
Peptide stereochemistry and channel mutational analysis of translocation. (A) Single-channel current records (black line) under an asymmetric ΔpH gradient of 2 units (pH_cis 5.6 and pH_trans 7.6) and an asymmetric KCl gradient (100 mM [added KCl]_cis, 0 mM [added KCl]_trans) for (Left) buffer alone, (Middle) 20 nM αl, and (Right) 60 nM αld peptides. Open (O) and closed (C) states are designated with blue lines. Note that scale bar for buffer and αl is given at left; larger time scale bar is given for αld, but the current scale is the same. (B) CDF of the single-channel blocked-state dwell times for the following peptide substrate and channel combinations: WT PA and αl (black), αd (red), αld (green), LF_N (blue), and LF (orange). Residuals to chemical kinetic modeling fits are given at top. (C) CDF of the single-channel of the blocked-state dwell times for αl peptide via WT (black) and the following mutant channels: PA R178A (blue), PA F427A (magenta), and PA R178A F427A (green). Individual CDFs were reproduced two to five times on individual membranes. (D) Activation free energy differences [i.e., ΔΔG^‡ = ΔG^‡(mutant PA) - ΔG^‡(WT)] for PA channel mutants from WT for the translocation of αl peptide. ΔΔG^‡ errors are propagated from SDs of t_1/2 values based on three to five CDF measurements per mutant.

Fig. S3.

Single-channel translocation record for αd and a buffer control. Single-channel current recordings (black trace) of PA channel without peptide (Buffer) and with 36 nM αd (d-enantiomer); representative recordings were performed at pH cis 5.6, 2-unit ΔpH, 0 mV Δψ, and asymmetric KCl (100 mM [added KCl]cis, 0 mM [added KCl]trans). Open (O) and closed (C) states are designated with blue lines. Note that scale bar for buffer and αd is given at left.

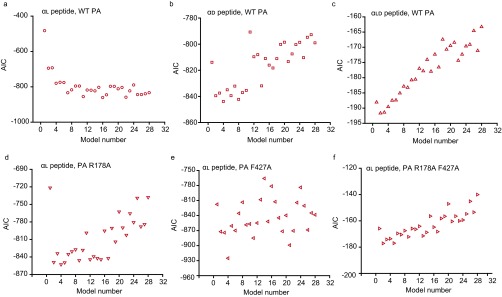
To investigate the translocation mechanism, CDFs for αl, αd, and αld peptide were fit to an extensive collection of 28 different chemical kinetic models (34) (Fig. 3B and Fig. S4). Each model began with a reversible binding step and ended with an irreversible dissociation to the trans side of the membrane. Akaike Information Criterion (AIC) was used to distinguish models for the αl, αd, and αld peptides (Fig. S5 A−C). Because the translocation kinetics were two-state, S-shaped, and not single-exponential, multiple-channel peptide complex (C·P) intermediates were populated during translocation as fully closed states. For αl, the most parsimonious scheme possessed a consecutive series of six irreversible first-order transitions of the C·P cocomplex

$$\text{C}+{\mathrm{P}}_{\mathrm{cis}}\leftrightarrow \text{C}\cdot {\mathrm{P}}_1\to \text{C}\cdot {\mathrm{P}}_2\to \text{C}\cdot {\mathrm{P}}_3\to \text{C}\cdot {\mathrm{P}}_4\to \text{C}\cdot {\mathrm{P}}_5\to \text{C}\cdot {\mathrm{P}}_6\to \text{C}+{\text{P}}_{\text{trans}}.$$

Although αd fit well to a model with three consecutive intermediates, the slower and less efficient αld used only two consecutive intermediates. Therefore, isotactic peptides moved through the channel by means of a multistep mechanism, but the syndiotactic one moved via a simpler, but slower, mechanism.

Fig. S4.

Potential chemical kinetic schemes for protein translocation. Twenty-eight possible kinetic schemes are diagramed. Each mechanism starts from the free channel state with peptide on the cis side of the membrane, P_cis, and each mechanism ends with peptide that translocated to the other side of the membrane, P_trans. The number designated to each scheme is used to reference the goodness of fits in Fig. S5.

Fig. S5.

Best-fit chemical kinetic schemes for translocation. To evaluate the quality of the fits to the closed-state CDFs (Fig. 3B) using the various translocation kinetic models (Fig. S4), the AIC was plotted for each model for the (A) αl, (B) αd, and (C) αld peptides in WT PA and (D) PA R178A, (E) PA F427A, and (F) PA R178A F427A with the αl peptide. AIC (y axis) is plotted against the x axis, which is numbered according to the schemes listed in Fig. S4. AIC is calculated by AIC = n log(RSS/n) + 2(k + 1), where RSS is residual sum of squares, n is number of data points, and k is number of parameters in each tested chemical kinetic model.

To determine if clamp allostery contributed to the observed rate acceleration of αl, kinetic measurements were made for the αl peptide using PA mutants (PA F427A and PA R178A) in the ϕ- and α-clamp sites, respectively (Fig. 3C). If the clamps were under allosteric control, then this would manifest as nonadditive activation free energies differences (ΔΔG^‡) from WT PA (35, 36). [The ΔG^‡ is estimated from the time for half the peptide to translocate (t_1/2) by ΔG^‡ = RT ln t_1/2 (37). AIC analysis of the PA mutants revealed they fit to different models than WT, making imperative the use of t_1/2 values to base kinetic comparisons (Fig. S5 D−F).] This effect was, in fact, observed, where individual mutants caused ∼0.5 kcal⋅mol⁻¹ changes in ΔΔG^‡(WT → MUT), but the double-mutant PA R178A F427A caused a ∼3-kcal⋅mol⁻¹ change (Fig. 3D). Indeed, double-mutant cycle analysis (35, 36) revealed that ΔG^‡(WT → F427A) was −0.8 (±0.1) kcal⋅mol⁻¹ and did not equal ΔG^‡(R178A → R178A F427A), which was −2.1 (±0.3) kcal⋅mol⁻¹. Hence the ϕ- and α-clamp sites were not independent. Overall, the coupling activation free energy for the distant ϕ- and α-clamp sites was 1.3 (±0.3) kcal⋅mol⁻¹. Also in agreement with the functional allosteric network model, PA K397Q showed a large defect in translocation, whereas PA K397Q D426Q restored function, reaffirming the role of the 397-loop/ϕ-clamp network (25). (Note that single-channel data could not be obtained with PA D426Q because its single-channel conductance was too low.) Thus, in support of the allosteric clamp model, the ϕ- and α-clamp sites worked synergistically through a long-distance network (38) (also including the 397 loop) to promote peptide translocation.

Discussion

This study is a single-channel analysis of peptide clamp allostery in a protein translocase or secretase. Here we find, in single-channel conductance experiments, that the central ϕ-clamp site gates between two different molecular configurations: a clamped state and an unclamped, dilated state. Based upon our thermodynamic analysis of peptide binding, we propose that the peptide binding properties of the clamped and unclamped states are remarkably distinct, as they differ by >300-fold in affinity for peptide. From our kinetic analysis of long blocked events in single-channel binding experiments, we found the allosterically triggered state is populated as the dissociation rate constants decrease. This result indicates that, when peptide binds to the α-clamp, it allosterically gates the ϕ-clamp to the tightly bound state. This property of the clamp is surprising albeit anticipated for a translocase, because it prevents the captured peptide from being released unproductively to the side of the membrane it initiated translocation from. Recently, in further support of this finding, a transcriptional coactivator was also shown to operate allosterically by decreasing dissociation rate constants (39). Hence this aspect of the allostery mechanism is not unprecedented.

As we have shown, in the absence of a proton gradient, dissociation from the channel could take hundreds of seconds. This timing is in stark contrast to the time to translocate under a proton gradient, which takes less than 1 s for the αl peptide. This dynamic, combined with the observation of multiple serial kinetic intermediates during translocation, suggests that there would need to be a means to reset the channel into the weaker affinity state. We propose that, under a ΔpH, proton dissociation down gradient allows the allosteric clamped state to reset to the weaker affinity unclamped state. The evidence for this aspect of the model is that allostery is diminished at higher pH. This weakening of the clamp would not, however, allow the peptide to release if it populated the deprotonated state, because a deprotonated and more anionic peptide would be trapped via the charge-clamp site located trans to the ϕ-clamp site.

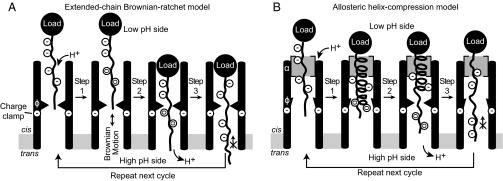
Between two plausible models, namely, the extended-chain (17) Brownian ratchet model (10, 18–23) (Fig. 4A) and the allosteric helix-compression model (8) (Fig. 4B), the current kinetic data on the αl peptide disfavor the former but favor the latter. This distinction between the two plausible models was made considering the relative speeds of the translocation kinetics data and not the thermodynamic binding data. Based upon the stereochemically altered peptide series tested, isotactic αl and αd peptides may cyclically populate sections of helical structure in the channel. This allosteric and stereochemistry-centered model is consistent with a recent functional analysis of synthetic anthrax toxin substrates (40) and a crystal structure revealing the LF_N–helix interactions with the α-clamp (9). An extended-chain model (17), by contrast, would not be selective of stereochemistry, as all three stereochemical configurations tested could easily make extended chain (32). Our detailed analysis of plausible chemical kinetic schemes consistent with efficient isotactic peptide translocation (αl and αd) suggests that the series of intermediates observed are consistent with a repeating coil-to-helix/helix-to-coil translocation cycle. It is known that isotactic peptides, αl and αd, have a unique ability to cooperatively transition between helix and random coil states, but the syndiotactic αld peptide cannot cooperatively cycle between the two structural extremes (33). Hence the alternating, syndiotactic peptide translocates poorly, presumably because it disrupts helix-to-coil/coil-to-helix cooperativity (33).

Fig. 4.

Translocation models. (A) Extended-chain Brownian ratchet mechanism. Peptide binds protons, reducing negative charges (−) in Asp/Glu residues to neutral ones (0). Brownian motion allows peptide to move past charge-clamp site. Peptide deprotonates down gradient and is electrostatically trapped for next iteration of translocation. (B) Allosteric helix-compression model. Helix populates within the channel, applies force on load, and triggers the allosteric α-clamp site. Asp/Glu (−) residues are neutralized (0) as the peptide protonates. Helix binding to the α-clamp site triggers the ϕ-clamp to convert to a high-affinity more closed state that collapses the helix into an extended chain. This action productively displaces the chain past the charge-clamp discriminator, trapping the Asp/Glu residues once they deprotonate down gradient. The transport cycle can then repeat when a new helix forms within the channel. Although multiple α-clamp sites exist, only one α-clamp site is diagramed in the above model. This simplification is meant to emphasize how kinetic allostery can be maintained when a single polypeptide chain is translocating.

Of course, an extended-chain Brownian ratchet mechanism may operate when required, albeit it does so much more slowly, i.e., with 10- to 100-fold slower kinetics. We propose that this is how the channel handles the syndiotactic αld peptide. Moreover, in the context of full-length LF, the channel may use the Brownian ratchet mechanism as a means to translocate peptide sequences with high β-sheet propensity. However, when a sequence with higher α helical propensity is present, the channel may take advantage of the allosteric helix compression mode of translocating.

Methods

Electrophysiology.

LF peptides were synthesized and verified with mass spectrometry by Elim Biopharmaceuticals, Inc. PA and mutants thereof were oligomerized and manipulated as described (9, 26, 37). Planar lipid bilayer currents were recorded using an Axopatch 200B (26, 37). Membranes were painted on a 50-μm aperture of a 1-mL, white Delrin cup with 3% (wt/vol) 1,2-diphytanoyl-sn-glycerol-3-phosphocholine in n-decane. Membranes were bathed in either bilayer buffer (BB: 5 mM succinate, 5 mM phosphate, 1 mM EDTA) or bilayer chloride buffer (BClB: 5 mM succinate, 5 mM phosphate, 1 mM EDTA, 100 mM potassium chloride). Single-channel recordings were acquired and filtered at 2 kHz. Ensemble recordings were made at 100 Hz. $\mathrm{\Delta }\mathrm{\psi }\equiv {\mathrm{\psi }}_{\mathrm{cis}}-{\mathrm{\psi }}_{\mathrm{trans}}\left({\mathrm{\psi }}_{\mathrm{trans}}\equiv 0\hspace{0.17em}\text{V}\right)\mathrm{;}\mathrm{\Delta }\text{pH}\equiv {\text{pH}}_{\text{trans}}-{\text{pH}}_{\text{cis}}$.

Thermodynamics.

Allosteric fits used the MWC model (31):

$${\mathrm{\theta }}_{\mathrm{obs}}=\left(K_{\mathrm{TR}}\left[\text{P}\right]/K_{\text{dT}}{\left(1+\left[\text{P}\right]/K_{\mathrm{dT}}\right)}^{n\mathrm{-}1}+\left[\text{P}\right]/K_{\text{dR}}{\left(1+\left[\text{P}\right]/K_{\mathrm{dR}}\right)}^{n\mathrm{-}1}\right)/\left(K_{\mathrm{TR}}{\left(1+\left[\text{P}\right]/K_{\mathrm{dT}}\right)}^n+{\left(1+\left[\text{P}\right]/K_{\mathrm{dR}}\right)}^n\right).$$

The MWC model assumes that, in the absence of peptide (P), the channel exists in the taut (T) or relaxed (R) state, and these states are in the equilibrium, R ↔ T, defined by K_TR. These states bind to peptide with respective K_dT and K_dR equilibrium dissociation constants. Observed fraction bound (θ_obs) versus [P] data were fit in ORIGIN9. Single-channel thermodynamic peptide binding data were obtained by measuring the total time the channel was blocked by peptide (t_block) and the total time the channel was not blocked by peptide (t_unblock), where θ_obs = t_block/(t_block + t_unblock).

Binding Kinetics.

In the single-channel equilibrium binding experiments, a single PA channel was inserted under a salt gradient ([Added KCl]_cis = 100 mM and [Added KCl]_trans = 0 mM). The ΔpH and Δψ were then set to 0 units and 0 mV, respectively. Approximately 1.5 nM peptide (either αL, αD, or αLD) was added to the cis chamber. Closed-state dwell times (t_obs) detected in CLAMPFIT10 were statistically analyzed by CDFs [defined as P(t_obs ≤ t)] using ORIGIN9. The closed-state dwell times from each experiment were divided into two different time domains: long-lived (>3 s) and short-lived (<3 s) closures. Analysis of peptide-dependent closed-state CDFs thus produced two different dwell-time distributions for each peptide, one corresponding to long block and the other for short block events. In both cases, opened-state CDF fit well to a single-exponential function, CDF = 1 – exp(−k_opent). Although both the short and long block CDF fit to double exponential functions, CDF = 1 – A₁exp(−k₁t) – A₂exp(−k₂t).

Translocation Kinetics.

Single-channel translocation data were collected under a +2-unit ΔpH with a 100-mM KCl gradient ([Added KCl]_cis = 100 mM and [Added KCl]_trans = 0 mM). Peptides were added to the cis chamber to a final concentration of 20 nM to 60 nM. Closed-state dwell times (t_obs) detected in CLAMPFIT10 were statistically analyzed by CDFs [defined by the probability P(t_obs ≤ t)] using ORIGIN9. The opened-state CDF fit well to a single-exponential function, CDF = 1 − exp(−k_obst). Short-lived closures (<10 ms) of a channel due to small contaminants were distinguished from long-lived events (>10 ms) caused by peptide binding to the channel. Analysis of the peptide-dependent closed-state CDFs revealed complex S-shaped kinetics, which could not be fit by a single-exponential function. Using GEPASI3, these were, instead, fit using a variety of chemical kinetic schemes (34). Because different peptides exhibited different chemical kinetic schemes, their translocation kinetics were compared on the basis of the time (in seconds) for half of the substrate to translocate (t_1/2) (37). Empirical activation energies of translocation (ΔG^‡) were estimated by ΔG^‡ = RT ln t_1/2/c, where c is 1 s (37).

SI Methods

Proteins.

LF peptides were synthesized, purified, and analyzed by mass spectrometry at Elim Biopharmaceuticals, Inc., requiring no further purification. Stock solutions of the peptides were made from freeze-dried powder in deionized water to prevent the introduction of unwanted buffer ions. Six-histidine (His₆)-tagged LF and LF_N (residues 1 to 263 of LF) were purified from overexpressing bacteria using standard Ni²⁺ nitrilotriacetic acid affinity chromatography and Q-Sepharose, anion-exchange chromatography (GE Healthcare) (18). The His₆ tags were removed with bovine α-thrombin treatment (0.5 units per milligram of protein) for 30 min at room temperature in 20 mM Tris⋅Cl, pH 8, 150 mM NaCl, 2 mM CaCl₂, and 1 M dextrose (37). WT PA, PA R178A (9), PA F427A (7), PA R178A F427A, PA K397Q (25), and PA K397Q D426Q (25), were overexpressed in the periplasm and purified on Q-Sepharose as described (7). PA₇ oligomers were produced on Q-Sepharose as described previously (26).

Planar Lipid Bilayer Apparatus.

Planar lipid bilayer currents were recorded using an Axopatch 200B amplifier and a Digidata 1440A acquisition system (Molecular Devices Corp.) (26, 37). Membranes were generally painted on a 50-μm aperture of a 1-mL, white Delrin cup with 3% (wt/vol) 1,2-diphytanoyl-sn-glycerol-3-phosphocholine (Avanti Polar Lipids) in n-decane (Sigma-Aldrich). Cis (side to which the PA₇ is added) and trans chambers were bathed generally in either BB (5 mM succinate, 5 mM phosphate, 1 mM EDTA) or BClB (5 mM succinate, 5 mM phosphate, 1 mM EDTA, 100 mM potassium chloride). Single-channel recordings were electronically filtered at 2,000 Hz using a multisection Bessel filter and recorded at 2,000 Hz using PCLAMP10 software. Ensemble recordings were similarly made at 100 Hz with matched filtering. $\mathrm{\Delta }\mathrm{\psi }\equiv {\mathrm{\psi }}_{\text{cis}}-{\mathrm{\psi }}_{\text{trans}}\left({\mathrm{\psi }}_{\mathrm{trans}}\equiv 0\hspace{0.17em}\text{V}\right)\mathrm{;}\mathrm{\Delta }\text{pH}\equiv {\text{pH}}_{\text{trans}}-{\text{pH}}_{\text{cis}}$.

Single-Channel Analysis of Unitary Currents.

A single PA channel was inserted into a painted bilayer at a Δψ of 0 mV by adding ∼1 fmol of PA₇ (freshly diluted from a 2 μM PA₇ stock) to the cis side of the membrane (37). For pH 5.6 experiments, the cis chamber was bathed in BClB at pH 5.6, but the trans chamber was bathed in relatively low-electrolyte BB at the same pH to maintain symmetrical pH conditions to establish a conducting ΔKCl gradient at symmetrical pH as described (9). For pH 7.6 experiments, single channels were inserted in BCIB at pH 5.6 in the cis chamber, and, after insertion, the cis chamber was perfused with 20 mL of fresh pH 7.6 BCIB. Individual channel recordings were made for WT PA and mutants thereof at 2,000-Hz acquisition and filtering. Before plotting the records, they were refiltered by a Gaussian filter in CLAMPFIT10 to 50 Hz. Gaussian fits to different current levels were made to judge unique states of the channel. Errors in differences of the two conducting states of the channel were made from at least three different measurements as SDs.

Ensemble Equilibrium Binding.

A prior method (9) was used to monitor LF_N and LF peptide binding to channels at symmetrical pH and a Δψ of 0 mV by means of an applied KCl gradient. A bilayer was formed in either a 50- or 100-μm white Delrin cup. The cis chamber was bathed in BClB, pH 5.6. During setup, the trans chamber was bathed in the low-electrolyte BB at either pH 5.6 or 7.6, depending on the desired target pH conditions of the experiment. PA channels were inserted by adding 20 nmol of PA₇ to the cis chamber at pH 5.6. Upon stabilization of the ensemble current, the cis chamber was perfused to exchange fresh BClB at the desired pH, depending on the experiment: For the acidic pH condition, pH_cis and pH_trans were 5.6, but, for the neutral pH conditions, pH_cis and pH_trans were 7.6. Peptide ligand (P), i.e., LF_N or LF peptide, was added in small increments to the cis side of the membrane, allowing for binding to reach equilibrium, as indicated by the observed decrease in current. Fractions of closed channels (θ_obs) versus [P] plots were initially fit to a simple single-site model, θ_obs = 1/(1 + K_d/[P]), to obtain an equilibrium dissociation constant, K_d. In cases where binding was shown to be cooperative, several other analyses were performed as described in SI Methods, Allosteric Binding Model.

Allosteric Binding Model.

In some cases, the single-site binding model failed in fitting the data and yielded large systematic deviations. Several binding cooperativity models were tested to better pinpoint the mechanism. The cooperativity phenomenon was first estimated with the empirical Hill equation, θ_obs = 1/[1 + (K_d/[P])ⁿ]. This model was only used to approximate the Hill coefficient, n. The MWC allostery model (31) was adopted once the α- and ϕ-clamp sites were established in the cooperative binding mechanism. Each of the α-clamp sites in the seven-subunit oligomer (n = 7) were assumed to be able to bind P; however, only P reaching the ϕ-clamp would block conductance, based on previous observations (7, 9). The MWC formalism assumes that, in the absence of P, the channel exists in the taut (C_T) or relaxed (C_R) state, and these states are in the equilibrium, C_R ↔ C_T, defined by K_TR. These states bind to peptide with respective K_dT and K_dR equilibrium dissociation constants. The θ_obs for the MWC model is given by

$${\mathrm{\theta }}_{\mathrm{obs}}=\left(K_{\mathrm{TR}}\left[\text{P}\right]/K_{\text{dT}}{\left(1+\left[\text{P}\right]/K_{\mathrm{dT}}\right)}^{n\mathrm{-}1}+\left[\text{P}\right]/K_{\text{dR}}{\left(1+\left[\text{P}\right]/K_{\mathrm{dR}}\right)}^{n\mathrm{-}1}\right)/\left(K_{\mathrm{TR}}{\left(1+\left[\text{P}\right]/K_{\mathrm{dT}}\right)}^n+{\left(1+\left[\text{P}\right]/K_{\mathrm{dR}}\right)}^n\right).$$

The θ_obs versus [P] data were fit in ORIGIN9 to estimate the binding equilibrium dissociation constants. Single-channel thermodynamic peptide binding data were obtained by measuring the total time the channel was blocked by peptide (t_block) and the total time the channel was not blocked by peptide (t_unblock), where θ_obs = t_block/(t_block + t_unblock).

Thermodynamics of Binding.

For thermodynamic analysis of binding in Fig. 2, the fractional population (f) of each state, long block (C_LB), short block (C_SB), and open (O), were determined as the total dwell time in each state (t_CLB, t_CSB, or t_O) over the entire length of the recording (t_total); e.g., f_CLB = t_CLB/t_total, where t_total = t_CLB + t_CSB + t_O. The partition function, Q, was defined as

$$\text{Q}=1+\text{exp}\left(\mathrm{-}\mathrm{\Delta }{G}_{\text{O}\to \text{CLB}}/RT\right)+\text{exp}\left(\mathrm{-}\mathrm{\Delta }{G}_{\text{O}\to \text{CSB}}/RT\right),$$

where O is chosen as the ground state. From the fractional populations, Q and the thermodynamic free energies ΔG_O→CLB and ΔG_O→CSB were estimated as follows, using

$${\mathit{f}}_{\text{O}}=1/\text{Q}$$

$$f_{\text{CLB}}=\exp \left(\mathrm{-}\mathrm{\Delta }{G}_{\text{O}\to \text{CLB}}/RT\right)/\text{Q}$$

$$f_{\text{CSB}}=\exp \left(\mathrm{-}\mathrm{\Delta }{G}_{\text{O}\to \text{CSB}}/RT\right)/\text{Q},$$

where R is the gas constant; and T is the temperature in kelvins.

Single-Channel ΔpH-Driven Translocation.

A single PA channel was inserted into a painted bilayer at a Δψ of 0 mV by adding ∼1 fmol of PA₇ (freshly diluted from a 2-μM PA₇ stock) to the cis side of the membrane; the cis chamber was bathed in BClB at pH 5.6 but the trans chamber was bathed in relatively low-electrolyte BB at pH 7.6. Hence both a ΔpH and ΔKCl gradient were established, as described (20). Some intermittent, short-lived (<10 ms) closures of the PA channel were observed and attributed to buffer molecules or other minor contaminants. These closure events were readily discriminated from the long-lived (>10 ms) events characteristic of the substrates, LF, LF_N, or LF peptides.

Closed-state dwell times (t_obs) were determined from individual recordings using the event detector in CLAMPFIT10. No intermediate states were detected. A CDF, the probability (P) that a t_obs is less than or equal to time, t, or P(t_obs ≤ t), was determined for each set of closed- and opened-state t_obs in ORIGIN9. The opened-state CDF fit well to a single-exponential function, P(t_obs ≤ t) = 1 − exp(−k_obst). The logarithm of the observed rate constants (k_obs) varied directly with the logarithm of [P], indicating the opened-state CDF reported on peptide binding to the channel. Occasional short-lived closures (<10 ms) of a channel due to buffer ions and contaminants were readily distinguished from long-lived events (>10 ms) caused by peptide binding to the channel. These buffer events were removed from the subsequent analysis of closed-state events for any given peptide.

Analysis of the peptide-dependent closed-state CDFs revealed complex S-shaped kinetics, which could not be fit by a single-exponential function. Using GEPASI3, these were, instead, fit using 28 different chemical kinetic schemes (34). Because different peptides exhibited different chemical kinetic schemes, their translocation kinetics were compared on the basis of the time (in seconds) for half of the substrate to translocate (t_1/2). Empirical activation energies of translocation (ΔG^‡) at different ΔpH or Δψ were estimated by ΔG^‡ = RT ln t_1/2/c, where c is 1 s.

CD Spectroscopy.

Peptide stock solutions of αl (626 μM), αd (342 μM), and αld (1268 μM) were prepared by dissolving freeze-dried peptide in deionized water. CD samples were prepared by diluting the stock solutions to 20 µM in 10 mM of phosphate buffer, pH 7, with and without 20% (vol/vol) TFE. CD spectra were measured at 25 °C in an AVIV spectropolarimeter.