Activated kinetics in a nonequilibrium thermal bath

Changing rates of activated transitions with changing temperature is at the heart of the theory of chemical reactions. It is commonly expressed by the Arrhenius law, which asserts that reactions overcoming a potential (activation) barrier slow down as temperature is lowered. The reason is that each activated event occurs by drawing, by a random fluctuation, the kinetic energy from the surrounding heat bath to overcome the barrier of the potential energy. The probability of such a fluctuation decreases with cooling, thus slowing the kinetics down. In this established paradigm, temperature is a thermodynamic equilibrium parameter, constant across the sample, something that is only controlled by adding or subtracting heat from the entire macroscopic vessel in which the experiment is performed. In PNAS, Craven and Nitzan (1) explore what happens if this standard picture is modified to allow different parts of the reacting system, the reactants and products, to possess different temperatures.

How can temperature be different between reactants and products? From the macroscopic perspective, any heat flow should be associated with a temperature gradient; the two quantities are connected by the Kapitza thermal resistance (2). Therefore, any reaction with the thermal heat flow between the reactants and products will produce a temperature gradient between them. This is the configuration that Craven and Nitzan (1) put forward by considering the reactants and products at their corresponding temperatures $T_R$ and $T_P$ (Fig. 1). In contrast to the standard formulation of nonequilibrium thermodynamics, where only the chemically reacting subsystem is far from the equilibrium and the bath (which is the source or sink of thermal energy) is fully equilibrated (3), one arrives at the picture of chemical reactions occurring in a nonequilibrium thermal bath.

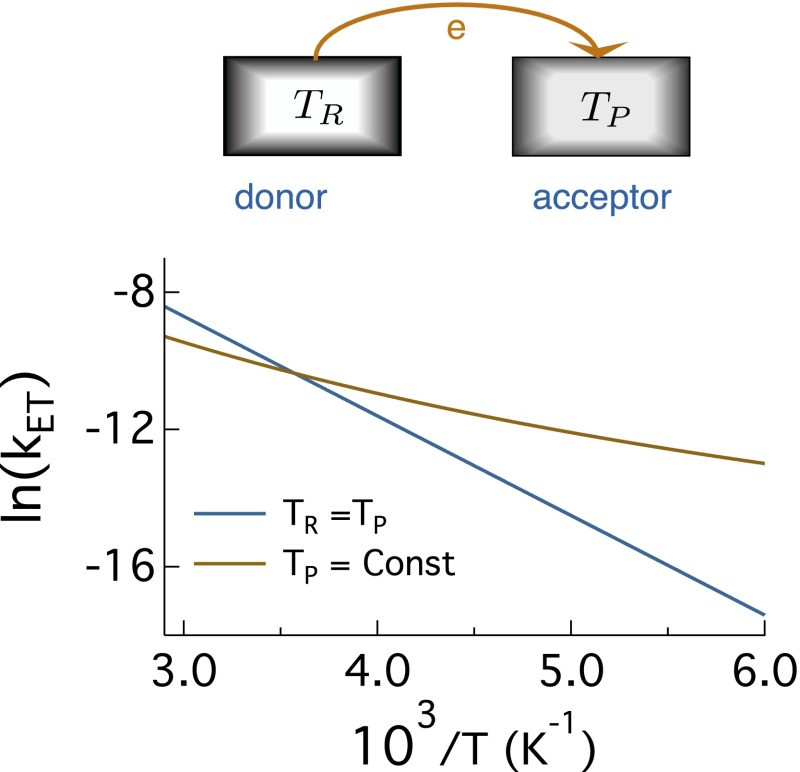
Fig. 1.

(Upper) Electron transfer between the donor and acceptor held at temperatures $T_R$ and $T_P$, respectively. (Lower) Arrhenius plot of the logarithm of the rate constant of electron transfer $\ln \left(k_{\text{ET}}\right)$ vs. $1/T$ for the equilibrium thermal bath with $T=T_R=T_P$ and for a nonequilibrium thermal bath, in which $T=T_R$ is varied and $T_P=280$ K is held fixed. The reaction is self-exchange electron transfer with zero reaction free energy and $E_{R1}=E_{R2}=0.5$ eV; $\text{ln}\left(k_{\text{ET}}\right)=-{\beta }_{\text{eff}}{F}^{†}$ is assumed for simplicity (the rate preexponential factor is put equal to unity).

To establish the transport of heat between molecules involved in chemical reactions, the length of the temperature change needs to scale down to nanometers (nanoscale) (2). In addition to practical difficulties of achieving this setup, one faces the challenging fundamental question of how to define temperature at such a small length scale. Temperature is well-defined in equilibrium thermodynamics of macroscopic materials, but the definitions of “nonequilibrium temperature” (4) and “local temperature” (5) differ between the applications and in general are not universal. The notion of a fictive temperature is often invoked in glass science, where it quantifies the amount of potential energy of a system trapped in a nonequilibrium state in excess to its equilibrium potential energy (6, 7). In this terminology, any activated event involves raising the system’s fictive temperature to the level consistent with the top of the activation barrier. In equilibrium systems, this occurs by spontaneous fluctuations (8), but the state of high fictive temperature can be alternatively achieved by either fast quenching of a hot system to a lower temperature or by bringing either reactants or products to a nonequilibrium state. The former scenario is realized in the preparation of glasses or in folding of proteins, whereas the latter scenario is routinely achieved in photochemistry, where absorption of light lifts the reactants to a state with a higher chemical potential. Part of light energy is typically deposited into vibrational degrees of freedom, leading to heating, that is, to an increase in the local temperature (9) relative to the temperature of the surrounding medium.

The effective temperature of an either driven or quenched nonequilibrium system has to exceed the equilibrium temperature to comply with the restrictions imposed by the second law of thermodynamics (4). This inequality implies greater thermal agitation within the system than work extracted in response to an external force. This general result has important consequences for energy chains of biology where barriers for moving electrons and, potentially, for other enzymatic reactions, are lowered by such excessive fluctuations (10). Because the nanometer length scale required for creating nonequilibrium states of the reactants and products is becoming increasingly accessible to experimentation, the natural question for this new emerging chemistry is how to describe chemical reactions at such conditions. The standard transition state theory (11) was not constructed to incorporate a nonequilibrium thermal bath and requires modification. Craven and Nitzan (1) take on this general theoretical challenge in application to electron-transfer reactions.

Electron transfer is a fundamental process for chemistry and biology, underlying essentially all chemical reactions altering oxidation states of the reactants and products (12). It is a basic elementary step in the production of energy by all forms of life (13) and is a critical step in the conversion of light’s energy to other forms in photosynthesis and photovoltaics (14).

At equilibrium, the basics are generally understood. The activation barrier of electron transfer is overcome by a spontaneous fluctuation deriving the kinetic energy from the thermal bath. According to Onsager’s regression hypothesis, this process is equivalent to applying a reversible work, or free energy, to bring the system to the nonequilibrium configuration at the top of the activation barrier (15). This free energy is calculated in the Marcus theory (8) from only two parameters: the free energy released to or absorbed from the bath (reaction free energy) and the free energy of electron-transfer reorganization $E_R$ (reorganization energy). The latter characterizes the breadth of the medium fluctuations, which scales linearly with the product of T and $E_R$. The probability of a spontaneous fluctuation is proportional to the Boltzmann factor $\text{exp}\left[-\beta F^{\mathrm{†}}\left(\beta \right)\right]$, where the inverse temperature $\beta =1/\left(k_{B}T\right)$ ($k_B$ is the Boltzmann constant) is uniform throughout the material.

The free energy $F^{†}\left(\beta \right)$ can be a complex function of temperature. It is known to increase with lowering temperature for activated relaxation of an external stress in glass-forming materials (7). The function $F^{†}\left(\beta \right)$ is also complex for electron-transfer reactions as a consequence of separate and distinct contributions to the overall activation barrier arising from molecular rotations and translations (16). The standard splitting $F^{†}=E^{†}-T{S}^{†}$ of the activation free energy into the temperature-independent energy and entropy often does not apply to electron-transfer reactions because both $E^{†}\left(T\right)$ and $S^{†}\left(T\right)$ are functions of temperature (17).

When the length scale for the temperature change becomes comparable to the distance between the donor and acceptor, one has to question the applicability of the Boltzmann distribution as the way to define probabilities of system configurations. Although this proposal seems to be far-reaching at first glance, it is perhaps quite common in electron transfer reactions occurring in biology’s energy chains (10). Proteins demonstrate a broad distribution of relaxation time scales. Some of them are slow enough to be practically frozen on the reaction time scale, making the nonequilibrium (fictive) temperature of the protein nearly universally higher than the equilibrium temperature of the surrounding bulk water. The rates of electron transfer measured in such systems invariably involve temperature-dependent $F^{†}\left(\beta \right)$, even though the Arrhenius plot of the logarithm of the reaction rate $\text{ln}\left(k_{\text{ET}}\right)$ vs. $1/T$ (Fig. 1) might seem to be linear in a narrow temperature range.

The challenge of formulating a theory involving a temperature gradient between the donor and acceptor subsystems is resolved in ref. 1 by assuming that Boltzmann statistics apply separately to the reactants and products, each characterized by a local temperature (Fig. 1). To connect this assignment to other problems of nonequilibrium thermodynamics, it is analogous to splitting the configuration space available to the system into basins (18), each

The standard transition state theory was not constructed to incorporate a nonequilibrium thermal bath and requires modification. Craven and Nitzan take on this general theoretical challenge in application to electron-transfer reactions.

characterized by a local Boltzmann distribution. The setup adopted by Craven and Nitzan (1) assigns a local temperature to each basin.

The theory in ref. 1 is formulated as the coupling of the electron to two harmonic oscillators characterized by their own reorganization energies $E_{R1}$ and $E_{R2}$ and equilibrated to different temperatures. The total reorganization energy of the bath becomes $E_R=E_{R1}+E_{R2}$. This physically attractive formalism predicts activated kinetics characterized by the effective temperature $T_{\text{eff}}=T_R\left(E_{R1}/E_R\right)+T_P\left(E_{R2}/E_R\right)$, which becomes the nonequilibrium (5) temperature for this specific problem. The general result of the theory is a weaker sensitivity of the activated kinetics to changes in temperature of either of the two heat reservoirs (reactants or products). This is illustrated in Fig. 1, where the Arrhenius kinetics of electron transfer in contact with an equilibrium thermal bath, $T=T_R=T_P$, is compared with the reaction in contact with a bath carrying a temperature gradient. In this latter case, the temperature of the reactant bath $T=T_R$ is varied, whereas the temperature of the product bath $T_P$ is held constant. The reaction enthalpy, given as the slope of the Arrhenius plot, is significantly reduced for the nonequilibrium bath. In addition, a slight curvature develops as a signature of a generally non-Arrhenius rate law in nonequilibrium systems (10).

The rules of performing the statistical averages are well-defined when two separate temperatures can be specified for reactants and products (1). This approach will not apply to reactions in which reactants and products couple to a single bath with a thermal gradient. One cannot assign a specific temperature to either reactions or products and only, at best, a range of temperatures. This problem falls under the general challenge of how to extend the theory of activated transitions beyond the equilibrium Boltzmann–Gibbs statistics (5, 10). Many applications, particularly those relevant to enzymatic reactions of biology, are characterized by the inability of the system to reach all parts of the phase space on the reaction time scale [the loss of ergodicity (18)]. The statistical consequence of this scenario is an excess of the fictive/effective temperature over the thermodynamic temperature (4). In addition, many reactions release heat (19), thus producing local excess of molecular kinetic energy and corresponding temperature gradients (9). All such scenarios demand advanced formalisms for describing reactions coupled to a nonequilibrium heat reservoir. We currently are taking only first steps in resolving this challenge. It holds promise for a deeper understanding of chemical reactivity in complex media and new capabilities in manipulating chemistry on the nanoscale.