Kinetic and thermodynamic framework for P4-P6 RNA reveals tertiary motif modularity and modulation of the folding preferred pathway

Significance

Many biological processes, including splicing, translation, and genome maintenance, require structured RNAs to fold into complex three-dimensional shapes. Our current understanding of these processes is based on distilling principles from descriptive folding studies. Moving toward predictive models will require coupling observed structural changes with kinetic and thermodynamic measurements. We have dissected P4-P6 RNA folding through distinct structural states and measured the rate and equilibrium constants for transitions between these states. Common kinetics found for RNA tertiary elements embedded in different structural contexts may help develop predictive folding models. Also, our results suggest that RNA folding may be well described by a model analogous to the diffusion-collision model for protein folding.

Abstract

The past decade has seen a wealth of 3D structural information about complex structured RNAs and identification of functional intermediates. Nevertheless, developing a complete and predictive understanding of the folding and function of these RNAs in biology will require connection of individual rate and equilibrium constants to structural changes that occur in individual folding steps and further relating these steps to the properties and behavior of isolated, simplified systems. To accomplish these goals we used the considerable structural knowledge of the folded, unfolded, and intermediate states of P4-P6 RNA. We enumerated structural states and possible folding transitions and determined rate and equilibrium constants for the transitions between these states using single-molecule FRET with a series of mutant P4-P6 variants. Comparisons with simplified constructs containing an isolated tertiary contact suggest that a given tertiary interaction has a stereotyped rate for breaking that may help identify structural transitions within complex RNAs and simplify the prediction of folding kinetics and thermodynamics for structured RNAs from their parts. The preferred folding pathway involves initial formation of the proximal tertiary contact. However, this preference was only ∼10 fold and could be reversed by a single point mutation, indicating that a model akin to a protein-folding contact order model will not suffice to describe RNA folding. Instead, our results suggest a strong analogy with a modified RNA diffusion-collision model in which tertiary elements within preformed secondary structures collide, with the success of these collisions dependent on whether the tertiary elements are in their rare binding-competent conformations.

Structured RNAs play central roles in biology, in the splicing and alternative splicing of eukaryotic pre-mRNAs, in the synthesis of proteins and their transport, and in chromosome maintenance (1–4). Beyond the RNAs and RNA–protein machines involved in these processes, it has been increasingly recognized that Nature has taken extensive advantage of RNA at multiple levels of gene regulation, and considerable current efforts are focused on uncovering the pathways and molecular mechanisms that underlie the functions of small RNAs and long noncoding RNAs (2, 5–8). The pervasive functions of RNA in biology underscore the importance of understanding RNA’s fundamental physical properties and, ultimately, of using this understanding to predict the kinetics and thermodynamics of folding and conformational transitions responsible for RNA function.

Decades of characterization of RNA folding and structure have led to generalizable principles and provided biological insights. The observations that RNA encodes genetic information, forms highly stable local structures, and can catalyze reactions provided support for the possibility that early life evolved using functional RNAs (9–12). This high stability was also recognized to lead to misfolding. Indeed, highly stable misfolded tRNAs were identified in the 1960s (13–15), and many subsequent studies supported a strong propensity of RNA to misfold (16–20). These observations and consideration of the physical properties of RNA (21) led to the “RNA chaperone hypothesis” (22), which predicted the existence of RNA chaperones to prevent and resolve deleterious misfolded states in vivo (20, 23–28).

Due to its complexity, most studies of RNA tertiary folding have been descriptive. Studies to date have identified misfolded intermediates (29–32), revealed multiple folding pathways (33, 34) and functional states (35), and led to the general perspective that RNA folds on a rugged energetic landscape (18). Nevertheless, these conclusions drawn from qualitative studies have been limited and, even at times, misleading. For example, evidence for new intermediates arising upon mutation and for changes in conditions that supported a rugged landscape for RNA folding instead has been shown, upon placement of results within the context of a kinetic folding framework, to represent formation of the same intermediate with altered stability (36). Additionally, an alternative base-pairing of the P3 helix was implicated in forming a long-lived misfolded state of the Tetrahymena group I intron (30) but could be isolated and probed only once the kinetic folding framework was established. Subsequent studies showed that the alternative P3 helix biased partitioning toward the long-lived misfolded state but that the final state contains the native P3 helix with its kinetic stability arising from an altered folding topology that requires near-complete unfolding to rectify (37, 38).

The above examples highlight the importance and power of quantitative analysis of individual reaction steps within complex processes. Such studies have been instrumental in many areas of biology and biochemistry—providing kinetics and frameworks to consolidate existing knowledge, aid the design of new experimental tests, anchor the interpretation of new results, and allow more precise and predictive models to be built (39–43). The power of this information is fully manifest when accompanied by structural information sufficient to allow molecular, and even biological, interpretation of kinetic and thermodynamic behavior (44, 45). However, the folding of RNAs, such as the group I ribozymes, RNase P RNA, and ribosomal RNAs, is extremely complex, with many structural elements, folding intermediates, and pathways, and there is limited structural information about these intermediates, precluding them as foundational models to connect kinetic and thermodynamic measurements with specific structural changes during folding.

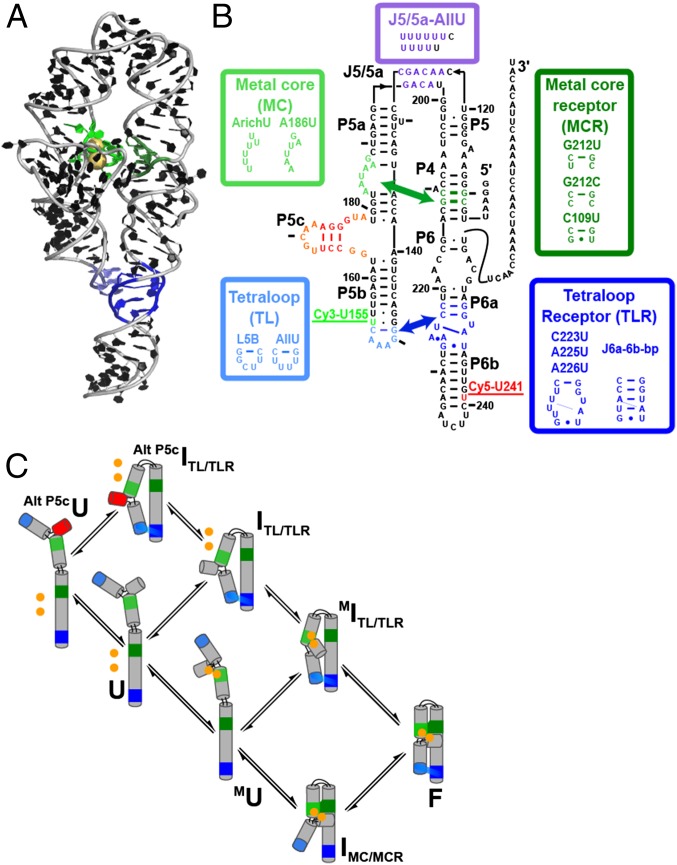
Decades of work on P4-P6 RNA (Fig. 1) have produced an X-ray structure of the folded state and rich structural information that delineate a set of potential folding intermediates and folding pathways (Fig. 1C) (47–57). Moreover, functional work has uncovered sets of mutations that allow ablation and isolation of these folding intermediates with high confidence (49, 51, 53, 56, 58–60). The control afforded by this well-behaved, established system provides an opportunity to deepen understanding and develop and test generalizable principles beyond this model system, provided that a detailed framework is in place to provide context for interpretation. Here, we use single-molecule FRET (smFRET) with a series of P4-P6 mutants to isolate and measure specific folding transitions, extending beyond measurements of overall folding rates (52–55, 61–65) and constructing a kinetic and thermodynamic framework for P4-P6 RNA. This framework defines a preferred folding pathway, allows this pathway and the partitioning of states to be interpreted in structural terms, helps to uncover the origin of the effects of mutations on folding rates and pathways, and suggests a generalized framework for considering RNA tertiary folding.

Fig. 1.

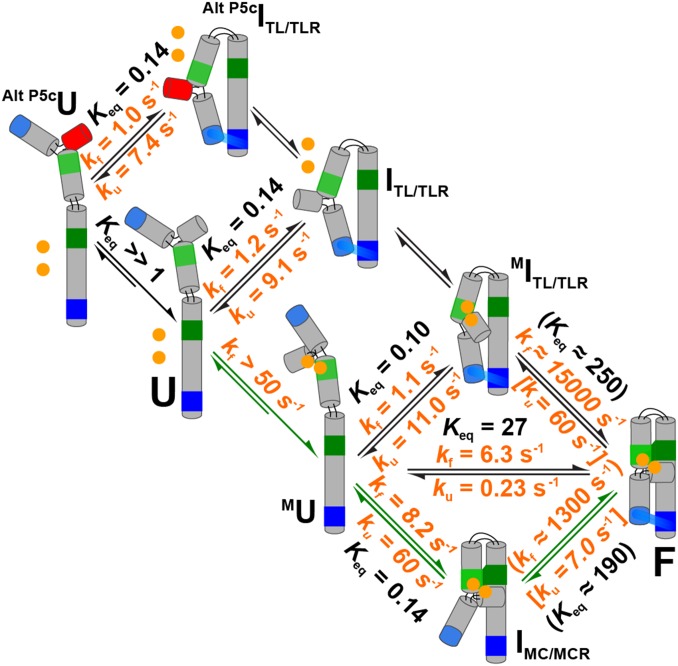
P4-P6 RNA and proposed framework. (A) P4-P6 crystal structure (PDB ID code 1GID). Tertiary contacts are colored as follows: tetraloop (TL, light blue), tetraloop receptor (TLR, dark blue), metal core (MC, light green), metal-core receptor (MCR, dark green). Crystallographically and functionally defined Mg²⁺ ions bound by the MC are shown as gold spheres (46, 50, 82). (B) P4-P6 secondary structure and variants used in this study to isolate specific folding intermediates (see also Fig. 2A). Tertiary contacts are colored as in A. The positions of the donor and acceptor dyes are shown. (C) Proposed thermodynamic and kinetic framework based on previously identified structural intermediates. P4-P6 is shown in a schematic depiction, color-coded as in A and B, and tertiary contacts are shown throughout as a green swatch and a blue swatch for the MC/MCR and TL/TLR, respectively. Intermediates include the following: ^{Alt P5c}U, unfolded state with an alternative P5c secondary structure; ^{Alt P5c}I_TL/TLR, intermediate with the TL/TLR interaction formed and the alternative P5c secondary structure; U, unfolded state with the native P5c secondary structure (states not notated “Alt P5c” have native P5c secondary structure); I_TL/TLR, intermediate with only the TL/TLR interaction formed; ^MU, unfolded state with the MC formed through binding of two Mg²⁺ ions (depicted as two bound gold spheres); ^MI_TL/TLR, intermediate in which the TL/TLR interaction and the MC are formed; I_MC/MCR, intermediate with the MC/MCR interaction formed; and F, the native folded state in which both tertiary contacts are formed (49, 56, 60, 77, 82, 118).

A further major goal in RNA folding, beyond a description of the kinetics and thermodynamics of individual structural transitions, is to obtain quantitative and predictive algorithms for RNA tertiary structure, akin to the predictive rules for RNA secondary structure formation. Although this problem is complex, several observations suggest that such a goal may be achievable due to a modular architecture and folding behavior of RNA (66, 67). This perspective is based on the observations that structures of tertiary contacts and junctions found in different RNA structures can be overlaid with little deviation (68–70) and that these substructures, or motifs, can be “cut and pasted” from one structural context to another with function retained (67–69, 71–75). From these observations, it has been proposed that it may be possible to predict the thermodynamics and kinetics of RNA tertiary structure formation from the energetic contributions of these motifs and other components of RNA structure (67). However, despite the structural similarity and transferability of motifs, there is as yet no quantitative assessment of whether the energetic properties of tertiary structure elements are the same in different structural contexts—a basic requirement for the viability of an energetic reconstruction of RNA tertiary structure from its components.

The P4-P6 kinetic and thermodynamic folding framework we derive provides an opportunity to assess whether components of RNA tertiary structure are energetically modular. Specifically, the P4-P6 framework isolates the formation and breaking of each of its two tertiary contacts, the tetraloop/tetraloop receptor and the metal core/metal-core receptor, allowing us to compare the rate constants for breaking these tertiary contacts in P4-P6 with those in simplified RNA constructs with each tertiary motif alone. We find kinetic properties of these motifs that are independent of structural context and thus may be transferrable, thereby providing an early step toward a predictive, energetic model for RNA tertiary structure.

Results and Discussion

We first developed the P4-P6 folding framework from structural states previously identified and measured the rate and equilibrium constants for transitions between these states with smFRET. We then used this framework to isolate the formation and dissolution of particular tertiary contacts to test whether the kinetics properties of this structural transition are transferable to other RNA contexts. Finally, we probed properties of the framework, in particular the flux through folding pathways in response to mutation, that suggest features of RNA folding that are analogous to simple protein-folding models and may be general.

Building and Determining a Kinetic and Thermodynamic Framework for P4-P6 RNA.

Building the structural states for the P4-P6 framework.

We first built on the large body of work on P4-P6 RNA (e.g., refs. 47–56, 59, 60, 65 and 76–82) to construct a framework of structural states, and we then probed transitions between these states to establish a kinetic and thermodynamic folding framework.

The P456 helical stack of P4-P6 (Fig. 1B, Right) connects to the P5abc helices (Fig. 1B, Left) via the two-way J5/5a junction, which enables a 180-degree turn that allows the P5abc helix to be roughly parallel to the P456 helices (Fig. 1A). This parallel configuration is enforced by two tertiary contacts of P4-P6, the metal core/metal-core receptor (MC/MCR) and the tetraloop/tetraloop receptor (TL/TLR). TL/TLR tertiary motifs are found in many structured RNAs (70), and, whereas the MC/MCR may be unique to this RNA (50), specific divalent binding sites are common in tertiary structures (83–87). In addition, many structured RNAs have junctions that, like J5/5a, exhibit distinct bending properties (51, 68, 88, 89).

The folding of P4-P6 has been followed in multiple studies, with folding rate constants of 2–30 s⁻¹ observed across a range of conditions (52–55, 61–65). However, interpretation of these overall rate constants has been stymied by a lack of knowledge of which individual folding steps were followed and rate limiting. Fig. 1C diagrams potential intermediates in the folding of P4-P6 suggested by prior structural work (47–57). States differ in whether an alternative secondary structure is present (Fig. 1C, Alt P5c, red), whether Mg²⁺ ions are bound to the metal core (Fig. 1C, gold circles), and whether each tertiary contact is formed (Fig. 1C, MC/MCR, green and TL/TLR, blue). NMR, small angle X-ray scattering, and chemical probing data with WT and mutant P4-P6 RNAs provide evidence for each of these structural states and conditions or mutations that allow each species to predominate (49, 51, 53, 56, 58–60).

Determining the P4-P6 kinetic and thermodynamic framework.

We studied the folding of the P4-P6 constructs depicted in Fig. 1B by smFRET.

smFRET allows determination of forward and reverse reaction rate constants and highly unfavorable and favorable equilibrium constants. This ability, along with homogenous molecular behavior (ref. 90 and Materials and Methods), allows construction of a folding framework under uniform conditions, avoiding uncertainties and complications from extrapolation of RNA behavior across conditions (62, 82, 91). Example traces and data quality analyses for all constructs can be found in Dataset S1. We emphasize the importance of reporting full characterization and analysis of all traces (92), rather than just representative traces and a final model, as well as the need to have single-molecule data in a common format and publically available for future analysis (93). In the following sections, we describe how individual steps and partition points in the overall folding framework have been assessed.

Determining the predominant unfolded state.

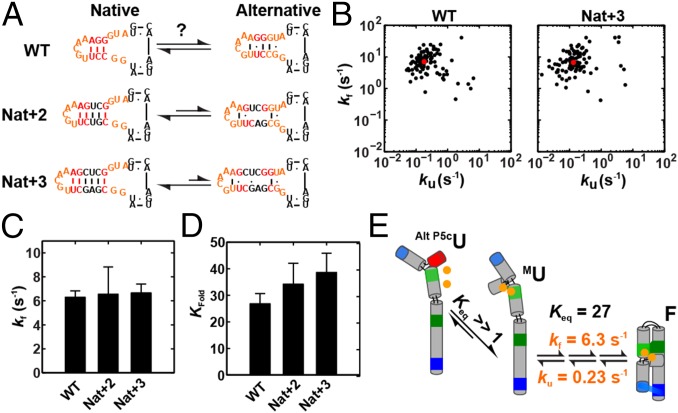
Prior studies by Wu and Tinoco (77) identified an alternative secondary structure within the P5c helix of an isolated P5abc construct in the absence of Mg²⁺ (Fig. 2A). Thus, it was necessary to determine, under the folding conditions used herein [5 mM Mg²⁺, 100 mM KCl, 50 mM 3-(N-morpholino)propanesulfonic acid (MOPS), pH 8.0], whether the unfolded state has P5c predominantly with the native or alternative secondary structure and whether the predominant folding pathway proceeded through the alternative secondary structure state (Fig. 1C). We therefore mutated P5c to stabilize the native form of P5c over the alternatively base-paired form (Nat+2 and Nat+3) (Fig. 2A) (94). If the alternative unfolded state (^{Alt P5c}U) were the prevalent unfolded state, then Nat+2 and Nat+3 would be predicted to increase the folding equilibrium constant and, in the simplest case of folding proceeding subsequently through U, increase the overall folding rate as well. In contrast, if P5c existed predominantly with its native base pairing in its predominant unfolded state (U or ^MU) (Fig. 1C), then further stabilizing the native base pairing would have little if any effect on the rate and equilibrium constants.

Fig. 2.

Overall folding of WT P4-P6 and constructs with the native P5c secondary structure enforced. (A) The local equilibrium between the native and alternative P5c secondary structure of WT P4-P6 and constructs with the native P5c secondary structure enforced by two (Nat+2) or three (Nat+3) base pairs (46, 50, 77, 82). (B) Scatter plot of folding versus unfolding rate constants for WT and Nat+3 P4-P6. Data for 100 randomly selected molecules with the median folding and unfolding rate constants denoted by red circles (Dataset S1). See SI Appendix, Fig. S1 for data for a variant with the alternative P5c secondary structure (Alt+2). (C and D) Comparison of the folding rate (C) and equilibrium (D) constants of WT, Nat+2, and Nat+3. Error bars correspond to the bootstrap-estimated 95% confidence intervals (SD = 2σ_bootstrap). See SI Appendix, Table S1 for data and SI Appendix, Supporting Methods for experimental details. Conditions were as follows: 50 mM MOPS, pH 8.0, 5 mM MgCl₂, and 100 mM KCl at 23 °C. (E) Overall P4-P6 folding occurs from an unfolded state with native P5c secondary structure (^MU).

Fig. 2B summarizes the overall folding and unfolding rate and equilibrium data for individual molecules of WT P4-P6 and Nat+3 P4-P6 (the data and analysis for all smFRET experiments are presented in Dataset S1). The rate constants for individual molecules are shown and demonstrate that the behavior of individual molecules is highly homogeneous for each construct. Nat+3 and Nat+2 P4-P6 give folding and unfolding rate and equilibrium constants that are nearly the same as WT P4-P6 (Fig. 2 C and D and SI Appendix, Table S1), suggesting that an unfolded state or states with native P5c secondary structure predominate over one with the alternative secondary structure (^{Alt P5c}U) under the conditions of our experiments.

Consistent with these results, an Mg_1/2 of ∼0.25 mM is observed for binding of Mg²⁺ to the metal-ion core (53), strongly suggesting that the predominant unfolded state at 5 mM Mg²⁺ has bound metal ions and the correct P5c secondary structure (77). This state is referred to as ^MU herein (Fig. 1C and Fig. 2E) and predominates over U. From the above, it seemed most likely that folding would proceed from ^MU to more folded states. Nevertheless, alternative pathways via the ^{Alt P5c}U or U states were possible. To rigorously assess these potential folding pathways, and others in subsequent sections, we took advantage of the fact that any step that is on the folding pathway must occur with a rate constant of 6.3 s⁻¹ or greater because no step on a pathway can occur slower than the overall rate constant (Fig. 2E).

To test the possibility that folding could involve fast formation of ^{Alt P5c}I_TL/TLR from the small fraction of P4-P6 in the ^{Alt P5c}U state (Fig. 1C), we measured the ^{Alt P5c}U-to-^{Alt P5c}I_TL/TLR transition, using a construct analogous to Nat+2 that stabilizes the ^{Alt P5c}U state instead (Alt+2). This construct folds at 1.0 s⁻¹, which is substantially slower than the overall folding rate of 6.3 s⁻¹ (SI Appendix, Fig. S1 and Table S1) and thus rules out folding via ^{Alt P5c}U as the preferred pathway (Fig. 2E).

Does P4-P6 fold via ^MU or I_TL/TLR?

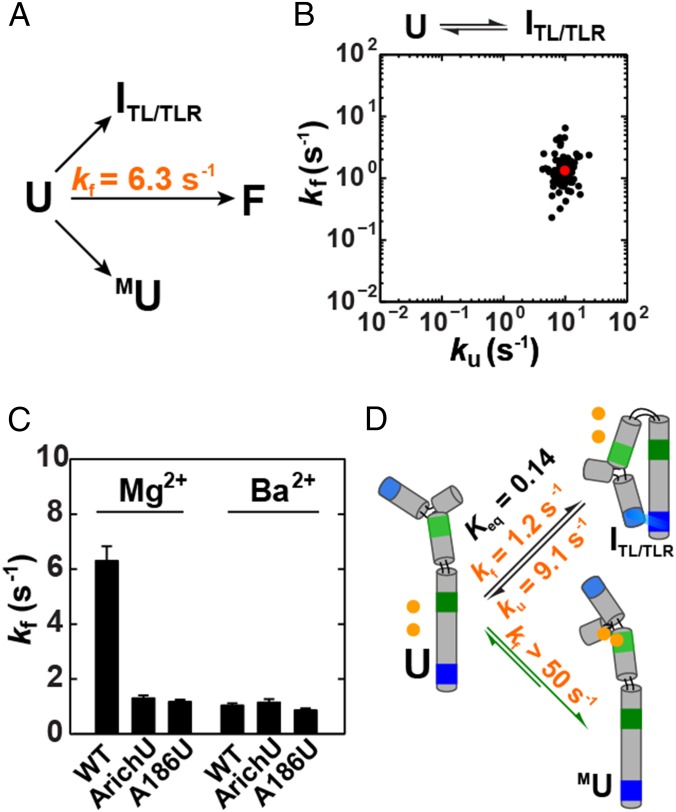
Having established ^MU as predominant over ^{Alt P5c}U and U, the simplest scenario would be predominant folding from it through one or both intermediates with a single tertiary interaction formed (^MI_TL/TLR and I_MC/MCR) (Fig. 1C). Nevertheless, a predominant folding from U to I^TL/TLR would also have been possible. Specifically, the small amount of U present could first form the TL/TLR tertiary interaction very rapidly to give I_TL/TLR, and subsequent folding could follow from that species (Fig. 3A).

Fig. 3.

Does the folding pathway proceed via formation of the tetraloop/tetraloop receptor (TL/TLR) or the metal core (MC)? (A) Folding from U could occur either through I_TL/TLR or ^MU. (B) Scatter plot of the folding versus unfolding rate constants of the ArichU mutant (Fig. 1C) that isolates the U-to-I_TL/TLR transition. (C) Comparison of the folding rate constants of WT, ArichU, and A186U P4-P6 in Mg²⁺ and Ba²⁺. Prior work has shown that Ba²⁺ does not bind to the metal core so the same folding behavior is predicted for WT P4-P6 and the ArichU and A186U mutants in Ba²⁺ (81). This expectation was met, suggesting that there are no unintended effects from the above mutations. Errors as in Fig. 2. Conditions were as follows: 50 mM MOPS, pH 8.0, 5 mM MgCl₂ or BaCl₂, and 100 mM KCl at 23 °C. (D) P4-P6 folds predominantly via formation of the ^MU intermediate (green arrows). The equilibrium and kinetic values shown for the U-to-I_TL/TLR pathway are average values from A186U and ArichU variants (SI Appendix, Table S1). Estimation of the limit for the U-to-^MU transition of >50 s⁻¹ was determined from previous literature data (SI Appendix, SI Text).

We isolated the folding of U to I_TL/TLR by mutating residues in the so-called A-rich bulge, an internal loop that binds Mg²⁺ ions; and these mutations were previously shown to prevent Mg²⁺ binding (Fig. 1B, ArichU) (56). Fig. 3B shows the folding and unfolding of individual ArichU RNA molecules, and Fig. 3C compares the folding rate constants for this mutant, an additional mutant that prevents Mg²⁺ binding (A186U) (58), and WT P4-P6. These mutants can fold only to I_TL/TLR whereas WT P4-P6 folds to its final state (F) with both contacts under these conditions (56). The MC mutants fold ∼10-fold slower than WT (Fig. 3C and SI Appendix, Table S1). Because an overall process cannot occur faster than its slowest step, a pathway involving a rare state such as U would need to be correspondingly faster than the overall folding rate. Thus, these data strongly suggest that a pathway via I_TL/TLR is not significantly traversed in WT P4-P6 folding—i.e., this pathway is not kinetically competent.

The observation that folding via I_TL/LTR is not kinetcally competent requires that folding of U to ^MU be at least as fast as the overall folding rate constant of 6.3 s⁻¹ because this step is on the pathway that must be traversed (Fig. 3D). Although our smFRET assay cannot detect the U-to-^MU transition, because there is no significant FRET difference between these states, prior time-resolved hydroxyl radical footprinting results (53) suggest that Mg²⁺ binding is fast relative to overall P4-P6 folding, with a rate constant of >50 s⁻¹ (Fig. 3D and SI Appendix, SI Text), further supporting the preferred folding pathway from U to ^MU.

Does folding proceed from ^MU via ^MI_TL/TLR or I_MC/MCR?

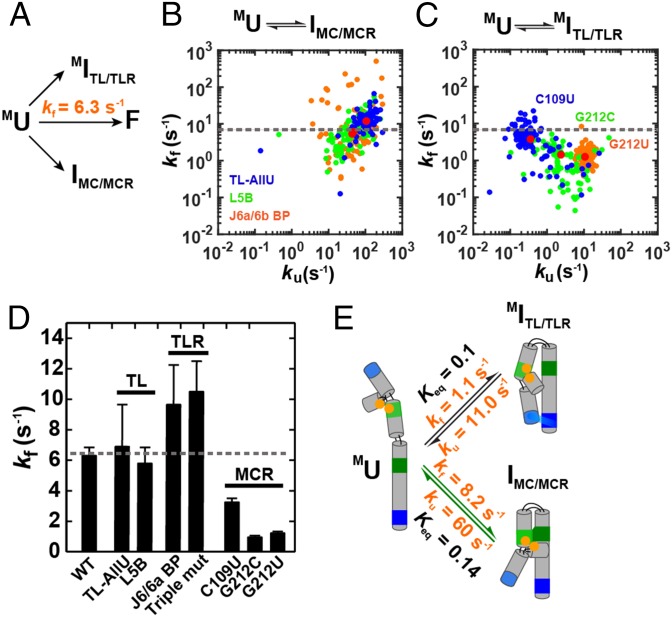
Once Mg²⁺ ions are bound to the metal core (MC) to give ^MU, two possible intermediates can form next, ^MI_TL/TLR or I_MC/MCR (Fig. 1C and Fig. 4A). We distinguished between these potential folding pathways from ^MU using mutations to isolate the transitions to ^MI_TL/TLR and I_MC/MCR (Fig. 4A). To isolate the ^MU-to-I_MC/MCR transition, we mutated the tetraloop (TL) and tetraloop receptor (TLR) (Fig. 1B). The folding of these mutants is as fast as that for overall folding (Fig. 4B, dashed line), and the same results were obtained for multiple constructs with mutations in the TL or TLR (Fig. 4D and SI Appendix, Table S1).

Fig. 4.

Does folding proceed from ^MU via formation of the tetraloop/tetraloop receptor (TL/TLR) or the metal core/metal-core receptor (MC/MCR)? (A) From ^MU, folding can proceed through ^MI_TL/TLR or I_MC/MCR. (B) Scatter plot of the folding versus unfolding rate constants for the TL-AllU (blue), L5B (green), and J6a/6b BP (orange) mutants that destabilizes the TL/TLR; and (C) MCR variants C109U (blue), G212C (green), and G212U (orange) that destabilize the formation of the MC/MCR contact (SI Appendix, Fig. S5). (D) Comparison of the folding rate constants of WT P4-P6 with those of the TL, TLR, and MCR mutants. Triple mut, the A225U/A226U/C223U variant. The dotted gray lines in C and D indicate the rate constant for WT P4-P6 folding. The values are from SI Appendix, Table S1, and the error estimates and conditions are as in Fig. 3. (E) Preferential folding via I_MC/MCR. The rate constants for the ^MU-to-^MI_TL/TLR transition are for the G212U mutant (SI Appendix, Table S1) because this mutant has rate constants and behavior similar to MC mutations that ablate the MC/MCR interaction (56). The rate constants for the ^MU-to-I_MC/MCR transition are averages of the values for the TL and TLR variants in D.

These results meet a necessary criterion for folding proceeding through the I_MC/MCR intermediate but alone are not sufficient to establish this pathway over pathways through the ^MI_TL/TLR intermediate (Fig. 4A): i.e., a downstream step subsequent to formation of the ^MI_TL/TLR intermediate could be slow and thereby render this path kinetically incompetent. Thus, we used MCR mutations previously shown to affect the formation of the MC/MCR (Fig. 1B) (79) to evaluate the potential for folding through the ^MI_TL/TLR intermediate (Fig. 4A). Each of the three MCR mutations led to different levels of destabilization (Fig. 4C and SI Appendix, Table S1), suggesting that the two least destabilizing mutants did not fully ablate the MC/MCR. Because the MC/MCR motif involves A-minor interactions between adenosine residues and 2′-hydroxyl groups of residues in Watson–Crick base pairs, it may be particularly refractory to full ablation (50, 79, 95, 96). Nevertheless, the most destabilizing mutant, G212U, has rate constants that are the same as variants with mutations in the MC that remove Mg²⁺ binding and ablate the MC/MCR (56)(SI Appendix, Table S1) (G212U vs. ArichU and A186U), suggesting that the G212U variant also ablates the MC/MCR interaction. The G212U mutant and other MCR mutants gave folding rate constants slower than overall folding (Fig. 4D, dashed line vs. MCR mutants), providing evidence that the pathway with TL/TLR formation before MC/MCR formation is not kinetically competent (Fig. 4E).

The MC and MCR tertiary contact partners that form first in folding are closer in secondary structure than the TL and TLR and are also closer to the major bend in the molecule mediated by the J5/5a junction (Fig. 1A) (49). This observation is reminiscent of the correlation over four orders of magnitude of folding rates with the closeness of tertiary contact partners in primary sequence for a subset of proteins (97). This concept has also been explored in, and suggested for, RNA folding, but only overall reaction rates were followed and effects were modest in scale (98, 99). Herein, we observed a pathway preference of only ∼10-fold (Figs. 4E and 5), despite the close positioning of the MC and MCR tertiary elements (Fig. 1), and, as shown below, this preference can be reversed by a single point mutation. These results underscore the need for more complex descriptions for the RNA folding process, and our results further suggest a general framework that may be appropriate (Analysis of Mutational Effects on Folding Pathways).

Fig. 5.

Thermodynamic and kinetic framework of P4-P6 folding (5 mM MgCl₂, 100 mM KCl, 23 °C). The preferred folding pathway is depicted with the green arrows. Values for each step are taken from results in Fig. 3D, Fig. 4E, and SI Appendix, Fig. S1. The value in the square bracket for F→I_MC/MCR is the average of the unfolding rate constants determined for constructs that isolate the TL/TLR (SI Appendix, Table S2). The value in the square bracket for F → ^MI_TL/TLR is the average of unfolding rate constants for constructs that isolate the MC/MCR (P4-P6, ^MU⇌I_MC/MCR) (SI Appendix, Table S1); (MC/MCR_iso, 5 mM Mg²⁺) (SI Appendix, Table S3). The value for ^{Alt P5c}I_TL/TLR→^{Alt P5c}U was corrected by a factor of two to account for the uniform twofold slower unfolding in 5 mM Ba²⁺ relative to 5 mM Mg²⁺ (Fig. 6C and SI Appendix, Table S1) because the experiment was carried out with Ba²⁺ to prevent Mg²⁺ occupancy of the metal core (MC) (81). Values in parentheses were calculated from completion of the thermodynamic cycle (SI Appendix, Supporting Methods).

The overall kinetic and thermodynamic framework for P4-P6 folding.

Fig. 5 presents the rate and equilibrium constants for individual reaction steps in the P4-P6 folding framework, combining the results described above with additional results and inferences from the following section (Modularity of Tertiary Contact Unfolding Kinetics). Our findings can be summarized as follows: The ^MU state predominates over the ^{Alt P5c}U and U states, and folding does not proceed through these less populated unfolded states because folding to ^{Alt P5c}I_TL/TLR and I_TL/TLR from ^{Alt P5c}U and U, respectively, is slower than overall folding. ^MU proceeds preferentially to I_MC/MCR, with a rate constant similar to that for overall folding, whereas folding to ^MI_TL/TLR from ^MU is not kinetically competent. Thus, the final step in the preferred folding pathway is formation of F from I_MC/MCR.

We could not measure the conversion of I_MC/MCR to F directly because I_MC/MCR does not accumulate sufficiently under conditions in which there is also significant formation of F. Nevertheless, we could calculate the equilibrium constant for the folding of I_MC/MCR to F based on the values of the thermodynamic cycle in Fig. 5 involving the overall folding equilibrium and the folding equilibrium between ^MU and I_MC/MCR (K_eq = [F]/[I_MC/MCR] = 190) (Fig. 5) (and see Eq. 2 in SI Appendix, Supporting Methods). In addition, commonalities in conformational steps described in the next section allow us to estimate rate constants for this step (Fig. 5, rate constants in parentheses and square brackets) and complete the P4-P6 folding framework.

Modularity of Tertiary Contact Unfolding Kinetics.

As noted in the Introduction, structured RNAs seem to be modular, made up of motifs that are seen across multiple RNAs, and are often structurally superimposable (68–70). A straightforward, but hitherto untested, extension of this perspective would be that these structural motifs are also energetically modular.

What is meant by “energetic modularity” and what would its signature be? One of course would not expect all structures that contain a given motif to have the same overall folding equilibrium. However, the rate constant for breaking of a particular tertiary motif could be independent of its surroundings: i.e., the same across different structured RNAs. Although more complex scenarios are possible, a common unfolding rate constant across different RNAs would be expected if a motif has the same structure in different RNAs and if the transition state for its dissolution entails disruption of interactions within the motif rather than distal rearrangements that induce disruption and do so differentially in different RNAs. The experiments described below use our folding framework to test this kinetic prediction of energetic modularity.

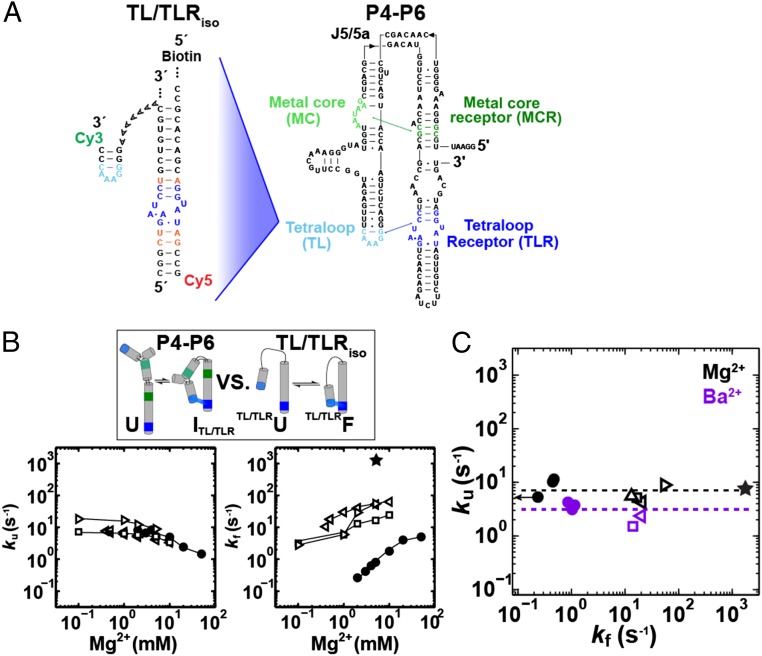
We determined the rate constants for formation and dissolution of the two tertiary contacts, the TL/TLR and the MC/MCR, in P4-P6 and in engineered constructs that isolate the folding of each tertiary contact (100–102). These engineered single-molecule FRET constructs, developed by Pardi, Nesbitt, and coworkers (100–102), contain a single tertiary contact connected by a simplified junction (Fig. 6A and SI Appendix, Fig. S3) (TL/TLR_iso and MC/MCR_iso) and allow us to obtain rate constants for unfolding of each contact alone.

Fig. 6.

Folding kinetics of tertiary contacts within different structural contexts. (A) Construct used to isolate the folding and unfolding of the TL/TLR (TL/TLR_iso). Residues are colored as in Fig.1, and residues that are the same as in P4-P6 are colored orange. (B, Top) Constructs that isolate TL/TLR formation (see SI Appendix, Fig. S2 for TL/TLR_iso sequences). (Bottom) Unfolding (Left) and folding (Right) rate constants for ArichU P4-P6 variant (●) and TL/TLR_iso constructs (A7 linker, □; T14 linker, left triangle; and an extended tetraloop helix, right triangle) across a range of Mg²⁺ concentrations. Published data for TL/TLR_iso are shown (A7 linker, □) (100). Lines are shown to guide the eye (published data for the TL/TLR_iso were taken with 100 mM NaCl instead of 100 mM KCl; see SI Appendix, Tables S1 and S3 for values and condition details). (C) Unfolding versus folding rate constants of P4-P6 variants (closed circles: ArichU, A186U, and J5/5a AllU/Arichu) and TL/TLR_iso constructs (open symbols, as in B, and including a P4-P6 helical context, △) in 5 mM Mg²⁺ (black) or Ba²⁺ (purple). The folding rate constant for J5/5a AllU/ArichU P4-P6 is an upper limit indicated by the left arrow. The folding rate constant for I_MC/MCR→F (★) was calculated as described in the SI Appendix, Supporting Methods, Eq. 3. The average unfolding rates in 5 mM Mg²⁺ or Ba²⁺ are shown as black and purple dashed lines, respectively, and were twofold slower in Ba²⁺ than Mg²⁺. Data are from SI Appendix, Tables S1–S3.

We measured the unfolding and folding rate constants for the simplified TL/TLR_iso construct previously studied (100) as well as several related TL/TLR_iso constructs (SI Appendix, Fig. S2), and we compared these values with those for P4-P6 constructs that form only the TL/TLR tertiary contact (ArichU, Fig. 6B). The unfolding rate constants measured for three TL/TLR_iso constructs and a mutant P4-P6 construct were nearly the same over an Mg²⁺ concentration range of ∼10-fold. Given the very shallow Mg²⁺ dependences, this correspondence likely holds over a considerably wider range (Fig. 6B, Left, open vs. closed symbols). In contrast, the folding rate constants varied considerably across this range of Mg²⁺ (Fig. 6B, Right), presumably reflecting the different probabilities of aligning the TL and TLR for formation (Implications).

We extended the comparisons of TL/TLR unfolding rates to include additional P4-P6 variants (Fig. 6C). For four TL/TLR_iso constructs (SI Appendix, Fig. S2) and three P4-P6 variants lacking the MC/MCR in 5 mM Mg²⁺, the unfolding rate constants varied less than threefold (4.3–9.5 s⁻¹) whereas the folding rate constants varied by over 100-fold (Fig. 6C, black). We also determined these rate constants with 5 mM Ba²⁺because Ba²⁺ does not bind the metal core (81) and thereby allows comparisons that include WT P4-P6. As in Mg²⁺, the unfolding rate constants were constant across Ba²⁺ concentration whereas the folding constants varied widely (Fig. 6C, purple). The above results suggest that the TL/TLR tertiary contact comes apart with the same probability in different structural contexts.

To test whether the observation of common unfolding rates for the TL/TLR also held for the MC/MCR, we compared the folding and unfolding rates of the MC/MCR in P4-P6 with that of the simplified MC/MCR_iso construct (SI Appendix, Fig. S3). We found that the unfolding rate constants for a P4-P6 variant that isolates the ^MU-to-I_MC/MCR (L5B, Fig. 1B) transition and the simpler construct were the same, within error, at each Mg²⁺ concentration over an ∼10-fold range (SI Appendix, Fig. S3). This observation is consistent with a common unfolding rate for the MC/MCR but does not provide as strong support for modular kinetic behavior as the TL/TLR results because the MC/MCR experiments required a construct more similar to the P4-P6 context to achieve measurable folding kinetics (SI Appendix, Fig. S3 A and D).

The close correspondence of unfolding rate constants for individual tertiary contacts in P4-P6 constructs and minimal isolated constructs allowed us to assign the two unfolding steps in the framework that we could not directly follow to these common values (Fig. 5, F→^MI_TL/TLR and F→I_MC/MCR). These values, the directly measured rate constants, and the measured overall folding equilibrium then allowed us to calculate the two remaining folding rate constants from thermodynamic cycles (^MI_TL/TLR→F and I_MC/MCR→F) (SI Appendix, Supporting Methods, Eq. 3).

Analysis of Mutational Effects on Folding Pathways.

Contact order has been, at least partially, a predictive model in protein folding (97) and has been invoked in RNA folding models (98, 99). Predictions of this model are consistent with the observation that the MC/MCR forms before the TL/TLR on the preferred folding pathway, although with a modest effect, as described above. Here, we use the WT P4-P6 RNA framework (Fig. 5) to analyze the destabilizing effects of a point mutation in the MCR. The results provide evidence that this single mutation changes the order of tertiary contact formation. These observations, additional observations from this study, and general properties of RNA tertiary folding led us to invoke an alternative formalism modified from the diffusion–collision model for protein folding (103). This model is described in Implications.

The G212C P4-P6 mutant unfolds faster than WT P4-P6 (Fig. 7A, orange). Nevertheless, it unfolds slower than variants with the MC ablated and slower than the G212U MCR mutant (SI Appendix, Table S1 and Fig. 4C), suggesting the presence of residual MC/MCR interactions in folded G212C P4-P6. Intriguingly, the G212C folding rate constant of 0.95 s⁻¹ is slower than that for WT P4-P6 and matches that for folding to form the TL/TLR from the unfolded state (U), as determined with mutants and conditions that do not allow MC/MCR formation (Fig. 4C and SI Appendix, Table S1). This congruence in folding rate constants introduced the possibility that folding of this variant follows a pathway in which the TL/TLR forms first followed by the mutant MC/MCR interaction, an order that would be opposite to that for WT P4-P6 folding (Fig. 5).

Fig. 7.

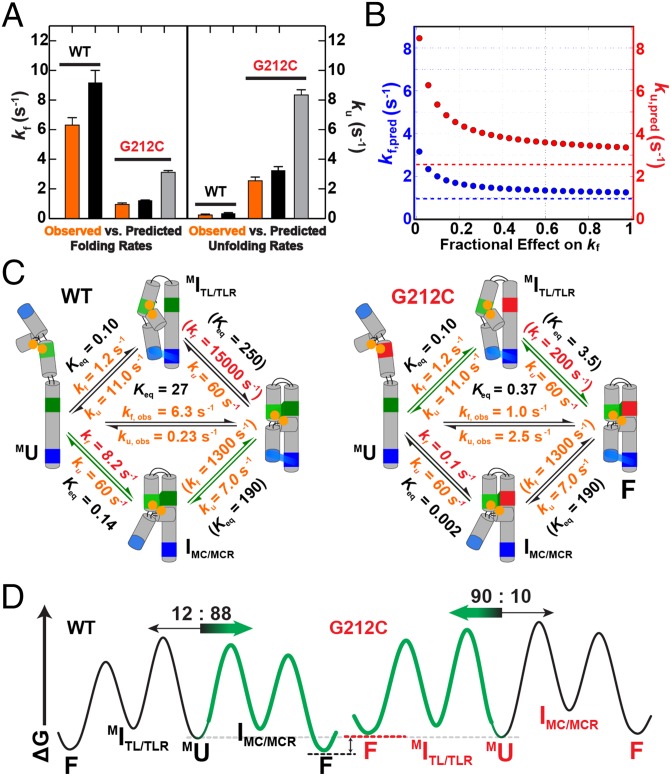
The kinetic effects of the G212C MCR mutation. (A) Comparison of the observed (orange) versus predicted (black and gray) overall folding (Left) and unfolding (Right) rate constants of WT P4-P6 and G212C P4-P6 (SI Appendix, Supporting Methods). For WT, the predicted rate constants are calculated from the values in Fig. 5 that are reproduced in C of this figure. For G212C, the predicted folding and unfolding rate constants assume the full equilibrium effect of the mutation either on the folding (black) or unfolding (gray) rate constant for the MC/MCR interaction. (B) Predicted values for the overall folding (blue) and unfolding (red) rate constants for the G212C mutant over a range of hypothetical MC/MCR folding and unfolding rate constants, assuming that the full equilibrium effect of the mutation (72-fold) is apportioned between these rate constants, ranging from the full effect of the mutation on the unfolding rate constant [(fractional effect on k_f) = 0] to the full effect on the folding rate constant [(fractional effect on k_f) = 1]. The observed overall folding and unfolding rate constants for G212C are represented by the dashed lines. (C) Simplified folding framework for WT P4-P6 (Left; values from Fig. 5) and G212C P4-P6 (Right). Values for G212C P4-P6 are the same as for WT except for steps for MC/MCR formation, which are decreased by the full equilibrium effect of the mutation (72-fold). (D) Free energy diagrams for WT P4-P6 (Left) and the G212C mutant (Right) folding. The preferred folding pathway is shown in green, and the flux through each pathway is given above each pathway and is designated by the relative arrow size. Profiles are to scale.

To assess whether this alternative pathway is indeed traversed, we calculated the overall folding rate constants (^MU→F) predicted based on the observed overall equilibrium effect of the G212C mutation (72-fold) (SI Appendix, Table S1), assuming that only the folding and/or unfolding steps involving MC/MCR formation are affected (Fig. 7) (i.e., that the steps involving TL/TLR formation are not affected). The predicted overall folding and unfolding rate constants vary when the overall equilibrium effect is apportioned differentially between MC/MCR folding versus unfolding (Fig. 7B): i.e., the overall equilibrium effect of 72-fold could arise with the full effect on folding [(fractional effect on k_f) = 1] or on unfolding [(fractional effect on k_f) = 0], or any combination of fractional effects that sum to one. The predicted values closely match the observed rate constants only when the equilibrium effect is predominantly apportioned to the MC/MCR folding rate constant (Fig. 7B, points vs. dashed lines; Fig. 7A, orange vs. black or gray).

The WT and G212C frameworks both predict overall folding and unfolding rate constants that are in good agreement with the observed rate constants for folding and unfolding (Fig. 7A, orange versus black bars), and the G212C framework has all rate constants identical to those for WT P4-P6 folding other than those involved in MC/MCR folding (Fig. 7C). Because the prediction assumes that the effects of the G212C mutation are only on steps involving its tertiary contact, this observation is also consistent with modularity in tertiary contact formation within P4-P6.

Fig. 7D shows free energy profiles for folding of WT and G212C P4-P6 RNA. For WT, folding proceeds 88% through the MC/MCR pathway whereas, for G212C P4-P6, the flux is 90% through the TL/TLR pathway. This dramatic change in the preferred folding pathway arises because the rate-limiting step for WT P4-P6 folding, formation of the MC/MCR interaction, is slowed to such an extent for the mutant that the barrier for this pathway becomes higher than the barrier for the alternative pathway through initial formation of the TL/TLR interaction. Our data suggest, most simply, that the G212C mutation renders formation of a binding-competent state of the MCR more unfavorable, and with an effect that is sufficiently large to favor formation of a more distal contact.

Implications

The folding framework for P4-P6 RNA developed herein and shown in Fig. 5 suggests kinetic properties of RNA elements that may hold across different RNAs, leads to simplifications that may aid in predicting RNA folding kinetics and thermodynamics, and provides a foundation for future fundamental studies of RNA folding. Such frameworks describing the kinetics and thermodynamics of individual steps in complex processes have been foundational in numerous areas of biology (e.g., refs. 39–45).

A Common Unfolding Rate Constant for a Tertiary Motif.

The TL/TLR tertiary motif is found in multiple RNAs and may be characteristic of at least a subset of RNA tertiary motifs. This interaction forms with rate constants spanning more than three orders of magnitude in different structural contexts and under different solution conditions but comes apart with a common unfolding rate of ∼10 s⁻¹ (Fig. 6C and SI Appendix, Fig. S3). Uncovering this commonality required an ability to interrogate individual folding steps. The results suggest that the identity of the base pairs in the helices surrounding this tertiary contact and the junctions that bring together the tertiary contact partners do not affect the final structure of the tertiary motif or the energetics of the transition state ensemble for its disengagement. This observed modularity in tertiary contact unfolding provides a first step toward using the energetic contributions of individual tertiary motifs to predict the overall folding kinetics and thermodynamics for complex RNAs (104).

Stated another way, the data suggest a common rate for dissolution of a TL/TLR, a conclusion that, if general, could enable the prediction of the rates of conformational steps of complex RNAs that involve breaking of a particular contact. Similarly, observing a conformational step with a rate constant that is stereotypical for the dissociation of a particular tertiary interaction could suggest the breaking of that motif in the rate-limiting step, a model that could then be specifically tested by mutation of that motif. Conversely, tertiary contacts that do not follow modular behavior would be suggested to have multiple folded states and/or complex folding pathways and merit further detailed structural and dynamic study.

A Generalized Model for RNA Tertiary Folding.

A general goal in developing an RNA folding model (or any model) is to incorporate the minimal number of features sufficient for accurate quantitative prediction. As described above, contact order is a predictive, yet simple, concept in protein folding (97). Although folding of WT P4-P6 RNA follows the general prediction for a contact order model because the tertiary contact pairs that are closest to one another within the secondary structure form first [i.e., the MC/MCR forms first followed by the TL/TLR (Fig. 5)], this simple model fails to account for the reversal in the order of tertiary contact formation with the G212C mutation (Fig. 7D).

Modification of another established formalism from protein folding, the diffusion–collision model, may better describe the folding behaviors observed for P4-P6 and may prove more general in RNA folding and assembly. This model applied to proteins posits that the rate of forming a tertiary interaction between alpha helices, beta strands, or hydrophobic clusters is determined by the rate of the regions of the protein colliding, weighted by the probability that the partner elements (e.g., two alpha helices) are in a conformation competent for the tertiary contact to form when the collision occurs (103, 105). There is evidence for intermediates in protein folding that are not accounted for by this model (e.g., refs. 106–108). In contrast, given the more hierarchical nature of RNA than protein folding and the discrete nature of RNA tertiary contacts, a diffusion–collision model may be more readily and quantitatively applied to RNA, as elaborated below.

RNA secondary is preformed and stable, and RNA tertiary contact partners come together due to diffusion of the RNA helices they are embedded in (66, 104, 109). RNA tertiary contact formation also typically requires local unfavorable conformational rearrangements (104, 110–115) such that the rates of formation of these interactions are orders of magnitude slower than diffusional collision (104, 116).

In this way, RNA tertiary elements are potentially analogous to protein secondary structure elements in the diffusion–collision model. (Long-range secondary structure is also involved in RNA 3D structure formation and can be considered along with tertiary contacts in this model.) The probability that RNA tertiary contact partners associate is determined by (i) the conformational properties of the helices and the junctions that connect the tertiary elements and thus determine their collisional frequencies and (ii) the properties of the tertiary elements that determine the probability that both partners are in binding-competent conformations and the lifetimes of these states, relative to the lifetime of the collisional state. This process is akin to the need for protein secondary structure elements to be formed to allow tertiary structure formation in the original diffusion–collision model (103).

Our P4-P6 folding results can be described in terms of this RNA diffusion–collision model. Formation of one of P4-P6’s tertiary interactions increases the rate constant (i.e., the probability) of forming the other, presumably because the first contact greatly restricts the conformational space explored by the second tertiary contact elements and thereby increases their collisional probability and thus the rate of forming the second contact (Fig. 5). Cooperativity, a fundamental feature of the folding of biological macromolecules, is an emergent property of this increased collisional probability (60, 104).

Mutations in J5/5a, which forms a bend in P4-P6 (Fig. 1 A and B) (49, 51), slow formation of the TL/TLR contact, and linking the TL and TLR elements by a flexible single strand increases the folding rate; in contrast, neither alteration affects the unfolding rate (Fig. 6C and SI Appendix, Table S2), consistent with different linkages imparting different collisional probabilities but not affecting the contacts themselves. Collisional probabilities for RNA, as a polyelectrolyte, are also expected to be dependent on ionic conditions, and accordingly we observe a steeper salt dependence on the rate constant for TL/TLR formation for the more highly charged P4-P6 construct than the TL/TLR_iso constructs (Fig. 6B and SI Appendix, Table S3). Finally, our results suggest that the G212C mutation decreases the probability of the MCR adopting its tertiary-competent conformation and thereby slows formation of the MC/MCR and reverses the order of tertiary contact formation in folding (Fig. 7D).

We have established a P4-P6 RNA folding framework and determined the effects of mutations within this RNA and also compared its folding to dramatically simplified constructs. The data emerging from these studies have allowed us to describe the folding of P4-P6 in terms of an RNA diffusion–collision model. Although this description is, to our knowledge, the first such description, there is no reason to think that such a description will not be generalizable because the model encompasses structural features that are common to folded RNAs. Certainly, additional complexities are expected, including parallel folding pathways from distinct secondary structure transitions, secondary structure transitions during tertiary folding, and influences from protein and other ligand binding. Thus, it will be of great interest to determine whether the RNA diffusion–collision model can be modified and adapted to describe this full range of behaviors and properties and whether it provides a foundation for building a quantitative and predictive understanding of RNA from the properties of its components.

Materials and Methods

Further details of the methods are provided in SI Appendix, Supporting Methods.

Preparation of P4-P6 smFRET (smP4-P6) Variants.

The smP4-P6 variants were prepared by a five-piece splinted ligation with protocols slightly altered from those described previously (60, 90, 117). Prior studies revealed that standard laboratory protocols introduce covalent differences in the RNA and that these modifications can affect the folding of individual molecules (90). Alterations in the protocol include substituting a synthetically derived 3′ and 5′ piece and removing intermediate gel purification and UV shadowing steps (SI Appendix, Supporting Methods). These changes increase the yield and throughput of the ligation procedure while producing RNA with the same purity, kinetics and thermodynamics as assayed by smFRET and compared with RNAs prepared by differed methods (SI Appendix, Fig. S4).

Preparation of Isolated Constructs.

Synthetic RNAs (SI Appendix, Tables S4 and S5) for each isolated construct were purchased from IDT with a 3′ primary amine, labeled with Cy3/Cy5 or Cy3b/Atto647N dyes with an NHS-ester reaction, and gel-purified.

smFRET Experiments.

smFRET measurements were performed on a custom-built prism-based total internal reflection microscope. Buffers used in smFRET measurements contained 1–50 mM MgCl₂ or 5 mM BaCl₂, 50 mM MOPS, pH 8.0, 100 mM KCl, 2 mg/mL glucose, 1.8 mM Trolox, 100 units/mL glucose oxidase (Sigma-Aldrich), and 1,000 units/mL catalase (Sigma-Aldrich). Depending on the folding equilibrium and change in FRET for each molecule, smFRET data were collected at an acquisition rate between 50 and 310 frames per second. Data were analyzed using the SMART data analysis package (92). See Dataset S1 for the imaging parameters and buffer conditions for each measurement reported herein. Before imaging, P4-P6 molecules were annealed to a DNA oligo containing a 5′ biotin (5′ biotin-AACCAAAATCAACCTAAAACTTACACA-3′) at 50 °C for 15 min and cooled at 0.1 °C/min to room temperature. Samples were diluted to ∼10–100 pM for imaging. Prior smFRET studies have shown that the unfolded states of P4-P6 have very low FRET (∼0.2) whereas states with the TL/TLR formed, including the fully folded state, have a high FRET value (∼0.8) and the intermediate with only the MC/MCR formed has an intermediate FRET value (∼0.5) (Fig. 1C) (60). Also, prior P4-P6 smFRET work revealed molecular heterogeneity from covalent damage caused by standard RNA treatments and showed that this damage could be avoided to yield highly homogeneous populations (90).

Data Analysis.

Thermodynamic and kinetic parameters were inferred from single-molecule FRET traces that were fit with a hidden Markov model (HMM)-based algorithm to a two-state model with a single unfolded (low FRET = 0.16) and single folded (high FRET = 0.45 or 0.8) state to extract transition probabilities, taking into account the noise observed in each intensity channel (92).

A subset of 20 traces for each construct and condition were also fit to a three-state linear model. In each case, the data were found to fit better to the two-state model than to a three-state model based on the difference in the Bayesian information criterion (BIC) (92), which includes a statistical penalty for including additional states, with the following exceptions that do not affect the conclusions of this work: WT P4-P6 folding with a Cy3b/Atto674N dye pair at 1 mM Mg, and MC/MCR_iso at 5 and 10 mM Mg²⁺. (Example traces can be found in Dataset S1.) For WT P4-P6 folding, this behavior may be related to the dye dynamics because the apparent three-state behavior is not seen in variants with the Cy3/Cy5 dye pair. For MC/MCR_iso, multistate behavior is seen only at low Mg²⁺ concentration, and not above 10 mM Mg²⁺. This construct has a lower folded FRET value than constructs that form the TL/TLR and fast transitions at lower [Mg²⁺], so that the signal-to-noise is relatively low; thus, the apparent three-state behavior may arise from noise in the data. We emphasize that elimination of the above data with potential three-state behavior would not change any of the conclusions of this work. We also note that, in general, best-fit models are sensitive to the penalty used for additional variables and the data quality and number of transitions (92).

Standard criteria for the identification of single-molecule traces were used: (i) single-step photobleaching, (ii) anticorrelated donor and acceptor channels, (iii) total intensity consistent with a single molecule, and (iv) stable total intensity. The folding rate constant reported for the J5/5a-AllU/ArichU P4-P6 variant is a limit because most traces for this molecule showed no folding behavior whereas traces that contained transitions had on average fewer than two transitions, preventing reliable estimation of the folding rate constant (92). All rate and equilibrium constants reported herein are the mean of the log distribution of the values for each molecule (118), and all other folding parameters are the mean of the distribution of each parameter for each molecule. Error estimates for all measurements, including the predictions of the overall folding and unfolding rate constants for WT and G212C, were determined by 95% confidence intervals of the mean from bootstrapping the parameters from individual molecules. Because the bootstrapped errors are asymmetric, the maximum of the two values is reported as the error for simplicity in the main text. Both errors are reported in SI Appendix. Signal-to-noise (SNR) cutoffs of 1 and 0.25 for molecules with high FRET states of 0.8 and 0.45, respectively, were used to minimize use of molecules for which fitting errors contributed disproportionately to the inferred rate constants. Evaluation of smFRET data for each construct is presented in Dataset S1. All smFRET data are available online for reanalysis in a standard single-molecule dataset (SMD) format (93).