Electron transfer across a thermal gradient

Significance

Electron transfer (ET) is a fundamental process that drives many physical, chemical, and biological transformations, as well as playing a ubiquitous role in the development of technologies for energy conversion and electronics. Recent advances in temperature measurement and control allow thermal gradients and heat flow to be addressed at the molecular level, making it possible to observe electron transfer across thermal gradients. Here, we develop a theory for ET between donor and acceptor sites, where each site has a different local temperature. The transfer of charge across the resulting thermal gradient is found to be coupled with an energy transfer mechanism that may alter heat conduction between sites, even for vanishing net electron current.

Abstract

Charge transfer is a fundamental process that underlies a multitude of phenomena in chemistry and biology. Recent advances in observing and manipulating charge and heat transport at the nanoscale, and recently developed techniques for monitoring temperature at high temporal and spatial resolution, imply the need for considering electron transfer across thermal gradients. Here, a theory is developed for the rate of electron transfer and the associated heat transport between donor–acceptor pairs located at sites of different temperatures. To this end, through application of a generalized multidimensional transition state theory, the traditional Arrhenius picture of activation energy as a single point on a free energy surface is replaced with a bithermal property that is derived from statistical weighting over all configurations where the reactant and product states are equienergetic. The flow of energy associated with the electron transfer process is also examined, leading to relations between the rate of heat exchange among the donor and acceptor sites as functions of the temperature difference and the electronic driving bias. In particular, we find that an open electron transfer channel contributes to enhanced heat transport between sites even when they are in electronic equilibrium. The presented results provide a unified theory for charge transport and the associated heat conduction between sites at different temperatures.

The study of electronic transport in molecular nanojunctions naturally involves consideration of inelastic transport, where the transporting electron can exchange energy with underlying nuclear motions (1, 2). Such studies have been motivated by the use of inelastic tunneling spectroscopy, and more recently Raman spectroscopy, as diagnostic tools on one hand, and by considerations of junction stability on the other. In parallel, there has been an increasing interest in vibrational heat transport in nanostructures and their interfaces with bulk substrates (3–11) focusing on structure–transport correlations (12–15), molecule–substrate coupling (16–18), ballistic and diffusive transport processes (11, 19), and rectification (20–22). More recently, noise (23–26), nonlinear response (e.g., negative differential heat conductance), and control by external stimuli (27, 28) have been examined. An important driving factor in this growing interest is the development of experimental capabilities that greatly improve on the ability to gauge temperatures (and “effective” temperatures in nonequilibrium systems) with high spatial and thermal resolutions (29–43) and to infer from such measurement the underlying heat transport processes. In particular, vibrational energy transport/heat conduction in molecular layers and junctions has recently been characterized using different probes (6, 19, 44–52).

The interplay between charge and energy (electronic and nuclear) transport (53–60) is of particular interest as it pertains to the performance of energy-conversion devices, such as thermoelectric, photovoltaic, and electromechanical devices. In particular, the thermoelectric response of molecular junctions, mostly focusing on the junction linear response as reflected by its Seebeck coefficient, has been recently observed (61–65) and theoretically analyzed (2, 20, 64, 66–77). Most of the theoretical work has focused on junctions characterized by coherent electronic transport in which the electronic and nuclear contribution to heat transport are assumed largely independent of each other. The few recent works that analyze electron–phonon interactions effects on the junction Seebeck coefficient (73, 78–81) do so in the limit of relatively weak electron–phonon interaction (in the sense that the electron is not localized in the junction), using the same level of treatment as applied in the theory of inelastic tunneling spectroscopy.

The present work considers the opposite limit of strong electron–phonon interaction, where electron transport is dominated by successive electron hops subjected to full local thermalization, that is, successive Marcus electron transfer (ET) processes (82–88). By their nature, such successive hops are independent of each other, so a single transfer event may be considered. Even in this well-understood limit different considerations apply under different conditions, and different levels of descriptions were applied to account for the molecular nature of the solvent (89), the dimensionality of the process (90–99), and the definition of the reaction coordinate. Extensions to equilibrium situations have ranged from considerations of deviation from transition state theory (TST) to the description of control by external fields (99–101).

Here, we generalize the standard Marcus (transition state) theory of ET to account for situations where the donor and acceptor sites are characterized by different local temperatures. Such generalization requires the use of multidimensional TST because nuclear polarization modes associated with the different sites are assumed to be equilibrated at their respective local temperatures. Our main results are as follows. (i) We obtain an analytical formula for the ET rate that depends on the two site temperatures and reduces to the standard Marcus form when these temperatures are equal. (ii) The corresponding activation energy does not correspond to the geometric activation energy, that is, the point of lowest (free) energy on the isoenergetic surface, and is instead a thermal quantity that depends on the local temperature of each site. (iii) ET between sites of different temperatures is found to be associated with energy transfer between the sites and may affect thermal conduction between sites even when the net electron flux between them vanishes.

We focus on a model that contains the essential ingredients of our theory: The donor and acceptor sites are taken to be at different local temperatures and the ET process is assumed to be dominated by two vibrational modes, one localized near the donor and the other near the acceptor site at the respective local equilibria. Coupling between these modes that is not associated with their mutual coupling to the ET process is disregarded. The ET rate for this bithermal model is obtained and analyzed, along with the implications of this ET process for the energy (heat) transfer between the corresponding sites. Although a general treatment of this problem for systems consisting of large numbers of vibrational modes with associated temperatures is tractable, we defer exposition of this formulation to later work.

Theory of ET Between Sites of Different Local Temperatures

Model.

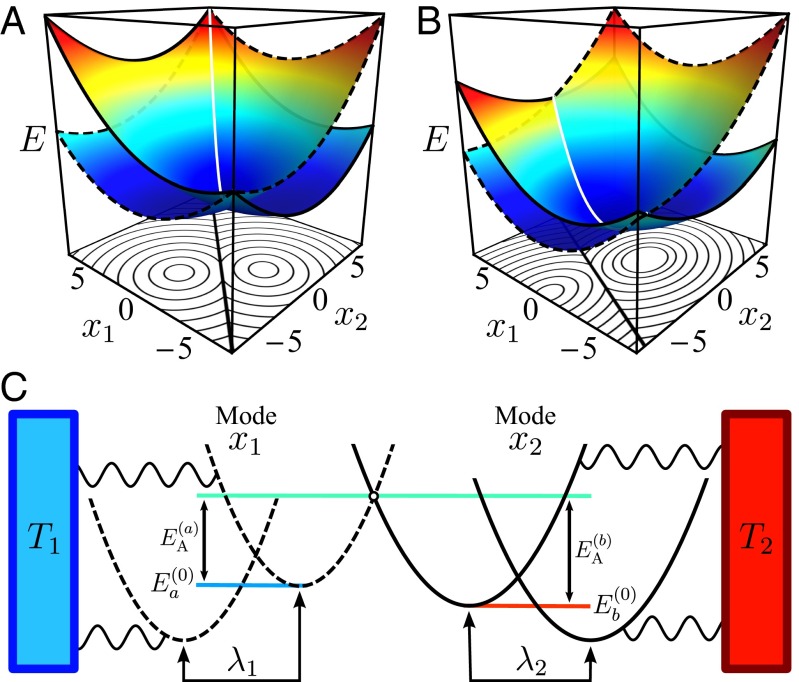
The system under consideration is similar to the model used in Marcus’ theory. It comprises two sites, 1 and 2, on which the transferred electron can localize, and the corresponding electronic states are denoted a (electron on site 1) and b (electron on site 2). The localization is affected by the response of nuclear modes, assumed harmonic, whose equilibrium positions depend on the electronic population. In the implementation of Marcus’ theory, this condition is often expressed in terms of a single reaction coordinate; however, the nature of our problem requires the use of at least two groups of modes: one localized near and in (local) thermal equilibrium with site 1 and another localized near and equilibrated with site 2. In the present discussion we consider a minimal model comprising two such modes, denoted $x_1$ and $x_2$, and assume that mode $x_1$ is sensitive to the temperature and charge on site 1 whereas mode $x_2$ “feels” the temperature and charging state of site 2. The diabatic electronic (free) energies in states a and b take the same form as in Marcus’ theory (Fig. 1):

$$E_a\left(x_1,x_2\right)=E_a^{\left(0\right)}+\frac{1}{2}{k}_1{\left(x_1-{\lambda }_1\right)}^2+\frac{1}{2}{k}_2{x}_2^2,$$ [1]

$$E_b\left(x_1,x_2\right)=E_b^{\left(0\right)}+\frac{1}{2}{k}_1{x}_1^2+\frac{1}{2}{k}_2{\left(x_2-{\lambda }_2\right)}^2.$$ [2]

In choosing these forms we have taken the equilibrium position of mode $x_j:j\in \left\{\mathrm{1,2}\right\}$ to be at the origin when the corresponding site j is unoccupied. A schematic of the geometric and energetic properties for ET using the considered multidimensional formalism is shown in Fig. 1C. The reorganization energies for each coordinate are

$$E_{\text{R}1}=\frac{1}{2}{k}_1{\lambda }_1^2\hspace{1em}\text{and}\hspace{1em}{E}_{\text{R}2}=\frac{1}{2}{k}_2{\lambda }_2^2,$$ [3]

and the total reorganization energy is

$$E_{\text{R}}=E_{\text{R}1}+E_{\text{R}2}.$$ [4]

As in Marcus’ theory, we assume that these modes are in thermal equilibrium with their environments; however, here the environments of sites 1 and 2 are at different local temperatures—$T_1$ and $T_2$—and modes $x_1$ and $x_2$ are in thermal equilibrium with their corresponding environments. Our aim is to investigate the effect of this thermal nonequilibrium on the ET process and to assess the contribution of the latter to the transport of thermal energy between the donor and acceptor sites. In considering the latter, we disregard direct coupling between modes localized near the different sites, so that coupling that may lead to energy transfer between such modes can arise only from their mutual interaction with the electronic subsystem. In reality, heat transport between sites occurs also by direct vibrational coupling.

Fig. 1.

Energy surfaces ($E_a$ and $E_b$) for ET between (A) symmetric ($\mathrm{\Delta }{E}_{ba}=0,E_{\text{R}1}=E_{\text{R}2}$) and (B) asymmetric ($\mathrm{\Delta }{E}_{ba}\ne 0,E_{\text{R}1}\ne E_{\text{R}2}$) donor–acceptor pair geometries. The boundary of the $E_a$ surface is shown dashed and the boundary of the $E_b$ surface is shown as a solid curve. The z axis corresponds to energy E and is normalized for visual clarity. Corresponding contour plots are shown below each surface and the CL is shown as a thick black line. (C) Schematic illustration of energy surfaces for ET between modes $x_1$ (dashed) and $x_2$ (solid). Each mode is in contact with an independent heat bath. The circular marker denotes a crossing point where $E_a=E_b$. In this and all other figures, values are shown in dimensionless reduced units. For convenience, energy may be taken in units of 0.25 eV (a characteristic reorganization energy) and length in units of 1 nm (a characteristic donor–acceptor distance).

Multidimensional TST.

Because of large disparity between electronic and nuclear timescales, electronic energy conservation is a condition for an ET event to occur. This implies that such events take place only at nuclear configurations that satisfy $E_a\left(x_1,x_2\right)=E_b\left(x_1,x_2\right)$, which, denoting $\mathrm{\Delta }{E}_{ba}=E_b^{\left(0\right)}-E_a^{\left(0\right)}$ and using Eqs. 1 and 2 can be expressed by the condition $f_{\text{c}}\left(x_1,x_2\right)=0$ where

$$f_{\text{c}}\left(x_1,x_2\right)=k_1{\lambda }_1{x}_1-k_2{\lambda }_2{x}_2+\mathrm{\Delta }{E}_{ba}-E_{\text{R}1}+E_{\text{R}2}.$$ [5]

Eq. 5 describes a line in the $x_1\times x_2$ space on which the two paraboloids displayed in Fig. 1 A and B cross. We call this subspace the crossing line (CL).

The Marcus expression for the activation energy is the lowest energy point on this line, and the multidimensional nature of the problem is manifested (in the unithermal case) by an entropic correction the the preexponential factor in the rate expression. Although this level of description is usually adequate, multidimensional variants of Marcus’ theory are developed and applied when a reaction proceeds through complex geometric configurations in which multiple reaction pathways are available (97). Zwickl et al. (98) have developed a theory for multiple particle transfer and have also examined to what extent the applicability of a one-dimensional picture persists as the number of intrinsic reaction coordinates is increased. When a charge transfer reaction occurs through a series of events, a univariate parameterization of the reaction progress must often be replaced by a set of reaction coordinates to adequately describe the mechanism (95). For concerted reaction events, numerical methods developed by Guthrie (96) have extended the parabolic Marcus formalism to quartic energy surfaces in hyperdimensional space. The interplay and competition between sequential and concerted events in ET mechanisms has also been investigated, with Lambert et al. (97) characterizing forbidden and allowed pathways in model systems. As will be seen below, the fact that different modes affected by the ET represent environments of different temperatures has important implications with regard to the multidimensional nature of the transition state.

Bithermal TST.

Here and below we use the term “bithermal” to refer to a two-mode model in which the different modes are coupled to environments of different temperatures. In classical TST for ET that disregards nuclear tunneling the ET rate from state m to state n is

$$k_{m\to n}=\frac{1}{2}\langle {\mathcal{T}}_m{v}_{\perp }\rangle P_{m\to n},$$ [6]

where $v_{\perp }$ is the velocity in the direction normal to the transition surface, $P_{m\to n}$ is the probability density about the transition state on the m potential surface calculated at the transition state for the $m\to n$ process, and ${\mathcal{T}}_m$ is the tunneling probability in the surface crossing event when coming from the m side and is a function of $v_{\perp }$ (102, 103). In the Arrhenius picture, this expression can be interpreted as a product of the frequency of reactive attempts multiplied by the probability that an attempt is successful. Using the Landau–Zener expression for the tunneling probability, we find that ${\mathcal{T}}_m{v}_{\perp }$ is a golden-rule type rate that does not depend on $v_{\perp }$ in the weak coupling (nonadiabatic) limit, and is linear in $v_{\perp }$ in the strong coupling (adiabatic, ${\mathcal{T}}_m=1$) limit (Supporting Information). For completeness we note that for the two-mode bithermal system considered here, the average velocity in the normal direction is (Supporting Information)

$$\langle v_{\perp }\rangle =\sqrt{\frac{4}{\pi }\left(\frac{m_2{\beta }_2{k}_1{E}_{\text{R}1}+m_1{\beta }_1{k}_2{E}_{\text{R}2}}{{\left|\nabla f_{\text{c}}\right|}^2{m}_1{\beta }_1{m}_2{\beta }_2}\right)},$$ [7]

where $m_j$ is the mass associated with mode $x_j$ and $\left|\nabla f_{\text{c}}\right|$ is the magnitude of the gradient of the CL constraint. In the unithermal, equal-mass case (${\beta }_1={\beta }_2=\beta ;m_1=m_2=m$) this expression reduces to the well-known form $\sqrt{2/\pi m\beta }$, which is the Boltzmann-weighted expected speed in one dimension (103, 104). Note, however, that donor and acceptor sites with significantly different temperatures are far enough from each other to make the nonadiabatic limit the more relevant.

Next, consider the probability density $P_{m\to n}$ to be at the transition surface when moving in the m electronic state. In the multidimensional version of Marcus theory this probability is given by the standard activation factor $\exp \left[-E_{\text{A}}/k_{\text{B}}T\right]$ ($k_{\text{B}}$ is Boltzmann’s constant), where the activation energy $E_{\text{A}}$ is the lowest energy on the transition surface multiplied by a pre-exponential term that can be calculated explicitly (Supporting Information). This term will generally also contain entropic corrections that are in the present harmonic model. In the multidimensional–bithermal case, the fact that modes of different temperature are weighted differently on the transition surface has to be taken into account. This is accomplished by using Eqs. 1 and 2 to write the required probability density for electronic state a as

$$\begin{array}{c}{P}_{a\to b}={\displaystyle {\iint }_{{\mathrm{ℝ}}^2}\left|\nabla f_{\text{c}}\right|e^{-{\beta }_1\left(\frac{1}{2}{k}_1{\left[x_1-{\lambda }_1\right]}^2\right)}{e}^{-{\beta }_2\left(\frac{1}{2}{k}_2{x}_2^2\right)}}\\ \times \delta \left(f_{\text{c}}\left(x_1,x_2\right)\right)d{x}_{1}d{x}_2/{\displaystyle {\iint }_{{\mathrm{ℝ}}^2}{e}^{-{\beta }_1\left(\frac{1}{2}{k}_1{\left[x_1-{\lambda }_1\right]}^2\right)}{e}^{-{\beta }_2\left(\frac{1}{2}{k}_2{x}_2^2\right)}d{x}_{1}d{x}_2}\\ =\sqrt{\frac{{\beta }_1{\beta }_2\left(k_1{E}_{\text{R}1}+k_2{E}_{\text{R}2}\right)}{2\pi \left({\beta }_1{E}_{\text{R}2}+{\beta }_2{E}_{\text{R}1}\right)}}\\ \times \exp \left[-{\beta }_1{\beta }_2\frac{{\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2}{4\left({\beta }_1{E}_{\text{R}2}+{\beta }_2{E}_{\text{R}1}\right)}\right],\end{array}$$ [8]

and for electronic state b,

$$\begin{array}{c}{P}_{b\to a}={\displaystyle {\iint }_{{\mathrm{ℝ}}^2}\left|\nabla f_{\text{c}}\right|e^{-{\beta }_1\left(\frac{1}{2}{k}_1{x}_1^2\right)}{e}^{-{\beta }_2\left(\frac{1}{2}{k}_2{\left[x_2-{\lambda }_2\right]}^2\right)}}\\ \times \delta \left(f_{\text{c}}\left(x_1,x_2\right)\right)d{x}_{1}d{x}_2/{\displaystyle {\iint }_{{\mathrm{ℝ}}^2}{e}^{-{\beta }_1\left(\frac{1}{2}{k}_1{x}_1^2\right)}{e}^{-{\beta }_2\left(\frac{1}{2}{k}_2{\left[x_2-{\lambda }_2\right]}^2\right)}d{x}_{1}d{x}_2}\\ =\sqrt{\frac{{\beta }_1{\beta }_2\left(k_1{E}_{\text{R}1}+k_2{E}_{\text{R}2}\right)}{2\pi \left({\beta }_1{E}_{\text{R}2}+{\beta }_2{E}_{\text{R}1}\right)}}\\ \times \exp \left[-{\beta }_1{\beta }_2\frac{{\left(\mathrm{\Delta }{E}_{ba}-E_{\text{R}}\right)}^2}{4\left({\beta }_1{E}_{\text{R}2}+{\beta }_2{E}_{\text{R}1}\right)}\right],\end{array}$$ [9]

where ${\beta }_j=1/k_{\text{B}}{T}_j$. The factor $\left|\nabla f_{\text{c}}\right|$ renders the constraint $\delta \left(f_{\text{c}}\left(x_1,x_2\right)\right)$ invariant (105, 106). Intervals of integration $\mathrm{ℝ}$ and ${\mathrm{ℝ}}^2$ denote integration over the regions $\left(-\infty ,\infty \right)$ and $\left(-\infty ,\infty \right)\times \left(-\infty ,\infty \right)$, respectively.

In the relevant nonadiabatic limit, Eqs. 8 and 9 illustrate how the bithermal ET rate is related to the inverse thermal energies ${\beta }_1$ and ${\beta }_2$ of the respective heat baths. Note that they can be written in the standard forms

$$P_{a\to b}\propto \exp \left[-{\beta }_{\text{eff}}\frac{{\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2}{4E_{\text{R}}}\right],$$ [10]

$$P_{b\to a}\propto \exp \left[-{\beta }_{\text{eff}}\frac{{\left(\mathrm{\Delta }{E}_{ba}-E_{\text{R}}\right)}^2}{4E_{\text{R}}}\right],$$ [11]

with ${\beta }_{\text{eff}}={\left(k_{\text{B}}{T}_{\text{eff}}\right)}^{-1}$, where the effective temperature is

$$T_{\text{eff}}=T_1\frac{E_{\text{R}1}}{E_{\text{R}}}+T_2\frac{E_{\text{R}2}}{E_{\text{R}}}.$$ [12]

An interesting consequence is that in the symmetric case ($\mathrm{\Delta }{E}_{ba}=0$) the ratio $P_{a\to b}/P_{b\to a}=1$, independent of the site temperatures, so the electron is as likely to reside on either the hot or the cold site. In the unithermal limit ($T_1=T_2=T$), $T_{\text{eff}}=T$ and we recover the functional form and temperature dependence predicted by classical Marcus theory (82, 107) (Supporting Information contains details of this calculation).

Note that one could naively try to evaluate the ET rates by considering the probability to reach the geometrical barrier, which is the lowest energy point on the transition surface measured relative to the bottom of the reactant surface. The coordinate of this point can be found by minimizing either $E_a$ or $E_b$ under the constraint $E_a=E_b$. This leads to

$$x_1^{\min }=-{\lambda }_1\frac{\mathrm{\Delta }{E}_{ba}-E_{\text{R}}}{2E_{\text{R}}}\hspace{1em}\text{and}\hspace{1em}{x}_2^{\min }={\lambda }_2\frac{\mathrm{\Delta }{E}_{ba}+E_{\text{R}}}{2E_{\text{R}}}.$$ [13]

The corresponding geometrical activation energies, $E_{\text{A}}^{\left(a\right)}=E_a\left(x_1^{\min },x_2^{\min }\right)-E_a^{\left(0\right)}$ and $E_{\text{A}}^{\left(b\right)}=E_b\left(x_1^{\min },x_2^{\min }\right)-E_b^{\left(0\right)}$, can be cast as additive contributions of energies in mode $x_1$ and in mode $x_2$. Using Eq. 1 we find that for state a

$$E_{\text{A}}^{\left(a\right)}=E_{\text{A}1}^{\left(a\right)}+E_{\text{A}2}^{\left(a\right)}=\frac{{\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2}{4E_{\text{R}}},$$ [14]

where

$$E_{\text{A}j}^{\left(a\right)}=E_{\text{R}j}{\left(\frac{\mathrm{\Delta }{E}_{ba}+E_{\text{R}}}{2E_{\text{R}}}\right)}^2:j\in \left\{\mathrm{1,2}\right\}.$$ [15]

Similarly, for state b,

$$E_{\text{A}}^{\left(b\right)}=E_{\text{A}1}^{\left(b\right)}+E_{\text{A}2}^{\left(b\right)}=\frac{{\left(\mathrm{\Delta }{E}_{ba}-E_{\text{R}}\right)}^2}{4E_{\text{R}}},$$ [16]

and

$$E_{\text{A}j}^{\left(b\right)}=E_{\text{R}j}{\left(\frac{\mathrm{\Delta }{E}_{ba}-E_{\text{R}}}{2E_{\text{R}}}\right)}^2:j\in \left\{\mathrm{1,2}\right\}.$$ [17]

It follows that the probabilities to reach the configuration $\left(x_1^{\min },x_2^{\min }\right)$ in the a and b states satisfy

$$P_{a\to b}\propto \exp \left[-\left({\beta }_1{E}_{\text{R}1}+{\beta }_2{E}_{\text{R}2}\right){\left(\frac{\mathrm{\Delta }{E}_{ba}+E_{\text{R}}}{2E_{\text{R}}}\right)}^2\right]$$ [18]

and

$$P_{b\to a}\propto \exp \left[-\left({\beta }_1{E}_{\text{R}1}+{\beta }_2{E}_{\text{R}2}\right){\left(\frac{\mathrm{\Delta }{E}_{ba}-E_{\text{R}}}{2E_{\text{R}}}\right)}^2\right],$$ [19]

which are clearly different from Eqs. 8 and 9, although like the latter they go to the Marcus forms in the limit ${\beta }_1={\beta }_2$. Interestingly, Eqs. 18 and 19 can also be written in the forms 8 and 9 but with an effective temperature that satisfies

$$\frac{1}{T_{\text{eff}}}=\frac{1}{T_1}\frac{E_{\text{R}1}}{E_{\text{R}}}+\frac{1}{T_2}\frac{E_{\text{R}2}}{E_{\text{R}}},$$ [20]

an interesting mismatch with Eq. 12. These differences imply that in the bithermal case the ET rates are no longer controlled by the geometrical barrier.

This can be also seen explicitly: The equal electronic energies condition defines the CL, which can be parametrized in terms of a coordinate α according to

$$\begin{array}{l}{x}_1\left(\alpha \right)=\frac{k_2{\lambda }_2}{k_1{\lambda }_1}\alpha +\frac{1}{k_1{\lambda }_1}\left(\frac{1}{2}{k}_1{\lambda }_1^2-\frac{1}{2}{k}_2{\lambda }_2^2-\mathrm{\Delta }{E}_{ba}\right),\\ x_2\left(\alpha \right)=\alpha .\end{array}$$ [21]

with a value of the parametric coordinate α specifying a unique transition point. The energy on the CL,

$$E^{‡}\left(\alpha \right)=E_a\left[x_1\left(\alpha \right),x_2\left(\alpha \right)\right]=E_b\left[x_1\left(\alpha \right),x_2\left(\alpha \right)\right],$$ [22]

is parametrized by α. The energies as a function of position α on the CL coming from states a and b, relative to the corresponding energy origins are

$$E^{‡}\left(\alpha \right)-E_a^{\left(0\right)}=\frac{1}{2}{k}_1{\left[x_1\left(\alpha \right)-{\lambda }_1\right]}^2+\frac{1}{2}{k}_2{\left[x_2\left(\alpha \right)\right]}^2,$$ [23]

$$E^{‡}\left(\alpha \right)-E_b^{\left(0\right)}=\frac{1}{2}{k}_1{\left[x_1\left(\alpha \right)\right]}^2+\frac{1}{2}{k}_2{\left[x_2\left(\alpha \right)-{\lambda }_2\right]}^2,$$ [24]

respectively. The probabilities to be at point α on the CL given that we are in the corresponding state satisfy

$$P_{a\to b}^{‡}\left(\alpha \right)=\frac{e^{-{\beta }_1\left(\frac{1}{2}{k}_1{\left[x_1\left(\alpha \right)-{\lambda }_1\right]}^2\right)}{e}^{-{\beta }_2\left(\frac{1}{2}{k}_2{\left[x_2\left(\alpha \right)\right]}^2\right)}}{{\displaystyle {\int }_{\mathrm{ℝ}}{e}^{-{\beta }_1\left(\frac{1}{2}{k}_1{\left[x_1\left(\alpha \right)-{\lambda }_1\right]}^2\right)}{e}^{-{\beta }_2\left(\frac{1}{2}{k}_2{\left[x_2\left(\alpha \right)\right]}^2\right)}\hspace{0.17em}d\alpha }},$$ [25]

$$P_{b\to a}^{‡}\left(\alpha \right)=\frac{e^{-{\beta }_1\left(\frac{1}{2}{k}_1{\left[x_1\left(\alpha \right)\right]}^2\right)}{e}^{-{\beta }_2\left(\frac{1}{2}{k}_2{\left[x_2\left(\alpha \right)-{\lambda }_2\right]}^2\right)}}{{\displaystyle {\int }_{\mathrm{ℝ}}{e}^{-{\beta }_1\left(\frac{1}{2}{k}_1{\left[x_1\left(\alpha \right)\right]}^2\right)}{e}^{-{\beta }_2\left(\frac{1}{2}{k}_2{\left[x_2\left(\alpha \right)-{\lambda }_2\right]}^2\right)}\hspace{0.17em}d\alpha }}.$$ [26]

For $P_{a\to b}^{‡}\left(\alpha \right)$, the point of maximum probability on the CL is found from Eq. 25 to be

$$x_{1,\max }^{\left(a\right)}=\frac{{\lambda }_1\left[{\beta }_2\left(-\mathrm{\Delta }{E}_{ba}+E_{\text{R}1}\right)-\left({\beta }_2-2{\beta }_1\right)E_{\text{R}2}\right]}{2\left(E_{\text{R}2}{\beta }_1+E_{\text{R}1}{\beta }_2\right)},$$ [27]

$$x_{2,\max }^{\left(a\right)}={\alpha }_{\max }^{\left(a\right)}=\frac{{\lambda }_2{\beta }_1\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}{2\left(E_{\text{R}2}{\beta }_1+E_{\text{R}1}{\beta }_2\right)}.$$ [28]

A similar procedure using Eq. 26 yields

$$x_{1,\max }^{\left(b\right)}=\frac{{\lambda }_1{\beta }_2\left(-\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}{2\left(E_{\text{R}2}{\beta }_1+E_{\text{R}1}{\beta }_2\right)},$$ [29]

$$x_{2,\max }^{\left(b\right)}={\alpha }_{\max }^{\left(b\right)}=\frac{{\lambda }_2\left[{\beta }_1\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}2}\right)-\left({\beta }_1-2{\beta }_2\right)E_{\text{R}1}\right]}{2\left(E_{\text{R}2}{\beta }_1+E_{\text{R}1}{\beta }_2\right)}.$$ [30]

For ${\beta }_1={\beta }_2$, the position of maximum probability is also the geometric minimum. When the temperatures differ, the position of maximum probability on the transition line shifts from this minimum. The shifts of these probability distributions from their unithermal forms is the reason for the difference between the correct probabilities given by Eqs. 8 and 9, and the forms in Eqs. 18 and 19 obtained under the assumption that the probabilities are dominated by the geometric minimum energy. A graphical representation of these results is shown in Figs. 2 and 3 for several illustrative examples. Fig. 2 shows the position of maximum probability as a function of the temperature difference. The probability densities themselves are shown in Fig. 3. These plots clearly show the essentials of the bithermal transition behavior as discussed above.

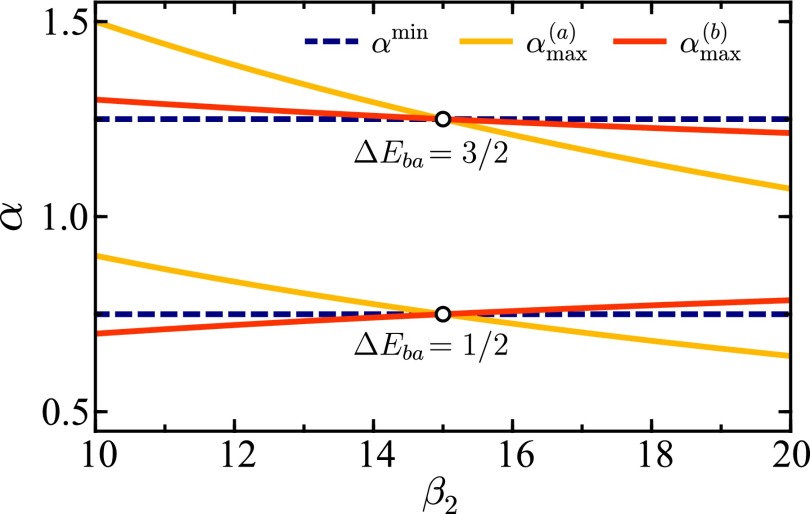
Fig. 2.

Parametric CL coordinate α shown as function of ${\beta }_2$, with ${\beta }_1=15$ held constant, for the geometrical energy minimum (dashed line) and the maximum probability (solid lines) on the $E_a$ and $E_b$ surfaces. In the top curves $\mathrm{\Delta }{E}_{ba}=3/2$ and in the bottom curves $\mathrm{\Delta }{E}_{ba}=1/2$. The circular markers denote the points where ${\beta }_1={\beta }_2$. Other parameters are $E_{\text{R}1}=E_{\text{R}2}=1/2$.

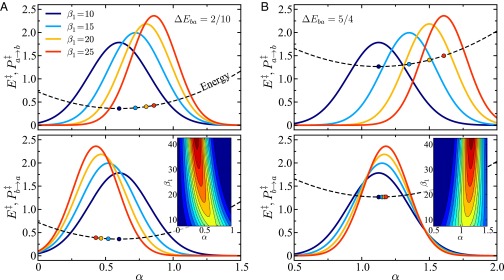
Fig. 3.

Crossing point probability densities $P^{‡}\left(\alpha \right)$ for (A) $\mathrm{\Delta }{E}_{ba}=2/10$ and (B) $\mathrm{\Delta }{E}_{ba}=5/4$ on the $E_a$ (Top) and $E_b$ (Bottom) energy surfaces as functions of the CL coordinate α (Eq. 21). Varying values of ${\beta }_1$ are shown with ${\beta }_2=10$ held constant in all cases. In each panel, the corresponding CL energy $E^{‡}$ is shown as a parabolic dashed curve. The circular markers on the energy curves denote the corresponding thermal energy minima (probability density maxima). In each bottom panel, the inset is a corresponding contour plot of $P_{b\to a}^{‡}\left(\alpha \right)$ that is normalized with colors varying from blue (minimum) to red (maximum). Other parameters are $E_{\text{R}1}=E_{\text{R}2}=1/2$.

The following observations are noteworthy:

• i)The point of maximum probability on the transition surface does not depend on the absolute temperatures $T_1$ and $T_2$, only on their ratios. When $T_1=T_2$ it becomes the geometrical point of minimum enegy, which is temperature-independent.
• ii)Considering the position of the maximum probability points relative to the minimum energy point on the CL, some general trends can observed. For reaction free energies below the total reorganization energy ($\left|E_{ba}\right|<E_{\text{R}}$) the points of maximum probability in the $a\to b$ and $b\to a$ directions are on opposite sides of the geometrical energy minimum for ${\beta }_2<{\beta }_1$, cross at the unithermal point, and finally continue on opposite sides for ${\beta }_2>{\beta }_1$. For reactions with reorganization energy above the reaction free energy ($\left|E_{ba}\right|>E_{\text{R}}$) the maximum probability points for both reaction directions are on same side of the geometrical energy minimum for all values of ${\beta }_2$ with ${\beta }_1$ held constant, except where they cross at the unithermal point.
• iii)As shown in Fig. 3, in addition to the shift in the transition line probability distribution function, another interesting feature is observed: both the $P_{a\to b}^{‡}$ and $P_{b\to a}^{‡}$ distributions become narrower (smaller variance) with increasing deviation from the unithermal point in the direction ${\beta }_1>{\beta }_2$ for finite ${\beta }_2$ held constant. The inset in each bottom panel of Fig. 3 illustrates this narrowing as ${\beta }_1\to \mathrm{\infty }$. In the opposite direction (${\beta }_1<{\beta }_2$), the complementary trend is observed with the distributions becoming increasingly broad. It is of note that in the limit ${\beta }_1\to 0$ $\left(T_1\to \mathrm{\infty }\right)$ the total distribution will be dominated by the respective distribution of the $x_2$ coordinate, that is, $P_{a\to b}^{‡}\left(x_1,x_2\right)\approx P_{a\to b}^{‡}\left(x_2\right)$.
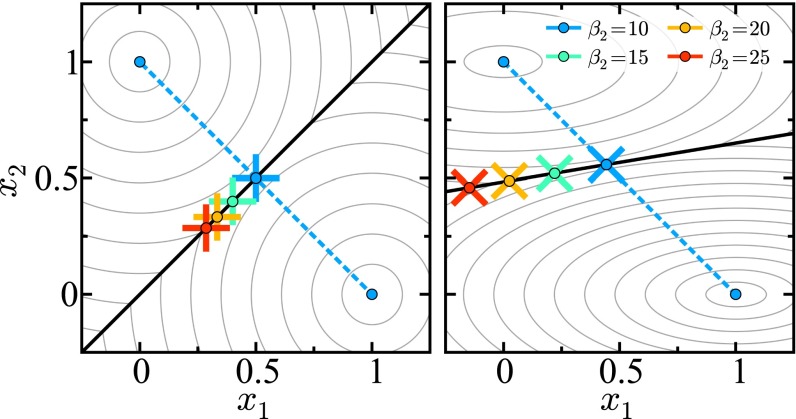
• iv)At the unithermal limit, the maximum probability path that connects stable states is linear and goes through ${\alpha }^{\min }$ as shown in Fig. 3. This holds in both the symmetric ($E_{ba}=0$) and asymmetric cases. In bithermal systems, this path is obviously nonlinear (because it deviates from the minimum energy point) and depends on the thermal characteristics. Fig. 4 demonstrates this observation. Note that unlike in the symmetric case, in an asymmetric system the path connecting minima is not necessarily normal to the CL. This is also the case in unithermal charge transfer reactions with asymmetric donor–acceptor geometry (108). The finding of a thermal energy minimum point that does not correspond to a geometrical energy minimum point is nonintuitive but is congruent with recent advances in TST that have shown that in nonequilibrium systems the traditional picture of a transition state as a stationary saddle point on a potential energy surface is flawed, and that the correct nature is a structure with different extremal properties (109–113).

Fig. 4.

Contour plots of energy surfaces for symmetric (Left) and asymmetric (Right) donor–acceptor pair geometries. The CL is shown as a thick black line. The crosses mark the point of maximum probability for the a→b transition on the CL for ${\beta }_2\in \left\{\mathrm{10,15,20,25}\right\}$ with ${\beta }_1=10$ held constant. The dashed line connects the two well minima through the geometrical minimum energy point.

Finally, an interesting interpretation of the results 8 and 9 can be found in terms of the Tolman activation energy (114), which accounts for statistical properties of the reaction mechanism and goes beyond the Arrhenius viewpoint of a single activation threshold. In the Tolman interpretation, the activation energy is defined as the average energy of all reacting systems minus the average energy of all reactants (114–116). In the present model this is

$$E_{\text{A}}^{\text{Tolman},\left(m\right)}={\langle E^{‡}\left(\alpha \right)\rangle }_m-E_m^{\left(0\right)}:m\in \left\{a,b\right\},$$ [31]

where $E^{‡}\left(\alpha \right)$ is the energy on the CL and the average is over the corresponding distribution ($m\in \left\{a,b\right\}$), namely,

$${\langle E^{‡}\left(\alpha \right)\rangle }_m={\displaystyle {\int }_{\mathrm{ℝ}}{E}^{‡}\left(\alpha \right)P_{m\to n}^{‡}\left(\alpha \right)d\alpha }.$$ [32]

Using Eqs. 25 and 26 these averages can be easily evaluated and can be cast as additive terms representing the division of the needed activation energy between modes $x_1$ and $x_2$,

$$E_{\text{A}}^{\text{Tolman},\left(m\right)}=\langle E_{\text{A}1}^{\left(m\right)}\rangle +\langle E_{\text{A}2}^{\left(m\right)}\rangle :m\in \left\{a,b\right\},$$ [33]

where

$$\begin{array}{l}\langle E_{\text{A}1}^{\left(a\right)}\rangle =\frac{2{\beta }_1{E}_{\text{R}2}^2+2{\beta }_2{E}_{\text{R}1}{E}_{\text{R}2}+{\beta }_2^2{E}_{\text{R}1}{\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2}{4{\left(E_{\text{R}2}{\beta }_1+E_{\text{R}1}{\beta }_2\right)}^2},\\ \langle E_{\text{A}2}^{\left(a\right)}\rangle =\frac{2{\beta }_2{E}_{\text{R}1}^2+2{\beta }_1{E}_{\text{R}1}{E}_{\text{R}2}+{\beta }_1^2{E}_{\text{R}2}{\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2}{4{\left(E_{\text{R}2}{\beta }_1+E_{\text{R}1}{\beta }_2\right)}^2},\\ \langle E_{\text{A}1}^{\left(b\right)}\rangle =\frac{2{\beta }_1{E}_{\text{R}2}^2+2{\beta }_2{E}_{\text{R}1}{E}_{\text{R}2}+{\beta }_2^2{E}_{\text{R}1}{\left(\mathrm{\Delta }{E}_{ba}-E_{\text{R}}\right)}^2}{4{\left(E_{\text{R}2}{\beta }_1+E_{\text{R}1}{\beta }_2\right)}^2},\\ \langle E_{\text{A}2}^{\left(b\right)}\rangle =\frac{2{\beta }_2{E}_{\text{R}1}^2+2{\beta }_1{E}_{\text{R}1}{E}_{\text{R}2}+{\beta }_1^2{E}_{\text{R}2}{\left(\mathrm{\Delta }{E}_{ba}-E_{\text{R}}\right)}^2}{4{\left(E_{\text{R}2}{\beta }_1+E_{\text{R}1}{\beta }_2\right)}^2}.\end{array}$$ [34]

It can be easily checked that defining the probabilities to be on the CL by

$$P_{a\to b}\propto \exp \left[-\left({\beta }_1\langle E_{\text{A}1}^{\left(a\right)}\rangle +{\beta }_2\langle E_{\text{A}2}^{\left(a\right)}\rangle \right)\right],$$ [35]

and

$$P_{b\to a}\propto \exp \left[-\left({\beta }_1\langle E_{\text{A}1}^{\left(b\right)}\rangle +{\beta }_2\langle E_{\text{A}2}^{\left(b\right)}\rangle \right)\right],$$ [36]

leads to the exact results 8 and 9 for the bithermal Boltzmann factors. A comparison of rates obtained from the geometrical minimum energy point and the point of maximum probability is shown in Fig. S1 in the Supporting Information.

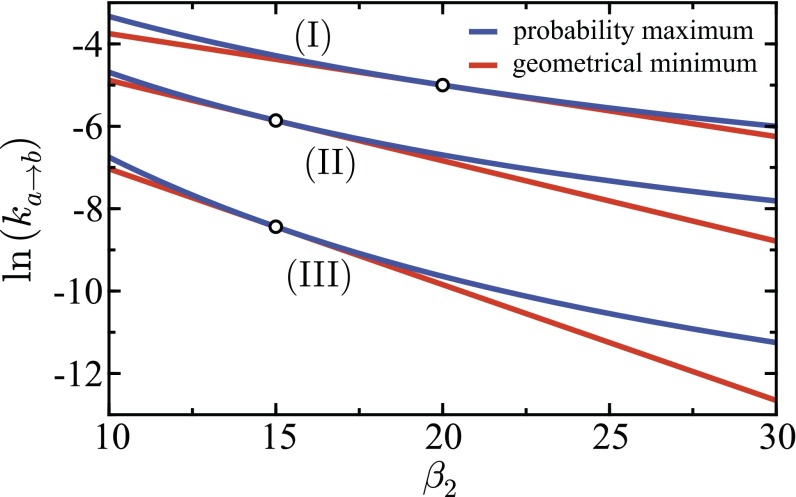
Fig. S1.

ET rate $\ln \left(k_{a\to b}\right)$ given by the geometrical energy minimum (red line) and probablity maximum (blue line) shown as function of ${\beta }_2$ with ${\beta }_1$ held constant. Parameters are (I) $\mathrm{\Delta }{E}_{ba}=0,{\beta }_1=20$, (II) $\mathrm{\Delta }{E}_{ba}=1/4,{\beta }_1=15$, and (III) $\mathrm{\Delta }{E}_{ba}=1/2,{\beta }_1=15$. The circular markers denote the points where ${\beta }_1={\beta }_2$. Other parameters are $E_{\text{R}1}=E_{\text{R}2}=1/2$. Preexponential factors in the rate expressions have been suppressed.

Energy Transfer.

As outlined in the introduction, the coupled transfer of charge and heat, and the interplay between the electric and heat currents, gives rise to unique electronic and thermoelectric phenomena (117, 118). When ET takes place across a thermal gradient, it can carry energy as well, implying heat ($\mathcal{Q}$) transfer between the donor and acceptor sites. Indeed, our model has disregarded direct coupling between the modes coupled to the electronic occupation of the different sites, so this coupling is the only potential source (in this model) of heat transfer. Here we explore this possibility.

During the $m\to n$ state transition, for mode $x_j$, the heat transferred is the sum of the heat released by the corresponding bath during the ascent to the transition state crossing point defined by α on the $E_m$ surface, and the heat absorbed by the bath during the descent to equilibrium on the $E_n$ surface,

$${\mathcal{Q}}_j^{(m\to n)}\left(\alpha \right)=-{\mathcal{Q}}_{\mathrm{rel}}^{\left(m\right)}+{\mathcal{Q}}_{\mathrm{abs}}^{\left(n\right)}.$$ [37]

For the two-mode, two-state system considered here the amounts of heat transfer into each bath during an ET event are

$$\begin{array}{c}{\mathcal{Q}}_1^{\left(a\to b\right)}\left(\alpha \right)=-{\mathcal{Q}}_1^{\left(b\to a\right)}\left(\alpha \right)\\ =-\frac{1}{2}{k}_1{\left[x_1\left(\alpha \right)-{\lambda }_1\right]}^2+\frac{1}{2}{k}_1{\left[x_1\left(\alpha \right)\right]}^2,\\ {\mathcal{Q}}_2^{\left(a\to b\right)}\left(\alpha \right)=-{\mathcal{Q}}_2^{\left(b\to a\right)}\left(\alpha \right)\\ =-\frac{1}{2}{k}_2{\left[x_2\left(\alpha \right)\right]}^2+\frac{1}{2}{k}_2{\left[x_2\left(\alpha \right)-{\lambda }_2\right]}^2.\end{array}$$ [38]

The signs in Eq. 38 are chosen such that $\mathcal{Q}$ is positive when energy enters the corresponding bath. The average values for these components are

$$\begin{array}{l}\langle {\mathcal{Q}}_j^{\left(a\to b\right)}\rangle ={\displaystyle {\int }_{\mathrm{ℝ}}{\mathcal{Q}}_j^{(a\to b)}\left(\alpha \right)P_{a\to b}^{‡}\left(\alpha \right)d\alpha },\\ \langle {\mathcal{Q}}_j^{\left(b\to a\right)}\rangle ={\displaystyle {\int }_{\mathrm{ℝ}}{\mathcal{Q}}_j^{(b\to a)}\left(\alpha \right)P_{b\to a}^{‡}\left(\alpha \right)d\alpha },\end{array}$$ [39]

where $j\in \left\{\mathrm{1,2}\right\}$ and $P_{m\to n}^{‡}\left(\alpha \right)$ is the probability density on the CL for the corresponding surface. Evaluating each of these integrals yields

$$\begin{array}{l}\langle {\mathcal{Q}}_1^{\left(a\to b\right)}\rangle =\frac{-E_{\text{R}1}{T}_1\mathrm{\Delta }{E}_{ba}+E_{\text{R}1}{E}_{\text{R}2}\left(T_2-T_1\right)}{E_{\text{R}1}{T}_1+E_{\text{R}2}{T}_2},\\ \langle {\mathcal{Q}}_2^{\left(a\to b\right)}\rangle =\frac{-E_{\text{R}2}{T}_2\mathrm{\Delta }{E}_{ba}-E_{\text{R}1}{E}_{\text{R}2}\left(T_2-T_1\right)}{E_{\text{R}1}{T}_1+E_{\text{R}2}{T}_2},\\ \langle {\mathcal{Q}}_1^{\left(b\to a\right)}\rangle =\frac{E_{\text{R}1}{T}_1\mathrm{\Delta }{E}_{ba}+E_{\text{R}1}{E}_{\text{R}2}\left(T_2-T_1\right)}{E_{\text{R}1}{T}_1+E_{\text{R}2}{T}_2},\\ \langle {\mathcal{Q}}_2^{\left(b\to a\right)}\rangle =\frac{E_{\text{R}2}{T}_2\mathrm{\Delta }{E}_{ba}-E_{\text{R}1}{E}_{\text{R}2}\left(T_2-T_1\right)}{E_{\text{R}1}{T}_1+E_{\text{R}2}{T}_2},\end{array}$$ [40]

which depend on the reaction free energy, the reorganization energy in each mode, and the temperature of each bath. It should be emphasized that the modes themselves are assumed to remain in thermal equilibrium. Expressions 40 give the heat transferred into the thermal bath with which the corresponding mode equilibrates for a single ET in the indicated direction. Note that the total heat transfer for the $a\to b$ transition is

$$\langle {\mathcal{Q}}^{\left(a\to b\right)}\rangle =\langle {\mathcal{Q}}_1^{\left(a\to b\right)}\rangle +\langle {\mathcal{Q}}_2^{\left(a\to b\right)}\rangle =-\mathrm{\Delta }{E}_{ba},$$ [41]

and correspondingly for the $b\to a$ transition,

$$\langle {\mathcal{Q}}^{\left(b\to a\right)}\rangle =\langle {\mathcal{Q}}_1^{\left(b\to a\right)}\rangle +\langle {\mathcal{Q}}_2^{\left(b\to a\right)}\rangle =\mathrm{\Delta }{E}_{ba},$$ [42]

which are just statements of energy conservation. The change in free energy of the baths associated with the $a\to b$ process ($-\mathrm{\Delta }{E}_{ba}$) is divided between the two baths with the ratio $E_{\text{R}1}{T}_1/E_{\text{R}2}{T}_2$. Interestingly, this ratio depends on their temperatures, reflecting the fact that the higher-temperature bath is more effective in promoting ET. Even more significant is the observation that there is a term in each expression in 40 that does not depend on $\mathrm{\Delta }{E}_{ba}$, and the sign of which does not depend on the direction of the ET process. Thus, there exists a nonzero heat transfer between baths associated with the ET process in bithermal systems. Over each ET event it is given by

$$\langle {\mathcal{Q}}_{2\to 1}\rangle \equiv \langle {\mathcal{Q}}_1^{\left(a\to b\right)}\rangle +\langle {\mathcal{Q}}_1^{\left(b\to a\right)}\rangle =\frac{2E_{R1}{E}_{\text{R}2}\left(T_2-T_1\right)}{E_{\text{R}1}{T}_1+E_{\text{R}2}{T}_2}$$ [43]

and

$$\langle {\mathcal{Q}}_{1\to 2}\rangle \equiv \langle {\mathcal{Q}}_2^{\left(a\to b\right)}\rangle +\langle {\mathcal{Q}}_2^{\left(b\to a\right)}\rangle =-\frac{2E_{R1}{E}_{\text{R}2}\left(T_2-T_1\right)}{E_{\text{R}1}{T}_1+E_{\text{R}2}{T}_2}.$$ [44]

To see the significance of this result, consider an ensemble of site pairs with probabilities $p_a$ that a pair is in state a (electron on site 1) and $p_b$ that the pair is in state b (electron on site 2). These probabilities obey the kinetic equations

$$\frac{d{p}_a}{dt}=-\frac{d{p}_b}{dt}=-{\mathcal{J}}_{a\to b}+{\mathcal{J}}_{b\to a},$$ [45]

where ${\mathcal{J}}_{a\to b}=k_{a\to b}{p}_a$ and ${\mathcal{J}}_{b\to a}=k_{b\to a}{p}_b$. Correspondingly, the rate of heat deposit on the respective site is given by

$$\frac{d{\mathcal{Q}}_j}{dt}={\mathcal{J}}_{a\to b}\langle {\mathcal{Q}}_j^{\left(a\to b\right)}\rangle +{\mathcal{J}}_{b\to a}\langle {\mathcal{Q}}_j^{\left(b\to a\right)}\rangle :j\in \left\{\mathrm{1,2}\right\}.$$ [46]

Now, consider the steady state at which the system is at electronic quasiequilibrium so that ${\mathcal{J}}_{a\to b}={\mathcal{J}}_{b\to a}={\mathcal{J}}_{\text{ss}}$, that is, the net electron flux between sites vanishes. Using Eqs. 43 and 44 it follows that at this state

$${\left(\frac{d{\mathcal{Q}}_1}{dt}\right)}_{\text{ss}}=-{\left(\frac{d{\mathcal{Q}}_2}{dt}\right)}_{\text{ss}}={\mathcal{J}}_{\text{ss}}\frac{2E_{R1}{E}_{\text{R}2}\left(T_2-T_1\right)}{E_{\text{R}1}{T}_1+E_{\text{R}2}{T}_2}\equiv {\mathcal{J}}_{\text{ss}}^{\mathcal{Q}}.$$ [47]

Thus, for $T_1\ne T_2$, even when the net electron flux vanishes, the presence of hopping electrons induces a net heat current from the hot bath to the cold bath. Of interest is the observation that there is no pure Seebeck effect in the model investigated here. This is seen in Eqs. 10–12, which imply that when $E_{\text{R}1}=E_{\text{R}2}$, changing $T_1$ relative to $T_2$ affects the forward and backward rates in the same way. Note that Eq. 47 is nonlinear in the temperature difference (although it is approximately so when the difference is small). In the high- and low-temperature limits of site 2, the steady-state heat flux becomes

$$\underset{T_2\to \mathit{\infty }}{\lim }{\mathcal{J}}_{\text{ss}}^{\mathcal{Q}}=2{\mathcal{J}}_{\text{ss}}{E}_{R1}\hspace{1em}\text{and}\hspace{1em}\underset{T_2\to 0}{\lim }{\mathcal{J}}_{\text{ss}}^{\mathcal{Q}}=-2{\mathcal{J}}_{\text{ss}}{E}_{R2},$$ [48]

respectively, each of which depends only on the reorganization energy of the respective cold mode. These results imply that in a system where electron hops between local sites there is a contribution to the heat conduction associated with the electronic motion. An assessment of this contribution to the heat conduction in such systems will be made elsewhere.

Conclusions

A unified theory for the rate and extent of ET and heat transport between bithermal donor–acceptor pairs has been constructed in an augmented Marcus framework. Through application of a multidimensional TST where different modes interact with environments of different temperatures, we have characterized the kinetics of the charge transfer process over various temperature gradients and geometries between reactant and product states. In a bithermal system, the traditional interpretation of the activation energy as a single point derived through geometric minimization of overall points where the donor and acceptor are equienergetic has been shown to not adequately describe the transfer mechanism, and, instead, a statistical interpretation of the activation energy threshold has been developed to account for the biasing of states that arises due to the temperature gradient. We find that entropic rate corrections, which are trivial in the unithermal case, are nontrivial for bithermal systems and are characteristic of the multithermal density of states. Surprisingly, for electron transport across a thermal gradient, the transfer of heat continues to occur even when there is no net transfer of charge. This effect could be harnessed, particularly through molecular junctions and wires (1, 53, 119, 120), to control the transfer of thermal energy in reaction networks with complex systems of heat reservoirs. In turn, the use of these reservoirs to control charge current in thermoelectric systems with nonzero Seebeck coefficients could result in the development of devices and electronics that can be harnessed for application in thermally controlled molecular machines.

A description of the transfer process across smoothly varying temperature gradients and the characterization of possible deviations from the assumed bithermal Boltzmann distribution on the transition state CL are possible areas for future research. The treatment of collective behaviors arising from anharmonic coupling between reactive modes, such as that observed in multiple particle transfer mechanisms (98), will require further characterization of the nature of thermalization (121) and temperature, specifically in systems that are in contact with multiple independent heat baths. The current description gives impetus for experimental verification of the constructed methodologies in bithermal systems.

The bithermal donor–acceptor model considered here can be generalized to systems with multiple reaction pathways. For example, a theoretical description of the transfer mechanism in a donor–bridge–acceptor model can be constructed by extending the dimension of the transition state structure on the crossing “line.” Developing a general description of thermal transition states in ET reactions with many reactive modes could be accomplished through implementation of the geometric transition state formalisms developed for classical reactions in high dimensionality (122). A conjecture supported by the bithermal biasing of the transition state structure predicted here is that multibody temperature gradients can be used to control which reaction pathway is taken in a complex network. The possibility of controlling reactions through multithermally induced deformation of transitions states is a significant finding of this study, and one that is primed for further exploration thorough computation and experiment.

Derivation of the Normal Velocity at the Crossing Line

In the rate expression given by Eq. 6, the frequency of activated events is proportional to the expectation value of the velocity normal to the transition state. For bithermal ET, the set of transition state structures is composed of equienergetic points between the $E_a$ and $E_b$ surfaces that are elements of the CL. A unit normal vector to the CL is

$$\begin{array}{c}{\widehat{\mathbf{u}}}_{\text{n}}=\left(n_1,n_2\right)\\ =\left(-\frac{1}{\left|\nabla g\right|},\frac{s}{\left|\nabla g\right|}\right)\\ =n_1{\widehat{\mathbf{e}}}_1+n_2{\widehat{\mathbf{e}}}_2,\end{array}$$ [S1]

and a unit tangent vector is

$$\begin{array}{c}{\widehat{\mathbf{u}}}_{\text{t}}=\left(n_2,-n_1\right)\\ =\left(\frac{s}{\left|\nabla g\right|},\frac{1}{\left|\nabla g\right|}\right)\\ =n_2{\widehat{\mathbf{e}}}_1-n_1{\widehat{\mathbf{e}}}_2,\end{array}$$ [S2]

where $g\left(x_1,x_2\right)=x_1-s{x}_2-c$ is a function that defines the crossing constraint $g\left(x_1,x_2\right)=0$. The slope s is the coefficient in front of α in Eq. 21 and intercept c represents the second term in the right-hand side of Eq. 21. The constant $\left|\nabla g\right|=\sqrt{1+s^2}$ is the magnitude of the gradient of the CL. The velocity vector

$$\dot{\mathbf{x}}={\dot{x}}_1{\widehat{\mathbf{e}}}_1+{\dot{x}}_2{\widehat{\mathbf{e}}}_2$$ [S3]

has a scalar component in the direction of the normal (102),

$${\dot{x}}_{\text{n}}\left({\dot{x}}_1,{\dot{x}}_2\right)=\dot{\mathbf{x}}\cdot {\widehat{\mathbf{u}}}_{\text{n}}={\dot{x}}_1{n}_1+{\dot{x}}_2{n}_2,$$ [S4]

and a scalar component in the direction of the tangent,

$${\dot{x}}_{\text{t}}\left({\dot{x}}_1,{\dot{x}}_2\right)=\dot{\mathbf{x}}\cdot {\widehat{\mathbf{u}}}_{\text{t}}={\dot{x}}_1{n}_2-{\dot{x}}_2{n}_1.$$ [S5]

We are interested calculating the expectation value of the normal component,

$$\langle {\dot{x}}_{\text{n}}\rangle =\frac{{\displaystyle {\iint }_{\mathcal{C}}{\dot{x}}_{\text{n}}\left({\dot{x}}_1,{\dot{x}}_2\right)\hspace{0.17em}{e}^{-{\beta }_1\left(\frac{1}{2}{m}_1{\dot{x}}_1^2\right)}{e}^{-{\beta }_2\left(\frac{1}{2}{m}_2{\dot{x}}_2^2\right)}d{\dot{x}}_{1}d{\dot{x}}_2}}{{\displaystyle {\iint }_{\mathcal{C}}{e}^{-{\beta }_1\left(\frac{1}{2}{m}_1{\dot{x}}_1^2\right)}{e}^{-{\beta }_2\left(\frac{1}{2}{m}_2{\dot{x}}_2^2\right)}\hspace{0.17em}d{\dot{x}}_{1}d{\dot{x}}_2}},$$ [S6]

where $\mathcal{C}$ is a domain of integration such that we only include the positive values of ${\dot{x}}_{\text{n}}$. In order satisfy this constraint we will transform from ${\dot{x}}_1\times {\dot{x}}_2$ space into a coordinate system with basis in the normal and tangential directions.

The normal and tangential velocity components can be defined through

$$\left(\begin{array}{c}{\dot{x}}_{\text{n}}\\ {\dot{x}}_{\text{t}}\end{array}\right)=\mathbf{M}\left(\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right),$$ [S7]

with

$$\mathbf{M}=\left(\begin{array}{cc}{n}_1& n_2\\ n_2& -n_1\end{array}\right),$$ [S8]

which allows the components ${\dot{x}}_1$ and ${\dot{x}}_2$ to be expressed as

$$\left(\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right)={\mathbf{M}}^{-1}\left(\begin{array}{c}{\dot{x}}_{\text{n}}\\ {\dot{x}}_{\text{t}}\end{array}\right),$$ [S9]

with

$$\text{det}\hspace{0.17em}\mathbf{M}=\left|\mathbf{M}\right|=-\left(n_1^2+n_2^2\right).$$ [S10]

and

$${\mathbf{M}}^{-1}=\frac{1}{\left|\mathbf{M}\right|}\left(\begin{array}{cc}-n_1& -n_2\\ -n_2& n_1\end{array}\right).$$ [S11]

Expanding Eq. S9 yields

$${\dot{x}}_1\left({\dot{x}}_{\text{n}},{\dot{x}}_{\text{t}}\right)=\frac{1}{\left|\mathbf{M}\right|}\left(-n_1{\dot{x}}_{\text{n}}-n_2{\dot{x}}_{\text{t}}\right),$$ [S12]

$${\dot{x}}_2\left({\dot{x}}_{\text{n}},{\dot{x}}_{\text{t}}\right)=\frac{1}{\left|\mathbf{M}\right|}\left(-n_2{\dot{x}}_{\text{n}}+n_1{\dot{x}}_{\text{t}}\right),$$ [S13]

which express the respective original coordinate in terms of the normal and tangential components. In the diagonal (normal-tangential) coordinate system, the expectation value of the normal velocity in the positive direction is

$$\langle {\dot{x}}_{\text{n}}\rangle =\frac{{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\dot{x}}_{\text{n}}\hspace{0.17em}{e}^{-{\beta }_1\left(\frac{1}{2}{m}_1{\left[{\dot{x}}_1\left({\dot{x}}_{\text{n}},{\dot{x}}_{\text{t}}\right)\right]}^2\right)}{e}^{-{\beta }_2\left(\frac{1}{2}{m}_2{\left[{\dot{x}}_2\left({\dot{x}}_{\text{n}},{\dot{x}}_{\text{t}}\right)\right]}^2\right)}\hspace{0.17em}d{\dot{x}}_{\text{t}}d{\dot{x}}_{\text{n}}}}}{{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{e}^{-{\beta }_1\left(\frac{1}{2}{m}_1{\left[{\dot{x}}_1\left({\dot{x}}_{\text{n}},{\dot{x}}_{\text{t}}\right)\right]}^2\right)}{e}^{-{\beta }_2\left(\frac{1}{2}{m}_2{\left[{\dot{x}}_2\left({\dot{x}}_{\text{n}},{\dot{x}}_{\text{t}}\right)\right]}^2\right)}\hspace{0.17em}\hspace{0.17em}d{\dot{x}}_{\text{t}}d{\dot{x}}_{\text{n}}}}},$$ [S14]

which upon evaluation yields

$$\langle {\dot{x}}_{\text{n}}\rangle =\sqrt{\frac{2}{\pi }\left(\frac{m_2{\beta }_2{n}_1^2+m_1{\beta }_1{n}_2^2}{m_1{\beta }_1{m}_2{\beta }_2}\right)}.$$ [S15]

At the unithermal (${\beta }_1={\beta }_2=\beta$) − equimass ($m_1=m_2=m$) limit, Eq. S15 reduces to the expected form

$$\langle {\dot{x}}_{\text{n}}\rangle =\sqrt{\frac{2}{\pi m\beta }},$$ [S16]

in agreement with known results (103, 104).

The result given by Eq. S15 is valid for both bithermal and unithermal systems. The algebraic components of the probability density P of velocities at the CL can be examined by expanding the bithermal Boltzmann factor in Eq. S14 in terms of ${\dot{x}}_{\text{n}}$ and ${\dot{x}}_{\text{t}}$,

$$P\left({\dot{x}}_{\text{n}},{\dot{x}}_{\text{t}}\right)\propto \text{exp}\left[-\left(\frac{m_1{\beta }_1{n}_1^2+m_2{\beta }_2{n}_2^2}{2{\left|\mathbf{M}\right|}^2}{\dot{x}}_{\text{n}}^2+\frac{m_1{\beta }_1{n}_2^2+m_2{\beta }_2{n}_1^2}{2{\left|\mathbf{M}\right|}^2}{\dot{x}}_{\text{t}}^2-\frac{n_1{n}_2\left(m_2{\beta }_2-m_1{\beta }_1\right)}{{\left|\mathbf{M}\right|}^2}{\dot{x}}_{\text{n}}{\dot{x}}_{\text{t}}\right)\right].$$ [S17]

It can be seen that for $m_1{\beta }_1=m_2{\beta }_2$ the coupling term disappears and, in this case, the probabilities of each component are separable, that is, $P=P\left({\dot{x}}_{\text{n}}\right)P\left({\dot{x}}_{\text{t}}\right)$. Moreover, for ${\dot{x}}_{\text{t}}=0$, the probability density $P=P\left({\dot{x}}_{\text{n}}\right)$ is a function of only the normal component. In all other cases the coupling term is nonlinear and the probability densities of each component are not separable. Note that the result derived by Jóhannesson and Jónsson (103) for the expectation value of the normal velocity in a unithermal system with multiple dimensions is in agreement with our result only for unithermal–equimass cases. Away from the equimass limit, discrepancies arise between their result and ours. The nature these discrepancies is that they effectively suppress the coupling term in their calculations by treating ${\dot{x}}_{\text{t}}=0$ only. In our result, we perform a rigorous transformation $\left({\dot{x}}_1,{\dot{x}}_2\right)\mapsto \left({\dot{x}}_{\text{n}},{\dot{x}}_{\text{t}}\right)$, thus including both the coupling term and the tangential component.

Geometrical Energy Minimum Activation Energy Derivation

At the low-temperature limit, the reaction rate probability will be dominated by the geometrical activation energy (the energy at the well minimum on the CL). To construct this term we want to minimize the energy $E_a$ subject to the crossing condition $E_a=E_b$. As noted by Zwickl et al. (98), this optimization can be accomplished using the standard method of Lagrange multipliers with the Lagrange function defined as

$$\begin{array}{c}\mathrm{ℒ}=E_a^{\left(0\right)}+\frac{1}{2}{k}_1{\left(x_1-{\lambda }_1\right)}^2+\frac{1}{2}{k}_2{x}_2^2\\ +\mu \left(\mathrm{\Delta }{E}_{ba}+\frac{1}{2}{k}_2{\lambda }_2^2-k_2{\lambda }_2{x}_2-\frac{1}{2}{k}_1{\lambda }_1^2+k_1{\lambda }_1{x}_1\right).\end{array}$$ [S18]

The corresponding system of equations for minimization is

$$\begin{array}{c}\frac{\partial \mathrm{ℒ}}{\partial x_1}=k_1\left(x_1-{\lambda }_1\right)+\mu k_1{\lambda }_1=0,\\ \frac{\partial \mathrm{ℒ}}{\partial x_2}=k_2{x}_2-\mu k_2{\lambda }_2=0,\end{array}$$ [S19]

and solving this system yields

$$x_1=\left(1-\mu \right){\lambda }_1\hspace{1em}\text{and}\hspace{1em}{x}_2=\mu {\lambda }_2.$$ [S20]

Substitution into $E_b\left(x_1,x_2\right)=E_a\left(x_1,x_2\right)$ gives

$$\mathrm{\Delta }{E}_{ba}+\frac{1}{2}{k}_1{\lambda }_1^2+\frac{1}{2}{k}_2{\lambda }_2^2=\mu \left(k_2{\lambda }_2^2+k_1{\lambda }_1^2\right),$$ [S21]

in terms of the multiplier μ. The sum of the free energy and reorganization energy can then be expressed as

$$\mathrm{\Delta }{E}_{ba}+E_{\text{R}}=\mu \left(2E_{\text{R}}\right).$$ [S22]

The multiplier is related to Eq. S22 through

$$\mu =\frac{\mathrm{\Delta }{E}_{ba}+E_{\text{R}}}{2E_{\text{R}}}\hspace{1em}\text{and}\hspace{1em}1-\mu =-\frac{\mathrm{\Delta }{E}_{ba}-E_{\text{R}}}{2E_{\text{R}}},$$ [S23]

from which it follows that the values of the reaction coordinates that allow crossing subject to the constraint are

$$x_1^{\text{min}}=-{\lambda }_1\frac{\mathrm{\Delta }{E}_{ba}-E_{\text{R}}}{2E_{\text{R}}},$$ [S24]

$$x_2^{\text{min}}={\lambda }_2\frac{\mathrm{\Delta }{E}_{ba}+E_{\text{R}}}{2E_{\text{R}}}.$$ [S25]

This point lies on a line that connects the metastable minima $E_a\left({\lambda }_1,0\right)$ and $E_b\left(0,{\lambda }_2\right)$ and is thus independent of reaction direction (98).

The total activation energy on the $E_a$ surface, $E_{\text{A}}^{\left(a\right)}$, can be separated into components corresponding to each mode,

$$E_{\text{A}}^{\left(a\right)}=E_{\text{A}1}^{\left(a\right)}+E_{\text{A}2}^{\left(a\right)},$$ [S26]

where A1 and A2 denote activation energy in the respective modes. Following Marcus’ theory, ET occurs at the point of minimum energy where $E_a=E_b$. As illustrated through the energy schematic in Fig. 1C, the activation energy $E_{\text{A}}^{\left(a\right)}$ is the difference between the occupation energy $E_a^{\left(0\right)}$ and the energy at the geometrical equienergetic minimum. In terms of the component energetics the crossing condition gives

$$\begin{array}{c}{E}_{\text{A}1}^{\left(a\right)}=\frac{1}{2}{k}_1{\left(-{\lambda }_1\frac{\mathrm{\Delta }{E}_{ba}-E_{\text{R}}}{2E_{\text{R}}}-{\lambda }_1\right)}^2\\ =E_{\text{R}1}{\left(\frac{\mathrm{\Delta }{E}_{ba}+E_{\text{R}}}{2E_{\text{R}}}\right)}^2\end{array}$$ [S27]

in the $x_1$ coordinate, and

$$\begin{array}{c}{E}_{\text{A}2}^{\left(a\right)}=\frac{1}{2}{k}_2{\lambda }_2^2{\left(\frac{\mathrm{\Delta }{E}_{ba}+E_{\text{R}}}{2E_{\text{R}}}\right)}^2\\ =E_{\text{R}2}{\left(\frac{\mathrm{\Delta }{E}_{ba}+E_{\text{R}}}{2E_{\text{R}}}\right)}^2\end{array}$$ [S28]

in the $x_2$ coordinate. By combining Eqs. S26–S28 we find the activation energy on the $E_a$ surface at the minimum energy point is

$$E_{\text{A}}^{\left(a\right)}=\frac{{\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2}{4E_{\text{R}}}.$$ [S29]

For a unithermal system this activation energy yields the familiar Marcus rate expression (82, 87, 88). For a bithermal system, the additivity of the total activation energy with respect to its components allows the transfer rate from $a\to b$ to be expressed as

$$\begin{array}{c}{k}_{a\to b}\propto \text{exp}[-{\beta }_1{E}_{\text{R}1}{\left(\frac{\mathrm{\Delta }{E}_{ba}+E_{\text{R}}}{2E_{\text{R}}}\right)}^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-{\beta }_2{E}_{\text{R}2}{\left(\frac{\mathrm{\Delta }{E}_{ba}+E_{\text{R}}}{2E_{\text{R}}}\right)}^2]\\ =\text{exp}\left[-\left({\beta }_1{E}_{\text{R}1}+{\beta }_2{E}_{\text{R}2}\right){\left(\frac{\mathrm{\Delta }{E}_{ba}+E_{\text{R}}}{2E_{\text{R}}}\right)}^2\right].\end{array}$$ [S30]

On the $E_b$ surface the activation energy is also a linear combination of components

$$E_{\text{A}}^{\left(b\right)}=E_{\text{A}1}^{\left(b\right)}+E_{\text{A}2}^{\left(b\right)}$$ [S31]

with the $x_1$ component

$$\begin{array}{c}{E}_{\text{A}1}^{\left(b\right)}=\frac{1}{2}{k}_1{\lambda }_1^2{\left(\frac{\mathrm{\Delta }{E}_{ba}-E_{\text{R}}}{2E_{\text{R}}}\right)}^2\\ =E_{\text{R}1}{\left(\frac{\mathrm{\Delta }{E}_{ba}-E_{\text{R}}}{2E_{\text{R}}}\right)}^2\end{array}$$ [S32]

and the $x_2$ component

$$\begin{array}{c}{E}_{\text{A}2}^{\left(b\right)}=\frac{1}{2}{k}_2{\lambda }_2^2{\left(\frac{\mathrm{\Delta }{E}_{ba}+E_{\text{R}}}{2E_{\text{R}}}-1\right)}^2\\ =E_{\text{R}2}{\left(\frac{\mathrm{\Delta }{E}_{ba}-E_{\text{R}}}{2E_{\text{R}}}\right)}^2.\end{array}$$ [S33]

The activation energy on the $E_b$ surface through the minimum energy point is

$$E_{\text{A}}^{\left(b\right)}=\frac{{\left(-\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2}{4E_{\text{R}}},$$ [S34]

and analogous to $k_{a\to b}$ the rate of transfer from surface $E_a$ to surface $E_b$ is

$$k_{b\to a}\propto \text{exp}\left[-\left({\beta }_1{E}_{\text{R}1}+{\beta }_2{E}_{\text{R}2}\right){\left(\frac{\mathrm{\Delta }{E}_{ba}-E_{\text{R}}}{2E_{\text{R}}}\right)}^2\right].$$ [S35]

If ${\beta }_1={\beta }_2$, then Eqs. S30 and S35 give the rate constants derived by Marcus.

Recovery of the Marcus Rate Expressions

Exact Rate Results.

For ET reactions in which donor and acceptor surfaces $E_a$ and $E_b$ are isogeometric ($k_1=k_2=k_{\text{M}}$) and both modes on each surface are in contact with baths of the same temperature (${\beta }_1={\beta }_2=\beta$), the bithermal probability densities for each reaction direction

$$\begin{array}{c}{P}_{a\to b}=\sqrt{\frac{{\beta }_1{\beta }_2\left(k_1{E}_{\text{R}1}+k_2{E}_{\text{R}2}\right)}{2\pi \left({\beta }_1{E}_{\text{R}2}+{\beta }_2{E}_{\text{R}1}\right)}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \hspace{0.17em}\text{exp}\left[-{\beta }_1{\beta }_2\frac{{\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2}{4\left({\beta }_1{E}_{\text{R}2}+{\beta }_2{E}_{\text{R}1}\right)}\right],\end{array}$$ [S36]

and

$$\begin{array}{c}{P}_{b\to a}=\sqrt{\frac{{\beta }_1{\beta }_2\left(k_1{E}_{\text{R}1}+k_2{E}_{\text{R}2}\right)}{2\pi \left({\beta }_1{E}_{\text{R}2}+{\beta }_2{E}_{\text{R}1}\right)}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \hspace{0.17em}\text{exp}\left[-{\beta }_1{\beta }_2\frac{{\left(\mathrm{\Delta }{E}_{ba}-E_{\text{R}}\right)}^2}{4\left({\beta }_1{E}_{\text{R}2}+{\beta }_2{E}_{\text{R}1}\right)}\right],\end{array}$$ [S37]

(which are Eqs. 8 and 9) reduce to

$$P_{a\to b}=\sqrt{\frac{\beta k_{\text{M}}}{2\pi }}\text{exp}\left[-\beta \frac{{\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2}{4E_{\text{R}}}\right],$$ [S38]

and

$$P_{b\to a}=\sqrt{\frac{\beta k_{\text{M}}}{2\pi }}\text{exp}\left[-\beta \frac{{\left(\mathrm{\Delta }{E}_{ba}-E_{\text{R}}\right)}^2}{4E_{\text{R}}}\right].$$ [S39]

In the adiabatic limit, the tunneling probability ${\mathcal{T}}_m\to 1$, and clearly the expectation value $\langle {\mathcal{T}}_m{v}_{\perp }\rangle$ is equal to $\langle v_{\perp }\rangle$. Moreover, the expression for the velocity term in rate formula given by Eq. 6 is

$$\frac{\langle v_{\perp }\rangle }{2}=\sqrt{\frac{1}{2\pi m\beta }},$$ [S40]

and, with ${\omega }_0=\sqrt{k_{\text{M}}/m}$, combining Eqs. S38 and S39 with Eq. S40 gives the expected TST forms

$$k_{a\to b}=\frac{{\omega }_0}{2\pi }\text{exp}\left[-\beta \frac{{\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2}{4E_{\text{R}}}\right],$$ [S41]

$$k_{b\to a}=\frac{{\omega }_0}{2\pi }\text{exp}\left[-\beta \frac{{\left(\mathrm{\Delta }{E}_{ba}-E_{\text{R}}\right)}^2}{4E_{\text{R}}}\right],$$ [S42]

in agreement with the adiabatic Marcus rates.

In the nonadiabatic limit, the tunneling probability can calculated using the Landau–Zener expression:

$${\mathcal{T}}_m^{\text{LZ}}=1-\text{exp}\left[-\frac{2\pi {\mathrm{\Delta }}^2}{\hslash {\left|\mathrm{\Delta }F\right|}_{{\alpha }_{\text{min}}}{v}_{\perp }}\right],$$ [S43]

where $\mathrm{\Delta }$ is the coupling constant between diabatic energy surfaces and ${\left|\mathrm{\Delta }F\right|}_{{\alpha }_{\text{min}}}$ is the difference in the forces normal to the CL on each surface evaluated at ${\alpha }_{\text{min}}$ (123, 124). A first-order approximation to ${\mathcal{T}}_m^{\text{LZ}}$ gives ${\mathcal{T}}_m\propto 1/v_{\perp }$ (87). In this limit, the expectation value $\langle {\mathcal{T}}_m{v}_{\perp }\rangle$ is proportional to a constant and the rate expressions given by combining Eqs. S38 and S39 with Eq. S40, a first-order approximation to Eq. S43, and Eq. 6 are

$$k_{a\to b}=\frac{{\mathrm{\Delta }}^2}{\hslash {\left|\mathrm{\Delta }F\right|}_{{\alpha }_{\text{min}}}}\sqrt{\frac{\pi \beta k_{\text{M}}}{2}}\text{exp}\left[-\beta \frac{{\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2}{4E_{\text{R}}}\right],$$ [S44]

$$k_{b\to a}=\frac{{\mathrm{\Delta }}^2}{\hslash {\left|\mathrm{\Delta }F\right|}_{{\alpha }_{\text{min}}}}\sqrt{\frac{\pi \beta k_{\text{M}}}{2}}\text{exp}\left[-\beta \frac{{\left(\mathrm{\Delta }{E}_{ba}-E_{\text{R}}\right)}^2}{4E_{\text{R}}}\right],$$ [S45]

which are in agreement with the known nonadiabatic Marcus rates (87, 107).

Approximate Rate Results Using the Tolman Activation Energy.

The rate expressions given by Eqs. S35 and S36 can also be applied to recover the Marcus rates. In the Marcus limit ($k_1=k_2=k_{\text{M}};{\lambda }_1={\lambda }_2=\lambda ;{\beta }_1={\beta }_2=\beta$), the geometric energy minimum corresponds to the probability maximum and also corresponds to the activation energy derived by Marcus. We will use this isogeometric–unithermal system to validate the Tolman interpretation of activation energy described in the main text by recovering the Marcus transfer rate. In this case, the total reorganization energy of the system is

$$E_{\text{R}}=k_{\text{M}}{\lambda }^2$$ [S46]

and the slope and intercept of the CL are

$$s=1\hspace{1em}\text{and}\hspace{1em}c=-\frac{\mathrm{\Delta }{E}_{ba}}{k_{\text{M}}\lambda }.$$ [S47]

Evaluating the expectation value of the activation energy on the CL gives

$$\begin{array}{c}\langle E_{\text{A}}^{\left(a\right)}\rangle =\frac{1}{2\beta }+\frac{k_{\text{M}}{\left(c-\lambda \right)}^2}{4}\\ =\frac{1}{2\beta }+\frac{{\left(\mathrm{\Delta }{E}_{ba}+k_{\text{M}}{\lambda }^2\right)}^2}{4k_{\text{M}}{\lambda }^2}\\ =\frac{1}{2\beta }+\frac{{\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2}{4E_{\text{R}}}.\end{array}$$ [S48]

The corresponding ET rate from site a to site b is

$$k_{a\to b}\propto \text{exp}\left[-\beta \frac{{\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2}{4E_{\text{R}}}\right].$$ [S49]

The factor ${\left(\mathrm{\Delta }{E}_{ba}+E_{\text{R}}\right)}^2/4E_{\text{R}}$ is the same as that derived by Marcus. Similarly, the activation energy on the $E_b$ surface is

$$\begin{array}{c}\langle E_{\text{A}}^{\left(b\right)}\rangle =\frac{1}{2\beta }+\frac{k_{\text{M}}{\left(c+\lambda \right)}^2}{4}\\ =\frac{1}{2\beta }+\frac{{\left(-\mathrm{\Delta }{E}_{ba}+k_{\text{M}}{\lambda }^2\right)}^2}{4k_{\text{M}}{\lambda }^2}\\ =\frac{1}{2\beta }+\frac{{\left(\mathrm{\Delta }{E}_{ba}-E_{\text{R}}\right)}^2}{4E_{\text{R}}},\end{array}$$ [S50]

which in turn gives the rate

$$k_{b\to a}\propto \text{exp}\left[-\beta \frac{{\left(\mathrm{\Delta }{E}_{ba}-E_{\text{R}}\right)}^2}{4E_{\text{R}}}\right],$$ [S51]

as expected. Thus, the exponential portions of the rate expressions derived using Eqs. 35 and 36 using the Tolman interpretation of the activation energy are in agreement with the Marcus rates for both the $a\to b$ and $b\to a$ transitions.

Comparison of Rates

Shown in Fig. S1 is a comparison between the rates for the $a\to b$ transfer process obtained using the geometrical energy minimum and those predicted using the maximum probability points on the CL with preexponential factors suppressed. At the unithermal limit, the rates are equivalent as expected from the previous analysis of the CL statistics. For bithermal systems, due to the inclusion of multiple states in the statistical evaluation, the rates are always greater than or equal to the rates predicted using the geometrical minimum. The activation of a larger portion of the reactant population will increase the flow from hot oscillator to the cold oscillator, and the movement of these electrons leads to the rate increase. Temperature-dependent activation energies (125) lead to nonlinearity in the slope of the corresponding Arrhenius plot, which is also observed for the shown bithermal systems. At the unithermal point, the slopes given by the geometrical and thermal activation energies are equal, but for ${\beta }_1\ne {\beta }_2$ the slopes, and hence the activation energies, deviate. These results give credence to the application of the Tolman interpretation (114, 115) to adequately describe activation energy in bithermal systems. Nonlinear Arrhenius plots with both convex and concave curvatures (116, 126) have been interpreted as arising from the redistribution of energy in sets of modes, so it is perhaps not surprising that a thermal gradient between modes leads to nonlinear activation energies.