Waltzing route toward double-helix formation in cholesteric shells

Significance

Droplets of chiral liquid crystals, or cholesterics, typically exhibit an intriguing radial defect which results from frustrations in the molecular order. This configuration shows a fascinating analogy to the Dirac monopole, a hypothetical magnetic charge, and plays a crucial role in the droplet optical properties, recently exploited to produce microlasers. Despite its evident interest, the nature of this disclination remains uncertain. We experimentally show, by studying spherical cholesteric shells, that it is composed of two line defects that wrap around each other on a double-helix structure. By tuning the system chirality, we can make this configuration dissociate into two independent stacks of disclination rings. The transition between configurations is reversible and entails an unexpected defect waltz dynamics.

Abstract

Liquid crystals, when confined to a spherical shell, offer fascinating possibilities for producing artificial mesoscopic atoms, which could then self-assemble into materials structured at a nanoscale, such as photonic crystals or metamaterials. The spherical curvature of the shell imposes topological constraints in the molecular ordering of the liquid crystal, resulting in the formation of defects. Controlling the number of defects, that is, the shell valency, and their positions, is a key success factor for the realization of those materials. Liquid crystals with helical cholesteric order offer a promising, yet unexplored way of controlling the shell defect configuration. In this paper, we study cholesteric shells with monovalent and bivalent defect configurations. By bringing together experiments and numerical simulations, we show that the defects appearing in these two configurations have a complex inner structure, as recently reported for simulated droplets. Bivalent shells possess two highly structured defects, which are composed of a number of smaller defect rings that pile up through the shell. Monovalent shells have a single radial defect, which is composed of two nonsingular defect lines that wind around each other in a double-helix structure. The stability of the bivalent configuration against the monovalent one is controlled by c = h/p, where h is the shell thickness and p the cholesteric helical pitch. By playing with the shell geometry, we can trigger the transition between the two configurations. This transition involves a fascinating waltz dynamics, where the two defects come closer while turning around each other.

Liquid crystals offer fascinating possibilities for producing materials that are organized at a mesoscopic scale, such as photonic crystals or metamaterials (1). In a seminal paper, Nelson (2) proposed to induce valency into simple spherical particles by coating their surfaces with a nematic liquid crystal shell. In this elegant approach, the spherical symmetry of the particle is broken by the presence of topological defects, which stem from frustrations in the liquid crystal orientational order due to the curvature of the particle surface. These defects, once functionalized, could act as sticky surface patches inducing directional particle bonding through patch–patch interactions, which would make possible the fabrication of complex materials by spontaneous self-assembly. The number of surface defects would set the valence of the particle, whereas their position would determine the directionality of the eventual bonds. The type of defect configuration in the shell, and thus its valence, results from a very subtle interplay between topological constraints and elastic free-energy minimization. For a two-dimensional nematic shell, theory predicts a tetravalent configuration where four defects are organized in a tetrahedral fashion (3). These defects have a winding number $s_i=1/2$, indicating a π-rotation of $\mathit{n}$, the average molecular orientation, around the defect (4). This is consistent with the Poincaré–Hopf theorem, which states that the total winding number for any spherical nematic must necessarily be ${\displaystyle {\sum }_i{s}_i}=2$ (5–7).

A beautiful experimental realization of Nelson’s ideas has been made by using double emulsions of nematic liquid crystal (8, 9). On the one hand, it has confirmed the existence of the tetrahedral configuration. On the other hand, it has underlined the key role of bulk effects in promoting new defect configurations. Cholesteric liquid crystals, where molecular chirality––lack of mirror symmetry––induces a three-dimensional helical organization in the system, is expected to provide an excellent playground to study the impact of bulk effects in the shell defect configuration. Even at the level of simple droplets, it is well known that molecular chirality can result in intricate defect structures. For instance, when $\mathit{n}$ is tangent to the drop surface, a sufficiently strong chirality induces an interesting monovalent configuration with a single defect that spans the droplet radius (10–12), analogous to a Dirac monopole (13), whereas achiral nematic droplets display a simple bivalent configuration, with two surface defects at opposite poles. However, despite recent numerical simulations showing that the radial defect has a double-helix structure (14), the cholesteric organization and the inner structure of the defects emerging in these droplets remain unclear (11, 14, 15).

In this article, we study monovalent and bivalent cholesteric shells by means of experiments and simulations. We take advantage of the possibility that liquid crystal shells offer, in terms of controlling defect positions, to zoom in on the defect cores and get information about their structures. By bringing together experimental observations and numerical results, we show that (i) bivalent shells possess two highly structured defects, which are composed of smaller disclination rings that pile up through the shell, whereas (ii) monovalent shells possess a radial defect composed of two distinct disclinations that wind around each other in a double-helix fashion. We demonstrate that the defect positions are only controlled by the shell geometry, independently of the cholesteric pitch, and propose a simple model that quantitatively captures this behavior. We also show that the transition between the two configurations is governed by the confinement ratio $c=h/p$, where h is the average shell thickness and p is the cholesteric pitch. Finally, we perform a dynamical study of this transition, and report a fascinating defect waltz where the defects wind around each other due to a chemical Lehmann effect (Fig. 1).

Fig. 1.

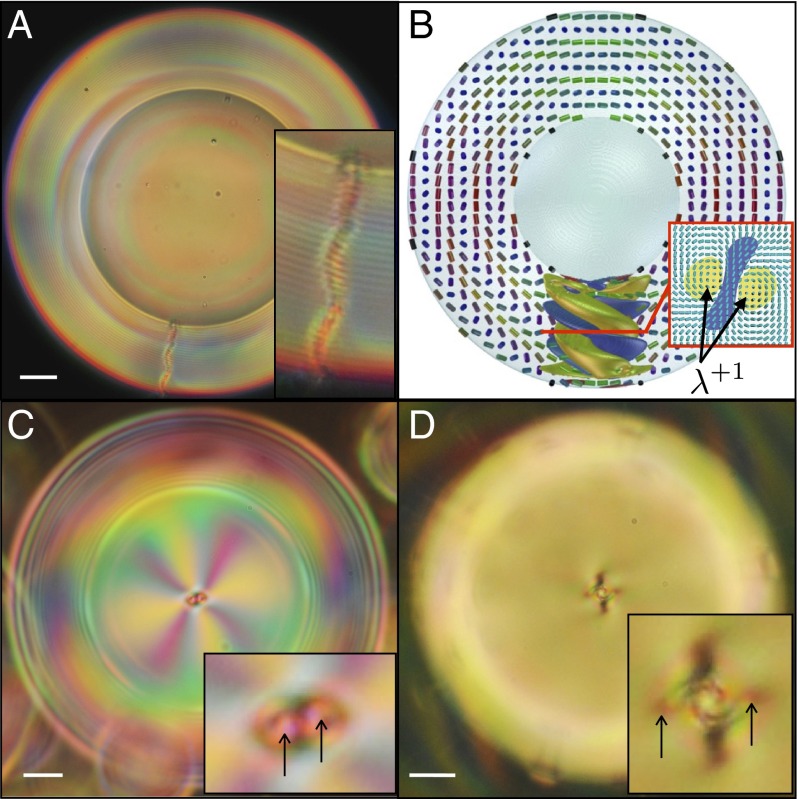
Cross-polarized image of a cholesteric shell (with $p=3.5\hspace{0.17em}\mu \text{m}$) during the formation of a double-helix structure, where two defect lines wind around each other to form a metastable braided structure. (Scale bar, $20\hspace{0.17em}\mu \text{m}$.)

Results and Discussion

Our cholesteric liquid crystal shells are double emulsions produced in an axisymmetric glass capillary device (16). Each shell is composed of an aqueous inner droplet, which is contained inside a bigger liquid crystalline droplet, in turn dispersed in an aqueous environment; see schematics in Fig. 2A. The liquid crystalline phase is composed of a mixture of 4-Cyano-4′-pentylbiphenyl (5CB), which is nematic at room temperature, and a chiral dopant (S)-4-Cyano-4′-(2-methylbutyl)biphenyl (CB15). The cholesteric pitch p is determined by the amount of dopant present in the solution (17). The two aqueous phases contain 1% wt polyvinyl alcohol (PVA) to (i) stabilize the double emulsions against coalescence and (ii) ensure that the liquid crystalline molecules are anchored parallel to the two surfaces confining the shell (18). Typical values of the outer radii, R, range from 50 to $100\hspace{0.17em}\mu \text{m}$. Due to a density mismatch between the inner aqueous phase and the liquid crystalline phase, the inner droplet either sinks or floats inside the liquid crystal. However, the PVA layer at the two interfaces induces a disjoining pressure that prevents contact between the two droplets, resulting in a nonzero minimal thickness denoted $h_0$. Our shells are thus heterogeneous in thickness, with an average thickness $h\equiv R-a$.

Fig. 2.

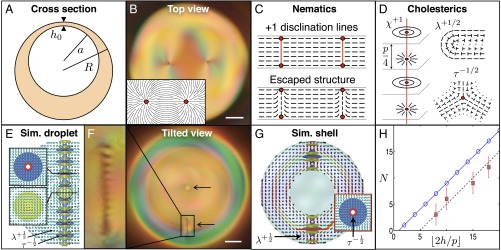
Cholesteric shells with bivalent defect structure. (A) Schematics showing the geometry of experimental shells. (B) Top view of a bivalent experimental cholesteric shell showing its two outer surface defects. (Inset) Sketch of the director field around those defects. (C) Planar and escaped structures of +1 disclinations in nematics. (D) ${\chi }^{+1}$-, ${\lambda }^{+1/2}$-, and ${\tau }^{-1/2}$-disclinations in cholesterics. The nails represent an out-of-plane director field, where the nail heads indicate the extremity pointing upwardly. (E) Simulated cholesteric droplet with diametrical spherical structure (DSS). Reproduced from ref. 14. (F) Tilted view of a bivalent experimental cholesteric shell, where the position of the defects is indicated by arrows and the inner structure of one of the two defects is zoomed in on. (G) Simulated cholesteric shell with DSS. (H) Number of disclination rings as a function of $\lfloor 2h/p\rfloor$ in a DSS structure, from numerical predictions (blue) and observations (red). B and F are cross-polarized images. (Scale bar, $20\hspace{0.17em}\mu \text{m}$.)

The type of defect structure in the produced shells depends on the cholesteric pitch. Here, we focus on two types of shells: monovalent shells, characterized by one defect, and bivalent shells, characterized by two defects.

Bivalent Shells.

Bivalent cholesteric shells appear when chirality is low. They possess two $+1$ surface defects at each of the shell boundaries, so that the total winding number on each sphere is $+2$, consistent with the topological requirements (5, 6). These defects appear close to each other, as imaged in Fig. 2B, which is a cross-polarized picture of the top of the shell. A similar configuration appears on the inner sphere. The director field around either pair of surface defects is sketched in Fig. 2B (Inset). Keeping this type of in-plane director field through the shell thickness would imply the formation of two $+1$ defect lines or disclinations spanning the shell. However, the liquid crystalline structure is free to evolve between the boundaries to minimize its free energy. In nematic shells, the bulk elastic energy associated with $+1$ disclinations is released by allowing $\mathit{n}$ to escape into the third dimension, as schematically represented in Fig. 2C, which shows a local cross-section of a nematic shell made by a plane containing the defects (19). In contrast, three types of disclinations are allowed by the symmetry of cholesterics: χ, τ, and λ (20). The χ- and τ-lines are singular in the sense that their cores correspond to a discontinuity in the order parameter, whereas λ-lines have no singular core. To investigate the bulk structure of the $+1$ defects appearing in our cholesteric shells, we induce a slight rotation in the double emulsions by gently moving the sample, which allows us to obtain a side view of the shell (Fig. 2F). Instead of a smooth optical texture (escaped structure) or a solid line (singular disclination), we observe an alternation of bright and dark parallel short lines when imaging the sample between cross-polarizers. This texture, zoomed in on in Fig. 2F (Left) remains unaltered after a rotation of the sample, or when removing the polarizers from the optical path, revealing the existence of a sequence of singular bulk defect cores. Our images show a close resemblance with simulated polarization micrographs recently reported for cholesteric droplets with diametrical spherical structure (DSS) (14). These droplets have a diametrical defect with a highly structured core, in which a number of ${\tau }^{-1/2}$-disclination rings pile up, while keeping certain separation distance, to form a structure that spans the whole droplet diameter, as shown in Fig. 2E, where the rings are represented in red.

We perform numerical simulations by using the Landau–de Gennes free-energy modeling (Material and Methods) to investigate the existence of the DSS in shells. We consider a simple geometry where the two spheres delimiting the shell are concentric. We find that all of the configurations reported for droplets in ref. 14 also appear in shells, in particular the DSS, which is shown in Fig. 2G. However, in the shell geometry, the diametrical defect is truncated by the inner sphere, producing two independent defects, as we observe in our experiments. In both Fig. 2 E and G, the cylinders represent the director field. The defects can be identified by the blue and yellow isosurfaces, which indicate the regions of large splay and bend deformations, respectively. The singular rings, represented in red, are surrounded by regions of large splay elastic deformation (Fig. 2 E and G, Insets). The structure of rings is periodically repeated along the defect, leading to an optical texture of alternating bright and dark spots and two $+1$ surface defects at the boundaries, in agreement with our experiments. The total number of singular rings in the defect is given by $N=\lfloor 2l/p\rfloor -1$, where $\lfloor \rfloor$ denotes the integer part and l is the length scale of the system (14), that is, $l=R$ in droplet and $l=h$ in a shell. To compare the structure that we observe experimentally with the simulated one, we count the number of rings N in four bivalent shells with different $h/p$ and plot it as a function of $\lfloor 2h/p\rfloor$ (Fig. 2H). We find the same tendency as in simulations, apart from an offset. We attribute this offset to the fact that the experimental shells are heterogeneous in thickness, and thus, the average shell thickness, $h\equiv R-a$, is not the real shell thickness at the defect sites, $h_{def}$. Actually, in our shells, h is typically larger than $h_{def}$, because defects have a tendency to regroup in the thinnest part of the shell (9), which explains the shift of the experimental curve toward larger values of $\lfloor 2h/p\rfloor$. All these results suggest that the observed structure indeed corresponds to the numerically predicted one.

Monovalent Shells.

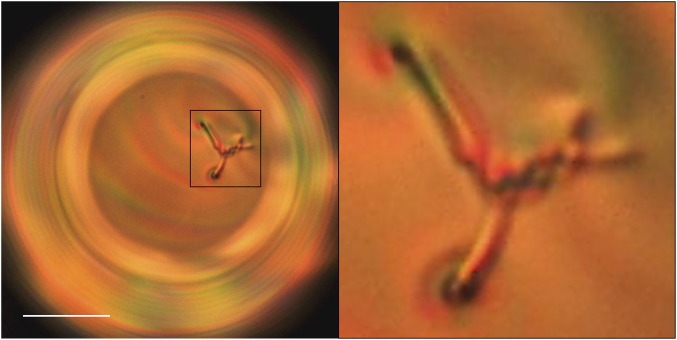
Monovalent cholesteric shells appear at higher chirality. They display an optical texture that is reminiscent of the spherulitic or Frank-Pryce texture (Fig. 3A), widely reported for droplets (11). This configuration is characterized by a radial defect of charge $+2$. Although initially considered as a singular disclination, the nature of this radial defect is still an open question (11, 14, 21). Recent numerical studies on cholesteric droplets have actually suggested that it is a nonsingular defect with double-helix structure (14). Our simulations in a shell-like geometry lead to the same conclusion, as shown in Fig. 3A, where the yellow isosurfaces correspond to two ${\lambda }^{+1}$-disclinations winding around each other. The ends of the ${\lambda }^{+1}$-lines produce two pairs of close $+1$ surface defects at the bounding spheres. Remarkably, experiments on shells seem to reveal the existence of such an intricate structure. Fig. 3C shows a top view of an experimental monovalent shell. The eight color brushes (pink and yellow) emerging from the center of the shell indicate a global topological charge of $+2$. However, a close view of the central defect (Fig. 3C, Inset) reveals that it is actually composed of two $+1$ surface defects. Interestingly, the distance between the two surface defects becomes larger with p. By making this distance sufficiently large, we are able to optically distinguish two lines winding around each other (Fig. 3D). Note that although ${\lambda }^{+1}$-lines are not singular, they provoke a strong distortion in the nearby director field, which explains why we see micrometer-thick lines under the microscope (22). By playing with the focal plane, we can see that the two lines keep winding around each other deeper down the shell. These experimental results are in accordance with the numerical simulations, supporting the idea that the radial defect is indeed composed of two distinct disclinations organized in a double helix structure.

Fig. 3.

Cholesteric shells with monovalent defect structure. (A, C, and D) Cross-polarized images of experimental shells with different helical pitch p: 2.7, 3.5, and $9.3\hspace{0.17em}\mu \text{m}$, respectively. (Scale bar, $20\hspace{0.17em}\mu \text{m}$.) A is a side view of the shell, showing a radial defect spanning the shell, whereas B and C are top views of the shell, showing the two disclinations composing the radial defect. The arrows point to the ends of the disclinations, which wind around each other deeper down the shell. (B) Simulated cholesteric shell with radial spherical structure (RSS).

Controlling the Number and Position of Defects.

The results mentioned above strongly suggest that the cholesteric pitch, p, has a determinant role in the type of defect configuration displayed by the shell. To find the exact parameters controlling the type of defect configuration in the shell, we consider all of the relevant length scales of our system, which are p, R, and h. We can assume that the minimum thickness of the shell, $h_0$, is the same for all of the shells. This assumption seems reasonable because $h_0$ is a small distance that results from the disjoining pressure appearing when the PVA layers coating the inner and outer droplets of the double emulsion get very close. Experimental measurements of $h_0$ indicate that this value is at the limit of resolution of the optical microscope, that is, $\sim 1\hspace{0.17em}\mu \text{m}$. Therefore, we investigate the effect of $h/R$ and $p/R$, which are the two dimensionless parameters that can be built if R is chosen as reference length scale.

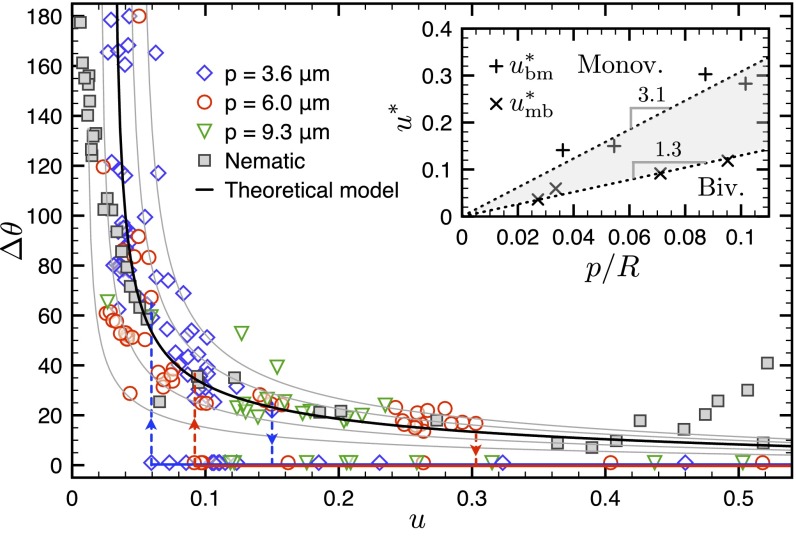
We characterize the type of defect configuration by the parameter $\mathrm{\Delta }\theta$, which is the angular distance between defects at the outermost surface of the shell. Positive values of $\mathrm{\Delta }\theta$ correspond to bivalent shells, where the two defects are separated by a certain nonzero angular distance, whereas $\mathrm{\Delta }\theta =0$ is ascribed to monovalent shells, where we consider that the two defects are fused into a single entity. We first plot $\mathrm{\Delta }\theta$ as a function of $u=h/R$ for different values of the cholesteric pitch (Fig. 4). Each point on this plot refers to a different shell, at equilibrium, with its specific geometry. Different symbols/colors correspond to different values of p, namely 9.3, 6, and 3.6 $\mu \text{m}$. The nematic case, corresponding to $p\to \infty$, is also included in the plot and represented by filled squares (9). Because $h_0$ is a constant, u is a measure of the shell thickness gradient: $u=\left(h_0+h_{\text{max}}\right)/2R$, where $h_{\text{max}}$ is the larger local thickness of the shell. For the shells considered in Fig. 4, $h_{\text{max}}$ varies between $1\hspace{0.17em}\mu \text{m}$ for low u values, and $100\hspace{0.17em}\mu \text{m}$ for high u values.

Fig. 4.

Evolution of $\mathrm{\Delta }\theta$ as a function of $u=h/R$ for different cholesteric mixtures of 5CB and CB15. Each point corresponds to a different experimental shell with a given geometry u, and each symbol/color corresponds to a different value of p (p = 9.3, 6, or 3.6 $\mu \text{m}$). The data for $p\to \infty$ (nematic) have been taken from ref. 9. The solid lines represent the theoretical curves, for different values of the minimal shell thickness $h_0$, obtained from solving $f=0$ in Eq. 1. The dashed lines containing down arrows indicate the critical values of u, denoted $u_{\text{bm}}\ast$, above which no bivalent shells are found. The dashed lines containing up arrows indicate the critical values of u, denoted $u_{\text{bm}}\ast$, below which no monovalent shells are found. To facilitate the reading of the image, we have plotted these lines only for the blue and red symbols. (Inset) Evolution of $u_{\text{bm}}\ast$ and $u_{\text{bm}}\ast$ as a function of $p/R$. The gray region corresponds to the zone where the two configurations coexist.

As a general trend, we observe that $\mathrm{\Delta }\theta$ decreases when increasing u, first rapidly and then slowly. This tendency is the same for all of the values of p, including $p\to \infty$, which indicates that in bivalent shells, the angular distance between defects only depends on the geometry of the shell. Interestingly, we observe that above a certain critical value $u_{\text{bm}}^{\ast }$, which depends on p, $\mathrm{\Delta }\theta$ drops to zero. This corresponds to the experimental fact that, above $u_{\text{bm}}^{\ast }$, we do not observe any shell with bivalent configuration. Conversely, below a critical value $u_{\text{mb}}^{\ast }$, which is smaller than $u_{\text{bm}}^{\ast }$ and also dependent on p, the monovalent configuration disappears. The discontinuity in $\mathrm{\Delta }\theta$ is represented by descending and ascending dashed lines in Fig. 4. If we now plot the critical values $u_{\text{bm}}^{\ast }$ and $u_{\text{mb}}^{\ast }$ as a function of the second dimensionless parameter, $p/R$, we observe a linear behavior, as shown in Fig. 4 (Inset). The slopes of these curves set two critical values of the confinement ratio, defined as $c=h/p$, at which discontinuous transitions between configurations are expected. Those values are $c_{\text{bm}}=3.1$ for the bivalent–monovalent transition, and $c_{\text{mb}}=1.3$ for the monovalent–bivalent transition, indicating the existence of hysteresis. From these results, we conclude that the transition between the bivalent and monovalent configurations is controlled by c. The regions of exclusive existence of each of the configurations, as well as the zone of coexistence, are indicated in Fig. 4 (Inset).

The above-mentioned continuous decrease of $\mathrm{\Delta }\theta$ as a function of u has also been observed in previous experimental (9) and numerical (23) works dealing with bivalent nematic shells. The equilibrium value of $\mathrm{\Delta }\theta$ has been thought to result from the balance of two opposing forces: (i) a repulsive defect interaction of elastic nature and (ii) an attractive force due to the shell thickness gradient, which tends to bring the defects to the thinnest part of the shell. To test this hypothesis with our experimental results, we develop a simple model that allows us to obtain an estimative expression of these forces. Because $\mathrm{\Delta }\theta$ seems to be independent of the nematic or cholesteric nature of the system (Fig. 4), we ignore the details of the molecular ordering in the system and consider the global cholesteric arrangement in the shell as a superposition of two-dimensional nematic layers. Actually, the value of p measured in experimental and simulated bivalent shells is very close to the spontaneous pitch of the liquid crystal, revealing a sort of layer organization in the shell (14). Although this approach means a great simplification of the problem, it captures its underlying physics, as shown thereafter.

We start from the surface energy $E_{/\text{u}.\text{l}.}$ associated with two +1 defects interacting on a sphere of radius R (2). For small angles $\mathrm{\Delta }\theta$, it becomes $E_{/\text{u}.\text{l}.}=2E_0-2\pi K\log \left(\theta /\sqrt{2}\right)$, where K is the single elastic constant, $2\theta =\mathrm{\Delta }\theta$, $E_0=\pi K\log \left(R/r_{\text{c}}\right)$ is the energy per unit length of each defect, and $r_{\text{c}}$ is the radius of the defect core (2, 3). We take $r_{\text{c}}\simeq 0.01R$, corresponding to the average thickness of the DSS lines that we measured ($\simeq 1\hspace{0.17em}\mu \text{m}$). At the first level of approximation, we write the integrated free energy of the eccentric shell as $E=E_{/\text{u}.\text{l}.}h\left(\theta ,u\right)$, where $h\left(\theta ,u\right)$ is the length of the defect lines calculated by a conformal mapping technique for nonconcentric shells (23). The latter technique uses an electrostatic analogy to map the equipotential lines to the inner and outer surfaces of the shell, and the electric field to the defect lines. We find that at small angles θ, $h\left(\theta ,u\right)=h_0+g\left(u\right)\hspace{0.17em}{\theta }^2/2+\text{o}\left({\theta }^2\right)$, where g is a function of u only. The force f between defect lines, derived from the free energy through $f=-{\partial }_{\theta }E/R$, then reads

$$f=\frac{2\pi K}{R}\left[\frac{h_0}{\theta }+\frac{g\left(u\right)\hspace{0.17em}\theta }{2}\left(1+2\log \left(\frac{\theta }{\sqrt{2}}\right)-\frac{2E_0}{\pi K}\right)\right].$$ [1]

The equilibrium position of the disclination lines is thus obtained by solving $f=0$, which yields $\mathrm{\Delta }{\theta }_{\text{th}}=F\left(u,h_0\right)$. Fig. 4 displays the obtained $\mathrm{\Delta }{\theta }_{\text{th}}$ as a function of u for different values of $h_0$, ranging from 0.01R to 0.05R (solid lines). We obtain a very good agreement with the experimental data for $h_0=0.03R\simeq 2\hspace{0.17em}\mu \text{m}$, which is a reasonable value for our system. The very good agreement between the experimental data and our model, together with the reasonable values obtained for the fitting parameter, shows that our simple approach captures the physics controlling the position of defects in bivalent experimental shells.

Transitions Between Configurations.

Finally, we take advantage of the fine control that we can achieve on u to force the transition between the monovalent and bivalent defect configurations. We consider a shell that initially has a bivalent defect configuration (Fig. 5A) where the two $+1$ outer surface defects are clearly visible. Then, we add an aqueous solution of CaCl₂ to the outer phase, which imposes a difference in osmotic pressure between the inner droplet and the outer continuous phase. Because the 5CB–CB15 mixture is slightly permeable to water, it acts as a membrane that allows the inner droplet to deswell. In this way, the inner radius of the shell a progressively decreases, and therefore u increases (10). We calculate the typical ratio of the viscous to elastic forces, namely the Ericksen number $Er=\eta vL/K$, associated with this deswelling experiment. In our case, η and K are, respectively, the viscosity and average elastic constant of the 5CB–CB15 mixture, $v\sim \mathrm{\Delta }h/\mathrm{\Delta }t$ is the fluid velocity, where $\mathrm{\Delta }h$ is the typical thickness variation over the time of the experiment $\mathrm{\Delta }t$, and $L\sim \mathrm{\Delta }h$ is the relevant length scale of the system. We find that $Er\simeq {10}^{-4}$, showing that our experiment can be considered as quasi-static. The continuous variation of u during the experiment has an impact on the shell defect configuration. As u increases, the two defects get progressively closer, as shown in the sequence of images of Fig. 5. Interestingly, the defects do not approach each other by following the shorter path––a geodesic––but by turning around each other (Movie S1). This fascinating defect waltz leads to the trajectories plotted in Fig. 5E, where each defect is represented by a different symbol and the progressive color variation indicates temporal evolution. Eventually, at a certain critical angular distance $\mathrm{\Delta }{\theta }_{\text{crit}}$, the two defects jump together toward the center of the shell and assemble to form a single defect of total winding number $+2$ (Fig. 5D). In rare cases, the system can get trapped in intermediate metastable states (Fig. 1), which allows us to get information on the structure of the $+2$ defect during its formation. The dynamics of the transition, where the two defects rotate around each other, together with the braided metastable structures that we observe, suggests that the final defect has a double-helix structure, as our numerical simulations suggest. Remarkably, the transition between the bivalent and monovalent defect configurations turns out to be reversible. When salt is added to the inner phase, so that the inner droplet swells and u progressively decreases, we observe that the $+2$ defect splits out into two independent $+1$ defects, which subsequently move away from each other by following the same type of waltz dynamics mentioned above.

Fig. 5.

Dynamical transition from a bivalent shell into a monovalent shell. (A–D) Top-view pictures of the shell taken during the transition. In this experiment, the disclinations are located at the bottom of the shell, where it is thinnest. (E) Renormalized trajectories of the outer surface defects obtained from plotting $Y_{\text{def}}=\left(y_{\text{def}}-y_{\text{cent}}\right)/R_{\text{init}}$ versus $X_{\text{def}}=\left(x_{\text{def}}-x_{\text{cent}}\right)/R_{\text{init}}$, where $R_{\text{init}}$ and $\left(x_{\text{cent}},y_{\text{cent}}\right)$, respectively, designate the initial outer radius and the $\left(x,y\right)$ coordinates of the center of mass of the trajectory. The progressive color variation indicates the temporal evolution of the system, from the beginning (blue) to the end (red) of the deswelling experiment. Each symbol––star or square––is associated with one defect. (A–D) Cross-polarized images. (Scale bar, $20\hspace{0.17em}\mu \text{m}$.)

The intricate rotational dynamics of the transition seems to be related to the chiral nature of our liquid crystal. A natural explanation for this rotation could be the so-called Lehmann effect (19, 24), and more specifically, its overlooked chemical version (25, 26). According to the latter, a current of matter, $\mathit{J}$, in the direction of the cholesteric helix can provoke a rotation of the director field. Due to the absence of mirror symmetry of the molecules, the current induces a torque $\mathbf{\Gamma }$ on the liquid crystal molecules, resulting in a global rotation of the director field. The torque is linearly related to the current through $\mathbf{\Gamma }=-\nu \mathit{J}$, where ν is called the Lehmann coefficient. In our geometry, the outward current $\mathit{J}$ of water molecules, which diffuse through the liquid crystal, is quasi-radial and directed along the helical axis, and therefore might lead to a Lehmann effect. To test this hypothesis, we compare the direction of rotation of the liquid crystal in swelling and deswelling experiments, where J has opposite signs. Consistently with a Lehmann effect, we observe that changing the sign of J provokes a change in the direction of rotation of the liquid crystal. In addition, we always find that $\mathbf{\Gamma }\cdot \mathit{J}>0$ (Fig. 5E), which is expected for a right-handed cholesteric liquid crystal, where $\nu <0$. Chirality therefore induces one main effect in the dynamics, namely the winding trajectory of the defects, clearly visible in Fig. 5E.

Conclusions

We have investigated cholesteric shells displaying bivalent and monovalent configurations. Our experiments were performed along with numerical simulations to reveal the intricacy of the observed defect textures. Our results suggest that bivalent shells are characterized by two highly structured defects, each of them composed of several disclination rings that pile up through the shell, whereas monovalent shells display a radial defect composed by two close disclination lines that wind around each other in a double-helix fashion. The stability of the bivalent configuration against the monovalent one is controlled by $c=h/p$, that is, the number of helical turns that can be accommodated in the shell thickness. The position of the defects in the bivalent configuration is controlled by the shell thickness gradient, which is well captured by a simple theoretical model. We have also shown that by continuously varying the shell geometry, it is possible to induce a transition between the two configurations. The transition involves a fascinating waltz dynamics, which seems to stem from a chemical Lehmann effect.

Our study on monovalent and bivalent cholesteric shells has highlighted the complexity of cholesteric structures in shell-like geometries. This complexity disappears at infinitely high cholesteric pitch, that is, in the nematic limit, where other types of defects have been reported (8, 9). Future research might consider cholesteric shells with very large helical pitch, because they are expected to display novel defect configurations, hybrid between those observed in nematics and highly chiral cholesterics (27).

Materials and Methods

Simulations were performed using the Landau–de Gennes (LdG) free-energy minimization on a finite-difference grid. As in the previous simulations in droplets (14), the following LdG free energy for the tensorial order parameter $Q_{ij}$ is used:

$$\begin{array}{c}F={\displaystyle {\int }_{bulk}\left\{\frac{A}{2}{Q}_{ij}{Q}_{ji}+\frac{B}{3}{Q}_{ij}{Q}_{jk}{Q}_{ki}+\frac{C}{4}{\left(Q_{ij}{Q}_{ji}\right)}^2\right\}\text{d}V}\\ +{\displaystyle {\int }_{bulk}\left\{\frac{L}{2}{Q}_{ij,k}{Q}_{ji,k}+2q_{0}L{\mathit{ϵ}}_{ikl}{Q}_{ij}{Q}_{lj,k}\right\}\text{d}V}\\ +{\displaystyle {\int }_{surface}\left\{\frac{W}{2}{\left({\tilde{Q}}_{ij}-{\tilde{Q}}_{ij}^{\perp }\right)}^2\right\}\text{d}S.}\end{array}$$

The first two contributions account for the phase transition and bulk elasticity, whereas the last one ensures planar degenerate anchoring. The auxiliary tensors ${\tilde{Q}}_{ij}$ and ${\tilde{Q}}_{ij}^{\perp }$, respectively, denote the Q tensor with added trace and its projection to the surface, as defined by Fournier and Galatola (28), and $q_0=2\pi /p$ is the intrinsic wave number of the cholesteric pitch.