Abstract
Multiple comparisons or multiple testing has been viewed as a thorny issue in genetic association studies aiming to detect disease-associated genetic variants from a large number of genotyped variants. We alleviate the problem of multiple comparisons by proposing a hierarchical modeling approach that is fundamentally different from the existing methods. The proposed hierarchical models simultaneously fit as many variables as possible and shrink unimportant effects towards zero. Thus, the hierarchical models yield more efficient estimates of parameters than the traditional methods that analyze genetic variants separately, and also coherently address the multiple comparisons problem due to largely reducing the effective number of genetic effects and the number of statistically ‘significant’ effects. We develop a method for computing the effective number of genetic effects in hierarchical generalized linear models, and propose a new adjustment for multiple comparisons, the hierarchical Bonferroni correction, based on the effective number of genetic effects. Our approach not only increases the power to detect disease-associated variants but also controls the Type I error. We illustrate and evaluate our method with real and simulated data sets from genetic association studies. The method has been implemented in our freely available R package BhGLM (http://www.ssg.uab.edu/bhglm/).
Keywords: Bayesian inference, Effective number of parameters, Effective number of hypothesis tests, Generalized linear models, Genetic association studies, Hierarchical modeling, Hierarchical Bonferroni correction, Multiple comparisons
Introduction
Genetic association studies usually genotype many genetic variants in candidate genes or across the entire genome, from which researchers want to identify disease-associated variants and characterize their genetic effects. Statistical analysis of genetic association data needs to estimate many effects and test many hypotheses, and thus requires multiple comparisons adjustments (Balding 2006; Rice et al. 2008). The main multiple comparisons problem is that the false positives or the Type I error rate increases with each additional test. This can be a serious concern in large-scale genetic association studies, because the genome includes a huge number of polymorphic variants and the genetic architecture of a disease or complex trait is unknown, and thus any variant is highly unlikely to be causally associated with any given phenotype (Balding 2006). Therefore, an appropriate adjustment for multiple testing plays a crucial role in avoiding a flood of false-positive claims or true associations being missed.
Various strategies have been proposed to address the multiple comparisons problem (Hsu 1996; Rice et al. 2008). A class of approaches to the problem is designed to control the family-wise error rate (i.e., the probability of making one or more false discoveries, or Type I error, among a family of hypotheses), mainly including the Bonferroni correction, the sequential Bonferroni procedure (Holm 1979), and the methods of Hochberg (Hochberg 1988) and Hommel (Hommel 1988). These methods adjust the overall significance level or equivalently the p-values based on the total number of tests being performed. The Bonferroni correction is one of the most basic and historically most popular methods, in which the adjusted significance level is calculated as the usual significance level divided by the number of tests, or equivalently the original p-values are multiplied by the number of tests to yield the working p-values. Another class of approaches focuses not on reducing the family-wise error rate but instead on controlling the expected proportion of false positives, the “false discovery rate” or FDR (Benjamini and Hochberg 1995; Benjamini and Yekutieli 2001).
The above general approaches have been applied or modified to genetic association studies (Sabatti et al. 2003; Benjamini and Yekutieli 2005; Roeder et al. 2007; Rice et al. 2008; Kang et al. 2009). Recently, geneticists have proposed special methods that take advantage of the relationship between markers (e.g., linkage disequilibrium) to define the effective number of independent tests and then adjust the original p-values using the Bonferroni correction (Gao et al. 2008; Galwey 2009; Gao et al. 2010). These methods are conceptually attractive, but may not be valid in complicated situations, for example, testing epistatic interactions and low-frequency or rare variants for which linkage disequilibrium is expect to be low.
Our approach, as described in this article, has fundamental differences from the existing methods. We simultaneously deal with the main issues that underlie the multiple comparisons problem: many parameters, many hypothesis tests and uncertainty about parameter estimates (If we knew the true effects, we wouldn’t be making any probabilistic statements). We propose hierarchical generalized linear models to simultaneously fit as many variables as possible and to account for the relationship between the variables. Thus, our hierarchical models yield more reliable estimates of parameters than the traditional methods that analyze genetic variants separately. Our hierarchical modeling can shrink many unimportant effects toward zero and largely reduce the effective number of parameters, and thus coherently address the multiple comparisons problem. We develop a method for computing the effective number of genetic effects in hierarchical generalized linear models and construct a new adjustment for multiple comparisons, the hierarchical Bonferroni correction, based on the effective number of genetic effects. Our approach is fully general, applicable to not only genetic association studies involving common variants, rare variants and epistatic interactions but also other disciplines.
The rest of the paper is organized as follows. We first introduce hierarchical generalized linear models for genetic association studies. We then describe our method for calculating the effective number of genetic effects and constructing our hierarchical Bonferroni procedure. We briefly describe our freely available R package BhGLM that has implemented the proposed method. We illustrate our approach with two real data sets, the sequencing data from Dallas Heart Study and a case-control study of adiponectin genes and colorectal cancer. Finally, we conclude and discuss potential extensions.
Methods
Generalized Linear Models (GLMs)
We consider generalized linear models with a large number of coefficients or highly correlated genetic variables constructed from the genotypes of common or rare genetic variants (e.g., single nucleotide polymorphisms (SNPs)). The observed values of a continuous or discrete response are denoted by y = (y1, ···, yn). We assume that the genetic predictor variables can be organized into K groups, Gk, k = 1, ···, K, and the k-th group Gk contains Jk variables, where K ≥ 1 and Jk > 1. In genetic association studies, the groups can be constructed based on candidate genes in which the variants are located and the types of the genetic effects (e.g., additive and dominance effects, and interactions). As discussed later, this hierarchical structure will be incorporated into our hierarchical framework to more efficiently estimate genetic effects. If the group information is not available, our method treats all the predictors as ungrouped variables or a single group and also can jointly estimate the coefficients. We assume that relevant non-genetic variables (e.g., gender indicator, age, etc.) are also measured for each individual and will be included as ungrouped covariates in the model to control for possible confounding effects.
The generalized linear model relates the linear predictor to the mean of the response variable via a link function (McCullagh and Nelder 1989; Gelman et al. 2003),
| (1) |
where h is a link function, n is the number of individuals, β0 is the intercept, and represent observed values of covariates and genetic variables, respectively, the coefficients and are non-genetic and genetic effects, respectively, the notation j ∈ Gk indicates the group of variable j, Xi contains all variables, and β is a vector of all the coefficients and the intercept. For simplicity, we denote Xi = (1, xi1, ···, xiJ) and β =(β0, β1, ···, βJ)′, where is the total number of variables.
The data distribution can be expressed as
| (2) |
where the distribution p(yi | Xi β, ϕ) can take various forms, including Normal, Gamma, Binomial, and Poisson distributions, and ϕ is a dispersion parameter. Some GLMs, for example the Poisson and binomial distributions, do not require a dispersion parameter; that is, ϕ is fixed at 1.
The standard algorithm for fitting GLMs is the iterative weighted least squares (IWLS) (McCullagh and Nelder 1989; Gelman et al. 2003). Given the current estimates of the parameters (β̂,ϕ̂), the IWLS algorithm constructs the pseudo-response zi and the pseudo-weight wi for each data point yi:
| (3) |
and approximates the likelihood p(yi | Xiβ, ϕ) by the weighted normal likelihood:
| (4) |
where η̂i = Xiβ̂, L(yi | η̂i) = log p(yi | Xi β̂, ϕ =1), L′ (yi | ηi) = dL(yi | ηi) / dηi, and L″(yi | ηi) =d2L(yi | ηi) / dηi2. The parameters (β, ϕ) are then updated by solving the normal linear regression (4) using the weighted least squares. For normal linear regressions, we have zi = yi and wi = 1, and thus the iterative procedure is not required.
Hierarchical Modeling
Generalized linear models with many coefficients or highly correlated variables can be nonidentifiable classically. An approach to overcoming the problem is to use Bayesian inference. We use a hierarchical framework to construct priors for coefficients. At the first level, we assume an independent normal distribution with mean 0 and variable-specific variance for each coefficient βj:
| (5) |
For the intercept β0 and the dispersion parameter ϕ, we can use any reasonable non-informative prior distributions; for example, with set to a large value, and p(logϕ) ∝ 1.
Given the prior variances , the conditional posterior of β can be approximated by the multivariate normal distribution N(β̂, Var(β̂)), where , and zi and wi are the pseudo-response and the pseudo-weight, respectively. Therefore, the coefficients β can be updated by β̂ (Gelman et al. 2003; Gelman et al. 2008; Yi and Banerjee 2009; Yi et al. 2011b; Yi and Zhi 2011). If the prior variances of some coefficients equal zero, , the coefficients are exactly shrunk to zero. The coefficients with zero prior variance should be removed to avoid infinites in the calculation of β̂ and Vβ. An alternative solution to avoid the problem of this extreme is to replace the zero variance by a very small positive value, say 10−10, and then apply the augmented regression to jointly update all coefficients β. Since the prior βj ~ N(0,10−10) can shrink βj very close to zero, this method can produce estimates that are essentially identical to those from the extreme.
If a dispersion parameter, ϕ, is present, we can update ϕ by . The resulting estimate β̂ is well defined and has finite variance, even if the original data are high-dimensional and have collinearity or separation that would result in nonidentifiability of the classical maximum likelihood estimate (Gelman et al. 2008).
The variance parameters, , j =1, ···, J, directly control the amount of shrinkage in the coefficient estimates and thus the model complexity; if , the coefficient βj is shrunk to zero and is essentially removed from the model, contributing zero degree of freedom to the model, and if , there is no shrinkage and thus βj contributes one degree of freedom. Although these variances are not the parameters of interest, they are useful intermediate quantities to estimate for fitting the proposed hierarchical GLMs and for calculating degrees of freedom. We treat the variances as unknowns and further assign prior distributions to these variances as described in Appendix A. Our prior distributions can include group-specific and variable-specific parameters. The group-specific parameters provide a way to pool the information among variables within a group, while the variable-specific parameters allow different shrinkage for different variables. This would allow us to obtain more reliable estimates of parameters (Yi et al. 2011b; Yi and Ma 2012). However, the proposed method for calculating the effective number of genetic effects can be applied to hierarchical GLMs with various other priors on the variances.
The full computation of the hierarchical GLMs is the EM-IWLS algorithm that incorporates an expectation-maximization (EM) algorithm into the above IWLS procedure by treating the unknown variances and the hyperparameters in the priors of as missing data and updating the parameters (β, ϕ) by averaging over the missing data at each iteration (Yi and Ma 2012). At convergence of the EM-IWLS algorithm, we obtain the latest estimates (β̂, ϕ̂) and the covariance matrix Var(β̂). As in the classical framework, the p-values for testing the hypotheses H0 : βj =0 can be calculated using the statistic , which approximately follows a standard normal distribution or a Student-t distribution with n degrees of freedom, if the dispersion ϕ is not or in the model, respectively. We describe the EM-IWLS algorithm in Appendix A.
Effective Number of Genetic Effects
The complexity of a Bayesian hierarchical model is measured by the effective number of parameters or degrees of freedom, which is generally defined as the posterior mean of deviance minus the deviance evaluated at the posterior mean or mode (Spiegelhalter et al. 2002; Gelman et al. 2003):
| (6) |
where θ includes all parameters, D (θ) = −2log{p(y | θ)}, D̄(θ) is the posterior mean of D(θ) averaging over the posterior distribution of θ, and θ̂ is the posterior mean or mode of θ. The effective number of parameters can be generally calculated using posterior simulations (Spiegelhalter et al. 2002; Gelman et al. 2003). However, we here approximately estimate the effective number of any subset of parameters conditional on the estimates of all other parameters from the EM-IWLS algorithm (Spiegelhalter et al. 2002; Gelman et al. 2003).
As discussed earlier, the generalized linear likelihood p(y | θ) is approximated by the weighted normal likelihood N(z | Xβ, Σzϕ), and thus the standardized deviance can be expressed as . To calculate the effective number of genetic effects, we take expectation of D with respect to the conditional posterior distribution of genetic effects p(βg | β0, βc, ϕ, τ2), where βg is a vector of all genetic effects , βc is a vector of all non-genetic effects , and τ2 is a vector of all variances . The conditional posterior distribution p(βg | β0, βc, ϕ, τ2) can be approximated by a multivariate normal with mean β̂g and covariance , where Xg is the design matrix of βg, , and Σβg is a diagonal matrix containing variances of genetic effects. Therefore, we obtain and thus the effective number of genetic effects
| (7) |
where is the total number of genetic effects (the row number of Vg). This expression can be simply modified to calculate the effective number of any subset of coefficients (for example, the genetic effects of the k-th group). We also can similarly derive the effective number of coefficients as , where (J + 1) is the total number of coefficients, , and (Spiegelhalter et al. 2002; Gelman et al. 2003).
From the above expression, we can see that 0 ≤ ρ ≤ Jg and thus is a measure of the reduction of the number of parameters due to shrinkage. The reduction term depends on the variances , which directly control the amount of shrinkage in the coefficient estimates. We can derive that ρ = Jg if , and ρ =0 if .
The Effective Number of Tests and Hierarchical Bonferroni Correction for Multiple Comparisons
There are at least two reasons that we have to deal with multiple comparisons issues: 1) we have uncertainty about estimates of parameters, and 2) we have to test a large number of hypotheses. Traditional methods that independently fit genetic variables in essence use only the information in each variant and thus are unlikely to precisely estimate genetic effects. The hierarchical models, however, jointly fit as many of genetic variables as possible and thus take the relationship between the variables into account. As a result we are actually able to get more reliable point estimates and their corresponding intervals. The hierarchical prior distribution has an infinite spike at zero and very heavy tails, thereby strongly shrinking ‘unimportant’ effects to zero while minimally shrinking ‘important’ effects (Park and Casella 2008; Yi and Xu 2008; Armagan et al. 2010; Kyung et al. 2010; Yi and Ma 2012). Therefore, the hierarchical modeling tends to reduce the number of statistically significant comparisons, but does not sap our power to detect true association signals (Gelman et al. 2012).
For a hierarchical generalized linear model simultaneously fitting genetic effects, we have to test Jg hypotheses H0: βj =0. However, it is inappropriate to adjust for multiple comparisons by directly using the traditional Bonferroni correction, because our hierarchical modeling induces dependences among parameters and thus reduces the number of independent hypothesis tests. We define the effective number of hypothesis tests as the effective number of genetic effects and then use ρ to construct the hierarchical Bonferroni correction:
| (8) |
where Jρ =max(ρ, (ρ + 0.05·Jg)/2), and and pj are the adjusted and the original p-values for testing H0: βj =0, respectively. Therefore, we reject the hypothesis H0: βj =0 if . This is equivalent to using the original p-values at the significance level 0.05/Jρ, i.e., we reject H0 if pj < 0.05/Jρ.
The reason we use Jρ rather than ρ as the ‘total number of tests’ is to better control Type I error. Under the null model where all the genetic effects are zero, the effective number of genetic effects can be estimated close to zero. This will deflate the p-value of the overall test because of the small number of independent tests. Because there would be about 0.05 · Jg effects to be significant at the 5% level under the null model, the hierarchical Bonferroni correction provides an effective way to compromise the small effective number of genetic effects and the expected number of Type I errors.
Implementation
We have developed a freely available R package BhGLM, Bayesian hierarchical GLMs with application to genetic data analysis, for setting up and fitting Bayesian hierarchical GLMs, and for numerically and graphically displaying the results (http://www.ssg.uab.edu/bhglm/). The function bglm() in the package BhGLM allows us to set up Bayesian hierarchical GLMs using various priors and to implement our EM-IWLS algorithm. The function summary.bglm() provides various numerical summaries for the hierarchical GLMs fits, including estimates of coefficients, their standard errors and p-values. The functions bglm() and summary.bglm() are simple alterations of the standard R functions glm() and summary.glm() for analyzing classical GLMs, respectively. We have created new functions df.adj() and mc.adj() for calculating the effective number of parameters in the hierarchical GLMs and the adjusted p-values for multiple comparisons, respectively. The function mc.adj() includes not only our hierarchical Bonferroni correction but also several other popular approaches (Holm 1979; Hochberg 1988; Hommel 1988; Benjamini and Hochberg 1995; Benjamini and Yekutieli 2001).
Results
We illustrate our method for hierarchical modeling and multiple comparisons using two real data sets for genetic association studies. We compare our approach to six commonly-used methods: Bonferroni correction, Holm (1979), Hochberg (1988), Hommel (1988), Benjamini and Hochberg (1995), and Benjamini and Yekutieli (2001).
Dallas Heart Study Sequencing Data
Romeo et al. (Romeo et al. 2007; Romeo et al. 2009) conducted a large-scale genetic association study to examine the role of sequence variations in four genes ANGPTL3, 4, 5, and 6 in lipid metabolism. The study sequenced the exons and the intron-exon boundaries of the four genes in 3551 individuals from the Dallas Heart Study (DHS), a multi-ethnic sample from Dallas County residents (consisting of 601 Hispanic, 1,830 African American, 1,045 European American and 75 other ethnicities). A total of 339 segregating sequence variants were uncovered in the four genes (88 in ANGPTL3, 91 in ANGPTL4, 84 in ANGPTL5, and 76 in ANGPTL6), including only 35 common variants (having minor allele frequency (MAF) above 1%), 125 rare non-synonymous variants and 179 rare synonymous variants (having MAF below 1%). The phenotype analyzed in our study is the log-transformed plasma levels of triglyceride. Our analyses included race, age, and gender as covariates in the model.
We first used the traditional single-SNP method to separately analyze each variant and then analyzed the data by simultaneously fitting all the main effects of 339 variants and the covariates using the proposed hierarchical normal linear model. The main-effect predictor of each variant was coded using the additive genetic model, i.e., the number of minor alleles in the observed genotype. For the missing genotypes, we filled in the variables using the expectation of the observed values in that marker. We divided the variants in each gene into three groups: common variants, rare non-synonymous and rare synonymous variants, resulting in a total of 12 groups with the number of variants from 4 to 50. This group structure was incorporated into our hierarchical normal linear model.
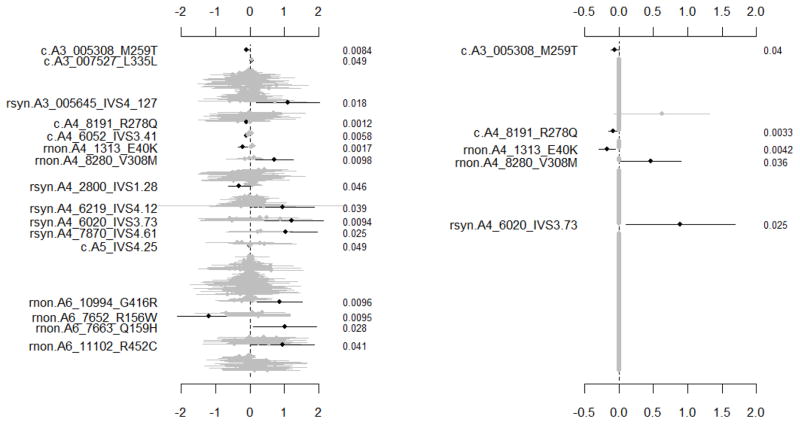
Figure 1 displays the coefficient estimates, standard errors, and original p-values for all the genetic variables. The traditional single-SNP method detected 16 additive effects with the p-values below the significance level 5%, including 5 common variants (with ‘c’), 6 rare non-synonymous variants (‘rnon’) and 5 rare synonymous variants (‘rsyn’). However, all these 16 ‘significant’ additive effects became insignificant after adjusted for multiple comparisons (Table 1a). Since linkage disequilibrium (LD) between rare variants is low (Pritchard 2001; Pritchard and Cox 2002), the previous methods that use LD to calculate the effective number of independent tests are unlikely to greatly reduce the multiple testing penalty, and thereby would produce results similar to the Bonferroni correction (Gao et al. 2008; Gao et al. 2010).
Figure 1.
Dallas heart study sequencing data. The left panel: the traditional single-SNP method separately analyzing each variant. The right panel: the proposed hierarchical normal linear model simultaneously fitting all the main effects of 339 variants. All the analyses include race, age, and gender as covariates in the model (not shown). The points, short lines and numbers at the right side represent estimates of effects, ± 2 standard errors, and original p-values, respectively. Only effects with p-value below 0.05 are labeled and blacked.
Table 1.
Dallas heart study sequencing data. Adjusted p-values using six commonly-used methods, bonferroni: Bonferroni correction, holm: Holm (1979), Hochberg: Hochberg (1988), hommel: Hommel (1988), BH: Benjamini & Hochberg (1995), and BY: Benjamini & Yekutieli (2001), and the proposed method ( bonferroni.adj). Only genetic effects with original p-values below 0.05 are shown. The column “none” presents the original p-values.
| a. The traditional single-SNP analysis
| |||||||
|---|---|---|---|---|---|---|---|
| none | bonferroni | holm | hochberg | hommel | BH | BY | |
| c.A3_005308_M259T | 0.008 | 1.000 | 1.000 | 0.998 | 0.998 | 0.416 | 1 |
| c.A3_007527_L335L | 0.049 | 1.000 | 1.000 | 0.998 | 0.998 | 0.940 | 1 |
| rsyn.A3_005645_IVS4_127 | 0.018 | 1.000 | 1.000 | 0.998 | 0.998 | 0.664 | 1 |
| c.A4_8191_R278Q | 0.001 | 0.415 | 0.415 | 0.415 | 0.414 | 0.292 | 1 |
| c.A4_6052_IVS3.41 | 0.006 | 1.000 | 1.000 | 0.998 | 0.998 | 0.416 | 1 |
| rnon.A4_1313_E40K | 0.002 | 0.584 | 0.582 | 0.582 | 0.579 | 0.292 | 1 |
| rnon.A4_8280_V308M | 0.010 | 1.000 | 1.000 | 0.998 | 0.998 | 0.416 | 1 |
| rsyn.A4_2800_IVS1.28 | 0.046 | 1.000 | 1.000 | 0.998 | 0.998 | 0.940 | 1 |
| rsyn.A4_6219_IVS4.12 | 0.039 | 1.000 | 1.000 | 0.998 | 0.998 | 0.940 | 1 |
| rsyn.A4_6020_IVS3.73 | 0.009 | 1.000 | 1.000 | 0.998 | 0.998 | 0.416 | 1 |
| rsyn.A4_7870_IVS4.61 | 0.025 | 1.000 | 1.000 | 0.998 | 0.998 | 0.848 | 1 |
| c.A5_IVS4.25 | 0.049 | 1.000 | 1.000 | 0.998 | 0.998 | 0.940 | 1 |
| rnon.A6_10994_G416R | 0.010 | 1.000 | 1.000 | 0.998 | 0.998 | 0.416 | 1 |
| rnon.A6_7652_R156W | 0.010 | 1.000 | 1.000 | 0.998 | 0.998 | 0.416 | 1 |
| rnon.A6_7663_Q159H | 0.028 | 1.000 | 1.000 | 0.998 | 0.998 | 0.848 | 1 |
| rnon.A6_11102_R452C | 0.041 | 1.000 | 1.000 | 0.998 | 0.998 | 0.940 | 1 |
| b. The hierarchical normal linear model
| ||||||||
|---|---|---|---|---|---|---|---|---|
| none | bonferroni | holm | hochberg | hommel | BH | BY | bonferroni.adj | |
| c.A3_005308_M259T | 0.040 | 1 | 1 | 1 | 1 | 1.000 | 1 | 0.423 |
| c.A4_8191_R278Q | 0.003 | 1 | 1 | 1 | 1 | 0.709 | 1 | 0.035 |
| rnon.A4_1313_E40K | 0.004 | 1 | 1 | 1 | 1 | 0.709 | 1 | 0.044 |
| rnon.A4_8280_V308M | 0.036 | 1 | 1 | 1 | 1 | 1.000 | 1 | 0.376 |
| rsyn.A4_6020_IVS3.73 | 0.025 | 1 | 1 | 1 | 1 | 1.000 | 1 | 0.260 |
The hierarchical normal linear model detected 5 additive effects at the significance level 5% and shrunk all other effects close to zero. Using the previous multiple comparisons corrections, the adjusted p-values for these 5 additive effects were all large. However, these corrections ignore the hierarchical modeling and are too conservative. The effective number of genetic effects was estimated to be 4.22, close to the number of non-zero effects. With our hierarchical Bonferroni correction, therefore, two variants in ANGPTL4, 8191_R278Q and 1313_E40K, remained significant (Table 1b). These two variants were previously identified in the previous studies (Romeo et al. 2007; King et al. 2010; Yi et al. 2011b), although they only analyzed the variants in ANGPTL4 and did not address the multiple comparisons. The hierarchical modeling can reduce the uncertainty in inferences and correspondingly controls the number of statistically significant comparisons.
Adiponectin Genes and Colorectal Cancer Risk
Kaklamani et al. (2008) investigated the association of genetic variants of the adiponectin (ADIPOQ) and adiponectin receptor 1(ADIPOR1) genes with colorectal cancer risk in a large case-control study (Yi et al. 2011a). This case-control study included a total of 441 patients with a diagnosis of colorectal cancer and 658 unrelated controls. All cases and controls were white and of Ashkenazi Jewish ancestry and from New York, New York. Information regarding gender, current age for controls, and age at colorectal cancer diagnosis for cases was recorded. Five haplotype-tagging SNPs were selected to capture variations in the major blocks in each of genes ADIPOQ and ADIPOR1. The selected SNPs have MAF above 10% and show low proportions of missing genotypes (from 0.3% to 3%).
We illustrate our method with this data by analyzing epistatic interactions, which shows the problem of multiple comparisons even with a small number of variants. We first used the traditional method for detecting epistatic interactions that analyze two variants at a time, and we then used the proposed hierarchical logistic regression to simultaneously fit all 20 main effects and 180 epistatic interactions of 10 variants. All the models also included gender and age as covariates. The main-effect predictors of each variant were coded using the Cockerham genetic model, which defines an additive effect and a dominance effect (Yi et al. 2011a). The epistatic predictors were constructed by multiplying two corresponding main-effect variables, introducing four interactions for a pair of SNPs, i.e., additive-additive, additive-dominance, dominance-additive, and dominance-dominance interactions. For the missing genotypes, we filled in the variables using the expectation of the observed values in that marker. We divided the main-effect variables in each gene into two groups: additive and dominance predictor groups. We then constructed 16 interaction groups based on the four main-effect groups. This group structure was incorporated into our hierarchical logistic model.
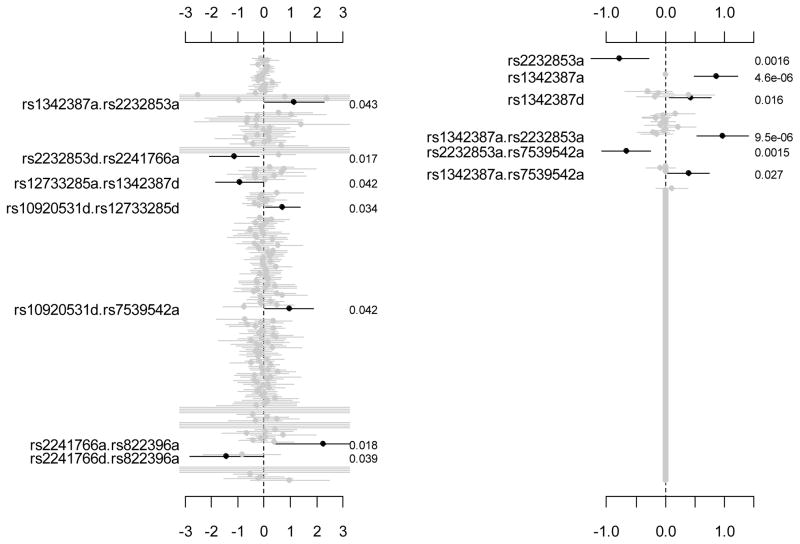
Figure 2 displays the coefficient estimates, standard errors, and original p-values for all the genetic variables. The traditional method detected 7 interaction effects with the p-values below the significance level 5%. However, the adjusted p-values for all these 7 ‘significant’ interactions were close to 1 (Table 2a), indicating that these interactions may be false positives.
Figure 2.
Adiponectin genes and colorectal cancer risk. The left panel: the traditional method analyzing two variants at a time. The right panel: the proposed hierarchical logistic regression simultaneously fitting all the main effects and the epistatic interactions. All the analyses include age and gender as covariates in the model (not shown). The points, short lines and numbers at the right side represent estimates of effects, ± 2 standard errors, and original p-values, respectively. Only effects with p-value below 0.05 are labeled and blacked.
Table 2.
Adiponectin genes and colorectal cancer risk. Adjusted p-values using six commonly-used methods, bonferroni: Bonferroni correction, holm: Holm (1979), Hochberg: Hochberg (1988), hommel: Hommel (1988), BH: Benjamini & Hochberg (1995), and BY: Benjamini & Yekutieli (2001), and the proposed method ( bonferroni.adj). Only genetic effects with original p-values below 0.05 are shown. The column “none” presents the original p-values.
| a. The tradition method analyzing two variants at a time
| |||||||
|---|---|---|---|---|---|---|---|
| none | bonferroni | holm | hochberg | hommel | BH | BY | |
| rs1342387a.rs2232853a | 0.043 | 1 | 1 | 0.984 | 0.984 | 0.983 | 1 |
| rs2232853d.rs2241766a | 0.017 | 1 | 1 | 0.984 | 0.984 | 0.983 | 1 |
| rs12733285a.rs1342387d | 0.042 | 1 | 1 | 0.984 | 0.984 | 0.983 | 1 |
| rs10920531d.rs12733285d | 0.034 | 1 | 1 | 0.984 | 0.984 | 0.983 | 1 |
| rs10920531d.rs7539542a | 0.042 | 1 | 1 | 0.984 | 0.984 | 0.983 | 1 |
| rs2241766a.rs822396a | 0.018 | 1 | 1 | 0.984 | 0.984 | 0.983 | 1 |
| rs2241766d.rs822396a | 0.039 | 1 | 1 | 0.984 | 0.984 | 0.983 | 1 |
| b. The hierarchical logistic regression
| ||||||||
|---|---|---|---|---|---|---|---|---|
| none | bonferroni | holm | hochberg | hommel | BH | BY | bonferroni.adj | |
| rs2232853a | 0.001576 | 0.315135 | 0.310408 | 0.310408 | 0.310408 | 0.078784 | 0.463093 | 0.024833 |
| rs1342387a | 0.000005 | 0.000926 | 0.000926 | 0.000926 | 0.000926 | 0.000926 | 0.005441 | 0.000073 |
| rs1342387d | 0.015835 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 0.633408 | 1.000000 | 0.249563 |
| rs1342387a.rs2232853a | 0.000010 | 0.001906 | 0.001897 | 0.001897 | 0.001897 | 0.000953 | 0.005603 | 0.000150 |
| rs2232853a.rs7539542a | 0.001482 | 0.296366 | 0.293403 | 0.293403 | 0.291921 | 0.078784 | 0.463093 | 0.023354 |
| rs1342387a.rs7539542a | 0.026981 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 0.899379 | 1.000000 | 0.425226 |
The hierarchical logistic model detected 3 main effects and 3 epistatic interactions as well as the two covariates with the p-values below 5% and shrunk all other effects close to zero. Only one of these significant effects was detected by the traditional two-SNP method. In our hierarchical logistic model, the effective number of genetic effects was estimated to be 14.76, much smaller than the total number of genetic effects. With our hierarchical Bonferroni correction, two additive effects, rs2232853a and rs1342387a, and two interactions, rs1342387a.rs2232853a and rs2232853a.rs7539542a, were still significant (Table 2b). The p-values adjusted by our correction were smaller than those by the previous methods, indicating that the proposed method would be more powerful.
Simulation Studies
To get further insight into our approach, we performed simulation studies. Our simulation studies used the real genotype data of the 10 SNPs and the two covariates, gender and age, in the above case-control study. We generated the case-control indicator yi for each individual using the latent-data formulation of the logistic regression (Gelman and Hill 2007; Yi and Zhi 2011); the logistic model logit(yi = 1) Xi βtrue is equivalent to the model, wi ~ N (Xi βtrue, 1.62), yi = 1 ⇔ wi > c, where Xi includes a constant (intercept), the two covariates, the 10 main-effect predictors and 180 interaction terms. Thus, we first sample n (= 441 + 658) latent normal phenotype wi and then set 441 individuals with the 40% (= 441 / n) largest wi as affected (i.e., yi = 1) and the other individuals as unaffected (i.e., yi = 0). This procedure is equivalent to repeatedly sampling from the binomial distribution Bin(1, logit−1(Xiβtrue)) until obtaining 441 cases and 658 controls. We considered two sets of βtrue as described below. For each situation, 1000 replicated datasets were simulated. For each simulated data set, we first used the traditional method to analyze two variants at a time, and we then used the proposed hierarchical logistic regression to simultaneously fit all 20 main effects and 180 epistatic interactions of 10 variants. All the models also included gender and age as covariates.
In our first simulation scenario, we set all the coefficients βtrue to zero, examining the ratio of false positives. We counted the number of coefficients that were statistically significant at the threshold level 5% for each simulation and also computed the family-wise error rate (FWER: the proportion of making at least one false discovery in 1000 simulations). The traditional analysis got 8 ‘significant’ effects on average with quantiles of 25% and 75% being 5 and 12, respectively, and had the FWER of 99%. This shows that multiple comparisons corrections are clearly crucial here. By comparison, our hierarchical model detected only 0.3 ‘significant’ effect on average with quantiles of 25% and 75% being 0 and 1, respectively, and had the FWER of 4.6% when we used the proposed correction Jρ (the FWER is 14% when we directly used the effective number of effects ρ ) (See Equation 12). The effective number of genetic effects was estimated to be 1.6 on average with quantiles of 25% and 75% being 0.8 and 2.2, respectively. Therefore, the hierarchical model approach can largely reduce the number of false positives and hence relieve the problem of multiple comparisons.
In the second scenario, we set the coefficients βtrue based on their estimates in the hierarchical logistic model fit of the real data (see the right panel of Figure 2); we set the coefficients with the original p-values below 5% to their estimated values, and the other coefficients to zero. Therefore, this simulation assumed 8 non-zero coefficients, including two covariates, three main effects, and three interactions. We calculated the frequency of each effect estimated with original or adjusted p-values smaller than 0.05 over 1000 replicates. These frequencies correspond to the empirical power for detecting the simulated non-zero effects and Type I error rate for other effects, respectively.
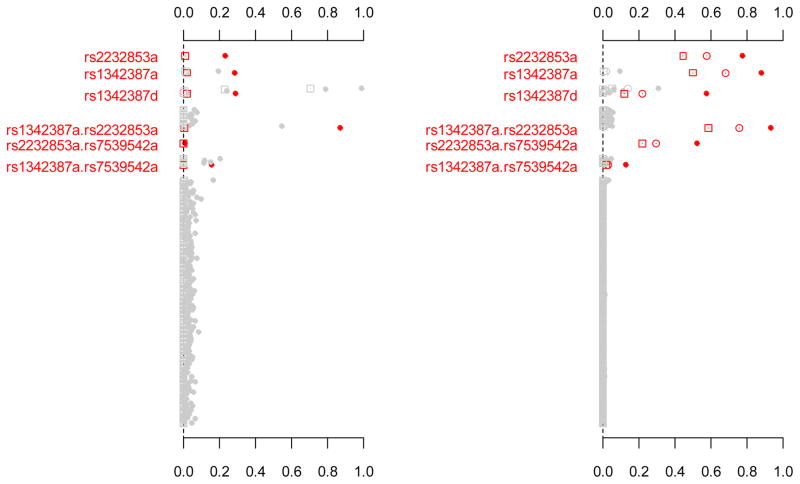
As shown in the left panel of Figure 3, the traditional analysis had low power to detect all the simulated genetic effects except the largest epistatic effect, rs1342387a.rs2232853a. With multiple comparisons corrections, the power of the traditional analysis was close to zero. It was found that the traditional analysis frequently detected several zero effects, resulting in high Type I error. By comparison, our hierarchical modeling approach detected most of the simulated genetic effects with reasonable power and had low rate of false positives (see the right panel of Figure 3). The effective number of genetic effects was estimated to be 13.0 on average with quantiles of 25% and 75% being 11.8 and 14.1, respectively. The hierarchical Bonferroni correction only slightly reduced the power, but was always more powerful than the previous methods. The hierarchical models jointly fit all possible predictors and can provide reliable estimates of parameters. As a result, our approach can relieve the problem of multiple comparisons.
Figure 3.
Frequency of each effect estimated with original or adjusted p-values smaller than 0.05 over 1000 replicates. The left panel: the traditional method analyzing two variants at a time. The right panel: the proposed hierarchical logistic regression simultaneously fitting all the main effects and the epistatic interactions. All the analyses include age and gender as covariates in the model (not shown). The points (●) represent frequencies estimated with original p-values. The squares (■) represent frequencies estimated with the minimum p-values adjusted by the six previous methods. The circles (○) represent frequencies estimated with the p-values of the hierarchical Bonferroni correction. Only effects with non-zero simulated value are labeled with red color.
Discussion
We have described in this article that the challenges of multiple comparisons can be substantially relieved when using the proposed hierarchical modeling approach. The hierarchical modeling framework appropriately models the relationship between the corresponding parameters and thus enables to yield more reliable point and interval estimates (Gelman and Hill 2007). In contrast, the traditional procedures insufficiently model the ensemble of the parameters and are unlikely to get reliable estimates which the multiple comparisons corrections are based on. A hierarchical model shrinks point estimates of unimportant effects and their corresponding intervals toward zero (the null hypothesis). Thus, hierarchical estimates make comparisons appropriately more conservative, and at the same time don’t reduce our power to detect true effects (Gelman et al. 2012). In addition, our hierarchical modeling approach is flexible, applicable to not only simple genetic models (e.g., additive models) but also complex genetic models involving common variants, rare variants and genetic interactions.
In genetic association studies, there are various valuable sources that can be used to appropriately set up hierarchical models (Hung et al. 2004; Thomas et al. 2009). Genome annotation can group genetic variants into genes and genes into biological pathways (Wang et al. 2010; Schaid et al. 2011). Variants (genes) within a group can be biologically related or statistically correlated and hence would influence phenotype more similarly than those in different groups. In addition to genotype data, there are various types of additional variables that may characterize biological importance of each variant or gene (Madsen and Browning 2009; Hoffmann et al. 2010; Price et al. 2010). However, these important sources have not been efficiently incorporated into genetic association studies. We believe that it is worthwhile to invest research time and effort towards developing hierarchical models for genetic association studies.
Applied researchers may worry about having to learn a different kind of model and technique. However, functions for implementing our hierarchical modeling approach are now available in the freely available R package BhGLM (http://www.ssg.uab.edu/bhglm/). The package BhGLM provides functions for setting up and fitting Bayesian hierarchical GLMs, for numerically and graphically displaying the results, and for genetic association analyses. Therefore, routinely using the hierarchical modeling procedure should be convenient.
A variety of prior distributions have been proposed for coefficients in high-dimensional models (Park and Casella 2008; Yi and Xu 2008; Armagan et al. 2010; Kyung et al. 2010; Yi and Ma 2012). Most of these priors can be expressed as a mixture of normal distributions, , with variances following certain hyper-prior distributions. The key contribution of this work is to introduce the effective number of genetic effects and the hierarchical Bonferroni correction that can be applied to hierarchical GLMs with various priors on the variance parameters . The effective number of genetic effects can be much smaller than the actual number of genetic effects, and thereby the hierarchical Bonferroni correction avoids the high penalty of the traditional Bonferroni correction. As described earlier, the effective number of genetic effects is estimated using all information included in the data and the model. Therefore, our method should be more appropriate and flexible than those existing methods that only use linkage disequilibrium (Gao et al. 2008; Gao et al. 2010).
Measuring the complexity of hierarchical models is an important and active research area in statistics (Spiegelhalter et al. 2002; Lu et al. 2007). Our method for estimating the effective number of parameters may provide a useful procedure in the area. Besides being used to construct our hierarchical Bonferroni correction, the effective number of genetic effects obviously has many other applications; for example, it can be used to create the adjusted versions of traditional model comparisons criteria (e.g., AIC) and test statistics for jointly testing a group of genetic effects. In the future, we will explore these applications.
Acknowledgments
We would like to thank Drs. Jonathan Cohen and Helen Hobbs for access to the Dallas Heart Study dataset, and Drs. Virginia G. Kaklamani and Boris Pasche for access to the Colorectal Cancer Case-Control dataset. This work was supported in part by the research grants: NIH 5R01GM069430-08 and NIH 5R01DA025095.
Appendix A
The hierarchical prior distributions and the EM-IWLS algorithm
A variety of prior distributions have been proposed for coefficients in high-dimensional models (Park and Casella 2008; Yi and Xu 2008; Armagan et al. 2010; Kyung et al. 2010; Yi and Ma 2012). Most of these priors can be expressed as a mixture of normal distributions, , with variances following certain hyper-prior distributions. Although our method can be used to various priors for the variances , we describe our algorithm for the hierarchical exponential distribution with group-specific hyperparameters:
| (A1) |
where the subscript k[j] indexes the group k that the j-th predictor belongs to. The hyperparameter sk controls the amount of shrinkage in the variance estimate; a large value of sk forces the variance closer to zero. This prior distribution includes group-specific parameters sk and variable-specific parameters .
We further treat the hyperparameters sk as unknown parameters with the Gamma hyper-prior distributions:
| (A2) |
As a typical default specification for the hyperparameters, one can let a = b = 1, which induces the standard double Pareto distributions for the coefficients and usually works well in high-dimensional settings (Armagan et al. 2010).
We fit the generalized linear models with the hierarchical priors by estimating the marginal posterior modes of the parameters (β, ϕ). We modify the usual iterative weighted least squares (IWLS) for fitting classical GLMs and incorporate an EM algorithm into the modified IWLS procedure. The EM-IWLS algorithm increases the marginal posterior density of the parameters (β, ϕ) at each step and thus converges to a local mode. Our EM algorithm treats the unknown variances and the hyperparameters sk[j] as missing data and estimates the parameters (β, ϕ) by averaging over these missing values. At each step of the iteration, we replace the terms involving the parameters (β, ϕ) and the missing values ( , sk[j]) by their conditional expectations, and then update the parameters (β, ϕ) by maximizing the expected value of the joint log-posterior density,
| (A3) |
For the E-step of the algorithm, we take the expectation of the above joint log-posterior density with respect to the conditional posterior distributions of the variances and the hyperparameters. The conditional posterior distributions are
| (A4) |
| (A5) |
Therefore, we have the conditional expectations
| (A6) |
| (A7) |
In the M-step, we update (β, ϕ) by maximizing , where , and for j =1, ···, J. This is equivalent to solving the generalized linear model yi ~ p (yi | Xi β, ϕ) with the normal priors . Thus, the parameters (β, ϕ) can be updated using the modified IWLS algorithm as described in the main text.
References
- Armagan A, Dunson D, Lee J. Bayesian generalized double Pareto shrinkage. Biometrika. 2010 [PMC free article] [PubMed] [Google Scholar]
- Balding DJ. A tutorial on statistical methods for population association studies. Nat Rev Genet. 2006;7:781–791. doi: 10.1038/nrg1916. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society Series B. 1995;57:289–300. [Google Scholar]
- Benjamini Y, Yekutieli D. The control of the false discovery rate in multiple testing under dependency. Annals of Statistics. 2001;29:1165–1188. [Google Scholar]
- Benjamini Y, Yekutieli D. Quantitative trait Loci analysis using the false discovery rate. Genetics. 2005;171:783–790. doi: 10.1534/genetics.104.036699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galwey NW. A new measure of the effective number of tests, a practical tool for comparing families of non-independent significance tests. Genet Epidemiol. 2009;33:559–568. doi: 10.1002/gepi.20408. [DOI] [PubMed] [Google Scholar]
- Gao X, Becker LC, Becker DM, Starmer JD, Province MA. Avoiding the high Bonferroni penalty in genome-wide association studies. Genet Epidemiol. 2010;34:100–105. doi: 10.1002/gepi.20430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao X, Starmer J, Martin ER. A multiple testing correction method for genetic association studies using correlated single nucleotide polymorphisms. Genet Epidemiol. 2008;32:361–369. doi: 10.1002/gepi.20310. [DOI] [PubMed] [Google Scholar]
- Gelman A, Carlin J, Stern H, Rubin D. Bayesian data analysis. Chapman and Hall; London: 2003. [Google Scholar]
- Gelman A, Hill J. Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge University Press; New York: 2007. [Google Scholar]
- Gelman A, Hill J, Yajima M. Why we (usually) don’t have to worry about multiple comparisons. Journal of Research on Educational Effectiveness. 2012;5:189–211. [Google Scholar]
- Gelman A, Jakulin A, Pittau MG, Su YS. A weakly informative default prior distribution for logistic and other regression models. Annals of Applied Statistics. 2008;2:1360–1383. [Google Scholar]
- Hochberg Y. A sharper Bonferroni procedure for multiple tests of significance. Biometrika. 1988;75:800–803. [Google Scholar]
- Hoffmann TJ, Marini NJ, Witte JS. Comprehensive approach to analyzing rare genetic variants. PLoS One. 2010;5:e13584. doi: 10.1371/journal.pone.0013584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holm S. A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics. 1979;6:65–70. [Google Scholar]
- Hommel G. A stagewise rejective multiple test procedure based on a modified Bonferroni test. Biometrika. 1988;75:383–386. [Google Scholar]
- Hsu JC. Multiple Comparisons: Theory and Methods. London: Chapman and Hall; 1996. [Google Scholar]
- Hung R, Brennan P, Malaveille C, Porru S, Donato F, et al. Using hierarchical modeling in genetic association studies with multiple markers: application to a case-control study of bladder cancer. Cancer Epidemiol Biomarkers Prev. 2004;13:1013–1021. [PubMed] [Google Scholar]
- Kang G, Ye K, Liu N, Allison DB, Gao G. Weighted multiple hypothesis testing procedures. Stat Appl Genet Mol Biol. 2009:8. doi: 10.2202/1544-6115.1437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King CR, Rathouz PJ, Nicolae DL. An evolutionary framework for association testing in resequencing studies. PLoS Genet. 2010;6:e1001202. doi: 10.1371/journal.pgen.1001202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kyung M, Gill J, Ghosh M, Casella G. Penalized Regression, Standard Errors, and Bayesian Lassos. Bayesian Analysis. 2010;5:369–412. [Google Scholar]
- Lu H, Hodges JS, Carlin BP. Measuring the complexity of generalized linear hierarchical models. The Canadian Journal of Statistics. 2007;35:69–87. [Google Scholar]
- Madsen BE, Browning SR. A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet. 2009;5:e1000384. doi: 10.1371/journal.pgen.1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCullagh P, Nelder JA. Generalized linear models. Chapman and Hall; London: 1989. [Google Scholar]
- Park T, Casella G. The Bayesian Lasso. Journal of the American Statistical Association. 2008;103:681–686. [Google Scholar]
- Price AL, Kryukov GV, de Bakker PI, Purcell SM, Staples J, et al. Pooled association tests for rare variants in exon-resequencing studies. Am J Hum Genet. 2010;86:832–838. doi: 10.1016/j.ajhg.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK. Are rare variants responsible for susceptibility to complex diseases? Am J Hum Genet. 2001;69:124–137. doi: 10.1086/321272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Cox NJ. The allelic architecture of human disease genes: common disease-common variant...or not? Hum Mol Genet. 2002;11:2417–2423. doi: 10.1093/hmg/11.20.2417. [DOI] [PubMed] [Google Scholar]
- Rice TK, Schork NJ, Rao DC. Methods for handling multiple testing. Adv Genet. 2008;60:293–308. doi: 10.1016/S0065-2660(07)00412-9. [DOI] [PubMed] [Google Scholar]
- Roeder K, Devlin B, Wasserman L. Improving power in genome-wide association studies: weights tip the scale. Genet Epidemiol. 2007;31:741–747. doi: 10.1002/gepi.20237. [DOI] [PubMed] [Google Scholar]
- Romeo S, Pennacchio LA, Fu Y, Boerwinkle E, Tybjaerg-Hansen A, et al. Population-based resequencing of ANGPTL4 uncovers variations that reduce triglycerides and increase HDL. Nat Genet. 2007;39:513–516. doi: 10.1038/ng1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romeo S, Yin W, Kozlitina J, Pennacchio LA, Boerwinkle E, et al. Rare loss-of-function mutations in ANGPTL family members contribute to plasma triglyceride levels in humans. J Clin Invest. 2009;119:70–79. doi: 10.1172/JCI37118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabatti C, Service S, Freimer N. False discovery rate in linkage and association genome screens for complex disorders. Genetics. 2003;164:829–833. doi: 10.1093/genetics/164.2.829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaid DJ, Sinnwell JP, Jenkins GD, McDonnell SK, Ingle JN, et al. Using the gene ontology to scan multilevel gene sets for associations in genome wide association studies. Genet Epidemiol. 2011 doi: 10.1002/gepi.20632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, Linde Avd. Bayesian measures of model complexity and fit (with discussion) Journal of the Royal Statistical Society Series B. 2002:64.
- Thomas DC, Conti DV, Baurley J, Nijhout F, Reed M, et al. Use of pathway information in molecular epidemiology. Hum Genomics. 2009;4:21–42. doi: 10.1186/1479-7364-4-1-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K, Li M, Hakonarson H. Analysing biological pathways in genome-wide association studies. Nat Rev Genet. 2010;11:843–854. doi: 10.1038/nrg2884. [DOI] [PubMed] [Google Scholar]
- Yi N, Banerjee S. Hierarchical generalized linear models for multiple quantitative trait locus mapping. Genetics. 2009;181:1101–1113. doi: 10.1534/genetics.108.099556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi N, V, Kaklamani G, Pasche B. Bayesian analysis of genetic interactions in case-control studies, with application to adiponectin genes and colorectal cancer risk. Ann Hum Genet. 2011a;75:90–104. doi: 10.1111/j.1469-1809.2010.00605.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi N, Liu N, Zhi D, Li J. Hierarchical generalized linear models for multiple groups of rare and common variants: jointly estimating group and individual-variant effects. PLoS Genet. 2011b;7:e1002382. doi: 10.1371/journal.pgen.1002382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi N, Ma S. Hierarchical Shrinkage Priors and Model Fitting for High-dimensional Generalized Linear Models. Stat Appl Genet Mol Biol. 2012 doi: 10.1515/1544-6115.1803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi N, Xu S. Bayesian LASSO for quantitative trait loci mapping. Genetics. 2008;179:1045–1055. doi: 10.1534/genetics.107.085589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi N, Zhi D. Bayesian analysis of rare variants in genetic association studies. Genet Epidemiol. 2011;35:57–69. doi: 10.1002/gepi.20554. [DOI] [PMC free article] [PubMed] [Google Scholar]