Abstract
The human soleus H-reflex is commonly tested as an indicator of the reflex excitability of the calf muscles with infrequent stimuli to a subject seated and at rest. However, the reflex varies widely with the level of voluntary contraction and with the time history of stimulation. We studied two aspects of this variation. Antagonist (tibialis anterior) activation decreases the response, while increasing agonist (soleus) activation increases the H-reflex to a peak after which it declines. In subjects with large H-reflexes at rest, the reflex peaked at low levels of contraction. In contrast, in subjects with small H-reflexes at rest, the reflex peaked at higher levels of contraction for reasons that were elucidated using a realistic computer model. A parabolic curve fitted the maximum amplitude of the H-reflex in the model and over the entire range of contractile levels studied. The second aspect studied was post-activation depression or homosynaptic depression (HD), which has been described previously as a reduction of a second H-reflex elicited shortly after an initial reflex. We confirmed the presence of HD in resting, seated subjects for intervals up to 4 s. However, by voluntarily activating the soleus muscle, HD was drastically reduced when seated and abolished when standing. This suggests that HD may be absent in normal, functional movements and perhaps in clinical conditions that alter H-reflexes. Meaningful, quantitative measurements of reflex excitability can only be made under voluntary activity that mimics the condition of interest.
Keywords: Post-activation depression, H-reflex, Neural models, Reflex modulation
Introduction
The most-studied excitatory reflex in human subjects is arguably the Hoffmann or H-reflex in the soleus muscle; see extensive review of past work by Pierrot-Deseilligny and Burke (2005). The H-reflex is the electrical analog of the tendon jerk that is routinely tested clinically. Yet the form of the dependence of the H-reflex on stimulus intensity, voluntary activity and inter-stimulus interval is rarely quantified. One exception is the study by Hoehler and Burger who fitted several models to the form of the H-reflex as a function of stimulus intensity (Hoehler and Buerger 1981). Controversy even remains about the best way to study the role of the reflex in common movements (Stein and Thompson 2006). Most commonly the reflex is tested at rest (Pierrot-Deseilligny and Burke 2005), but Hoffmann in his original study (Hoffmann 1918) and many subsequent studies found that the reflex is enhanced when the calf muscles are activated voluntarily and reduced when antagonist muscles are activated. Also, the H-reflex rises to a peak and then declines as the agonist muscles are activated more (Capaday and Stein 1987; Slot and Sinkjaer 1994). We show here that the values are well fitted with a parabola over the entire range of agonist and antagonist activations studied. Furthermore, the stimulus level at which the peak occurs varies inversely with the level of the H-reflex at rest. The physiological reasons for some of these results have been suggested previously based on simple models of a motor neuron pool (Capaday and Stein 1987; Matthews 1999), but are all confirmed here with a more detailed and realistic model.
Another controversial topic is the significance of the phenomenon of post-activation depression. Essentially, if one H-reflex is applied to a resting subject, then a second stimulus will produce a smaller reflex at intervals up to as much as 10 s; see review by Pierrot-Deseilligny and Burke (2005). This depression is also referred to as homosynaptic depression because only the synapses that are activated become depressed (Hultborn et al. 1996). We will use the abbreviation HD, rather than PAD, because the latter abbreviation is commonly used for primary afferent depolarization (Eccles 1964). HD is less evident in patients with spasticity produced by several clinical conditions. Although the mechanism for this change is not clear, Pierrot-Deseilligny and Burke reviewed a number of studies suggesting that the decrease in HD was a major factor in spasticity after spinal cord injury or stroke. However, we show here that HD is reduced in normal subjects activating the calf muscles while sitting (see also Hultborn and Nielsen 1998) and virtually abolished in standing subjects. Burke et al. (1989) also found that voluntary contraction abolished HD in a number of muscles. We feel, as discussed elsewhere (Stein and Thompson 2006), that HD is probably an epiphenomenon of the resting state and may not be important clinically. In short, the purpose of the paper is to quantify two methodological issues that have significance in terms of normal and clinical reflex function in humans.
Methods
Nine subjects between 21 and 65 years of age with no neurological problems took part in the first part of this study. Surface self-adhesive Ag–AgCl electrodes (Kendall LTP, Chicopee, MA) were placed on the tibialis anterior (TA) and soleus muscles. The TA recording electrodes were positioned over the motor point, located approximately one-third of the distance from the knee to the ankle joint, while the soleus recording electrodes were aligned with the Achilles tendon about 2–3 cm below the gastrocnemius muscle. The electromyogram (EMG) from the stimulated muscle was amplified, high-pass filtered at 30 Hz, low-pass filtered at 1 kHz, and recorded at a sample rate of 5 kHz with Axoscope (Axon Instruments, Union City, CA). In addition, EMG from these electrodes was rectified, low-pass filtered at 3 Hz, and displayed on an oscilloscope so subjects could monitor their level of contraction. The maximum voluntary contractions (MVCs) of the soleus and TA were determined as the maximum rectified EMG levels the subject could produce via plantar flexion and dorsiflexion, respectively. Tibial nerve stimulation was achieved using surface self-adhesive Ag–AgCl electrodes (Kendall LTP). The stimulus electrode for the tibial nerve was positioned in the popliteal fossa. The specific locations were chosen to achieve the greatest response at the lowest voltage. Stimuli were 1 ms, rectangular pulses delivered by a Grass SD9 isolated stimulator (Grass Instruments, Quincy, MA). Results were analyzed throughout the course of each experiment to ensure the validity of each trial using a custom-made Matlab program (Mathworks Inc., Natick, MA).
Quantification of soleus H-reflex relative to level of voluntary contraction
To examine the effect of increasing the magnitude of either voluntary agonist or antagonist contraction on the soleus H-reflex, various levels of muscle contraction were tested from rest up to 60% of soleus MVC, and up to 40% of TA MVC. The tested range differed slightly between subjects due to variations in their ability to maintain high levels of contraction. Subjects were seated with their leg held in a brace and were asked to monitor their contraction on the oscilloscope. Two different trials were conducted at each level of contraction. First, multiple voltage levels of tibial nerve stimulation were administered in sets of four stimuli each, ranging from motor threshold (MT) to a level that elicited the maximal M-wave (Mmax). Peak-to-peak M-wave and H-reflex amplitudes were plotted as a function of stimulus intensity and the Mmax and Hmax were noted. Intervals between stimuli were varied randomly between 2 and 5 s, so that subjects could not anticipate when the next stimulus would occur. The stimulus intensity at which the Hmax occurred was used in a second trial at the same level of contraction using 16 stimuli to determine Hmax more accurately. For subsequent levels of contraction, the stimulus intensity was adjusted slightly, if needed to maintain the M-wave constant throughout the course of the experiment.
To further quantify changes that occurred under different conditions the values for M and M + H were fitted with a sigmoid curve, also known as the Boltzmann equation of the form (Capaday 1997):
| (1) |
where r is response, which reaches an asymptotic, maximum value m, s stimulus, h stimulus level at which half the maximum response is reached, and w measure of the steepness (width) of the curve. When w = ±(h − s), r = m/(1 + exp(±1)), the two values are 0.732 and 0.269, so w is approximately the half-width. The prediction for the H-reflex is then obtained as the difference of the fitted curves for M and M + H. All three fitted curves are shown in Fig. 1 for one trial. A second approach, proposed by (Hoehler and Buerger 1981), calculated the H-reflex response directly as a product of two factors: one similar to Eq. (1) and a second multiplicative factor, assuming that the occlusion of the H-reflex was directly proportional to the fraction of the motor pool (1 − M/Mmax) that had not been activated at that stimulus level
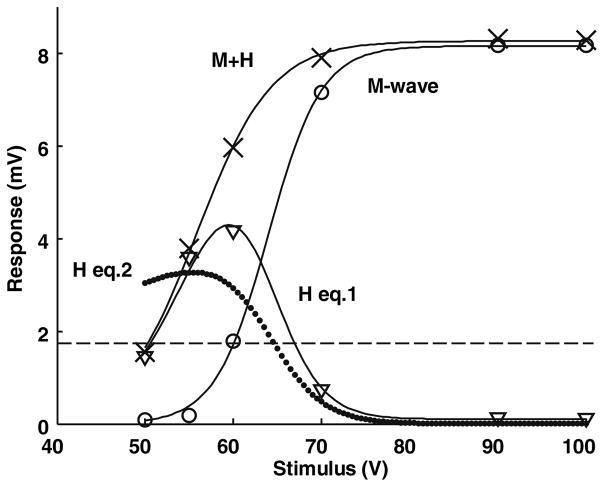
Fig. 1.
A representative example of M, H and M + H curves for one subject at rest over a range of tibial nerve stimulus intensities. The M-wave and the sum M + H were fitted with Eq. (1). The difference between these two curves was well-fitted to the H-reflex. Equation (2) in the text fitted the H-reflex less well. The H-reflex reached 0.2 Mmax (dashed line) with a stimulus of approximately 50 V, compared to 60 V for the M-wave in this subject. Such differences are quantified in the text for the population data
| (2) |
Equation (2) assumes implicitly that motor units are recruited at random into the M-wave, an assumption that Hoehler and Buerger found worked better than an inverse recruitment from large to small. The value m is the maximum size that the H-reflex would reach, if there were no occlusion by the M-wave, and is different from the measured Hmax in the presence of occlusion. The value of m was limited in the fitting procedure to be no greater than Mmax, since the reflex can not recruit more than the maximum produced by direct stimulation of the nerve (Mmax). All fitting was done with a nonlinear, least mean squares algorithm (lsqnonlin) in Matlab (Math Works).
The Hmax/Mmax ratios were plotted against the recorded background level of contraction and fitted using least mean square methods with a second order polynomial of the form y = a + bx + cx2, where y is Hmax/Mmax, a is the y-intercept, or the value of Hmax/Mmax at rest, and x represents the level of background contraction. For graphical purposes, dorsiflexion was considered a negative value of plantar flexion. The peak of the curves occurs when the derivative dy/dx = b + 2cx is zero so xmax = −b/2c. Thus the parameters b and c determine the value xmax at which the peak Hmax/Mmax occurred. A linear relation was found between the parameter a (the H-reflex at rest) and xmax, the contraction level at which the H-reflex reached its maximum.
Homosynaptic depression
A second goal of this study was to examine the functional significance of HD in the soleus H-reflex, using 12 neurologically normal subjects. Larger numbers were required in the HD study to verify the statistical significance of some of the measurements. Three conditions were tested: seated with one leg braced and at rest, seated with one leg braced and contracting to 15–20% soleus MVC, and standing with 15–20% soleus MVC. As in the previous section, an M–H curve was generated for each condition by tibial nerve stimulation at gradually increasing intensities, ranging from motor threshold (MT) to a level that elicited Mmax. From this curve, a stimulus level was chosen to elicit approximately 0.5× Hmax. At this level, excitatory and inhibitory influences can easily increase or decrease the H-reflex (Zehr and Stein 1999a). The tibial nerve was then activated by pairs of stimuli separated by variable intervals, including 0.1, 0.2, 0.5, 1, 2, and 4 s. The stimuli were repeated every 9 s, so the time between the second stimulus of one sweep and the first stimulus of the next sweep was also effectively tested. For example, if the stimuli were 2 s apart on a given trial, there was also a 7 s interval being tested prior to the onset of the next stimulus. The M-wave and H-reflex amplitudes for 15 stimulus pairs were averaged for each interval.
For each subject, the mean of the H-reflex amplitudes obtained during the 7–8.9 s delay periods was calculated. Since there is little or no HD at these intervals, all other H-reflexes were normalized to this value. The normalized values at each delay were averaged between subjects, and the trends in HD over the various delay intervals for the three conditions were compared. Statistical analysis was performed to determine whether the normalized H-reflex amplitude was below 1.0 (i.e., whether HD was significant) with a one-sample t test for each condition. Furthermore, the effects of contraction and posture on HD were analyzed by comparing results from the three conditions at a given inter-stimulus interval, using a paired-samples t test. Results were significant when P ≤ 0.05.
Results
Quantification of soleus H-reflex relative to levels of voluntary contraction
Figure 1 shows a plot of the M and H curves as a function of stimulus voltage for one subject at rest. The standard errors were typically less than the symbol size in this figure and have therefore not been plotted. The M-wave was fitted with Eq. (1) and the values are: the maximum M-wave, m = 8.2 mV, the stimulus that produces a half-maximum M-wave, h = 64.0 V, and half-width, w = 3.0 V. The half-width is a measure of the steepness of the curve, as described in the “Methods”. This equation accounts for 99.9% of the variance (also referred to as Pearson’s R2). As the M-wave increases, the H-reflex decreases due to occlusion, so the true level of reflex activation is uncertain. We also fitted the sum (M + H) with Eq. (1) and the variance accounted for (vaf) was also 99.9%. Finally, the difference between these curves was well-fitted to the H-reflex (H eq.1). The H-reflex is activated at lower stimulus levels than the M-wave, as can be quantified by measuring the shift in stimulus required to activate the M-wave and the sum M + H to 0.2 Mmax. This level was chosen because the M-wave tended to be very small when H = 0.2 Mmax so there was little occlusion. The calculated values for nine subjects to recruit 0.2 Mmax were 54.3 ± 4.5 V and 39.9 ± 3.7 V for the M-wave and H-reflex, respectively. In other words, the recruitment curve for the H-reflex was shifted by 14.4 V, or 26.6%, on average compared to the M-wave. The half-widths (voltage range to go from approximately 0.25–0.75 of the maximum value) were 3.4 ± 0.4 for the M-wave and 7.4 ± 2.0 V for M + H.
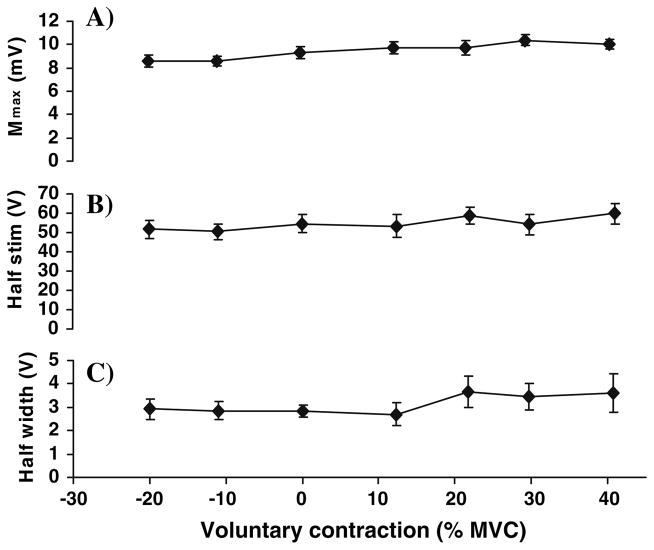
Figure 1 also shows an alternative method for fitting the H-reflex (H eq.2) that is described in the “Methods” and will be discussed later. In this trial the fit was not nearly as good as with the first equation. Values of vaf for the fits to the M-waves were highest with nearly all trials having a vaf > 95%. Values for M + H were next with 70% having vaf > 95% and most of the rest having vaf > 90%, Values of vaf for the H-reflex were lower, but still good with the results from Eq. (1) (about 70% having a vaf > 90%) generally higher than Eq. (2) (about 50% having a vaf > 90%). Thus, Eq. (1) is a convenient way to quantify the results from these experiments and will be used in the following sections. Figure 2 shows the parameters of the curves fitted to the M-wave as a function of the level of voluntary contraction. The parameters m and h had a small but significant trend (P < 0.05), but the parameters of the M-wave are relatively independent of the level of voluntary contraction.
Fig. 2.
The parameters of the curves fitted to the M-waves as a function of voluntary contraction for nine subjects. Valid data from all subjects were sorted according to contraction level into groups of eight. Thus each point shows the mean ± SE of eight values. Negative values indicate antagonist TA contraction, while positive values represent levels of soleus contraction. Relative to Eq. (1): a Mmax = m, b Half Stim = h, and c Half Width = w. These parameters change little over the levels of voluntary contraction studied
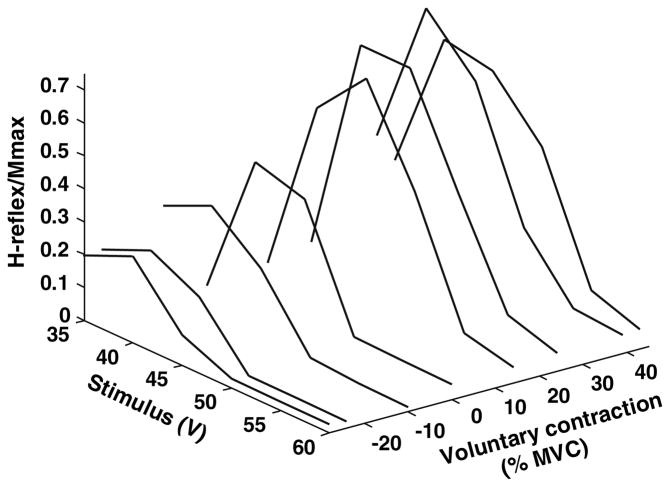
In contrast, Fig. 3 illustrates for one subject how the H-reflex varies both with the level of measured background contraction and the stimulus intensity in a 3D graph. The actual values are shown connected by straight line segments for clarity. Activating the antagonist TA decreased the magnitude of the H-reflex sharply. Increasing the contraction of the agonist, soleus, initially increased the H-reflex, but subsequently decreased it. In this subject the peak occurred at about 30% MVC and decreased at 40%. The stimulus intensity at which the peak H-reflex was elicited varied somewhat with the level of voluntary contraction, but the shape of the curve was largely unchanged. This was verified for the population as a whole using the fitted parameters.
Fig. 3.
A representative example of a 3D plot comparing the magnitude of the soleus H-reflex to both tibial nerve stimulus intensity and the level of voluntary antagonist (negative values) or agonist (positive values) contraction. TA contraction diminishes the soleus H-reflex; increasing soleus contraction increases the H-reflex to a peak and then reduces it
Figure 4a shows that increasing activation of soleus muscle caused the reflex to peak and subsequently decline with further contraction. Increasing activation of TA diminished the H-reflex. Since TA and soleus are antagonists and contribute to torques with opposite signs, the EMGs have been plotted with opposite signs, as has been done for some years (e.g., Kearney and Chan 1982). In this figure modulation of the H-reflex with the level of voluntary contraction had a parabolic shape. The parabolic trend lines fitted the data well, with the group mean of the vaf values equal to 0.95 (P < 0.0001). The fitted curves for all nine subjects are shown in Fig. 4b.
Fig. 4.
A representative example (a) and a compilation of nine subjects (b) illustrating the parabolic form of the normalized soleus H-reflex over a range of antagonist and agonist activation. Negative and positive values indicate the level of tibialis anterior and soleus contraction, respectively. The solid black boxes and trend line in a represent the data obtained from the constant stimulus intensity trials, while the open circles and dotted line serve as a consistency check from the input–output trials (see “Quantification of soleus H-reflex relative to level of voluntary contraction”)
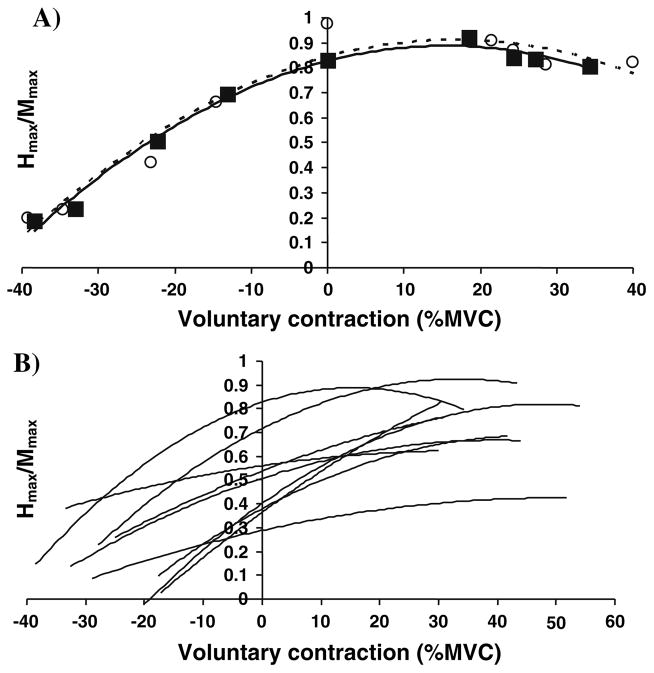
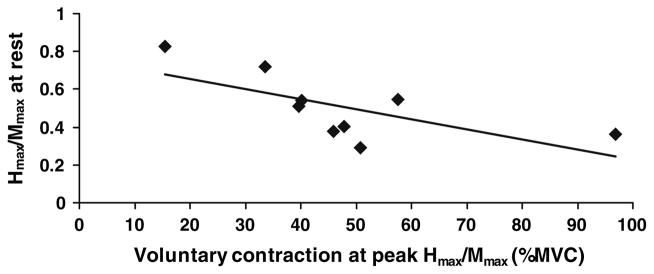
Figure 5 shows that the level of agonist contraction that produced the peak H-reflex was inversely related to the level of the H-reflex at rest (Fig. 5). The linear trend line (vaf = 0.45, P = 0.02) displayed a relatively large y-intercept, or Hmax/Mmax at rest, of 0.76 (P ≤ 0.001). In other words, subjects with large reflexes at rest experienced peak reflexes at lower levels of soleus contraction. Those with lesser responses at rest experienced peak H-reflexes at higher contractile levels, although these maxima were generally still smaller than for subjects with large responses at rest.
Fig. 5.
The soleus H-reflex at rest was inversely related to the level of agonist background contraction at which the peak Hmax/Mmax occurred. Subjects with large H-reflexes at rest had a peak response at low levels of soleus activation, while those with smaller H-reflexes at rest reached their peak reflex at larger levels of contraction. The values were obtained from the equations of the parabolic trend lines fitted to the results of the trials using a constant stimulus intensity (see “Methods” and Fig. 4)
Homosynaptic depression
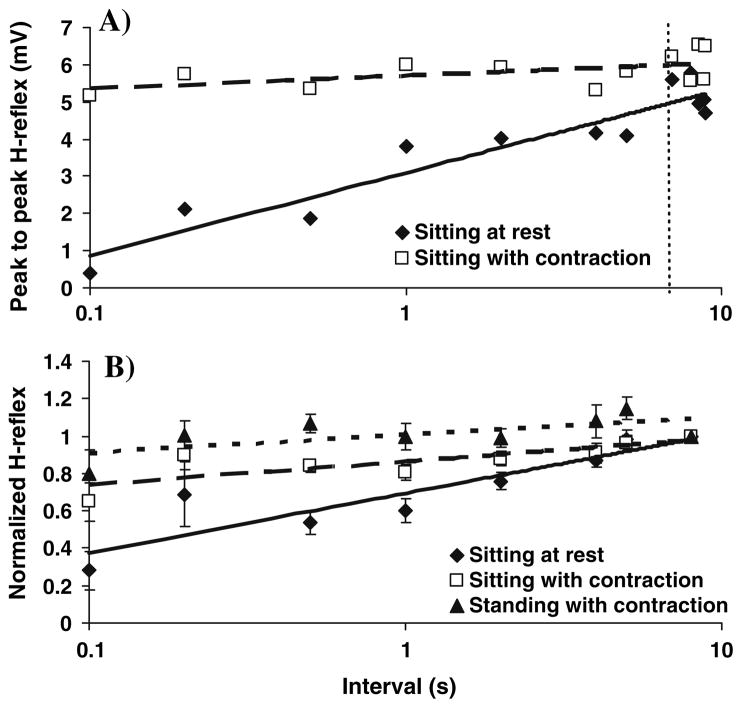
We now turn to the effects of voluntary contraction and interval between stimuli on the H-reflex. As the interval between stimuli to the tibial nerve decreased (Fig. 6a), the reflex to the second stimulus was more and more depressed, when subjects were seated at rest. However, with voluntary soleus contraction in either seated or standing positions, this HD was greatly reduced or abolished. After normalization of the H-reflexes to the average of the values measured with delays of 7–8.9 s (Fig. 6b), the modulation of HD with posture and time could be analyzed statistically. For subjects seated at rest, significant depression was found at all inter-stimulus intervals up to 4 s (P < 0.05). When subjects were seated while maintaining voluntary soleus contraction, significant HD was noted only at intervals of 0.1, 0.5, 1, and 2 s (P < 0.01). In contrast, no significant HD was found at any interval (P > 0.05) when subjects were standing with the same level of voluntary contraction; significant excitation was even noted at the 5 s interval (P = 0.015). HD was significantly greater when seated at rest than in other positions at intervals of 0.1, 0.5, 1, and 2 s (P < 0.05). At 4 and 5 s, subjects also showed greater HD when sitting at rest, compared to that when standing (P < 0.05). Finally, HD was significantly greater with voluntary contraction while seated, compared to standing while contracting at intervals of 0.1, 0.5, 1, 2, and 5 s (P < 0.05).
Fig. 6.
a A representative example of HD data from one subject. The values determined between 7–8.9 s (after the dotted line) were averaged, and the H-reflexes obtained with intervals of 0.1, 0.2, 0.5, 1, 2, 4 and 5 s were normalized to this value. b HD was reduced with 15–20% soleus MVC when seated and virtually abolished upon standing with the same level of contraction. Group mean ± SE are shown (n = 12)
Discussion
The “simple”, largely monosynaptic H-reflex actually has considerable complexity. Typically, reflexes are measured at rest (Pierrot-Deseilligny and Burke 2005), despite evidence of task-, phase-, and context-dependency (Stein and Capaday 1988; Zehr and Stein 1999b). Measurements at rest do not accurately represent the H-reflex during motor tasks. Additional factors must be considered when measuring an H-reflex, including stimulus intensity, level of voluntary agonist or antagonist contraction, and postural state. Because the H-reflex is often tested clinically (Pierrot-Deseilligny and Burke 2005), reflex function in healthy, neurologically normal individuals must be understood to recognize when something is wrong. For this purpose we have quantified the reflex under various behavioral conditions.
Quantification of the H-reflex
First, we fit the well-known M–H curve (Fig. 1) that relates both the M-wave and the H-reflex to stimulus intensity. The M-wave was fit to the Boltzmann equation that has been used for example to describe the input–output properties of the human corticospinal pathway (Devanne et al. 1997). Since vaf ≥ 95%, the fits are excellent. The parameters of the Boltzmann equation were relatively independent of the level of voluntary contraction (Fig. 2), although the value of Mmax, for example, does vary more dramatically with the length of the muscle (Inman et al. 1952; Simonsen and Dyhre-Poulsen 1999; Frigon et al. 2007). Some but not all studies have indicated an increase in Mmax with increasing voluntary contraction (Nagata and Christianson 1995; Linnamo et al. 2001; Frigon et al. 2007), as found here (Fig. 2a).
The sum, M + H, was also fitted to the same curve (Fig. 2) and gave nearly as high values of vaf. This was less expected because the sum of two Boltzmann equations is not another Boltzmann equation. However, because of the overlap of the M and H curves, the fit is reasonably good. The larger value of the half-width is probably a reflection of the composite nature of the curve. Also, we could obtain a good approximation to the measured H-reflex by subtraction. Hoehler and Buerger (1981) presented a number of alternative methods. Their preferred method assumed that motor axons in the nerve were recruited randomly so that the measured H-reflex was scaled by a factor that depended on the proportion of motor fibers that were not activated directly at any stimulus strength [see Eq. (2)]. This method gave a better fit than when they assumed that motor axons were recruited in inverse order of size (from large to small). In addition, the situation is complicated by the presence of F-waves or other factors (Hoehler and Buerger 1981). The method we have used for fitting the sum M + H avoids these issues and generally gave a better fit.
Having fitted the M–H curves and estimated Hmax the next step was to examine the variation of Hmax with contraction of agonist and antagonist muscles (Fig. 2). As has been shown repeatedly (Hoffmann 1918; Slot and Sinkjaer 1994; Pierrot-Deseilligny and Burke 2005), Hmax decreases with increasing antagonist activation. It increases with increasing agonist contraction up to a maximum and then declines (Slot and Sinkjaer 1994). Many pathways could be involved; as well as changes in excitatory pathways, both recurrent inhibition and presynaptic inhibition, for example, change with voluntary activation (Hultborn and Pierrot-Deseilligny 1979; Katz et al. 1988). Whatever the pathways involved, a similar result was recently found for motor evoked potentials elicited by transcortical magnetic stimulation (Martin et al. 2006). We found that the change in Hmax with contraction level was well fitted by a parabola over the entire range of voluntary contractions studied. Furthermore, the peak of the parabola (the overall peak value of Hmax) varied inversely with the value of Hmax at rest (Fig. 5). In other words, subjects, who had large reflexes at rest, showed only small increases and Hmax soon began to decline with increasing activation of the agonist muscles. In contrast, subjects, who had small reflexes at rest, continued to increase Hmax up to much higher levels of agonist activation. Common activities such as walking require alternating activation and inhibition of different muscle groups so the reflex activation can only be determined as part of the activities of interest (Stein and Thompson 2006).
The parabolic relationship with the presence of a peak and its dependence on the resting reflex can be understood qualitatively as follows. With voluntary contraction, motor neurons are depolarized closer to threshold so the probability that an excitatory post-synaptic potential (EPSP) reaches threshold upon electrical stimulation rises. If large EPSPs are already generated reliably at rest, then fewer motor neurons will still be available for voluntary activation than in people with smaller reflexes at rest. However, once motor neurons are recruited to fire repetitively, they will sometimes be refractory or hyperpolarized enough that they are not activated by the sensory stimulus in a manner that depends on the frequency–current (f–I) relationship. When a sufficient number are active and do not respond reflexly on a fraction of trials, the H-reflex will decline. In the “Appendix” we show that the parabolic relationship and the relationship between the location in the peak of the parabola and the level of voluntary contraction emerge from a realistic model that is consistent with these qualitative ideas.
The wide variation in the H-reflexes at rest is well known (Pierrot-Deseilligny and Burke 2005). To reduce the effect of this variability, Crone et al. suggested using a fixed value such as H/Mmax = 0.25 (Crone et al. 1990). However, this value may be at or above the maximum H-reflex that can be generated in some subjects, while it may only be a small fraction of Hmax for others. We prefer using a stimulus that generates a value near 0.5 Hmax so that excitatory and inhibitory effects can both be readily observed (Zehr and Stein 1999a). The reason for the wide variation in healthy individuals is unknown, but several factors can be cited. One factor may be age differences between subjects. Values of Hmax/Mmax decrease with increasing age; see Kido et al. (2004) and their references to earlier work. Also, the location of the nerve in different subjects with respect to the skin may vary and make activation of spindle afferents more or less effective. Another factor may be training; for instance, increased excitability of H-reflexes during maximum voluntary contraction occurs following a heavy-resistance strength training program (Aagaard et al. 2002) and professional ballet dancers have reduced reflex excitability compared to other groups (Nielsen et al. 1993a). However, H-reflex amplitude measured at rest has repeatedly been found to be unaffected by such training (Voigt et al. 1998; Aagaard et al. 2002). This further supports the importance of measuring H-reflexes during the activities of interest.
Homosynaptic depression
After eliciting one H-reflex, a second reflex could be reduced for a number of reasons: refractoriness due to the afterhyperpolarization, recurrent inhibition, inhibitory feedback from Golgi tendon organs and presynaptic inhibition. However, these effects would not be expected to last for several seconds, so the prolonged HD has been attributed to a decreased release of transmitter that reduces the excitability of the H-reflex for a period of time ranging from 1 to 2 s (Lamy et al. 2005) to over 10 s (Hultborn et al. 1996). Yet, some pathways in humans are not depressed at long intervals (Pierrot-Deseilligny and Burke 2005) so the functional significance of HD remains uncertain.
In human experiments EPSPs are not directly measurable. However, the effects of preceding length changes and contractions, which can modify spindle firing rates have been interpreted to support the idea that increasing firing rates lead to reduced EPSPs and hence reduced H-waves; see for example (Gregory et al. 1990; Wood et al. 1996). In reviewing his classic studies on the effects of eliciting EPSPs at different frequencies, Eccles (p. 84–87) found synapses that either increased or decreased the size of their EPSPs with increasing frequency (Eccles 1964). Luscher et al. (1983) reported that as the rate of stimulation increased up to 2–5 Hz, the EPSPs in cat motor neurons decreased progressively. However, at higher rates the EPSPs increased and reach a maximum at approximately 10–20 Hz, but then declined again at frequencies of up to 100 Hz. Clearly, synaptic transmission is a complex, dynamic process involving the interplay of facilitation and depression; see review by Zucker and Regehr (2002).
Despite the mixed results, HD has been considered a potential confounding variable in the accurate measurement of H-reflexes that could lead to inappropriate medical diagnoses and treatments. Reduced HD has been noted in spastic patients (Nielsen et al. 1993b), stroke patients (Masakado et al. 2005), and the normal elderly (Robertson and Koceja 2003), and has been considered a major factor in the development of spasticity (Pierrot-Deseilligny and Burke 2005). Furthermore, Lamy et al. (2005) argued that HD may be important in limiting the extent to which muscle contraction is controlled by muscle afferents. Our results question the validity of such assumptions. Most studies have examined HD with subjects in the resting state, but studies involving maintained voluntary contractions have all found HD greatly reduced or abolished (see the “Introduction”). Moreover, these states are closer to those involved in functional activities such as standing and walking. Our results confirm significant depression in resting, seated subjects at all intervals up to 4 s, suggesting that intervals of as much as 10 s between stimuli (Hultborn et al. 1996) are needed for reliable H-reflex measurements. Although the interval of 0.2 s still showed significant depression, the HD appeared considerably less than expected from the trend line. Taborikova and Sax (1969) suggested that there are long-loop pathways that would produce excitation at times of about 0.2 s. Whatever the mechanism, HD at this and other intervals was much reduced when subjects voluntarily contracted the soleus muscle while seated.
When standing and maintaining the same level of contraction, HD was essentially abolished. A plausible explanation for the elimination of HD during functional motor activity (Stein and Thompson 2006) is that spindle afferents are active with voluntary contraction alone, often firing at high frequencies. As explained above, the EPSPs produced at these frequencies may be increased or decreased compared to rest. In either case, the addition of electrical stimulation that produces one or two extra imp./s will have little impact on a neuron that is already firing at a relatively high rate, thus failing to induce measurable changes in HD. To further validate the suggestion that HD is not a clinically important variable, neurological patients should be studied at various states of rest, voluntary contraction, and posture.
In conclusion, the amplitude of the human soleus H-reflex is greatly modulated depending on the level of activation of agonist or antagonist muscles and we have quantified the relationships involved. We have also confirmed the importance of measuring the reflex at a contractile level and postural state similar to that involved in the activity of interest. This will avoid confounding by HD, a phenomenon that we doubt is involved in functional movements or clinically important conditions such as spasticity.
Acknowledgments
We thank Dr. Monica Gorassini for helpful comments on the manuscript. Ms SuLing Chong and Mr Robert Rolf provided technical assistance. This research was supported by grants from the Canadian Institutes of Health Research and the Christopher Reeve Foundation.
Appendix
The modeling was done using the NEURON simulation environment with 250 motor neurons in the pool (Carnevale and Hines 2006). Each MN had three sections: initial segment (threshold for spike generation), soma and an equivalent dendritic cable. The morphology of the models was illustrated previously (Jones and Bawa 1997) and is similar to those used by others (Slot and Sinkjaer 1994). To simulate a range of sizes the diameter of the stem dendrite was calculated as
where di is diameter of the ith MN and the range of stem diameters, 1.6, was the range of diameters between the largest and smallest MNs.
The passive (leak) conductance of the pool of MNs was also varied over a range of two to generate the experimentally measured range of input resistance. The passive leak conductance (S/cm2) for each MN was calculated as
where g is specific conductance of the ith MN. This has to be combined with surface area and cable properties to generate the input resistance of the neuron. The resulting values for input resistance match the experimentally measured range (0.7–4 MΩ) for cat medial gastrocnemius MNs; e.g., (Fleshman et al. 1988). Corresponding values are not available for the human soleus muscle. After generating the pool of 250 MNs and setting the passive parameters, each section of the model was spatially divided into segments with a length constant (λ) less than 0.1 at a frequency of 100 Hz. This was done to ensure that spatial resolution meets the assumption of isopotentiality in each compartment of the model.
To simulate the composite Ia EPSP that is generated by the H-reflex stimulus a current pulse input was used rather than synaptic conductance changes; for validation see Jones and Bawa (1997). The current pulse input is located in the dendrite so that the resulting transient depolarizing potential measured in the soma has the same time course as a composite Ia EPSP generated using the observed distribution of synapses. This results in an H-reflex stimulus that evokes an EPSP that is 1.8 times larger in the lowest threshold (MN[1]) compared to the highest threshold MN (MN[250]).
Active properties were added using the Hodgkin–Huxley formalism (Jones and Bawa 1997). The initial segment and soma have fast transient Na+ and delayed rectifier K+ channels and the soma also has an AHP current generated by a K+ conductance. This current is a simplified version of the calcium-dependent K+ channel that underlies the AHP and is based on previous studies (Baldissera and Gustafsson 1974a, b). Across the pool of 250 MNs the AHPs vary from a duration of 160 ms in MN[1] to 90 ms in MN[250]. The time to peak AHP is shorter in the high threshold MNs and varies monotonically across the pool of MNs.
Voluntary input to the pool of 250 MNs was simulated as a current source in the soma with equal input to all MNs. The difference in passive and active properties across the pool resulted in an exponential distribution of thresholds, i.e., relatively more low threshold units. The minimal rhythmic firing rate for the lowest threshold MN (MN[1]) was 6 imp./s and this unit increased it’s firing rate to 19 imp./s when the highest threshold MN (MN[250]) was recruited with a minimal rhythmic firing rate of 13 imp./s. The amplitude of the voluntary input needed to recruit the MNs varied exponentially over a range of 2.5 from the lowest to highest threshold MNs. The shape of the motor unit action potential (MUAP) was not simulated, since the H-reflex is quite synchronous. MNs that responded to the stimulus occurred at a fixed latency after the stimulus within a window of 3–4 ms. The MUAP size had an exponential distribution across the pool with a range of 10.
Simulations were done to match the experimental paradigm; the MN pool was either at rest or subject to voluntary input that would recruit a subset of the pool. Stimuli were delivered after the onset of voluntary contraction at a time when the firing rates of the active MNs had accommodated to a steady state. The voluntary current input needed to recruit the lowest threshold MN was 2.5 nA and the highest threshold MN was recruited with an input of 6.25 nA. Currents were used from −2 nA (to simulate antagonist contraction) up to +5 nA for agonist contractions. This is a rather narrow range of currents because of the narrow range of thresholds chosen. However, the range of thresholds was increased to 2.5–35 nA while maintaining the relative spacing between MNs. The results were similar, except that the scale in Fig. 8 was extended.
Fig. 8.
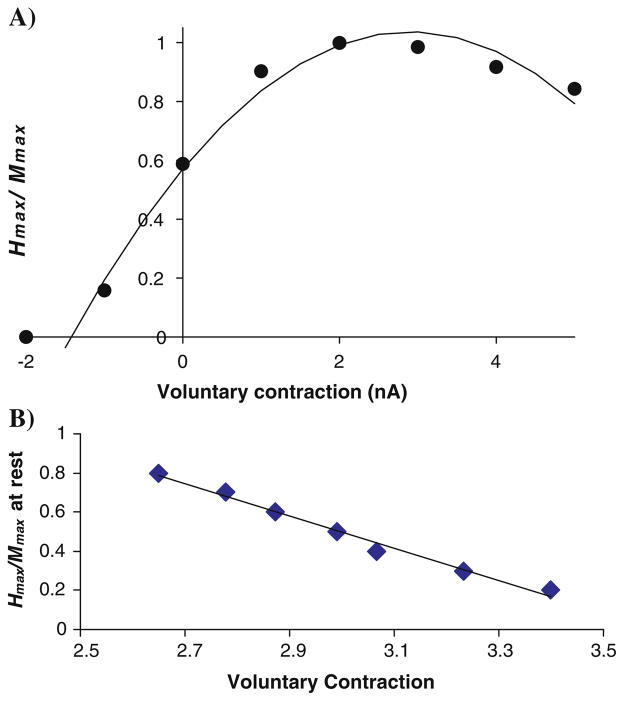
a The calculated ratio Hmax/Mmax varies with the level of voluntary contraction in a parabolic fashion, as was observed experimentally (Fig. 5). b Shifting the relative positions of the M-wave and H-reflex curves changes the ratio Hmax/Mmax at rest and the voluntary contraction level at which the maximum level is reached (cf. Fig. 5)
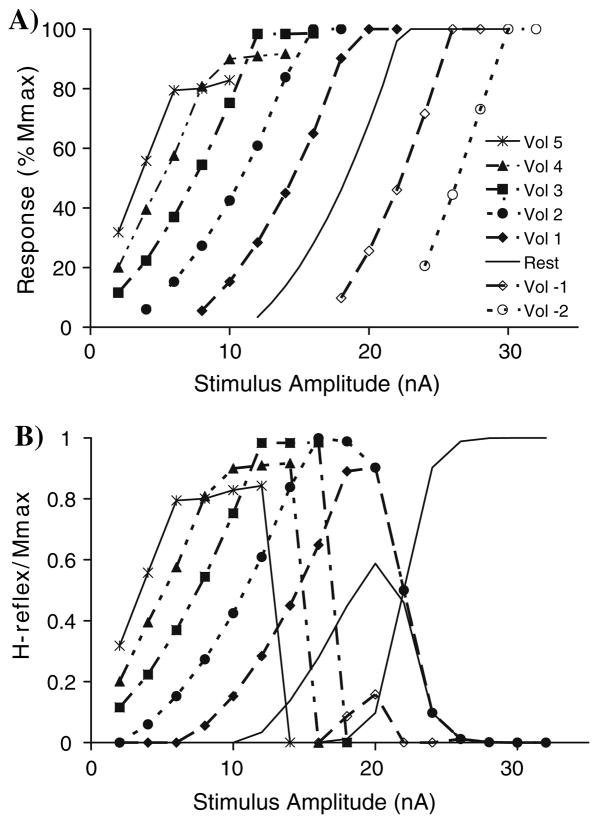
As the stimulus amplitude increased at rest the response increased until all 250 MNs were recruited via the reflex pathway, i.e., reflex curve at rest in Fig. 7a. With a simulated low level of voluntary (Vol) contraction (Vol 3) the reflex curve was shifted to the left and the final plateau amplitude was similar to rest. The reflex curve continued to shift to the left at higher levels of simulated voluntary contraction and the final plateau level decreased (Vol 4 = 89.8%, Vol 5 = 82.5% of Mmax). In contrast, simulations of antagonist contraction shifted the reflex curve to the right, but did not change the final plateau level. In the model all 250 MNs were still recruited, although this may not be plausible physiologically.
Fig. 7.
a Stimulus–response curves for the calculated H-reflexes (y-axis) with different levels of agonist (Vol > 0) or antagonist activity (Vol < 0). The stimulus in the model can be made arbitrarily large, so that full activation is achieved even with antagonist voluntary activity. b Adding a curve for the M-wave will occlude the firing of some motor neurons and therefore reduce the observed H-reflex. The magnitude of the H-reflex has been normalized relative to the maximum M-wave
Thus, in the simulations with the MN pool model the recruitment curve shifts to the left and the final amplitude decreases as voluntary contraction increases. With antagonist contraction, the curve shifts to the right. Since the M-wave curve changes little with voluntary contraction level experimentally (Fig. 2), an M-wave can be added to the simulation results and the H-reflex calculated by subtraction (Fig. 7b). With this set of parameters Hmax is 86% of Mmax at rest. With moderate contraction (Vol 3) the Hmax increases to almost 100% but with further increases in voluntary contraction the peak of the H-reflex curve goes down slightly (Vol 4 and 5). The stimulus amplitude for evoking the maximum H-reflex systematically decreases as voluntary contraction levels increase. Hmax declines much more precipitously with antagonist contraction (Vol = −1) but is elicited with a stimulus amplitude similar to that evoking Hmax in the rest condition. Figure 8a shows that Hmax/Mmax at different levels of voluntary contraction is well fitted by a second order polynomial, as was done for the experimental data (Fig. 5). Assuming that the only difference between individuals is the relative position of the M-wave and H-reflex curves, one can generate a range of resting values of Hmax/Mmax from 0.2 to 0.8. The peak of the curve also shifts with the value of Hmax at rest, as was found experimentally (compare Fig. 5 with Fig. 8b). In conclusion, a realistic model of the motor pool is able to reproduce the changes in H-reflexes with voluntary contraction that are found experimentally.
Contributor Information
Richard B. Stein, Department of Physiology, University of Alberta, Edmonton, Canada. Department of Biomedical Engineering, University of Alberta, Edmonton, Canada. Centre for Neuroscience, University of Alberta, Edmonton, Canada. 513 Heritage Medical Research Centre, University of Alberta, Edmonton, AB, Canada T6G 2S2
Kristen L. Estabrooks, Department of Physiology, University of Alberta, Edmonton, Canada
Steven McGie, Department of Physiology, University of Alberta, Edmonton, Canada.
Michael J. Roth, Department of Physiology, University of Alberta, Edmonton, Canada
Kelvin E. Jones, Department of Biomedical Engineering, University of Alberta, Edmonton, Canada. Centre for Neuroscience, University of Alberta, Edmonton, Canada
References
- Aagaard P, Simonsen EB, Andersen JL, Magnusson P, Dyhre-Poulsen P. Neural adaptation to resistance training: changes in evoked V-wave and H-reflex responses. J Appl Physiol. 2002;92:2309–2318. doi: 10.1152/japplphysiol.01185.2001. [DOI] [PubMed] [Google Scholar]
- Baldissera F, Gustafsson B. Firing behaviour of a neurone model based on the afterhyperpolarization conductance time course and algebraical summation. Adaptation and steady state firing. Acta Physiol Scand. 1974a;92:27–47. doi: 10.1111/j.1748-1716.1974.tb05720.x. [DOI] [PubMed] [Google Scholar]
- Baldissera F, Gustafsson B. Firing behaviour of a neurone model based on the afterhyperpolarization conductance time course. First interval firing. Acta Physiol Scand. 1974b;91:528–544. doi: 10.1111/j.1748-1716.1974.tb05708.x. [DOI] [PubMed] [Google Scholar]
- Burke D, Adams RW, Skuse NF. The effects of voluntary contraction on the H reflex of human limb muscles. Brain. 1989;112:417–433. doi: 10.1093/brain/112.2.417. [DOI] [PubMed] [Google Scholar]
- Capaday C. Neurophysiological methods for studies of the motor system in freely moving human subjects. J Neurosci Methods. 1997;74:201–218. doi: 10.1016/s0165-0270(97)02250-4. [DOI] [PubMed] [Google Scholar]
- Capaday C, Stein RB. A method for simulating the reflex output of a motoneuron pool. J Neurosci Methods. 1987;21:91–104. doi: 10.1016/0165-0270(87)90107-5. [DOI] [PubMed] [Google Scholar]
- Carnevale NT, Hines ML. The NEURON book. Cambridge University Press; Cambridge: 2006. [Google Scholar]
- Crone C, Hultborn H, Mazieres L, Morin C, Nielsen J, Pierrot-Deseilligny E. Sensitivity of monosynaptic test reflexes to facilitation and inhibition as a function of the test reflex size: a study in man and the cat. Exp Brain Res. 1990;81:35–45. doi: 10.1007/BF00230098. [DOI] [PubMed] [Google Scholar]
- Devanne H, Lavoie BA, Capaday C. Input–output properties and gain changes in the human corticospinal pathway. Exp Brain Res. 1997;114:329–338. doi: 10.1007/pl00005641. [DOI] [PubMed] [Google Scholar]
- Eccles JC. The physiology of synapses. Springer; Berlin: 1964. [Google Scholar]
- Fleshman JW, Segev I, Burke RB. Electrotonic architecture of type-identified alpha-motoneurons in the cat spinal cord. J Neurophysiol. 1988;60:60–85. doi: 10.1152/jn.1988.60.1.60. [DOI] [PubMed] [Google Scholar]
- Frigon A, Carroll TJ, Jones KE, Zehr EP, Collins DF. Ankle position and voluntary contraction alter maximal M-waves in soleus and tibialis anterior. Muscle Nerve. 2007;35:756–766. doi: 10.1002/mus.20747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gregory JE, Mark RF, Morgan DL, Patak A, Polus B, Proske U. Effects of muscle history on the stretch reflex in cat and man. J Physiol. 1990;424:93–107. doi: 10.1113/jphysiol.1990.sp018057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoehler FK, Buerger AA. A quantitative model of the Hoffmann reflex. Neurol Res. 1981;3:251–266. doi: 10.1080/01616412.1981.11739602. [DOI] [PubMed] [Google Scholar]
- Hoffmann P. Ueber die Beziehungen der Sehnenreflexe zur willkuerlichen Bewegung und zum Tonus. Zeitschrift fuer Biologie. 1918;68:351–370. [Google Scholar]
- Hultborn H, Nielsen JB. Modulation of transmitter release from Ia afferents by their preceding activity—a ‘postactivation depression’. In: Rudomin P, Romo R, Mendell L, editors. Presynaptic inhibition and neural control. Oxford University Press; New York: 1998. pp. 178–191. [Google Scholar]
- Hultborn H, Pierrot-Deseilligny E. Changes in recurrent inhibition during voluntary soleus contractions in man studied by an H-reflex technique. J Physiol. 1979;297:229–251. doi: 10.1113/jphysiol.1979.sp013037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hultborn H, Illert M, Nielsen J, Paul A, Ballegaard M, Wiese H. On the mechanism of the post-activation depression of the H-reflex in human subjects. Exp Brain Res. 1996;108:450–462. doi: 10.1007/BF00227268. [DOI] [PubMed] [Google Scholar]
- Inman VT, Ralston HJ, Saunders JB, Feinstein B, Wright EW., Jr Relation of human electromyogram to muscular tension. Electroencephalogr Clin Neurophysiol Suppl. 1952;4:187–194. doi: 10.1016/0013-4694(52)90008-4. [DOI] [PubMed] [Google Scholar]
- Jones KE, Bawa P. Computer simulation of the responses of human motoneurons to composite 1A EPSPS: effects of background firing rate. J Neurophysiol. 1997;77:405–420. doi: 10.1152/jn.1997.77.1.405. [DOI] [PubMed] [Google Scholar]
- Katz R, Meunier S, Pierrot-Deseilligny E. Changes in presynaptic inhibition of Ia fibres in man while standing. Brain. 1988;111:417–437. doi: 10.1093/brain/111.2.417. [DOI] [PubMed] [Google Scholar]
- Kearney RE, Chan CW. Contrasts between the reflex responses to tibialis anterior and triceps surae to sudden ankle rotation in normal human subjects. Electroencephalogr Clin Neurophysiol. 1982;54:301–310. doi: 10.1016/0013-4694(82)90179-1. [DOI] [PubMed] [Google Scholar]
- Kido A, Tanaka N, Stein RB. Spinal excitation and inhibition decrease as humans age. Can J Physiol Pharmacol. 2004;82:238–248. doi: 10.1139/y04-017. [DOI] [PubMed] [Google Scholar]
- Lamy JC, Wargon I, Baret M, Ben Smail D, Milani P, Raoul S, Penicaud A, Katz R. Post-activation depression in various group I spinal pathways in humans. Exp Brain Res. 2005;166:248–262. doi: 10.1007/s00221-005-2360-4. [DOI] [PubMed] [Google Scholar]
- Linnamo V, Strojnik V, Komi PV. Electromyogram power spectrum and features of the superimposed maximal M-wave during voluntary isometric actions in humans at different activation levels. Eur J Appl Physiol. 2001;86:28–33. doi: 10.1007/s004210100462. [DOI] [PubMed] [Google Scholar]
- Luscher HR, Ruenzel P, Henneman E. Composite EPSPs in motoneurons of different sizes before and during PTP: implications for transmission failure and its relief in Ia projections. J Neurophysiol. 1983;49:269–289. doi: 10.1152/jn.1983.49.1.269. [DOI] [PubMed] [Google Scholar]
- Martin PG, Gandevia SC, Taylor JL. Output of human motoneuron pools to corticospinal inputs during voluntary contractions. J Neurophysiol. 2006;95:3512–3518. doi: 10.1152/jn.01230.2005. [DOI] [PubMed] [Google Scholar]
- Masakado Y, Kagamihara Y, Takahashi O, Akaboshi K, Muraoka Y, Ushiba J. Post-activation depression of the soleus H-reflex in stroke patients. Electromyogr Clin Neurophysiol. 2005;45:115–122. [PubMed] [Google Scholar]
- Matthews PB. The effect of firing on the excitability of a model motoneurone and its implications for cortical stimulation. J Physiol. 1999;518:867–882. doi: 10.1111/j.1469-7793.1999.0867p.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagata A, Christianson JC. M-wave modulation at relative levels of maximal voluntary contraction. Eur J Appl Physiol Occup Physiol. 1995;71:77–86. doi: 10.1007/BF00511236. [DOI] [PubMed] [Google Scholar]
- Nielsen J, Crone C, Hultborn H. H-reflexes are smaller in dancers from The Royal Danish Ballet than in well-trained athletes. Eur J Appl Physiol Occup Physiol. 1993a;66:116–121. doi: 10.1007/BF01427051. [DOI] [PubMed] [Google Scholar]
- Nielsen J, Petersen N, Ballegaard M, Biering-Sorensen F, Kiehn O. H-reflexes are less depressed following muscle stretch in spastic spinal cord injured patients than in healthy subjects. Exp Brain Res. 1993b;97:173–176. doi: 10.1007/BF00228827. [DOI] [PubMed] [Google Scholar]
- Pierrot-Deseilligny E, Burke D. The circuitry of the human spinal cord: its role in motor control and movement disorders. Cambridge University Press; Cambridge: 2005. [Google Scholar]
- Robertson CT, Koceja DM. Post-activation depression of the soleus H-reflex in the elderly. Electromyogr Clin Neurophysiol. 2003;43:103–111. [PubMed] [Google Scholar]
- Simonsen EB, Dyhre-Poulsen P. Amplitude of the human soleus H reflex during walking and running. J Physiol. 1999;515:929–939. doi: 10.1111/j.1469-7793.1999.929ab.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slot PJ, Sinkjaer T. Simulations of the alpha motoneuron pool electromyogram reflex at different preactivation levels in man. Biol Cybern. 1994;70:351–358. doi: 10.1007/BF00200332. [DOI] [PubMed] [Google Scholar]
- Stein RB, Capaday C. The modulation of human reflexes during functional motor tasks. Trends Neurosci. 1988;11:328–332. doi: 10.1016/0166-2236(88)90097-5. [DOI] [PubMed] [Google Scholar]
- Stein R, Thompson A. Muscle reflexes in motion: how, what and why? Exerc Sport Sci Rev. 2006;34:145–153. doi: 10.1249/01.jes.0000240024.37996.e5. [DOI] [PubMed] [Google Scholar]
- Taborikova H, Sax DS. Conditioning of H-reflexes by a preceding subthreshold H-reflex stimulus. Brain. 1969;92:203–212. doi: 10.1093/brain/92.1.203. [DOI] [PubMed] [Google Scholar]
- Voigt M, Chelli F, Frigo C. Changes in the excitability of soleus muscle short latency stretch reflexes during human hopping after 4 weeks of hopping training. Eur J Appl Physiol Occup Physiol. 1998;78:522–532. doi: 10.1007/s004210050455. [DOI] [PubMed] [Google Scholar]
- Wood SA, Gregory JE, Proske U. The influence of muscle spindle discharge on the human H reflex and the monosynaptic reflex in the cat. J Physiol. 1996;497:279–290. doi: 10.1113/jphysiol.1996.sp021767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zehr EP, Stein RB. Interaction of the Jendrássik maneuver with segmental presynaptic inhibition. Exp Brain Res. 1999a;124:474–480. doi: 10.1007/s002210050643. [DOI] [PubMed] [Google Scholar]
- Zehr EP, Stein RB. What functions do reflexes serve during human locomotion? Prog Neurobiol. 1999b;58:185–205. doi: 10.1016/s0301-0082(98)00081-1. [DOI] [PubMed] [Google Scholar]
- Zucker RS, Regehr WG. Short-term synaptic plasticity. Annu Rev Physiol. 2002;64:355–405. doi: 10.1146/annurev.physiol.64.092501.114547. [DOI] [PubMed] [Google Scholar]