Transethnic Genetic-Correlation Estimates from Summary Statistics

Abstract

The increasing number of genetic association studies conducted in multiple populations provides an unprecedented opportunity to study how the genetic architecture of complex phenotypes varies between populations, a problem important for both medical and population genetics. Here, we have developed a method for estimating the transethnic genetic correlation: the correlation of causal-variant effect sizes at SNPs common in populations. This methods takes advantage of the entire spectrum of SNP associations and uses only summary-level data from genome-wide association studies. This avoids the computational costs and privacy concerns associated with genotype-level information while remaining scalable to hundreds of thousands of individuals and millions of SNPs. We applied our method to data on gene expression, rheumatoid arthritis, and type 2 diabetes and overwhelmingly found that the genetic correlation was significantly less than 1. Our method is implemented in a Python package called Popcorn.

Introduction

Many complex human phenotypes vary dramatically in their distributions between populations as a result of a combination of genetic and environmental differences. For example, northern Europeans are on average taller than southern Europeans,¹ and African Americans have an higher rate of hypertension than European Americans.² Differences in allele frequencies, effect sizes, and genetic architectures drive the genetic contribution to population phenotypic differentiation. Understanding the root causes of phenotypic differences worldwide has profound implications for biomedical and clinical practice in diverse populations, the transferability of epidemiological results, aiding multi-ethnic disease mapping,^{3, 4} assessing the contribution of non-additive and rare-variant effects, and modeling the genetic architecture of complex traits. In this work, we consider a central question in the global study of phenotype: do genetic variants have the same phenotypic effects in different populations?

Although the vast majority of genome-wide association studies (GWASs) have been conducted in European populations,^{5, 6} the growing number of non-European and multi-ethnic studies^{4, 7, 8} provide an opportunity to study distributions of genetic effects across populations. For example, one recent study used mixed-model-based methods to show that the genome-wide genetic correlation of schizophrenia between European and African Americans is nonzero.⁹ Although powerful, computational costs and privacy concerns limit the utility of genotype-based methods. In this work, we make two significant contributions to studies of transethnic genetic correlation. First, we expand the definition of genetic correlation to better account for a transethnic context. Second, we develop an approach that uses only summary-level GWAS data to estimate genetic correlation across populations. Like other recent methods based on summary statistics,^{10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21} our approach supplements summary association data with linkage disequilibrium (LD) information from external reference panels, avoids privacy concerns, and is scalable to hundreds of thousands of individuals and millions of markers. Unlike traditional approaches that focus on the similarity of GWAS results,^{22, 23, 24, 25, 26} we use the entire spectrum of GWAS associations while accounting for LD to avoid filtering correlated SNPs.

In a single population, the genetic correlation of two phenotypes is defined as the correlation coefficient of SNP effect sizes.^{19, 27} In multiple populations, differences in allele frequency motivate multiple possible definitions of genetic correlation. Because a variant can have a higher effect size but lower frequency in one population, we consider both the correlation of allele effect sizes and the correlation of allelic impact. We define the transethnic genetic-effect correlation (ρ_ge, previously defined by Lee et al.²⁷ and implemented in Genome-wide Complex Trait Analysis [GCTA]) as the correlation coefficient of the per-allele SNP effect sizes. Similarly, we define the transethnic genetic-impact correlation (ρ_gi) as the correlation coefficient of the population-specific allele-variance-normalized SNP effect sizes.

Intuitively, the genetic-effect correlation measures the extent to which the same variant has the same phenotypic change, whereas the genetic-impact correlation gives more weight to common alleles than to rare ones separately in each population. Consider the case of a SNP that is rare in population 1 but common in population 2 and has an identical effect size in both populations. In this case, the correlation of effect sizes (genetic-effect correlation, ρ_ge) is 1. This, however, provides an incomplete picture of the relationship between the two populations, given that the allele has a much bigger impact on the distribution of the phenotype in population 2. Therefore, we define the genetic-impact correlation, ρ_gi, as the correlation of effect sizes after genotypes are normalized to have mean 0 and variance 1. In our hypothetical case, ρ_gi < ρ_ge, but the opposite can also be true. Consider again the case of a SNP rare in population 1 but common in population 2. If the effect size is large in the first population but small in the second, then ρ_ge might be much less than 1, but the impact of the allele in the two populations will be similar. Therefore, ρ_gi will be close to 1. Although other definitions of the genetic correlation are possible (see Discussion), these quantities capture two important questions about the study of disease in multiple populations: to what extent do the same mutations in multiple populations differ in their phenotypic effects, and to what extent are these differences mitigated or exacerbated by differences in allele frequency?

To estimate genetic correlation, we take a Bayesian approach wherein we assume genotypes are drawn separately from within each population and effect sizes have a normal prior (the infinitesimal model²⁸). Although this model is unlikely to represent reality, it has been used successfully in practice.^{9, 17, 18, 29, 30} The infinitesimal assumption yields a multivariate normal distribution on the observed test statistics (Z scores), where the covariance matrix is a function of the heritability and genetic correlation. Rather than pruning SNPs in LD,^{11, 31, 32} this allows us to explicitly model the resulting inflation of Z scores. We then maximize an approximate weighted likelihood function to find the heritability and genetic correlation. This method is implemented in a Python package called Popcorn. Although it is derived for quantitative phenotypes, Popcorn extends easily to binary phenotypes under the liability threshold model. We show via extensive simulation that Popcorn produces unbiased estimates of the genetic correlation and the population-specific heritabilities with a SE that decreases as the number of SNPs and individuals in the studies increases. Furthermore, we show that our approach is robust to violations of the infinitesimal assumption.

We applied Popcorn to European and Yoruban gene-expression data,³³ as well as GWAS summary statistics from European and East Asian cohorts affected by rheumatoid arthritis (RA) and type 2 diabetes (T2D).^{34, 35} Our analysis of GEUVADIS (Genetic European Variation in Health and Disease) data showed that our summary-statistic-based estimator is concordant with the mixed-model-based estimator. We found that the mean transethnic genetic correlation across all genes was low (ρ_ge = 0.320 [0.009]) but increased substantially when the gene was highly heritable in both populations (ρ_ge = 0.772 [0.017]). In RA and T2D, we found ρ_ge to be 0.463 (0.058) and 0.621 (0.088), respectively.

Across all phenotypes considered, we overwhelmingly found that the transethnic genetic correlation is significantly less than 1. This observation highlights the need to study phenotypes in multiple populations because it implies that, up to the effects of unobserved variants, effect sizes at common SNPs tend to differ between populations. This indicates that results might not transfer between populations, and therefore predicting disease risk in non-Europeans on the basis of current GWAS results could be problematic. Our results provide further evidence that gaining insight into the genetic architecture of complex traits will require a multi-population approach.

Material and Methods

Our method takes as input summary association statistics from two studies of a phenotype in two different populations, along with two sets of reference genotypes each matching one of the populations in the study. Our method has two steps: first, we estimate the diagonal elements of the LD-matrix products ${\Sigma }_1^2$, ${\Sigma }_2^2$, and Σ₁Σ₂; second, using these estimates, we find the maximum-likelihood values and estimate SEs of the parameters of interest: $h_1^2$ or $h_2^2$ and ρ_ge or ρ_gi. The details follow.

Consider two GWASs conducted on the same phenotype in different populations. Assume we have N₁ individuals genotyped on M SNPs in study 1 and N₂ individuals genotyped on the same SNPs in study 2. Let X₁ and X₂ be the matrices of mean-centered genotypes in studies 1 and 2, respectively, and let Y₁ and Y₂ be their normalized phenotypes. Let f₁ and f₂ be vectors of the allele frequencies of the M SNPs common to both populations. If we assume Hardy-Weinberg equilibrium within each population separately, the allele variances are ${\sigma }_1^2=2f_1\left(1-f_1\right)$ and ${\sigma }_2^2=2f_2\left(1-f_2\right)$. Let β₁ and β₂ be the (unobserved) per-allele effect sizes for each SNP in studies 1 and 2, respectively. The heritability in study 1 is then $h_1^2={\Sigma }_i{\sigma }_{li}^2{\beta }_{li}^2$ (and likewise for study 2). The objective of this work is to estimate transethnic genetic correlation from summary statistics of common variants, $Z_1=\left[{\left(X_1/{\sigma }_1\right)}^{\mathrm{T}}{Y}_1\right]/\sqrt{N_1}$ (and likewise for study 2), and estimates of population LD matrices (Σ₁ and Σ₂) from external reference panels. Define the genetic-effect correlation as ρ_ge = Cor(β₁, β₂) and the genetic-impact correlation as ρ_gi = Cor(σ₁β₁, σ₂β₂).

We assume that the genotypes are drawn randomly from each population and that phenotypes are generated by the linear model Y₁ = X₁β₁ + ε₁ (likewise for phenotype 2). When effect sizes β are assumed to be inversely proportional to allele frequency, as is commonly done,^{17, 30} we show (Appendix A) that under the linear infinitesimal genetic architecture, the joint distribution of the Z scores from each study is asymptotically multivariate normal with mean $\overrightarrow{0}$ and variance

$$\text{Var}\left(Z\right)=\left[\begin{array}{cc}{\Sigma }_1+\frac{N_1+1}{M}{h}_1^2{\Sigma }_1^2& {\rho }_{\text{gi}}\sqrt{h_1^2{h}_2^2}\frac{\sqrt{N_1{N}_2}}{M}{\Sigma }_1{\Sigma }_2\\ {\rho }_{\text{gi}}\sqrt{h_1^2{h}_2^2}\frac{\sqrt{N_1{N}_2}}{M}{\Sigma }_2{\Sigma }_1& {\Sigma }_2+\frac{N_2+1}{M}{h}_2^2{\Sigma }_2^2\end{array}\right].$$ (Equation 1)

However, when effect sizes are assumed to be independent of allele frequency, we show

$$\text{Var}\left(Z\right)=\left[\begin{array}{cc}{\Sigma }_1+\frac{N_1+1}{{\Vert {\sigma }_1^2\Vert }_1}{h}_1^2{\Sigma }_1{\sigma }_1^2{\Sigma }_1& {\rho }_{\text{ge}}\sqrt{h_1^2{h}_2^2}\frac{\sqrt{N_1{N}_2}}{\sqrt{{\Vert {\sigma }_1^2\Vert }_1{\Vert {\sigma }_2^2\Vert }_1}}{\Sigma }_1\sqrt{{\sigma }_1^2{\sigma }_2^2}{\Sigma }_2\\ {\rho }_{\text{ge}}\sqrt{h_1^2{h}_2^2}\frac{\sqrt{N_1{N}_2}}{\sqrt{{\Vert {\sigma }_1^2\Vert }_1{\Vert {\sigma }_2^2\Vert }_1}}{\Sigma }_2\sqrt{{\sigma }_2^2{\sigma }_1^2}{\Sigma }_1& {\Sigma }_2+\frac{N_2+1}{{\Vert {\sigma }_2^2\Vert }_1}{h}_2^2{\Sigma }_2{\sigma }_2^2{\Sigma }_2\end{array}\right].$$ (Equation 2)

Given these equations for variance, we can estimate the quantities ρ_gi or ρ_ge and $h_1^2$ or $h_2^2$ by maximizing the multivariate normal likelihood, $l\left({\rho }_{\text{g}\left\{\text{i},\text{e}\right\}},h_1^2,h_2^2|Z,\Sigma ,\sigma \right)\propto -\text{ln}\left(\left|C\right|\right)-Z^{\text{T}}{C}^{-1}Z$, where C is either of the above covariance matrices in Equation 1 or 2. Because Σ₁ and Σ₂ are estimated from finite external reference panels, estimating the maximum likelihood of the above multivariate normal distribution leads to over-fitting. We employ two optimizations to avoid this problem. First, we maximize an approximate weighted likelihood that uses only the diagonal elements of each block of Var(Z). This allows us to account for the LD-induced inflation of tests statistics, but it discards covariance information between pairs of Z scores and therefore leads to over-counting Z scores of SNPs in high LD. To compensate for this, we downweight Z scores of SNPs in proportion to their LD. Second, rather than compute the full products ${\Sigma }_1^2$, ${\Sigma }_2^2$, and Σ₁Σ₂ over all M SNPs in the genome, we choose a window size W and approximate the product by ${\left({\Sigma }_a{\Sigma }_b\right)}_{ii}={\sum }_{w=i-W}^{w=i+W}{r}_{aiw}{r}_{biw}$. These optimizations are similar to those employed by LD-score regression.¹⁷ The full details of the derivation and optimization are provided in Appendix A.

Results

Simulated Genotypes and Simulated Phenotypes

Using HAPGEN2,³⁴ we simulated 50,000 European (EUR)-like and 50,000 East Asian (EAS)-like individuals at 248,953 chromosome 1–3 SNPs with an allele frequency above 1% in both EUR and EAS HapMap 3 populations. HAPGEN2 implements a model that combines haplotype recombination with mutation and results in excess local relatedness among the simulated individuals. To account for this local structure, we used PLINK 2³⁵ to filter individuals with genetic relatedness above 0.05, resulting in 4,499 EUR-like individuals and 4,837 EAS-like individuals. From these simulated individuals, 500 per population were chosen uniformly at random to serve as an external reference panel for estimating Σ₁ and Σ₂.

In each simulation, effect sizes were drawn from a “spike and slab” model, where ${\beta }_{1i},{\beta }_{2i}\sim \mathcal{N}\left(0,\left[\begin{array}{cc}{h}_1^2& {\rho }_{\text{ge}}\sqrt{h_1^2{h}_2^2}\\ {\rho }_{\text{ge}}\sqrt{h_1^2{h}_2^2}& h_2^2\end{array}\right]\right)$ with probability p and ${\beta }_{1i},{\beta }_{2i}=\left(\mathrm{0,0}\right)$ with probability 1 − p. ρ_gi were analytically computed from the simulated effect sizes and allele frequencies in the simulated reference genotypes. Quantitative phenotypes were generated under a linear model with independent and identically distributed noise and normalized to have mean 0 and variance 1, whereas binary phenotypes were generated under a liability threshold model where individuals are labeled as case subjects when their liability exceeds a threshold $\tau ={\Phi }^{-1}\left(1-K\right)$, in which K is the population disease prevalence.³⁶

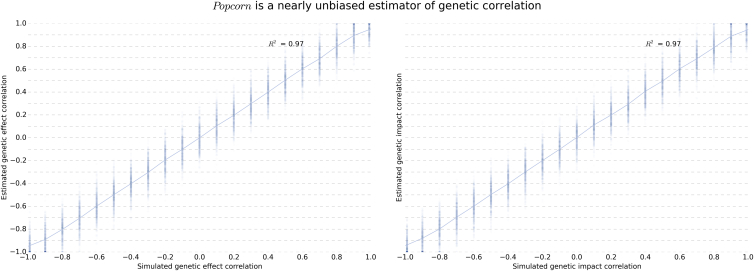
We varied $h_1^2$, $h_2^2$, ρ_ge, and ρ_gi, as well as the number of individuals in each study (N₁ and N₂), the number of SNPs (M), the population prevalence (K), and proportion of causal variants (p) in the simulated GWASs, and generated summary statistics for each study. The results shown in Figure 1 and Figure S1 demonstrate that the estimators are nearly unbiased as the genetic correlation and heritabilities vary. Furthermore, by varying the proportion of causal variants p, we show that our estimator is robust to violations of the infinitesimal assumption (Figure S2). In Figure S3, we show that the SE of the estimator decreases as the number of SNPs and individuals in the study increases. In Figure S4, we simulate data for 4,499 EUR-like individuals and 15,101 EAS-like individuals for a range of genetic correlations to show that our estimators remain nearly unbiased when the sample sizes of the two populations are very different. Finally, we show in Table S1 that our estimates of the heritability of liability in case-control studies are nearly unbiased.

Figure 1.

True and Estimated Genetic-Impact and Genetic-Effect Correlations

All simulations were conducted with a simulated EUR and EAS heritability of 0.5 with 4,499 simulated EUR and 4,836 simulated EAS individuals at 248,953 SNPs.

Simulations with Nonstandard Disease Models

Our approach, as well as genotype-based methods such as GCTA, makes assumptions about the genetic architecture of complex traits. Previous work has shown that violations of these assumptions can lead to bias in heritability estimation;³⁷ therefore, we sought to quantify the extent to which this bias might affect our estimates. We simulated phenotypes under six different disease models: (1) independent, where the effect size is independent of allele frequency; (2) inverse, where the effect size is inversely proportional to allele frequency; (3) rare, where only SNPs with an allele frequency under 10% affect the trait; (4) common, where only SNPs with an allele frequency between 40% and 50% affect the trait; (5) difference, where effect size is proportional to the difference in allele frequency; and (6) adversarial, a difference model where the sign of β is set to increase the phenotype in the population where the allele is most common. Additional genetic architectures, including ones where effect sizes are not a direct function of MAF,³⁸ are possible.

We simulated phenotypes by using genotypes with an allele frequency above 1% or 5% and compared the true and estimated genetic-impact and genetic-effect correlations among all models (Table 1). We found that when only SNPs with a frequency above 5% in both populations were used, the difference in ρ_ge and ρ_gi was minimal except in the most adversarial cases. Even in the adversarial model, the true difference was only 7%. Although they are unlikely to represent reality, the four nonstandard disease models result in substantial bias in our estimators. When SNPs with an allele frequency above 1% in both populations are included, the differences are more pronounced. This is because the normalizing constant 1/σ rapidly increases as the SNP becomes more rare. Indeed, as SNPs become more rare, having an accurate disease model becomes increasingly important. Therefore, we proceeded with a 5% MAF cutoff in our analysis of real data and used the notation $h_c^2$ to refer to the heritability of SNPs with an allele frequency above 5% in both populations (the common-SNP heritability). Note, however, that one of the advantages of maximum-likelihood estimation in general is that the likelihood can be reformulated to mimic the disease model of interest.

Table 1.

True and Estimated Values of Genetic-Impact and Genetic-Effect Correlations in Simulated EUR-like and EAS-like Genotypes

Model	MAF > 0.01				MAF > 0.05
ρge	ρgi	${\hat{\mathit{\rho }}}_{\mathbf{ge}}$	${\hat{\mathit{\rho }}}_{\mathbf{gi}}$	ρge	ρgi	${\hat{\mathit{\rho }}}_{\mathbf{ge}}$	${\hat{\mathit{\rho }}}_{\mathbf{gi}}$
Independent	0.500	0.478	0.500	0.460	0.500	0.488	0.509	0.469
Inverse	0.431	0.500	0.567	0.496	0.479	0.500	0.555	0.482
Rare	0.500	0.467	0.382	0.863	0.500	0.496	0.998	0.756
Common	0.500	0.500	0.522	0.493	0.500	0.500	0.502	0.496
Difference	0.500	0.416	0.354	0.435	0.500	0.461	0.410	0.412
Adversarial	0.710	0.604	0.525	0.651	0.714	0.667	0.601	0.675

Results are the average of 100 simulations with a phenotype heritability of 0.5 in each population.

Validating Popcorn by Using Gene Expression in GEUVADIS

We compared the common-SNP heritability $\left(h_c^2\right)$ and genetic-correlation estimates of Popcorn to those of GCTA in the GEUVADIS dataset, for which raw genotypes are publicly available. GEUVADIS consists of RNA-sequencing (RNA-seq) data for 464 lymphoblastoid cell line (LCL) samples from five populations in the 1000 Genomes Project. Of these, 375 are of European ancestry (CEU [Utah residents with ancestry from northern and western Europe from the CEPH collection], FIN [Finnish in Finland], GBR [British in England and Scotland], and TSI [Toscani in Italia]), and 89 are of African ancestry (YRI [Yoruba in Ibadan, Nigeria]). Raw RNA-seq reads obtained from the European Nucleotide Archive (accession number ENA: ERP001942) were aligned to the transcriptome with hg19 coordinates from the UCSC Genome Browser. RSEM³⁹ was used for estimating the abundances of each annotated isoform, and total gene abundance was calculated as the sum of all isoform abundances normalized to one million total counts or transcripts per million (TPM). For mapping of expression quantitative trait loci (eQTLs), European and Yoruban samples were analyzed separately. For each population, we median normalized TPMs to account for differences in sequencing depth in each sample and standardized to mean 0 and variance 1. Of the 29,763 total genes, 9,350 with TPM > 2 in both populations were chosen for this analysis.

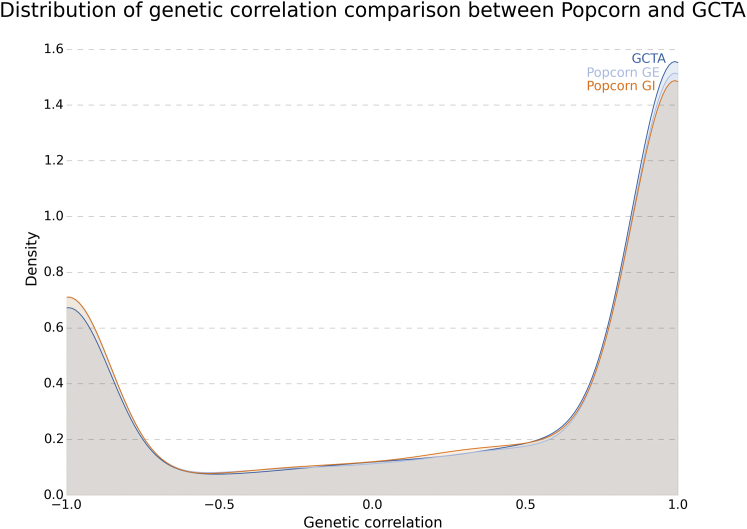
For each gene and using 30 principal components as covariates, we conducted a cis-eQTL association study at all SNPs within 1 Mb of the gene body and with an allele frequency above 5% in both populations. We found that GCTA and Popcorn agreed on the global distribution of heritability (Figure S5) and that GCTA’s estimates of genetic correlation had a similar distribution to Popcorn’s estimates of genetic-effect and genetic-impact correlation (Figure 2). Although the number of SNPs and individuals included in each gene analysis is too small for obtaining accurate point estimates of the genetic correlation on a per-gene basis (N = 464, M = 4279.5), the large number of genes enables accurate estimation of the global mean heritability and genetic correlation.

Figure 2.

The Distributions of the Estimates of Genetic Correlation Computed with Popcorn and GCTA Are Compared

The distribution was computed via Gaussian kernel density estimation on the set of genetic-correlation estimates.

Common-SNP Heritability and Genetic Correlation of Gene Expression in GEUVADIS

We found that the average cis-$h_c^2$ of the expression of the genes we analyzed was 0.093 (0.002) in EUR and 0.088 (0.002) in YRI. Our estimates are higher than previously reported average cis-heritability estimates of 0.055 in whole blood and 0.057 in adipose,⁴⁰ which could have arisen for several reasons. First, we removed 68% of the transcripts that are lowly expressed in either YRI or EUR data. Second, estimates from RNA-seq analysis of cell lines might not be directly comparable to microarray data from tissue.

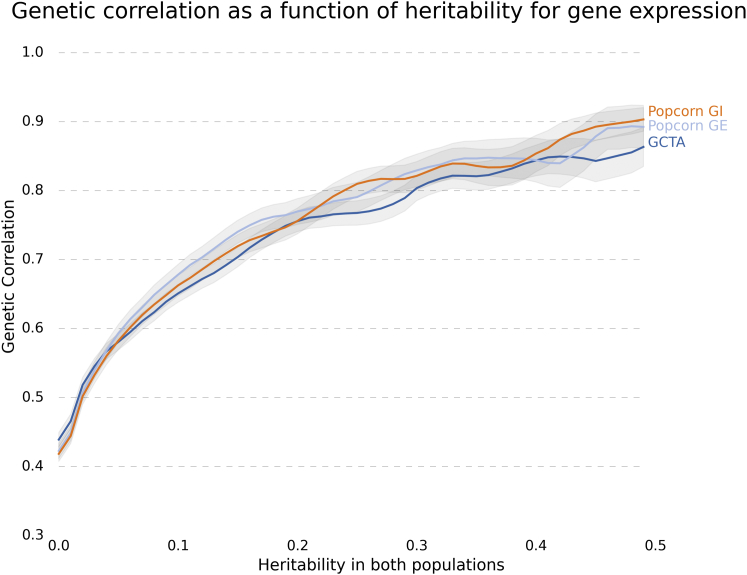
The average genetic-effect correlation was 0.320 (0.010), whereas the average genetic-impact correlation was 0.313 (0.010). Notably, the genetic correlation increased as the cis-$h_c^2$ of expression in both populations increased (Figure 3). In particular, when the cis-$h_c^2$ of the gene was at least 0.2 in both populations, the genetic-effect correlation was 0.772 (0.017), whereas the genetic-impact correlation was 0.753 (0.018).

Figure 3.

Genetic Correlation as a Function of Heritability for Gene Expression

The mean and SE of the genetic correlation of the set of genes with $h_1^2$ and $h_2^2$ exceeding threshold h in each analysis (y axis) are plotted against h (x axis).

In order to verify that our analysis did not contain any small-sample-size or conditioning biases, we analyzed the genetic correlation of simulated phenotypes over the GEUVADIS genotypes. We sampled pairs of heritabilities from the distribution of estimated expression heritability and simulated pairs of phenotypes to have the given heritability and a genetic-effect correlation of 0.0 over randomly chosen 4,000 bp regions from chromosome 1 of the GEUVADIS genotypes. Without conditioning, the average estimated genetic-effect correlation was −0.002 (0.003), indicating that the estimator remained unbiased. Furthermore, with conditioning on the heritability estimates above a certain threshold, the average estimated genetic-effect correlation was not significantly different from 0.0 (Figure S6).

We found that although the average genetic correlation was low, the genetic correlation increased with the cis-$h_c^2$ of the gene, indicating that as cis-genetic regulation of gene expression increases, it does so similarly in both YRI and EUR populations. This could help interpret the recent observation that although the global genetic correlation of gene expression across tissues is low,⁴⁰ cis-eQTLs tend to replicate across tissues.⁴¹ Because the presence of a cis-eQTL indicates substantial cis-genetic regulation, an analysis of eQTL replication across tissues implicitly conditions on a high heritability of gene expression and therefore might indicate a much higher genetic correlation than the average.

Summary Statistics of RA and T2D

Finally, we sought to examine the transethnic ρ_gi and ρ_ge in RA and T2D cohorts for which raw genotypes are not available. We obtained summary statistics from a RA GWAS of 58,284 individuals of European descent and 22,515 individuals of East Asian descent⁸ and from T2D GWASs of 69,033 individuals of European descent (DIAGRAM stage 1⁴²) and 18,817 individuals of East Asian descent.⁴³ We used genotypes from 504 East Asian and 503 European individuals sequenced as part of the 1000 Genomes Project as population-specific external reference panels for our EAS and EUR summary statistics, respectively. We removed the major histocompatibility region (chromosome 6, 25–35 Mb) from the RA summary statistics. We estimated the common-SNP heritability and genetic correlation by using 2,539,629 strand-unambiguous SNPs genotyped or imputed in both RA studies and 1,054,079 strand-unambiguous SNPs genotyped or imputed in both T2D studies; all SNPs had an allele frequency above 5% in 1000 Genomes EUR and EAS populations. The $h_c^2$ and genetic-correlation estimates are presented in Table 2. Our RA $h_c^2$ estimates of 0.177 (0.015) and 0.221 (0.026) for EUR and EAS, respectively, are lower than a previously reported mixed-model-based heritability estimate of 0.32 (0.037) in Europeans.⁴⁵ Similarly, our T2D $h_c^2$ estimates of 0.242 (0.013) and 0.105 (0.021) for EUR and EAS, respectively, are lower than a previously reported mixed-model-based estimate of 0.51 (0.065) in Europeans.⁴⁵ We stress that this discrepancy is most likely due to the correction of genomic control in summary association data (such correction does not affect genetic-correlation estimates¹⁹) and the difference between common-SNP heritability $h_c^2$ and total narrow-sense heritability $h^2$. Furthermore, estimates of the heritability of T2D from family studies can vary significantly.^{46, 47}

Table 2.

Heritability and Genetic Correlation of RA and T2D between EUR and EAS Populations

		hEUR2Liability	hEAS2Liability	ρge	ρgi
RA	estimate (SE)	0.18 (0.02)	0.22 (0.03)	0.46 (0.06)	0.46 (0.06)
95% CI	[0.15, 0.21]	[0.16, 0.28]	[0.34, 0.58]	[0.34, 0.58]
p > 0	3.90e−32	1.89e−17	1.37e−15	8.16e−16
p < 1	0.0	3.1e−197	2.53e−20	4.87e−22
T2D	estimate (SE)	0.24 (0.01)	0.11 (0.02)	0.62 (0.09)	0.61 (0.08)
95% CI	[0.22, 0.26]	[0.07, 0.15]	[0.44, 0.80]	[0.45, 0.77]
p > 0	2.41e−77	5.73e−7	1.70e−12	2.85e−13
p < 1	0.0	0.0	1.066e−5	2.06e−6

EUR RA data contained 8,875 case and 29,367 control subjects for a study prevalence of 0.23. EAS RA data contained 4,873 case and 17,642 control subjects for a study prevalence of 0.22. RA prevalence was assumed to be 0.5% in both populations.⁸ T2D EUR data contained 12,171 case and 56,862 control subjects for a study prevalence of 0.18. T2D EAS data contained 6,952 case and 11,865 control subjects for a study prevalence of 0.37. T2D EUR prevalence was assumed to be 8%,⁴² whereas T2D EAS prevalence was assumed to be 9%.⁴⁴ CI, confidence interval.

We found the genetic-effect correlation in RA and T2D to be 0.463 (0.058) and 0.621 (0.088), respectively, and the genetic-impact correlation was not significantly different at 0.455 (0.056) and 0.606 (0.083), respectively. The transethnic genetic-impact and genetic-effect correlations for both phenotypes were significantly different from both 1 and 0 (Table 2), showing that although the phenotypes have clear genetic overlap, the per-allele effect sizes differ significantly between the two populations.

Summary Statistics of Height and BMI

To further validate that our observations were not a statistical artifact, we used Popcorn to estimate the genetic correlation of one trait in one population across studies and compared it with those of GCTA and LDSC (LD Score). We obtained sex-stratified summary statistics of height and BMI from the GIANT consortium⁴⁸ and used Popcorn and LDSC to estimate the genetic correlation of height and BMI. Values for GCTA were taken from Yang al.⁴⁹ Scores for Popcorn and LDSC were computed from variants with an allele frequency above 5% in 1000 Genomes European-descent individuals, and genetic correlation was computed with all strand-unambiguous variants with an allele frequency above 5% in HapMap 3 (these are supplied with the summary statistics). Popcorn’s sex-stratified genetic correlations of height and BMI were not significantly different from 1.0 or from those of LDSC or GCTA (Table S2).

Discussion

We have developed transethnic genetic-effect and genetic-impact correlations and provided a method for estimating these quantities on the basis of only summary-level GWAS information and suitable reference panels. We have applied our estimator to several phenotypes: RA, T2D, and gene expression. Although the GEUVADIS dataset lacks enough power for inferring the genetic correlation of single or small subsets of genes, we can make inferences about the global structure of genetic correlation of gene expression. We have found that the global mean genetic correlation is low but that it increases substantially when the heritability is high in both populations. In all phenotypes analyzed, the genetic correlation was significantly different from both 0 and 1. Our results show that global differences in SNP effect size of complex traits can be large. In contrast, effect sizes of gene expression appear to be more conserved where there is strong genetic regulation.

It is not possible to draw conclusions about polygenic selection from estimates of transethnic genetic correlation. The effect sizes can be identical $\left({\rho }_{\text{ge}}=1\right)$ while polygenic selection acts to change only the allele frequencies. Similarly, the effect sizes can be different $\left({\rho }_{\text{ge}}<1\right)$ without selection. Differences in effect sizes at common SNPs can result from many phenomena. We expect that untyped and unimputed variants that are differentially linked to observed SNPs, along with rare or population-specific variants differentially linked to observed SNPs, will contribute significantly. If a gene-gene or gene-environment interaction exists but only marginal effects are tested, the observed marginal effects could be different in each population as a result of differences in allele frequency, even if the interaction effect is the same in both populations, and this will result in decreased genetic correlation. Although within-locus (dominance) interactions might also play a role,⁵⁰ the magnitude of this effect has been debated.⁵¹ Statistical noise could also be to blame, given that within-population meta-analyses of the same trait do not always show identical effects; however, we estimated the sex-stratified genetic correlation of height and BMI and found that neither was significantly different from 1, which agrees with previous results.⁴⁹ We emphasize that we cannot differentiate between these effects on the basis of this analysis alone, and establishing how much each of these effects contributes to inter-population differences in effect size will require further research.

Estimates of the transethnic genetic correlation are important for several reasons. They might help inform best practices for transethnic meta-analysis and potentially offer improvements over current methods that use F_ST to cluster populations for analysis.⁴ Further, the transethnic genetic correlation constrains the limit of out-of-sample phenotype predictive power. If the maximum within-population correlation of predicted phenotype P to true phenotype Y is ${\rho }_{YP}^{\text{max}}=\sqrt{h_1^2}$, then the maximum out-of-population correlation is ${\rho }_{YP}^{\text{max}}={\rho }_{\text{ge}}\sqrt{h_1^2}$ (Appendix A). Our observation that the genetic correlation is low for RA, T2D, and gene expression shows that out-of-population phenotypic predictive power is quite low. Similarly, it implies that assessing disease risk in non-Europeans on the basis of current GWAS results might be problematic; gaining insight into differences in genetic architecture and improving risk assessment will necessitate increased study of disease in many populations.

Although the genetic correlation of multiple phenotypes in one population has a relatively straightforward definition, extending this to multiple populations motivates multiple possible extensions. In this work, we have provided estimators for the correlation of genetic effect and genetic impact, but other quantities related to the shared genetics of complex traits between populations include the correlation of explained variance, ${\rho }_{\text{ge}}=\text{Cor}\left({\sigma }_1^2{\beta }_1^2,{\sigma }_2^2{\beta }_2^2\right)$, and the proportion of causal variants shared by the two populations. Interestingly, although our goal was to construct an estimator that determines the extent of genetic sharing independently of allele frequency, we have observed that the correlations of genetic effect and genetic impact are similar. Furthermore, our simulations show that under a random-effects model utilizing only SNPs with an allele frequency above 5% in both populations, the true genetic-effect and genetic-impact correlations are similar. We conclude that at variants common in both populations, differences in effect size and not allele frequency are driving the transethnic phenotypic differences in these traits.

Our approach to estimating genetic correlation has two major advantages over mixed-model-based approaches. First, utilizing summary statistics allows application of the method without data-sharing and privacy concerns that come with raw genotypes. Second, our approach is linear in the number of SNPs and thus avoids the computational bottleneck required for estimating the genetic relationship matrix. Conceptually, our approach is very similar to that taken by LD-score regression. Indeed, the diagonal of the LD-matrix product in one population is exactly the LD scores $\left({\sum }_{1ii}^2=l_i\right)$. One could ignore our likelihood-based approach and define cross-population scores as $c_i={\sum }_m{r}_{1im}{r}_{2im}$ in order to exploit the linear relationship $\mathbb{E}\left[Z_{1i}{Z}_{2i}\right]=\left(\sqrt{N_1{N}_2}/M\right){\rho }_{\text{gi}}\sqrt{h_1^2{h}_2^2}{c}_i$ (a similar approach can be taken for the genetic-effect correlation). Given that LD-score regression has been successfully used for computing the genetic correlation of two phenotypes in a single population, this derivation can be viewed as an extension of LD-score regression to one phenotype in two different populations. The main difference in our approach is choosing maximum likelihood rather than regression in order to fit the model. A comparison of our method to the LDSC software shows that they perform similarly as heritability estimators (Figure S7).

Of course, our method is not without drawbacks. First, it requires a large sample size and large number of SNPs to achieve SEs low enough for accurate estimation. Until recently, large-sample GWASs have been rare in non-European populations, although they are becoming more common. Similarly, the quality of reference panels could suffer in non-European populations, which could affect downstream analysis.⁵² Second, our method is limited to analyzing relatively common SNPs, both because having an accurate disease model is important for the analysis of rare variants and because estimates of effect size and correlation coefficients have a high SE at rare SNPs.¹⁷ Third, our analysis is currently limited to SNPs that are present in both populations. Indeed, it is currently unclear how best to handle population-specific variants in this framework. Fourth, our estimator of ρ is bounded between −1 and 1. This could induce bias when the true value is close to the boundary and the sample size is small. Fifth and finally, admixed populations induce very long-range LD that is not accounted for in our approach, and we are therefore limited to unadmixed populations.¹⁷

Our analysis leaves open several avenues for future work. We approximately maximize the likelihood of an $M\times M$ multivariate normal distribution via a method that uses only the diagonal elements of each block and discards covariance information between Z scores. A better approximation might lower the SE of the estimator, facilitating an analysis of the genetic correlation of functional categories, pathways, and genetic regions. We would also like to extend our analysis to include population-specific variants and variants with frequencies from 1% to 5% or lower than 1%. Our simulations indicate that having an accurate disease model is important for determining the difference between genetic-effect and genetic-impact correlations when rare variants are included. Maximum-likelihood approaches are well suited to different genetic architectures. For example, one could estimate both the global relationship between allele frequency and effect size and the global relationship between per-SNP F_ST and genetic correlation by incorporating parameters α and ϒ into the prior distribution of the effect sizes:

$${\beta }_{1i},{\beta }_{2i}\sim \mathcal{N}\left(0,\left[\begin{array}{cc}{h}_1^2{\sigma }_{1i}^{\alpha }& {\rho }_{\text{ge}}\sqrt{h_1^2{h}_2^2}{F}_{STi}^{\gamma }\\ {\rho }_{\text{ge}}\sqrt{h_1^2{h}_2^2}{F}_{STi}^{\gamma }& h_2^2{\sigma }_{1i}^{\alpha }\end{array}\right]\right).$$

We expect that incorporating these parameters will improve estimates of heritability and genetic correlation while revealing important biological insights.

Published: June 16, 2016

Appendix A

Consider two GWASs of a phenotype conducted in different populations. Assume we have N₁ individuals genotyped or imputed to M SNPs in study 1 and N₂ individuals genotyped or imputed to M SNPs in study 2. Let X₁ and X₂ and Y₁ and Y₂ be the matrices of mean-centered genotypes and phenotypes, respectively, of the individuals in studies 1 and 2, respectively. Let f₁ and f₂ be the allele frequencies of the M SNPs common to both populations. If we assume Hardy-Weinberg equilibrium, the allele variances are ${\sigma }_1^2=2f_1\left(1-f_1\right)$ and ${\sigma }_2^2=2f_2\left(1-f_2\right)$. Let β₁ and β₂ be the (unobserved) per-allele effect size for each SNP in studies 1 and 2, respectively. Define the genetic-impact correlation as ${\rho }_{\text{gi}}=\text{Cor}\left(\sqrt{{\sigma }_1^2}{\beta }_1,\sqrt{{\sigma }_2^2}{\beta }_2\right)$ and the genetic-effect correlation as ${\rho }_{\text{ge}}=\text{Cor}\left({\beta }_1,{\beta }_2\right)$. We present a maximum-likelihood framework for estimating the heritability of the phenotype in study 1 and its SE, the heritability of the phenotype in study 2 and its SE, and the genetic-effect and genetic-impact correlations of the phenotype between the studies and their SEs given only the summary statistics Z₁ and Z₂ and reference genotypes G₁ and G₂ representing the populations in the studies. We assume that genotypes are drawn randomly from populations with expected correlation matrices Σ₁ and Σ₂ and that every SNP is causal with a normally distributed effect size (although this assumption is not necessary in practice; see Figure S1).

Genetic-Impact Correlation

Let $X_1^{\prime }=X_1/\sqrt{{\sigma }_1^2}$ (and similarly for study 2) be normalized genotype matrices. We consider the standard linear model for the generation of phenotypes, where $Y_1=X_1^{\prime }{\beta }_1+{\mathit{\epsilon }}_1$ and $Y_2=X_2^{\prime }{\beta }_2+{\mathit{\epsilon }}_2$.

For convenience of notation, let $h_{\text{ix}}={\rho }_{\text{gi}}\sqrt{h_1^2{h}_2^2}$. We assume that the SNP effects follow the infinitesimal model, where every SNP has an effect size drawn from the normal distribution, and that the residuals are independent for each individual and normally distributed:

$$\left(\begin{array}{c}{\beta }_1\\ {\beta }_2\end{array}\right)\sim \mathcal{N}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\frac{1}{M}\left[\begin{array}{cc}{h}_1^2{\mathbb{I}}_M& h_{\text{ix}}{\mathbb{I}}_M\\ h_{\text{ix}}{\mathbb{I}}_M& h_2^2{\mathbb{I}}_M\end{array}\right]\right)$$ (Equation A1)

$$\left(\begin{array}{c}{\mathit{\epsilon }}_1\\ {\mathit{\epsilon }}_2\end{array}\right)\sim \mathcal{N}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}\left(1-h_1^2\right){\mathbb{I}}_M& 0\\ 0& \left(1-h_2^2\right){\mathbb{I}}_M\end{array}\right]\right),$$ (Equation A2)

where $h_1^2$ and $h_2^2$ are the heritability of the disease in studies 1 and 2, respectively, and ${\rho }_{\text{gi}}$ is the genetic-impact correlation.

Using the above model, we compute the distribution of the observed Z scores as a function of the reference-panel correlations and the model parameters ($h_1^2$, $h_2^2$, and ${\rho }_{\text{gi}}$). Given a distribution for Z and an observation of Z, we can then choose parameters that give the highest probability of observing Z. First, we compute the distribution of Z. It is well known that the Z scores of a linear regression are normally distributed given β when the sample size is large enough. Because $\mathrm{\mathbb{P}}\left(Z\right)\propto \mathrm{\mathbb{P}}\left(Z|\beta \right)\mathrm{\mathbb{P}}\left(\beta \right)$ and the product of normal distributions is normal, we need to compute only the unconditional mean and variance of Z to know its distribution. Specifically, let $Z={\left[Z_1^{\text{T}},Z_2^{\text{T}}\right]}^{\text{T}}$. Then, its mean is

$$\mathbb{E}\left[Z\right]=\mathbb{E}\left[\begin{array}{c}\frac{X_1^{\prime \text{T}}{Y}_1}{\sqrt{N_1}}\\ \frac{X_2^{\prime \text{T}}{Y}_2}{\sqrt{N_2}}\end{array}\right]=\left[\begin{array}{c}\frac{1}{\sqrt{N_1}}\left(\mathbb{E}\left[X_1^{\prime \text{T}}{X}_1^{\prime }\right]\mathbb{E}\left[{\beta }_1\right]+\mathbb{E}\left[X_1^{\prime \text{T}}\right]\mathbb{E}\left[{\mathit{\epsilon }}_1\right]\right)\\ \frac{1}{\sqrt{N_2}}\left(\mathbb{E}\left[X_2^{\prime \text{T}}{X}_2^{\prime }\right]\mathbb{E}\left[{\beta }_2\right]+\mathbb{E}\left[X_2^{\prime \text{T}}\right]\mathbb{E}\left[{\mathit{\epsilon }}_2\right]\right)\end{array}\right]=0.$$

The within-population variance is

$$\text{Cov}\left[Z_{1i},Z_{1j}\right]=\mathbb{E}\left[Z_{1i}{Z}_{1j}\right]={\mathbb{E}}_{X,\beta ,\mathit{\epsilon }}\left[\mathbb{E}\left[Z_{1i}{Z}_{1j}|X,\beta ,\mathit{\epsilon }\right]\right]$$

$$=\frac{1}{N_1}{\mathbb{E}}_{X,\beta ,\mathit{\epsilon }}\left[X_{1i}^{\text{′T}}\left(X_1^{\prime }{\beta }_1+{\mathit{\epsilon }}_1\right){\left(X_1^{\prime }{\beta }_1+{\mathit{\epsilon }}_1\right)}^{\text{T}}{X}_{1j}^{\prime }\right]$$

$$=\frac{1}{N_1}{\mathbb{E}}_{X,\beta }\left[X_{1i}^{\text{′T}}{X}_1^{\prime }{\beta }_1{\beta }_1^{\text{T}}{X}_1^{\text{T}}{X}_{2j}\right]+\frac{1}{N_1}{\mathbb{E}}_{X,\mathit{\epsilon }}\left[X_{1i}^{\text{′T}}{\mathit{\epsilon }}_1{\mathit{\epsilon }}_1^{\text{T}}{X}_{1j}^{\prime }\right]$$

$$=\frac{h_1^2}{M{N}_1}{\mathbb{E}}_X\left[X_{1i}^{\text{′T}}{X}_1^{\prime }{X}_1^{\text{′T}}{X}_{1j}^{\prime }\right]+\frac{1-h_1^2}{N_1}{\mathbb{E}}_X\left[X_{1i}^{\text{′T}}{X}_{1j}^{\prime }\right]$$

$$=\frac{h_1^2}{M{N}_1}\left(N_{1}M{r}_{1ij}+N_1\stackrel{M}{\sum _{m=1}}{r}_{1im}{r}_{1jm}+N_1^2\stackrel{M}{\sum _{m=1}}{r}_{1im}{r}_{1jm}\right)+\frac{1-h_1^2}{N_1}{r}_{1ij}$$

$$=r_{1ij}+\frac{N_1+1}{M}{h}_1^2{\Sigma }_{1\left(i\right)}{\Sigma }_1^{\left(j\right)},$$

where $r_{pij}={\Sigma }_{pij}$ is the correlation coefficient of SNP i and j in population p. Similarly, the between-population variance is

$$\text{Cov}\left[Z_{1i},Z_{2j}\right]=\frac{1}{\sqrt{N_1{N}_2}}{\mathbb{E}}_{X,\beta }\left[X_{1i}^{\text{′T}}{X}_1^{\prime }{\beta }_1{\beta }_2^{\mathrm{\top }}{X}_2^{\prime \text{T}}{X}_{2j}^{\prime }\right]+\frac{1}{\sqrt{N_1{N}_2}}{\mathbb{E}}_{X,\mathit{\epsilon }}\left[X_{1i}^{\prime \mathrm{\top }}{\mathit{\epsilon }}_1{\mathit{\epsilon }}_2^{\mathrm{\top }}X{\prime }_{2j}\right]$$

$$=\frac{h_{\text{ix}}}{M\sqrt{N_1{N}_2}}{\mathbb{E}}_X\left[X_{1i}^{\prime \mathrm{\top }}{X}_1^{\prime }{X}_2^{\prime \text{T}}{X}_{2j}^{\prime }\right]$$

$$=\frac{h_{\text{ix}}}{M\sqrt{N_1{N}_2}}\left(N_1{N}_2\stackrel{M}{\sum _{m=1}}{r}_{1im}{r}_{2jm}\right)$$

$$=\frac{\sqrt{N_1{N}_2}}{M}{h}_{\text{ix}}{\Sigma }_{1\left(i\right)}{\Sigma }_2^{\left(j\right)},$$

where ${\Sigma }_{\left(i\right)}$ denotes the i^th row of Σ, and ${\Sigma }^{\left(j\right)}$ denotes the j^th column. The covariance of the Z scores is thus

$$C=\text{Var}\left(Z\right)=\left[\begin{array}{cc}{\Sigma }_1+\frac{N_1+1}{M}{h}_1^2{\Sigma }_1^2& h_{\text{ix}}\frac{\sqrt{N_1{N}_2}}{M}{\Sigma }_1{\Sigma }_2\\ h_{\text{ix}}\frac{\sqrt{N_1{N}_2}}{M}{\Sigma }_2{\Sigma }_1& {\Sigma }_2+\frac{N_2+1}{M}{h}_2^2{\Sigma }_2^2\end{array}\right]$$ (Equation A3)

and $Z\sim \mathcal{N}\left(0,C\right)$.

Genetic-Effect Correlation

Let $h_{\text{ex}}={\rho }_{\text{ge}}\sqrt{h_1^2{h}_2^2}$. We modify the procedure above to use mean-centered instead of normalized genotype matrices and model the distribution of the effect sizes as

$$\left(\begin{array}{c}{\beta }_1\\ {\beta }_2\end{array}\right)\sim \mathcal{N}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}\frac{h_1^2}{{\Vert {\sigma }_1^2\Vert }_1}{\mathbb{I}}_M& \frac{h_{\text{ex}}}{\sqrt{{\Vert {\sigma }_1^2\Vert }_1{\Vert {\sigma }_2^2\Vert }_1}}{\mathbb{I}}_M\\ \frac{h_{\text{ex}}}{\sqrt{{\Vert {\sigma }_1^2\Vert }_1{\Vert {\sigma }_2^2\Vert }_1}}{\mathbb{I}}_M& \frac{h_2^2}{{\Vert {\sigma }_2^2\Vert }_1}{\mathbb{I}}_M\end{array}\right]\right).$$ (Equation A4)

Notice that a linear model with effect sizes acting on unnormalized genotypes is the same as a linear model with effect sizes acting on normalized genotypes under the substitution ${\beta }_{\mathrm{1,2}}\to \sqrt{{\sigma }_{\mathrm{1,2}}^2}{\beta }_{\mathrm{1,2}}$. Therefore, the covariance of Z scores on the per-allele scale can be immediately inferred from the prior derivation:

$$C=\text{Var}\left(Z\right)=\left[\begin{array}{cc}{\Sigma }_1+\frac{N_1+1}{{\Vert {\sigma }_1^2\Vert }_1}{h}_1^2{\Sigma }_1{\sigma }_1^2{\Sigma }_1& h_{\text{ex}}\frac{\sqrt{N_1{N}_2}}{\sqrt{{\Vert {\sigma }_1^2\Vert }_1{\Vert {\sigma }_2^2\Vert }_1}}{\Sigma }_1\sqrt{{\sigma }_1^2{\sigma }_2^2}{\Sigma }_2\\ h_{\text{ex}}\frac{\sqrt{N_1{N}_2}}{\sqrt{{\Vert {\sigma }_1^2\Vert }_1{\Vert {\sigma }_2^2\Vert }_1}}{\Sigma }_2\sqrt{{\sigma }_2^2{\sigma }_1^2}{\Sigma }_1& {\Sigma }_2+\frac{N_2+1}{{\Vert {\sigma }_2^2\Vert }_1}{h}_2^2{\Sigma }_2{\sigma }_2^2{\Sigma }_2\end{array}\right].$$

Approximate Maximum-Likelihood Estimation

Let $C=\left[\begin{array}{cc}{C}_{11}& C_{12}\\ C_{21}& C_{22}\end{array}\right]$ be either of the above covariance matrices written in block form. We approximately optimize the above likelihood as follows: first, we find $h_1^2$ and $h_2^2$ by maximizing the likelihood corresponding to C₁₁ and C₂₂, and then we find ${\rho }_{\text{gi}}$ or ${\rho }_{\text{ge}}$ by maximizing the likelihood corresponding to C₁₂:

$$l\left(h_1^2|Z_1,\Sigma ,\sigma \right)\approx -\stackrel{M}{\sum _{i=1}}{w}_{11i}\left(\text{ln}\left(C_{11ii}\right)+\frac{Z_{1i}^2}{C_{11ii}}\right)$$

$$l\left(h_2^2|Z_2,\Sigma ,\sigma \right)\approx -\stackrel{M}{\sum _{i=1}}{w}_{22i}\left(\text{ln}\left(C_{22ii}\right)+\frac{Z_{2i}^2}{C_{22ii}}\right)$$

$$l\left({\rho }_{\text{g}\left\{\text{i,e}\right\}}|Z,\widehat{h_1^2},\widehat{h_2^2},\Sigma ,\sigma \right)\approx -\stackrel{M}{\sum _{i=1}}{w}_{12i}\left(\text{ln}\left(C_{12ii}\right)+\frac{Z_{1i}{Z}_{2i}}{C_{12ii}}\right).$$

Because we are discarding between-SNP covariance information $\left(\text{Cov}\left(Z_{1i},Z_{1j}\right)\right)$, highly correlated SNPs will be over-counted in our approximate likelihood. As a simple example, notice that two SNPs in perfect LD will each contribute identical terms to the approximate likelihood and therefore should be downweighted by a factor of 1/2. The extent to which SNP i is over-counted is exactly the i^th entry in its corresponding LD-matrix product. Therefore, we let $w_{jki}^{\text{gi}}=1/{\left({\Sigma }_j{\Sigma }_k\right)}_{ii}$ and $w_{jki}^{\text{ge}}=1/{\left({\Sigma }_j\sqrt{{\sigma }_j^2{\sigma }_k^2}{\Sigma }_k\right)}_{ii}$ to reduce the variance in our estimates of the parameters $h_1^2$, $h_2^2$, ${\rho }_{\text{gi}}$, and ${\rho }_{\text{ge}}$.

Furthermore, rather than compute the full products ${\Sigma }_1^2$, ${\Sigma }_2^2$, and ${\Sigma }_1{\Sigma }_2$ over all M SNPs in the genome, we choose a window size W and approximate the product by ${\left({\Sigma }_a{\Sigma }_b\right)}_{ii}={\sum }_{w=i-W}^{w=i+W}{r}_{aiw}{r}_{biw}$. Although maximum-likelihood estimation admits a straightforward estimate of the SE via the fisher information, we found these estimates to be inaccurate in practice. Instead, we use a block jackknife with a block size equal to min $\left(100,\left(M/200\right)\right)$ SNPs to ensure that blocks are large enough for the removal of residual correlations.

Out-of-Population Prediction of Phenotypic Values

Consider using the results of a GWAS with perfect power in population 2 to predict the phenotypic values of a set of individuals from population 1. This defines the upper limit of the correlation of true and predicted phenotypic values. Let the true values of the effect sizes in population 2 be β₂. Let the true phenotypes in population 1 be $Y=X_1{\beta }_1+{\mathit{\epsilon }}_1$ and the predicted phenotypes be P = X₁β₂. We are interested in the correlation of the predicted and true phenotypes ${\rho }_{YP}^{\text{MAX}}=\text{Cor}\left(Y,P\right)$. Notice that given X, the true and predicted phenotype of each individual is an affine transformation of a multivariate normal random variable (β):

$$\left[\begin{array}{c}{Y}_i\\ P_i\end{array}\right]=\left[\begin{array}{cc}{X}_{\left(i\right)}& 0_M\\ 0_M& X_{\left(i\right)}\end{array}\right]\left[\begin{array}{c}{\beta }_1\\ {\beta }_2\end{array}\right]+\left[\begin{array}{c}{\mathit{\epsilon }}_i\\ 0\end{array}\right].$$

Therefore, (Y_i, P_i) for individual i is multivariate normal with the expected covariance matrix

$${\mathbb{E}}_X\left[\text{Cov}\left(Y_i,P_i\right)\right]={\mathbb{E}}_X\left[\begin{array}{cc}{X}_{\left(i\right)}& 0_M\\ 0_M& X_{\left(i\right)}\end{array}\right]\left[\begin{array}{cc}\frac{1}{{\Vert {\sigma }_1^2\Vert }_1}{\mathbb{I}}_M& \frac{h_{\text{ex}}}{\sqrt{{\Vert {\sigma }_1^2\Vert }_1{\Vert {\sigma }_2^2\Vert }_1}}{\mathbb{I}}_M\\ \frac{h_{\text{ex}}}{\sqrt{{\Vert {\sigma }_1^2\Vert }_1{\Vert {\sigma }_2^2\Vert }_1}}{\mathbb{I}}_M& \frac{h_2^2}{{\Vert {\sigma }_2^2\Vert }_1}{\mathbb{I}}_M\end{array}\right]{\left[\begin{array}{cc}{X}_{\left(i\right)}& 0_M\\ 0_M& X_{\left(i\right)}\end{array}\right]}^{\text{T}}$$

$$={\mathbb{E}}_X\left[\begin{array}{cc}\frac{{\sum }_m{X}_{im}^2}{{\Vert {\sigma }_1^2\Vert }_1}& \frac{h_{\text{ex}}{\sum }_m{X}_{im}^2}{\sqrt{{\Vert {\sigma }_1^2\Vert }_1{\Vert {\sigma }_2^2\Vert }_1}}\\ \frac{h_{\text{ex}}{\sum }_m{X}_{im}^2}{\sqrt{{\Vert {\sigma }_1^2\Vert }_1{\Vert {\sigma }_2^2\Vert }_1}}& \frac{h_2^2{\sum }_m{X}_{im}^2}{{\Vert {\sigma }_2^2\Vert }_1}\end{array}\right]$$

$$=\left[\begin{array}{cc}1& h_{\text{ex}}\sqrt{\frac{{\Vert {\sigma }_1^2\Vert }_1}{{\Vert {\sigma }_2^2\Vert }_1}}\\ h_{\text{ex}}\sqrt{\frac{{\Vert {\sigma }_1^2\Vert }_1}{{\Vert {\sigma }_2^2\Vert }_1}}& h_2^2\frac{{\Vert {\sigma }_1^2\Vert }_1}{{\Vert {\sigma }_2^2\Vert }_1}\end{array}\right].$$

Therefore, the expected correlation $\mathbb{E}\left[\text{Cor}\left(Y_i,P_i\right)\right]$ is

$$\frac{h_{\text{ex}}}{\sqrt{h_2^2}}\sqrt{\frac{{\Vert {\sigma }_1^2\Vert }_1}{{\Vert {\sigma }_2^2\Vert }_1}\frac{{\Vert {\sigma }_2^2\Vert }_1}{{\Vert {\sigma }_1^2\Vert }_1}}={\rho }_{\text{ge}}\sqrt{h_1^2}.$$

The expected population correlation tends to the sample correlation as the number of samples increases; therefore,

$${\rho }_{YP}^{\text{MAX}}=\text{Cor}\left(Y,P\right)\to {\rho }_{\text{ge}}\sqrt{h_1^2}$$ (Equation A5)

as $N\to \infty$.

Web Resources

• DIAGRAM stage 1 data, http://diagram-consortium.org/downloads.html

• Popcorn, https://github.com/brielin/popcorn

• Summary statistics of height and BMI, https://www.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files

• Summary statistics of RA, http://plaza.umin.ac.jp/∼yokada/datasource/software.htm