Boosting the Power of the Sequence Kernel Association Test by Properly Estimating Its Null Distribution

Abstract

The sequence kernel association test (SKAT) is probably the most popular statistical test used in rare-variant association studies. Its null distribution involves unknown parameters that need to be estimated. The current estimation method has a valid type I error rate, but the power is compromised given that all subjects are used for estimation. I have developed an estimation method that uses only control subjects. Named SKAT+, this method uses the same test statistic as SKAT but differs in the way the null distribution is estimated. Extensive simulation studies and applications to data from the Genetic Analysis Workshop 17 and the Ocular Hypertension Treatment Study demonstrated that SKAT+ has superior power over SKAT while maintaining control over the type I error rate. This method is applicable to extensions of SKAT in the literature.

Introduction

Since the proliferation of DNA microarray technology about a decade ago, genome-wide association studies (GWASs) have successfully discovered many genetic variants associated with numerous human diseases and traits.¹ However, these identified variants explain only a small fraction of the overall heritability for most complex traits.^{2, 3, 4, 5} Because DNA microarray technology targets only common SNPs, it is possible that the “missing heritability” is due to variants that are rare. The rapid development of next-generation sequencing technology provides a great opportunity for studying rare variants.

Because a single SNP can provide only limited power, it is important to simultaneously leverage multiple SNPs in a gene or a region in rare-variant association studies. One approach is to test for the cumulative effect of rare variants.^{6, 7, 8, 9, 10} Such burden tests are most powerful when the effects of all variants are in the same direction. When some variants are protective but others are deleterious, this approach is no longer optimal.

An alternative approach is to test for the cumulative quadratic effect of rare variants. Examples include the C-alpha test¹¹ and the sequence kernel association test (SKAT).¹² SKAT is a score-based variance-component test and is computationally efficient. It includes the C-alpha test as a special case. It has a solid theoretical foundation.^{13, 14} It can handle both dichotomous traits and continuous traits and is able to control for covariates. SKAT has been generalized in many ways for the purposes of incorporating burden tests,¹⁵ conducting meta-analysis,¹⁶ analyzing extreme continuous traits¹⁷ and survival outcomes,^{18, 19, 20} performing family-based association tests,²¹ and studying gene-gene and gene-environmental interactions.^{22, 23}

One advantage of SKAT is that the form of its limiting distribution is known. It is a linear combination of a certain number of independent and identically distributed random variables, each of which follows a chi-square distribution with 1 degree of freedom (df). Although these combination coefficients are unknown, once they are estimated, one is able to compute the theoretical p value right away^{24, 25} without using computation-intensive techniques such as permutation. The focus of this report concerns ways to estimate these coefficients.

The current practice used by SKAT is to use all subjects in estimating these coefficients. However, as I will show, although the type I error rate is maintained, the power of SKAT is compromised in such a practice. Recognizing this fact, I propose a general approach to estimating these coefficients by using only control subjects. I demonstrate how this approach can be applied to dichotomous traits with and without covariates, as well as continuous traits. Its performance is assessed by extensive simulation studies. I further illustrate the utility of this method by applying it to data from the Genetic Analysis Workshop 17 (GAW17)²⁶ and the Ocular Hypertension Treatment Study (OHTS).²⁷

Material and Methods

Let m be the number of SNPs in a candidate region or a pathway. The genotype score of subject i at SNP j is denoted by g_ij, which takes value 0, 1, or 2, the number of copies of the minor allele. The genotypes of all subjects can be summarized by an n × m matrix G = (g_ij), where n is the number of subjects.

Case-Control Data with No Covariates

Let n₁ be the number of case subjects and n₀ be the number of control subjects. The total number of subjects is n = n₁ + n₀. Phenotypes are represented by an n × 1 vector y, whose elements are equal to 1 for case subjects and 0 for control subjects. Define $\hat{\pi }=n_1/n$ as the proportion of case subjects. The most popular version of the SKAT statistic is the one with linear kernel¹² and has the following form:

$$\text{SKAT}={\left(\mathbf{y}-\hat{\pi }1\right)}^t\mathbf{G}{\mathbf{G}}^t\left(\mathbf{y}-\hat{\pi }1\right).$$

When none of the m SNPs is associated with the case-control status (i.e., the null hypothesis), the distribution of SKAT can be approximated by that of ${\sum }_{k=1}^n{\lambda }_k{\chi }_{k,1}^2$, where ${\left\{{\lambda }_k\right\}}_{k=\mathrm{1,2},\dots ,n}$ are eigenvalues of the n × n matrix ${\mathbf{P}}^{1/2}\mathbf{G}{\mathbf{G}}^t{\mathbf{P}}^{1/2}$, which has $\mathbf{P}=\hat{\pi }\left(1-\hat{\pi }\right)\left(\mathbf{I}-n^{-1}{11}^t\right)$, an n × n matrix, and ${\left\{{\chi }_{k,1}^2\right\}}_{k=\mathrm{1,2},\dots ,n}$ as independent 1-df chi-square-distributed random variables.¹² Here, I is an n × n identity matrix, and 1 is an n × 1 vector of values of 1. The rank of matrix ${\mathbf{P}}^{1/2}\mathbf{G}{\mathbf{G}}^t{\mathbf{P}}^{1/2}$ is min {m, n}. Because the non-zero eigenvalues ${\left\{{\lambda }_k\right\}}_{k=\mathrm{1,2},\dots ,n}$ are the same as the non-zero eigenvalues from G^tPG, the distribution of ${\sum }_{k=1}^n{\lambda }_k{\chi }_{k,1}^2$ is completely determined by the eigenvalues of G^tPG. Note that the dimension of G^tPG, which is m × m, is smaller than that of ${\mathbf{P}}^{1/2}\mathbf{G}{\mathbf{G}}^t{\mathbf{P}}^{1/2}$ in the usual case of m < n. It is computationally more convenient to use G^tPG.

Define the sample variance matrix of G as S. We have

$$\mathbf{S}=\frac{1}{n-1}{\mathbf{G}}^t\left(\mathbf{I}-n^{-1}{11}^t\right)\mathbf{G}$$

$$=\frac{1}{\left(n-1\right)\hat{\pi }\left(1-\hat{\pi }\right)}{\mathbf{G}}^t\mathbf{P}\mathbf{G}.$$

That is, ${\mathbf{G}}^t\mathbf{P}\mathbf{G}=\left(n-1\right)\hat{\pi }\left(1-\hat{\pi }\right)\mathbf{S}$. The matrix S is an estimate of the underlying variance matrix of m SNPs when the null hypothesis of no association is true. When none of the SNPs is associated with the phenotype (the null hypothesis), it makes sense to use all subjects to compute S for the null distribution because none of the subjects carries a variant, and all of them are expected to share a common variance of genotype scores. However, when some SNPs are associated with the phenotype, using all subjects is no longer appropriate because case and control subjects are expected to have different mean SNP scores at these SNPs. Their variance matrices of the genotype scores are expected to be different as well. In this situation, a reasonable estimation of the null variance matrix of the m SNPs is the sample variance matrix of the genotypes scores for the control subjects.

I propose the following method for approximating the null distribution of SKAT. Let S₀ be the sample variance matrix of the genotype scores on the m SNPs among the n₀ control subjects:

$${\mathbf{S}}_0=\frac{1}{n_0-1}{\mathbf{G}}_0^t\left({\mathbf{I}}_0-n_0^{-1}{1}_0{1}_0^t\right){\mathbf{G}}_0,$$

where G₀ is an n₀ × m matrix of genotype scores of control subjects, I₀ is an n₀ × n₀ identity matrix, and 1₀ is an n₀ × 1 vector of values of 1. Let ${\left\{{\tilde{\lambda }}_k\right\}}_{k=\mathrm{1,2},\dots ,n_0}$ be the eigenvalues of matrix $\left(n-1\right)\hat{\pi }\left(1-\hat{\pi }\right){\mathbf{S}}_0$. The null distribution of the SKAT statistic is approximated by ${\sum }_{k=1}^m{\tilde{\lambda }}_k{\chi }_{k,1}^2$ provided that n₀ > m. I call this method SKAT+.

Apparently, when none of the SNPs is associated with the phenotype, S₀ and S converge to the same variance matrix as n₀ and n get large. That is, using either S₀ or S will give a valid type I error rate. However, when the null hypothesis is not true, S₀ and S no longer converge to the same variance matrix. The trace of the limiting matrix of S is larger than that of S₀. Using S instead of S₀ tends to get a distribution with larger variance and a larger p value and hence a less powerful testing procedure.

Case-Control Data with Covariates

Let x_i be a p × 1 vector of the values of p covariates for subject i. To remove their confounding effect, the following logistic regression is fit first:

$$\text{logit}\text{Pr}\left(y_i=1\right)={\alpha }_0+{\mathit{\alpha }}^t{\mathbf{x}}_i.$$

Let ${\hat{\pi }}_i$ be the estimated probability of y_i = 1:

$${\hat{\pi }}_i=\frac{\text{exp}\left\{{\hat{\alpha }}_0+{\hat{\mathit{\alpha }}}^t{\mathbf{x}}_i\right\}}{1+\text{exp}\left\{{\hat{\alpha }}_0+{\hat{\mathit{\alpha }}}^t{\mathbf{x}}_i\right\}},$$

where ${\hat{\alpha }}_0$ and $\hat{\mathbf{\alpha }}$ are estimates of ${\alpha }_0$ and $\mathbf{\alpha }$, respectively. Let $\hat{\mathit{\pi }}={\left({\hat{\pi }}_1,{\hat{\pi }}_2,\dots ,{\hat{\pi }}_n\right)}^t$. The SKAT¹² statistic is now defined by

$$\text{SKAT}={\left(\mathbf{y}-\hat{\mathit{\pi }}\right)}^t\mathbf{G}{\mathbf{G}}^t\left(\mathbf{y}-\hat{\mathit{\pi }}\right).$$

When the sample size is large enough, the distribution of SKAT can be approximated by that of ${\sum }_{k=1}^n{\lambda }_k{\chi }_{k,1}^2$, where ${\left\{{\lambda }_k\right\}}_{k=\mathrm{1,2},\dots ,n}$ are eigenvalues of ${\mathbf{P}}^{1/2}\mathbf{G}{\mathbf{G}}^t{\mathbf{P}}^{1/2}$ or, equivalently, those of ${\mathbf{G}}^t\mathbf{P}\mathbf{G}$. Here,

$$\mathbf{P}=\mathbf{V}-\mathbf{V}\tilde{\mathbf{X}}{\left({\tilde{\mathbf{X}}}^t\mathbf{V}\tilde{\mathbf{X}}\right)}^{-1}{\tilde{\mathbf{X}}}^t\mathbf{V},$$

which has $\tilde{\mathbf{X}}=\left[1\mathbf{X}\right]$, an n × (p + 1) matrix, and

$$\mathbf{V}=\text{diag}\left({\hat{\pi }}_1\left(1-{\hat{\pi }}_1\right),{\hat{\pi }}_2\left(1-{\hat{\pi }}_2\right),\dots ,{\hat{\pi }}_n\left(1-{\hat{\pi }}_n\right)\right).$$

Define $\mathbf{\Sigma }$ as

$$\mathbf{\Sigma }=\frac{1}{n-p-1}{\mathbf{G}}^t\mathbf{P}\mathbf{G}.$$

Σ is the variance matrix of the residuals of the projection of ${\mathbf{V}}^{1/2}\mathbf{G}$ on the linear space spanned by ${\mathbf{V}}^{1/2}\tilde{\mathbf{X}}$, where ${\mathbf{V}}^{1/2}=\text{diag}\left(\sqrt{{\hat{\pi }}_1\left(1-{\hat{\pi }}_1\right)},\dots ,\sqrt{{\hat{\pi }}_n\left(1-{\hat{\pi }}_n\right)}\right)$. Following the same idea as in the previous subsection, we substitute Σ with its counterpart computed with subjects whose value of $y_i-{\hat{\pi }}_i$ is low. One decision we have to make is the threshold for selection. For instance, we can use those subjects whose $y_i-{\hat{\pi }}_i$ value is below the median or third quartile of ${\left\{\left(y_i-{\hat{\pi }}_i\right)\right\}}_{i=1,\dots ,n}$. Another choice is to use control subjects only. This is equivalent to using 0 as the threshold given that all control subjects satisfy $y_i-{\hat{\pi }}_i\le 0$.

Let n₀ be the number of such chosen subjects. Let G₀, V₀, and ${\tilde{\mathbf{X}}}_0$ denote the sub-matrices of G, V, and $\tilde{\mathbf{X}}$, respectively, corresponding to the selected subjects. Let P₀ and Σ₀ be defined as

$${\mathbf{P}}_0={\mathbf{V}}_0-{\mathbf{V}}_0{\tilde{\mathbf{X}}}_0{\left({\tilde{\mathbf{X}}}_0^t{\mathbf{V}}_0{\tilde{\mathbf{X}}}_0\right)}^{-1}{\tilde{\mathbf{X}}}_0^t{\mathbf{V}}_0.$$

and

$${\mathbf{\Sigma }}_0=\frac{1}{n_0-p-1}{\mathbf{G}}_0^t{\mathbf{P}}_0{\mathbf{G}}_0,$$

respectively. Let ${\left\{{\tilde{\lambda }}_k\right\}}_{k=\mathrm{1,2},\dots ,m}$ be the eigenvalues of matrix (n − p − 1)Σ₀. Because G^tPG can be expressed as ${\mathbf{G}}^t\mathbf{P}\mathbf{G}=\left(n-p-1\right)\mathbf{\Sigma }$, the null distribution of the SKAT statistic is approximated by ${\sum }_{k=1}^m{\tilde{\lambda }}_k{\chi }_{k,1}^2$ when n₀ > m. This is because when the null is true, the residuals ${\left\{y_i-{\hat{\pi }}_i\right\}}_{i=1,\dots ,n}$ are independent of the covariate-corrected genotypes. Hence, Σ₀ and Σ converge to the same matrix as $n_0$ and n get large.

When there are no covariates, we have $\tilde{\mathbf{X}}=1$ and $\mathbf{P}=\hat{\pi }\left(1-\hat{\pi }\right)\left(\mathbf{I}-n^{-1}{11}^t\right)$, where $\hat{\pi }=n_1/n$. This method reduces to the method proposed in the previous subsection.

Continuous Traits

First, we fit the following null linear regression that has covariates only (that is, no genotype scores are used):

$$y_i={\alpha }_0+{\alpha }^t{\mathbf{X}}_i+{\mathit{ϵ}}_i,$$

where ${\mathit{ϵ}}_i\sim N\left(0,{\sigma }^2\right)$. Let ${\hat{y}}_i$ denote the predicted value of $y_i$ and $\hat{\mathbf{y}}={\left({\hat{y}}_1,{\hat{y}}_2,\dots ,{\hat{y}}_n\right)}^t$. The estimates of ${\alpha }_0$, $\mathit{\alpha }$, and ${\sigma }^2$ are denoted by ${\hat{\alpha }}_0$, $\hat{\mathit{\alpha }}$, and ${\hat{\sigma }}^2$, respectively. The SKAT statistic with linear kernel is defined as¹²

$$\text{SKAT}={\left(\mathbf{y}-\hat{\mathbf{y}}\right)}^t\mathbf{G}{\mathbf{G}}^t\left(\mathbf{y}-\hat{\mathbf{y}}\right).$$

Its asymptotic distribution is ${\sum }_{k=1}^n{\lambda }_k{\chi }_{k,1}^2$, where ${\left\{{\lambda }_k\right\}}_{k=1,\dots ,n}$ are the eigenvalues of G^tPG, in which $\mathbf{P}={\hat{\sigma }}^2\left(\mathbf{I}-\tilde{\mathbf{X}}{\left({\tilde{\mathbf{X}}}^t\tilde{\mathbf{X}}\right)}^{-1}{\tilde{\mathbf{X}}}^t\right)$ and $\tilde{\mathbf{X}}=\left[1\mathbf{X}\right]$.

We write the matrix G^tPG as ${\mathbf{G}}^t\mathbf{P}\mathbf{G}=\left(n-p-1\right){\hat{\sigma }}^2\mathbf{S}$, where

$$\mathbf{S}=\frac{1}{n-p-1}{\mathbf{G}}^t\left(\mathbf{I}-\tilde{\mathbf{X}}{\left({\tilde{\mathbf{X}}}^t\tilde{\mathbf{X}}\right)}^{-1}{\tilde{\mathbf{X}}}^t\right)\mathbf{G}$$

denotes the variance matrix of the genotype scores after the effects of the covariates are removed. Assuming that higher phenotypic value is positively associated with disease severity, we can choose subjects whose residual $y_i-{\hat{y}}_i$ is low. Denote the matrices of the genotypes and the covariates of these selected subjects as G₀ and X₀, respectively. Define ${\tilde{\mathbf{X}}}_0=\left[1{\mathbf{X}}_0\right]$. Furthermore, denote their covariate-corrected genotype-score variance matrix as S₀. The asymptotic distribution of SKAT is then estimated by ${\sum }_{k=1}^n{\tilde{\lambda }}_k{\chi }_{k,1}^2$, where $\left\{{\tilde{\lambda }}_k\right\}$ are the eigenvalues of $\left(n-p-1\right){\hat{\sigma }}^2{\mathbf{S}}_0$. S₀ and S converge to the same matrix under the null given that the residuals $\left\{y_i-{\hat{y}}_i\right\}$ are independent of the genotypes, and selection based on $\left\{y_i-{\hat{y}}_i\right\}$ doesn’t bias S₀ as an estimate of the underlying genotype covariance matrix.

A Resampling Procedure

To obtain a resampling p value, we can use the following procedure. Given the n₀ selected subjects and their genotype-score matrix G₀, we randomly select n₀ phenotype residuals $\left\{y_i-{\hat{\pi }}_i\right\}$ (or $\left\{y_i-{\hat{\mathbf{y}}}_i\right\}$ for continuous traits). Let ${\tilde{\mathbf{y}}}_0={\mathbf{y}}_0-{\hat{\mathit{\pi }}}_0$ denote the vector of selected phenotype residuals. A resampling version of the SKAT statistic is computed as

$$\frac{n-p-1}{n_0-p-1}{\tilde{\mathbf{y}}}_0^t\left({\mathbf{I}}_0-n_0^{-1}{1}_0{1}_0^t\right){\mathbf{G}}_0{\mathbf{G}}_0^t\left({\mathbf{I}}_0-n_0^{-1}{1}_0{1}_0^t\right){\tilde{\mathbf{y}}}_0.$$

Repeat this process the desired number of times. The resampling p value is computed as the proportion of the resampled SKAT statistic that is equal to or larger than the observed SKAT statistic.

Results

Simulation Studies

I simulated dichotomous traits and continuous traits under various configurations in order to evaluate the performance of the proposed SKAT+ method. I calculated both the p value based on the asymptotic distribution and the resampling p value based on 1,000 resamples. I compared SKAT+ with SKAT, SKAT-O,²⁸ and aSPU,²⁹ a recent competitor to SKAT. The aSPU method depends on the best p value of a number of sums of powered score statistics at each SNP. For the SKAT method, I used the R package SKAT (version 1.1.2). Small-sample adjustment was turned off, and no weights were applied to SNPs, although such tricks can be used in SKAT+ as well. For the aSPU method, I downloaded (on November 30, 2015) the permutation-based aSPU R code aSPUperm.R from Dr. Wei Pan’s website. This aSPU R code works only for dichotomous traits, although in theory it works for continuous traits as well. The number of permutations for aSPU is fixed at 1,000. Under each configuration, the number of simulation replications for all methods is fixed at 1,000. Rejection rates at significance levels 0.05 and 0.01 are reported unless otherwise noted.

For the assessment of type I error rate and power for dichotomous traits, I used an R code used previously³⁰ and many other publications coauthored by Dr. Wei Pan. This R code (simRareSNP.R) was downloaded (on November 30, 2015) from Dr. Wei Pan’s website. Specifically, there are eight disease-susceptibility variants whose odds ratios for each additional copy of the minor allele are pre-specified. For instance, an odds ratio equal to 1 for each of these variants implies that none of them is associated with the simulated trait. So, this is a setup used for the study of type I error rate. The disease probability can be expressed via the following logistic-regression model:

$$\text{logit}\left[\text{Pr}\left(\text{disease}\right)\right]={\beta }_0+{\beta }_1{g}_1+\dots +{\beta }_8{g}_8,$$

where ${\beta }_0=-\text{log}\left(0.05/0.95\right)$ corresponds to a background disease probability of 0.05, and $\text{exp}\left({\beta }_1\right),\dots ,\text{exp}\left({\beta }_8\right)$ are the odds ratios for the eight disease-susceptibility variants, respectively. In addition, a varying number of neutral rare variants whose minor allele frequencies (MAFs) were randomly chosen from a uniform distribution on interval (0.001, 0.01) were simulated. All variants were in linkage equilibrium. A total of 500 case and 500 control subjects were simulated. A similar simulation setup has also been used elsewhere.^{12, 31} Only control subjects were used for the SKAT+ method. Simulated type I error rates with odds ratios equal to 1 for each of the eight disease-susceptibility variants are reported in the first half of Table 1. They are under control for all four statistics except that the resampling p values for SKAT+ are slightly liberal in some situations.

Table 1.

Simulated Type I Error Rate for Dichotomous Traits over 1,000 Replicates

Method	α = 0.05					α = 0.01
No. of Neutral Rare Variants					No. of Neutral Rare Variants
0	4	8	16	32	0	4	8	16	32
Without Covariates
SKAT+	0.046	0.040	0.047	0.043	0.040	0.007	0.005	0.013	0.005	0.006
SKAT+ (rs)	0.063	0.046	0.059	0.062	0.049	0.017	0.012	0.017	0.014	0.013
SKAT	0.050	0.036	0.049	0.049	0.040	0.007	0.006	0.011	0.004	0.006
SKAT-O	0.041	0.041	0.052	0.052	0.045	0.009	0.008	0.010	0.004	0.005
aSPU	0.037	0.037	0.047	0.048	0.041	0.005	0.007	0.009	0.005	0.005
With Covariates
SKAT+	0.050	0.042	0.038	0.051	0.039	0.004	0.011	0.002	0.012	0.004
SKAT+ (rs)	0.062	0.047	0.049	0.066	0.050	0.012	0.016	0.010	0.017	0.008
SKAT	0.042	0.039	0.044	0.049	0.045	0.006	0.008	0.003	0.013	0.008
SKAT-O	0.055	0.046	0.054	0.057	0.051	0.006	0.013	0.005	0.012	0.008
aSPU	0.045	0.046	0.049	0.053	0.051	0.005	0.011	0.007	0.016	0.011

SKAT+ (rs) represents the SKAT+ method based on resampling p values.

I also considered the case where there are two covariates, X₁ and X₂. The disease probability is determined by

$$\text{logit}\left[\text{Pr}\left(\text{disease}\right)\right]={\beta }_0+0.5X_1+0.5X_2+{\beta }_1{g}_1+\dots +{\beta }_8{g}_8,$$

where X₁ follows a standard normal distribution, and X₂ follows a binary distribution taking value 0 or 1 with probability 0.5. This way of adding covariates has been used elsewhere.¹² To accommodate covariates X₁ and X₂, I modified Dr. Wei Pan’s R code accordingly. Subjects whose $y_i-\hat{\pi }$ values were not higher than the third quartile of ${\left\{\left(y_i-\hat{\pi }\right)\right\}}_{i=1,\dots ,\mathrm{1,000}}$ were selected for the SKAT+ method. Simulated type I error rates are reported in the second half of Table 1. Again, they are under control except that the resampling p values for SKAT+ are slightly liberal in some situations.

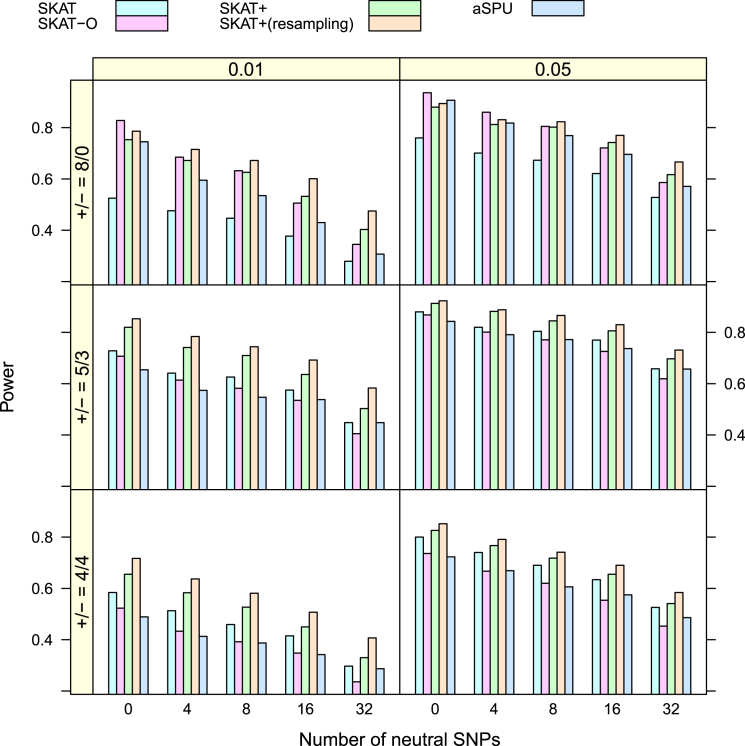
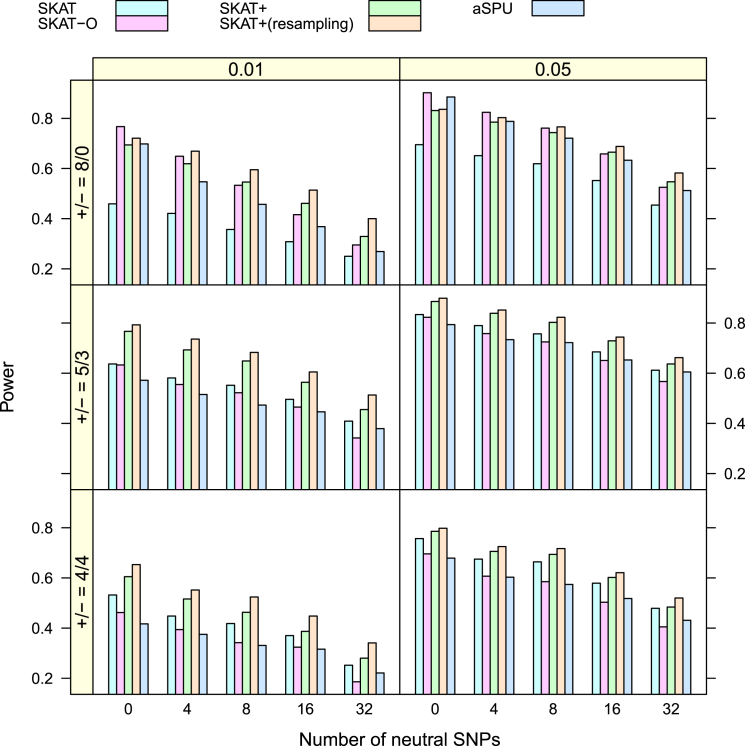
For the power analysis, I considered three scenarios in terms of the odds ratios of the eight disease-causing SNPs. They were (1) ORs = (2, 2, 2, 2, 2, 2, 2, 2), (2) ORs = (3, 3, 2, 2, 2, 1/2, 1/2, 1/2), and (3) ORs = (3, 1/3, 2, 2, 2, 1/2, 1/2, 1/2). These are typical scenarios used in the literature.^{29, 30} Scenario 1 mimics the situation where all causal variants work in the same direction, whereas the other two allow their directions to be different with different deleterious/protective ratios. The power is presented in Figure 1 and Figure 2 for situations without and with covariates, respectively. The SKAT+ method performed apparently better—in some cases much better—than SKAT across the board. It also performed better than SKAT-O and aSPU in almost all cases even when ORs = (2, 2, 2, 2, 2, 2, 2, 2), a case in favor of SKAT-O and aSPU because this is a situation for which they are optimized.^{28, 30}

Figure 1.

Simulated Power of Dichotomous Traits over 1,000 Replicates

There are no covariates. Only control subjects were selected for SKAT+.

Figure 2.

Simulated Power of Dichotomous Traits over 1,000 Replicates

There are two covariates. The third quartile of ${\left\{y_i-{\hat{\pi }}_i\right\}}_{i=1,\dots ,\mathrm{1,000}}$ was used for selecting subjects for SKAT+.

Continuous traits were simulated according to the following model:¹²

$$y=0.5X_1+0.5X_2+{\beta }_1{g}_1+\dots +{\beta }_8{g}_8,$$ (Equation 1)

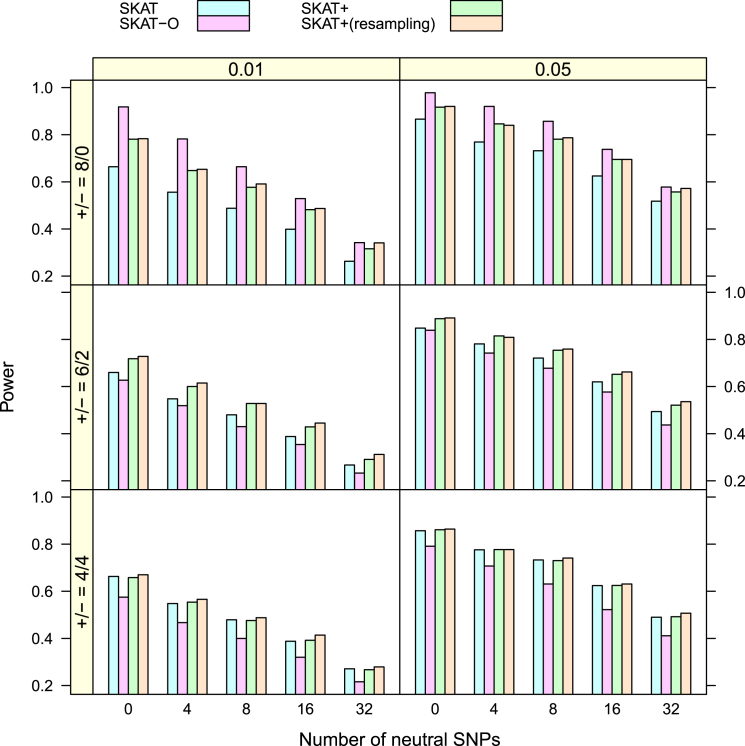
where X₁ and X₂ were generated in the same way as in the case of dichotomous traits, and g₁, …, g₈ were genotype scores at eight causal rare variants. The MAFs of these causal variants were selected uniformly from the interval (0.001, 0.01). For the study of type I error rate, ${\beta }_1,\dots ,{\beta }_8$ were set at 0. For the study of power, the magnitude of ${\beta }_j$ was equal to $\left|0.2{\text{log}}_{10}\left(\text{MAF}\right)\right|$, and the signs of these β values were in one of the following three configurations: (1) signs = (+, +, +, +, +, +, +, +), (2) signs = (+, +, +, +, +, +, −, −), or (3) signs = (+, +, +, +, −, −, −, −). Additional neutral SNPs were simulated with MAFs uniformly chosen from the interval (0.001, 0.01). Sample size was 1,000, and subjects whose $y_i-{\hat{y}}_i$ values were below the third quartile of the residuals were selected for SKAT+. That is, 75% were selected. The type I error rates are presented in Table 2. All are in line with the nominal levels. The simulated power is presented in Figure 3. SKAT+ performed better than SKAT when the ratio of positive β values to negative β values was 8:0 (configuration 1) or 6:2 (configuration 2). When this ratio was 4:4 (configuration 3), the performance of SKAT+ was almost identical to that of SKAT. This is because at this ratio, the simulated trait according to model 1 is symmetric with respect to 0. After the effect of covariates is removed, the sample covariance matrix of the selected subjects is expected to be the same as that of the whole sample. Compared with SKAT-O, SKAT+ performed worse only in configuration 1, a situation optimized for SKAT-O. In other situations, SKAT-O performed even worse than SKAT.

Table 2.

Simulated Type I Error Rate for Continuous Traits over 1,000 Replicates

Method	α = 0.05					α = 0.01
No. of Neutral Rare Variants					No. of Neutral Rare Variants
0	4	8	16	32	0	4	8	16	32
SKAT+	0.054	0.055	0.052	0.042	0.048	0.009	0.010	0.007	0.011	0.006
SKAT+ (rs)	0.051	0.058	0.051	0.040	0.056	0.011	0.011	0.008	0.013	0.010
SKAT	0.048	0.048	0.045	0.036	0.043	0.008	0.006	0.005	0.009	0.006
SKAT-O	0.039	0.049	0.037	0.038	0.043	0.008	0.008	0.005	0.009	0.006

Subjects whose $y_i-{\hat{y}}_i$ values were among the lowest 75% were selected for the SKAT+ method. SKAT+ (rs) represents the SKAT+ method based on resampling p values. The aSPU method was not computed because the R code from its authors doesn’t handle continuous traits.

Figure 3.

Simulated Power of Continuous Traits over 1,000 Replicates

There are two covariates. The third quartile of ${\left\{y_i-{\hat{y}}_i\right\}}_{i=1,\dots ,\mathrm{1,000}}$ was used for selecting subjects for SKAT+.

Application to GAW17 Data

GAW17 provided 200 phenotype datasets²⁶ simulated with mini-exome genotype data on 697 subjects selected from the 1000 Genomes Project. There were 24,487 SNPs in 3,205 genes. Four phenotypes were simulated on the basis of the genotypes of these subjects. Three of them (denoted by Q1, Q2, and Q4) were quantitative, and one was dichotomous such that the affection status was determined by Q1, Q2, and Q4 and a latent liability through a liability threshold model. Q1 was influenced by 39 SNPs in 9 genes. Q2 was influenced by 72 SNPs in 13 genes. Q4 was not influenced by any of the genotyped SNPs. The latent liability was influenced by 51 SNPs in 15 genes. As a result, the dichotomous trait was influenced by 162 genotyped SNPs in 36 genes (Q1 and the latent liability shared one common gene). Age, gender, and smoking status were confounders to Q1, Q4, and the latent liability, but not to Q2. I compared the proportion of times SKAT+, SKAT, and SKAT-O were significant at level 0.05 at each causal gene across 200 simulated datasets. I focused on the continuous traits Q1, Q2, and Q4. The following linear null model was considered:

$$y={\alpha }_0+{\alpha }_1\text{age}+{\alpha }_2\text{smoke}+{\alpha }_3\text{gender}.$$

Note that covariates were controlled for although they were known to have no effect on Q2. Q4 was used here for confirming that the type I error rate of SKAT+ was under control. The effects of the genotyped causal SNPs were all in the same direction of increasing the continuous traits. Only SNPs whose MAFs were no larger than 1% were used. Genes with only one genotyped SNP were excluded. Because the majority of the MAFs at the causal genes were extremely rare at a magnitude of 1 × 10⁻⁴, the 95^th percentile of the residuals was used for selecting subjects for SKAT+. The proportion of rejecting the null hypothesis at level 0.05 out of the 200 simulated replicates is presented in Table 3. Given that the power was not high for most causal genes even at level 5% for all methods, only those genes at which the maximum power of the three statistics was greater than 10% are presented. It is clear that SKAT+ has higher power than SKAT. Its power is less than SKAT-O in most situations. This is very possibly because the direction of the causal variants in these genes is simulated to be the same, a situation SKAT-O is optimized for. The results for trait Q4 suggest that the type I error rates for all three methods are under control, especially given that there were only 200 replicates.

Table 3.

Proportion of Significant Test Results at Level 0.05 out of the 200 Simulated GAW17 Datasets

Gene	Q1			Q2			Q4
SKAT+	SKAT	SKAT-O	SKAT+	SKAT	SKAT-O	SKAT+	SKAT	SKAT-O
FLT1 (MIM: 165070)	1.000	1.000	1.000	–	–	–	0.045	0.045	0.035
FLT4 (MIM: 136352)	0.500	0.430	0.570	–	–	–	0.055	0.065	0.045
HIF1A (MIM: 603348)	0.110	0.100	0.195	–	–	–	0.070	0.060	0.065
KDR (MIM: 191306)	0.995	0.995	1.000	–	–	–	0.075	0.065	0.075
BCHE (MIM: 177400)	–	–	–	0.400	0.340	0.410	0.050	0.040	0.055
PDGFD (MIM: 609673)	–	–	–	0.710	0.680	0.715	0.035	0.025	0.035
RARB (MIM: 180220)	–	–	–	0.440	0.420	0.345	0.065	0.055	0.050
SIRT1 (MIM: 604479)	–	–	–	0.625	0.600	0.640	0.080	0.055	0.075
SREBF1 (MIM: 184756)	–	–	–	0.425	0.375	0.670	0.065	0.065	0.075
VLDLR (MIM: 192977)	–	–	–	0.185	0.175	0.180	0.035	0.030	0.040
VNN1 (MIM: 603570)	–	–	–	0.195	0.185	0.150	0.075	0.065	0.085
VWF (MIM: 613160)	–	–	–	0.335	0.300	0.300	0.025	0.030	0.035

Application to OHTS

Primary open-angle glaucoma (POAG [MIM: 137760]) is a leading cause of irreversible blindness. Although a genetic basis has been established for a substantial fraction of POAG, no risk alleles of major effect have been identified.³² The etiology of POAG is likely to be complex. Because POAG is assessed through quantitative measures such as central corneal thickness (CCT), intraocular pressure, and cup-to-disc ratio, one promising research direction is to map genes underlying these quantitative measures. Indeed, large-scale GWASs have identified genes that affect CCT.^{33, 34, 35} Using data from the OHTS,²⁷ I applied the methods SKAT+, SKAT, and SKAT-O to a gene-based GWAS of CCT.

OHTS is a multi-center, randomized clinical trial sponsored by the National Eye Institute. Its goal is to investigate the efficacy of medical treatment in delaying or preventing the onset of POAG in individuals with elevated intraocular pressure. A total of 1,636 individuals between 40 and 80 years old were enrolled, and 1,077 of them were genotyped in a subsequent study. Data for this genetic study are available from dbGaP (study accession number dbGaP: phs000240.v1.p1). Both genotype data and baseline phenotype data are available for 1,057 subjects. The vast majority of these subjects are non-Hispanic white (752) and black (249).

There were 1,051,295 genotyped SNPs and 30,562 autosomal genes. The HGNC gene symbols were obtained with the R/Bioconductor package biomaRt (version 2.26.1). As in Lee et al.,²⁸ genes that contained fewer than three SNPs were excluded from further consideration. This reduced the number of genes to 23,778.

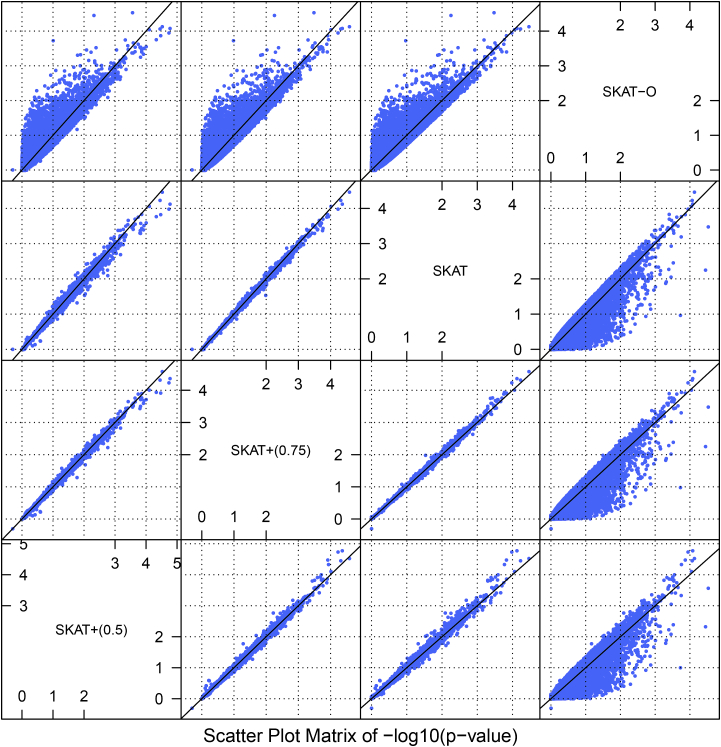
Because a thinner CCT increases the risk of POAG,³² subjects with higher CCT measurements were used as control subjects in calculations of the null distribution for SKAT+. In particular, two inclusion criteria were used: the first and second quartiles. CCT measurements from both eyes were averaged and used as the response, and age and gender were used as covariates. The analysis was done on non-Hispanic white samples only, given that this group is much larger than other ethnic groups. A scatterplot matrix of the genome-wide gene-based p values from SKAT+ (with two different inclusion criteria), SKAT, and SKAT-O is shown in Figure 4. SKAT-O behaved rather differently from the others. The other three behaved pretty similarly to each other, but they did differ, especially SKAT+ with 50% of the subjects, which is not surprising. Most importantly, there doesn’t seem to exist a systematic bias in favor of SKAT+. Those genes at which at least one of SKAT+, SKAT, and SKAT-O had a p value less than 0.0001 are listed in Table 4. These genes warrant further investigation. Unfortunately, they do not overlap ZNF469 (MIM: 612078), COL5A1 (MIM: 120215), COL8A2 (MIM: 120252), AKAP13 (MIM: 604686), or AVGR8, genes for which association with CCT has been reported previously.^{33, 34, 35} I also conducted a simulation study to confirm that the type I error rate of SKAT+ is under control at a much higher level. For this purpose, genes TRERF1 (MIM: 610322) and IQUB in Table 4 were arbitrarily selected. A continuous trait following a standard normal distribution and a dichotomous trait with disease probability 0.3 were each generated with 5 × 10⁶ replicates. For the continuous trait, 75% of the subjects were used as control subjects. For the dichotomous trait, all simulated control subjects were used for the SKAT+ method. The expected proportion of control subjects is equal to 1 − 0.3 = 0.7. The type I error rates are presented in Table 5. They are clearly under control.

Figure 4.

Scatterplots of Genome-wide Gene-Based p Values for the OHTS

SKAT+ (0.5) refers to the SKAT+ method using 50% of the subjects for its p value calculation. SKAT+ (0.75) uses 75% of the subjects.

Table 4.

A Summary of Gene-Based Association p Values with Data from the OHTS

Chromosome	Gene	SKAT+ (0.5)	SKAT+ (0.75)	SKAT	SKAT-O
2	HAGLROS	3.525 × 10−5	4.821 × 10−5	5.918 × 10−5	8.619 × 10−5
6	EXOC2 (MIM: 615329)	2.725 × 10−4	3.285 × 10−4	3.327 × 10−4	2.951 × 10−5
TRERF1 (MIM: 610322)	2.976 × 10−5	2.586 × 10−5	3.427 × 10−5	7.390 × 10−5
7	NDUFA5 (MIM: 601677)	1.822 × 10−5	5.848 × 10−5	1.042 × 10−4	1.129 × 10−4
IQUB	1.680 × 10−5	4.322 × 10−5	7.473 × 10−5	8.301 × 10−5
15	MTMR10 (MIM: 208500)	4.767 × 10−3	5.528 × 10−3	5.592 × 10−3	3.536 × 10−5
SNAP23 (MIM: 602534)	3.355 × 10−5	1.217 × 10−4	1.486 × 10−4	1.359 × 10−4
HAUS2 (MIM: 613429)	9.859 × 10−5	1.930 × 10−4	2.581 × 10−4	2.784 × 10−4
MYL12BP1	4.672 × 10−5	1.155 × 10−4	1.693 × 10−4	1.748 × 10−4
16	TXNDC11	7.867 × 10−5	9.746 × 10−5	8.708 × 10−5	9.013 × 10−5

Genes were selected if any statistic had a p value less than 0.0001 in the non-Hispanic white-only sample. SKAT+ (0.5) refers to SKAT+ method using 50% of the subjects for its p value calculation. SKAT+ (0.75) uses 75% of the subjects.

Table 5.

Simulated Type I Error Rates of SKAT+ for Two Top Genes in Table 4 over 5 × 10⁶ Replicates

Trait Type	Gene	Nominal Level
10−4	10−5	2.5 × 10−6
Continuous	TRERF1	8.1800 × 10−5	2.8000 × 10−6	1.2000 × 10−6
IQUB	1.0120 × 10−4	7.6000 × 10−6	2.0000 × 10−6
Dichotomous	TRERF1	9.7600 × 10−5	4.6000 × 10−6	3.0000 × 10−6
IQUB	1.1128 × 10−4	9.6000 × 10−6	2.0000 × 10−6

Only non-Hispanic white subjects were used. The continuous trait followed a standard normal distribution, and the dichotomous trait had a disease probability equal to 0.3. 75% of subjects were used as controls subjects.

Discussion

I have proposed the SKAT+ method for gene-based association testing. This method uses the same test statistic as SKAT but estimates the null distribution differently. By using a properly selected subset of subjects, this estimation method leads to a more powerful testing procedure. The selection is based on the residuals of the phenotype after the effect of covariates has been removed. The null distribution depends only on the second moments of the phenotype and the genotypes controlling for the effect of covariates. Selection based on phenotype residuals does not affect the validity of the test but has an effect on the power.

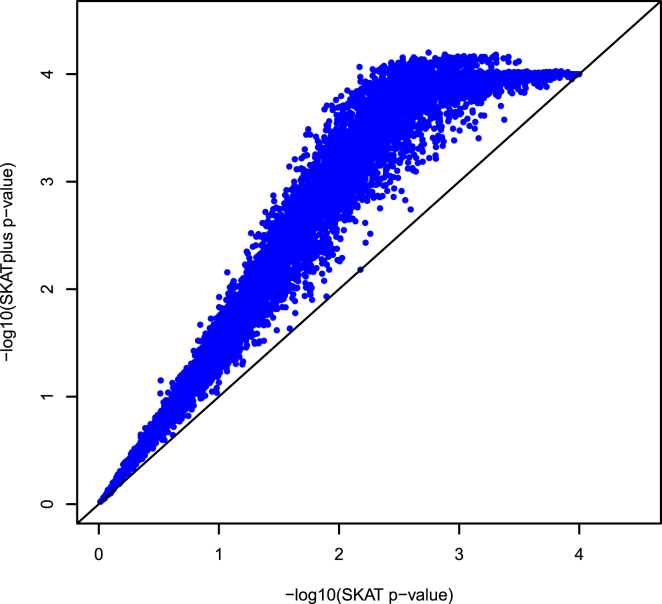
The current estimation method has a valid type I error rate, but the power is compromised because the estimated distribution does not correspond to the desired one when the null hypothesis is not true. It is contaminated by the distribution of SKAT under the alternative hypothesis. Because of this, the proposed SKAT+ method is almost surely destined to be more powerful than SKAT as sample size increases. No other SKAT competitors can make such a statement given that they perform better in only certain situations. To demonstrate this point, I simulated 10,000 datasets from the covariate-free dichotomous-trait model (Simulation Studies) used in the simulation studies with ORs = (2, 2, 2, 2, 2, 2, 2, 2) and no neutral SNPs. The −log₁₀-transformed 10,000 p values for SKAT+ were plotted against SKAT p values transformed in the same way (Figure 5). The vast majority of the 10,000 p values from SKAT+ were much more significant than those from SKAT, and almost none of them were apparently worse.

Figure 5.

The p Values from SKAT+ versus the p Values from SKAT over 10,000 Replicates

The vast majority of the 10,000 p values from SKAT+ are much more significant than those from SKAT, given that the points are almost all above the 45° line. The simulation model is 1, with ORs = (2, 2, 2, 2, 2, 2, 2, 2) and no neutral SNPs.

Selection of subjects for the SKAT+ method is critical for power improvement. For case-control studies without covariates, the selection seems to be obvious. When there are covariates or the trait is continuous, the selection is less so. For the simulation studies, I selected subjects whose trait values were not higher than the third quartile after the effect of covariates had been removed. I also tried other thresholds, such as the median and the 80% quantile. The results are not shown, but they were consistent with the intuition that SKAT+ becomes more similar to SKAT as more subjects are selected. Generally, a lower threshold leads to fewer subjects and less accuracy in p value computation. The larger the sample size, the lower the threshold one can afford while still having enough selected subjects for estimating the null distribution with certain accuracy. SKAT+ contains SKAT as a special case. If small sample size is a concern, one is recommended to use SKAT instead of SKAT+. Furthermore, one can use the recently proposed small-sample method.³⁶ A previous method²⁸ for small-sample situations “can overcorrect and lead to inflated type I error.”³⁶

A related issue in selecting control subjects is the allele frequencies of the variants. The rarer they are, the more sensitive the sample variance matrix of genotype scores is to the selected control subjects. Hence, a larger number of control subjects should be used. For an MAF of 1%, there are on average two copies of the minor allele per 100 subjects. So, 500 subjects would have ten copies of the minor allele. If the MAFs are rarer, having a more stable sample variance matrix would require more subjects for the control group.

Note that when there are no covariates, it is possible to estimate the unknown null-distribution parameters by using data from a reference database, such as the 1000 Genomes Project or the International HapMap Project. One can compute the variance matrix for the SNPs used in the study and use it in place of the matrix S₀. In this way, there is no need to select subjects for the SKAT+ method, but one needs to use an appropriate matching data sample. When there are covariates, generally it is not possible to use a reference database this way.

Also note that the basic principle behind SKAT+ is applicable to extensions of SKAT, as mentioned in the Introduction. It can also be generalized to phenotype with a distribution in the exponential family if the diagonal matrix V is replaced with a diagonal matrix of proper estimates of ${\left\{\text{var}\left(y_i\right)\right\}}_{i=1,\dots ,n}$.¹⁴

An implementation of the SKAT+ method is provided in the R package iGasso.

Published: June 9, 2016

Web Resources

• 1000 Genomes Project, http://www.1000genomes.org/

• Dr. Wei Pan’s website, http://www.biostat.umn.edu/∼weip/prog

• International HapMap Project, https://hapmap.ncbi.nlm.nih.gov/

• OMIM, http://www.omim.org

• R package iGasso, http://cran.r-project.org/web/packages/iGasso/index.html