Contrasting the Genetic Architecture of 30 Complex Traits from Summary Association Data

Abstract

Variance-component methods that estimate the aggregate contribution of large sets of variants to the heritability of complex traits have yielded important insights into the genetic architecture of common diseases. Here, we introduce methods that estimate the total trait variance explained by the typed variants at a single locus in the genome (local SNP heritability) from genome-wide association study (GWAS) summary data while accounting for linkage disequilibrium among variants. We applied our estimator to ultra-large-scale GWAS summary data of 30 common traits and diseases to gain insights into their local genetic architecture. First, we found that common SNPs have a high contribution to the heritability of all studied traits. Second, we identified traits for which the majority of the SNP heritability can be confined to a small percentage of the genome. Third, we identified GWAS risk loci where the entire locus explains significantly more variance in the trait than the GWAS reported variants. Finally, we identified loci that explain a significant amount of heritability across multiple traits.

Introduction

Large-scale genome-wide association studies (GWASs) have identified thousands of SNPs associated with hundreds of traits and diseases.^{1, 2, 3, 4} However, only a fraction of the trait variance can be explained by the risk SNPs reported by GWASs. The so-called “missing-heritability problem” is partly due to the fact that GWASs impose a stringent significance threshold, which neglects small-effect variants that fail to reach genome-wide significance at current sample sizes. As an alternative, analysis of variance components aggregates the effect of all SNPs regardless of their significance⁵ and has yielded important insights into the genetic architecture of complex traits.^{6, 7, 8, 9, 10, 11}

Heritability has been traditionally estimated with twins or pedigree¹² information, and more recent works have shown that SNP-based heritability (i.e., the proportion of trait variance explained by a given set of SNPs) can be estimated from unrelated individuals.⁸ Standard approaches for estimating SNP heritability rely on estimating the genetic relationships between pairs of individuals (estimated genome-wide or across a subset of the genome).^{8, 13, 14} Therefore, these analyses require individual-level genotype data, which prohibits their applicability to ultra-large GWASs that, as a result of privacy concerns, are typically available only at the summary level. To solve this bottleneck, recent methods have shown that SNP heritability, both across the genome and for different functional categories in the genome, can be accurately estimated with only summary GWAS data.^{6, 7} Although these methods have enabled powerful analyses making insights into the genetic basis of complex traits, they rely on the infinitesimal-model assumption (i.e., that all SNPs contribute to the trait), which is invalid at most risk loci.^{6, 7} To overcome this drawback, alternative approaches have proposed imposing a prior on the sparsity of effect sizes to further increase accuracy of estimating SNP heritability.¹⁵ A potentially more robust approach is to not assume any distribution for the effect sizes at causal variants and treat them as fixed effects in the estimation procedure. Indeed, recent works have shown that SNP heritability can be estimated under maximum likelihood from polygenic scores under a fixed-effects model assuming no linkage disequilibrium (LD) among SNPs.¹¹

Here, we introduce Heritability Estimator from Summary Statistics (HESS), an approach for estimating the trait variance explained by all typed SNPs at a single locus in the genome while accounting for LD among SNPs. We build upon recent works^{11, 16} that have treated causal effect sizes as fixed effects and model the genotypes at the locus as random correlated variables. Our estimator can be viewed as a weighted summation of the squares of the projection of GWAS effect sizes onto the eigenvectors of the LD matrix at the considered locus, where the weights are inversely proportional to the corresponding eigenvalues. Through extensive simulations, we show that HESS is unbiased when in-sample LD is available, regardless of disease architecture (i.e., the number of causals and distribution of effect sizes). We extend our method to use LD estimated from reference panels¹⁷ and show that a principal-component-based regularization of the LD matrix¹⁸ yields approximately unbiased and more consistent estimates of local SNP heritability than existing methods.⁶

We applied HESS to partition common SNP heritability at each locus in the genome by using GWAS summary data for 30 traits spanning over 10 million SNPs and 2.4 million phenotype measurements. First, we show that common SNPs explain a large fraction (ranging anywhere from 20% to 90% across the studied quantitative traits) of the total familial heritability estimated from twin studies. Second, we showcase the utility of estimates of local SNP heritability in finding loci that explain more trait variance than the top associated SNP at the locus—an effect likely due to multiple signals of association. Third, we contrast the polygenicity of all 30 traits by comparing the fraction of total SNP heritability attributable to loci with the highest local SNP heritability. We have found that most of the 30 selected traits are highly polygenic and that a small number of traits are driven by a small number of loci. Finally, we report 36 “heritability hotspots”—genomic regions that attain a significant contribution to the SNP heritability of multiple traits. Taken together, our results provide insights into traits where further GWASs and/or fine-mapping studies are likely to recover a significant amount of the missing heritability.

Material and Methods

Overview of Methods

We introduce estimators for the trait variance explained by typed variants at a single locus (local SNP heritability, $h_{g,\text{local}}^2$) from summary GWAS data (i.e., Z scores, effect sizes, and their SEs). We derive our estimator under the assumption that effect sizes at typed variants are fixed and genotypes are drawn from a distribution with a pre-specified covariance structure. The covariance (i.e., the pairwise correlation between any variants at a locus, LD) can be estimated in sample from the GWAS genotype data or from external reference panels (e.g., 1000 Genomes Project¹⁷). Our estimator can be viewed as a weighted summation of the squared projections of GWAS effect sizes onto the eigenvectors of the LD matrix at the considered locus. The finite sample size of a GWAS, as well as the reference panels used for estimating LD, induces statistical noise that needs to be accounted for if estimation is to be accurate. Given that the top projections make up the bulk of the summation, truncated singular value decomposition (SVD) lends itself as an appropriate regularization method to account for noise in the estimated LD matrices. Finally, we extend our approach to consider multiple independent loci each contributing to the trait and show how our local estimator can be employed when the total genome-wide SNP heritability is known (or estimated from other methods).

Estimating SNP Heritability at a Single Locus from GWAS Summary Data

Let $y_i={\mathbf{x}}_{\mathbf{i}}^T\mathit{\beta }+{\mathit{ϵ}}_i$, where y_i is the trait value for individual i, x_i are the standardized (i.e., mean 0 and unit variance) genotypes of individual i at p typed SNPs in the locus, $\mathit{\beta }=\left({\beta }_1,\cdots ,{\beta }_p\right)$ is the vector of fixed effect sizes for the p SNPs, and ${\mathit{ϵ}}_i\sim N\left(0,{\sigma }_e^2\right)$ is the environmental effect. If we assume that β is fixed and X is random, the phenotypic variance is

$$\text{Var}\left[\mathbf{y}\right]=\text{Var}\left[\mathbf{X}\mathit{\beta }\right]+{\sigma }_e^2={\mathit{\beta }}^T\text{Cov}\left[\mathbf{X}\right]\mathit{\beta }+{\sigma }_e^2={\mathit{\beta }}^T\mathbf{V}\mathit{\beta }+{\sigma }_e^2,$$ (Equation 1)

where V is a p × p variance-covariance matrix of the genotype vector (i.e., the LD matrix). If we make a standard assumption that the phenotypes are standardized (i.e., Var[y] = 1), it follows that the amount of variance contributed by the p SNPs to the trait (i.e., local SNP heritability) is $h_{g\text{,local}}^2={\mathit{\beta }}^T\mathbf{V}\mathit{\beta }$. If the true effect-size vector β and the LD matrix V are given, then computing $h_{g,\text{local}}^2$ is trivial. In reality, however, the vector β is unknown and is estimated in a GWAS involving n samples and p SNPs, where ${\hat{\beta }}_{\text{GWAS},i}$ is estimated as the marginal standardized regression coefficient for SNP i:

$$\begin{array}{c}{\hat{\beta }}_{\text{GWAS},i}=\frac{1}{n}{\mathbf{X}}_i^T\mathbf{y}=\frac{1}{n}{\mathbf{X}}_i^T\left(\left[\begin{array}{ccc}{\mathbf{X}}_1& \cdots & {\mathbf{X}}_p\end{array}\right]\mathit{\beta }+\mathrm{ϵ}\right)\\ =\left[\begin{array}{ccc}\frac{1}{n}{\mathbf{X}}_i^T{\mathbf{X}}_1& \cdots & \frac{1}{n}{\mathbf{X}}_i^T{\mathbf{X}}_p\end{array}\right]\mathit{\beta }+\frac{1}{n}{\mathbf{X}}_i^T\mathrm{ϵ}=\stackrel{p}{\sum _{j=1}}{r}_{ij}{\beta }_j+\frac{1}{n}{\mathbf{X}}_i^T\mathrm{ϵ},\end{array}$$ (Equation 2)

where X_i denotes standardized genotypes for SNP i across the n individuals, and r_ij denotes the LD between SNPs i and j. If we extend to p SNPs at the locus, it follows that ${\hat{\mathit{\beta }}}_{\text{GWAS}}=\mathbf{V}\mathit{\beta }+\left(1/n\right){\mathbf{X}}^T\mathrm{ϵ}$, where V is the LD matrix. When β is fixed and $\mathbf{ϵ}$ is random, ${\hat{\mathit{\beta }}}_{\text{GWAS}}$ is a random variable with $\text{E}\left[{\hat{\mathit{\beta }}}_{\text{GWAS}}\right]=\text{E}\left[\mathbf{V}\mathit{\beta }+\left(1/n\right){\mathbf{X}}^T\mathrm{ϵ}\right]=\mathbf{V}\mathit{\beta }$ and $\text{Cov}\left[{\hat{\mathit{\beta }}}_{\text{GWAS}}\right]=\text{Var}\left[\mathbf{V}\mathit{\beta }+\left(1/n\right){\mathbf{X}}^T\mathrm{ϵ}\right]=\left(1/n^2\right){\mathbf{X}}^T\text{Cov}\left[\mathrm{ϵ}\right]\mathbf{X}=\left({\sigma }_e^2/n\right)\mathbf{V}=\mathbf{V}(1-h_{g,\text{local}}^2)/n$. By central limit theorem, ${\hat{\mathit{\beta }}}_{\text{GWAS}}\sim N\left(\mathbf{V}\mathit{\beta },\mathbf{V}(1-h_{g,\text{local}}^2)/n\right)$.

As the GWAS sample size (n) increases, ${\hat{\mathit{\beta }}}_{\text{GWAS}}$ converges to ${\mathit{\beta }}_{\text{GWAS}}=\mathbf{V}\mathit{\beta }$. By simple substitution in Equation 1, it follows that an estimator for $h_{g,\text{local}}^2$ is

$$\left({\mathit{\beta }}_{\text{GWAS}}^T{\mathbf{V}}^{-1}\right)\mathbf{V}\left({\mathbf{V}}^{-1}{\mathit{\beta }}_{\text{GWAS}}\right)={\mathit{\beta }}_{\text{GWAS}}^T{\mathbf{V}}^{-1}{\mathit{\beta }}_{\text{GWAS}}.$$ (Equation 3)

Unfortunately, the finite sample size of the GWAS induces statistical noise in the estimation of ${\mathit{\beta }}_{\text{GWAS}}$, which leads to biased estimation if we simply replace ${\mathit{\beta }}_{\text{GWAS}}$ with ${\hat{\mathit{\beta }}}_{\text{GWAS}}$ above as $\text{E}\left[{\hat{\mathit{\beta }}}_{\text{GWAS}}^T{\mathbf{V}}^{-1}{\hat{\mathit{\beta }}}_{\text{GWAS}}\right]=\text{tr}\left({\mathbf{V}}^{-1}\text{Cov}\left[{\hat{\mathit{\beta }}}_{\text{GWAS}}\right]\right)+{\mathit{\beta }}^T\mathbf{V}\mathit{\beta }$. However, we can correct for the bias $\text{tr}\left({\mathbf{V}}^{-1}\text{Cov}\left[{\hat{\mathit{\beta }}}_{\text{GWAS}}\right]\right)$ as follows.

Let ${\hat{h}}_{g,\text{local}}^2$ be an unbiased estimator of $h_{g,\text{local}}^2$; then by definition, $E\left[{\hat{h}}_{g\text{,local}}^2\right]$ must satisfy $E\left[{\hat{h}}_{g\text{,local}}^2\right]=h_{g\text{,local}}^2$. Then it follows that

$$\text{E}\left[{\hat{\mathit{\beta }}}_{\text{GWAS}}^T{\mathbf{V}}^{-1}{\hat{\mathit{\beta }}}_{\text{GWAS}}\right]=\text{tr}\left(\frac{1-h_{g,\text{local}}^2}{n}{\mathbf{V}}^{-1}\mathbf{V}\right)+h_{g\text{,local}}^2=\frac{1-\text{E}\left[{\hat{h}}_{g,\text{local}}^2\right]}{n}p+\text{E}\left[{\hat{h}}_{g\text{,local}}^2\right].$$ (Equation 4)

A sufficient condition for Equation 4 to hold is $(1-{\hat{h}}_{g\text{,local}}^2)p/n+{\hat{h}}_{g\text{,local}}^2={\hat{\mathit{\beta }}}_{\text{GWAS}}^T{\mathbf{V}}^{-1}{\hat{\mathit{\beta }}}_{\text{GWAS}}$. Solving for ${\hat{h}}_{g,\text{local}}^2$ gives an unbiased estimator for $h_{g,\text{local}}^2$:

$${\hat{h}}_{g,\text{local}}^2=\frac{n{\hat{\mathit{\beta }}}_{\text{GWAS}}^T{\mathbf{V}}^{-1}{\hat{\mathit{\beta }}}_{\text{GWAS}}-p}{n-p}.$$ (Equation 5)

Following quadratic form theory,¹⁹ the variance of ${\hat{h}}_{g,\text{local}}^2$ is

$$\text{Var}\left[{\hat{h}}_{g,\text{local}}^2\right]={\left(\frac{n}{n-p}\right)}^2\left(2p\left(\frac{1-h_{g,\text{local}}^2}{n}\right)+4h_{g,\text{local}}^2\right)\left(\frac{1-h_{g,\text{local}}^2}{n}\right).$$ (Equation 6)

Because $h_{g,\text{local}}^2$, the true local SNP heritability, is unknown, we use ${\hat{h}}_{g,\text{local}}^2$ instead. For $h_{g,\text{local}}^2$ near 0, $\text{Var}\left[{\hat{h}}_{g,\text{local}}^2\right]\approx \left(4/{\left(n-p\right)}^2\right)h_{g,\text{local}}^2+\left(2p/{\left(n-p\right)}^2\right)$ through Taylor expansion around 0. Thus, the plug-in principle yields an estimation of $\text{Var}\left[{\hat{h}}_{g,\text{local}}^2\right]$ approximately equal to the truth in the expectation. For small ${\hat{h}}_{g,\text{local}}^2$ (as expected for most loci and traits), $\text{Var}\left[{\hat{h}}_{g,\text{local}}^2\right]$ is dominated by $2p/{\left(n-p\right)}^2$.

Accounting for Rank Deficiencies in LD

In the above derivation, we made the assumption that the inverse of the LD matrix V exists. In practice, however, as a result of pairs of SNPs in perfect LD, V is usually rank deficient, and thus V⁻¹ does not exist. In such cases, we use the Moore-Penrose pseudoinverse²⁰ V^†. Let q = rank (V); by rank decomposition, V = V_AV_B, where ${\mathbf{V}}_A\in {\mathbf{R}}^{p\times q}$ and ${\mathbf{V}}_B\in {\mathbf{R}}^{q\times p}$ are matrices with full column rank and full row rank, respectively. Then, $\text{tr}\left({\mathbf{V}}^{†}\mathbf{V}\right)=\text{tr}\left({\mathbf{V}}_B^{†}{\mathbf{V}}_A^{†}{\mathbf{V}}_A{\mathbf{V}}_B\right)=\text{tr}\left({\mathbf{V}}_B{\mathbf{V}}_B^{†}{\mathbf{V}}_A^{†}{\mathbf{V}}_A\right)=\text{tr}\left({\mathbf{I}}_q\right)=q$. Accounting for the rank-deficient LD matrix, we obtain an unbiased estimator, ${\hat{h}}_{g,\text{local}}^2=(n{\hat{\mathit{\beta }}}_{\text{GWAS}}^T{\mathbf{V}}^{†}{\hat{\mathit{\beta }}}_{\text{GWAS}}-q)/(n-q)$. We make the same adjustment (replacing p with q) in the variance estimator for ${\hat{h}}_{g,\text{local}}^2$.

Adjusting for Noise in External Reference LD

When genotype data of GWAS samples are not available, we substitute the in-sample LD matrix V with external reference LD matrix $\hat{\mathbf{V}}$ estimated from the 1000 Genomes Project¹⁷ with a population that matches the GWAS samples. However, because of limited sample size, external reference LD matrices contain statistical noise that biases our estimate. We apply truncated-SVD regularization to remove noise from the external reference LD matrix as follows.

First, note that ${\hat{\mathit{\beta }}}_{\text{GWAS}}^T{\mathbf{V}}^{†}{\hat{\mathit{\beta }}}_{\text{GWAS}}={\sum }_{i=1}^q{s}_i={\sum }_{i=1}^q\left(1/w_i\right){\left({\hat{\mathit{\beta }}}_{\text{GWAS}}^T{\mathbf{u}}_i\right)}^2$, where w_i and u_i are the eigenvalues and eigenvectors, respectively, of the LD matrix V, and q = rank (V). For external reference LD matrix $\hat{\mathbf{V}}$ with eigenvalues and eigenvectors ${\hat{w}}_i$ and ${\hat{\mathbf{u}}}_i$, respectively, the same decomposition holds except that s_i is replaced with ${\hat{s}}_i=\left(1/{\hat{w}}_i\right){\left({\hat{\mathit{\beta }}}_{\text{GWAS}}^T{\hat{\mathbf{u}}}_i\right)}^2$. In our previous works,^{21, 22} we proposed regularizing $\hat{\mathbf{V}}$ by using ridge-regression penalty. This regularization method is equivalent to replacing ${\hat{w}}_i$ with ${\hat{w}}_i+\lambda$, where λ is the ridge-regression penalty. The ridge-regression penalty shrinks the quadratic term ${\hat{\mathit{\beta }}}_{\text{GWAS}}{\hat{\mathbf{V}}}^{†}{\hat{\mathit{\beta }}}_{\text{GWAS}}$ toward 0, which can lead to downward bias. We also notice that a large λ is needed to drive down the noise (${\hat{s}}_i$ for large i), which diminishes the true signal at the same time. Here, we show through simulations that most of the signal in ${\hat{\mathit{\beta }}}_{\text{GWAS}}^T{\mathbf{V}}^{†}{\hat{\mathit{\beta }}}_{\text{GWAS}}$ comes from $s_i$, where $i\ll q$, and that ${\hat{s}}_i\approx s_i$ for $i\ll q$ (see Figure S1). These results motivate us to apply truncated SVD to remove noise in $\hat{\mathbf{V}}$, i.e., we estimate ${\hat{\mathit{\beta }}}_{\text{GWAS}}^T{\mathbf{V}}^{†}{\hat{\mathit{\beta }}}_{\text{GWAS}}$ by ${\sum }_{i=1}^{k}1/{\hat{w}}_i{\left({\hat{\mathit{\beta }}}_{\text{GWAS}}^T{\hat{\mathbf{u}}}_i\right)}^2$, where $k\ll q$. Let $g\left({\hat{\mathit{\beta }}}_{\text{GWAS}},k\right)={\sum }_{i=1}^k\left(1/{\hat{w}}_i\right){\left({\hat{\mathit{\beta }}}_{\text{GWAS}}^T{\hat{\mathbf{u}}}_i\right)}^2$; through eigen decomposition of $\hat{\mathbf{V}}$, it can be shown that

$$\text{E}\left[g\left({\hat{\mathit{\beta }}}_{\text{GWAS}},k\right)\right]=\frac{k\left(1-h_{g,\text{local}}^2\right)}{n}+\sum _{i=1}^k{\hat{w}}_i{\left({\hat{\mathbf{u}}}_i^T\mathit{\beta }\right)}^2.$$ (Equation 7)

Because the true local SNP heritability is $h_{g,\text{local}}^2={\sum }_{i=1}^q{w}_i{\left({\mathbf{u}}_i^T\mathit{\beta }\right)}^2$, if we assume ${\hat{\mathbf{u}}}_i={\mathbf{u}}_i$ for $i\ll q$, Equation 7 is an approximation of $h_{g,\text{local}}^2$ with bias $k\left(1-h_{g,\text{local}}^2\right)/n$. Correcting for this bias yields the estimator for the single-locus case:

$${\tilde{h}}_{g,\text{local}}^2=\frac{ng\left({\hat{\mathit{\beta }}}_{\text{GWAS}},k\right)-k}{n-k}.$$ (Equation 8)

In theory, the variance of ${\tilde{h}}_{g,\text{local}}^2$ is $\text{Var}\left[{\tilde{h}}_{g,\text{local}}^2\right]\approx \left(4/{\left(n-k\right)}^2\right){\hat{h}}_{g,\text{local}}^2+\left(2k/{\left(n-k\right)}^2\right)$. In practice, however, this gives an underestimation of the truth. Thus, we replace k with q = rank (V).

Extension to Multiple Independent Loci

For genomes partitioned into m independent loci, the linear model for individual i’s trait value becomes $y_i={\mathbf{x}}_{i,1}^T{\mathit{\beta }}_1+\dots +{\mathbf{x}}_{i,m}^T{\mathit{\beta }}_m+{\mathit{ϵ}}_i$, where ${\mathbf{x}}_{i,j}$ denotes the genotypes at the p_i SNPs in the i^th locus for individual i, and ${\mathit{\beta }}_i$ denotes the effect sizes of SNPs in this locus. On the basis of the revised model, we decompose Var[y] into

$$\text{Var}\left[\mathbf{y}\right]=\text{Var}\left[{\mathbf{X}}_1{\mathit{\beta }}_1\right]+\cdots +\text{Var}\left[{\mathbf{X}}_m{\mathit{\beta }}_m\right]+{\sigma }_e^2=h_{g,\text{local},1}^2+\cdots +h_{g,\text{local},m}^2+{\sigma }_e^2,$$ (Equation 9)

where $h_{g\text{,local},i}^2$ denotes the local SNP heritability contributed by the i^th locus. In the case of multiple independent loci, the noise term ${\sigma }_e^2$ is equal to $1-{\sum }_{j=1}^m{h}_{g,\text{local},j}^2$. Thus, in order to correct for the bias generated by ${\sigma }_e^2$, we need to know $h_{g,\text{local},j}^2$ for all j. After accounting for bias and adjusting for noise in external reference LD $\left({\hat{\mathbf{V}}}_i\right)$ according to the strategies outlined in previous sections, we arrive at the estimator

$${\hat{h}}_{g,\text{local},i}^2=\frac{ng\left({\hat{\mathit{\beta }}}_{\text{GWAS},i},k_i\right)-\left(1-{\sum }_{j=1,j\ne i}^m{\hat{h}}_{g,\text{local},j}^2\right)k_i}{n-k_i},$$ (Equation 10)

which defines a system of linear equations involving m variables $\left({\hat{h}}_{g,\text{local},i}^2\right)$ and m equations. We can solve a similar system of linear equations to obtain the variance estimate

$$\text{Var}\left[{\hat{h}}_{g,\text{local},i}^2\right]={\left(\frac{n}{n-k_i}\right)}^2\left(2k_i\frac{{\hat{\sigma }}_e^2}{n}+4{\hat{h}}_{g,\text{local},i}^2\right)\frac{{\hat{\sigma }}_e^2}{n}+{\left(\frac{k_i}{n-k_i}\right)}^2\sum _{j=1,j\ne i}^m\text{Var}\left[{\hat{h}}_{g,\text{local},j}^2\right],$$ (Equation 11)

where ${\hat{\sigma }}_e^2=1-{\sum }_{j=1}^m{\hat{h}}_{g,\text{local},j}^2$.

In the special case when $k_1=\cdots =k_m=k$ (i.e., all loci use the same number of eigenvectors in the truncated-SVD regularization of LD matrices), Equation 10 simplifies as follows: ${\hat{h}}_g^2={\sum }_{i=1}^m{\hat{h}}_{g,\text{local},i}^2={\sum }_{i=1}^m\left(ng\left({\hat{\mathit{\beta }}}_{\text{GWAS},i},k\right)-\left(1-{\hat{h}}_g^2+{\hat{h}}_{g,\text{local},i}^2\right)k)/(n-k\right)=\left(n/(n-k)\right){\sum }_{i=1}^{m}g\left({\hat{\mathit{\beta }}}_{\text{GWAS,i}},k\right)-\left(k/(n-k)\right)\left(m-m{\hat{h}}_g^2+{\hat{h}}_g^2\right).$ This yields the following estimate for the total genome-wide SNP heritability:

$${\hat{h}}_g^2=\frac{n}{n-mk}\sum _{i=1}^{m}g\left({\hat{\mathit{\beta }}}_{\text{GWAS},i},k\right)-\frac{mk}{n-mk},$$ (Equation 12)

which has variance

$$\text{Var}\left[{\hat{h}}_g^2\right]={\left(\frac{n}{n-mk}\right)}^2\sum _{i=1}^m\text{Var}\left[g\left({\hat{\mathit{\beta }}}_{\text{GWAS},i},k\right)\right]\approx {\left(\frac{n}{n-mk}\right)}^2\frac{2mk}{{\left(n-k\right)}^2}.$$ (Equation 13)

Thus, if k is chosen such that n − mk is small (i.e., n/(n − mk) is large), the estimates of genome-wide SNP heritability become unstable with large variance. To ensure stable estimates and reduce variance (at the cost of some bias), we recommend choosing k such that n/(n − mk) is less than 2 when using our estimator for genome-wide estimation.

Known Genome-wide SNP Heritability

In many cases, the estimate of total genome-wide SNP heritability $\left(h_g^2\right)$ and its variance $\left(\text{Var}\left[h_g^2\right]\right)$ are known (e.g., estimated from individual-level data). In those cases, one can simply plug $h_g^2$ into Equation 10 to obtain local estimates of heritability $h_{g\text{,local},i}^2$:

$${\hat{h}}_{g,\text{local},i}^2=g\left({\hat{\mathit{\beta }}}_{\text{GWAS},i},k\right)-\frac{k}{n}\left(1-h_g^2\right),$$ (Equation 14)

from which we conclude

$$\text{Var}\left[{\hat{h}}_{g,\text{local},i}^2\right]=\text{Var}\left[g\left({\hat{\mathit{\beta }}}_{\text{GWAS,i}},k\right)\right]+{\left(\frac{k}{n}\right)}^2\text{Var}\left[h_g^2\right].$$ (Equation 15)

In general, the sum of local SNP heritability ${\hat{h}}_g^2={\sum }_{i=1}^m{\hat{h}}_{g,\text{local,}i}^2$ is not necessarily equal to $h_g^2$ as a result of variance in ${\hat{h}}_{g,\text{local},i}^2$. Given that $\text{Var}\left[{\hat{h}}_g^2\right]=\text{Var}\left[{\sum }_{i=1}^m{\hat{h}}_{g,\text{local},i}^2\right]\approx \left(2mk/{\left(n-k\right)}^2\right)+{\left(mk/n\right)}^2\text{Var}\left[h_g^2\right]$, we recommend choosing k such that mk/n is less than 0.5 to ensure stable estimate and reduce variance. We assessed estimation of the local SNP heritability with or without known genome-wide SNP heritability by using the height GWAS data (see Table 1) with a previously reported $h_g^2$ = 0.50.² The estimates of local SNP heritability were virtually indistinguishable between the two approaches (R = 1.0; see Figure S8).

Table 1.

Estimates of Total SNP Heritability and the Amount of ${\mathit{h}}_{\mathit{g}}^{\mathbf{2}}$ Attributable to Loci Containing GWAS Index SNPs, ${\mathit{h}}_{\mathit{g},\text{local,GWAS}}^{\mathbf{2}}$, and Index SNPs Only, ${\mathit{h}}_{\text{GWAS}}^{\mathbf{2}}$

Trait	${\mathit{h}}_{\mathit{g}}^{\mathbf{2}}$(% SE)	${\mathit{h}}_{\mathbf{pub}}^{\mathbf{2}}$(%)	${\mathit{h}}_{\mathit{g}}^{\mathbf{2}}\mathbf{/}{\mathit{h}}_{\mathbf{pub}}^{\mathbf{2}}$	${\mathit{h}}_{\mathbf{GWAS}}^{\mathbf{2}}$(% SE)	${\mathit{h}}_{\mathit{g}\mathbf{,}\mathbf{local,GWAS}}^{\mathbf{2}}$(% SE)	${\mathit{h}}_{\mathit{g}\mathbf{,}\mathbf{local,GWAS}}^{\mathbf{2}\mathbf{\ast }}$(% SE)	Enrichmenta(SE)
BMI1	16.5 (0.5)	4223	0.39	1.6 (0.001)	3.1 (0.1)	3.1 (0.1)	3.7 (0.4)
Height2	59.4 (0.3)	6923	0.86	13.9 (0.002)	32.0 (0.2)	24.0 (0.2)	1.5 (0.1)
Hemoglobin24	17.9 (2.1)	3725	0.48	2.2 (0.003)	1.9 (0.3)	1.8 (0.3)	7.6 (1.4)
Mean cell hemoglobin24	29.3 (2.2)	5226	0.56	7.2 (0.003)	6.2 (0.4)	6.1 (0.4)	9.9 (1.9)
Concentration of mean cell hemoglobin24	10.9 (2.5)	4827	0.23	0.4 (0.003)	0.5 (0.2)	0.5 (0.2)	6.7 (1.8)
Mean cell volume24	26.3 (2.0)	5226	0.51	6.5 (0.004)	5.7 (0.4)	5.6 (0.4)	8.1 (1.3)
Packed cell volume24	16.7 (2.5)	3025	0.56	1.4 (0.003)	0.9 (0.2)	0.8 (0.2)	6.0 (1.4)
Red blood cell count24	22.0 (2.3)	5626	0.39	3.6 (0.004)	2.6 (0.3)	2.6 (0.3)	6.4 (1.6)
Number of platelets28	27.5 (1.5)	5725	0.48	3.5 (0.003)	3.9 (0.3)	3.9 (0.3)	5.7 (0.9)
Fasting glucose29	22.3 (2.3)	6630	0.34	2.6 (0.002)	1.7 (0.2)	1.6 (0.2)	8.0 (2.5)
Fasting insulin29	19.9 (2.4)	3631	0.55	–	–	–	–
HBA1C32	20.8 (2.3)	7530	0.28	1.8 (0.003)	0.9 (0.2)	0.9 (0.2)	6.6 (1.9)
HOMA-B29	20.3 (2.4)	7233	0.28	0.6 (0.001)	0.4 (0.1)	0.4 (0.1)	7.5 (1.9)
HOMA-IR29	19.9 (2.4)	3831	0.52	–	–	–	–
HDL3	39.4 (0.9)	4234	0.94	5.8 (0.002)	10.7 (0.2)	10.5 (0.2)	4.6 (1.3)
LDL3	33.0 (1.0)	4034	0.82	7.8 (0.002)	8.4 (0.2)	8.3 (0.2)	5.1 (0.9)
TC3	35.5 (0.9)	5035	0.71	8.0 (0.002)	9.3 (0.2)	9.3 (0.2)	4.3 (0.6)
TG3	34.8 (0.9)	4036	0.87	5.2 (0.002)	8.0 (0.2)	8.0 (0.2)	5.8 (1.4)
Education years37	19.9 (0.8)	4037	0.50	0.1 (0.002)	0.2 (0.0)	0.2 (0.0)	3.2 (1.4)
Forearm BMD38	17.4 (2.2)	8439	0.21	0.3 (0.001)	0.5 (0.1)	0.5 (0.1)	22.4 (7.7)
Femoral-neck BMD38	24.1 (2.1)	8439	0.29	2.0 (0.003)	2.0 (0.2)	2.0 (0.2)	7.1 (1.0)
Lumbar spine38	25.1 (2.0)	8439	0.30	2.2 (0.003)	2.2 (0.3)	2.2 (0.3)	6.1 (0.8)
Age at menarche40	27.8 (0.7)	4941	0.57	2.6 (0.002)	3.8 (0.2)	3.7 (0.2)	2.9 (0.2)
College37	19.4 (0.8)	4037	0.48	0.1 (0.001)	0.1 (0.0)	0.1 (0.0)	3.5 (0.9)
RA42	66.3 (0.9)	5543	1.21	11.2 (0.003)	22.0 (0.3)	22.1 (0.3)	9.8 (4.3)
SCZ44	64.5 (0.7)	8145	0.80	6.2 (0.004)	9.2 (0.2)	9.2 (0.2)	2.3 (0.1)
Crohn disease46	35.9 (1.8)	5347	0.68	3.8 (0.002)	5.9 (0.4)	5.9 (0.4)	4.8 (0.7)
Inflammatory bowel disease46,b	35.3 (1.4)	–	–	4.9 (0.002)	6.7 (0.3)	6.6 (0.3)	4.6 (0.5)
Ulcerative colitis46	31.9 (2.1)	5847	0.55	2.7 (0.002)	4.1 (0.3)	4.1 (0.3)	5.4 (1.0)
Type 2 diabetes48	25.4 (1.6)	2649	0.98	1.3 (0.002)	1.1 (0.2)	1.1 (0.2)	3.9 (0.7)

$h_{g,\text{local,GWAS}}^{2\ast }$ is the same as $h_{g,\text{local,GWAS}}^2$ except that GWAS index SNPs were excluded from the computation. In Table S2, we report $h_{g,\text{local,GWAS}}^{2†}$, which we obtained by excluding all GWAS hits. We also report estimates of familial heritability $\left(h_{\text{pub}}^2\right)$ obtained from twin or family studies. At the bottom of the table, we list case-control traits where our estimate of $h_g^2$ is biased as a result of ascertainment.

^aSimilar to Finucane et al.,⁷ we define enrichment as the ratio between the fraction of $h_g^2$ attributable to $h_{g,\text{local,GWAS}}^{2\ast }$ and the genomic fraction covered by these loci. We obtained SEs by a jackknife over the loci.

^bInflammatory bowel disease refers to the union of Crohn disease and ulcerative colitis.

Simulation Framework

We used HAPGEN2⁵⁰ to simulate genotypes for 50,000 individuals by starting with half of the 505 European (EUR) individuals in the 1000 Genomes Project¹⁷ for SNPs with minor allele frequency (MAF) greater than 5% in randomly selected regions spanning 0.75–1.5 Mb on chromosome 1. We reserved the other half of the EUR individuals as an external reference panel. From the simulated genotypes of the 50,000 individuals, we then simulated phenotypes according to the linear model $\mathbf{y}=\mathbf{X}\mathit{\beta }+\mathrm{ϵ}$, where X is the standardized genotype matrix with mean 0 and variance 1 at each column.

We investigated the performance of our method under a wide range of simulations. We first selected a subset C of $\left|C\right|$ causal SNPs at random and then simulated the effect sizes at these SNPs as ${\mathit{\beta }}_C\sim N\left(0,\left(h^2/\left|C\right|\right){\mathbf{I}}_{\left|C\right|}\right)$, where $h^2$ is the heritability to be simulated. We drew $\mathrm{ϵ}$ from $N\left(0,\left(1-h^2\right){\mathbf{I}}_n\right)$ such that $\text{E}\left[\mathbf{y}\right]=0$, $\text{Var}\left[\mathbf{y}\right]=1$, and the SNP heritability for this locus is h². For fixed β, we then generated replications of trait values y by re-drawing $\mathrm{ϵ}$. Finally, we computed summary statistics, ${\hat{\mathit{\beta }}}_{\text{GWAS}}$, according to the procedures outlined in previous sections. We simulated 500 sets of summary statistics for each simulation scenario. Although C and β were fixed within each of the 500 sets of simulated summary statistics, they varied across different set of simulations.

We also investigated simulations where β varied across simulated individuals. In each of the 500 sets of simulated GWAS summary statistics, we first selected a subset C of $\left|C\right|$ causal SNPs at random. Then, for each individual, we drew ${\mathit{\beta }}_{C,i}$ from $N\left(0,{\mathit{\alpha }}_i{h}^2\right)$ for $i=1,\cdots ,\left|C\right|$, where α governs the proportion of heritability contributed by each SNP and satisfies ${\sum }_{i=1}^{\left|C\right|}{\mathit{\alpha }}_i=1$. In the special case when ${\mathit{\alpha }}_i=1/\left|C\right|$ for all i, each causal SNP contributes the same proportion of heritability. Here, C and α were fixed in each simulation set but varied across the 500 sets of simulations.

Given that in simulations we assume that all SNPs are typed and that environmental effect $\left(\mathrm{ϵ}\right)$ is drawn independently for each individual, cryptic relatedness among individuals in the 1000 Genomes Project¹⁷ will have minimal effect on our estimates.

Empirical Datasets

We obtained publicly available GWAS summary data for 30 traits in individuals of European ancestry from 11 GWAS consortia (see Table 1). For quality control, we restricted our analysis to GWASs involving at least 20,000 samples and excluded sex chromosomes. We used the same definition of independent loci as in Berisa and Pickrell⁵¹ (1.6 Mb on average). To reduce statistical noise in the LD matrix, we focused on estimating heritability attributable to common SNPs (i.e., SNPs with a MAF greater than 5% in the EUR 1000 Genomes data¹⁷). Prior to estimating heritability, we also removed SNPs with ambiguous alleles in comparison to the reference panel (Table S1) and applied our estimator as defined in Equation 10. For each trait, we chose k, the number of eigenvectors used for estimating local heritability across all loci, on the basis of the GWAS sample size (see Material and Methods)—a large k for a GWAS with a large sample size and a small k for a GWAS with a small sample size. To avoid inflation due to noise in LD, we capped k at a maximum of 50 (see Table S2). To ensure stable estimates, we also recommend filtering out eigenvectors with corresponding eigenvalues less than 1.

Most GWASs apply a genomic control (GC) factor $\left({\lambda }_{\text{GC}}\right)$ to ${\chi }^2$ statistics to correct for inflation due to population structure⁵² and publish GC-corrected effect-size estimation $\left({\hat{\mathit{\beta }}}_{\text{GWAS,GC}}\right)$. We note that all of the summary GWAS data we analyze in this work are adjusted for population structure to various degrees and have at least one round of genomic correction. However, recent works^{6, 53} have shown that ${\lambda }_{\text{GC}}$ cannot distinguish between inflation and true polygenicity and overestimates the correction factor needed for population stratification. Although dividing the ${\chi }^2$ statistics by ${\lambda }_{\text{GC}}$ has little effect on computing the ratios between local and genome-wide heritability,⁷ it can result in underestimation of both local and genome-wide SNP heritability—when applied on GC-corrected summary data directly, our method can produce negative and uninformative estimates of local and total SNP heritability. To account for this, we first estimate ${\lambda }_{\text{GC}}$ from summary GWAS data and re-inflate the effect sizes $\left({\hat{\mathit{\beta }}}_{\text{GWAS,GC}}\right)$ with estimated $\sqrt{{\lambda }_{\text{GC}}}$ before obtaining estimates of local SNP heritability. We estimate ${\lambda }_{\text{GC}}$ on the basis of the observation that at a locus with no heritability (i.e., $h_{g,\text{local},i}^2=0$), $\text{E}\left[{\hat{\mathit{\beta }}}_{\text{GWAS,GC},i}^T{\mathbf{V}}_i^{†}{\hat{\mathit{\beta }}}_{\text{GWAS,GC},i}\right]=\left(1/{\lambda }_{\text{GC}}\right)\left(q_i/n\right)$, where ${\hat{\mathit{\beta }}}_{\text{GWAS,GC},i}={\hat{\mathit{\beta }}}_{\text{GWAS},i}/\sqrt{{\lambda }_{\text{GC}}}$ denotes the GC-corrected effect-size vector, and $\text{E}\left[{\hat{\mathit{\beta }}}_{\text{GWAS},i}^T{\mathbf{V}}_i^{†}{\hat{\mathit{\beta }}}_{\text{GWAS},i}\right]=q_i/n$, where ${\hat{\mathit{\beta }}}_{\text{GWAS},i}$ is the vector of effect-size estimation without GC correction. To estimate ${\lambda }_{\text{GC}}$, we treat the bottom 50% of all loci with the smallest estimated local SNP heritability as loci for which $h_{g,\text{local},i}^2=0$ and regress the vector $\left(q_i/n\right)$ against the vector $\left({\hat{\mathit{\beta }}}_{\text{GWAS,GC},i}^T{\mathbf{V}}_i^{†}{\hat{\mathit{\beta }}}_{\text{GWAS,GC},i}\right)$. We note that using the bottom 50% of all loci is a conservative measure to account for ascertainment in choosing loci and can result in estimated ${\lambda }_{\text{GC}}$ less than 1. In practice, we only re-inflate ${\hat{\mathit{\beta }}}_{\text{GWAS,GC}}$ if the estimated ${\lambda }_{\text{GC}}$ is greater than 1. We report estimated ${\lambda }_{\text{GC}}$ for all 30 traits in Table S1. Overall, our estimated ${\lambda }_{\text{GC}}$ is consistent with the reported ${\lambda }_{\text{GC}}$. For example, our estimated ${\lambda }_{\text{GC}}$ for BMI (1.33), high-density lipoprotein (HDL; 1.13), low-density lipoprotein (LDL; 1.16), total cholesterol (TC; 1.16), and triglycerides (TG; 1.18) are consistent with the reported ${\lambda }_{\text{GC}}$ for BMI (1.38)¹ and lipid traits (1.10–1.15).³

We define GWAS hits as SNPs with p values less than 5 × 10⁻⁸. To avoid overestimation due to LD tagging, for each locus, we only select the most significant (i.e., smallest p value) GWAS hit as the index SNP. Heritability attributable to index SNPs, $h_{\text{GWAS}}^2$, is then estimated as ${\sum }_{i=1}^I{\hat{\beta }}_i^2$, where ${\hat{\beta }}_i$ is the effect size of the i^th index SNP, and I is the number of index SNPs. We estimate the variance of ${\hat{h}}_{\text{GWAS}}^2$ as $\text{Var}\left[{\hat{h}}_{\text{GWAS}}^2\right]={\sum }_{i=1}^I\text{Var}\left[{\hat{\beta }}_i^2\right]={\sum }_{i=1}^I\text{Var}\left[{\left(Z_i/\sqrt{n}\right)}^2\right]={\sum }_{i=1}^I\text{Var}\left[\left(1/n\right){\chi }_i^2\right]=2I/n^2$.

For case-control traits, an adjustment factor is needed to correct for ascertainment.⁵⁴ We note that this adjustment factor is derived on the basis of the infinitesimal model and does not apply to our method, which assumes a fixed-effects model. Therefore, we report only unadjusted heritability estimates for case-control traits. However, we note that the ratio between local and genome-wide SNP heritability is not affected by this scaling factor.

Results

Performance of HESS in Simulations

We used simulations to assess the performance of our proposed approach under a variety of disease architectures. First, we confirmed that by accounting for rank deficiency in the LD matrix, we obtained unbiased estimation, whereas the approach that uses the number of SNPs to correct for bias generated by the quadratic form¹⁶ leads to a severe underestimation of heritability (Figure S2). Second, we found that using the top 10–50 eigenvectors of the LD matrix (see Material and Methods) provides a good approximation of the estimated heritability when LD is estimated from external reference panels (Figure S1).

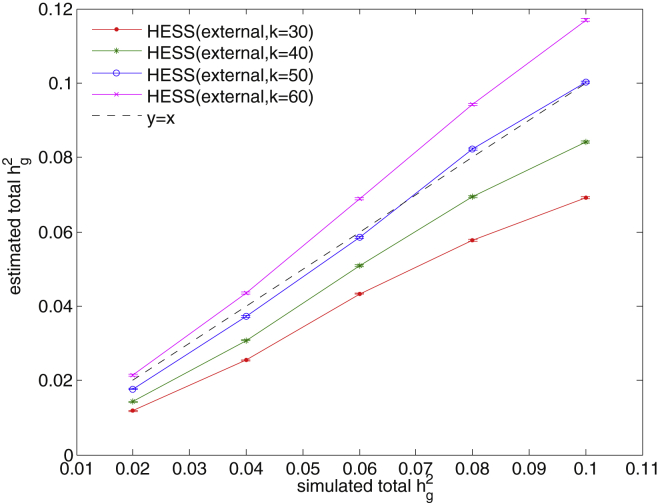
Because we used approximately independent loci,⁵¹ we also assessed potential bias due to cross-tagging of heritability resulting from LD across adjacent loci. We simulated summary statistics based on 10,000 randomly selected SNPs spread across the entire chromosome 22; 20% of these SNPs were causal, and total SNP heritability varied from 2% to 10%. For each simulation scenario, we simulated 500 sets of summary statistics and used Equation 10 to estimate local SNP heritability. We estimated total SNP heritability by summing all local estimates of SNP heritability. We found that when HESS used the top k = 30 eigenvectors in the truncated-SVD regularization of LD matrices, it yielded a downwardly biased estimate of total SNP heritability, whereas at k = 50, HESS was approximately unbiased (Figure 1). Therefore, we used k = 50 as the default unless otherwise noted.

Figure 1.

Estimates of Total SNP Heritability in the Whole-Chromosome Simulation for Different Numbers of Eigenvectors Included

We saw a slight downward bias when the number of eigenvectors, k, was small (e.g., k = 30) and an upward bias when k was large (e.g., k = 60). When k = 50, we attained an approximately unbiased estimate of total SNP heritability. Error bars represent twice the SE.

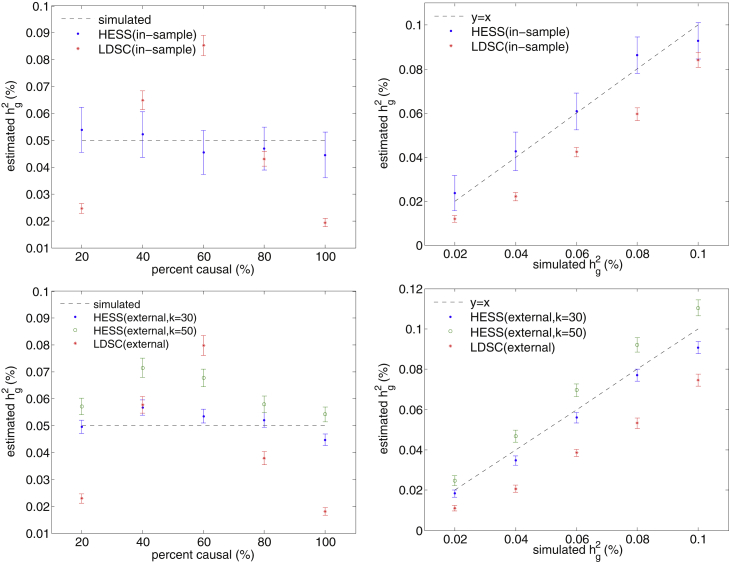
Next, we compared HESS to the recently proposed LD Score Regression (LDSC),^{6, 7} which provides estimates of heritability from GWAS summary data. Although LDSC is not designed for local analyses as a result of model assumptions on polygenicity, it is able to estimate the trait variance attributable to any sets of SNPs. As expected, in our simulations, where all individuals shared the same effect-size vector (β), we found that LDSC was sensitive to the underlying polygenicity and, in general, yielded biased estimation of heritability. In contrast, HESS provided an unbiased estimation of heritability across all simulated disease architectures when in-sample LD was available. For example, in simulations where 20% of the variants at the locus were causal and explained 0.05% of the heritability, HESS yielded an estimate of 0.054% (SE = 0.004%), whereas LDSC yielded 0.025% (SE = 0.0009%) (Figure 2). We attribute this to the fact that HESS does not make an assumption on the distribution of effect sizes at causal variants by treating them as fixed effects in the model. When LD from the sample was unavailable and had to be estimated from reference panels, both methods were biased, but HESS (with k = 30 or 50 eigenvectors in the truncated-SVD regularization of the LD matrix) yielded results closer to the simulated heritability at randomly selected loci with different widths (Figure 2, Figure S3, and Figure S4). Similar results were obtained in simulations where β was drawn independently for each individual (see Figure S5). This is expected because when conditioned on a fixed β, HESS is unbiased (i.e., $\text{E}\left[{\hat{h}}_g^2|\mathit{\beta }\right]=h_g^2$), and then the expectation of the HESS estimate across all possible β is still unbiased (i.e., $\text{E}\left[{\hat{h}}_g^2\right]=\text{E}\left[\text{E}\left[\widehat{h_g^2}|\mathit{\beta }\right]\right]=\text{E}\left[h_g^2\right]=h_g^2$).

Figure 2.

HESS Provides Superior Accuracy over LDSC in Estimating Local Heritability

HESS attains unbiased estimates when in-sample LD is used (top) and approximately unbiased estimates when reference LD is used (bottom). The mean and SE in these figures were computed on the basis of 500 simulations, each involving 50,000 simulated GWAS datasets. Error bars represent twice the SE.

Finally, unlike LDSC, which employs a jackknife approach to estimate variance in the estimated heritability (thus requiring multiple loci), HESS provides a variance estimator according to quadratic form theory (see Material and Methods). Because external reference LD is typically computed on the basis of much smaller samples than in-sample LD, subtle patterns in in-sample LD cannot be captured by external reference LD. Thus, external reference LD matrices usually have lower rank than their corresponding in-sample LD matrices, resulting in underestimation of $\text{Var}\left[{\hat{h}}_{g,\text{local,}i}^2\right]$ (see Equation 11). We verified this in simulations and found that the variance estimator yielded unbiased estimates when in-sample LD was available and underestimated theoretical variance when external reference LD was used (Figure S6). We also note that cryptic relatedness in GWAS samples can drive down the effective sample size (n); thus, our estimates of SEs could be deflated for GWASs in which the effective sample size is significantly smaller than the actual sample size.

Common Variants Explain a Large Fraction of Heritability

Having demonstrated the utility of HESS in simulations, we next applied our method to empirical GWAS summary data across 30 complex traits and diseases spanning more than two million phenotypic measurements (see Material and Methods, Table 1, and Table S1). We estimated the local SNP heritability at 1,703 approximately independent loci⁵¹ by using EUR individuals from 1000 Genomes to estimate LD.¹⁷ We first investigated the total contribution of common variants (MAF > 5%) to the heritability of complex traits. We summed up the local estimates provided by our method to obtain an estimate for the total genome-wide heritability for all genotyped SNPs. For traits where the SNP heritability was previously reported, we found a broad consistency between our estimate and the existing estimates from the literature (see Table 1). For example, HESS estimated a genome-wide SNP heritability $\left(h_g^2\right)$ of 16.5% (SE = 0.5%) for BMI and 59.4% (SE = 0.3%) for height, whereas the previously reported estimates were 21.6% (2.2%) for BMI¹ and 62.5% for height.² We also found that our estimates of total SNP heritability broadly correlate with those obtained by LDSC (see Figure S7). Most importantly, we found that common SNPs explain a large fraction (ranging from 21% for forearm bone mineral density [BMD] to 94% for HDL) of the previously reported familial heritability for all quantitative traits we interrogated (Table 1). Although we observed a very high contribution of common SNPs to case-control traits as well, we note that our estimator can be biased as a result of ascertainment in this case (see Material and Methods).

Hidden Heritability at Known Risk Loci

Recent works^{10, 55} have shown that the total heritability explained by all variants at GWAS risk loci $\left(h_{g,\text{local,GWAS}}^2\right)$ is higher than heritability explained by GWAS index SNPs $\left(h_{\text{GWAS}}^2\right)$. This suggests that a fraction of the missing heritability is due to multiple causal variants or poor tagging of hidden causal variants at known risk loci. We used HESS to quantify the gap between these two estimates of heritability at known risk loci. We found several traits for which $h_{g,\text{local,GWAS}}^2$ was significantly larger than $h_{\text{GWAS}}^2$. For example, $h_{g,\text{local,GWAS}}^2$ was over two times higher (32.0% [SE = 0.2%]) than $h_{\text{GWAS}}^2$ (13.9% [SE = 0.002%]) for height (Table 1). The difference can be accounted for by incomplete tagging of hidden causal variant(s) or allelic heterogeneity (i.e., multiple causal variants). Indeed, conditional analysis identified 36 GWAS loci containing multiple signals of association (for a total of 87 GWAS risk SNPs at these loci) for height.⁵⁶ Restricting to the 28 loci containing at least 2 of the 87 GWAS risk SNPs, we estimated $h_{g,\text{local,GWAS}}^2$ at 4.6% (SE = 0.06%), a 2.4-fold increase over $h_{\text{GWAS}}^2$ = 1.9% (SE = 0.003%). These loci, 5.8% of all GWAS loci for height, contributed to 14.2% of the difference between $h_{g,\text{local,GWAS}}^2$ and $h_{\text{GWAS}}^2$ across all loci, thus suggesting that the difference is most likely due to multiple signals of association. To confirm this hypothesis, we applied a conditional analysis from summary GWAS data by using GCTA-COJO⁵⁶ for the traits HDL, TG, rheumatoid arthritis (RA), and schizophrenia (SCZ). We observed that a moderate fraction (2%–16%) of GWAS loci showed multiple signals of association (see Table 2), thus confirming that contrasting $h_{g,\text{local,GWAS}}^2$ with $h_{\text{GWAS}}^2$ is indicative of multiple signals of association.

Table 2.

GCTA-COJO Analysis of Summary Statistics for the Traits HDL, TG, RA, and SCZ

Trait	No. of Loci with GWAS Hits	No. of GWAS Loci with Multiple Signals	$h_{g,\text{local,GWAS}}^2$(% SE)	$h_{\text{GWAS}}^2$(% SE)	Fraction (%)a
HDL3	92	15	6.1 (0.14)	2.8 (0.003)	67.3
TG3	66	9	4.6 (0.12)	3.0 (0.002)	57.1
RA42	51	4	14.8 (0.19)	4.3 (0.005)	97.3
SCZ44	103	2	0.3 (0.003)	0.2 (0.003)	3.6

We define loci with multiple association signals as loci containing at least two of the risk SNPs reported by GCTA-COJO.⁵⁶ Here, we computed $h_{g,\text{local,GWAS}}^2$ and $h_{\text{GWAS}}^2$ by restricting to the loci with multiple association signals.

^aThe fraction of difference between $h_{g,\text{local,GWAS}}^2$ and $h_{\text{GWAS}}^2$ across all loci that is accounted for by loci with multiple signals of association.

In contrast, the majority of traits showed similar $h_{g,\text{local,GWAS}}^2$ and $h_{\text{GWAS}}^2$ (see Table 1), suggesting that these loci have a single causal variant that is very well tagged by the index GWAS variant. For example, it is known that LDL is strongly regulated by a single non-coding functional variant at the SORT1 locus^{3, 57} and that BMD (femoral neck) is strongly regulated by WNT16.^{58, 59} We also observed traits (e.g., mean cell hemoglobin, mean cell volume, and red blood cell count) for which $h_{g,\text{local,GWAS}}^2$ was estimated to be less than $h_{\text{GWAS}}^2$. This seemingly contradictory result is due to the fact that fewer eigenvectors in the truncated-SVD regularization of LD matrices were used for estimating $h_{g,\text{local,GWAS}}^2$ for GWASs with small sample sizes (see Table S2), resulting in downward bias (see Material and Methods).

Contrasting Polygenicity across Multiple Complex Traits

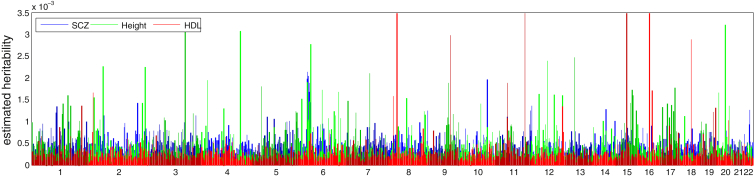
Most studied common traits exhibit a strong polygenic architecture (i.e., an abundance of small-effect loci contributing to a trait).^{1, 2, 3, 9} We recapitulated this observation by using the HESS analysis (Figures 3, S16, and S17) and found a strong correlation between chromosome length and the fraction of heritability it explains for most traits that we have analyzed here (Figures 4 and 5). Consistent with previous findings,⁶⁰ we also observed regions (such as fat mass and obesity associated [FTO] on chromosome 16 and human leukocyte antigen [HLA] on chromosome 6) contributing disproportionately to the fraction of heritability for HDL, BMI, and RA.

Figure 3.

Manhattan-Style Plots of Regional Heritability across the Genome for the Traits Height, HDL, and SCZ

See Figures S16 and S17 for results across all traits.

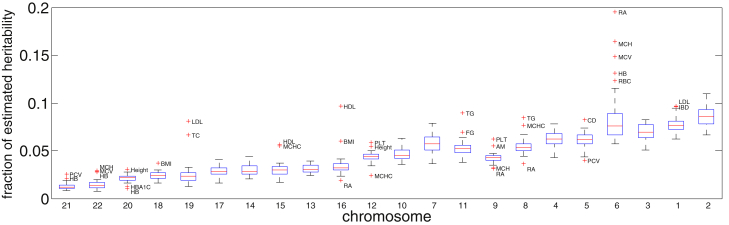
Figure 4.

Fraction of $h_g^2$ per Chromosome across the 30 Traits Studied

Here, we obtained the chromosomal heritability by summing local heritability at loci within the chromosome. For each chromosome, we plot the box plots of estimates at the 30 considered traits. Chromosomes are ordered by size. With some notable exceptions, all traits show a strong polygenic signature of genetic architecture.

Figure 5.

Heritability Attributable to Each Chromosome for Four Example Traits

We obtained the chromosomal heritability by summing local heritability at loci within the chromosome. We obtained SE by taking the square root of the sum of variance estimation. See Figures S13–S15 for results across all traits. Error bars represent twice the SE.

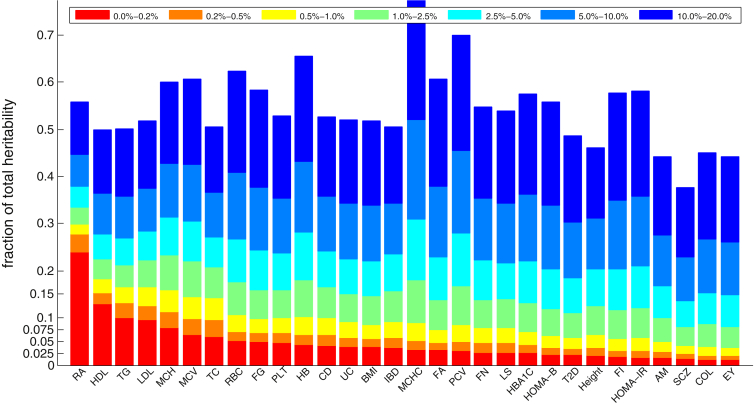
Next, we sought to quantify the variability in polygenicity across traits. We rank ordered loci on the basis of their estimated local SNP heritability, summed their contribution, and plotted it against the percentage of genome they occupy (Figure 6). For highly polygenic traits, we expected the cumulative fraction of total SNP heritability to be proportional to the fraction of genome covered, whereas for less polygenic traits, we expected to see a small genomic fraction accounting for a large fraction of the total SNP heritability. For example, in SCZ and height, the top 1% of loci with the highest local SNP heritability contributed to 4.2% (SE = 1.0%) and 6.5% (SE = 1.5%), respectively, of the total SNP heritability of these traits. This is consistent with previous reports on the degree of polygenicity of these traits.^{2, 3, 9} At the other extremes, RA and lipid traits (HDL, LDL, TC, and TG) had a lower degree of polygenicity, such that the top 1% of loci accounted for 14%–30% of the total SNP heritability. However, the low polygenicity of RA was mostly driven by the HLA region on chromosome 6. After removing estimates of local SNP heritability at loci overlapping the HLA region for all traits, we observed that RA showed a moderate degree of polygenicity for the rest of the genome (see Figure S9). We also note that the different degrees of polygenic signals across traits reflect both a difference in disease architecture (i.e., distribution of effect sizes) and a difference in the sample sizes for the GWAS summary data.

Figure 6.

Stacked Bar Plot Showing the Percentage of Total Heritability Attributable to Different Fractions of the Genome

We rank ordered all genomic loci by their explained heritability and quantified the fraction of total heritability attributable to different percentile ranges. Traits with high polygenicity (e.g., height and SCZ) tend to have bars with a height proportional to bin size, whereas less polygenic traits (e.g., RA and HDL) tend to have bars much larger than bin size.

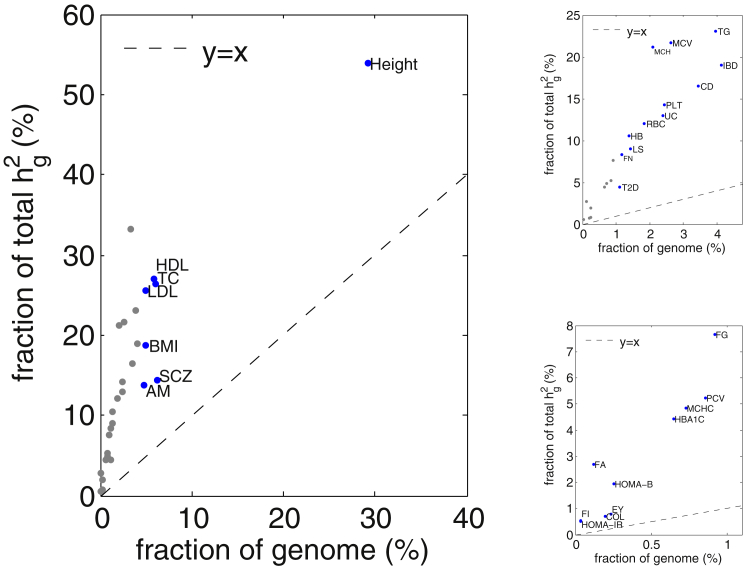
A different perspective of polygenicity is to restrict to GWAS risk loci (because they clearly contain risk variants) and contrast the proportion of explained variance with the proportion of the genome they occupy. We observed a wide distribution across traits reflecting diverse genetic architectures, as well as different sample sizes for the GWASs performed for these traits. For example, approximately 30% of loci across the genome harbored a risk variant for height and accounted for 50% of the total SNP heritability (a 1.5-fold enrichment). On the other hand, although only 5% of the loci contained GWAS risk variants for HDL, these loci collectively explained 25% of the SNP heritability of HDL (a 4.6-fold enrichment; Figure 7).

Figure 7.

Fraction of $h_g^2$ Explained by All Loci Containing a GWAS Hit versus the Fraction of Genome Covered by These Loci

Images on the right focus successively on the traits near the bottom left.

Loci Contributing to Heritability of Multiple Traits

It has been previously established that a number of the 30 traits investigated in this study share a genetic basis.⁶¹ Correlating estimates of local SNP heritability across the entire genome can serve as a proxy for the magnitude of pleiotropy, and we can identify pairs of traits whose genetic components tend to localize within the same regions of the genome (Figure S10). Motivated by this, we searched for specific pleiotropic loci that we define as loci that contribute significant non-zero SNP heritability (one-tailed p value < 0.05, Bonferroni corrected for 1,703 loci) for at least 3 out of the 30 analyzed traits. In total, we identified 36 such loci distributed genome-wide (see Figure 8 and Figure S11).

Figure 8.

Heatmap Showing the Fraction of Total SNP Heritability, $h_g^2$, Contributed by Each of the 36 “Pleiotropic” Loci

For each locus, we only display traits to which the locus contributes a significant amount of heritability. We mark traits to which the locus contributes more than 5% of the total SNP heritability in dark blue.

As expected, the HLA region (chr6: 26–34 Mb) displayed strong pleiotropic signal, particularly for immunologically relevant phenotypes (see Figure 8). For instance, the locus chr6: 32–33 Mb contributed a significant amount of SNP heritability for eight traits and had exceptionally strong signals for RA, ulcerative colitis, and inflammatory bowel disease (see Figure 8). We also observed several other pleiotropic loci, including chr2: 199–202 Mb (contributing to age at menarche, SCZ, and height), chr6: 134–136 Mb (contributing to multiple red blood cell traits), and chr19: 45–46 Mb (contributing to multiple lipid traits). It is well known that genetic correlations exist among red blood cell traits,^{24, 62, 63} as well as among lipid traits.^{3, 61} Interestingly, previous research has also revealed that early age at menarche is associated with later onset of SCZ.⁶⁴ Our results suggest that these genetic correlations and associations might be caused in part by the pleiotropic effect of these loci.

We note that the selection of traits can bias the identification of pleiotropic loci toward over-represented traits such as height and lipid traits. Nevertheless, analyzing local SNP heritability is still a useful tool for quantifying the fraction of total SNP heritability contributed by a single locus and provides valuable insights into identifying pleiotropic loci.

Discussion

We have presented HESS, an unbiased estimator of local SNP heritability from GWAS summary data. We extend existing work¹⁶ that estimates heritability under the fixed-effects model by proposing to regularize the external reference LD matrix via truncated SVD and generalizing the estimator to multiple independent loci. Through extensive simulations, we demonstrate that HESS is unbiased when given in-sample LD and yields more consistent and less biased estimates of local SNP heritability than LDSC given external reference LD. We applied HESS on GWAS summary data of 30 complex traits from 12 GWAS consortia and showed that our results recapitulate previous findings. We then used these estimates of local SNP heritability to contrast polygenicity of complex traits, found loci with multiple causal variants, and identified heritability hotspots. We note that enrichment of heritability at GWAS risk loci could be leveraged into prioritizing GWASs or fine mapping; for example, traits with small enrichment of heritability at GWAS risk loci are more suitable for larger GWASs, whereas traits with large enrichment of heritability at known risk loci could be investigated further through fine mapping.

In this work, we focus on estimating local heritability attributable to common autosomal variants (MAF > 5%) and ignore potential heritability captured by the sex chromosomes and rare variants. We also note that our heritability estimates for case-control traits are not adjusted for ascertainment because it is unclear whether adjustment derived from the infinitesimal model can be directly applied for the fixed-effects model. Thus, our reported heritability estimation for case-control traits can be biased as a result of ascertainment. Future work that addresses estimation of local heritability including both common and rare variants, sex chromosomes, and adjustment of heritability estimates under the fixed-effects model for case-control traits will further improve the utility of our approach.

We conclude with several caveats and limitations of our work. First, our method relies on independent LD blocks, which are often hard to define as a result of LD leakage across multiple loci. In this work, we attempt to minimize LD leakage by using principled approaches to define approximately independent loci. Second, when only external reference LD is available, our method can yield biased estimates because external reference LD usually has a lower rank than its corresponding in-sample LD. Furthermore, cryptic relatedness in the GWAS data could also bias our estimation procedure. This makes hypothesis testing difficult. However, with in-sample LD and larger reference panels, such as the Haplotype Reference Consortium,⁶⁵ this bias will be reduced because LD can be inferred more precisely. We also note that our estimated ${\lambda }_{\text{GC}}$ can be a potential source of bias; thus, our genome-wide estimate should be interpreted with caution. Third, for stable estimation, the number of eigenvectors used (k) in the truncated-SVD regularization should be chosen on the basis of the GWAS sample size—GWASs with large sample sizes can afford a large k, whereas GWASs with small sample sizes should use a small k. We recommend applying our method to summary data obtained from GWASs involving around or above 50,000 samples. For GWASs with small sample sizes, when genome-wide SNP heritability is known, one can still apply Equation 14 to obtain stable estimates of local heritability. We also note that although using the same number of eigenvectors for all loci facilitates the study of the statistical properties of our estimator, this approach might not be optimal for all loci. We conjecture that selecting k according to a more principled approach (e.g., on the basis of the distribution of eigenvalues) might reduce bias, and we leave such investigation as future work.

Published: June 23, 2016

Web Resources

• HESS, http://bogdan.bioinformatics.ucla.edu/software/hess