PADRE: Pedigree-Aware Distant-Relationship Estimation

Abstract

Accurate estimation of shared ancestry is an important component of many genetic studies; current prediction tools accurately estimate pairwise genetic relationships up to the ninth degree. Pedigree-aware distant-relationship estimation (PADRE) combines relationship likelihoods generated by estimation of recent shared ancestry (ERSA) with likelihoods from family networks reconstructed by pedigree reconstruction and identification of a maximum unrelated set (PRIMUS), improving the power to detect distant relationships between pedigrees. Using PADRE, we estimated relationships from simulated pedigrees and three extended pedigrees, correctly predicting 20% more fourth- through ninth-degree simulated relationships than when using ERSA alone. By leveraging pedigree information, PADRE can even identify genealogical relationships between individuals who are genetically unrelated. For example, although 95% of 13^th-degree relatives are genetically unrelated, in simulations, PADRE correctly predicted 50% of 13^th-degree relationships to within one degree of relatedness. The improvement in prediction accuracy was consistent between simulated and actual pedigrees. We also applied PADRE to the HapMap3 CEU samples and report new cryptic relationships and validation of previously described relationships between families. PADRE greatly expands the range of relationships that can be estimated by using genetic data in pedigrees.

Introduction

Accurate prediction and verification of relationships among individuals is essential in a variety of genetic studies. Errors in pedigrees are common^{1, 2, 3} and have adverse consequences, including biased phasing and family-based imputation results, inaccurate identification of Mendelian errors, and reduction of power to detect linkage⁴ or family-based associations. Therefore, ensuring that the genetic relationships among the DNA samples match the reported pedigree structure is critical for accurate family-based genetic analysis.⁵ Detecting cryptic relationships can be important as well.⁶ Genetic relationships identified in population studies can be leveraged for improved haplotype phase inference, detection of population structure, genotype imputation, and study designs such as identical-by-descent (IBD) mapping and tests to detect multiple rare and common variants that contribute to disease.^{7, 8, 9, 10, 11, 12, 13} The identification of relatives also plays an important role in forensics in criminal investigations,¹⁴ identification of victims of mass disaster,¹⁵ and discovery of family history.

With close relationships (first through third degree), pedigree reconstruction can provide the kinship structure of the individuals in a genetic dataset.⁵ However, genetic datasets often contain relationships that are more distant than third degree, resulting in sparsely connected pedigrees that are unsuitable for reconstruction. Algorithms that consider IBD segment data, such as ERSA (estimation of recent shared ancestry),^{16, 17} can accurately predict pairwise relationships up to ninth-degree relatives (e.g., fourth cousins), but do not reconstruct pedigrees, nor can they utilize information from known or observed pedigree structures in the data. Here, we introduce PADRE (pedigree-aware distant-relationship estimation), which leverages the pedigree reconstruction of known or cryptic first- to third-degree relatives by PRIMUS (pedigree reconstruction and identification of a maximum unrelated set)⁵ along with the accurate distant relationship predictions by ERSA.¹⁷ PADRE, which has been implemented as an extension of PRIMUS and ERSA, uses ERSA-generated relationship likelihoods to identify the highest composite likelihood connection between family networks reconstructed by PRIMUS (Figure S1), significantly improving the accuracy of the predictions and expanding the range of relationships that can be predicted.

Subjects and Methods

PADRE Algorithm

PADRE combines reconstructed pedigree information with distant pairwise relationship predictions to identify distant relationships between pedigrees and requires results from PRIMUS (v.1.8.0) and ERSA (v.2.1) as input (Figure S1). PRIMUS identifies family-based networks of individuals within a dataset, where each family network consists of the set of individuals with a detected first- through third-degree relationship to at least one other individual in the network. When PRIMUS reconstructs a dataset into family networks (i.e., Net₁, Net₂, … Net_n), each network can be represented by one or more possible pedigrees that fit the genetic data, annotated here with subscripts (i.e., Net₁₁, Net₁₂, … and Net_1j). PADRE tests for significant relationships between each pair of networks by using the likelihood ratio test in ERSA. This test compares the null model that two founders in two different networks, x and y, are unrelated to the alternative model that the two individuals are N^th-degree relatives. If a significant relationship is detected between any two founders, PADRE will then identify the best fitting relationship between the two networks by using a composite likelihood framework. The significance threshold is 0.05 by default but can be adjusted for the number of founder-to-founder relationships tested by application of a Bonferroni correction with the command-line argument adding “--PADRE_multiple_test_correct.” For a significant relationship detected between founders x and y, PADRE calculates the maximum composite likelihood for each possible N^th-degree relationship between x and y by multiplying the cross-network pairwise relationship likelihoods in ERSA for each pair of pedigrees Net_1i and Net_2j:

$${\hat{L}}_{1i2j}\left(x,y\text{|}N\right)=L_{Ne{t}_{1i}}{L}_{Ne{t}_{2j}}\prod _{\begin{array}{c}\forall a\in Net{1}_i\\ \forall b\in Net{2}_j\end{array}}{\hat{L}}_{ab}\left(s_{ab}\text{|}{D}_{ab}\right),$$ (Equation 1)

where $a$ and $b$ are individuals in the pedigrees Net_1i and Net_2j, respectively, $D_{ab}$ is the degree of relatedness between $a$ and $b$ given the two pedigrees and that founders x and y are N^th-degree relatives, and s_ab is a set containing the length of each detected IBD segment between a and b. ${\hat{L}}_{ab}\left(s_{ab}\text{|}{D}_{ab}\right)$ is the maximum likelihood of the observed IBD segments shared by a and b conditioned on the degree of relationship distance D_ab specified by N, Net_1i and Net_2j. L_Net1i and L_Net2j are the composite pedigree likelihoods consisting of the product of the PRIMUS likelihoods for each pairwise relationship specified by Net_1i and Net_2j, respectively. When D_ab is less than 10, ${\hat{L}}_{ab}$ includes two additional estimated parameters compared to the model with no relationship (relationship distance and number of shared segments conditioned on relationship distance); these likelihoods are calculated by ERSA.¹⁶

Because many 10^th- and most 11^th-degree human relatives share no autosomal IBD segments from their most recent common ancestor,¹⁶ models involving relationships more distant than ninth degree require special consideration. Although such models also include two additional parameters, the maximum likelihood estimate for the number of shared genetic segments is typically 0, resulting in a compressed free parameter space. Maximizing the likelihood of such models without accounting for the reduced free parameter space over-penalizes such distant relationships. We address this problem with the following approximation. Given that two individuals, a and b, are genetic ninth-degree relatives, the unconditional maximum likelihood of a 10^th-degree relationship for individual a and the offspring of individual b is as follows: with 50% probability, the shared segment is inherited by the offspring of individual b, and the likelihood is equal to the ninth-degree relationship likelihood. Otherwise, the likelihood is equal to the unrelated likelihood. This approximation holds for relationship distances detectable by PADRE and beyond (see Figure S2) and leads to the following formula to approximate the likelihood of 10^th-degree and more-distant relationships in PADRE:

$${\hat{L}}_{ab}\left(s_{ab}\text{|}{D}_{ab}>9\right)={\left(0.5\right)}^{D_{ab}-9}{\hat{L}}_{ab}\left(s_{ab}\text{|}{D}_{ab}^{\prime }=9\right)+\left(1-{\left(0.5\right)}^{D_{ab}-9}\right){\hat{L}}_{ab}\left(s_{ab}\text{|unrelated}\right),$$ (Equation 2)

where the effective degrees of freedom is given by:

$$g\left(D_{ab}\right)=\left[\begin{array}{cc}2,& D_{ab}\le 9\\ {\left(0.5\right)}^{D_{ab}-9},& D_{ab}>9\end{array}\right].$$ (Equation 3)

To identify the best fitting model, PADRE calculates the composite likelihood Akaike information criterion (CL-AIC) for each possible fourth- through ninth-degree relationship between the founders of the two family networks via Equation 1.¹⁸ Because each network could have more than one possible pedigree, we evaluate all pairs of possible pedigrees identified by PRIMUS for each network and identify the pair of pedigrees that minimizes the CL-AIC of the two networks. For a given pair of pedigrees Net_1i and Net_2j, the CL-AIC is calculated according to Equation 4:

$$AI{C}_{1i2j}\left(x,y\text{|}N\right)=2k_{1i2j}\left(x,y,N\right)-2ln{\hat{L}}_{1i2j}\left(x,y\text{|}N\right)-ln{L}_{Ne{t}_{1i}}-ln{L}_{Ne{t}_{2j}},$$ (Equation 4)

where k is equal to the effective number of parameters in ${\hat{L}}_{1i2j}\left(x,y\text{|}N\right)$. The value for k is given by Equation 5:

$$k_{1i2j}\left(x,y,N\right)=\sum _{\begin{array}{c}\forall a\in Net{1}_i\\ \forall b\in Net{2}_j\end{array}}g\left(D_{ab}\right).$$ (Equation 5)

Finally, PADRE evaluates all pairs of possible pedigrees identified by PRIMUS for each network to identify the model that minimizes the CL-AIC of the two networks:

$$AI{C}_{\text{min}}\left(Net1,Net2\right)=\underset{\begin{array}{c}x\in Net1\\ y\in Net2\\ 4\le N\le 9\\ 1\le i\le Net{1}_n\\ 1\le j\le Net{2}_n\end{array}}{\min }AI{C}_{1i2j}\left(x,y\text{|}N\right).$$ (Equation 6)

For each pair of family networks, PADRE reports the pair of founders, their degree of relatedness, and the two pedigrees from the model specified by the $AI{C}_{\text{min}}$. In a separate output file, PADRE provides the degree of relatedness between each pair of samples in the model specified by the $AI{C}_{\text{min}}$.

PADRE takes, as a command line option, the maximum degree of relatedness PRIMUS uses to reconstruct and then adjusts the range of ERSA predictions to test all relationships greater than the maximum degree of relatedness in PRIMUS. By default, the maximum degree of relatedness is three, and PADRE thus considers all fourth- through ninth-degree relationships in ERSA.

Simulations

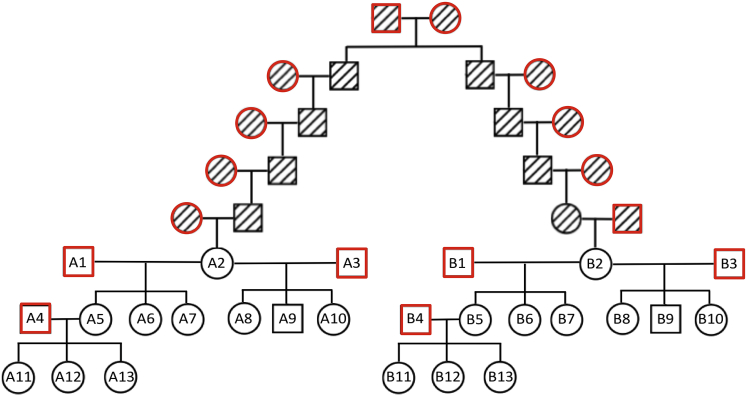
We simulated pedigrees to evaluate the accuracy and relative benefit of using PADRE to detect distant relationships. We used two identical 13-person, three-generation pedigree structures and connected a founder in each pedigree by varying the number of generations to their recent common ancestor. Figure 1 illustrates a simulated pedigree in which founders A2 and B2 are ninth-degree relatives. To test the full range of predictions beyond the third degree, we generated versions of the pedigree in which individuals A2 and B2 are fourth- through ninth-degree relatives. For each of these versions of simulated pedigree structures, we created 100 different sets of genotypes by using the method described in Morrison.¹⁹ We randomly selected haplotypes with ∼1 M SNPs from among the unrelated HapMap3²⁰ CEU (Utah residents with ancestry from northern and western Europe from the CEPH collection) samples and assigned them to the all founders (individuals with red symbols in Figure 1). The unrelated set of CEU samples was determined by running ERSA (v.2.1) on all the HapMap3 CEU samples and then running the IMUS algorithm within PRIMUS²¹ to identify the maximum unrelated set of individuals. We then used Morrison’s recombination simulation software to propagate the founder genotypes through the pedigree. This method simulates recombination events as a homogeneous Poisson process by using the genetic map provided with the HapMap3 data, disregarding the centromere. Genotypes were removed for all individuals not included in either of the 13-person pedigrees. IBD estimates were calculated with PLINK v.1.9²²

$$\text{plink}\text{-}\text{-}\text{file}\left[\text{data}\_\text{file}\_\text{root}\_\text{name}\right]\text{-}\text{-}\text{genome}\text{-}\text{-}\text{maf}0.05\text{-}\text{-}\text{geno}0.1\text{-}\text{-}\text{out}\left[\text{data}\_\text{file}\_\text{root}\_\text{name}\right],$$

and all simulated pedigrees were reconstructed with PRIMUS (v.1.8):

$$\text{run}\_\text{PRIMUS}.\text{pl}\text{-}\text{-}\text{p}\left[\text{data}\_\text{file}\_\text{root}\_\text{name}\right].\text{genome}.$$

Figure 1.

Pedigree Structure Used to Simulate Ninth-Degree Pedigrees

100 ninth-degree pedigrees, each with different genotypes, were generated with A2 and B2 related as ninth-degree relatives. The same pedigree structures for samples A1–A13 and B1–B13 were also used to generate 100 pedigrees, each with different genotypes, where A2 and B2 were fourth-, fifth-, sixth-, seventh-, eighth-, and ninth-degree relatives. The number of ancestral relatives was adjusted to account for the different degree of relatedness.

We obtained ERSA (v.2.1) results for each simulation as described below.

To test improvements in relationship predictions by PADRE as the size and density of genotyped individuals increased, we first used PRIMUS, ERSA, and PADRE to analyze individuals A6 and B6 in each simulated pedigree (Figure 1). We repeated the analyses iteratively, including genotypes of an additional randomly selected first- or second-degree relative of A6 and B6 in each iteration. We then performed a final analysis using all 13 individuals in each pedigree (see Figure 1).

Runtime

We evaluated PADRE runtime on a machine with Intel Xeon CPU E5-2670 v.2 at 2.50 GHz with 14 GB of memory, subtracting the time needed to load the ERSA likelihood files. The number of comparisons is the number of pairwise likelihoods that were looked up during the PADRE analysis and is the single best estimate of runtime. Each comparison is conducted at the lowest level of five nested for loops: (1) for each pair of networks, (2) for each pair of possible pedigrees within the networks, (3) for each pair of founders between each of the pedigrees in different networks, (4) for degrees of relatedness between the fourth and ninth degrees, and (5) for each pair of non-missing individuals between the two pedigrees.

The variability in the comparisons per second is due to variability in the other PADRE calculations. PRIMUS reconstruction was unable to complete for all family networks when it was run on the European ancestry dataset using third-degree relationships as a cutoff because some family networks resulted in too many possible pedigree structures consistent with the genetic dataset. The results of these runtime comparisons are shown in Table S1.

Extended Pedigree Samples

We analyzed Affymetrix 6.0 SNP microarray data on 169 individuals from three previously described extended pedigrees with predominantly northern European ancestry.¹⁶ The three pedigrees were validated as described in Huff et al.,¹⁶ are composed of 24, 30, and 115 genotyped individuals, and included a total of 7,266 previously described relationships between pairs of individuals.

HapMap3 CEU Samples

Using 165 CEU individuals from HapMap3 release 2²⁰ obtained from the HapMap website (see Web Resources), we reconstructed pedigree structures in this dataset with PRIMUS as described below by using the default settings. We applied a Bonferroni correction when detecting initial relationships between family networks identified in PRIMUS of p = 5.5 × 10⁻⁶ (0.05/9,074 founder-to-founder relationships).

Pedigree Reconstruction with PRIMUS

PRIMUS uses genome-wide IBD estimates to identify families and reconstruct all possible pedigrees that fit the genetic data by using relationships as distant as third-degree relatives. We used the prePRIMUS IBD pipeline⁵ to generate genome-wide average IBD estimates between all samples in each pedigree and used PRIMUS (v.1.8) to reconstruct pedigrees. The command line options used were “--file [data_file_root_name] and --genome.” Due to the sparse number of individuals genotyped in the three European ancestry pedigrees and in many of the simulations which lead to long runtimes in PRIMUS, we applied a relatedness threshold of second degree in PRIMUS to both datasets by adding the command line option “--degree_rel_cutoff 2.” We used the default relatedness cutoff of third-degree relatives for the HapMap3 CEU dataset.²⁰

Distant Relationships Prediction with ERSA

We applied the IBD detection pipeline described by Glusman et al.¹⁷ by first phasing all genetic data with Beagle (v.3.3.2)¹¹ by using the phasing pipeline provided on the GERMLINE website (see Web Resources). We analyzed the phased data in GERMLINE (v.1.4.0)²³ for each chromosome with the following command:

$$\begin{array}{l}\text{germline}–\text{homoz}–\text{err}\_\text{het}1–\text{err}\_\text{hom}2–\text{map}\\ \left[\text{data}\_\text{root}\_\text{name}\_\text{chrN}\right].\text{map}–\text{min}\_\text{m}2.5<\\ \left[\text{data}\_\text{root}\_\text{name}\_\text{chrN}\_\text{options}\right].\text{txt}\end{array}$$

We analyzed the GERMLINE output files with ERSA (v.2.1) to calculate the likelihood of each possible pairwise relationship (from the first through 39^th degrees) among all samples in the dataset. We controlled for potential false-positive IBD segments by masking genomic regions from the 1000 Genomes Project²⁴ CEU samples with greater than a 4-fold excess of pairwise IBD (mask_region_threshold = 4) as previously described:¹⁷

$$\begin{array}{l}\text{ersa}\text{-}\text{-}\text{segment}\_\text{files}=\left[\text{sample}\_\text{data}\_\text{germline}.\text{match}\_\text{files}\right]\text{-}\text{-}\\ \text{model}\_\text{output}\_\text{file}\text{model}\_\text{likelihoods}.\text{txt}\text{-}\text{-}\text{output}\_\text{file}=\text{ersa}\_\text{results}\text{-}\text{-}\\ \text{confidence}\_\text{level}0.999\text{-}\text{-}\text{mask}\_\text{common}\_\text{shared}\_\text{regions}\text{true}\text{-}\text{-}\\ \text{control}\_\text{files}=\left[\text{CEU}\_\text{germline}.\text{match}\_\text{files}\right]\end{array}$$

Results

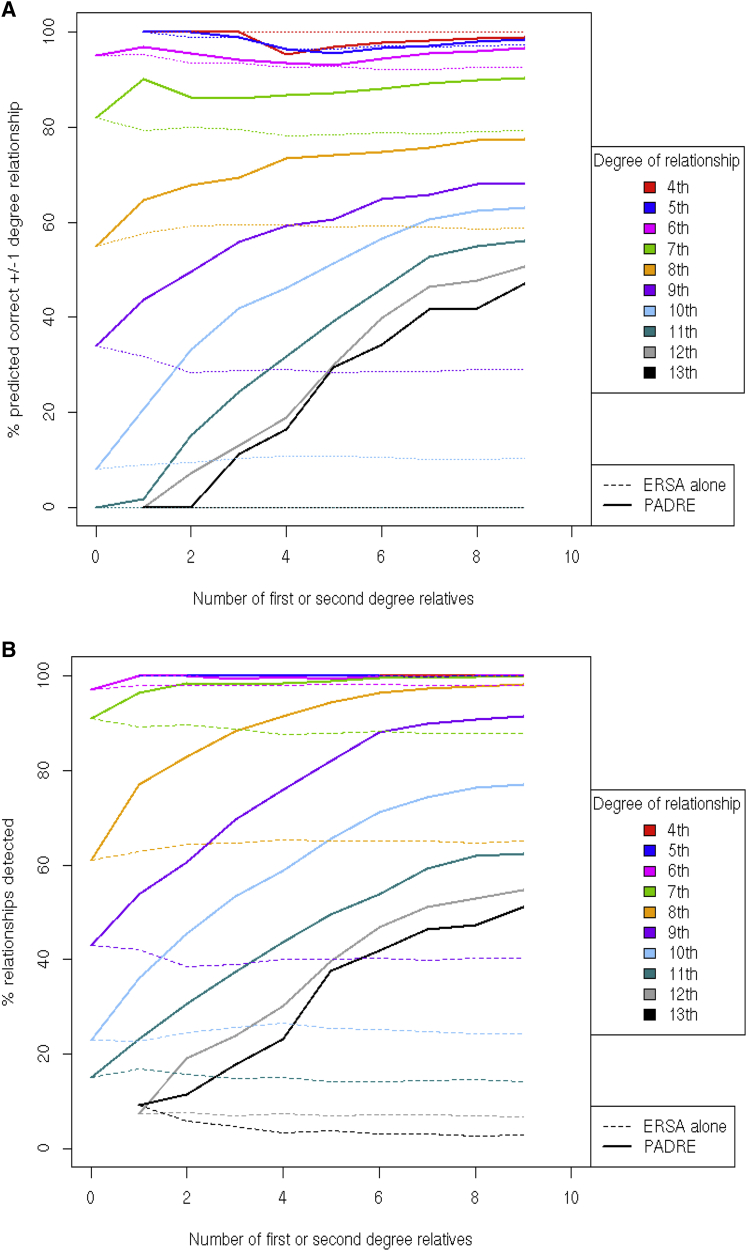
To evaluate the improvements in relationship prediction, we ran PADRE on 600 simulated pedigrees, each with ten different patterns of genotyped individuals, and compared the accuracy of the resulting pairwise relationship predictions (see Subjects and Methods). Figure 2A shows that PADRE and ERSA alone exhibited the same accuracy when the individuals had no other first- or second-degree relatives in the pedigree. However, as additional genotyped individuals were included in the pedigrees, PADRE accurately predicted up to 56% more of the simulated relationships. In addition to higher relationship prediction accuracy, Figure 2A demonstrates that PADRE predicted relationships that are undetectable by methods that consider only pairwise genetic data. For example, PADRE detected over 50% of 13^th-degree relationships, although 95% of 13^th-degree relatives share no genetic material through their most recent common ancestors (in humans). PADRE provided a substantial increase in power by correctly detecting up to 83% of seventh- through 13^th-degree relationships in our simulations (Figure 2B).

Figure 2.

Comparison of PADRE versus ERSA Accuracy in Simulated Data by Degree of Relationships

(A) The observed accuracy in the pedigree predictions increases as additional first- and second-degree relatives are added.

(B) Power of PADRE and ERSA alone to detect simulated relationships as additional first- and second-degree relatives were added to the pedigree. The ERSA results fluctuate slightly because additional pairwise estimates are added as more individuals are included, as described with the generation of the simulations.

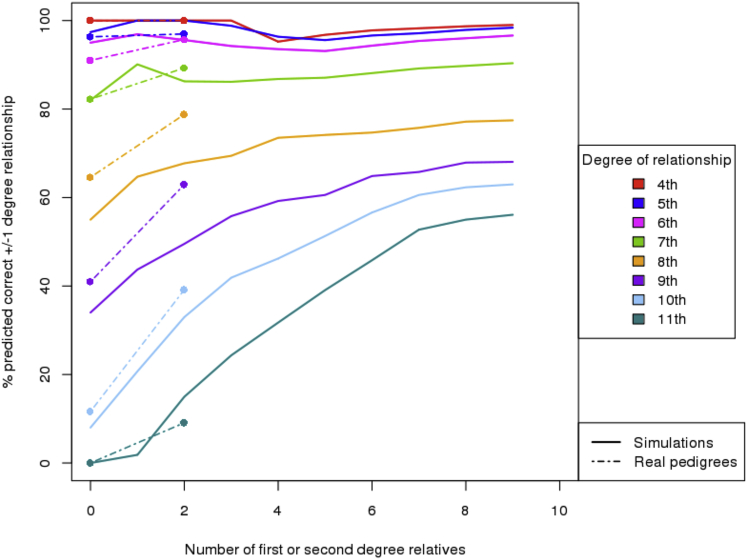
Figure 2 displays the ERSA and PADRE results for simulated pedigrees as large as 20 individuals, and Figure 3 summarizes the results for the simulated pedigrees with all 26 individuals. PADRE predicted the exact degree of relationship for 20% additional fourth- through ninth-degree relationships, relative to ERSA alone. For 10^th- through 13^th-degree relationships, ERSA accurately predicted only 4% of relationships to within one degree. In comparison, PADRE accurately predicted 59% of the simulated 10^th- through 13^th-degree relationships to within one degree, even though approximately 71% of such relatives share no DNA segments that are IBD (additional comparative data are shown in Figure S3). This can be accomplished because genetic relationships across pedigree founders propagate through pedigrees, allowing for multiple pairwise comparisons, which improves accuracy and results in accurate estimates of distant genealogical relationships even in pairs of descendants who inherited no genomic segments in common. Thus, by utilizing the pairwise sharing across all members of both pedigrees, PADRE is frequently able to predict very distant genealogical relationships between deeply genotyped pedigrees that are undetectable from single pairwise genetic comparisons.

Figure 3.

PADRE and ERSA Prediction Accuracy on Simulated Pedigrees Where All Individuals Have Been Genotyped

PADRE more accurately predicts fifth- through tenth-degree relationships relative to ERSA and frequently identifies 11^th- through 13^th-degree relatives who were undetectable in ERSA.

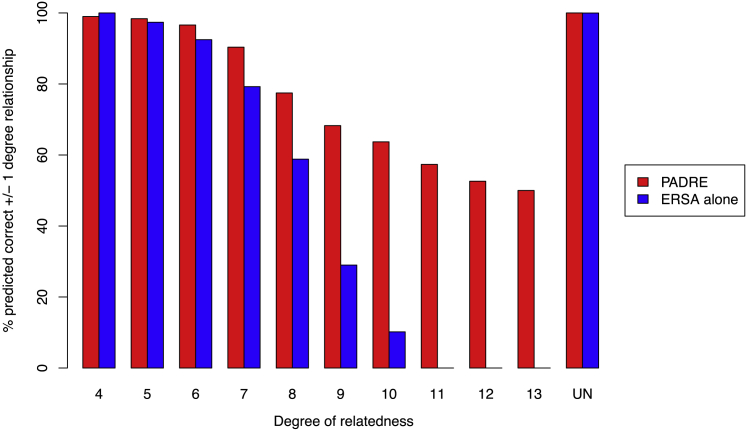
We also analyzed Affymetrix 6.0 microarray data from 169 individuals in three previously described extended pedigrees with predominantly northern European ancestry.¹⁶ The three pedigrees were composed of 24, 30, and 115 genotyped individuals and included a total of 7,266 pairs of related individuals. As expected, ERSA and PADRE attained the same accuracy for pairs of individuals with no genotyped first- or second-degree relatives. However, when we considered pairs of individuals who had two first- or second-degree relatives, we observed a substantial improvement in accuracy with PADRE (Figure 4), whereas ERSA’s accuracy rate was unchanged. PADRE correctly predicted 39% (95% confidence interval: 38% to 40%) of the 10^th-degree relationships within one degree of relatedness when the individuals had two first- or second-degree relatives in the pedigree, in comparison to 23% (95% confidence interval: 22% to 24%) for ERSA alone. In addition, PADRE was able to detect 9% of the 11^th-degree relationships, whereas ERSA did not detect any. The relationship prediction accuracy in this dataset increased as the number of first- and second-degree relatives in the pedigree increased, broadly matching the improvement we observed in our simulations (Figure 4). Effects of Bonferroni correction on relationship estimation accuracy in these data are shown in Figure S4.

Figure 4.

Percentage of Relationships Correctly Predicted by PADRE to Within ± One Degree in Real Pedigrees of European Ancestry and Simulated Pedigrees

Relationship detection accuracy was broadly consistent between the real and simulated pedigrees. Because the real pedigrees included two or fewer first- or second-degree relatives, PADRE’s estimated relationship detection accuracy for pedigrees with three or more sampled relatives is based solely on simulated data.

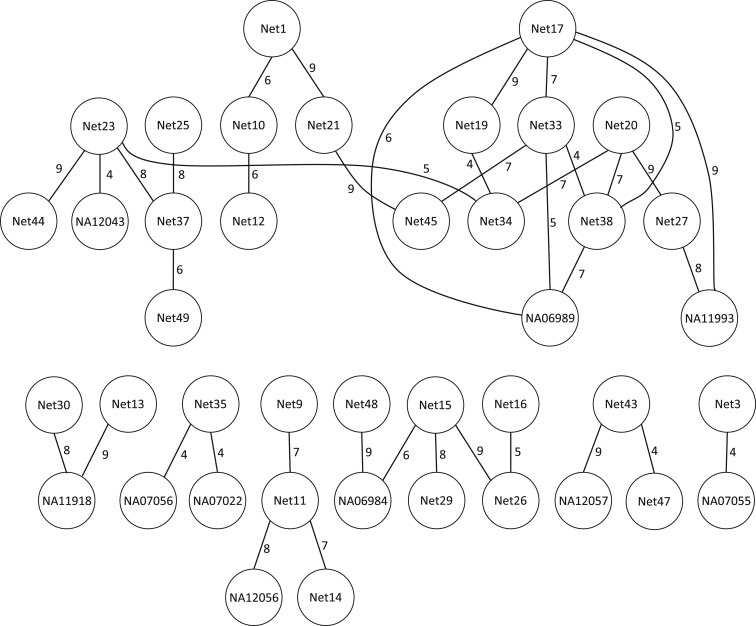
We previously reconstructed 51 separate pedigrees within the HapMap3 CEU dataset.²⁰ These pedigrees contain between two and six individuals. PADRE identified relationships between 40 pairs of pedigrees consisting of 594 pairs of individuals via previously unknown fourth- through ninth-degree relationships (Figure 5). Figure 6 illustrates one example in which PADRE predicts relationships connecting founders from four previously described CEU pedigrees.

Figure 5.

A Graph of PADRE-Estimated Relationships among the CEU Samples with a Bonferroni-Adjusted Threshold of α = 0.05/9,090 = 5.5 × 10⁻⁶

Each node corresponds to a PRIMUS reconstructed network number, and an edge between nodes indicates a significant relationship predicted by PADRE using pairwise relationship likelihoods obtained by ERSA. The number next to each edge indicates the degree of relationship connecting a founder in the reconstructed pedigree of each network. This type of network graph is the standard output of PADRE.

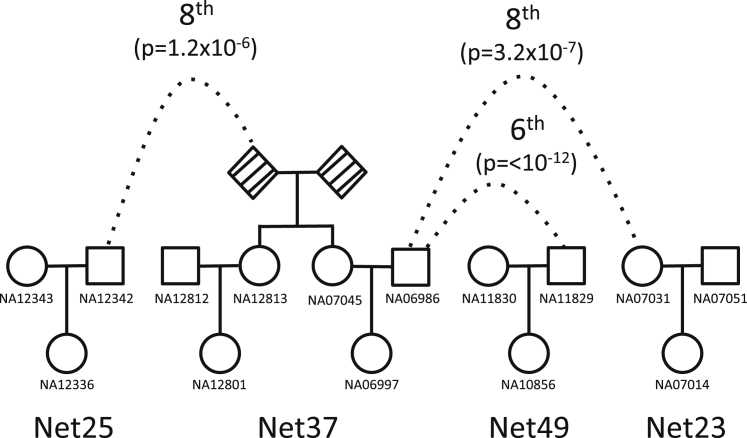
Figure 6.

An Example of Four Distantly Related HapMap3 CEU Pedigrees with Relationships Predicted by PADRE

Although the trios and the full-sibling relationship between NA12813 and NA07045 have been previously reported, PADRE is able to identify statistically significant relationships connecting these distantly related pedigrees. The related pairs of founders are marked with the dotted lines, and the degree of relationship is labeled next to the line.

We have demonstrated through simulated and actual data that PADRE can leverage pedigree reconstruction results from PRIMUS and distant pairwise relationship predictions from ERSA to improve both the sensitivity and accuracy of distant relationship estimation. The power to detect relationships more distant than ninth-degree relatives was dependent on the number of generations in the pedigrees with genotype data. For instance, PADRE detected up to 13^th-degree relationships in the simulated pedigrees with three generations of genotype data and the founders of the pedigrees (A2 and B2, Figure 1). As the depth of the pedigrees connected by PADRE increases, so will the distance of relationships that PADRE will be able to predict. Relationship estimation accuracy in PADRE improved as the number of genotyped individuals within each pedigree increased (Figures 2 and 4) and was most accurate when all individuals within a pedigree were genotyped (Figure 3).

We note that PADRE assumes absence of consanguinity and thus does not look for distant relationships within the reconstructed pedigree structures identified by PRIMUS. However, these types of relationships can be detected in other ways, for example, by using ISCA²⁵ and ERSA (v.2) to evaluate regions of the genome that are shared IBD on both chromosomes (IBD2) between founders within a pedigree. Although PADRE can connect a single pedigree, and even a single founder, to multiple other pedigrees, the algorithm is currently limited to establishing a maximum of one distant relationship between founders of any given pair of pedigrees. Allowing for multiple relationships between founders of a pair of pedigrees will require modeling of independently inherited shared segments to prevent confounding and is a direction of work for future releases of PADRE.

Discussion

PADRE has several important and immediate applications in human genetic analysis, especially in large case-control studies. PADRE can detect cryptic fourth- through 13^th-degree relationships, even in small datasets, as shown in our analysis of the CEU data (Figures 5 and 6). By identifying and appropriately modeling these relationships, studies can avoid findings biased by relatedness²⁶ and in some cases might be able to leverage familial relationships to improve power.²⁷ This is particularly important for detecting relatively high-penetrance risk alleles segregating in distantly related pedigrees.

Existing prediction algorithms for detecting distant pairwise relationships use the number and size of shared IBD segments between two individuals to estimate their degree of relatedness.^{16, 28} However, as the degree of relatedness increases, the number of shared segments drops to zero. Most 11^th-degree human relatives share no segments of their autosomal DNA IBD;¹⁶ therefore, their degree of relatedness cannot be estimated by existing pairwise comparison programs. In some scenarios, PADRE can leverage reconstructed pedigrees to identify genealogical relationships between individuals who are genetically unrelated, i.e., share no portion of their genome IBD through their most recent common ancestors.

PADRE runtime increases combinatorially depending on the number of family networks, the number of possible pedigrees within each family network, the number of founders in each of the pedigrees, and the number of non-missing individuals in each pedigree structure in the PRIMUS results. These numbers are difficult to predict prior to running PRIMUS and depend heavily on how densely the pedigrees have been sampled (Figure S5). For some datasets, it will be necessary to use a closer relatedness cutoff for the PRIMUS reconstruction in order to limit the number of possible pedigrees generated. This adjustment will in turn improve the runtime of PADRE. We have employed this technique with the European ancestry pedigrees due to the sparse sampling of individuals. Table S1 and accompanying text provides additional information on runtimes and computational limitations of PADRE.

There has been a resurgence of interest in large and deeply genotyped pedigrees in the search for genetic heritability of complex disease traits. Pedigrees have become especially relevant in the detection of rare variant effects on diseases because pedigrees are well-suited for the study of rare variation.⁹ Under the hypothesis that multiple rare and common variants contribute to complex disease, projects such as the Alzheimer’s Disease Sequencing Project, the San Antonio Mexican American Family Studies, and the Jackson Heart Study have all undertaken deep whole-genome sequencing of members of clinically ascertained pedigrees. Projects such as these could particularly benefit directly from verification and detection of distant relatedness in PADRE.

PADRE leverages genome-wide average IBD sharing, as well as the size and distribution of shared IBD segments, to achieve a substantial improvement in accuracy over existing methods. PADRE has immediate relevance to a host of applications within genetics, allowing investigators to more accurately estimate cryptic relatedness, verify very distant relationships, and maximize power in analytic design. PADRE is freely available for academic use (see Web Resources).

Data Access

Access to PADRE input data for the extended pedigrees has been made publicly available. The ERSA-derived shared segments (as described in Huff et al. 2011¹⁶) as well as the PRIMUS-derived pedigree likelihoods for the extended pedigree samples are available on the PADRE website (see Web Resources).

Published: June 30, 2016

Web Resources

• GERMLINE, http://www.cs.columbia.edu/∼gusev/germline/phasing_pipeline.tar.gz

• HapMap, http://hapmap.ncbi.nlm.nih.gov

• PADRE, http://www.hufflab.org/software/padre