Abstract
The purpose of this study was to develop regression-based prediction equations for estimating dual-energy X-ray absorptiometry (DXA)-derived appendicular lean soft tissue mass (aLM) using ultrasound and to investigate the validity of these equations in 102 Caucasian adults aged 50 to 76 years. The subjects were randomly separated into two groups: 71 in the model-development group (41 men and 30 women) and 31 in the cross-validation group (18 men and 13 women). aLM was measured using a DXA, and muscle thickness (MT) was measured using ultrasound at 9 sites. Stepwise linear regression analysis was used to determine predictive models for DXA-derived aLM from MT variables, sex, and age. A number of ultrasound prediction equations for estimation of aLM were developed and then cross-validated in a subsample of older adults. The results indicated that ultrasound MT and MT × height can be used to accurately and reliably estimate DXA-derived aLM in older Caucasian adults.
Keywords: Aging, Skeletal muscle mass, B-mode ultrasonography, DXA
Introduction
Lean soft tissue mass of upper and lower extremities, termed appendicular lean soft tissue mass (aLM), measured using a dual-energy X-ray absorptiometry (DXA) is widely used as a standard technique for estimating age-related change in muscle mass of the human body. aLM declines with increasing age in different ethnicities (Gallagher et al. 1997), especially after the age of 60 (Kyle et al. 2001). In both men and women, reduced aLM is closely associated with increased risks of future physical disability (Baumgartner et al. 1998; Tanimoto et al. 2012), metabolic disorders (Park et al. 2009), cognitive impairment (Burns et al. 2010), and mortality (Bunout et al. 2011; Vetrano et al. 2014). The aLM measured by DXA, however, contains non-skeletal muscle tissue components such as a fat-free component of adipose tissue mass (Abe et al. 2015c), which accounts for 15 % of total adipose tissue (Heymsfield et al. 2002). In addition, DXA measurements are costly, expose individuals to radiation, and access to the equipment is limited.
Ultrasound is a non-invasive, low cost, and safe imaging technique to estimate body composition such as body fat and lean body mass (Abe et al. 1994). Unless the muscle being imaged is small, a single image from a portable ultrasound only measures muscle thickness but not muscle cross-sectional area and muscle volume. Consequently, a few studies have developed ultrasound prediction equations for estimating total body and regional muscularity in adults (Abe et al. 1994; Sanada et al. 2006; Takai et al. 2013, 2014). Recently, we reported that three of the four selected equations have systematic bias and only one equation had a relatively small total error with no systematic error (Abe et al. 2015b). The ultrasound prediction equation developed by Sanada et al. (2006), which has no systematic error described above, used magnetic resonance imaging (MRI) measured total body and regional muscle volume as a reference criterion. On the other hand, two of the three selected equations with systematic error used DXA-derived leg lean mass (Takai et al. 2013) or total fat-free body mass (Takai et al. 2014) as a reference criterion. Thus, ultrasound equations for predicting aLM have not been currently published. aLM divided by height squared (aLM index) is one criterion for defining age-related muscle loss (i.e., sarcopenia). DXA-derived aLM does not include trunk muscle as well as bone mineral mass, although the shoulder and hip joint muscles are included in the aLM. Additionally, all prediction equations reported previously were developed on Japanese samples. Therefore, development of new equations for predicting DXA-derived aLM would be required in addition to the previous studies. The purpose of the present study was to develop regression-based prediction equations for estimating DXA-derived aLM using ultrasound and to investigate the validity of these equations in Caucasian adults.
Methods
Subjects
One hundred and two healthy Caucasian adults (59 men and 43 women) aged 50 to 76 years were randomly separated into two groups: 71 in the model-development group and 31 in the cross-validation group (Table 1). According to a previous study (Dupler and Tolson 2000), the ratio for the number of subjects in the development group to the validation group was two to one. The subjects were recruited from the university campus and surrounding area. Prior to obtaining informed consent, a written description of the purpose of the study and its safety was distributed to potential subjects. All subjects were free of overt chronic disease (e.g., neuromuscular, diabetes, angina, myocardial infarction, cancer, stroke, etc.) as assessed by self-report. Because adipose tissue mass in the extremities may falsely inflate the DXA-derived aLM (Abe et al. 2015c), volunteers with a higher body fat percentage (>35 % body fat) measured by DXA were excluded. The rate of regular sports activity (at least twice a week), including running and cycling exercise, was approximately 67 % of the subjects (48 men and 20 women). This study was conducted according to the World Medical Association Declaration of Helsinki and was approved by the University’s Institutional Review Board, and written informed consent was obtained from subjects. Body mass and standing height were measured to the nearest 0.1 kg and 0.1 cm, respectively, by using a height scale and an electronic weight scale. Body mass index (BMI) was defined as body mass (kg)/height2 (m2).
Table 1.
Physical characteristics of the subjects
| Variables | Model development (n = 71) | Cross-validation (n = 31) | ||
|---|---|---|---|---|
| Men (n = 41) | Women (n = 30) | Men (n = 18) | Women (n = 13) | |
| Age (years) | 59.3 (6.5) | 58.3 (6.4) | 60.6 (6.9) | 57.1 (5.4) |
| Height (m) | 1.77 (0.06) | 1.63 (0.05) | 1.77 (0.07) | 1.61 (0.06) |
| Weight (kg) | 82.1 (13.8) | 63.6 (11.7) | 80.3 (8.9) | 67.0 (16.4) |
| BMI (kg/m2) | 26.1 (3.5) | 23.9 (5.7) | 25.5 (2.1) | 26.0 (6.3) |
| Body fat (%) | 19.4 (5.1) | 29.7 (6.2) | 19.1 (3.5) | 30.4 (9.4) |
| tLM (kg) | 62.2 (9.3) | 41.7 (6.2) | 61.0 (6.9) | 42.9 (6.9) |
| aLM (kg) | 28.2 (4.2) | 17.5 (2.7) | 27.8 (3.4) | 18.4 (3.1) |
| Muscle thickness (cm) | ||||
| Forearm (radius) | 2.50 (0.38) | 1.78 (0.24) | 2.37 (0.39) | 1.81 (0.24) |
| Forearm (ulna) | 4.29 (0.35) | 3.38 (0.27) | 4.19 (0.36) | 3.37 (0.27) |
| Upper-arm anterior | 3.48 (0.39) | 2.39 (0.31) | 3.36 (0.34) | 2.41 (0.25) |
| Upper-arm posterior | 3.99 (0.52) | 2.71 (0.50) | 3.92 (0.62) | 2.73 (0.64) |
| Trunk anterior | 1.34 (0.30) | 0.97 (0.15) | 1.39 (0.28) | 0.92 (0.19) |
| Trunk posterior | 2.30 (0.54) | 1.87 (0.43) | 2.17 (0.43) | 2.02 (0.46) |
| Thigh anterior | 5.25 (0.58) | 4.11 (0.58) | 5.35 (0.49) | 4.77 (0.63) |
| Thigh posterior | 6.69 (0.53) | 5.84 (0.66) | 6.49 (0.61) | 5.90 (0.78) |
| Lower-leg anterior | 3.10 (0.36) | 2.61 (0.24) | 3.07 (0.29) | 2.75 (0.24) |
| Lower-leg posterior | 7.45 (0.61) | 6.33 (0.52) | 7.11 (0.69) | 6.42 (0.45) |
Values are means ± standard deviations (SD)
BMI body mass index, tLM total lean soft tissue mass, aLM appendicular lean soft tissue mass
Ultrasound measurements
Muscle thickness (MT) was measured using B-mode ultrasound (Aloka SSD-500, Tokyo, Japan) at nine sites [anterior forearm (at 30 % proximal between the styloid process and the head of the radius), anterior and posterior upper arm (at 60 % distal between the lateral epicondyle of the humerus and the acromial process of the shoulder), anterior and posterior thigh (midway between the lateral condyle of the femur and greater trochanter), anterior and posterior lower leg (at 30 % proximal between the lateral malleolus of the fibula and the lateral condyle of the tibia), anterior trunk (about 3 cm lateral to the umbilicus), and posterior trunk (about 5 cm below to the inferior angle of the scapula)] on the right side of the body as described previously [Abe et al. 1994]. After measurement of limb length using anatomical landmarks described above, all measurement sites were marked with a marker pen. The measurements were taken while the subjects stood quietly relaxed with their elbows and knees extended and weight evenly distributed on both legs. A linear transducer with a 5-MHz scanning head was coated with water-soluble transmission gel to provide acoustic contact and reduce pressure by the scanning head to achieve a clear image. The scanning head was placed on the skin surface of the measurement site using the minimum pressure required, and cross-sections of each muscle were imaged. Two images from each site were printed (SONY UP-897MD, Tokyo, Japan), and mean values of each site were used for data analysis. The subjects were standing approximately 5 min for the ultrasound measurement. The subcutaneous adipose tissue–muscle interface and muscle-bone interface were identified from the ultrasonic image, and the distance between the two interfaces was accepted as MT for limb muscles. For measurements in the trunk, MT was defined as the distance between the adipose tissue-muscle interface and the deep muscle fascia interface. In the anterior forearm, two MTs were measured as the perpendicular distance between the subcutaneous adipose tissue-muscle interface and muscle-bone interface of the radius (forearm radius MT) and ulna (forearm ulna MT). The distance between the two interfaces was measured with a ruler. Precision and linearity of the image reconstruction have been described and confirmed elsewhere [Abe et al. 2014b]. Test-retest reliability of MT measurements using intraclass correlation coefficient (ICC3,1), standard error of measurement (SEM), and the minimal difference needed to be considered real was previously determined from young and middle-aged subjects for forearm radius (0.92, 0.10, and 0.27 cm) and ulna (0.99, 0.05, 0.15 cm) [Abe et al. 2015a], anterior (0.88, 0.08, and 0.22 cm) and posterior (0.96, 0.08, and 0.22 cm) upper arm and anterior (0.98, 0.07, and 0.19 cm) and posterior (0.95, 0.10, and 0.28 cm) thigh [Abe et al. 2014a].
Dual-energy X-ray absorptiometry measurements
Subjects underwent DXA scans (Discovery A, Hologic Inc., Bedford, MA, USA) to determine percent body fat (%fat), total body fat mass, arms and legs LM, aLM, and total LM (tLM). Quality assurance testing and calibration was performed the morning of data collection days to ensure that the DXA was operating properly. Subjects were asked to refrain from eating for at least 4 h prior to scans and were offered water ad libitum. Also, subjects were asked to refrain from moderate/vigorous exercise for at least 48 h prior to the scans. DXA scans were conducted immediately before or after ultrasound measurements. Test-retest reliability using ICC3,1, SEM, and the minimal difference to be considered real was previously determined from 17 subjects scanned twice for aLM (0.99, 0.21, and 0.58 kg), tLM (0.99, 0.36, and 0.71 kg), and %Fat (0.99, 0.49, and 0.95 %) [Abe et al. 2015b].
Statistical analysis
Data were analyzed using IBM SPSS statistics 21, and variability was represented using standard deviation (SD). Stepwise linear regression analysis was used to determine predictive models for DXA-derived aLM from MT variables, sex, and age. As the equation to calculate the volume of a cylinder is π × r2 × h, it would be suitable for MT2 × limb length to estimate aLM. When body segments (length of forearm, upper-arm, thigh and lower leg) were analyzed, the predicted accuracy (r2 value) was similar to using standing height. Thus, standing height was used to express the length factor of the muscle. The overall agreement between the predicted aLM and the measured aLM on a continuous scale was evaluated using Lin’s concordance correlation coefficient (CCC) [Lin 1989]. Independent t tests were used to analyze physical characteristic differences among the developmental and cross-validation groups and between means of measured and predicted aLM models. Total error (the average deviation of individual scores from the line of identity) of aLM prediction equations was also calculated. Bland-Altman plots were also used such that the differences between measured aLM and predicted aLM were plotted against the mean of the measured and predicted aLM. Significance was set at an alpha level of p < 0.05.
Results
The physical characteristics of the subjects in the model-development and cross-validation groups are presented in Table 1. There were no significant differences between the development and validation groups for men and women.
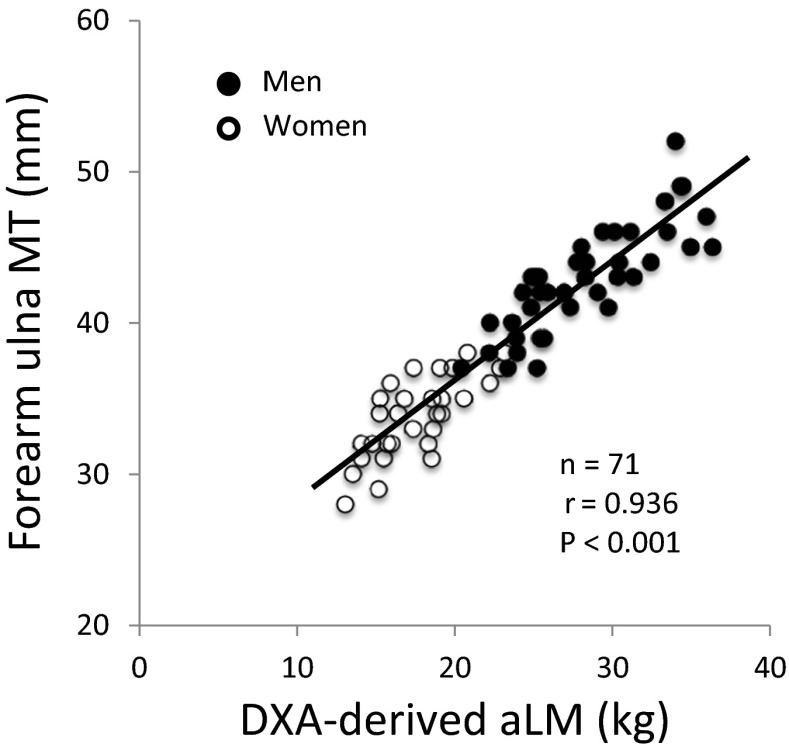
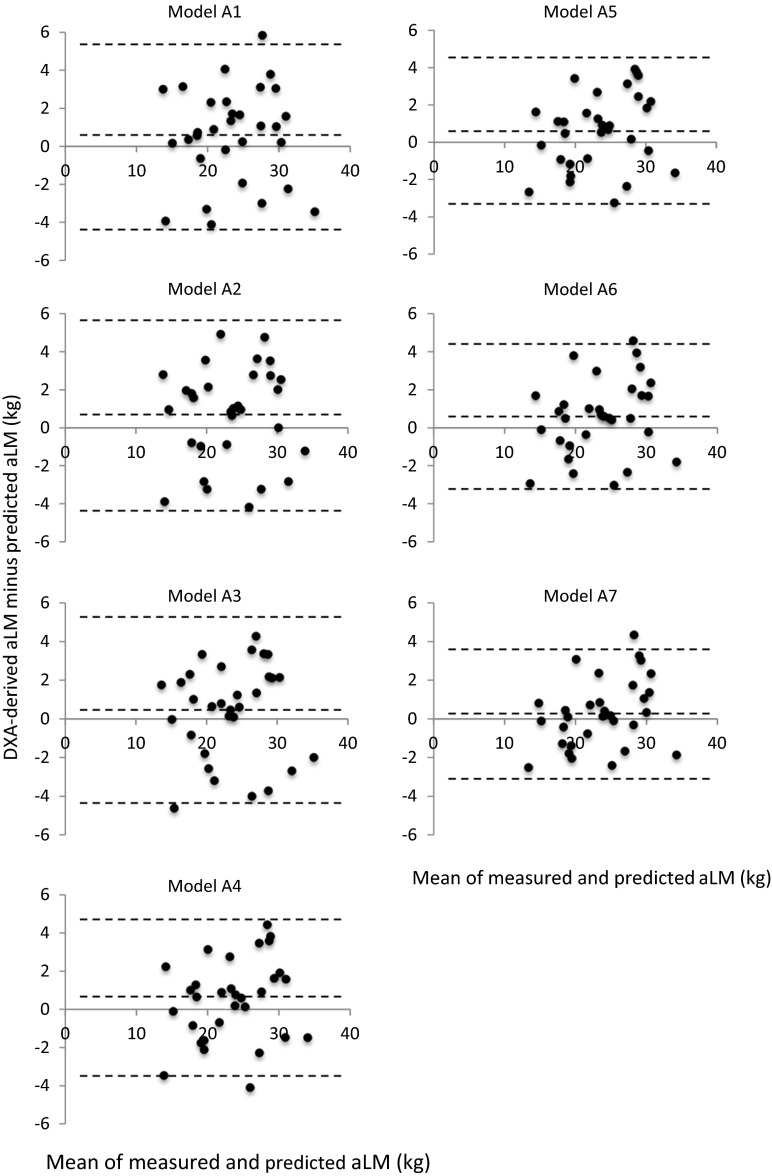
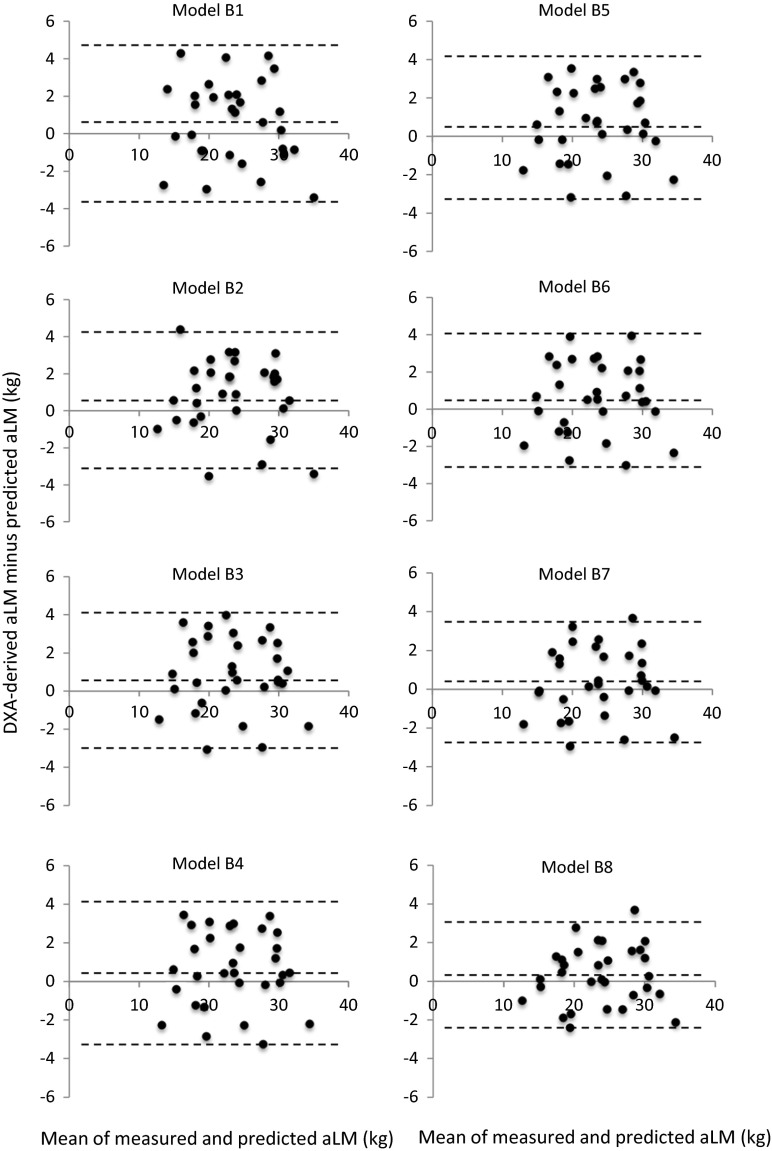
Significant simple correlations (p < 0.05) were observed between DXA-derived aLM and ultrasound MT measured at 10 sites (r = 0.379–0.936) in the model-development group (n = 71). The highest correlation was found between the aLM and forearm-ulna MT (Fig. 1). Stepwise multiple-regression analyses produced seven equations predicting the DXA-derived aLM from ultrasound MT with age and sex (series A, Table 2) and eight equations predicting the aLM from MT × standing height with age and sex (series B, Table 3). The aLM prediction equations were applied to the validation group (n = 31), and the predicted aLM did not significantly differ from the measured aLM in model series A (Table 4). In model series B, however, four of the eight equations were significantly lower in the predicted aLM than in the DXA-derived aLM (Table 4). Total errors of the prediction models were ranged from 1.78 to 2.54 kg for model series A and 1.53 to 2.23 kg for model series B (Table 4). Bland-Altman analysis did not indicate a bias in prediction of the aLM for the validation group (Figs. 2 and 3).
Fig. 1.
Relationship between DXA-derived appendicular lean soft tissue mass (aLM) and ultrasound forearm-ulna muscle thickness (MT)
Table 2.
The predicted equations (series A) of DXA-derived appendicular lean soft tissue mass (aLM) in the development group (n = 71) with aLM in kg and muscle thickness (MT) in centimeter
| Entered predictor variables | Stepwise regression equation | R 2 | Adjusted R 2 | SEE (kg) |
|---|---|---|---|---|
| Age, sex, MT-FA (radius), MT-FA (ulna), MT-UA, MT-UP, MT-A, MT-P, MT-TA, MT-TP, MT-LA, MT-LP | Model A1 | |||
| aLM = 10.90 × MT-FA (ulna) − 18.83 | 0.877 | 0.875 | 2.26 | |
| Model A2 | ||||
| aLM = 6.83 × MT-FA (ulna) + 3.96 × MT-UA − 14.94 | 0.916 | 0.913 | 1.89 | |
| Model A3 | ||||
| aLM = 5.15 × MT-FA (ulna) + 3.62 × MT-UA + 3.73 × MT-LA − 18.10 | 0.938 | 0.935 | 1.63 | |
| Model A4 | ||||
| aLM = 4.68 × MT-FA (ulna) + 3.32 × MT-UA + 3.48 × MT-LA + 1.00 × MT-TP − 21.02 | 0.944 | 0.941 | 1.56 | |
| Model A5 | ||||
| aLM = 4.32 × MT-FA (ulna) + 2.98 × MT-UA + 2.85 × MT-LA + 0.97 × MT-TP + 0.94 × MT-LP − 23.12 | 0.948 | 0.944 | 1.51 | |
| Model A6 | ||||
| aLM = 4.09 × MT-FA (ulna) + 3.16 × MT-UA + 2.79 × MT-LA + 0.95 × MT-TP + 1.04 × MT-LP + 0.061 × age − 26.71 | 0.952 | 0.947 | 1.46 | |
| Model A7 | ||||
| aLM = 3.67 × MT-FA (ulna) + 2.84 × MT-UA + 2.58 × MT-LA + 1.05 × MT-TP + 0.93 × MT-LP + 0.069 × age + 0.79 × MT-TA − 27.63 | 0.955 | 0.950 | 1.43 | |
SEE standard error of estimate, FA forearm, UA upper-arm anterior, UP upper-arm posterior, A trunk anterior, P trunk posterior, TA thigh anterior, TP thigh posterior, LA lower-leg anterior, LP lower-leg posterior
Table 3.
The predicted equations (series B) of DXA-derived appendicular lean soft tissue mass (aLM) in the development group (n = 71) with aLM in kg and muscle thickness (MT in centimeter) × standing height (Ht in meter)
| Entered predictor variables | Stepwise regression equation | R 2 | Adjusted R 2 | SEE (kg) |
|---|---|---|---|---|
| Age, sex, MT-FA (radius) × Ht, MT-FA (ulna) × Ht, MT-UA × Ht, MT-UP × Ht, MT-A × Ht, MT-P × Ht, MT-TA × Ht, MT-TP × Ht, MT-LA × Ht, MT-LP × Ht | Model B1 | |||
| aLM = 4.89 × MT-FA (ulna) × Ht − 9.15 | 0.908 | 0.907 | 1.95 | |
| Model B2 | ||||
| aLM = 3.15 × MT-FA (ulna) × Ht + 1.33 × MT-LP × Ht − 13.38 | 0.939 | 0.937 | 1.61 | |
| Model B3 | ||||
| aLM = 2.11 × MT-FA (ulna) × Ht + 1.00 × MT-LP × Ht + 1.51 × MT-UA × Ht − 10.36 | 0.953 | 0.951 | 1.41 | |
| Model B4 | ||||
| aLM = 1.71 × MT-FA (ulna) × Ht + 0.72 × MT-LP × Ht + 1.53 × MT-UA × Ht + 1.25 × MT-LA × Ht − 10.56 | 0.960 | 0.957 | 1.32 | |
| Model B5 | ||||
| aLM = 1.54 × MT-FA (ulna) × Ht + 0.83 × MT-LP × Ht + 1.32 × MT-UA × Ht + 1.13 × MT-LA × Ht + 0.54 × MT-P × Ht − 11.05 | 0.964 | 0.961 | 1.27 | |
| Model B6 | ||||
| aLM = 1.40 × MT-FA (ulna) × Ht + 0.88 × MT-LP × Ht + 1.40 × MT-UA × Ht + 1.09 × MT-LA × Ht + 0.58 × MT-P × Ht + 0.053 × age − 14.18 | 0.966 | 0.963 | 1.23 | |
| Model B7 | ||||
| aLM = 1.23 × MT-FA (ulna) × Ht + 0.82 × MT-LP × Ht + 1.27 × MT-UA × Ht + 0.99 × MT-LA × Ht + 0.53 × MT-P × Ht + 0.060 × age + 0.40 × MT-TA × Ht − 14.67 | 0.969 | 0.965 | 1.19 | |
| Model B8 | ||||
| aLM = 0.98 × MT-FA (ulna) × Ht + 0.77 × MT-LP × Ht + 1.13 × MT-UA × Ht + 0.89 × MT-LA × Ht + 0.45 × MT-P × Ht + 0.058 × age + 0.48 × MT-TA × Ht + 0.44 × MT-TP × Ht − 16.11 | 0.972 | 0.969 | 1.13 | |
SEE standard error of estimate, FA forearm, UA upper-arm anterior, UP upper-arm posterior, A trunk anterior, P trunk posterior, TA thigh anterior, TP thigh posterior, LA lower-leg anterior LP lower-leg posterior
Table 4.
The predicted appendicular lean soft tissue mass (aLM) and DXA-derived aLM in the cross-validation group (n = 31)
| Regression equation | Predicted aLM (kg) | DXA-derived aLM (kg) | p for significance | Total error (kg) | Concordance correlation coefficient (95 % CI) | ||
|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | ||||
| Model A1 | 23.2 | 5.6 | 23.8 | 5.7 | NS | 2.54 | 0.897 (0.799–0.949) |
| Model A2 | 23.1 | 5.6 | NS | 2.61 | 0.808 (0.787–0.945) | ||
| Model A3 | 23.4 | 5.4 | NS | 2.46 | 0.899 (0.804–0.950) | ||
| Model A4 | 23.3 | 5.3 | NS | 2.18 | 0.920 (0.843–0.959) | ||
| Model A5 | 23.2 | 5.2 | NS | 2.08 | 0.926 (0.856–0.962) | ||
| Model A6 | 23.2 | 5.2 | NS | 2.05 | 0.928 (0.860–0.964) | ||
| Model A7 | 23.5 | 5.1 | NS | 1.78 | 0.945 (0.893–0.972) | ||
| Model B1 | 23.2 | 6.0 | 23.8 | 5.7 | NS | 2.23 | 0.926 (0.855–0.959) |
| Model B2 | 23.0 | 5.9 | <0.05 | 2.10 | 0.933 (0.868–0.967) | ||
| Model B3 | 22.9 | 5.8 | <0.05 | 2.10 | 0.932 (0.866–0.966) | ||
| Model B4 | 23.1 | 5.7 | <0.05 | 2.03 | 0.936 (0.872–0.968) | ||
| Model B5 | 23.1 | 5.7 | <0.05 | 2.04 | 0.934 (0.869–0.967) | ||
| Model B6 | 23.2 | 5.7 | NS | 2.02 | 0.936 (0.872–0.968) | ||
| Model B7 | 23.4 | 5.6 | NS | 1.76 | 0.950 (0.900–0.976) | ||
| Model B8 | 23.5 | 5.6 | NS | 1.53 | 0.963 (0.924–0.982) | ||
CI confidence interval
Fig. 2.
Bland-Altman plots of measured and predicted appendicular lean soft tissue mass (aLM) (series A). The middle dotted line represents the mean difference between measured and predicted aLM while the outside dotted lines represent 95 % limits of agreement
Fig. 3.
Bland-Altman plots of measured and predicted appendicular lean soft tissue mass (aLM) (series B). The middle dotted line represents the mean difference between measured and predicted aLM while the outside dotted lines represent 95 % limits of agreement
Discussion
In the present study, we developed ultrasound prediction equations to estimate DXA-derived aLM in a sample of healthy older Caucasian adults. To the best of our knowledge, this is the first study to develop ultrasound prediction equations for estimating aLM. Validation of the newly developed equations in a cross-validation subgroup showed that the equations predicted aLM with high precision and relatively low error. Ultrasound is a non-invasive, quick, and safe imaging technique that can be easily applied in clinical assessment and field survey. The precision and linearity of ultrasound image reconstruction have been confirmed (Abe et al. 2014b). Thus, these newly developed equations could be a valuable tool in population-based studies to assess a criterion for defining age-related muscle loss (i.e., sarcopenia), although validation in other ethnic groups must be investigated in the future.
The findings of the present study indicated that aLM estimated by ultrasound was not different between men and women (Fig. 1). A previous study (Shih et al. 2000) reported that there were no sex differences in estimated lower limb skeletal muscle mass using the DXA-derived prediction equations in 207 healthy men and women (90 Caucasian, 64 African-American, 31 Asian, and 21 Hispanic). Similarly, Sanada et al. (2006) observed that the relationship between MRI-measured skeletal muscle mass and ultrasound MT (sum of nine sites × height) overlapped in men and women (48 Japanese) and suggested that total muscle mass estimated by ultrasound was not different between sexes. In addition, a study revealed that there are strong correlations (r = 0.95–0.99) between MRI-measured whole body and regional (thigh, lower-leg, arm, and trunk) muscle mass in men and women (Abe et al. 2003). The linear relationship between MT and muscle CSA or muscle volume has been observed in upper and lower extremity muscles in both sexes (Abe et al. 2014b). As a result, our newly developed equations mainly included MT from the extremities, as DXA-derived aLM does not include trunk muscle.
A study (Baumgartner et al. 1998) proposed a definition for severe sarcopenia using a DXA-derived aLM index in men and women (7.26 and 5.45 kg/m2, respectively). In the present study, a small number of the subjects (4 men and 3 women) were below the cutoff values described above, which may be due to the fact that many subjects (approximately 70 %) performed regular sports activity (at least twice a week). We reconfirmed classification of the severe sarcopenia using the newly developed prediction equations. Six of the seven subjects (4 men and 2 women) were still classified as having severe sarcopenia, and an additional two women who were originally classified as moderate sarcopenia (1 standard deviation below the mean for young adult women) were newly classified as having severe sarcopenia.
Recently, Kulkarni et al. (2013) developed a model for prediction of DXA-derived aLM that used anthropometrical variables (height, weight, circumference, and skinfold) in Indian adults (18–79 years). Data from the present study were applied to Kulkarni et al.’s equations, and predicted aLM was significantly higher than the DXA-derived aLM in men (3.1 kg difference, p < 0.05) and in women (4.3 kg difference, p < 0.05). Although the authors of the anthropometrical study suggest the future validation studies in different populations, the anthropometric prediction equations may provide a low degree of accuracy in older Caucasian adults. More recently, BIA-derived prediction equations have also been reported to show excellent standard error of the estimate (SEE) and r2 values (Sergi et al. 2015). Our newly developed equations are in agreement with the accuracy of the BIA study. The ultrasound prediction models developed in this study indicate an excellent r2 value, which are similar to that of the previously reported DXA or ultrasound prediction models to estimate total and regional skeletal muscle mass (Sanada et al. 2006; Kim et al. 2002).
A previous study (Sanada et al. 2006) reported ultrasound prediction equations for predicting muscle mass using MT at nine sites including the forearm. However, forearm MT was measured only at the forearm-radius site. In the present study, we measured both forearm-ulna and forearm-radius MT and found that the highest correlation was observed between the DXA-derived aLM and forearm-ulna MT (r = 0.936), whereas only a moderate correlation was found between aLM and forearm-radius MT (r = 0.748). Three major flexor muscles are the prime movers of the digits, and the forearm-ulna MT mainly includes two muscles (flexor digitorum profundus, flexor digitorum superficialis), which produce flexion movement for the middle phalanges of the fingers. Furthermore, the forearm-ulna MT is strongly correlated with handgrip strength in young men and women (Abe et al. 2015a). These results suggest that the forearm-ulna MT may be positively associated with physical activity level of daily living, which may contribute to higher muscle mass or maintenance of skeletal muscle during aging.
It is known that muscle mass loss with increased age is greater in the lower extremities than in the upper extremities (Janssen et al. 2000), especially in the anterior thigh (Abe et al. 2014a). Thus, it was expected that the anterior thigh MT would be involved as a major predictor in the developed prediction equations. However, the anterior and posterior lower-leg MT and upper extremity MT were selected as major predictors in the equations. Ambulatory activity with moderate and vigorous intensities is positively associated with anterior and posterior lower-leg MT in older women (Abe et al. 2012). In addition, our subjects who performed regular cycling (Ozaki et al. 2015) and running (Oguri et al. 2004) exercise may have prevented the age-related thigh muscle mass loss. Therefore, use of the developed equations in older adults who perform different physical activity must be preceded by their validation in those populations.
In summary, a number of ultrasound prediction equations for estimation of aLM were developed in the present study and then cross-validated in a subsample of older adults. The results indicated that ultrasound MT and MT × height can be used to accurately and reliably estimate DXA-derived aLM in older Caucasian adults.
Acknowledgments
The authors thank the individuals who participated in this study. We also thank Dr. Paul D. Loprinzi in the Department of HESRM, The University of Mississippi, for his helpful statistical analysis comments.
References
- Abe T, Kondo M, Kawakami Y, Fukunaga T. Prediction equations for body composition of Japanese adults by B-mode ultrasound. Am J Hum Biol. 1994;6:161–170. doi: 10.1002/ajhb.1310060204. [DOI] [PubMed] [Google Scholar]
- Abe T, Kearns CF, Fukunaga T. Sex differences in whole body skeletal muscle mass measured by magnetic resonance imaging and its distribution in young Japanese adults. Br J Sports Med. 2003;37:436–440. doi: 10.1136/bjsm.37.5.436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abe T, Mitsukawa N, Thiebaud RS, Loenneke JP, Loftin M, Ogawa M. Lower body site-specific sarcopenia and accelerometer-determined moderate and vigorous physical activity: the HIREGASAKI study. Aging Clin Exp Res. 2012;24:657–662. doi: 10.3275/8758. [DOI] [PubMed] [Google Scholar]
- Abe T, Loenneke JP, Thiebaud RS, Fukunaga T. Age-related site-specific muscle wasting of upper and lower extremities and trunk in Japanese men and women. AGE (Dordr) 2014;36:813–821. doi: 10.1007/s11357-013-9600-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abe T, Loenneke JP, Thiebaud RS, Loftin M. Morphological and functional relationships with ultrasound measured muscle thickness of the upper extremity and trunk. Ultrasound. 2014;22:229–235. doi: 10.1177/1742271X14554678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abe T, Counts BR, Barnett BE, Dankel SJ, Lee K, Loenneke JP. Associations between handgrip strength and ultrasound-measured muscle thickness of the hand and forearm in young men and women. Ultrasound Med Biol. 2015;41:2125–2130. doi: 10.1016/j.ultrasmedbio.2015.04.004. [DOI] [PubMed] [Google Scholar]
- Abe T, Loenneke JP, Young KC, Thiebaud RS, Nahar VK, Hollaway KM, Stover CD, Ford MA, Bass MA, Loftin M. Validity of ultrasound prediction equations for total and regional muscularity in middle-aged and older men and women. Ultrasound Med Biol. 2015;41:557–564. doi: 10.1016/j.ultrasmedbio.2014.09.007. [DOI] [PubMed] [Google Scholar]
- Abe T, Patterson KM, Stover CD, Young KC. Influence of adipose tissue mass on DXA-derived lean soft tissue mass in middle-aged and older women. AGE (Duedr) 2015;37:2. doi: 10.1007/s11357-014-9741-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baumgartner RN, Koehler KM, Gallagher D, Romero L, Heymsfield SB, Ross R, Garry PJ, Linderman RD. Epidemiology of sarcopenia among the elderly in New Mexico. Am J Epidemiol. 1998;147:755–763. doi: 10.1093/oxfordjournals.aje.a009520. [DOI] [PubMed] [Google Scholar]
- Bunout D, de la Maza MP, Barrera G, Leiva L, Hirsch S. Association between sarcopenia and mortality in healthy older people. Australas J Ageing. 2011;30:89–92. doi: 10.1111/j.1741-6612.2010.00448.x. [DOI] [PubMed] [Google Scholar]
- Burns JM, Johnson DK, Watts A, Swerdlow RH, Brooks WM. Reduced lean mass in elderly Alzheimer disease and its association with brain atrophy. Arch Neurol. 2010;67:428–433. doi: 10.1001/archneurol.2010.38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupler TL, Tolson H. Body composition prediction equations for elderly men. J Gerontol A Biol Sci Med Sci. 2000;55:M180–M184. doi: 10.1093/gerona/55.3.M180. [DOI] [PubMed] [Google Scholar]
- Gallagher D, Visser M, De Meersman RE, Sepulveda D, Baumgartner RN, Pierson RN, Harris T, Heymsfield SB. Appendicular skeletal muscle mass: effect of age, gender, and ethnicity. J Appl Physiol. 1997;83:229–239. doi: 10.1152/jappl.1997.83.1.229. [DOI] [PubMed] [Google Scholar]
- Heymsfield SB, Gallagher D, Kotler DP, Wang Z, Allison DB, Heshka S. Body-size dependence of resting energy expenditure can be attributed to nonenergetic homogeneity of fat-free mass. Am J Physiol Endocrinol Metab. 2002;282:E132–E138. doi: 10.1152/ajpendo.2002.282.1.E132. [DOI] [PubMed] [Google Scholar]
- Janssen I, Heymsfield SB, Wang ZM, Ross R. Skeletal muscle mass and distribution in 468 men and women aged 18–88 yr. J Appl Physiol. 2000;89:81–88. doi: 10.1152/jappl.2000.89.1.81. [DOI] [PubMed] [Google Scholar]
- Kim J, Wang Z, Heymsfield SB, Baumgartner RN, Gallagher D (2002) Total-body skeletal muscle mass: estimation by a new dual-energy X-ray absorptiometry method. Am J Clin Nutr 76:378–383 [DOI] [PubMed]
- Kyle UG, Genton L, Hans D, Karsegard L, Slosman DO, Pichard C. Age-related differences in fat-free mass, skeletal muscle, body cell mass and fat mass between 18 and 94 years. Eur J Clin Nutr. 2001;55:663–672. doi: 10.1038/sj.ejcn.1601198. [DOI] [PubMed] [Google Scholar]
- Kulkarni B, Kuper H, Taylor A, Wells JC, Radhakrishna KV, Kinra S, Ben-Shlomo Y, Smith GD, Ebrahim S, Byrne NM, Hills AP. Development and validation of anthropometric prediction equations for estimation of lean body mass and appendicular lean soft tissue in Indian men and women. J Appl Physiol. 2013;115:1156–1162. doi: 10.1152/japplphysiol.00777.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin LI. A concordance correlation coefficient to evaluate reproducibility. Biometrics. 1989;45:255–268. doi: 10.2307/2532051. [DOI] [PubMed] [Google Scholar]
- Oguri K, Zhao L, Du N, Kato Y, Miyamoto M, Kurokawa J, Nagasaki S, Matsuoka T. Association of habitual long-distance running with the thickness of skeletal muscles and subcutaneous fat in the body extremities and trunk in middle-aged men. J Sports Med Phys Fitness. 2004;44:417–423. [PubMed] [Google Scholar]
- Ozaki H, Loenneke JP, Thiebaud RS, Abe T. Cycle training induces muscle hypertrophy and strength gain: strategies and mechanisms. Acta Physiol Hung. 2015;102:1–22. doi: 10.1556/APhysiol.102.2015.1.1. [DOI] [PubMed] [Google Scholar]
- Park SW, Goodpaster BH, Lee JS, Kuller LH, Boudreau R, de Rekeneire N, Harris TB, Kritchevsky S, Tylavsky FA, Nevitt M, Cho YW, Newman AB, Health, Aging, and Body Composition Study Excessive loss of skeletal muscle mass in older adults with type 2 diabetes. Diabetes Care. 2009;32:1993–1997. doi: 10.2337/dc09-0264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanada K, Kearns CF, Midorikawa T, Abe T. Prediction and validation of total and regional skeletal muscle mass by ultrasound in Japanese adults. Eur J Appl Physiol. 2006;96:24–31. doi: 10.1007/s00421-005-0061-0. [DOI] [PubMed] [Google Scholar]
- Sergi G, De Rui M, Veronese N, Bolzetta F, Berton L, Carraro S, Bano G, Manzato E, Perissinotto E. Assessing appendicular skeletal muscle mass with bioelectrical impedance analysis in free-living Caucasian older adults. Clin Nutr. 2015;34:667–673. doi: 10.1016/j.clnu.2014.07.010. [DOI] [PubMed] [Google Scholar]
- Shih R, Wang Z, Heo M, Wang W, Heymsfield SB. Lower limb skeletal muscle mass: development of dual-energy X-ray absorptiometry prediction model. J Appl Physiol. 2000;89:1380–1386. doi: 10.1152/jappl.2000.89.4.1380. [DOI] [PubMed] [Google Scholar]
- Takai Y, Ohta M, Akagi R, Kato E, Wakahara T, Kawakami Y, Fukunaga T, Kanehisa H. Validity of ultrasound muscle thickness measurements for predicting leg skeletal muscle mass in healthy Japanese middle-aged and older individuals. J Physiol Anthropol. 2013;32:12. doi: 10.1186/1880-6805-32-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takai Y, Ohta M, Akagi R, Kato E, Wakahara T, Kawakami Y, Fukunaga T, Kanehisa H. Applicability of ultrasound muscle thickness measurements for predicting fat-free mass in elderly population. J Nutr Health Aging. 2014;18:579–585. doi: 10.1007/s12603-013-0419-7. [DOI] [PubMed] [Google Scholar]
- Tanimoto Y, Watanabe M, Sun W, Sugiura Y, Tsuda Y, Kimura M, Hayashida I, Kusabiraki T, Kono K. Association between sarcopenia and high-level functional capacity in daily living in community-dwelling elderly patients in Japan. Arch Gerontol Geriatr. 2012;55:e9–e13. doi: 10.1016/j.archger.2012.06.015. [DOI] [PubMed] [Google Scholar]
- Vetrano DL, Landi F, Volpato S, Corsonello A, Meloni E, Bernabei R, Onder G. Association of sarcopenia with short- and long-term mortality in older adults admitted to acute care words results from the CRIME study. J Gerontol A Biol Sci Med Sci. 2014;69:1154–1161. doi: 10.1093/gerona/glu034. [DOI] [PubMed] [Google Scholar]