Abstract
Many hormones, including stress hormones, are intermittently secreted as pulses. The pulsatile location process, describing times when pulses occur, is a regulator of the entire stress system. Characterizing the pulse location process is particularly difficult because the pulse locations are latent; only hormone concentration at sampled times is observed. In addition, for stress hormones the process may change both over the day and relative to common external stimuli. This potentially results in clustering in pulse locations across subjects. Current approaches to characterizing the pulse location process do not capture subject-to-subject clustering in locations. Here we show how a Bayesian Cox cluster process may be adapted as a model of the pulse location process. We show that this novel model of pulse locations is capable of detecting circadian rhythms in pulse locations, clustering of pulse locations between subjects, and identifying exogenous controllers of pulse events. We integrate our pulse location process into a model of hormone concentration, the observed data. A spatial birth-and-death Markov chain Monte Carlo algorithm is used for estimation. We exhibit the strengths of this model on simulated data and adrenocorticotropic and cortisol data collected to study the stress axis in depressed and non-depressed women.
Keywords: Bayesian analysis, Deconvolution, Mixture models, Point processes, Pulsatile hormones
1. Introduction
Regulation of the human stress system is maintained by signaling between the hormones in the hypothalamic–pituitary–adrenal (HPA) axis (Walker and others, 2010, 2012; Lightman, 2008). The primary hormones in this axis, adrenocorticotropic hormone (ACTH) and cortisol, are intermittently secreted in boluses, called pulses (McMaster and others, 2011; Lightman and Conway-Cambell, 2010; Spiga and others, 2011). Alterations in the hormone secretion patterns have been implicated in many health conditions, e.g., depression (Carroll and others, 1976; Young and others, 2001, 2004), post-traumatic stress disorder (Yehuda, 2002), and sleep apnea (Henley and others, 2009). New treatment strategies are beginning to focus on pulsatile delivery (Russell and others, 2014; Henley and Lightman, 2014). Thus, it is clinically important to be able to adequately model the pulse location processes of HPA axis hormones.
To study pulsatile secretion, hormone concentration values are obtained every few minutes for a period up to 24 h (Figure 1). Although the observed data are hormone concentrations, biologic and clinical interest is often on the latent pulse locations. In our motivating study ACTH and cortisol time series were generated from blood samples collected every 10 min for 24 h on 52 women, 26 depressed and 26 healthy controls (Young and others, 2001). This is a typical design. In the primary analysis the pulse location model was summarized using a simple frequency count over the period of observation. This may be overly simplistic for ACTH and cortisol. The pulse locations of these hormones exhibit circadian patterns and potentially other inhomogeneities over the period of observation (see Figure S1 of supplementary material available at Biostatistics online). These patterns may differ between groups even when the overall frequencies remain similar.
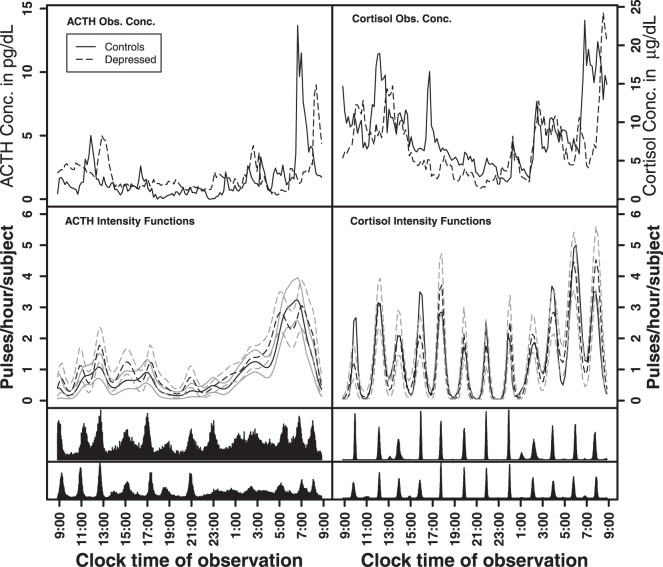
Fig. 1.
Observed ACTH and cortisol hormone concentration data for one pair of control and depressed subjects (top panel). Fitted intensity functions for ACTH and cortisol (second panel) with random effects for cluster size and width and the strict repulsion prior on the cluster locations. The gray lines are the 10% and 90% pointwise credible intervals. The bottom two panels are the joint posterior distributions of the cluster centers for the controls (top histogram) and depressed subjects (bottom histogram).
Models of the pulse location process have generally focused on characterizing the inter-event distribution within subjects or 24-h circadian rhythms in the location process (Anderson and O'Sullivan, 1993; Keenan and Veldhuis, 1997; Liu and Wang, 2007). We are interested in developing a more general model of the pulse location process that is able to characterize circadian rhythms in the pulse location model when present, but also is capable of identifying and quantifying temporal clustering of pulse locations across subjects. The subject-to-subject clustering of the pulse locations is of interest because various external stimuli (e.g., feeding, light, and sleep cycles) are known to influence cortisol levels (Greenspan and Gardner, 2004) and are tightly regulated and common across subjects in typical studies (including our motivating study). More (or less) clustering in pulse locations across subjects may indicate that the regulation of the hormone is more (or less) sensitive to external stimuli.
Our new model of pulse locations is based on the Cox cluster point process (Cox, 1955; Møller and Waagepetersen, 2004). Given pulse locations are latent, we embed the pulse location model into an existing deconvolution model of hormone concentration values. A spatial birth-and-death Markov chain Monte Carlo (MCMC) algorithm (Preston, 1977; Geyer and Møller, 1994) is used for estimation.
2. Methods
We first develop the pulse location model and then show how we integrate it with a hormone concentration model. Table 1 provides notation and definitions for the parameters in the model.
Table 1.
Notation
| Pulse location model notation | |
|---|---|
 |
Set of pulse locations for a population of subjects |
 |
Set of pulse locations for subject
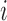
|
Parameters defining the
population intensity function
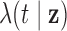
|
|
 |
Set of cluster centers common to all subjects |
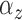 |
Expected number of pulses in cluster
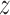
|
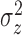 |
Variance of the pulse locations in cluster
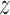
|
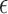 |
Rate of non-clustered pulse locations/hour |
Parameters defining the
subject-level intensity function
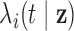
|
|
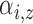 |
Expected number of pulses in cluster
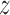 for subject for subject
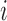 ; ; 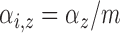
|
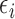 |
Rate of non-clustered pulse locations for
subject 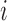 ; ; 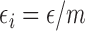
|
Hormone concentration model notation for subject
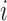
|
|
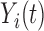 |
Observed hormone concentration at time
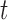
|
Pulsatile secretion
function, 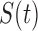
|
|
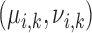 |
Pulse mass and width for pulse
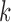
|
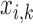 |
Pulse location for pulse
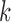
|
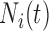 |
Number of pulses to time
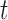
|
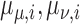 |
Mean pulse mass and width, respectively |
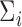 |
Variance–covariance matrix for the pulse mass and width |
Elimination
function
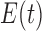
|
|
 |
Half-life |
Baseline
concentration, 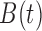
|
|
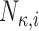 |
Number of knots in b-spline |
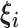 |
Set of 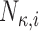 knot locations knot locations |
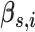 |
Set of b-spline coefficients |
| Model error | |
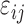 |
Model error for log hormone concentration at
time 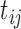
|
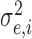 |
Model error variance |
2.1. The pulse location model
2.1.1. Overview and notation
The Cox cluster process is a Poisson process (Cox and Isham, 1984), which is defined by its intensity function,
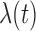 , where
, where 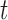 is time.
The intensity function defines the rate at which events occur in time. In our
case, the latent pulse locations for each subject serve as “the
data” that the Cox cluster process is modeling.
is time.
The intensity function defines the rate at which events occur in time. In our
case, the latent pulse locations for each subject serve as “the
data” that the Cox cluster process is modeling.
There are two levels defining the intensity function of our Cox cluster process.
Level 1 is the subject level and involves the pulse locations for each subject
(see right panel of Figure S2 of supplementary material available at Biostatistics online, the x's mark pulse locations). Level 2 is the population
level and is a model of locations where pulses cluster in time across subjects
(see right panel of Figure S2 of supplementary material available at Biostatistics online,
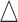 's mark latent cluster locations). The Level 1
model conditions on a realization from the Level 2 model, so we first define Level
2 and then Level 1.
's mark latent cluster locations). The Level 1
model conditions on a realization from the Level 2 model, so we first define Level
2 and then Level 1.
Level 2 (population level):The population cluster
locations are modeled as a marked Strauss process (Strauss, 1975) on time interval
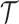 , which is slightly larger than the
observation time period to accommodate boundary issues. The Strauss process was
chosen because it is a repulsive process that reduces the likelihood that cluster
locations occur too close together in time. Strauss processes are defined by a
temporal range of repulsion (
, which is slightly larger than the
observation time period to accommodate boundary issues. The Strauss process was
chosen because it is a repulsive process that reduces the likelihood that cluster
locations occur too close together in time. Strauss processes are defined by a
temporal range of repulsion (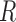 ), the strength of repulsion
(
), the strength of repulsion
(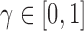 ), and a rate parameter
), and a rate parameter
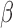 . Strict repulsion results when
. Strict repulsion results when
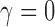 and there is no repulsion when
and there is no repulsion when
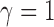 . The number of clusters generally increases
as
. The number of clusters generally increases
as 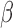 increases. These parameters are user-specified
and sensitivity to the choices of these parameters should be investigated when
fitting the data.
increases. These parameters are user-specified
and sensitivity to the choices of these parameters should be investigated when
fitting the data.
Notation:Let 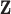 be a realization of cluster locations from the Strauss process
be a realization of cluster locations from the Strauss process
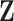 on
on 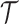 that is common for all subjects. For subject
that is common for all subjects. For subject
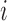 ,
, 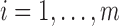 , each cluster,
, each cluster,
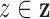 , is defined by two marks,
, is defined by two marks,
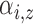 and
and 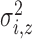 , which describe the size and spread,
respectively, of a Gaussian-shaped contribution to the intensity function centered
at cluster center
, which describe the size and spread,
respectively, of a Gaussian-shaped contribution to the intensity function centered
at cluster center 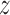 . The joint density of
. The joint density of
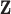 ,
, 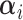 , and
, and 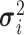 is defined in Section 2.1.2. The
is defined in Section 2.1.2. The 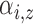 and
and
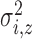 are often modeled as random effects
with a mean and variance that is common for all subjects, but additional
restrictions are possible (e.g., a common
are often modeled as random effects
with a mean and variance that is common for all subjects, but additional
restrictions are possible (e.g., a common 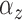 across subjects for each cluster).
across subjects for each cluster).
Level 1 (subject level):For subject
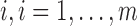 , the set of latent pulse locations,
, the set of latent pulse locations,
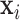 , is a realization of a Cox cluster
process
, is a realization of a Cox cluster
process 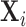 on
on 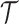 . The
. The 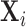 are driven by random subject-specific
intensity functions, which we now derive. For each
are driven by random subject-specific
intensity functions, which we now derive. For each 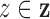 , let
, let 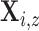 be an inhomogeneous Poisson process with
random intensity function
be an inhomogeneous Poisson process with
random intensity function 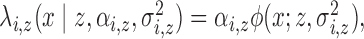 where
where 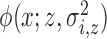 is the density of a Gaussian
distribution with mean
is the density of a Gaussian
distribution with mean 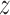 and variance
and variance
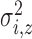 . The expected number of pulse
secretion events in
. The expected number of pulse
secretion events in 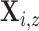 is by definition
is by definition
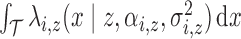 . Thus, except at the boundaries,
. Thus, except at the boundaries,
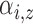 is the expected number of pulses in
cluster
is the expected number of pulses in
cluster 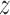 for subject
for subject 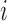 . Pulses
not associated with a population cluster are also allowed. Let this process
. Pulses
not associated with a population cluster are also allowed. Let this process
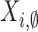 be modeled as an independent homogeneous
Poisson process with random time-constant intensity function
be modeled as an independent homogeneous
Poisson process with random time-constant intensity function
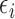 . Then, by the superposition principle (Cox and Isham, 1984), the pulse location
process for subject
. Then, by the superposition principle (Cox and Isham, 1984), the pulse location
process for subject 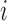 ,
, 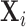 , is the union of the clustered and
non-clustered processes across population cluster centers (i.e.,
, is the union of the clustered and
non-clustered processes across population cluster centers (i.e.,
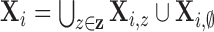 ) with random intensity function,
) with random intensity function,
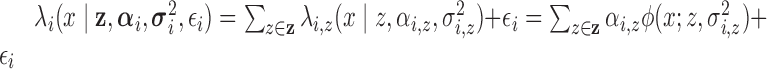 .
.
2.1.2. Defining the density of the pulse location model
Here we develop the density of the Cox process for a population of subjects to (1) show how to combine information across subjects and (2) develop other constraints necessary for estimation.
Combining Level 1 densities for all subjects:As
developed above, let 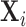 be the subject level Cox
cluster process on
be the subject level Cox
cluster process on 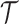 driven by random intensity
function
driven by random intensity
function 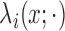 , where
“
, where
“ ”
” 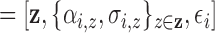 .
Conditioned on
.
Conditioned on 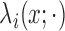 , the density of the
(latent) pulse locations for subject
, the density of the
(latent) pulse locations for subject 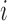 has the form
has the form
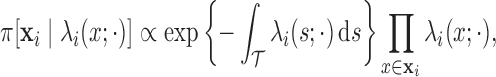 |
(2.1) |
where (2.1) is defined with respect to the measure of a unit-rate Poisson process instead of the standard Lebesgue measure (Cox and Isham, 1984; Møller and Waagepetersen, 2004).
Given that the Level 1 processes are independent across subjects conditioned on
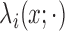 , the joint density of the pulse
locations for all
, the joint density of the pulse
locations for all 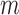 subjects is the product of the
subject-level densities from (2.1):
subjects is the product of the
subject-level densities from (2.1):
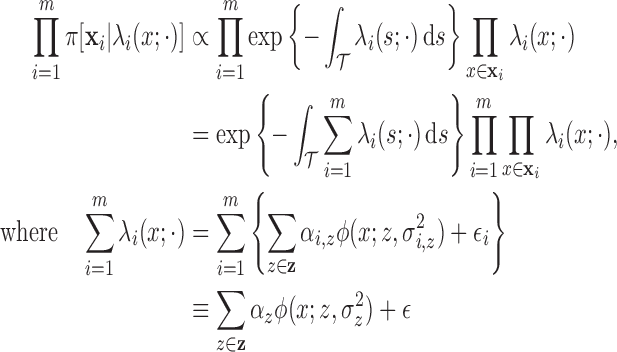 |
and 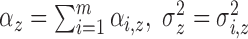 , and
, and 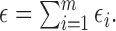
The identifiable parameters are 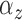 ,
,
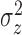 , and
, and 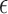 because each subject contributes only a small number of pulses to each cluster and
a small number of non-clustered pulses. In other words, the population intensity
function is better defined than the subject-level intensity functions. To move
between the population and subject models, we further assume that both
because each subject contributes only a small number of pulses to each cluster and
a small number of non-clustered pulses. In other words, the population intensity
function is better defined than the subject-level intensity functions. To move
between the population and subject models, we further assume that both
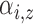 and
and 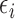 are equivalent for all subjects. Thus,
are equivalent for all subjects. Thus,
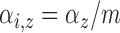 and
and 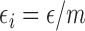 , and with these assumptions the subject-level
intensity function is a scaling of the population-level intensity function
(
, and with these assumptions the subject-level
intensity function is a scaling of the population-level intensity function
(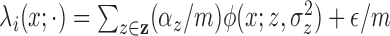 ).
).
2.2. Integrating the pulse location model with the hormone concentration model
2.2.1. Deconvolution model of hormone concentration
We use an existing deconvolution model (Veldhuis and Johnson, 1992; Johnson, 2003, 2007; Carlson and others, 2009); however, integration with other hormone concentration models (Keenan and others, 1998; O'Sullivan and O'Sullivan, 1988) is also plausible.
As in Johnson (2007), let
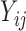 be the observed hormone concentration
for subject
be the observed hormone concentration
for subject 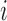 at time
at time 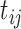 ,
where
,
where 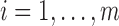 and
and 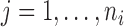 . The times of observations are generally
similar for all subjects and so to simplify notation we use
. The times of observations are generally
similar for all subjects and so to simplify notation we use
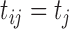 for all
for all 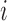 . The
convolution model for hormone concentration for subject
. The
convolution model for hormone concentration for subject 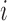 at time
at time
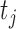 is as follows:
is as follows:
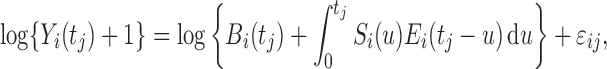 |
(2.2) |
where 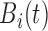 is a slowly changing
baseline component representing non-pulsatile hormone secretion and
is a slowly changing
baseline component representing non-pulsatile hormone secretion and
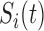 is the pulsatile secretion rate
function. By
is the pulsatile secretion rate
function. By 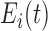 is denoted the hormone elimination
function, and
is denoted the hormone elimination
function, and 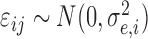 is
the model error at time
is
the model error at time 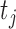 consisting of both
biological and technical components. Each of these components also depends on a
set of parameters whose notation is shown in Table 1 but has been suppressed here for brevity. We model
hormone concentration on the log scale because hormone concentrations are positive
and the error structure is likely multiplicative on the natural scale (Rodbard and
others, 1970). The one is added to aid in model fitting.
consisting of both
biological and technical components. Each of these components also depends on a
set of parameters whose notation is shown in Table 1 but has been suppressed here for brevity. We model
hormone concentration on the log scale because hormone concentrations are positive
and the error structure is likely multiplicative on the natural scale (Rodbard and
others, 1970). The one is added to aid in model fitting.
The pulse secretion rate function is defined as
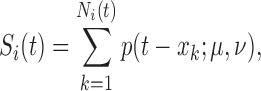 |
with 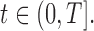 The function
The function
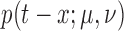 is the pulse shape function and is
assumed Gaussian in shape, i.e.,
is the pulse shape function and is
assumed Gaussian in shape, i.e., 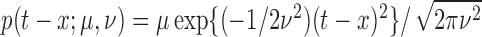 (Johnson, 2003, 2007; Carlson
and others, 2009). Each pulse is
defined by a location,
(Johnson, 2003, 2007; Carlson
and others, 2009). Each pulse is
defined by a location, 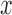 , a mass
, a mass
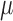 , and a duration
, and a duration 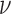 . The
number of pulses up to time
. The
number of pulses up to time 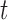 for subject
for subject
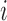 is denoted as
is denoted as 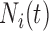 and
is modeled by the counting process derived from the Cox process pulse location
model (Section 2.1).
and
is modeled by the counting process derived from the Cox process pulse location
model (Section 2.1).
To integrate the pulse location and secretion models, we extend the Cox pulse
location process to be a marked process (Cox
and Isham, 1984). Thus, for the subject-level process
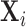 the marked Cox process includes both the
population level parameters in the Cox process and the pulse mass and width
parameters (and their priors).
the marked Cox process includes both the
population level parameters in the Cox process and the pulse mass and width
parameters (and their priors).
The hormone elimination function is modeled as a single exponential decay, i.e.,
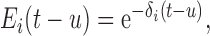 where
where
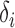 is the decay rate for subject
is the decay rate for subject
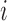 and
and 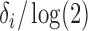 is the half-life. For this application, the
baseline concentration function,
is the half-life. For this application, the
baseline concentration function, 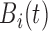 , is modeled by a
b-spline as described in Johnson
(2007) and defined by b-spline basis coefficients
, is modeled by a
b-spline as described in Johnson
(2007) and defined by b-spline basis coefficients
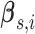 and corresponding knot locations
and corresponding knot locations
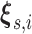 ; however, a constant baseline
could also be used when appropriate.
; however, a constant baseline
could also be used when appropriate.
2.3. Parameter priors
2.3.1. Prior factorization
The priors for a population of subjects factor as follows:
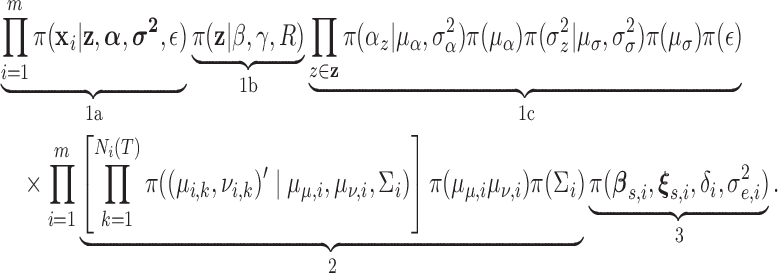 |
In this factorization, (1) and (2) are the components defining the marked Cox process for the pulse location model. (1a) and (1b) are the Cox process developed in Section 2.1 and (1c) are the prior distributions for the parameters in the Cox process. The parameters in (1b and c) are the new features that are characterized using this approach. (2) defines the priors on the parameters in the pulsatile secretion function (the marks of the Cox process); (3) defines the priors on the other hormone concentration parameters (baseline, half-life, and model error). Together (2) and (3) defined the deconvolution model for concentration.
2.3.2. Priors for parameters defining the Cox cluster process (1c)
We implemented two models for the Cox cluster process. In the first model, the
priors on the expected number of pulses in each cluster in the population,
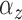 , and the variance of the pulse locations in
each cluster,
, and the variance of the pulse locations in
each cluster, 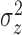 , vary from cluster to cluster and
are defined hierarchically as follows:
, vary from cluster to cluster and
are defined hierarchically as follows:
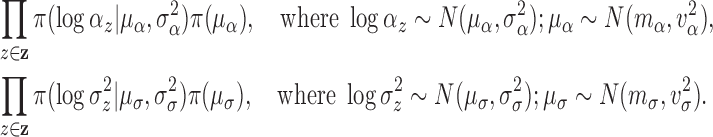 |
Values for 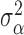 and
and
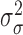 could also be estimated and have
corresponding priors, but for this work are fixed and set to reflect that there is
similarity in the expected number and spread across clusters.
could also be estimated and have
corresponding priors, but for this work are fixed and set to reflect that there is
similarity in the expected number and spread across clusters.
In the second model, the expected number of points in each cluster and the
variance of each cluster were common across clusters (i.e.,
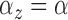 and
and 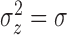 ) and were defined as follows:
) and were defined as follows:
 |
and 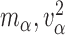 and
and
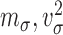 are set by the user. When
are set by the user. When
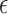 was estimated, the prior was
was estimated, the prior was
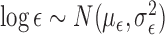 . The
specific values chosen for these parameters can be found in Section 3.2. We used the same priors for (2) and (3) as
in previous work (Johnson, 2007). For
brevity, the exact prior distributions and values of the parameters in (2) and (3)
can be found in Table S1 of supplementary material available at Biostatistics online.
. The
specific values chosen for these parameters can be found in Section 3.2. We used the same priors for (2) and (3) as
in previous work (Johnson, 2007). For
brevity, the exact prior distributions and values of the parameters in (2) and (3)
can be found in Table S1 of supplementary material available at Biostatistics online.
3. Estimation
We developed a spatial birth-and-death MCMC (SBDMCMC) algorithm to estimate our posterior distribution. Convergence of this sampler follows from arguments similar to Geyer and Møller (1994) and Stephens (2000). Implementation details are provided in Section 3.2. The steps of the algorithm are provided in Section 1 of supplementary material available at Biostatistics online.
3.1. The simulated data
We simulated data to impose either strong (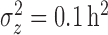 ) or weak (
) or weak (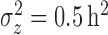 ) clustering of pulse locations across subjects.
The number of pulses for each individual for each cluster was modeled as a Bernoulli
with a success probability of 0.8. Thus, the expected number of pulses in each
population cluster,
) clustering of pulse locations across subjects.
The number of pulses for each individual for each cluster was modeled as a Bernoulli
with a success probability of 0.8. Thus, the expected number of pulses in each
population cluster, 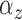 , was 20.8. The underlying cluster
center process,
, was 20.8. The underlying cluster
center process, 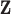 , was simulated as a multiscale
Strauss process (Penttinen, 1984); i.e.,
, was simulated as a multiscale
Strauss process (Penttinen, 1984); i.e.,
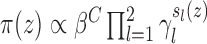 , where
, where
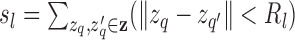 . We set
. We set 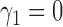 and
and 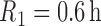 ,
, 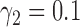 and
and
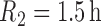 , and
, and 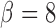 . In
a third simulation, we simulated pulse locations using a renewal process, which
resulted in no clustering in pulse locations across subjects. Figure 2 shows representative pulse location
intensity functions for the three simulations. When generating data with clustered
pulse locations, 100 sets of 26 subjects' pulse locations were simulated. When
generating from the renewal process, 20 sets of 26 subjects' pulse locations were
simulated. Hormone concentration profiles were generated using the deconvolution
model (Equation (2.2)) with
sampling every 10 min for 24 h. Information on the pulse and
hormone-specific parameters can be found in Section 2 of supplementary material available at Biostatistics
online.
. In
a third simulation, we simulated pulse locations using a renewal process, which
resulted in no clustering in pulse locations across subjects. Figure 2 shows representative pulse location
intensity functions for the three simulations. When generating data with clustered
pulse locations, 100 sets of 26 subjects' pulse locations were simulated. When
generating from the renewal process, 20 sets of 26 subjects' pulse locations were
simulated. Hormone concentration profiles were generated using the deconvolution
model (Equation (2.2)) with
sampling every 10 min for 24 h. Information on the pulse and
hormone-specific parameters can be found in Section 2 of supplementary material available at Biostatistics
online.
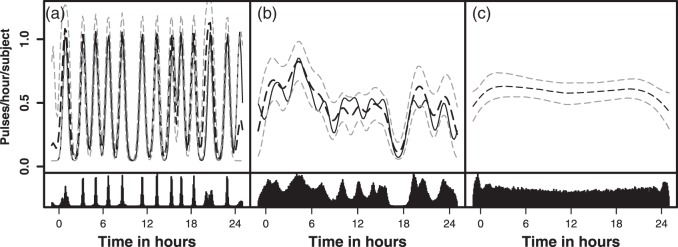
Fig. 2.
Simulated and fitted intensity function for a randomly selected simulation
for each model: (a) Strong clustering, (b) Weaker clustering, and (c) No
clustering. Each simulated dataset had 26 subjects. The top panel represents
the true intensity function (solid line) and the estimated intensity
function (dashed line). The gray lines are the 10% and 90% pointwise
credible intervals. The height of the peaks is 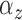 . The width of the peaks is
. The width of the peaks is
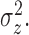 The peak center locations make up
The peak center locations make up
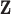 . The second panel shows the posterior
distributions of the estimated cluster
centers.
. The second panel shows the posterior
distributions of the estimated cluster
centers.
3.2. Implementation and summarization for simulated and experimental data
The prior on the cluster locations imposed strict repulsion between cluster locations
(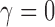 ,
, 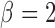 ,
,
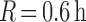 , no clusters could be
within 36 min of each other). This increased the chance of identifying
distinct cluster regions rather than slight deviations from the Gaussian assumption.
These parameters were chosen to correspond to the expected number of pulses over the
period of observation for each subject based on previous clinical knowledge. Another
approach to choosing
, no clusters could be
within 36 min of each other). This increased the chance of identifying
distinct cluster regions rather than slight deviations from the Gaussian assumption.
These parameters were chosen to correspond to the expected number of pulses over the
period of observation for each subject based on previous clinical knowledge. Another
approach to choosing 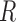 is to assume no repulsion and visually assess
the distance between distinct clustering regions. We investigated sensitivity to the
repulsion assumption by also fitting a no-repulsion model (
is to assume no repulsion and visually assess
the distance between distinct clustering regions. We investigated sensitivity to the
repulsion assumption by also fitting a no-repulsion model (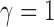 ).
The sensitivity to the rate parameter in the cluster center prior was investigated by
doubling
).
The sensitivity to the rate parameter in the cluster center prior was investigated by
doubling 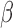 and halving it. The shape of the intensity
function was not dependent on
and halving it. The shape of the intensity
function was not dependent on 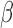 ; however, when there was
no repulsion and
; however, when there was
no repulsion and 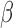 was much larger than truth, clusters were
occasionally modeled by two smaller clusters closer in time. In practice it may be
useful to set
was much larger than truth, clusters were
occasionally modeled by two smaller clusters closer in time. In practice it may be
useful to set 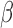 lower than might be expected.
lower than might be expected.
When fitting the simulated data, we assumed that cluster parameters were common
across clusters (i.e., 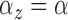 and
and 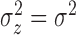 , model 2 described in Section 2.3.2). The prior on
, model 2 described in Section 2.3.2). The prior on 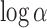 was set to a mean of
was set to a mean of 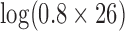 with a variance of 100 log
pulses
with a variance of 100 log
pulses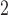 and the prior mean of
and the prior mean of
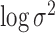 was
was 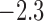 with a
variance of 10 log hours
with a
variance of 10 log hours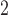 . When fitting the experimental data, we
fitted a variety of models where
. When fitting the experimental data, we
fitted a variety of models where 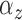 and
and
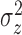 varied from cluster to cluster (model 1 in
Section 2.3.2) and where
varied from cluster to cluster (model 1 in
Section 2.3.2) and where
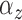 and
and 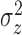 were common across clusters (model 2 in Section 2.3.2). The priors on the means of the cluster size and spread were as
above. The variances of
were common across clusters (model 2 in Section 2.3.2). The priors on the means of the cluster size and spread were as
above. The variances of 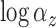 and
and 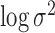 were set to 1.0 and 0.5, respectively, and not
estimated. In addition, we fitted models where the non-clustered process rate
parameter,
were set to 1.0 and 0.5, respectively, and not
estimated. In addition, we fitted models where the non-clustered process rate
parameter, 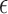 , was fixed and estimated. The prior mean for
, was fixed and estimated. The prior mean for
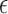 was set at
was set at  pulses/24 h with a variance of 10 when
pulses/24 h with a variance of 10 when 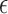 was
estimated. The values in these priors were chosen based on visual assessment of
previous analyses. In general, there is limited sensitivity to the priors when they
are vague. One exception is if the mean of the prior on
was
estimated. The values in these priors were chosen based on visual assessment of
previous analyses. In general, there is limited sensitivity to the priors when they
are vague. One exception is if the mean of the prior on 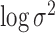 is quite large compared with the distance between
the clusters. This makes it more likely that extremely large variances may be
simulated early in the algorithm and quick convergence of the MCMC algorithm becomes
questionable.
is quite large compared with the distance between
the clusters. This makes it more likely that extremely large variances may be
simulated early in the algorithm and quick convergence of the MCMC algorithm becomes
questionable.
Parameters were initialized based on the estimates from the primary analyses of these
data (Young and
others, 2001). In addition, subjects were initialized to have
one randomly located pulse for each subject, and the Cox cluster model was
initialized to have one randomly located cluster. The starting value of the variance
of the pulse locations in each cluster in the Cox process (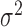 )
was sometimes important. When the starting value of the variance is high (e.g.,
larger than the typical distance between clusters),
)
was sometimes important. When the starting value of the variance is high (e.g.,
larger than the typical distance between clusters), 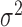 often becomes extremely large, making it difficult to identify the cluster centers.
We recommend starting the variance at a small value (e.g.,
0.05–
often becomes extremely large, making it difficult to identify the cluster centers.
We recommend starting the variance at a small value (e.g.,
0.05–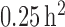 ) allowing for convergence from
below and did this for both the simulations and the experimental data fits. Model fit
was assessed graphically by generating a sample from the posterior predictive
distribution and plotting the mean and 80% credible interval with the observed
hormone concentration data.
) allowing for convergence from
below and did this for both the simulations and the experimental data fits. Model fit
was assessed graphically by generating a sample from the posterior predictive
distribution and plotting the mean and 80% credible interval with the observed
hormone concentration data.
For the simulated data, one chain of 150 000 iterations was run for each of
the 100 sets of data. For the experimental data, one chain of 225 000
iterations was run for each model estimated. The first 20 000 iterations of
each chain were treated as burn-in and discarded. Thereafter, every 50th iteration
was saved and used for summarizing the posterior distributions. We assessed
convergence and mixing visually using trace plots of the draws (see Figure S4 of supplementary material available at Biostatistics online). Each simulation took
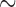 16 h to run on a single 2.93 GHz
processor. Run times increased the more parameters that varied across clusters.
16 h to run on a single 2.93 GHz
processor. Run times increased the more parameters that varied across clusters.
4. Results
4.1. Simulation
The bias and coverage of the individual parameters in the Cox process were small
under strong clustering (Table 2) and
the estimates of the individual cluster centers were unbiased [average bias of
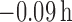 (
(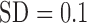 ), data not shown].
The slight biases in the parameters resulted in an upward bias in the expected number
of pulses over the day (Table 2). The
false-positive and -negative rates for finding individual pulse locations were both
8%. When the clustering was weaker, the parameters were unbiased with the exception
of the number of clusters, which was biased high. The estimates of the individual
cluster centers were unbiased [average bias of
), data not shown].
The slight biases in the parameters resulted in an upward bias in the expected number
of pulses over the day (Table 2). The
false-positive and -negative rates for finding individual pulse locations were both
8%. When the clustering was weaker, the parameters were unbiased with the exception
of the number of clusters, which was biased high. The estimates of the individual
cluster centers were unbiased [average bias of 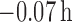 (
(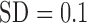 ), data not shown]
and the bias in the expected number of pulses over the day was similar to the strong
clustering model. This suggests that the additional clusters estimated partially in
the boundary regions. The fits of the intensity functions were good for both models
(Figure 2). The results for the
individual-level parameters can be found in Table S2 of supplementary material available at Biostatistics online. The results were similar under a
no-repulsion model of the cluster centers (see Table S3 of supplementary material available at Biostatistics online).
), data not shown]
and the bias in the expected number of pulses over the day was similar to the strong
clustering model. This suggests that the additional clusters estimated partially in
the boundary regions. The fits of the intensity functions were good for both models
(Figure 2). The results for the
individual-level parameters can be found in Table S2 of supplementary material available at Biostatistics online. The results were similar under a
no-repulsion model of the cluster centers (see Table S3 of supplementary material available at Biostatistics online).
Table 2.
Estimation properties of intensity function parameters for simulated data assuming strict repulsion in the cluster locations and common cluster parameters. Values are medians and interquartile ranges. Coverage was obtained using 95% equal-tails credible intervals
| Truth | PM | Width 95% CI | Bias of PM | Coverage of | |
|---|---|---|---|---|---|
| Parameter | (IQR) | (IQR) | (IQR) | (IQR) | 95% CI |
| Strong clustering | |||||
| Exp. number of pulses | 10.1 (9.8, 10.8) | 11.9 (10.9, 12.9) | 3.1 (2.9, 3.3) | 1.6 (1.1, 2.2) | 39 |
Number of clusters (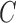 ) ) |
13 (12, 14) | 13 (12, 14) | 3 (3, 4) | 0 (0, 1) | 99 |
Number of pulses/cluster
(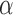 ) ) |
0.80 | 0.88 (0.85, 0.92) | 0.31 (0.29, 0.33) | 0.08 (0.05, 0.12) | 85 |
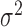 (hours
(hours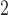 ) ) |
0.10 | 0.10 (0.09, 0.12) | 0.07 (0.06, 0.07) | 0.00 (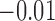 , 0.02) , 0.02) |
91 |
| Weaker clustering | |||||
| Exp. number of pulses | 10.0 (9.4, 10.9) | 11.1 (10.2, 12) | 3.0 (2.7, 3.1) | 0.94 (0.6, 1.3) | 80 |
Number of clusters (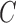 ) ) |
12 (11, 13) | 14 (13, 14) | 8 (7, 9) | 2 (1, 3) | 96 |
Number of pulses/cluster
(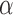 ) ) |
0.80 | 0.80 (0.72, 0.88) | 0.53 (0.44, 0.77) | 0.00 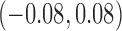
|
100 |
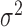 (hours
(hours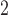 ) ) |
0.50 | 0.46 (0.39, 0.78) | 0.94 (0.56, 6.20) |
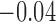
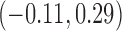
|
88 |
| No clustering | |||||
| Exp. number of pulses | 14 (13,14) | 14.4 (14.2, 14.6) | 3.3 (3.3, 3.4) | 0.55 (0.46, 0.77) | – |
Number of clusters (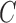 ) ) |
– | 13 (13, 13) | 7 (7, 7) | – | – |
Number of pulses/cluster
(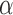 ) ) |
– | 1.4 (1.3, 1.5) | 6.2 (4.5, 8.5) | – | – |
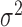 (hours
(hours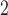 ) ) |
– | 14.5 (11.2, 17.4) | 3380 (1979, 6516) | – | – |
PM, posterior median; IQR, interquartile; CI, credible interval; Exp., expected.
We assessed the models' ability to differentiate between strong and weak clustering. These two models only differed in the cluster variance parameter. The posterior distributions were nearly completely separated in all 100 simulations, with the posteriors for the strong clustering simulations concentrating around higher values in every case.
Assuming a clustering model when the data were not clustered resulted in an essentially flat estimated intensity function (Figure 2). The posterior of the locations of the cluster centers was uniform over the period of observation (bottom panel of Figure 2(c)). The posterior distributions of the number of events in a cluster and the variance of the clusters often covered implausibly large values (e.g., interquartile ranges containing values that were longer than the period of observation). These findings show that assuming clustering when fitting does not induce clustering when it is not present. Further, the estimated intensity function provides an expected number of pulses that are consistent with truth, and the fits have low false-positive (8%) and -negative (1%) rates.
4.2. Example: ACTH and Cortisol in depression
4.2.1. Differences in depressed and non-depressed
The posterior distributions for the parameters defining a depressed and non-depressed groups pulse locations model largely overlapped, indicating the parameters defining the intensity functions for the depressed and non-depressed groups were similar (Table 3). Visually both depressed and non-depressed groups exhibited an increase in the number of pulses per hour during the early morning hours (Figure 1). For ACTH, there was some visual clustering in the depressed subjects. A more diffuse intensity pattern was seen in the non-depressed. For Cortisol, the depressed and non-depressed subjects had essentially identical patterns in the estimated intensity function. (Figure 1).
Table 3.
Summary of posterior distributions of parameters in the Cox cluster process for ACTH and cortisol for control and depressed subjects assuming strict repulsion and allowing cluster parameters to vary across clusters
| Pulse location model
parameters |
||||||||
|---|---|---|---|---|---|---|---|---|
| ACTH | Cortisol | |||||||
| Control | Depressed | Control | Depressed | |||||
| Parameter | PM | 95% CI | PM | 95% CI | PM | 95% CI | PM | 95% CI |
| Expected number of | ||||||||
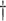 Pulse events Pulse events |
21.3 | (17.2, 25.8) | 26.6 | (21.8, 32.2) | 31.9 | (27.0, 37.7) | 30.4 | (25.8, 35.5) |
Number of clusters
(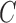 ) ) |
13.3 | (10, 16) | 14.4 | (12, 17) | 12.7 | (12, 14) | 12.7 | (12, 15) |
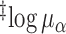 |
3.2 | (2.4, 4.0) | 3.5 | (2.9, 4.2) | 3.9 | (3.3, 4.5) | 3.9 | (3.3, 4.5) |
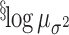 |
-0.7 | (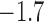 , 0.5) , 0.5) |
-1.1 | 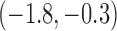 |
-2.3 | 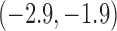 |
-2.3 | 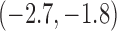 |
| Individual-level hormone concentration and pulse parameters | ||||||||
| ACTH | Cortisol | |||||||
| Control | Depressed | Control | Depressed | |||||
| Parameter | MPM | SE | MPM | SE | MPM | SE | MPM | SE |
| Number of pulses | 22.6 | 0.5 | 27.8 | 0.5 | 32.4 | 0.7 | 31.5 | 0.7 |
¶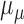
|
3.0 | 0.3 | 2.8 | 0.3 | 5.2 | 0.4 | 5.1 | 0.5 |
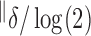 |
19.5 | 1.5 | 19.1 | 1.3 | 23.8 | 1.5 | 28.3 | 1.9 |
PM, posterior mean; CI, equal-tails credible interval; MPM, mean of the posterior means; SE, standard error of the posterior means.
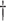 Events per subject per day.
Events per subject per day.
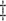 Log of the mean # of secretion events
per cluster.
Log of the mean # of secretion events
per cluster.
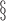 Log of the mean of the variances of
the clusters.
Log of the mean of the variances of
the clusters.
¶Mean pulse mass.
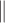 Half-life.
Half-life.
4.2.2. Differences in ACTH and cortisol patterns
The parameters defining the intensity functions were similar for ACTH and
cortisol, with the exception of the mean of the cluster widths
(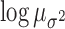 ; Table 3). The posterior distributions for the mean cluster
widths were nearly separate for ACTH and cortisol. The posterior for cortisol
concentrated around a smaller cluster width (posterior medians:
; Table 3). The posterior distributions for the mean cluster
widths were nearly separate for ACTH and cortisol. The posterior for cortisol
concentrated around a smaller cluster width (posterior medians:
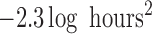 for cortisol vs.
for cortisol vs.
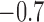 and
and 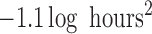 for ACTH controls and depressed,
respectively). The average cluster width for cortisol was more consistent with
strong clustering in pulse times across subjects. For cortisol, pulses for each
subject were more likely to occur around 10 am and approximately every 2 h
afterwards (Figure 1). For ACTH, the
average cluster width was more consistent with a weak to no-clustering model. Both
ACTH and cortisol exhibited circadian rhythms in the intensity function with more
events occurring per hour in the early morning hours. For ACTH, peak intensities
were
for ACTH controls and depressed,
respectively). The average cluster width for cortisol was more consistent with
strong clustering in pulse times across subjects. For cortisol, pulses for each
subject were more likely to occur around 10 am and approximately every 2 h
afterwards (Figure 1). For ACTH, the
average cluster width was more consistent with a weak to no-clustering model. Both
ACTH and cortisol exhibited circadian rhythms in the intensity function with more
events occurring per hour in the early morning hours. For ACTH, peak intensities
were 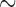 3 events/hour/subject in the early morning
surge and fell to
3 events/hour/subject in the early morning
surge and fell to 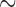 0.25 events/hour/subject in the evening
period. For cortisol, peak intensities were also in the early morning surge (4.5
events/hour/subject) and fell to 2 events/hour/subject in the evening hours.
0.25 events/hour/subject in the evening
period. For cortisol, peak intensities were also in the early morning surge (4.5
events/hour/subject) and fell to 2 events/hour/subject in the evening hours.
4.2.3. Sensitivity analyses
We fitted models where the cluster parameters were (1) common across clusters (Model 2 in Section 2.3.2) and (2) varied from cluster to cluster (Model 1 in Section 2.3.2) to investigate the necessity of less versus more flexibility in the cluster-specific features. We also investigated strict repulsion and no repulsion in the cluster center prior.
All of the models fitted resulted in a similar shape of the intensity function
defining the pulse location model (see Figure S5 of supplementary material available at Biostatistics online). However, the parameters defining
the intensity functions differed. The overall expected number of pulses per day
per subject for cortisol ranged from 29.5 (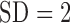 ) to 45.4 (
) to 45.4 (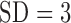 ) pulses/day/subject. Further inspection of the
estimated pulse locations revealed that the models differed in the number of
Gaussian components used to model each pulse rather than an increase in
biologically independent pulse events. Pulses being modeled with more than one
Gaussian component were more frequent for models with restrictions on
) pulses/day/subject. Further inspection of the
estimated pulse locations revealed that the models differed in the number of
Gaussian components used to model each pulse rather than an increase in
biologically independent pulse events. Pulses being modeled with more than one
Gaussian component were more frequent for models with restrictions on
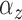 and
and 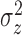 (e.g., the same
(e.g., the same 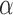 and
and 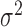 for all clusters).
for all clusters).
As expected, the mean number of clusters, 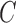 , was
higher for the no-repulsion priors (see Table S4 of supplementary material available at Biostatistics online). There were also slightly fewer
pulses per cluster,
, was
higher for the no-repulsion priors (see Table S4 of supplementary material available at Biostatistics online). There were also slightly fewer
pulses per cluster, 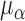 , and a slightly narrower spread
of the pulses in a cluster,
, and a slightly narrower spread
of the pulses in a cluster, 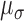 . These patterns
held for both hormones and for both groups of subjects. Visual assessment of the
intensity functions and posterior distributions of cluster locations indicated
that the additional clusters were modeling slight deviations from the assumed
normal distribution shape of the clusters. Thus, the strict repulsion prior was
more useful for identifying distinct regions of clustering.
. These patterns
held for both hormones and for both groups of subjects. Visual assessment of the
intensity functions and posterior distributions of cluster locations indicated
that the additional clusters were modeling slight deviations from the assumed
normal distribution shape of the clusters. Thus, the strict repulsion prior was
more useful for identifying distinct regions of clustering.
5. Discussion
We developed a new more flexible model of the latent pulse location process governing pulsatile hormone data. Although we focused on Cox cluster processes, other Cox processes (e.g., log Gaussian Cox processes) should produce similar results. This approach is unique in that it is flexible enough to capture both circadian changes and strong-to-weak clustering in pulse release times in the population.
A strength of our approach is that it integrates the latent pulse-generating process with the deconvolution model. This approach incorporates estimation uncertainty of all parameters in the estimation of all other parameters. One challenge in jointly modeling the pulse location and hormone concentration processes is that the deconvolution model (Equation (2.2)) does not restrict a pulse to be modeled by only one secretion event. While this is advantageous in that any shape and size pulse can be accurately modeled, it presents an identifiability challenge when estimating the pulse location model. Careful investigation of the subject pulse locations and the intensity function is necessary to examine whether differences in patterns are more likely due to changes in the intensity versus just differences in the number of events used to model each pulse.
It is possible to impose a firm time constraint between pulses by changing the distribution of the number of events in a cluster from a Poisson to a Bernoulli. The intensity function would be an independent cluster model (Lawson and Denison, 2002). This approach is being investigated in future work.
We uncovered a common temporal component in the pulse location times where subjects often have pulses at similar clock times, particularly in cortisol. This pattern has not been previously characterized. We interpret these results as evidence of the existence of one or more external regulators such as feeding or waking, which were common across subjects by the study protocol. A competing explanation may be that subjects are just tightly regulated in their inter-pulse intervals, although this explanation requires a mechanism to coordinate pulse times, not just frequencies. We investigated the plausibility of this second explanation via simulation. We simulated hormone release patterns on 25 subjects. Each subject had the same first pulse location and subsequent locations were generated using a common inter-pulse interval distribution with a mean and variance similar to the original analysis of these data (Young and others, 2001). Within 2 h, the pulse locations quickly disperse in clock time, and thus lack the visual clustering evident in simulated pulse locations from our Cox model (data not shown), and in the real data. This brief exercise provides further support to our interpretation that clustering in the locations indicates an influence of external factors on the pulse regulator.
Previous analyses of the pulse location model were performed in Liu and Wang (2007). Their intensity function for ACTH were similar; however, their intensity function for cortisol was smoother and had limited evidence of clustering in pulse locations compared with ours. There were several differences in the hormone concentration models that could explain this difference. Of importance, our model incorporates a changing baseline for cortisol, while the previous analysis assumes a constant baseline. Ignoring the circadian baseline pattern may result in additional pulses being added to achieve the correct hormone level. This could disrupt the clustering signaling because additional pulses may be added in more random locations.
We fitted each group and hormone separately. Gains in posterior precision of the parameters of interest may be possible by modeling both groups together in a single model. This is because parameters that are similar across groups could be estimated by all available data. Implementation of this extension is being investigated as future work.
We have presented a new approach to modeling pulsatile hormone data that is capable of characterizing complex temporal and clustering patterns in the pulse locations. This new approach uncovered previously unseen patterns in cortisol secretion that may be informative as biomedical investigators consider future hypotheses and treatments involving the stress axis.
6. Software
Software in the form of C code, together with a sample dataset and documentation is available as Supplementary Material.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
This work was supported by National Institutes of Health (NCRR KL2 RR025779, NIMH R21MH094994). Contents are the authors' sole responsibility and do not necessarily represent official NIH views.
Supplementary Material
Acknowledgments
The authors thank Dr. Elizabeth Young, posthumus, for allowing us to use the ACTH and cortisol hormone data, and the Associate Editor and reviewers for their thoughtful comments. Conflict of Interest: None declared.
References
- Anderson K. W., O'Sullivan F. (1993). A point process approach to pulsatile hormone data. Presented at the ASA meeting, San Fransisco.
- Carlson N. E., Johnson T. D., Brown M. B. (2009). A Bayesian approach to modeling associations between pulsatile hormones. Biometrics 65, 650–659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll B. J., Curtis G. C., Mendels J. (1976). Neuroendocrine regulation in depression I. Limbic system-adrenocortical dysfunction. Archives of General Psychiatry 33, 1039–1044. [DOI] [PubMed] [Google Scholar]
- Cox D. R. (1955). Some statistical models related with series of events. Journal of the Royal Statistical Society, Series B 17, 129–164. [Google Scholar]
- Cox D. R., Isham V. (1984) Point Processes. London: Chapman and Hall/CRC. [Google Scholar]
- Geyer C. J., Møller J. (1994). A new look at the statistical model identification. Scandinavian Journal of Statistics 21, 359–373. [Google Scholar]
- Greenspan F. S., Gardner D. G. (2004) Basic and Clinical Endocrinology, 7th edition New York: McGraw-Hill. [Google Scholar]
- Henley D. E., Lightman S. L. (2014). Cardio-metabolic consequences of glucocorticoid replacement: relevance of ultradian signaling. Clinical Endocrinology 80, 621–628. [DOI] [PubMed] [Google Scholar]
- Henley D. E., Russell G. M., Douthwaite J. A., Wood S. A., Buchanan F., Gibson R., Woltersdorf W. W., Catterall J. R., Lightman S. L. (2009). Hypothalamic–pituitary–adrenal axis activation in obstructive sleep apnea: the effect of continuous positive airway pressure therapy. Journal of Clinical Endocrinology and Metabolism 94, 4234–4242. [DOI] [PubMed] [Google Scholar]
- Johnson T. D. (2003). Bayesian deconvolution analysis of pulsatile hormone concentration profiles. Biometrics 59, 650–660. [DOI] [PubMed] [Google Scholar]
- Johnson T. D. (2007). Analysis of pulsatile hormone concentration profiles with nonconstant basal concentration: a Bayesian approach. Biometrics 63, 1207–1217. [DOI] [PubMed] [Google Scholar]
- Keenan D. M., Veldhuis J. D. (1997). Stochastic model of admixed basal and pulsatile hormone secretion as modulated by a deterministic oscillator. American Journal Physiology 273, R1182–R1192. [DOI] [PubMed] [Google Scholar]
- Keenan D. M., Veldhuis J. D., Yang R. (1998). Joint recovery of pulsatile and basal hormone secretion by stochastic nonlinear random-effects analysis. American Journal Physiology 275, R1939–R1949. [DOI] [PubMed] [Google Scholar]
- Lawson A. B., Denison D. G. T. (2002) Spatial Cluster Modeling. London: Chapman and Hall/CRC. [Google Scholar]
- Lightman S. L. (2008). The neuroendocrinology of stress: a never ending story. Journal of Neuroenocrinology 20, 880–884. [DOI] [PubMed] [Google Scholar]
- Lightman S. L., Conway-Cambell B. L. (2010). The crucial role of pulsatile activity of the hpa axis for continuous dynamic equilibrium. Nature Reviews Neuroscience 11, 710–718. [DOI] [PubMed] [Google Scholar]
- Liu A., Wang Y. (2007). Modeling of hormone secretion-generating mechanisms with splines: a psuedo-likelihood approach. Biometrics 63, 201–208. [DOI] [PubMed] [Google Scholar]
- McMaster A., Jangani M., Sommer P., Han N., Brass A., Beesley S., Lu W., Berry A., Loudon A., Donn R.. and others (2011). Ultradian cortisol pulsatility encodes a distinct, biologically important signal. PLoS ONE 6, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Møller J., Waagepetersen R. P. (2004) Statistical Inference and Simulation for Spatial Point Processes. London: Chapman and Hall/CRC. [Google Scholar]
- O'Sullivan F. O., O'Sullivan J. (1988). Deconvolution of episodic hormone data: an analysis of the role of season on the onset of puberty in cows. Biometrics 44, 339–353. [PubMed] [Google Scholar]
- Penttinen A. (1984).
Modelling interaction in spatial point patterns: parameter estimation by
the maximum likelihood method. In: Number 7 in
Jyv
 skyl
skyl Studies in Computer Science, Economics,
and Statistics. Jyväskylän yliopisto: University of
Jyv
Studies in Computer Science, Economics,
and Statistics. Jyväskylän yliopisto: University of
Jyv skyl
skyl .
. - Preston C. J. (1977). Spatial birth-and-death processes. Bulletin of the International Statistical Institute 46, 371–391. [Google Scholar]
- Rodbard D., Rayford P. L., Ross G. T. (1970). Statistical quality control. In: McArthur, J. W. and Colton, T. (editors), Statistics in Endocrinology. Cambridge, Massachusetts: The MIT Press, pp. 411–429.
- Russell G. M., Durant C. A., Atay A., Papastathi C., Bhake R., Wolfram W., Lightman S. (2014). Subcutaneous pulsatile glucocorticoid replacement therapy. Clinical Endocrinology 81, 289–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spiga F., Waite E. J., Liu Y., Kershaw Y. M., Aguilera G., Lightman S. L. (2011). Acth-dependent ultradian rhythm of corticosterone secretion. Endocrinology 152, 1448–1457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strauss D. J. (1975). A model for clustering. Biometrika 63, 467–475. [Google Scholar]
- Veldhuis J. D., Johnson M. L. (1992). Deconvolution analysis of hormone data. Methods in Enzymology 210, 539–575. [DOI] [PubMed] [Google Scholar]
- Walker J. J., Spiga F., Waite E., Zhao Z., Kershaw Y., Terry J. R., Lightman S. L. (2012). The origin of glucocorticoid hormone oscillations. PLoS Biology 10, e1001341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker J. J., Terry J. R., Lightman S. L. (2010). Origin of ultradian pulsatility in the hypothalamic–pituitary–adreal axis. Proceedings of the Royal Society B 277, 1627–1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yehuda R. (2002). Current status of cortisol findings in post-traumatic stress disorder. Psychiatric Clinics of North America 25, 341–368. [DOI] [PubMed] [Google Scholar]
- Young E. A., Abelson J., Lightman S. L. (2004). Cortisol pulsatility and its role in stress regulation and health. Frontiers in Neuroendocrinology 25, 69–76. [DOI] [PubMed] [Google Scholar]
- Young E. A., Carlson N. E., Brown M. B. (2001). Twenty-four hour ACTH and cortisol pulsatility in depressed women. Neuropsychopharmacology 25, 267–276. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.