Common polygenic variation enhances risk prediction for Alzheimer’s disease

Heritability estimates for Alzheimer’s disease in genome-wide association studies increase substantially when weak effect loci are also considered. Escott-Price et al. investigate the polygenic architecture of Alzheimer’s disease and the accuracy of prediction models, and show that including the polygenic component of risk significantly improves accuracy of case prediction.

Heritability estimates for Alzheimer’s disease in genome-wide association studies increase substantially when weak effect loci are also considered. Escott-Price et al. investigate the polygenic architecture of Alzheimer’s disease and the accuracy of prediction models, and show that including the polygenic component of risk significantly improves accuracy of case prediction.

Abstract

The identification of subjects at high risk for Alzheimer’s disease is important for prognosis and early intervention. We investigated the polygenic architecture of Alzheimer’s disease and the accuracy of Alzheimer’s disease prediction models, including and excluding the polygenic component in the model. This study used genotype data from the powerful dataset comprising 17 008 cases and 37 154 controls obtained from the International Genomics of Alzheimer’s Project (IGAP). Polygenic score analysis tested whether the alleles identified to associate with disease in one sample set were significantly enriched in the cases relative to the controls in an independent sample. The disease prediction accuracy was investigated in a subset of the IGAP data, a sample of 3049 cases and 1554 controls (for whom APOE genotype data were available) by means of sensitivity, specificity, area under the receiver operating characteristic curve (AUC) and positive and negative predictive values. We observed significant evidence for a polygenic component enriched in Alzheimer’s disease (P = 4.9 × 10⁻²⁶). This enrichment remained significant after APOE and other genome-wide associated regions were excluded (P = 3.4 × 10⁻¹⁹). The best prediction accuracy AUC = 78.2% (95% confidence interval 77–80%) was achieved by a logistic regression model with APOE, the polygenic score, sex and age as predictors. In conclusion, Alzheimer’s disease has a significant polygenic component, which has predictive utility for Alzheimer’s disease risk and could be a valuable research tool complementing experimental designs, including preventative clinical trials, stem cell selection and high/low risk clinical studies. In modelling a range of sample disease prevalences, we found that polygenic scores almost doubles case prediction from chance with increased prediction at polygenic extremes.

Introduction

Genome-wide association (GWA) studies have proved a powerful method to identify susceptibility alleles for complex diseases. The most powerful currently undertaken study, provided by the International Genomics of Alzheimer’s Project (IGAP), has identified over 20 Alzheimer’s disease susceptibility loci (Lambert et al., 2013). GWA study datasets can be used to determine a polygenic contribution of common single nucleotide polymorphisms (SNPs) that show disease association but fail to meet the accepted P-value threshold for genome-wide significance (P < 5 × 10⁻⁸). Recent studies confirm that the estimated heritability detected in Alzheimer’s disease GWA studies (24–35%) (Lee et al., 2013) increases substantially when weak effect loci are also considered. This strongly implies that a large proportion of the genetic signal must lie below the genome-wide significance threshold.

The polygenic score approach encompasses more of the causal variance, as a genetic risk score is calculated based not solely on genome-wide significant polymorphisms, but on all nominally associated variants at a defined significance threshold (typically thousands of variants). This type of analysis has recently shown significant polygenic contribution in other complex genetic diseases. For example in Parkinson’s disease, a polygenic basis was confirmed and shown to correlate with age at disease onset (Escott-Price et al., 2014). The method can also be used to identify overlap in genetic determinants between related disorders, e.g. schizophrenia and bipolar disorder; depression and anxiety (Demirkan et al., 2011). While the polygenic method undoubtedly introduces noise by including some variants that are not involved in disease susceptibility (i.e. false positives), this is more than offset by the increased power to identify those at highest/lowest risk of disease. Trait differences between those with highest/lowest polygenic risk scores have also been identified. For example, in a study of the Lothian Birth Cohort, increased polygenic risk of schizophrenia was associated with lower cognitive ability at age 70 and greater relative decline in general cognitive ability between the ages of 11 and 70 (McIntosh et al., 2013).

We investigated the polygenic architecture of Alzheimer’s disease using the powerful IGAP GWA dataset (Lambert et al., 2013). The IGAP dataset was split into two independent subsets before the polygenic contribution to Alzheimer’s disease was investigated by assessing whether score alleles identified in one subset were significantly enriched in cases from another subset.

We also investigated the prediction accuracy of the model, which includes the number of ε4 and ε2 alleles at the APOE gene, a polygenic score component based upon genome-wide significant loci, and a polygenic score component constructed using all independent markers within the dataset including statistically not-significant SNPs. For this analysis we used 3049 cases and 1554 controls for whom APOE genotype data were available. Furthermore we looked at the utility of the polygenic score when the analysis was restricted to subjects with ε2 and ε3 alleles only. As age is a strong predictor of Alzheimer’s disease, we tested the prediction models in samples stratified by age. To test the sensitivity of the prediction models to population differences we ran the same analyses for subjects from the UK, USA and Germany separately.

We also modelled the predictive utility of the polygenic score using a range of disease prevalences reflecting those incubating disease in different age groups (e.g. 17% Alzheimer’s disease prevalence in those aged 75–84 or those with early stage of the disease who are 60–65 years now). We modelled early stage disease incubation as we now aware that Alzheimer’s disease may begin between 10–30 years before clinical symptoms are observed (Frisoni et al., 2010; Weiner et al., 2015). Different disease prevalences may also reflect groups that already have biomarker indicators of disease e.g. plaque deposition, mild cognitive impairment, of which 50% are early Alzheimer’s disease. We also estimated positive (PPV) and negative predictive values (NPV) for polygenic score and extreme cut-off of polygenic score, but point out that these values are just estimates and may differ in the sample populations modelled.

Materials and methods

We used the discovery dataset reported by the IGAP consortium (Lambert et al., 2013), comprising 17 008 Alzheimer’s disease cases and 37 154 controls. This sample of Alzheimer’s disease cases and controls comprises four datasets taken from GWA studies performed by GERAD (Genetic and Environmental Risk for Alzheimer’s disease), EADI (European Alzheimer ’s disease Initiative), CHARGE (Cohorts for Heart and Aging Research in Genomic Epidemiology) and ADGC (Alzheimer's Disease Genetics Consortium) (Lambert et al., 2013). Full details of each study including the samples and methods used are provided elsewhere (Harold et al., 2009; Lambert et al., 2009; Seshadri et al., 2010; Hollingworth et al., 2011; Naj et al., 2011). Each of the four datasets were imputed with either Impute2 (Howie et al., 2009) or MACH (Li et al., 2010) software, using the 1000 Genomes data (release Dec 2010) as a reference panel.

Polygenic score analysis

We followed the approach previously described by the International Schizophrenia Consortium (International Schizophrenia et al., 2009). The polygenic score analysis requires two independent datasets. For the first, result data are sufficient as this dataset is used to select the SNPs, the risk score alleles and their genetic effects. The second dataset is used to test whether the polygenic risk scores differ in cases and controls and requires the genotypes for each individual. The meta-analysed results data of the EADI, CHARGE and ADGC consortia (13 831 cases and 29 877 controls, hereafter referred to as IGAP.noGERAD) were used for SNP selection. We used the individual genotypes of the GERAD consortium (Harold et al., 2009) data (3177 cases and 7277 controls); we used the GERAD data as the test sample.

We included only autosomal SNPs that passed stringent quality control criteria, i.e. minor allele frequencies ≥ 0.01 and imputation quality score ≥ 0.5 in each study. This resulted in 6 928 531 SNPs, which were present in at least 40% of the Alzheimer’s disease cases and 40% of the controls, being included in the analysis. The summary statistics across the three datasets were combined using fixed-effects inverse variance-weighted meta-analysis.

Using GERAD study data we performed (i) random linkage disequilibrium pruning using r² > 0.2; and (ii) ‘intelligent’ pruning [–clump option in PLINK (Purcell et al., 2007) genetic analysis tool] using the same r² parameter and a physical distance threshold for clumping SNPs of 1 Mb. The random linkage disequilibrium pruning resulted in 401 584 SNPs that are in relative linkage equilibrium (r² ≤ 0.2) and common between GERAD and IGAP.noGERAD datasets. The ‘intelligent’ pruning allows one to capture SNPs that are most (even if not-significantly) associated with the disease in a linkage disequilibrium block. This ‘intelligent’ pruning identified 538 363 independent SNPs that were most significantly associated with Alzheimer’s disease in IGAP.noGERAD data. We selected markers, based upon significance thresholds, to construct a polygenic score in the GERAD data. The polygenic score was calculated from the effect size (β)-weighted sum of associated alleles within each subject. Polygenic scores were normalized by subtracting the mean and dividing by the standard deviation.

We assessed a variety of significance thresholds for the selection of markers for polygenic score construction; overlapping panels of markers were used (e.g. significant at P ≤ 0.01, 0.05, 0.1,…, 1 in the IGAP.noGERAD) in the construction of a subject-level score in GERAD case/control sample. The ability of each panel-based score distribution to distinguish those with disease from cognitively normal individuals was assessed using logistic regression analysis while adjusting for age, sex, country of origin and three principal components (Harold et al., 2009), reflecting underlying stratification in the sample due to population and/or genotyping technique differences.

Analysis of predictive accuracy

To find the best predictors of the Alzheimer’s disease, we tested a variety of regression models. For this analysis we used the genotyped (rather than imputed) SNP data for the following reasons. Imputed genotype data contain probabilities of each of three genotypes, rather than the actual genotype. As the relevant software suitable for this analysis requires actual genotypes [e.g. intelligent pruning (–clump) option in PLINK], the probabilities were converted to actual genotype data, only if the probability was >0.9. This conversion increased missing value rates and, therefore SNPs with >10% missing values were excluded from the analysis. We ran the predictive analyses on imputed data, and note that the prediction accuracy is sensitive to the number of missing genotypes, which was exacerbated by the uncertainty of imputation aggregated across large numbers of SNPs contributing to the polygenic score. The intelligent pruning was performed using summary statistics for IGAP.noGERAD data, and thus the most significant SNPs in this dataset were not necessarily the same as genome-wide significant SNPs in the full IGAP data. Therefore, to represent genome-wide significant results in our analyses, we chose the best proxies to the genome-wide significant SNPs (Lambert et al., 2013) from the ‘intelligently’ pruned data.

As the genotyped data at the APOE locus contained only proxy SNPs for the APOE-ε4 and APOE-ε2 variants (rs429358 and rs7412), we limited our analysis to those individuals (3049 Alzheimer’s disease cases and 1554 controls) for whom we had APOE genotype data. For the other 21 genome-wide significant SNPs (Lambert et al., 2013), proxies with r² > 0.8 were available for 11 SNPs in the GERAD data, for an additional seven loci we had genotyped markers that were in modest linkage disequilibrium (r² between 0.5 and 0.8) with a genome-wide significant marker. Two genome-wide significant SNPs in the SLC24A4/RIN3 and CD33 loci had proxies with r² ∼ 0.3 (Supplementary Table 1). We excluded the DSG2 gene as this association did not replicate in IGAP stage 2 (Lambert et al., 2013), and the best proxy to the putative genome-wide significant SNP was in low linkage disequilibrium (r² = 0.06) in the GERAD sample.

We calculated sensitivity, specificity, area under the receiver operating characteristic curve (AUC), PPV and NPV by comparing the observed case/control status and the predicted probability estimated by logistic regression models using the prediction() and performance() functions in R-statistical software. PPV and NPV values were calculated adjusting for the lifetime risk of Alzheimer’s disease with BDtest() function, ‘bdpv’ package in R. We chose to use lifetime risk (17%) and prevalence at age 85 and above (32%) (Hebert et al., 2013) to prioritise subjects of age 60–65 for clinical trials. These people may not have Alzheimer’s disease yet, but are at early stage of the disease, which may manifest 20–30 years later.

As heterogeneity across cohorts comprising the discovery (IGAP.noGERAD) and validation (GERAD) datasets may introduce bias in the prediction modelling, we assessed heterogeneity between the UK, German and USA studies by means of I² values and chi-squared test for heterogeneity for each SNP, as well as performed calibration analysis with Hosmer-Lemeshow test [hoslem.test() function in R] for each regression model which we run in the validation data. For the discovery dataset we had only summary statistics for each SNP, which were adjusted for population covariates prior to analyses performed here.

We used as predictors a number of explanatory variables including APOE-ε4, APOE-ε2, age, gender, polygenic score based upon 20 genome-wide significant SNP proxies, and polygenic score calculated using SNPs with Alzheimer’s disease association P-values ranging from 0.0001 to 0.9 in the IGAP.noGERAD sample (APOE and GWA study loci were excluded; Supplementary Table 1). We assessed significance of model improvements over APOE (ε4 + ε2) and over GWA study proxies via DeLong’s method [roc.test() function in R].

We performed similar analyses on imputed data however the prediction accuracy using this dataset was marginally lower due to noise introduced through a number of missing values as a result of genotypes imputed with low certainty (results are not shown). To test the sensitivity of our results to possible bias due to age and population stratification, we ran the same models in subsamples stratified by geographical region (UK, USA and Germany), and age groups <60, 60–69, 70–79, 80–89 and 90+ years.

Results

Polygenic risk score analysis

In this study we investigated whether the polygenic score alleles identified in one Alzheimer’s disease GWA study were significantly enriched in the cases relative to the controls of an independent Alzheimer’s disease dataset. Our analysis revealed significant evidence for an overall enrichment of the Alzheimer’s disease polygenic risk score alleles of the IGAP.noGERAD data in the independent GERAS (Harold et al., 2009) cohort of 3177 Alzheimer’s disease cases and 7277 controls from the UK, Europe and USA (Table 1). The pattern of the polygenic score association was similar to those seen in studies of other complex diseases shown to have a polygenic signal (International Schizophrenia et al., 2009; Stergiakouli et al., 2012; Heilmann et al., 2013; Michailidou et al., 2013). Our most significant evidence for association was observed when SNPs with a selection threshold (P_T) of P ≤ 0.5 in the IGAP.noGERAD sample were included. The P-values for a significant enrichment in the polygenic score ranged from 3.9 × 10⁻²⁰ to 4.9 × 10⁻²⁶ dependent on the P_T used (Table 1). For all significant associations the B-coefficients (Effects) were positive, indicating that a higher polygenic score in the IGAP.noGERAD discovery dataset corresponds to a higher score in the independent GERAD replication dataset and provides evidence for a polygenic contribution to the development of Alzheimer’s disease.

Table 1.

Results of polygenic score analysis based upon a set of independent SNPs (at r² ≤ 0.2) pruned to retain those most significantly associated with the disease.

PTa	Effect	SE	P	R2	NSNPs
0.01	0.283	0.0308	3.9 × 10−20	0.016	16 749
0.05	0.311	0.0308	5.9 × 10−24	0.019	61 552
0.1	0.321	0.0309	2.6 × 10−25	0.020	107 834
0.2	0.327	0.0309	3.6 × 10−26	0.021	185 737
0.3	0.317	0.0308	7.9 × 10−25	0.020	251 850
0.4	0.323	0.0308	1.0 × 10−25	0.020	308 780
0.5	0.327	0.0310	4.9 × 10−26	0.021	359 500
0.6	0.326	0.0310	6.2 × 10−26	0.021	404 626
0.7	0.325	0.0309	9.3 × 10−26	0.020	444 663
0.8	0.328	0.0310	4.1 × 10−26	0.021	480 271
0.9	0.323	0.0309	1.9 × 10−25	0.020	511 297
1	0.321	0.0309	3.0 × 10−25	0.020	538 362

^aSelection threshold of ‘score’ SNPs taken from the IGAP.noGERAD discovery sample.

NSNPs = number of SNPs; SE = standard error.

As the 538 363 independent SNPs that we used to identify Alzheimer’s disease polygenic risk score alleles included those most significantly associated with the disease, it is plausible that our results are artificially biased by SNPs whose evidence for association is a consequence of linkage disequilibrium with a known genome-wide significant SNPs. To investigate this possibility we repeated our analysis using identical analysis thresholds but excluding all 5006 SNPs that, after linkage disequilibrium pruning, were present at the 24 genomic regions previously reported to be strongly associated with Alzheimer’s disease (Lambert et al., 2013; Escott-Price et al., 2014). The regions were defined as ±500 kb of both sides of the GWA SNPs (Lambert et al., 2013) or GWA genes (Escott-Price et al., 2014) and between 44 400–46 500 kb on chromosome 19 for the APOE locus (Supplementary Table 1). Given that each of these excluded regions is likely to contain at least one true Alzheimer’s disease susceptibility allele, this approach is highly conservative. Nevertheless, this analysis again revealed significant evidence that individuals with higher polygenic risk scores had greater probability of Alzheimer’s disease, with our most significant result P = 3.4 × 10⁻¹⁹ (Table 2). Moreover, we obtained analogous results when we used an alternative method of linkage disequilibrium pruning, which ignores the strength to which SNPs are associated with Alzheimer’s disease, and thus excludes SNPs from the 24 associated regions (Supplementary Table 2). These analyses suggest that our findings are not dependent on either the previously identified susceptibility loci or the SNPs that are associated with Alzheimer’s disease merely as a consequence of linkage disequilibrium with the genome-wide significant loci.

Table 2.

Results of polygenic score analysis based upon a set of relatively independent SNPs (at r² ≤ 0.2) pruned to retain those most significantly associated with the disease, excluding the genome-wide associated loci

PTa	Effect	SE	P	R2	NSNPs
0.01	0.154	0.0304	4.01 × 10−7	0.005	16 412
0.05	0.232	0.0305	2.50 × 10−14	0.011	60 750
0.1	0.256	0.0307	5.92 × 10−17	0.013	106 587
0.2	0.270	0.0307	1.23 × 10−18	0.014	183 808
0.3	0.263	0.0305	6.47 × 10−18	0.014	249 314
0.4	0.271	0.0306	7.26 × 10−19	0.014	305 741
0.5	0.275	0.0307	3.45 × 10−19	0.015	356 033
0.6	0.274	0.0307	4.66 × 10−19	0.015	400 785
0.7	0.273	0.0307	6.76 × 10−19	0.014	440 473
0.8	0.276	0.0308	2.93 × 10−19	0.015	475 769
0.9	0.271	0.0307	1.13 × 10−18	0.014	506 532
1	0.269	0.0307	1.67 × 10−18	0.014	533 356

^aSelection threshold of ‘score’ SNPs taken from the IGAP.noGERAD discovery sample. Exact positions of the excluded regions are given in Supplementary Table 1.

Analysis of predictive accuracy

The identification of subjects at high risk for Alzheimer’s disease is important for prognosis and early intervention, identifying biomarkers and disease mechanisms. We used logistic regression analysis to establish predictive values (sensitivity, specificity, AUC, PPV, NPV) of genetic risk factors in a subset of GERADdata (3049 cases and 1554 controls) for whom APOE genotype data were available. The results of this analysis are summarized in Table 3. All regression models’ P-values were highly significant (P < 10⁻⁹⁴). We also note that addition of the polygenic score to the regression model has significantly improved all regression models over and above APOE (ε4 + ε2) alone. Inclusion of the polygenic score based upon proxies to GWA studies significant SNPs improved the model by P = 2.7 × 10⁻¹² (Table 3). We have also tested model improvements over APOE + GWAS when added polygenic score based upon less significant SNPs (Table 3). A nominally significant improvement (P = 0.048) was observed adding polygenic score constructed from 130 SNPs with Alzheimer’s disease association P < 10⁻⁴. A clear change was observed between adding polygenic score based on genome-wide significant SNPs and SNPs with Alzheimer’s disease association P < 0.05 (model improvement P = 3.6 × 10⁻⁹), gradually improving with adding more SNPs with P-values up to 0.5 (model improvement P = 1.3 × 10⁻¹¹).

Table 3.

Predictive accuracy for 3049 Alzheimer’s disease cases versus 1554 controls

Model	NSNPs	Sensitivity	Specificity	AUC	AUC	Improve over APOE	Improve over APOE and GWA study	Hosmer-Lemeshow test
					95% CI			P-value*
ε4	1	0.593	0.746	0.678	0.66–0.69	-	-	0.987
ε4 + ε2	2	0.593	0.746	0.688	0.67–0.70	-	-	0.969
ε4 + ε2 + sex + age	2	0.669	0.662	0.717	0.70–0.73	8.5 × 10−13	-	0.067
ε4 + ε2 + 20 GWAS SNPs	22	0.666	0.666	0.715	0.70–0.73	2.7 × 10−12	-	0.234
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.0001	130	0.669	0.669	0.717	0.70–0.73	2.5 × 10−14	0.048	0.218
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.001	549	0.668	0.668	0.720	0.71–0.74	2.8 × 10−16	0.0082	0.415
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.01	3388	0.672	0.672	0.729	0.71–0.74	1.1 × 10−21	9.5 × 10−6	0.855
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.05	13273	0.677	0.677	0.738	0.72–0.75	7.4 × 10−27	3.6 × 10−9	0.633
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.1	23676	0.682	0.682	0.740	0.73–0.76	3.5 × 10−28	5.9 × 10−10	0.575
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.2	42273	0.683	0.683	0.743	0.73–0.76	1.5 × 10−29	3.6 × 10−11	0.211
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.3	58963	0.684	0.683	0.744	0.73–0.76	2.0 × 10−29	3.9 × 10−11	0.139
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.4	73941	0.684	0.684	0.744	0.73–0.76	1.1 × 10−29	2.1 × 10−11	0.213
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.5	87605	0.686	0.686	0.745	0.73–0.76	7.2 × 10−30	1.3 × 10−11	0.225
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.6	99724	0.685	0.685	0.745	0.73–0.76	4.4 × 10−30	9.4 × 10−12	0.155
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.7	110431	0.685	0.685	0.745	0.73–0.76	1.0 × 10−29	1.7 × 10−11	0.076
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.8	119616	0.683	0.683	0.745	0.73–0.76	6.2 × 10−30	1.2 × 10−11	0.095
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.9	127585	0.684	0.684	0.745	0.73–0.76	6.3 × 10−30	1.2 × 10−11	0.185
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.5 + age + sex	87605	0.704	0.703	0.782	0.77–0.80	1.9 × 10−57	6.5 × 10−33	0.829

* Non-significant Hosmer-Lemeshow test P-value indicates that the model is correctly specified. The polygenic scores (PS) were constructed using independent SNPs associated with Alzheimer’s disease in IGAP.noGERAD at different significance levels (Model column), excluding APOE and 20 GWA study regions (Supplementary Table 2). Numbers of SNPs participating in the predictive model are given in column SNPs.

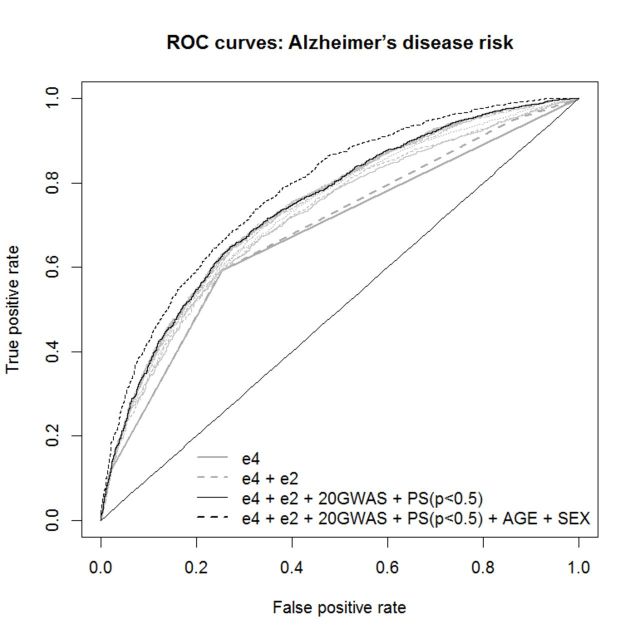
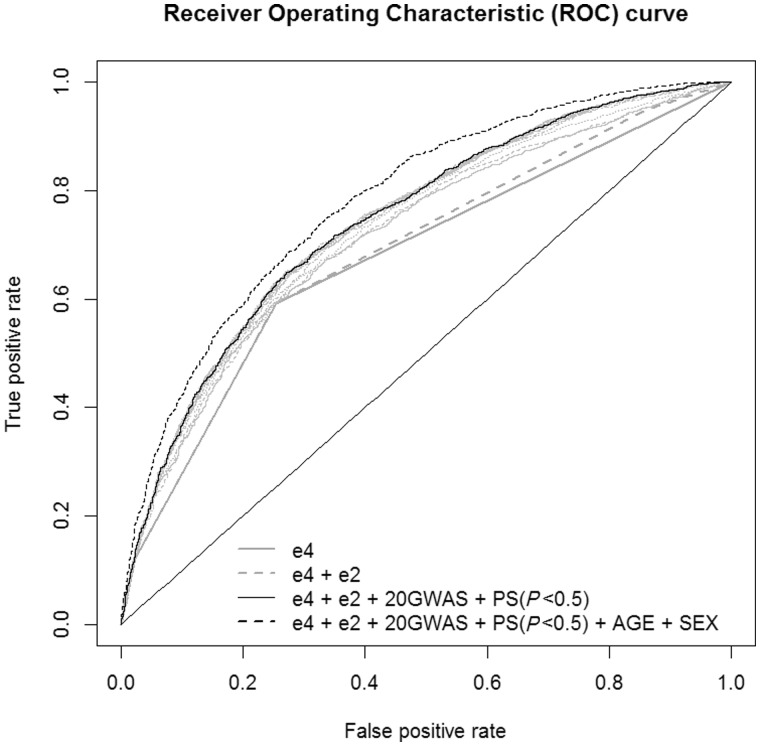
The APOE-ε4 allele is the strongest known genetic risk factor for Alzheimer’s disease. In the presence of APOE-ε4 alleles, the sensitivity was 0.59 the specificity 0.75 and the AUC = 0.678 (95% CI = 0.66–0.69) (Table 3). Inclusion of the numbers of APOE-ε2 alleles in the logistic regression model slightly increases all prediction accuracy values, in particular, the AUC increased to 0.688 (95% CI = 0.67–0.70). As expected, prediction accuracy was further enhanced [AUC = 0.715 (95% CI = 0.70–0.73), model improvement P = 2.7 × 10⁻¹²] when we added the genome wide significant polygenic score variable based upon proxies for the 20 genome-wide significant SNPs, where the weights of the SNP risk alleles were identified from the independent dataset IGAP.noGERAD (Fig. 1).

Figure 1.

ROC curves for predictive models with different predictors for risk of Alzheimer’s disease. GWAS = GWA study; PS = polygenic score.

We further investigated whether the polygenic score based on risk alleles of small effect identified in one study (IGAP.noGERAD) were improving the prediction accuracy in an independent dataset (GERAD). For this we used polygenic scores calculated excluding the known Alzheimer’s disease associated regions (Supplementary Table 2). The best prediction accuracy AUC = 0.745 (95% CI = 0.73–0.79) was achieved when we included the polygenic score for SNPs with Alzheimer’s disease association P-values < 0.5, with highly significant improvement over APOE alone (P = 7.2 × 10⁻³⁰) and over the APOE + GWAS model (P = 1.3 × 10⁻¹¹). As a result of logistic the prediction probability values between 0 and 1 are provided for each individual. Sensitivity and specificity (proportions of correctly predicted cases and controls) depend on the prediction probability threshold—a number between 0 and 1, which classifies all subjects into two groups ‘predicted cases’ and ‘predicted controls’. Clearly the lower this threshold, the more subjects are classified as cases, and therefore the more likely it predicts the majority of actual cases correctly, i.e. sensitivity increases (and vice versa for specificity). The commonly used (‘best’) approach to identify this threshold is to find a compromise between sensitivity and specificity by minimizing the difference between these two measures. The values of sensitivity and specificity were about 0.69 when estimated with the minimized difference probability threshold (MDT = 0.64).

The value AUC for the possible confounders such as sex, age and principal components, was not excessive, ranged between 52–56% (Supplementary Table 3), reaching maximum for the model with age and principal components, the latter indicating possible population stratification.

As age and sex have prediction value for Alzheimer’s disease, it made sense to include them as predictors into the model, rather than adjust for them. As expected, our results show that inclusion of sex and age in the regression model further improved the prediction accuracy (AUC = 0.782) (Table 3 and Fig. 1).

The population stratification might inflate prediction accuracy so we calculated the mean of heterogeneity I² values, which was 13.8% and the proportion of heterogeneity nominally significant SNPs was 7%, indicating slight inflation as compared to the nominal 5%. Table 3 also presents Hosmer-Lemeshow’s test P-values for each regression model. All P-values are non-significant indicating that the models are correctly specified.

To investigate possible population differences in the prediction of Alzheimer’s disease risk, we looked at UK, German and USA subjects separately. The pattern of predictive modelling results was similar to the main analyses results in all strata (Supplementary Table 4). Interestingly, the prediction in the USA strata was extremely good (the best AUC = 0.95%). This might be due to the fact that the majority of subjects (about 80%) in the training set were of USA origin in contrast to 17% in the test set. We performed the prediction modelling on the whole sample excluding SNPs with heterogeneity P-value < 0.05. The results and conclusions were similar.

In the context of practical application, e.g. in experimental designs comparing cases with high or low polygenic risk of Alzheimer’s disease, age has to be taken into account. Supplementary Table 5 presents the results of the genetic predictive modelling stratified by age groups. The results of the stratified analyses show a similar pattern of prediction accuracy. As before, the best accuracy in each stratum was achieved when the numbers of APOE-ε4, APOE-ε2 alleles, the polygenic score variable based upon proxies for the 20 genome-wide significant SNPs, and the polygenic score for SNPs with Alzheimer’s disease association P-values < 0.5 were included as predictors. The AUC value ranged from 73% to 79%, with the highest in the 60–69 age group (Supplementary Table 5). The best prediction might indicate that this particular age group has the strongest common genetic effect, with the younger age group (<60 years) potentially due to Mendelian forms of the disorder, and the older age groups confounded by general ageing effects.

Another way to look at the utility of the polygenic score as a predictor for Alzheimer’s disease is to exclude the strongest predictor, namely the ε4 allele, from the analysis. There were 1242 cases and 1160 controls in the sample without ε4 allele. When looking at these individuals only, the AUC was 65.0% when we included the polygenic scores based upon proxies for the 20 genome-wide significant SNPs and for SNPs with Alzheimer’s disease association P-values < 0.5, increasing to 65.8% when the number of ε2 alleles was added as a predictor. Similar accuracy was achieved (64.5% and 65.8%) when we ran the analysis on the whole sample without ε4 as a predictor.

Positive and negative predictive values

Using sensitivity and specificity, a practitioner can make statements such as ‘assuming that the individual has Alzheimer’s disease, the test has accuracy 69%’ (here 69% is the sensitivity; Table 3.) However, this statement might not be helpful for designing an experiment because, for new samples, all that is known is the prediction. The PPV answers the question ‘what is the probability that this person has (or is incubating) Alzheimer’s disease?’ With regard to the practical use of polygenic score in the identification of subjects at high and low risk for Alzheimer’s disease, we investigated the prediction accuracy in terms of PPV and NPV: the percentage of predicted patients who actually have the disease and the percentage of predicted who are actually controls, respectively. The results of these analyses are shown in Table 4. In our sample PPV reached 81% and NPV = 53% (see Table 4, line corresponding to the model with APOE, GWAS and SNPs with P ≤ 0.5).

Table 4.

Positive and negative predictive values, adjusted for prevalence of Alzheimer’s disease in different risk drops for Alzheimer’s disease.

	In our sample		17% prevalence		33% prevalence		50% prevalence
			(age 75–84)a		(age 85+)a		(MCI)b
Model	PPV	NPV	PPV	NPV	PPV	NPV	PPV	NPV
ε4	0.821	0.483	0.273	0.919	0.474	0.826	0.647	0.700
ε4 + ε2	0.821	0.483	0.273	0.919	0.474	0.826	0.647	0.700
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.0001	0.796	0.504	0.290	0.907	0.496	0.802	0.666	0.666
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.001	0.798	0.507	0.292	0.908	0.499	0.804	0.669	0.669
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.01	0.798	0.506	0.292	0.908	0.498	0.803	0.668	0.668
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.05	0.801	0.511	0.296	0.909	0.502	0.806	0.672	0.672
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.1	0.804	0.516	0.300	0.911	0.508	0.810	0.677	0.677
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.2	0.808	0.522	0.305	0.913	0.514	0.813	0.682	0.682
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.3	0.808	0.523	0.306	0.913	0.514	0.814	0.683	0.683
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.4	0.809	0.524	0.307	0.913	0.515	0.814	0.683	0.683
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.5	0.809	0.525	0.307	0.914	0.516	0.815	0.684	0.684
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.6	0.811	0.527	0.309	0.914	0.518	0.816	0.686	0.686
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.7	0.810	0.526	0.309	0.914	0.518	0.816	0.685	0.685
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.8	0.810	0.525	0.308	0.914	0.517	0.815	0.685	0.685
ε4 + ε2 + 20 GWAS SNPs + PS P < 0.9	0.809	0.523	0.306	0.913	0.515	0.814	0.683	0.683

^aHebert et al. (2013).

^bYesavage et al. (2002).

PS = polygenic score; GWAS = GWA study; MCI = mild cognitive impairment.

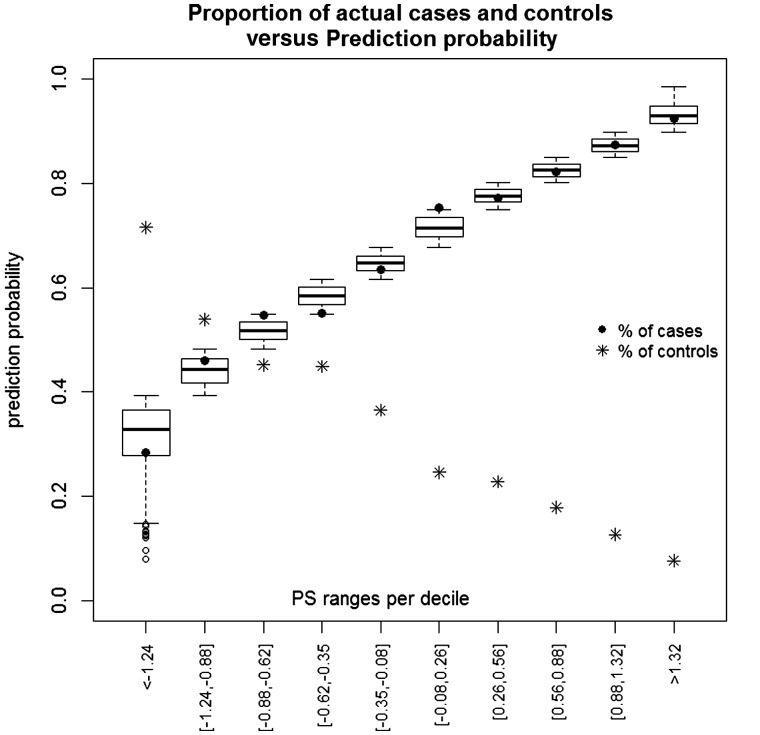
We recognize that the validating sample used here (3049 Alzheimer’s disease cases and 1554 controls) may not represent the range of samples with Alzheimer’s disease or those in the early stage of Alzheimer’s disease. We have therefore attempted to model potential scenarios with practical utility. Thus, we modelled samples in which 17% have or are in the early stage of Alzheimer’s disease, as well as 33% and 50%. This provides an estimate only and would need to be tested in appropriate sample populations. A crucial point is that prevalence affects the predictive value of any test. This means that the same diagnostic test will have a different predictive accuracy according to the clinical setting in which it is applied. With sensitivity and specificity values at 69% (Table 3), as prevalence rises from 17% (e.g. prevalence of Alzheimer’s disease among 75–84 year olds) to 33% (e.g. among those aged 85+), PPV will rise from 31% to 52% (Table 4): a huge difference in the clinical interpretation of the same test result. Furthermore, if the sample is enriched for Alzheimer’s disease cases, e.g. subjects are preselected for clinical trials on the basis of deposition of amyloid plaques or have mild cognitive impairment, with a high percentage estimated to convert to Alzheimer’s disease (Yesavage et al., 2002). Thus modelling with prevalence of 50%, will increase the PPV to 68% (Table 4), meaning that if the sample is enriched for cases, then with help of polygenic score, 68% of the sample will be correctly predicted as cases, as compared to 50% if chosen at random. Importantly, we will also correctly predict 68% of controls as the negative predictive value in this example is 0.684. The prediction accuracy can be enhanced by including individuals with extreme polygenic score cut-offs. We looked at deciles of the polygenic score distribution, estimated the range of predictive probabilities per decile and looked at the proportion of cases (and controls) correctly predicted. Figure 2 shows the results of this analysis. According to Fig. 2 our predictive modelling is fairly accurate (cf. black circle points with the box-plots in Fig. 2). The minimum polygenic score in the last decile is 1.32.

Figure 2.

Deciles of the polygenic score distribution with estimated range of predictive probabilities per decile (box-plots) and the proportion of cases (and controls) correctly predicted. PS = polygenic score.

To demonstrate utility of polygenic score we looked at most extreme polygenic score cut-offs and estimated PPV and NPV values, adjusted for (i) 17% lifetime risk of Alzheimer’s disease, approximately representing a general population at age 60–65, who will potentially get Alzheimer’s disease later; (ii) 33% prevalence; and (iii) 50% prevalence, representing a sample with high percentage subjects, estimated to convert to Alzheimer’s disease (Supplementary Tables 6 and 7). Adjusting for 17% prevalence, PPV and NPV values were PPV = 36%, NPV = 94% and PPV = 66% and NPV = 93% for polygenic score >2.3 and polygenic score >2.4, respectively. Increasing prevalence to 33% and 50% increased the PPV values to 82% and 90%, respectively (Supplementary Table 6), for subjects with normalized total polygenic score >2.4. Of course, these predictive values are just an indication of the possible achievable accuracy, as their estimations were based upon very small numbers (43 cases and four controls with polygenic score >2.3; and 32 cases and one control with polygenic score >2.4). Similar estimations were made for subjects with very low polygenic score, aiming to classify controls with a high precision (Supplementary Table 6).

Discussion

The molecular genetic data reported in this study provide strong support for a large polygenic contribution to the overall heritable risk of Alzheimer’s disease. This implies that the genetic architecture of Alzheimer’s disease includes many common variants of small effect that are likely to reflect a large number of susceptibility genes and a complex set of biological pathways related to disease.

First, we have shown that including genetic variants to a P-value ≤ 0.5, as well as age and sex, produces the best AUC = 78.2%. Second, we show that including full polygenic score (P < 0.5) significantly improves AUC over APOE + 20 proxies to genome-wide significant SNPs (P = 1.3 × 10⁻¹¹) and APOE alone (P = 7.2 × 10⁻³⁰). Third, our data also indicate that prediction can be further improved by limiting sample selection polygenic extremes.

However, it must be noted that our case-control dataset (3049 Alzheimer’s disease cases and 1554 controls) does not reflect other populations in which different proportions of Alzheimer’s disease cases or those at the early stage of the disease. We therefore attempted to model other data samples that may be of use. We modelled 17% of caseness reflecting prevalence of Alzheimer’s disease at ages 75–84 years, or in those possibly incubating Alzheimer’s disease at an early age range of 60–65 years. We observed that using more extreme polygenic scores, we increased the predictive value from 31% to 36% and almost doubled (66%) for a more extreme polygenic score cut-off. We also estimated PPV and NPV at 33% and 50% of caseness. At 33% caseness adding polygenic score estimated to increase PPV to 52% in the whole range of polygenic score and up to 82% for more extreme cut-off, thus indicating that polygenic scores have utility alongside other predictors of Alzheimer’s disease in a variety of experimental designs including: preventative clinical trials, the selection of induced pluripotent stem cell lines to model Alzheimer’s disease, and the investigation of biomarkers throughout disease development. However, these are estimates extrapolated from our data and need to be tested in actual population samples.

The Alzheimer’s disease polygenic score alleles identified in the GERAD cohort are not significantly enriched (minimum P = 0.14) in an independent GWA study for Parkinson’s disease (Moskvina et al., 2013) indicating that the identified polygenic component of Alzheimer’s disease is disease-specific. Our results are unlikely to be due to population stratification, although we observe greater predictive accuracy in samples enriched for individuals from the same population in both the discovery and validating dataset (AUC = 95% in subset of USA subjects used for validation).

Further studies are required if we are to progress from the knowledge that there is a polygenic contribution to Alzheimer’s disease, to understanding the specific genetic factors that comprise the polygenic component. Increasing the discovery sample size will allow more loci with increasingly small individual effect sizes to pass the threshold of genome-wide significance, and should substantially refine the polygenic scores derived here. Moreover, as we have previously shown, using approaches such as gene pathway analyses it is possible to use the captured polygenic signal and identify genes or biological systems relevant to Alzheimer’s disease (International Genomics of Alzheimer's Disease, 2015).

It is possible that our findings are influenced by rare Alzheimer’s disease susceptibility variants that are in linkage disequilibrium with the common alleles analysed in this study. The ongoing efforts of studies performing exome and whole genome sequencing in large numbers of Alzheimer’s disease case–control cohorts will allow us to establish the haplotype structure of common and rare alleles an in turn, to understand which loci are subject to ‘synthetic association’ (Dickson et al., 2010). To date, we have not observed a significant excess of rare copy number variants in cases in our GERAD sample and did not replicate findings of previous Alzheimer’s disease copy number variant studies (Chapman et al., 2013). We also found no excess of homozygous tracts in Alzheimer’s disease cases compared to controls and no individual run of homozygosity showed association to Alzheimer’s disease in the GERAD sample (Sims et al., 2011). However, as previously demonstrated in other complex diseases (Purcell et al., 2014), future polygenic score analysis of variants identified by exome/genome sequencing are expected to further inform our understanding of the genetic underpinnings of Alzheimer’s disease.

In conclusion, the derived polygenic scores have demonstrated utility for calculating an individual level genetic risk profile that can predict disease development. Measures of polygenic burden could prove useful in distinguishing patients with Alzheimer’s disease whose disease liability is most likely to carry a large or small genetic component. This utility of the developed polygenic score is increased among subjects aged 60–69, which is a desirable target group for identification and preventative intervention of Alzheimer’s disease. Identifying these individuals would benefit study recruitment into clinical trials and could facilitate a better understanding of how gene-gene and gene-environment interactions increase risk for Alzheimer’s disease.

Glossary

Abbreviations

AUC

area under the receiver operating characteristic curve

GERAD

Genetic and Environmental Risk for Alzheimer’s disease

GWA

genome-wide association

IGAP

International Genomics of Alzheimer’s Project

N/PPV

negative/positive predictive value

SNP

single nucleotide polymorphism

Appendix I

Authors who contributed to the generation of original study data for GERAD, ADGC, CHARGE and EADI, but not to the current publication are included herein. Author affiliations can be found in the Supplementary material.

GERAD Consortium

Richard Abraham¹, Paul Hollingworth¹, Amy Gerrish¹, Jade Chapman¹, Giancarlo Russo¹, Marian Hamshere¹, Jaspreet Singh Pahwa¹, Kimberley Dowzell¹, Amy Williams¹, Nicola Jones¹, Charlene Thomas¹, Alexandra Stretton¹, Angharad Morgan¹, Sarah Taylor¹, Simon Lovestone², Petroula Proitsi², Michelle K. Lupton², David C. Rubinsztein⁴, Brian Lawlor⁵, Aoibhinn Lynch⁵, Kristelle Brown⁶, David Craig⁷, Bernadette McGuinness⁷, Stephen Todd⁷, Janet Johnston⁷, David Mann⁸, A. David Smith⁹, Seth Love¹⁰, Patrick G. Kehoe¹⁰, Nick Fox¹¹, Martin Rossor¹¹, John Collinge¹², Frank Jessen¹³, Reiner Heun¹³, Britta Schürmann¹³, Tim Becker¹⁴, Christine Herold¹⁴, André Lacour¹⁴, Dmitriy Drichel¹⁴, Hendrik van den Bussche¹⁵, Isabella Heuser¹⁶, Johannes Kornhuber¹⁷, Jens Wiltfang¹⁸, Martin Dichgans^19,20, Lutz Frölich²¹, Harald Hampel^22,23, Michael Hüll²⁴, Dan Rujescu²⁵, John S. K. Kauwe²⁷, Petra Nowotny²⁶, John C. Morris²⁵, Kevin Mayo²⁵, Gill Livingston³⁰, Nicholas J. Bass³⁰, Hugh Gurling³⁰, Andrew McQuillin³¹, Rhian Gwilliam³², Panagiotis Deloukas³², Ammar Al-Chalabi³³, Christopher E. Shaw³³, Andrew B. Singleton³⁴, Rita Guerreiro^34,35, Thomas W. Mühleisen^36,37, Markus M. Nöthen^36,37, Susanne Moebus³⁸, Karl-Heinz Jöckel³⁸, Norman Klopp³⁹, H-Erich Wichmann^39,40,41, Minerva M. Carrasquillo⁴², V. Shane Pankratz⁴³, Steven G. Younkin⁴², Michael ODonovan¹, Michael J. Owen¹.

ADGC Consortium

Regina M. Carney¹, Deborah C. Mash², Marilyn S. Albert³, Roger L. Albin^4,5, Liana G. Apostolova⁶, Steven E. Arnold⁸, Clinton T. Baldwin⁸, Michael M. Barmada⁹, Lisa L. Barnes^10,11, Thomas G. Beach¹², Eileen H. Bigio¹³, Thomas D. Bird¹⁴, Bradley F. Boeve¹⁵, James D. Bowen¹⁶, Adam Boxer¹⁷, James R. Burk¹⁸, Nigel J. Cairns¹⁹, Chuanhai Cao²⁰, Chris S. Carlson²¹, Steven L. Carroll²², Lori B. Chibnik^23,24, Helena C. Chui²⁵, David G. Clark²⁶, Jason Corneveaux²⁷, David G. Cribbs²⁸, Charles DeCarli²⁹, Steven T. DeKosky³⁰, F. Yesim Demirci⁹, Malcolm Dick³¹, Dennis W. Dickson³², Ranjan Duara³³, Nilufer Ertekin-Taner^32,34, Kenneth B. Fallon²², Martin R. Farlow³⁵, Steven Ferris³⁶, Matthew P. Frosch³⁷, Douglas R. Galasko³⁸, Mary Ganguli³⁹, Marla Gearing^40,41, Daniel H. Geschwind⁴², Bernardino Ghetti⁴³, Sid Gilman⁴, Jonathan D. Glass⁴⁴, Robert C. Green⁴⁵, John H. Growdon⁴⁶, Ronald L. Hamilton⁴⁷, Chiao-Feng Lin⁴⁸, Lindy E. Harrell²⁶, Elizabeth Head⁴⁹, Lawrence S. Honig⁵⁰, Christine M. Hulette⁵¹, Bradley T. Hyman⁴⁶, Gail P. Jarvik^52,53, Gregory A. Jicha⁵⁴, Lee-Way Jin⁵⁵, Anna Karydas¹⁷, John S. K. Kauwe⁵⁶, Jeffrey A. Kaye^57,58, Ronald Kim⁵⁹, Edward H. Koo³⁸, Neil W. Kowall^60,61, Joel H. Kramer⁶², Patricia Kramer^57,63, Frank M. LaFerla⁶⁴, James J. Lah⁴⁴, James B. Leverenz⁶⁵, Allan I. Levey⁴⁴, Ge Li⁶⁶, Andrew P. Lieberman⁶⁷, Constantine G. Lyketsos⁶⁸, Wendy J. Mack⁶⁹, Daniel C. Marson²⁶, Frank Martiniuk⁷⁰, Eliezer Masliah^38,71, Wayne C. McCormick⁷², Susan M. McCurry⁷³, Andrew N. McDavid²¹, Ann C. McKee^60,61, Marsel Mesulam⁷⁴, Bruce L. Miller¹⁷, Carol A. Miller⁷⁵, Brian Kunkle⁷⁶, Joshua W. Miller⁵⁵, John C. Morris^19,77, Jill R. Murrell^43,78, John M. Olichney²⁹, Vernon S. Pankratz⁸⁰, Joseph E. Parisi^81,82, Elaine Peskind⁶⁶, Tricia A. Thornton-Wells^83,15, Ronald C. Petersen15⁸³, Aimee Pierce²⁸, Wayne W. Poon³¹, Huntington Potter⁸⁴, Joseph F. Quinn⁵⁷, Ashok Raj⁸⁴, Murray Raskind⁶⁶, Eric M. Reiman^27,85,86, Barry Reisberg^36,87, John M. Ringman⁶, Erik D. Roberson^26,48, Howard J. Rosen¹⁷, Roger N. Rosenberg⁸⁸, Mary Sano⁸⁹, Andrew J. Saykin^43,90, Julie A. Schneider^10,91, Lon S. Schneider^6,92, William W. Seeley¹⁷, Amanda G. Smith⁸⁴, Joshua A. Sonnen⁶⁵, Salvatore Spina⁴³, Robert A. Stern⁶⁰, Rudolph E. Tanzi⁴⁶, John Q. Trojanowski⁹³, Juan C. Troncoso⁹⁴, Vivianna M. Van Deerlin⁹³, Linda J. Van Eldik⁹⁵, Harry V. Vinters^6,96, Jean Paul Vonsattel⁹⁷, Sandra Weintraub⁷⁴, Robert Green⁹⁸, Kathleen A. Welsh-Bohmer^18,99, Jennifer Williamson⁵⁰, Randall L. Woltjer¹⁰⁰, Chang-En Yu⁷², Robert Barber¹⁰¹, Adam C. Naj^102,103, Gyungah Jun^104,105,106, Gary W. Beecham^1,107, Badri N. Vardarajan¹⁰⁴, Otto Valladares⁴⁸, Christiane Reitz^108,109, Joseph D. Buxbaum^110,111,112, Clinton Baldwin¹⁰⁴, Najaf Amin¹¹³, Philip L. De Jager^114,115, Denis Evans¹¹⁶, Matthew J. Huentelman¹¹⁷, M. Ilyas Kamboh^118,119, Amanda J. Myers¹²⁰, Ekaterina Rogaeva¹²¹, Peter St George-Hyslop^121,122, Lei Yu¹²³, John R. Gilbert^1,107, Hakon Hakonarson¹²⁴, Kara L. Hamilton-Nelson¹, Kelley M. Faber¹²⁵, Laura B. Cantwell⁴⁸, Deborah Blacker^126,127, David A. Bennett^123,128, Thomas J. Montine¹²⁹, Tatiana M. Foroud¹²⁵, Walter A. Kukull¹³⁰, Kathryn L. Lunetta¹⁰⁶, John S. K. Kauwe¹³¹, Eric Boerwinkle^132,133, Eden R. Martin^1,107, Li-San Wang⁴⁸.

CHARGE Consortium

Rhoda Au¹, Philip A. Wolf¹, Alexa Beiser², Stephanie Debette^1,3, Qiong Yang², Galit Weinstein¹, Andrew D. Johnson⁴, Jing Wang², Andre G. Uiterlinden^5,6,7, Fernando Rivadeneira⁵, Peter J. Koudstaal⁸, William T. Longstreth Jr^9,10,11, James T. Becker¹², Lewis H. Kuller¹³, Thomas Lumley¹⁴, Kenneth Rice¹⁵, Melissa Garcia¹⁶, Thor Aspelund¹⁷, Josef J. M. Marksteiner¹⁸, Peter Dal-Bianco¹⁹, Anna Maria Töglhofer²⁰, Paul Freudenberger²⁰, Gerhard Ransmayr²¹, Thomas Benke²², Anna M. Toeglhofer²⁰, Jan Bressler²³, Monique M. B. Breteler²⁴, Myriam Fornage²⁵, Reinhold Schmidt²⁶, Reposo Ramírez-Lorca²⁷, Antonio González-Perez²⁷, Carla A. Ibrahim-Verbaas²⁸, Anita L. DeStefano²⁹, Tamara B. Harris³⁰, Albert V. Smith^31,32, M. Arfan Ikram^33,34, Helena Schmidt²⁰, Seung-Hoan Choi²⁹, Annette L. Fitzpatrick^30,35, Paul K. Crane³⁶, Vilmundur Gudnason^31,32, Oscar L. Lopez³⁷, Francisco J. Morón²⁷, Gudny Eiriksdottir³², Eric B. Larson^36,38, Debby W. Tsuang³⁹, Duane Beekly⁴⁰, Palmi V. Jonsson^31,41, Thomas H. Mosley Jr⁴², Renee FAG de Bruijn⁴³, Jerome I. Rotter⁴⁴, Michael A. Nalls⁴⁵, Albert Hofman^33,34, Bruce M. Psaty^30,46.

EADI Consortium Authors

Benjamin Grenier-Boley^1,2,3, Florence Pasquier^2,4, Vincent Deramecourt^2,4, Nathalie Fiévet^1,3, Diana Zelenika⁵, Yoichiro Kamatani⁶, Marie-Thérèse Bihoreau⁵, Mark Lathrop^5,6,7, Olivier Hanon⁸, Dominique Campion⁹, Claudine Berr¹⁰, Luc Letenneur¹¹, Kristel Sleegers^12,13, Lina Keller¹⁴, Pascale Barberger-Gateau¹¹, Carole Dufouil¹¹, David Wallon⁹, Jordi Clarimon^15,16, Alberti Lleo^15,16, Paola Bossù¹⁷, Gianfranco Spalletta¹⁷, Sandro Sorbi^18,19, Florentino Sanchez Garcia²⁰, Maria Candida Deniz Naranjo²⁰, Paolo Bosco²¹, Daniela Galimberti²², Michelangelo Mancuso²³, Patrizia Mecocci²⁴, Maria Del Zompo²⁵, Alberto Pilotto²⁶, Maria Bullido^27,28,29, Francesco Panza³⁰, Paolo Caffarra^31,32, Benedetta Nacmias^18,19, Lars Lannfelt³³, Martin Ingelsson³³, Victoria Alvarez³⁴, Cristina Razquin³⁵, Pau Pastor^35,36, Ignacio Mateo³⁷, Eliecer Coto³⁴, Onofre Combarros³⁷, Hilkka Soininen^38,39, Laura Fratiglioni^14,40, Karolien Bettens^12,13, Alexis Brice^41,42, Didier Hannequin⁹, Karen Ritchie^10,43, Mikko Hiltunen^38,39, Jean-François Dartigues^11,44, Christophe Tzourio⁴⁵, Caroline Graff^40,46, Annick Alpérovitch⁴⁷, Anne Boland⁵, Marc Delépine⁵, Bruno Dubois⁴⁸, Emmanuelle Duron⁴⁹, Jacques Epelbaum⁵⁰, Caroline Van Cauwenberghe^12,51, Sebastiaan Engelborghs^51,52, Rik Vandenberghe^53,54, Peter P. De Deyn^51,52, Raffaele Ferri⁵⁵, Carmelo Romano⁵⁵, Carlo Caltagirone⁵⁶, Maria Donata Orfei⁵⁶, Antonio Ciaramella⁵⁶, Elio Scarpini^57,58, Chiara Fenoglio^57,58, Gabriele Siciliano²³, Ubaldo Bonuccelli²³, Silvia Bagnoli^19,59, Laura Bracco^19,59, Valentina Bessi^19,59, Roberta Cecchetti²⁴, Patrizia Bastiani²⁴, Alessio Squassina⁶⁰, Davide Seripa⁶¹, Ana Frank-García^28,29,62, Isabel Sastre,^28,29,63, Rafael Blesa^16,64, Daniel Alcolea^16,64, Marc Suárez-Calvet^16,64, Pascual Sánchez-Juan³⁷, Carmen Muñoz Fernandez⁶⁵, Yolanda Aladro Benito⁶⁵, Caroline Graff^68,67, Laura Fratiglioni⁶⁸, Håkan Thonberg^66,67, Charlotte Forsell⁶⁷, Lena Lilius⁶⁷, Anne Kinhult-Ståhlbom^66,67, Vilmantas Giedraitis³³, Lena Kilander³³, Rose Marie Brundin³³, Letizia Concari^69,70, Seppo Helisalmi^39,71, Anne Maria Koivisto^39,71, Annakaisa Haapasalo^39,71, Vincenzo Solfrizzi⁷², Vincenza Frisardi⁷³, Jurg Ott⁷⁴, Christine Van Broeckhoven^12,13.

Funding

Cardiff University was supported by the Medical Research Council (MRC) grant (MR/K013041/1), the EU Joint Programme – Neurodegenerative Disease Research (JPND) grant (MR/L501517/1), the Alzheimer’s Research UK (ARUK) grant (ARUK-PG2014-1), and the Health and Care Research Wales funded Centre for Ageing and Dementia Research (CADR). C.B. and E.M. were supported by the Medical Research Council (MRC) via the UK Dementia’s Platform (DPUK, reference MR/L023784/1). S.M. was supported by the National Institute of Health Research's Biomedical Research Unit - Dementia at Queen Square.

Supplementary material

Supplementary material is available at Brain online.