The discordant method: a novel approach for differential correlation

Abstract

Motivation: Current differential correlation methods are designed to determine molecular feature pairs that have the largest magnitude of difference between correlation coefficients. These methods do not easily capture molecular feature pairs that experience no correlation in one group but correlation in another, which may reflect certain types of biological interactions. We have developed a tool, the Discordant method, which categorizes the correlation types for each group to make this possible.

Results: We compare the Discordant method to existing approaches using simulations and two biological datasets with different types of –omics data. In contrast to other methods, Discordant identifies phenotype-related features at a similar or higher rate while maintaining reasonable computational tractability and usability.

Availability and implementation: R code and sample data are available at https://github.com/siskac/discordant.

Contact: katerina.kechris@ucdenver.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Many strategies exist for analyzing high-throughput —omics data in order to explore the complexity that differentiates biological groups. The most common analysis is differential expression, which is defined by molecular features that experience large changes in expression or abundance between groups (Malone and Oliver, 2011; Oshlack et al., 2010). In addition to differential variance (i.e. groups may not have different mean levels but dissimilar variance) (Ho et al., 2008), another analysis that may be relevant is differential correlation or coexpression (DC), which is the change of association of molecular feature pairs between groups (e.g. healthy and disease). These differential associations may indicate molecular interactions that characterize or reflect biological or disease state.

Examples of DC can be found in both low- and high-throughput studies. For instance, one study using chromatin immunoprecipitation determined the effect of mutant p53 on wild-type p53 in the cell. Mutated p53 reduces the binding of wild-type p53 to the p53 response element of p21, MDM2 and PIG3, causing DC of p53 and these targets between samples with wild-type p53 and mutant p53 (Willis et al., 2004). Another study using ELISA and a lymphoproliferation assay determined that patients with treated paracoccidioidomycosis had correlation between interleukins and tumor necrosis factor, but there was no correlation in untreated patients (Silva et al., 1995).

Larger-scale studies have identified DC to study how transcription factors can influence the expression of a transcript. In a myeloma study, transcription factor coexpression with genes in pathways was found to be different between the two major subtypes of myeloma (Wang et al., 2014). Another transcriptomic study that examined expression differences between lean and obese siblings found that NEGR1 is a central hub in obesity-related DC networks (Walley et al., 2012).

DC has been investigated with a myriad of approaches. These methods have been reviewed recently (Kayano et al., 2014). The classical method by Fisher transforms the correlation coefficients into z scores and then determines the statistical dissimilarity between the two groups (Fisher, 1915). Software implementing this method is now available (Fukushima, 2013). Wang et al. (2014) makes similar assumptions and uses a Hotteling test.

Another popular method uses linear models and determines significant interaction terms between groups (Cho et al., 2009; Ruggeri and Eng, 2015; Jauhiainen et al., 2012). Linear models have been shown to be effective, however, there are deficiencies when there is large differences in variability between groups, which may be relevant when examining —omics data from different types of platforms and/or data from humans or non-experimental model systems. It has been shown that large variability results in incorrect slope estimates (Cornbleet and Gochman, 1979; Ludbrook, 2010). Furthermore, slope estimates can be different depending on what feature is considered the dependent or independent variable in the linear model.

Alternative methods use Bayesian models (Bradley et al., 2009; Dawson and Kendziorski, 2012). For example, Bradley et al. uses pathway information as a prior, which can be beneficial for identification, but pathway knowledge can also be incomplete. Very few pathway databases combine interactions between multiple types of molecular features (Bader, 2006) except for KEGG (Kanehisa, 2000). Dawson et al. implemented EBcoexpress, which uses Empirical Bayes estimation and returns a posterior probability of differential coexpression for each pair of molecular features.

Another statistical method to determine DC is the Expected Conditional F-statistic, which modifies the F-statistic from analysis of variance for multiple groups (Fang et al., 2010; Ho et al., 2008; Lai et al., 2004). The F-statistic was adapted to determine molecular feature pairs that share the least variance instead of single features that share dissimilar mean across groups.

Other methods use partial correlations, hierarchical clustering, principal component analysis and other models to determine DC modules rather than individual pairs (Kayano et al., 2013; Kostka and Spang, 2004; Tesson et al., 2010; Watson, 2006). Although these types of analyses are informative, they only describe the average behavior of molecular features instead of specific pairs.

Missing from all of these methods is categorizing the different types of DC scenarios, commonly referred to as ‘binning’, where each pair is categorized into all possible paired correlation scenarios. The following are different examples: (i) Group 1: +, Group 2: −, (ii) Group 1: +, Group 2: 0, (iii) Group 1: +, Group 2: +. Example 1 is an extreme version of DC, where the correlation is in opposite directions between groups. Example 2 also illustrates DC, except that in Group 2 the correlation is zero. Finally, Example 3 is where there is no DC because the correlation is in the same direction for both groups. Most methods are well suited to detect molecular feature pairs with a pattern similar to Example 1 (i.e. cross), but are less likely to identify DC molecular feature pairs with a pattern similar to Example 2 (i.e. disrupted). Molecular feature pairs in Example 2 could be biologically relevant since they indicate an interaction in one group that is disrupted in the other group.

In this work, we develop a method that uses binning to not only improve the identification of molecular feature pairs that exhibit more significant cross DC as in Example 1, but also disrupted DC as in Example 2. Our method is based on a mixture model originally developed to assess whether microarray experiments could be combined (Lai et al., 2007, 2014). We have altered the application of this method to determine DC of molecular feature pairs between groups and have named it the Discordant method. Using the EM algorithm (Dempster et al., 1977), the Discordant method estimates a posterior probability for each possible paired correlation scenario to achieve binning. Binning increases power since it identifies all possible DC pairs rather than the most extreme. Other advantages of the Discordant method are computational tractability and ease in choosing initial parameters.

We compare our method to Fisher’s method, linear interaction models and EBcoexpress (Dawson and Kendziorski, 2012; Fisher, 1915) with simulations to assess specificity and sensitivity for all three methods. We also use the Cancer Genome Atlas (TCGA) glioblastoma miRNA and transcriptomic data (McLendon et al., 2008) and Chronic Obstructive Pulmonary Disease (COPD) metabolomic and transcriptomic data (Bahr et al., 2013) as a biological validation of the methods.

2 Methods

2.1 Fisher’s transformation

Fisher’s transformation is used (Fisher, 1915) to convert Pearson’s sample correlation coefficient r into z score with the following equation:

$$z=\frac{1}{2}ln\frac{(1+r)}{(1-r)}$$ (1)

The resulting z score has an approximately normal distribution (Hotelling, 1953). Fisher’s transformation is applied to all possible feature pairs for each biological group, which may be subsets of disease, biological or treatment samples. For example, in the biological applications of the methods in this study, the groups are defined by the presence or absence of disease.

2.2 Discordant

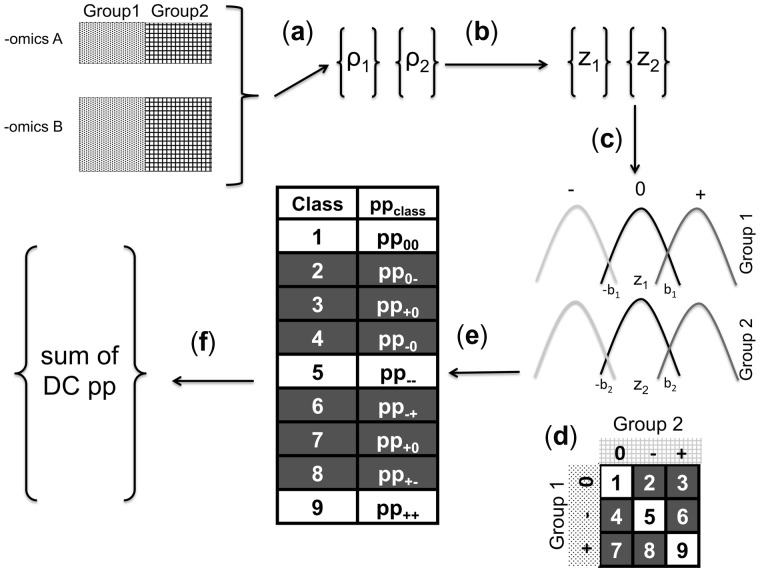
The model is adapted from Lais et al. which was developed to test for concordance between microarrays (Lai et al., 2007, 2014). Our method is based on a mixture model with three classes: 0, − and + as seen in Figure 1. Given a class i, the density for one feature pair, with Fisher’s transformed correlations z¹ and z^2, for group 1 and group 2, respectively, is:

$$f\left[z^{\left(1\right)},z^{\left(2\right)}\right]={\displaystyle \sum }_{i=0}^2{\displaystyle \sum }_{j=0}^2{\left({\pi }_{ij}{\varphi }_{{\mu }_i,{\sigma }_i^2}\left[z^1\right]{\varphi }_{{\eta }_j,{\tau }_j^2}[z^2]\right)}^{1(w_{ij}=1)}$$ (2)

where ${\varphi }_{\mu ,{\sigma }^2}$ is the normal probability distribution function (pdf) for group 1 with mean $\mu$ and variance ${\sigma }^2$, ${\varphi }_{\eta ,{\tau }^2}$ is the normal pdf for group 2 with mean $\eta$ and variance ${\tau }^2$ and ${\pi }_{ij}$ is the frequency that the feature pair is in class i for group 1 and class j for group 2. The three classes (represented by i and j) are 0 (i or j = 0),−(i or j = 1), and + (i or j = 2). Class 0 correlations are distributed around 0, class − correlations are distributed around an unknown negative mean and class + correlations are distributed around an unknown positive mean. The three classes are combined into the 3 by 3 class matrix in Figure 1d to explain all correlation scenarios between the groups (Supplementary Fig. S1) represented by w_ij. The DC scenarios are those on the off-diagonal of the class matrix (i.e. when the correlations are different between the groups). In the mixture model, the unobserved variable is the class membership for each feature pair.

Fig. 1.

Discordant algorithm pipeline. (a) Pearson’s correlation coefficients for all A and B pairs. (b) Fisher’s transformation. (c) Mixture model based on z scores. (d) Class matrix describing between group relationships. (e) EM Algorithm to estimate posterior probability of each class for each pair. (f) Features of —omics A and B that have high pp of DC

In the E-step, posterior probabilities are determined for each class and group:

$$q_{ij}^r\left(k\right)=p\left(w_{ij}\left(k\right)=1|{\theta }^{r-1},\left[z^1\right],\left[z^2\right]\right)$$ (3)

where k is the molecular feature pair, r the r^th iteration, z¹ and z² are the z scores for groups 1 and 2, θ is the set of parameters $[{\mu }_1,{\mu }_2,{\mu }_3,{\sigma }_1,{\sigma }_2,{\sigma }_3,{\eta }_1,{\eta }_2,{\eta }_3,{\tau }_1,{\tau }_2,{\tau }_3]$, and $q_{ij}^r(k)$ is the updated posterior probability of molecular feature pair k being in class w_ij in iteration r. The posterior probabilities from the E-step are used for the M-step to update the parameters (Supplementary Materials). Once these are re-estimated, the likelihood is determined using the density function in Equation (2):

$$L={\displaystyle \prod }_{k=1}^{K}f[z^1(k),z^2(k)]$$ (4)

After convergence of the EM algorithm (squared difference in parameters <0.01), we report the summed differential coexpressed posterior probabilities (i.e. off-diagonal in Fig. 1d):

$$p(D{C}_k)={\displaystyle \sum }_{i\ne j}{q}_{ij}^r\left(k\right)$$ (5)

To compare with the other methods described below, we subtract the posterior probabilities from one.

2.3 Comparison of discordant to other methods

Leading methods, Fisher, linear interaction models and EBcoexpress, were chosen to compare to the Discordant method. These methods have a similar output to Discordant, which is a P-value or posterior probability of a molecular feature pair being DC. They were compared based on q-values and ranks from simulations and biological validations, which are further explained below.

2.3.1 Fisher

The dissimilarity between Fisher-transformed z scores is measured with the following statistic, which has an approximately normal distribution (Fisher, 1915).

$$z^{*}=\frac{z_2-z_1}{\sqrt{\frac{1}{{(n_2-1)}^2}-\frac{1}{{(n_1-1)}^2}}}$$ (6)

We report P-values from testing H₀: z₁ = z₂ versus H₁: z₁ ≠ z₂.

2.3.2 Linear interaction model

Linear models were fit by regression of the feature y on main effects of feature x, disease group and the interaction between x and disease group. The follow linear model was used:

$$E\left[y\right]=\alpha +x{\beta }_1+g{\beta }_2+xg{\beta }_3$$ (7)

where β₁ is the linear parameter for feature x, β₂ is the group effect and β₃ is the interaction term. Using lm() in R, significance of x and y interactions between groups was evaluated by determining if the interaction β₃ had a significant contribution to the model. This term indicates group specific slopes and would reflect DC.

Linear interaction models were only applied to Glioblastoma multiforme (GBM) data because it is assumed that the independent and dependent variables are respectively miRNAs and transcripts. Because it is unknown what should be the dependent and independent variable for metabolites and transcripts, linear interaction models were not applied to the COPD data.

2.3.3 EBcoexpress

EBcoexpress is a bivariate mixture model for two groups to determine molecular feature pairs that are DC (Dawson and Kendziorski, 2012). EBcoexpress is based on a hierarchical model that uses Empirical Bayes to estimate the posterior probabilities. Further explanation on how initial parameters were chosen for EBcoexpress is in Supplementary Materials. To compare EBcoexpress to the Discordant and Fisher's methods, the posterior probability for equivalent coexpression was examined.

2.4 Validations

2.4.1 Simulations

Bivariate normal n by m matrices with n features and m samples were first simulated using the function mvrnorm from R package MASS. The means were set to 0 and the covariance matrix was a diagonal matrix of 1. We assumed independence for all samples in groups and across all features. The features were separated into two different sections, where these sections were treated as different types of —omics data (Supplementary Fig. S2a). The Pearson’s correlation coefficients were calculated (Supplementary Fig. S2b) and then they were swapped to create pairs that simulate the nine different situations of Figure 1d within the data (Supplementary Fig. S2c). This resulted in known DC pairs, so we could observe how categorizing association types in Discordant affected power compared with the other methods.

All methods were run on the simulated data and compared using a Receiver Operating Characteristic (ROC) curve and sensitivity/specificity by rank of P-values/1—posterior probabilities. Simulations were run 100 times and results were averaged over the runs. The simulations were altered to take into account how the methods were affected by feature size, sample size, proportion of forced DC and correlation method as summarized in Supplementary Table S1. We also ran the simulations with a positive definite matrix for the covariance matrix to account for relationships between features and found no qualitative differences in the simulation results (data not shown).

2.4.2 Glioblastoma multiforme miRNA and transcriptomic data

From The Cancer Genome Atlas (TCGA, http://cancergenome.nih.gov/) we accessed normalized GBM miRNA and mRNA expression data that had matched subjects (McLendon et al., 2008). This dataset was selected because it had the largest sample size of organ-specific control samples between the two arrays on TCGA. The miRNA data was generated on an Agilent miRNA array and was normalized using quantile normalization and available at TCGA. The mRNA data was generated on custom Agilent 244 K array and normalized using lowess normalization. In the datasets, there are 470 miRNA and 90 797 mRNA. Grubbs’ outlier test (Grubbs, 1969) was used to eliminate any molecular features with outliers that could skew correlation, which reduced the feature size to 331 miRNA and 72 656 mRNA (Grubbs’ P-value > 0.05). The number of matched samples between the—omics datasets are 10 control samples and 21 tumor samples.

Cancer-related miRNAs were accessed from multiMiR and miRcancer (Ru et al., 2014; Xie et al., 2013). We collected miRNAs on four cancers, including GBM as well as breast cancer, prostate cancer and melanoma as negative controls. There were 47 total cancer-related miRNA for GBM, but only four were unique to GBM and not occurring in any of the other cancers. After running each method, the top rank, and respective P-value/posterior probability and q-value of unique GBM-related miRNA-transcript pair was reported.

2.4.3 COPD transcriptomic and metabolomic data

Through COPDGene (http://www.copdgene.org/), a nation-wide genetic epidemiologic study, we were able to acquire metabolomic and transcriptomic data from COPD patients. The peripheral blood mononuclear cell (PBMC) transcriptomic data was generated on the Affymetrix HGU133 Plus 2.0 array and normalized by measuring the geometric mean (Bahr et al., 2013). Metabolomic data from plasma was processed and generated using LC/MS Agilent software and tools and pre-processed and filtered using MSPrep (Bowler et al., 2015; Hughes et al., 2014). Both datasets were filtered based on Grubbs’ outlier test, leaving 38 852 transcripts and 1640 metabolites (Grubbs’ P-value > 0.05). COPDGene subjects were separated by spirometry, which indicates the severity of COPD in a patient. The control group contained subjects with normal spirometry (FEV1/FVC > 0.7 and FEV1 percent predicted > 80% after bronchodilator) and disease group contained subjects with abnormal spirometry (FEV1/FVC < 0.7 and FEV1 percent predicted < 50% after bronchodilator). The final sample size for each group was control: 39 and COPD: 39.

Previous studies by COPDGene have implicated sphingolipids and their related pathways in COPD (Bowler et al., 2015). Sphingolipid-related metabolites were determined using ID Browser in Mass Profiler Professional (MPP) software (Agilent). Sphingolipid-related transcripts were determined using the Gene Ontology to collect transcripts with a GO term related to sphingolipids, and the probes acquired from Ensembl BioMart. The final number of sphingolipid-related metabolites and transcripts is 37 and 188, respectively. We examined the top ranks and respective P-values/posterior probability and q-values of the sphingolipid-related feature pairs.

3 Results

We applied DC analysis to simulations and biological data to identify the ability for each method to determine true positives defined by the simulations and identify pairs that have been previously validated in the respective phenotype. P-values and posterior probabilities are not directly comparable, therefore, molecular feature pairs were ranked by statistical significance for comparison by the respective value depending on the method and ranked lists (Käll et al., 2008), i.e. in order of increasing P-values and decreasing posterior probabilities.

3.1 Simulations

The basic parameters for the simulations were sample size 20 for both groups, 0.2 of feature pairs differentially correlated, 1000 pairs and correlation measured with Pearson’s correlation coefficient. These parameters were adjusted to determine if any would alter the methods’ power (Supplementary Table S1).

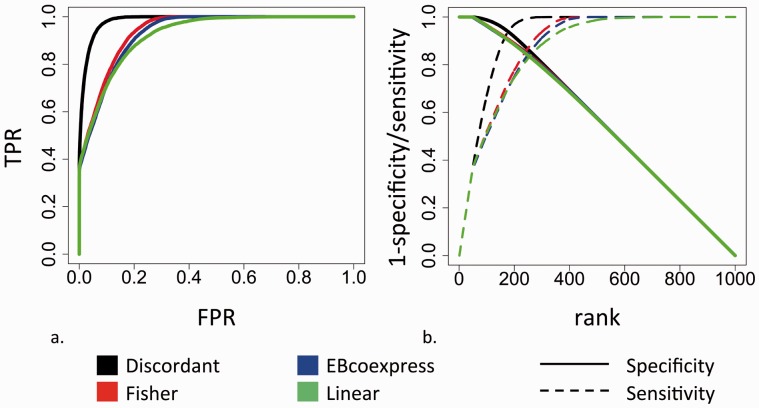
Statistical performance of simulations was evaluated by observing the prediction of known true positives and true negatives. In the ROC curve Discordant has more area under the curve (AUC) than any of the methods, and Fishers, linear interaction models and EBcoexpress have similar AUC (Fig. 2a). Sensitivity and specificity were plotted to determine why the Discordant method has a better ROC curve (Fig. 2b). Although specificity is the same for all three methods, Discordant method performs better with respect to sensitivity demonstrating that the Discordant method identifies more true positives than the other methods.

Fig. 2.

Simulation analysis. (a) ROC curve. Discordant AUC = 0.985, EBcoexpress AUC = 0.931, Fisher AUC = 0.940, Linear AUC = 0.930. (b) Senstivity/1-Specifcity plot

The ROC curves and plots of sensitivity and specificity for adjusted parameters are in Supplementary Figures S3 and S4. From the plots, change in sample size, the type of correlation used and the number of forced DC pairs and feature pairs in the simulation did not affect power except for disparate sample size in linear models.

To explore the predictions of paired correlation scenarios in the class matrix (Fig. 1d), the distribution of the ranks for each class was plotted in each method. As an example, for class 3, group 1 has a positive correlation and in group 2 has a correlation close to 0 (Supplementary Fig. S5a), while in class 6, group 1 has a positive correlation and group 2 has a negative correlation (Supplementary Fig. S5b). In Supplementary Figure S5a the distribution of ranks for Discordant is much smaller than Fisher or EBcoexpress, but in Supplementary Figure S5b the distribution of ranks is similar across all three methods. This affirms that binning in Discordant achieves greater power for identifying differentially correlated pairs where the correlation in one group is absent, whereas all methods identify all the most extreme differential correlated pairs, i.e. negative in one group and positive in the other group.

3.2 GBM miRNA and transcript pairs

3.2.1 Validation

The top ranks, P-values and q-values of the four unique GBM-related miRNAs pairs in Discordant, EBcoexpress, Fisher, miRNA-independent and transcript-independent linear interaction models were examined (Supplementary Table S2). The mean and median of these ranks are found in Table 1. It was found that Discordant had a smaller mean and median rank than the other methods, indicating that overall Discordant identifies unique GBM-related miRNAs earlier than any other method. Furthermore, at q-value < 0.05 Discordant identified all four GBM-related miRNAs, whereas EBcoexpress, Fisher and linear interaction models identify 3, 1 and 1, respectively. The top unique GBM-related miRNA pair, hsa-miR-92b and Agilent probe A_32_P56375, is plotted in Supplementary Figure S7.

Table 1.

Summary of the top ranks of biologically-validated features

Data	Method	Mean	Median
GBM	Discordant	464.75	347.5
	EBcoexpress	815	607
	Fisher	781	801
	Linear (miRNA-independent)	1095	532.5
	Linear (transcript-independent)	2596.5	787.5
COPD	Discordant	5.08e5	2.14e5
	EBcoexpress	4.91e5	3.21e5
	Fisher	5.42e5	4.41e5

Boxes shaded grey to point out most significant results based on mean and median ranks.

The linear interaction models identify miRNAs at an earlier rank than Discordant but the results are inconsistent between the linear interaction models when the independent and dependent variables are swapped (Supplementary Table S2). This was further confirmed using a Wilcoxon Signed-rank test on the –log₁₀(P-values) between the two models (P-value < 0.05).

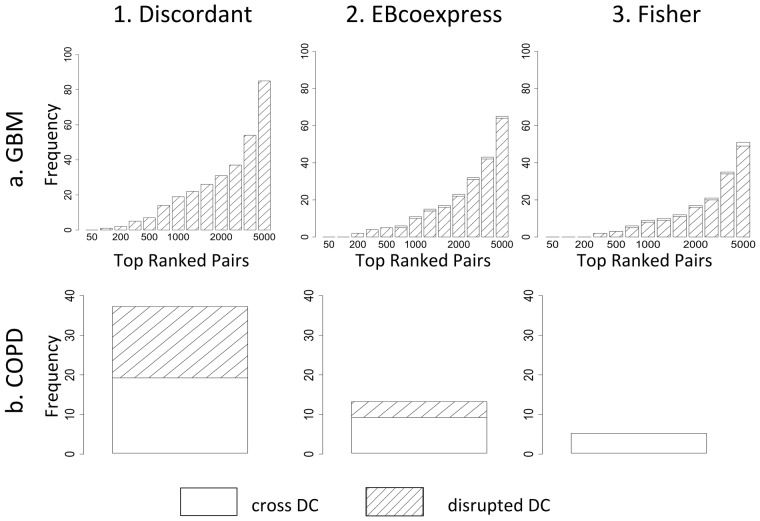
The frequency of GBM-related miRNAs and their associated classes were compared in Discordant and Fishers to determine the effect of binning on the analysis. It was found that the differentially correlated pairs with a GBM-related miRNA were more likely to be class 2 or 3, or disrupted DC, in Discordant (Fig. 3a.1), in contrast to Fishers and EBcoexpress where there were some pairs that were class 6 or 8, or cross DC (Fig. 3a.2 and 3a.3). Linear interaction terms had a similar pattern to Fisher and EBcoexpress (data not shown).

Fig. 3.

Effect of binning in methods. (a) Increasing frequency of classes in GBM. (b) Classes of sphingolipid-related metabolite and gene pairs in top ranked 100 000 pairs (Discordant q-value = 0.08, EBcoexpress q-value = 0.35, Fisher FDR = 1)

3.2.2 Known and novel targets

Pairs with Discordant posterior probability > 0.99 were used to investigate which features had the most connections, or hubs. The top four genes that were the biggest hubs with over 30 connections are: AGAP2, CRY2, GRIN1 and UPF3A (Supplementary Table S3). Most of these genes have functions that are central to the brain, where GBM occurs. AGAP2 is an Arf GAP that has anti-apoptotic effects of nerve growth factor (Inoue and Randazzo, 2007), CRY2 is a circadian rhythm gene that principally is localized in the brain, GRIN1 is a ligand-gated ion channel that facilitates signals through neurons (Wahlsten, 1999). UPF3A is found in the UPF complex that is implicated in pathways altered in cancer such as post-splicing, mRNA decay and nuclear export (Dreyfuss et al., 2002). None of these genes have been implicated in GBM.

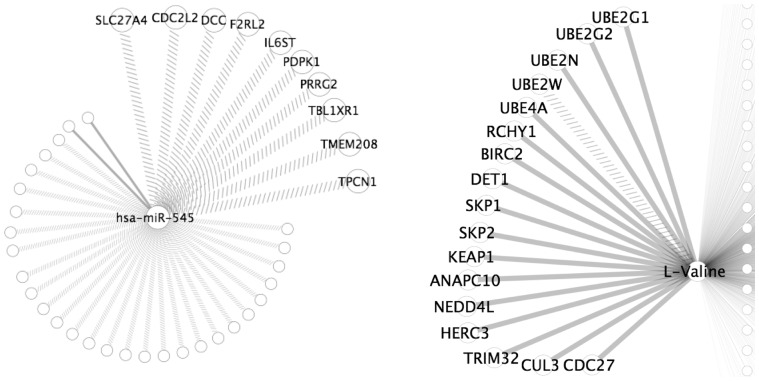
The miRNA hsa-miR-545 was the biggest hub connected to 39 genes, which is visualized in Figure 4a. hsa-miR-545 has not been found to be involved in GBM. Ten of the connected genes are annotated as being transmembrane proteins, and three of these are serine/threonine kinases (CDC2L2, PDPK1 and BMPR2). Tyrosine kinases have been found to be involved in GBM and are similar to serine/threonine kinases (Hamza and Gilbert, 2014).

Fig. 4.

Hubs found in COPD and GBM. Solid edges cross DC, dashed edges disrupted DC. (a) hsa-miR-545.and its connected genes (transmembrane genes shown). (b) Genes involved in ubiquitin mediated proteolysis connected to L-Valine in COPD, L-Valine connected to 1667 genes

3.3 COPD sphingolipid-related transcript and metabolite pairs

3.3.1 Validation

The sphingolipid pathway has been previously implicated in COPD (Bowler et al., 2015). A list of sphingolipid-related metabolites and genes was acquired, and the top rank and respective P-value/posterior probability and q-value when sphingolipid-related pairs identified by the three methods was evaluated (Supplementary Table S4). In Table 1, it was found that the median sphingolipid-related pair rank is smaller for Discordant compared with EBcoexpress and Fisher. EBcoexpress’ mean rank is smaller than Discordant, but only by 2e4 where the median rank between Discordant and EBcoexpress differs by 1e5. The expected mean and median rank of non-phenotype related features that were randomly chosen was 3.6e5 and 2.6e5, less than sphingolipid pairs. This may be reflecting the quality of the validation set (Section 4). At q-value < 0.10 Discordant identified 146 sphingolipid pairs, whereas EBcoexpress identified 1 and Fisher 0. Similarly to GBM, the findings here indicate that overall Discordant identifies sphingolipid-related feature pairs earlier than the other two methods. The top ranked sphingolipid-related metabolite-transcript pair determined by Discordant, a sphingenine and PSAPL1, is plotted in Supplementary Figure S8. Unlike GBM, the ranks are much later in the hundred thousands. This may indicate that although the sphingolipid pathway could be relevant to COPD, there may be other pathways that contribute to the complexity of the disease that may appear earlier on in the ranked list.

Because the sphingolipid pathway is not as significantly differentially coexpressed in COPD as the GBM-related miRNAs were in GBM, instead we examined the classes of sphingolipid-related metabolite and gene pairs that were in the top ranked 100 000 pairs. We found that Discordant identified relatively more disrupted classes than EBcoexpress or Fisher (Fig. 3b).

3.3.2 Known and novel targets

Molecular features that had the largest hubs were identified and listed in Supplementary Table S5. IGHG1, or immunoglobulin heavy constant gamma 1 is considered a true positive since immunity plays a central role in COPD (Rovina et al., 2013). Another gene identified as a hub is SARDH, or sarcosine dehydrogenase which has been implicated previously in COPD (Ubhi et al., 2012). The metabolite that has the largest hub has yet to be formally annotated; its chemical formula is C20 H33 N9 P2 S. The other metabolite that was a large hub is L-Valine, a metabolite involved in multiple biochemical pathways.

Genes connected to L-Valine were investigated using DAVID to determine if they were enriched in a biological pathway that is implicated in COPD (Huang et al., 2008, 2009). The ubiquitin mediated proteolysis KEGG pathway was enriched in the L-Valine differential coexpressed gene set with q-value = 0.001. In Figure 4b the genes involved in this pathway are highlighted from the rest of the other genes, which total to 17 out of 1667 in the gene set. In previous studies, the ubiquitin protease degradation pathway has been associated with COPD (Ottenheijm et al., 2006).

4 Discussion

We have presented the Discordant method for identifying DC pairs. Discordant categorizes the paired coexpression scenarios by ‘binning’, enabling it to determine more DC pairs than the other methods and improves power of detecting disrupted interactions. Binning not only improves performance for the Discordant method but also facilitates biological interpretation of results. As seen in Figure 3, Discordant identifies more disrupted DC pairs than EBcoexpress and Fisher, a trend also found in the simulations (Supplementary Fig. S5). Discordant also identifies more significant phenotype-related feature pairs in general for both GBM and COPD.

The GBM dataset produced more significant DC results for phenotype-related features than the COPD dataset. The GBM validation set is well curated because there are experimentally validated miRNAs involved in GBM, whereas for COPD there is less known about the molecular pathways. The sphingolipid-related genes and metabolites were determined by annotation for being in sphingolipid pathways, because there is limited experimental data for specific genes and metabolites. Despite the challenges of the COPD dataset, we did observe that sphingolipid metabolite-gene pairs were identified earlier in Discordant than EBcoexpress and Fisher (Table 1) and that there were more sphingolipid metabolite-gene pairs in the top 100 000 pairs in Discordant than EBcoexpress and Fisher (Fig. 3).

Both GBM and COPD have promising results of known and novel targets from Discordant. This confirms Discordant’s ability to identify phenotype-related biological processes and indicates the potential that Discordant can produce further testable hypotheses.

A similar method is to apply linear models with interaction terms. One of the benefits of linear models is that it assumes conditional normality instead of joint normality, meaning that the dependent variable can be non-normal. Linear models identified GBM-related miRNA pairs in earlier ranks than Discordant in the GBM data, but linear models can be difficult to use since it is unclear what should be the dependent and independent variable. We explored this by switching miRNA and transcript as the dependent and independent variable and we found it changed the results. We also found that the ranks of unique GBM-related miRNA pairs were different between the two analyses. It is highly suggested to only use linear models if it is known what is the independent and dependent variable, such as miRNA and transcript, respectively.

In terms of run-time, Fisher is notably faster than the rest of the methods, EBcoexpress is the slowest and Linear and Discordant only differ slightly (Supplementary Table S5). The Big O notation for Fisher is linear, O(n), where n is the number of feature pairs. For the linear interaction model and Discordant it is polynomial, O(n²) and O(2n + 3n²). The Big O notation for EBcoexpress is not as simple to identify since there are nested EM algorithms. EBcoexpress runs about 3-fold longer than Discordant in the GBM and COPD datasets and it also requires a grid approach to determine hyperparameters. Although Discordant does not run faster than Fisher and its run-time is comparable to linear interaction models, it still performs either equally or better with consistent results.

There are some limitations to Discordant. We assume independence between pairs, which is not true since features show up in multiple pairs. This assumption is critical to reducing computational complexity, and has been made by others (Dawson et al., 2012). Appropriate sample size is necessary for Discordant or any other DC method to work effectively to accurately estimate r between two features. Finally, the model assumes there are three Gaussian components in the mixture model. To explore the Gaussian assumption, we suggest that users apply the R package mixtools or lcmix, which can assess alternative or non-parametric densities (Benaglia et al., 2009, Dvorkin et al., 2013). Assuming the Gaussian case, we then recommend users to first run a mixture model fitting method (such as mclust) on each group to check that there is more than one mixture component (k > 1) by comparing the Bayesian Information Content (BIC) for different values of k. For the simulations and GBM, we found evidence of k > 1, while for COPD there was less evidence (data not shown) which is not unexpected considering the more challenging nature of that dataset.

Future directions for the Discordant method is to add more classes (−− and ++) that would contain correlation coefficients that were highly negative and highly positive to identify cases where there is a stronger linear association in one group versus the other. A challenge with adding these extra classes is that increasing the number of classes and parameters also increases complexity, which means longer run-time. We also want to investigate using discrete data, such as counts from RNA-Seq experiments.

Overall, when investigating DC pairs, Discordant performs well with respect to usability and accuracy. EBcoexpress, the most analogous method to Discordant, was not originally developed to investigate large —omics datasets, so it is possible that it could be optimized for that purpose. The Fisher method has short run-time but does not perform as well as similar methods. Linear interactions terms are effective, but should only be used when the dependent and independent variable are known when used to integrate different types of —omics data. The Discordant method fills in the drawbacks to all of these methods, in addition to providing a binning of results for easier interpretation.

Funding

Research reported in this publication was supported by National Library of Medicine and National Heart, Lung, and Blood Institute of the National Institutes of Health under award numbers T15LM009451 (C.S.) and P20HL113445 (K.K., R.B.). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Conflict of Interest: none declared.