A novel bi-level meta-analysis approach: applied to biological pathway analysis

Abstract

Motivation: The accumulation of high-throughput data in public repositories creates a pressing need for integrative analysis of multiple datasets from independent experiments. However, study heterogeneity, study bias, outliers and the lack of power of available methods present real challenge in integrating genomic data. One practical drawback of many P-value-based meta-analysis methods, including Fisher’s, Stouffer’s, minP and maxP, is that they are sensitive to outliers. Another drawback is that, because they perform just one statistical test for each individual experiment, they may not fully exploit the potentially large number of samples within each study.

Results: We propose a novel bi-level meta-analysis approach that employs the additive method and the Central Limit Theorem within each individual experiment and also across multiple experiments. We prove that the bi-level framework is robust against bias, less sensitive to outliers than other methods, and more sensitive to small changes in signal. For comparative analysis, we demonstrate that the intra-experiment analysis has more power than the equivalent statistical test performed on a single large experiment. For pathway analysis, we compare the proposed framework versus classical meta-analysis approaches (Fisher’s, Stouffer’s and the additive method) as well as against a dedicated pathway meta-analysis package (MetaPath), using 1252 samples from 21 datasets related to three human diseases, acute myeloid leukemia (9 datasets), type II diabetes (5 datasets) and Alzheimer’s disease (7 datasets). Our framework outperforms its competitors to correctly identify pathways relevant to the phenotypes. The framework is sufficiently general to be applied to any type of statistical meta-analysis.

Availability and implementation: The R scripts are available on demand from the authors.

Contact: sorin@wayne.edu

Supplementary Information: Supplementary data are available at Bioinformatics online.

1 Introduction

With rapid advances in high-throughput technologies, the generation of various kinds of high-throughput genomic data is prevalent in most biomedical research. Advanced techniques in sequencing (e.g. RNA-Seq, miRNA-Seq, DNA-Seq) and microarray assays (e.g. gene expression, methylation) have transformed biological research by enabling comprehensive monitoring of biological systems. Vast amounts of data of all types have accumulated in many public repositories, such as Gene Expression Omnibus (GEO) (Barrett et al., 2013), Array Express (Rustici et al., 2013) and The Cancer Genome Atlas (TCGA) (http://cancergenome.nih.gov/). Gene expression data, as measured by microarray and high-throughput sequencing, are particularly abundant in public repositories, such that many diseases are represented by half a dozen studies or more.

It would be tremendously beneficial if all datasets associated with a given condition could be analyzed together because of the increase in power expected to be associated with the much larger number of measurements in the combined dataset. However, batch effects, patient heterogeneity and disease complexity all complicate the integration of data from different sources. Indeed, for the same disease, different studies produce different sets of differentially expressed (DE) genes (Ein-Dor et al., 2005, 2006; Tan et al., 2003), and we will show that this problem is not resolved at the systems level, as pathway analysis results are often inconsistent as well.

Meta-analysis techniques, which are statistical methods for the quantitative analysis of independent but related studies (Normand, 1999), have already proven to be very useful for combining gene expression studies (Ramasamy et al., 2008; Tseng et al., 2012), and will be critical to decipher the biological knowledge contained in vast amounts of often conflicting studies, independent of the data type. In this manuscript, we describe a novel meta-analysis, and apply it to gene expression data in the context of pathway analysis.

Meta-analysis of gene expression data has primarily been used for DE gene detection (Tseng et al., 2012). Early meta-analyses simply performed the intersection or union of DE gene lists obtained from individual studies (Borovecki et al., 2005; Manoli et al., 2006), resulting in a single list which is either too conservative or too inclusive, respectively. Rhodes et al. (2002) were among the earliest to apply sophisticated meta-analysis methods for DE gene detection. In their work, P-values from multiple prostate cancer datasets were combined using Fisher’s method (Fisher, 1925). Since then, other P-value-based meta-analysis methods have been applied, such as Stouffer’s method (Stouffer et al., 1949), minP (Tippett, 1931), maxP (Wilkinson, 1951), weighted Fisher’s method (Li and Tseng, 2011), and latent variable approaches (Choi et al., 2007). A recent literature review (Tseng et al., 2012) revealed that P-value-based meta-analysis for gene detection accounts for approximately twice as many studies as any other type of meta-analysis, and is favored for its simplicity and extensibility. Therefore, we will focus on this type of P-value-based meta-analysis, investigate its limitations, and address them with our new approach.

Pathway analysis belongs to a family of statistical hypothesis testing (Goeman and Bühlmann, 2007) methods that have been developed to leverage molecular pathway knowledge bases such as the Kyoto Encyclopedia of Genes and Genomes (KEGG) (Kanehisa and Goto, 2000; Ogata et al., 1999) or Reactome (Croft et al., 2014). These knowledge bases contain graphs that describe how genes interact together to accomplish specific biological processes. Over-Representation Analysis (ORA) (Drǎghici et al., 2003), Gene Set Enrichment Analysis (GSEA) (Subramanian et al., 2005), Gene Set Analysis (GSA) (Efron and Tibshirani, 2007) and Impact Analysis (Drǎghici et al., 2007), are examples of approaches designed to identify the pathways that are relevant in a given condition. All of them take gene expression changes and a list of pathways as input, and produce a ranked list of pathways along with their P-values.

Recently, meta-analysis has also been used to combine multiple experiments at the pathway level (Kaever et al., 2014; Shen and Tseng, 2010). The work in (Kaever et al., 2014) uses classical methods, such as Fisher’s method and Stouffer’s method, to combine P-values of pathways from independent studies. The work in (Shen and Tseng, 2010), named MetaPath, is a dedicated approach that performs meta-analysis at both the gene and pathway level separately, and then combines the results to give the final P-value and ranking of pathways. For gene level analysis, MetaPath calculates a t-statistic for each gene in each study, then combines them using the maxP method (Wilkinson, 1951). A pathway enrichment score is calculated using these genes, for each pathway, using a Kolmogorov–Smirnov test, and assessed for significance with a sample-wise permutation test. At the pathway level, MetaPath calculates pathway enrichment for each individual study, then combines the P-values, again using the maxP method (Wilkinson, 1951). Finally, P-values from the gene and pathway level are integrated using minP (Tippett, 1931) to give the final P-value and ranking of pathways.

One practical drawback of many P-value-based meta-analysis methods, including Fisher’s, Stouffer’s, minP and maxP, is that they are sensitive to outliers. For example, Fisher’s method employs the log product of individual P-values and thus, a single P-value of zero in one individual case will result in a combined P-value of zero regardless of the other P-values. This can be a serious problem for pathway analysis methods that employ a finite number of iterations to construct an empirical distribution of a statistic which is then used to calculate an empirical P-value. If the observed value of the statistic is more extreme than any of the values obtained by the iterations, such methods may report a P-value of zero, which will, in turn, dramatically influence the meta P-value.

Another drawback of most P-value-based meta-analysis approaches is that, because they perform just one statistical test for each individual experiment, they may not fully exploit the potentially large number of samples within each study. A statistical test which is not powerful enough to reject the null hypothesis in one individual experiment can only derive power by amassing a large number of experiments. Low power in the case of a single experiment can be due in part to a mathematical design which favors a moderate number of samples, but may fail to fully exploit large sample sizes. For example, the basic t-test is designed to do well even with a small number of samples in each group. While the power of the t-test increases as the number of samples increases, a set of 20 experiments with 5 samples each has more power than a single experiment comprised of the same 100 samples (see Fig. S4 in Supplementary Materials).

Here we propose a P-value-based meta-analysis framework which addresses the mentioned shortcomings and thus provides more reliable results. As we will demonstrate, the proposed method is not sensitive to outliers. To gain power from the large number of samples within each experiment, the proposed meta-analysis integrates multiple independent studies on two levels: an intra-experiment analysis, and an inter-experiment analysis. First, for each individual experiment, the intra-experiment analysis splits the dataset into smaller datasets, performs a statistical test on each of the newly created small datasets, then combines the P-values. Next, the inter-experiment analysis combines those processed P-values, from each of the individual experiments. We demonstrate the power of our bi-level meta-analysis in the context of pathway analysis.

We illustrate our approach using one of the most popular statistical methods for pathway analysis, Gene Set Enrichment Analysis (GSEA), applying it to KEGG pathways, and 21 public gene expression datasets, conducted in independent laboratories, from three conditions: acute myeloid leukemia (9 datasets), type II diabetes (5 datasets) and Alzheimer’s disease (7 datasets). We compare the result of the proposed framework with three classical meta-analysis methods (Fisher’s, Stouffer’s, and the additive method), plus the standalone meta-analysis method—MetaPath. For all three conditions, our framework outperforms other approaches and correctly identifies the pathways designed to describe the biological processes responsible for these diseases.

2 Methods

2.1 P-value-based meta-analysis

We first describe Fisher’s method and the additive method for combining P-values, then discuss some of their limitations. Subsequently, we introduce our technique, and discuss how it addresses these limitations.

Fisher’s method is one of the most widely used methods for combining multiple independent studies based on their P-values. Under the null hypothesis, the log product of individual P-values follows a χ² distribution with 2m degrees of freedom (Fisher, 1925). This distribution is used to calculate the probability of observing the log product of individual P-values. One practical drawback of this approach is that if one of the individual P-values approaches zero, the combined P-value approaches zero as well, regardless of other individual P-values. Another drawback is that this method is very sensitive to bias under the null (i.e. the P-values under the null do not follow a uniform distribution). This results in a high false positive rate (see Fig. S8 in Supplementary Materials).

The additive method (Edgington, 1972; Hall, 1927; Irwin, 1927) uses the sum of the P-values as the test statistic, instead of the log product. Let us denote the P-values resulting from the m independent significance tests as P₁, P₂,…, P_m. These P-values are independent and uniformly distributed between zero and one under the null (i.e. all P-values between zero and one are equally probable when the null hypothesis is true). Denote the sum of these P-values, $X={\sum }_{i=1}^m{P}_i$ ($X\in [0,m]$), as the new random variable. X is known to follow the Irwin-Hall distribution (Hall, 1927; Irwin, 1927) with the following probability density function (pdf):

$$f(x)=\frac{1}{(m-1)!}{\displaystyle \sum _{i=0}^{\lfloor x\rfloor }{(-1)}^i}\left(\begin{array}{c}m\\ i\end{array}\right){(x-i)}^{m-1}$$ (1)

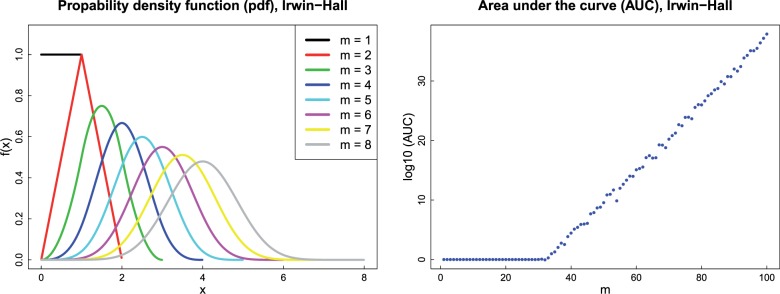
Unlike Fisher’s method, the additive method is not sensitive to small individual P-values. However, we note that the additive method faces a different practical problem. For large values of m, Eq. (1) involves some intensive computation due to a sum of combinatorial and division by a factorial, the result of which can lead to an ‘arithmetic underflow’. In other words, the result can be a number smaller than what a computer can actually store in memory. Figure 1 displays the Irwin-Hall probability density function (pdf) (left panel) and the area under the pdf curve (AUC) (right panel) for different m values. For each value of m, the area under the curve, $F(X=m)$, should be 1 and therefore the log absolute value of $F(X=m)$ should be 0. However, the calculation is not accurate for large values of m and the area under the curve increases very rapidly (right panel). The calculation of the additive method is not reliable when m > 30.

Fig. 1.

Probability density functions (pdf) of the Irwin-Hall distribution (left panel) and the area under the pdf curve (AUC) (right panel), for different values of m. The left panel shows the density of X, when $X\in [0,m]$. For each value of m, the density function is symmetrical and takes values between 0 and m. The right panel shows the area under the pdf curve calculated by a 64-bit implementation of R (version 3.1.1, 2014-Jul-10). For each value of m, the AUC should be 1 and therefore the $lo{g}_{10}(AUC)$ should be 0. However, due to the complexity of the Irwin-Hall formula and arithmetic underflow, the calculation is not accurate for large values of m and the AUC increases very rapidly. The figure shows that the calculation is completely unreliable when m > 30

Here we describe an enhancement to the additive method that makes it more reliable for larger values of m. First, we change the random variable from the sum of the P-values to the average of the P-values. Second, when m is large, we replace the additive method with the Central Limit Theorem (CLT). The reason for the modification is that the additive method is accurate for small values of m, while the Central Limit Theorem is more accurate for large values of m. We select m = 20 as a conservative cut-off. In other words, we will use the additive method when m < 20, and the Central Limit Theorem when $m\ge 20$.

To show the validity of using the Central Limit Theorem for large m, we define a new random variable $Y=\frac{{\sum }_{i=1}^m{P}_i}{m}$ ($Y\in [0,1]$), which is the average of P-values. Since $Y=\frac{X}{m}$, we can derive the probability density function (pdf) of Y using a linear transformation of X as follows:

$$g(y)=\frac{m}{(m-1)!}{\displaystyle \sum _{i=0}^{\lfloor m·y\rfloor }{(-1)}^i}\left(\begin{array}{c}m\\ i\end{array}\right){(m·y-i)}^{m-1}$$ (2)

The corresponding cumulative distribution function (cdf) can be calculated as:

$$G(y)=\frac{1}{m!}{\displaystyle \sum _{i=0}^{\lfloor m·y\rfloor }{(-1)}^i}\left(\begin{array}{c}m\\ i\end{array}\right){(m·y-i)}^m$$ (3)

The variable Y is the mean of m independent and identically distributed (i.i.d.) random variables (the P-values from each individual experiment), that follow a uniform distribution with a mean of $\frac{1}{2}$ and a variance of $\frac{1}{12}$. From the Central Limit Theorem (Kallenberg, 2002), the average of such m i.i.d. variables follows a normal distribution with mean $\mu =\frac{1}{2}$ and variance ${\sigma }^2=\frac{1}{12m}$, i.e. $Y\sim \mathcal{N}\left(\frac{1}{2},\frac{1}{12m}\right)$ for sufficiently large values of m.

In the rest of the manuscript, we refer to our proposed combination of the Irwin-Hall distribution and the Central Limit Theorem as ‘add-CLT’, for ‘additive-Central Limit Theorem’, in order to distinguish it from the classical additive method. As noted above, the transition from the additive method to the Central Limit Theorem takes place at the $m\ge 20$ threshold.

The pdf of Y for different m values and the corresponding AUCs are displayed in Figure S1 in Supplementary Materials. The data show that the AUC is 1 as it should be, for all values of m. We can see that add-CLT overcomes the computational problem of the classical additive method using the Irwin-Hall distribution.

2.2 Bi-level meta-analysis framework

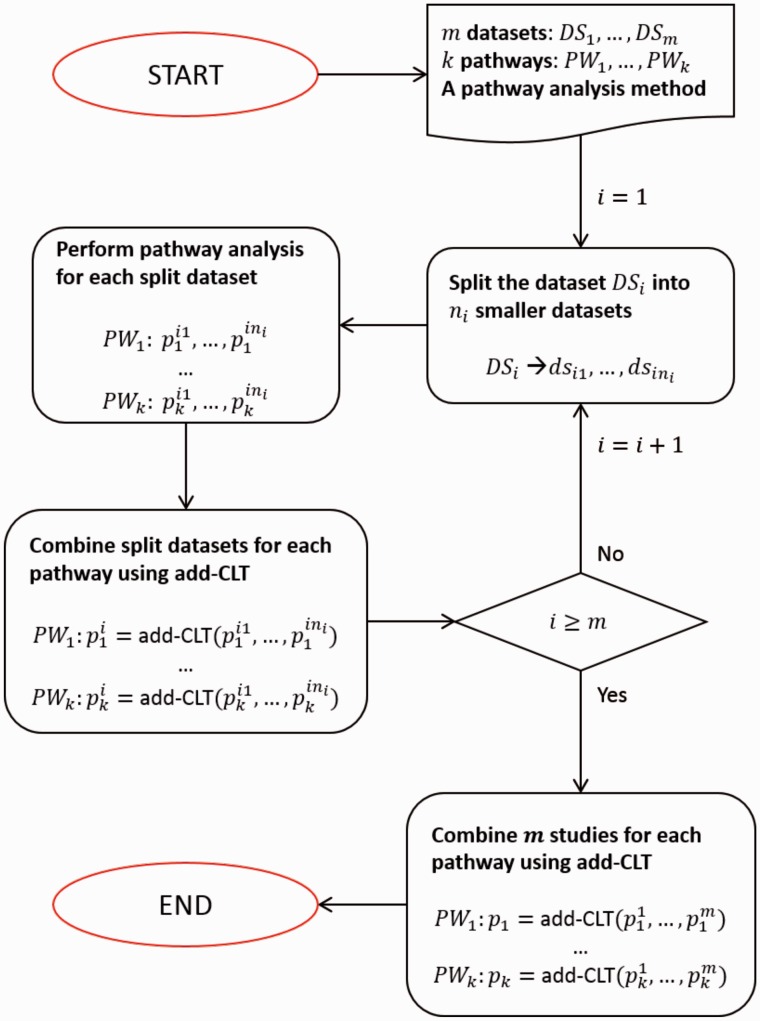
In this section we describe the bi-level meta-analysis framework in the context of pathway analysis. The input of the framework is as follows. First, we have m studies (datasets) of the same disease. Each dataset consists of a group of healthy samples and a group of disease samples. Second, we have a list of k pathways from an existing pathway database. Third, we have a pathway analysis method that can be used to identify the significantly impacted pathways in a given dataset. This pathway analysis method is used for each dataset, thus calculating a P-value for each of the k pathways in each of the m datasets.

Figure 2 displays the overall procedure of our framework. The framework is divided into two stages: intra-experiment analysis and inter-experiment analysis. The intra-experiment analysis works with one dataset at a time. Given a dataset DS_i ($i\in [\mathrm{1..}m]$), we divide the disease samples into n_i smaller groups. Each data subset consists of a small group of disease samples and all the control samples in the dataset. We impose that each small group include at least 5 disease samples, therefore, n_i approximately equals the number of disease samples divided by 5. Using the chosen pathway analysis method, we calculate the P-values for the k pathways for each of the n_i small datasets. The result is n_i lists of P-values, each with k P-values for the k pathways. Therefore, each pathway will have n_i P-values, one from each of the n_i lists. The n_i P-values are then combined into a single P-value for each pathway using the add-CLT described above.

Fig. 2.

Bi-level meta-analysis framework to identify significant pathways. The input includes m datasets, k pathways and a pathway analysis method. The intra-experiment analysis divides the dataset DS_i ($i\in [\mathrm{1..}m]$) into smaller datasets $d{s}_{i1},\dots ,d{s}_{i{n}_i}$ and then performs pathway analysis for each of the small datasets, resulting in n_i P-values for each pathway. The intra-experiment analysis combines the n_i P-values into one P-value for each pathway using add-CLT. After this process is done for all m studies (datasets), each pathway has m independent P-values – one per study. The inter-experiment analysis then combines the m P-values for each pathway into one meta P-value using the add-CLT method. This meta P-value for each pathway represents the overall significance of the pathway. The output of the framework is a list of k pathways ranked according to the meta P-values

After performing intra-level-analysis on all m studies (datasets), we have m lists of P-values—one per study, and each pathway has m independent P-values. Using add-CLT, the inter-experiment analysis combines the m P-values of each pathway into one meta P-value that represents the significance of the pathway. The output of the whole framework is a list of k pathways ranked according to the meta P-values.

While our bi-level framework is described in the context of pathway analysis, it can be modified and applied in any context. For example, the pathway analysis method can be substituted with another statistical test, or applied in totally different field. In addition, our add-CLT method maybe replaced by another meta-analysis method. However, we favor add-CLT for several reasons. First, it is robust against small P-values and against bias under the null. Second, it is more powerful than Fisher’s method in detecting changes in signal (see Figs S8, S9 in Supplementary Materials).

3 Experimental studies

In order to provide a deeper understanding of why intra-experiment analysis improves results on a mathematical level, we applied it to a two-sample t-test and compared the results to a standard t-test. We show that splitting datasets and combining P-values using add-CLT results in a gain of power. We also investigated the false positive rate of the bi-level meta-analysis and the robustness with respect to various split sizes. Furthermore, we compared add-CLT against the popular Fisher’s method. The results show that add-CLT is more reliable than Fisher’s method in terms of both false positive rate (FPR) and true positive rate (TPR) (see Figs S4–S9 in Supplementary Materials).

For the experiments based on real expression data, we compare 5 different meta-analysis approaches in the context of pathway analysis: our bi-level approach with add-CLT, three classical meta-analysis methods (Fisher’s, Stouffer’s and the additive method), and one standalone, dedicated, pathway meta-analysis method—MetaPath. We use the KEGG pathway database (version 65, 150 human pathways). For the 4 methods that need a pathway analysis algorithm, we select GSEA (Subramanian et al., 2005), which is currently one of the most popular methods.

We chose 21 datasets related to three human diseases: type II diabetes (5 datasets), acute myeloid leukemia (AML) (9 datasets) and Alzheimer’s disease (7 datasets). These disease datasets were chosen for several reasons—not only are they well suited for meta-analysis, but we have a good way to evaluate the results. For each disease, there is a dedicated pathway in KEGG that was created in order to describe the known mechanisms involved in these specific diseases. Thus, the five analysis methods can be assessed by their ability to identify these ‘target pathways’ in their respective conditions.

3.1 Pathway analysis using type II diabetes data

The diabetes datasets we use in our data analysis were obtained from Gene Expression Omnibus (GEO) with IDs: GSE25462 (skeletal muscle, 10 cases and 15 controls), GSE19420 (skeletal muscle, 10 cases and 12 controls), GSE18732 (skeletal muscle, 45 cases and 47 controls), GSE23343 (liver biopsy, 10 cases and 7 controls) and GSE22309 (skeletal muscle, 30 cases and 40 controls). Details of all datasets are provided in Supplementary Materials.

We use Gene Set Enrichment Analysis (GSEA) to analyze the 5 diabetes datasets individually, before performing the meta-analysis. For each dataset, GSEA produces a list of 150 KEGG pathways ranked by P-values. The rankings and FDR-corrected P-values of the target pathway Type II diabetes are displayed in Figure S2 in Supplementary Materials. The target pathway gets an FDR-corrected P-value higher than 0.5 in every single one of the diabetes datasets. The target pathway is ranked between 4th (in GSE23343) and 133th (in GSE19420). This is a clear case in which the correct pathway is missed in every single one of the 5 individual datasets available; such a situation calls for meta-analysis.

Proceeding to meta-analysis of these 5 datasets, the most straightforward approach is to combine the 5 P-values produced by GSEA for each pathway, using classical P-value-based meta-analysis methods. Here we use three classical approaches to combine the independent P-values: Fisher’s (Fisher, 1925), Stouffer’s (Stouffer et al., 1949) and the additive method (Edgington, 1972; Hall, 1927; Irwin, 1927). Fisher’s and Stouffer’s method have been used in (Kaever et al., 2014) to combine P-values of pathways in independent experiments. Stouffer’s method is similar to Fisher’s method, with the difference that, as the random variable, it uses the sum of P-values transformed into standard normal variables instead of the log product. Alongside these three classical meta-analysis techniques, we juxtapose our bi-level meta-analysis. The result of each is a list of all 150 pathways ranked according to the combined P-values, which we adjust for multiple comparisons using FDR.

Table 1 lists the top 5 ranked pathways and FDR-corrected P-values obtained by combining the 5 diabetes datasets using the 4 meta-analysis approaches. The pathway highlighted green is the target pathway Type II diabetes mellitus, which was created in order to describe the phenomena involved in this disease. The horizontal line marks the cutoff of 0.05 of the FDR-corrected P-values. All three classical meta-analysis approaches, Fisher’s, Stouffer’s, and the additive method, fail to identify the target pathway as significant (P > 0.4) with rankings 7, 10 and 12, respectively. The Oocyte meiosis pathway has a combined P-value equal to zero for Fisher’s and Stouffer’s methods because the P-value was zero for one of the datasets (GSE22309). As discussed in the Methods section, these approaches are sensitive to such occurrences. The bi-level meta-analysis approach identifies the target pathway Type II diabetes mellitus as the most significant pathway (P = 0.0151). Also, this is the only significant pathway at the 5% significance threshold.

Table 1.

Results of combining GSEA P-values using 4 meta-analysis approaches for type II diabetes data

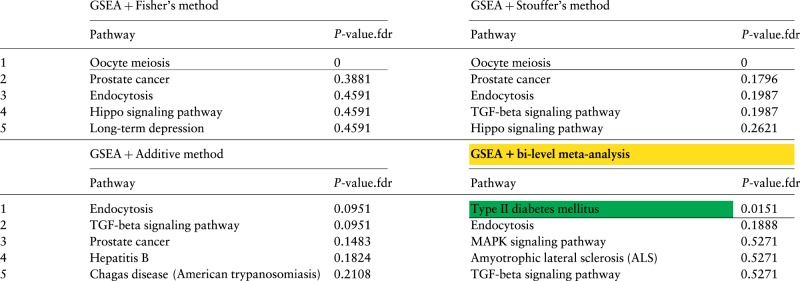The top 5 pathways and their FDR-corrected P-values obtained by combining the P-values of GSEA using 4 meta-analysis approaches: Fisher’s, Stouffer’s, the additive method and bi-level meta-analysis. In the first three approaches, the 5 P-values for a pathway (one of each of the 5 datasets) were combined into a single p-value using Fisher’s, Stouffer’s, or the additive method. This is done for all of the 150 signaling pathways in KEGG. The P-values are then adjusted for multiple comparisons using FDR. The pathways are sorted by the combined P-values, from low to high. The horizontal lines show the 5% significance threshold. The target pathway Type II diabetes mellitus is highlighted in green. The target pathway Type II diabetes mellitus is the only significant pathway using the bi-level meta-analysis. The three classical approaches, Fisher’s, Stouffer’s and the additive method, fail to identify the target pathway as significant and rank it in positions 7th, 10th and 12th, respectively.

As a fifth method, we employ MetaPath (Shen and Tseng, 2010), to combine the 5 studies. MetaPath (Shen and Tseng, 2010) is a dedicated pathway meta-analysis which is open source and does not require an external pathway analysis method. In our work, we use the R package provided in (Wang et al., 2012). MetaPath performs meta-analysis at both gene and pathway levels with a GSEA-like approach, and then combines the results to give the final P-value and ranking of pathways. Table 2 lists the top 5 pathways using MetaPath. The target pathway Type II diabetes mellitus is ranked 80th out of 150 with an FDR-corrected P-value of 1.

Table 2.

MetaPath results for 5 diabetes datasets

	MetaPath
	Pathway	P-value.fdr
1	Maturity onset diabetes of the young	0.9975
2	Lysosome	0.9988
3	Ribosome biogenesis in eukaryotes	1.0000
4	RNA transport	1.0000
5	mRNA surveillance pathway	1.0000

The target pathway Type II diabetes mellitus is ranked 80th.

3.2 Pathway analysis using AML data

The following AML datasets from GEO were used for our analysis: GSE14924 (CD4 T-cells, 10 cases and 9 controls, and CD8 T-cells, 10 cases and 11 controls), GSE17054 (hematopoietic stem cells, 5 cases and 4 controls), GSE12662 (fractionated bone marrow: CD34 + cells, promyelocytes, neutrophils and the PR9 cell line, 75 cases and 24 controls), GSE57194 (primary CD34 + cells, 6 cases and 6 controls), GSE33223 (peripheral blood mononuclear cells, 20 cases and 10 controls), GSE42140 (peripheral blood mononuclear cells, 26 cases and 5 controls), GSE8023 (CD34 + cells from cord blood, 9 cases and 3 controls) and GSE15061 (bone marrow, 201 cases and 68 controls).

We use Gene Set Enrichment Analysis (GSEA) (Subramanian et al., 2005) to analyze the 9 AML datasets individually. The rankings and FDR-corrected P-values of the target pathway Acute myeloid leukemia for the 9 datasets are displayed in Figure S3 in the Supplementary Materials. The AML pathway is assigned an FDR-corrected P-value ranging from 0.23 (GSE57194) to 1 (GSE33223) and a ranking between 12 (GSE42140) and 114 (GSE14924) across the 9 datasets analyzed. In essence, the AML pathway, which was created precisely to describe the most important biological mechanisms involved in AML, is neither found to be significant, nor ranked anywhere close to the top in any of the individual datasets.

We again use the 4 meta-analysis approaches to combine GSEA results: Fisher’s, Stouffer’s, the additive method, and the bi-level meta-analysis. The output for each of these 4 approaches is a list of 150 pathways ranked according to the combined P-values. Table 3 lists the top 5 ranked pathways and FDR-corrected global P-values yielded by the 4 meta-analysis approaches. The green highlight shows the target pathway Acute myeloid leukemia. The horizontal line is the selected significance cutoff of 0.05.

Table 3.

Results of combining GSEA P-values using 4 meta-analysis approaches for acute myeloid leukemia (AML)

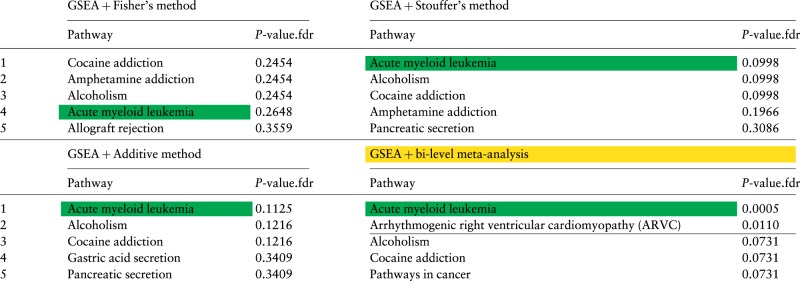The 5 top ranked pathways and FDR-corrected P-values obtained by combining the P-values of GSEA using 4 meta-analysis approaches: Fisher’s, Stouffer’s, the additive method and bi-level meta-analysis. In the first three approaches, the 9 P-values for a pathway (one of each of the 9 datasets) were combined into a single P-value using Fisher’s, Stouffer’s and the additive method. This is done for all of the 150 signaling pathways in KEGG. The P-values are then adjusted for multiple comparisons using FDR. The pathways are sorted by the combined P-values, from low to high. The horizontal lines show the 5% significance threshold. The target pathway Acute myeloid leukemia is highlighted in green. The target pathway Acute myeloid leukemia is significant only when using bi-level meta-analysis.

None of the three classical meta-analysis approaches identify the target pathway Acute myeloid leukemia as significant. Fisher’s yields a global P-value of 0.264, Stouffer’s yield a global P-value of 0.099 and the additive method yields a P-value of 0.112. Fisher’s method ranked the target pathway as 4th out of 150. The bi-level meta-analysis with add-CLT identifies the target pathway as significant with a P-value of 0.0005, and also ranks it 1st.

Again, we also provide the results of MetaPath (Shen and Tseng, 2010) when analyzing the 9 studies together. Table 4 lists the top 5 pathways using MetaPath for the 9 acute myeloid leukemia datasets. The target pathway Acute myeloid leukemia is highlighted green. This pathway is not significant (P = 0.4), and is ranked 3rd.

Table 4.

MetaPath results for 9 acute myeloid leukemia datasets

The target pathway Acute myeloid leukemia is not significant and is ranked 3rd.

3.3 Pathway analysis using Alzheimer’s data

As a final case, we selected Alzheimer’s disease because we want to give an example of a situation with more than one expected pathway. Alzheimer’s disease, Parkinson’s disease and Huntington’s disease are three neurological disorders that share many signaling mechanisms and affect the same tissue (brain). The common elements include abnormal protein folding, endoplasmic reticulum stress, and ubiquitin mediated breakdown of proteins, leading to programmed cell death (Swerdlow, 2011; Maruszak and Żekanowski, 2011; Zhu et al., 2013; Querfurth and Laferla, 2010). Furthermore, previous studies have shown the presence of a strong cross-talk that makes these three neurological disease pathways appear as significant simultaneously, due to their dominant mitochondrial module (Donato et al., 2013). Therefore, we expect a good analysis method to find all three of these pathways as significant in this meta-analysis of Alzheimer’s data.

The Alzheimer’s datasets we use in our data analysis were obtained from Gene Expression Omnibus (GEO) with IDs: GSE1297 (hippocampus, 22 cases and 9 controls), GSE28146 (hippocampus, 22 cases and 8 controls) and GSE5281 (a mixture of entorhinal cortex, hippocampus, medial temporal gyrus, posterior cingulate, superior frontal gyrus and primary visual cortex, 87 cases and 74 controls), GSE16759 (parietal lobe cortex, 4 cases and 4 controls), GSE48350 (a mixture of post central gyrus, superior frontal gyrus, hippocampus and entorhinal cortex, 80 cases and 173 controls), GSE39420 (brain tissues, 14 cases and 7 controls) and GSE4757 (entorhinal cortex, 10 cases and 10 controls).

Again, we use the 5 meta-analysis approaches, Fisher’s, Stouffer’s, the additive method, the bi-level meta-analysis and MetaPath, to combine the 7 Alzheimer’s studies. Table 5 lists the top 5 ranked pathways and FDR-corrected P-values obtained by combining the 7 Alzheimer’s datasets using the 4 existing meta-analysis approaches. Table 6 lists the top 5 ranked pathways using MetaPath. The horizontal line marks the 5% cutoff for the FDR-corrected P-values.

Table 5.

Results of combining GSEA P-values using 4 meta-analysis approaches for Alzheimer’s data

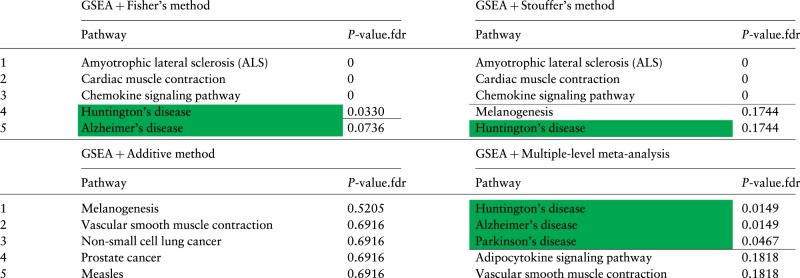The 5 top ranked pathways and FDR-corrected P-values obtained by combining the P-values of GSEA using 4 meta-analysis approaches: Fisher’s, Stouffer’s, the additive method and bi-level meta-analysis. In the first three approaches, the 7 P-values for a pathway (one of each of the 7 datasets) were combined into a single P-value using Fisher’s, Stouffer’s and the additive method. This is done for all of the 150 signaling pathways in KEGG. The P-values are then adjusted for multiple comparisons using FDR. The pathways are sorted by the combined P-values, from low to high. The horizontal lines show the 5% significance threshold. The target pathway Alzheimer’s disease and two neurological disease pathways, Parkinson’s disease and Huntington’s disease, are highlighted in green. Only the bi-level meta-analysis identifies all three neurological disease pathways, Alzheimer’s disease, Parkinson’s disease and Huntington’s disease, as significant.

Table 6.

MetaPath results for Alzheimer’s data

None of the three neurological disease pathways, Huntington’s disease, Alzheimer’s disease and Parkinson’s disease, appears as significant. They are ranked on positions 4th, 40th, 16th, respectively.

All 4 meta-analysis approaches, Fisher’s, Stouffer’s, the additive method and MetaPath, fail to identify the primary target pathway Alzheimer’s disease as significant, and rank it on positions 5, 11, 28 and 40, respectively. They also fail to identify Parkinson’s disease as significant. Among 4 existing meta-analysis approaches, only Fisher’s method identifies Huntington’s disease as significant.

In contrast, the bi-level meta-analysis approach identifies the target pathway Alzheimer’s disease as significant (P = 0.0149) with ranking 2. In addition, the pathways Huntington’s disease and Parkinson’s disease also appear as significant in the results of the bi-level meta-analysis. Furthermore, the proposed approach does not produce any false positives.

For all three disease conditions, diabetes, AML and Alzheimer’s disease, the classical meta-analysis approaches and MetaPath were unable to identify the target pathway as significant. Only the proposed bi-level meta-analysis identifies the target pathway as significant. This is likely due to two reasons. First, the combination of the additive method and the Central Limit Theorem is reliable in terms of both false positive rate and true positive rate. Second, the intra-experiment analysis performed within each of the individual studies increases the power of the pathway analysis.

4 Conclusion

In this article, we present a novel meta-analysis approach that combines multiple studies to gain more statistical power. The new framework exploits not only the vast number of studies performed in independent laboratories, but also makes better use of the available number of samples within individual studies. In addition, the use of the additive method and the Central Limit Theorem makes the framework robust to outliers and keeps the false positive rate under the desired threshold.

To evaluate the proposed framework for pathway analysis applications, we analyze 5 diabetes datasets, 9 acute myeloid leukemia datasets and 7 Alzheimer’s datasets using 5 different approaches: Fisher’s, Stouffer’s, the additive method, MetaPath and the bi-level meta-analysis. For each of these three diseases, there is a KEGG pathway, referred to as the target pathway, that describes the phenomena associated with these conditions. All 4 existing meta-analysis methods fail to identify the target pathways as significant after combining all available datasets for each condition. In contrast, the proposed bi-level meta-analysis identifies the target pathways as significant in all three conditions. These results confirm the increased power of the bi-level meta-analysis with respect to the other meta-analysis approaches.

Although the bi-level meta-analysis framework is illustrated in the context of pathway analysis, it is in fact a general meta-analysis method that can easily replace existing meta-analysis procedures in a wide range of research areas, such as biomarker/oncogene detection, genome-wide association studies (GWAS), enrichment analysis (Gene Ontology, gene set analysis), or even clinical trials to assess the effect of a therapy in complex diseases.

Funding

This work was supported by the National Institutes of Health [R01 DK089167, R42 GM087013]; National Science Foundation [DBI-0965741] and the Robert J. Sokol Endowment in Systems Biology.

Conflict of Interest: none declared.