3DRobot: automated generation of diverse and well-packed protein structure decoys

Abstract

Motivation: Computationally generated non-native protein structure conformations (or decoys) are often used for designing protein folding simulation methods and force fields. However, almost all the decoy sets currently used in literature suffer from uneven root mean square deviation (RMSD) distribution with bias to non-protein like hydrogen-bonding and compactness patterns. Meanwhile, most protein decoy sets are pre-calculated and there is a lack of methods for automated generation of high-quality decoys for any target proteins.

Results: We developed a new algorithm, 3DRobot, to create protein structure decoys by free fragment assembly with enhanced hydrogen-bonding and compactness interactions. The method was benchmarked with three widely used decoy sets from ab initio folding and comparative modeling simulations. The decoys generated by 3DRobot are shown to have significantly enhanced diversity and evenness with a continuous distribution in the RMSD space. The new energy terms introduced in 3DRobot improve the hydrogen-bonding network and compactness of decoys, which eliminates the possibility of native structure recognition by trivial potentials. Algorithms that can automatically create such diverse and well-packed non-native conformations from any protein structure should have a broad impact on the development of advanced protein force field and folding simulation methods.

Availiablity and implementation: http://zhanglab.ccmb.med.umich.edu/3DRobot/

Contact: jiay@phy.ccnu.edu.cn; zhng@umich.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

It has been more than 50 years since Anfinsen first showed that the native structure of protein molecules corresponds to the state with the lowest free energy (Anfinsen et al., 1961). However, ab initio folding of proteins from the first principle remains a significant unsolved problem in biophysics and computational biology. One of the major barriers is the difficulty in designing accurate force fields that can recognize the native state as the lowest energy, and meanwhile possess an energy funnel with a medium-range energy-RMSD correlation that can guide the folding simulation towards the native state (Bradley et al., 2005; Zhang, 2008).

A critical step to protein folding force field development is the preparation of a set of non-native protein structures, usually generated by computer (called structure decoys), which can be used to guide the design, train and benchmark of the energy terms (Park and Levitt, 1996; Rajgaria et al., 2008; Simons et al., 1997; Teodorescu et al., 2004; Zhang et al., 2003). However, creating appropriate structure decoys is highly non-trivial and many efforts have been made to address the problem. For example, Park and Levitt (1996) proposed to construct structure decoys by randomly rotating structural segments of known native structures around a set of selected flexible hinges. Since native structure features, such as hydrophobic core and contact specificities of amino acids, can be destroyed in the segment permutations, the native structure can be quite easily recognized by knowledge-based potentials that were extracted from the statistics of experimental structures (Lu and Skolnick, 2001). To partly amend this issue, Simons et al. (1997) and Xu and Zhang (2012) generated structure decoys by ab initio folding simulations through Rosetta and QUARK programs, respectively. Because extensive energy optimizations are conducted in the folding simulations, one advantage of the folding-based decoy set is that the native states cannot be easily recognized from the decoys by simple knowledge-based potentials (Deng et al., 2012). However, one issue of such decoy sets is that ab initio folding simulations cannot generate near-native structure conformations (say < 3 Å) due to the inherent difficulties in ab initio folding, in particular for the medium- to large-size proteins with complicated topology; this renders the decoys useless for the potential development that aims to recognize near-native structures (e.g. for high-resolution refinement).

To enrich near-native decoy generation, John and Sali (2003) proposed to generate decoys by mutations of threading alignments followed by comparative modeling using Modeller; similarly, Wu et al. (2007) constructed structure decoys by iterative threading assembly simulations based on I-TASSER. Because these decoys are built on specific homologous templates, the conformations are often aggregated into a few clusters around the template structures, which make it difficult to examine the continuous energy funnel and the energy-RMSD correlation of the force field—such energy funnel and correlation are critical in guiding successful protein folding simulations (Bradley et al., 2005; Zhang, 2008).

Even though many decoy sets used in literature were generated by extensive folding simulations, somewhat surprisingly, almost all the currently existing decoy sets have some level of correlations between the RMSD to the native and the radius of gyration or secondary structure distribution (see Supplementary Fig. S1). This means that the structure deviations have been created by sacrificing the hydrogen-bonding networks and/or the compactness of the native structures in the decoy construction simulation processes. Therefore, the native structure can be easily discriminated from the decoys by simply counting their secondary structure density or the compactness score. Energy training based on such decoys may introduce extra bias to the secondary structure and compactness weights that are not reflected in the native structures. To improve the quality of the decoy structures, Yeh et al. (2015) proposed a strategy to refine existing decoy sets by extra energy minimization simulations; meanwhile, additional decoy structures were added from the native structure perturbation and random dihedral angle sampling to increase the difficulty of decoy recognition by various scoring functions.

Finally, it is important to note that many protein folding and structure prediction studies need structure decoys for specific protein targets that the authors are interested in. However, most decoy sets in literature have been pre-generated, which further limits their use for more general studies.

In this work, we aim to develop a new algorithm, 3DRobot, dedicated for high-quality protein decoy generation by the extension of I-TASSER-based fragment structure assembly simulations. To increase structure diversity, multiple continuously distributed structure scaffolds will be collected from the PDB library, with new energy terms introduced to enhance the hydrogen-bonding and residue packing interactions. The on-line server and the executable program are freely available at http://zhanglab.ccmb.med.umich.edu/3DRobot, which allow users to generate high-quality structure decoys from any given target structures.

2 Methods

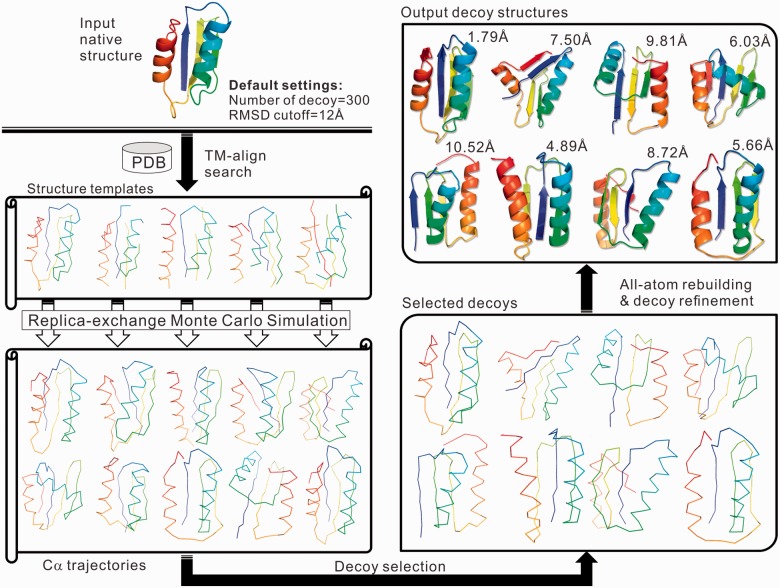
3DRobot is a hierarchical algorithm for protein 3D structure decoy generation, which consists of three steps of structure scaffold identification, fragment structure reassembly simulation, and model selection and refinement. A pipeline of 3DRobot is depicted in Figure 1.

Fig. 1.

3DRobot protocol for protein structure decoy construction

2.1. Identification of initial structure scaffolds

Starting from the native structure of the target protein, we use TM-align (Zhang and Skolnick, 2005) to thread the structure through a representative PDB library, which consists of 27  822 non-redundant protein structures with a pair-wise sequence identity <70%. Up to 100 non-redundant structure scaffolds (or templates) are selected from the top structure alignments ranked by TM-score to the native structure. To ensure the diversity of scaffolds and meanwhile keep sufficient structures in the low RMSD regions, we required a pair-wise RMSD of the selected scaffolds to be larger than R_target/2, where R_target is the RMSD between the TM-align scaffolds and the target native structure.

2.2 Structure decoy reassembly simulations

Starting from the TM-align scaffolds, the full-length structure decoys are assembled by replica-exchange Monte Carlo simulations, based on a protocol extended from I-TASSER (Roy et al., 2010; Yang et al., 2015). The target sequence is split into structurally aligned and unaligned regions. The structure in the continuously aligned regions with a length >5 residues will be excised from the scaffolds and modeled off-lattice with the local structure kept unchanged. The structure in the unaligned regions are constructed from scratch and modeled on a lattice system with grid = 0.87 Å. The force field of the 3DRobot simulations contains generic knowledge-based energy terms of solvation, hydrogen-bonding, short-range Cα correlations, electrostatic and pair-wise contacts, extended from I-TASSER. But different from I-TASSER simulations that were constrained by the threading template restraints, the spatial constraint potential is excluded in 3Drobot to enhance the conformational diversity of the assembly simulations.

To enhance the hydrogen-bonding networks and compactness of the decoys, we introduce two new energy terms into the 3DRobot structure assembly simulations.

2.2.1 Hydrogen-bond interactions

To enhance the hydrogen-bonding network of the structure decoys, we collected a list of residue pairs using STRIDE (Frishman and Argos, 1995), which have the hydrogen-bonding interactions in either the native or the TM-align scaffold structures. A distance potential is implemented to ensure the hydrogen bonds in the residue pairs:

$$E_{\text{HB}}={\displaystyle \sum _{I=1}^{n_{\text{HB}}}{w}_{\text{HB}}|d_i-d_{i0}| }$$ (1)

where n_HB is the total number of hydrogen-bonding pairs collected from the native and scaffold structures; d_i and d_i0 are the Cα distance of the ith hydrogen-bonded residue pairs in the decoy and the native (or scaffold if the target hydrogen bond is from the template scaffold) structures respectively; the weighting scale w_HB was set by trial and error as twice of the weight used in the generic hydrogen-bonding term.

The hydrogen-bonding network of the 3Drobot decoys is also enhanced by generic hydrogen-bonding terms implemented by the secondary structure propensity. Different from I-TASSER that has the secondary structure predicted by neural network training, the secondary structure in 3Drobot is taken from the PDB structures as defined by STRIDE, where a non-coil secondary structure element (helix or strand) is assigned if the structure element appears in either the native or the scaffold structure following the TM-align alignments.

2.2.2 Enhanced compactness

Because most decoy sets generated by computational simulations have a strong negative correlation between the compactness and the deviation from the native, an additional score is introduced to enhance the compactness of high structure deviations, i.e.

$$E_{\text{comp}}=\frac{1}{L}{\displaystyle \sum _{i=1}^{\text{L}}{w}_{\text{c}}{d}_i}$$ (2)

where d_i is the distance of the ith residue to the center of mass of the structure decoy. The weight factor is set as

$$w_{\text{c}}=\{\begin{array}{ll}0.2{\left(R_{\text{G}}/R_{\text{G}}^{\text{nat}}\right)}^{R_{\text{G}}/R_{\text{G}}^{\text{nat}}},& \text{if}\hspace{0.17em}{R}_{\text{G}}>R_{\text{G}}^{\text{nat}}\\ 0,& \text{otherwise}\end{array}$$ (3)

where R_G and $R_{\text{G}}^{\text{nat}}$ are the radiuses of gyration of the decoy and the native structures, respectively. The radius of gyration of a protein structure is defined by

$$R_{\text{G}}=\sqrt{\frac{1}{L}{\displaystyle \sum _{i=1}^{\text{L}}{\left({\mathit{r}}_i-{\mathit{r}}_0\right)}^2}}$$ (4)

where r_i is the position vector of the Cα atom of the ith residue, and r₀ is the centroid of all Cα atoms in the structure.

2.3 Decoy selection and atomic-level structure refinement

Because spatial restraints have not been used, the 3DRobot structure assembly simulations can generate decoys with folds very different from the starting scaffolds. Nevertheless, 3DRobot attempts to start the simulations from different scaffold conformations to maximize the diversity of the architecture of decoy generations. A new decoy is accepted only if it has a RMSD higher than R_target/2 to all existing decoys in the decoy pool. The simulation starting with specific scaffolds will be terminated if the number of decoys reaches to 2 N/N_scaffold, where N and N_scaffold are the total number of decoys required and the number of used TM-align scaffolds (up to 100 in this study). This cutoff allows a quick generation of at least two times of the requested decoys. We split the requested RMSD range into n_b bins, each with a RMSD interval 1 Å. The decoys in each RMSD bin are then adopted from different templates by numeration till the number of decoys in the bin reaches N/n_b. Supplementary Figure S2 shows an illustrative example of the decoy distribution starting from 13 scaffolds, where decoys from each RMSD bin are almost evenly adopted from different templates. In case that an even TM-score distribution is required, the decoys will be adopted by the same procedure, but in the evenly split TM-score bins each with an interval of 0.1.

The decoys generated by the 3DRobot simulations are reduced models with each residue specified by its Cα atom and side-chain center of mass. ModRefiner (Xu and Zhang, 2011) is extended to construct full-atom structures from the Cα traces, which also aims to refine the local structure clashes and hydrogen-bonding networks. The backbone atoms are quickly constructed using a look-up table that involves four neighboring Cα atoms. The overall structures are then relaxed and refined iteratively by a two-step energy minimization procedure: the first step is designed for backbone structure refinement and the second for side-chain rotamer optimization, which are guided by a composite physics- and knowledge-based force field as described by Xu and Zhang (2011). The structure refinement does not change the global fold of the structure decoys (typically with a Cα-RMSD to the initial model below 1–2 Å); therefore the evenness of the decoy distribution is not affected. But the hydrogen-bonding networks (as assessed by the HB-score) and the physical quality [as assessed by MolProbity score (Chen et al., 2010)] can be significantly improved as demonstrated by the large-scale benchmark tests (Xu and Zhang, 2011).

3 Results

3.1 Decoy datasets

To examine 3DRobot, we chose to test the method in control with three widely used decoy sets, which were generated by the representative structure modeling methods, including ab initio folding by Rosetta (Simons et al., 1997), homology modeling by Modeller (John and Sali, 2003), and multiple threading assembly simulation from I-TASSER (Wu et al., 2007).

3.1.1 Rosetta sets

The original Rosetta decoy sets (referred as ‘Rosetta_set’) contains decoys for 58 proteins ranging in length from 50 to 146 residues, with each containing 100 structure decoys by the Rosetta ab initio structure prediction. Since structures with a super-high RMSD (e.g. >∼12 Å) are usually considered equally bad and useless to most applications, we made an arbitrary but uniform RMSD cutoff at 12 Å for both decoy generation and evaluation. We further exclude 17 proteins in Rosetta_set whose number of decoys with RMSD < 12 Å is fewer than 50. The remaining 41 decoy sets have an average of 90 structure decoys for each set after removing the decoys with RMSD > 12 Å.

3.1.2 Modeller sets

The Modeller decoy sets (referred as ‘Modeller_set’) contains decoys for 20 proteins with length from 81 to 340 residues, which include on average 194 decoys for each target with RMSD < 12 Å. These decoys were built by the homology-modeling tool Modeller, combined with alignment mutation and refinement.

3.1.3 I-TASSER sets

The I-TASSER decoy sets (referred as ‘I-TASSER_set’) contains decoys for 56 proteins with length from 47 to 118 residues; each protein contains 300–500 decoys which were first generated by I-TASSER simulations and then refined by GROMACS4.0 MD energy minimization (Hess et al., 2008; Zhang et al., 2011). On average, 401 decoys for each protein are evaluated after removing those with RMSD > 12 Å.

3.1.4 3DRobot sets

For each of the three decoy sets, 3DRobot generates a set of N structure decoys with N equal to the average number of decoys in the corresponding sets. In addition, we implement 3DRobot on a set of 200 non-redundant proteins culled by PISCES (Wang and Dunbrack, 2003) from the PDB with a pair-wise sequence identity <20%, containing 48 α, 40 β and 112 α/β single-domain proteins with length from 80 to 250 residues. 300 decoys are constructed by 3DRobot for each target. All the 3DRobot decoys can be downloaded at http://zhanglab.ccmb.med.umich.edu/3DRobot/decoys.

3.2 Evenness of decoy distributions

Ideal structure decoys should have the structural conformations scattered in all interested regimes from near- to distant-native states so that the entire landscape of protein folding force fields could be appropriately assessed. Because the structural space is nearly infinite, however, it is not possible to have a limited number of decoys covering all the structural space. When projecting the high-dimension structural space to the 1D RMSD space, the number of decoys increases rapidly with the increase of RMSD. On the other hand, the decoys with a smaller RMSD are generally more important than the decoys with a larger RMSD when they are used for training protein folding potentials where sufficient near-native structures are needed to parameterize the subtle atomic interactions. Considering the two reverse tendencies, a relatively even distribution in the RMSD space should be desirable for decoy generation. Meanwhile, the requirement for an even RMSD distribution can help avoid significant gaps in the RMSD space and thus allow the assessment of energy potential in various resolutions ranging from near- to distant-native states.

To evaluate the evenness of decoy distributions, we divide the RMSD space into n_b bins (each with an interval 1 Å), and define an Evenness score of a set of N decoys as

$$\text{Evenness}=1-\sqrt{\frac{{\displaystyle \sum }_{i=1}^{n_b}{\left(n_i-\overline{n}\right)}^2}{{\overline{n}}^2{n}_b\left(n_b-1\right)}}$$ (5)

where n_i is the number of decoys in the ith RMSD bin, $\overline{n}=N/n_{\text{b}}$ is the average number of decoys in each bin. Here, we only consider the decoys in [0, 12Å] and n_b = 12. The Evenness score has value in [0, 1], with 1 corresponding to the decoys eventually distributed among all bins, and 0 to the extreme case that has all decoys aggregated into a single bin.

Column 4 of Table 1 lists the Evenness value of different decoys. The average Evenness for the Rosetta_set and I-TASSER_set are 0.502 and 0.475, respectively, which indicates significant gaps existing in the space of structural resolution. The low Evenness in Rosetta_set is mainly due to the difficulty of ab initio protein folding in generating low-RMSD structures, especially for proteins with a large size of complicated topology. Although 17 proteins with none or only a few decoys with RMSD < 12 Å have been excluded, there are still many proteins in the remaining 41 sets where no decoy has a RMSD, 5 Å. In contrast to Rosetta_set, the majority of the I-TASSER decoys are near native since the I-TASSER simulation started from LOMETS threading templates with strong spatial restraints. But there are no sufficient structures in the I-TASSER_set with a high RMSD to the native, where 10 out of the 56 proteins have no decoys with RMSD above 4 Å. The Evenness score in the Modeller_set is slightly higher (0.696), but there are still more than 50% of the proteins having no decoys with RMSD below 3 Å. The same issue exists for many other frequently used decoy sets, including the QUARK set (Xu and Zhang, 2012), the ModEM sets (Topf et al., 2005), the Decoys ‘R’ Us (Samudrala and Levitt, 2000), and the CASP10 decoys generated by the participant servers, which all have an average Evenness score below 0.5.

Table 1.

Evaluations and comparisons of decoy sets from Rosetta_set, Modeller_set, I-TASSER_set and the corresponding sets generated by 3DRobot

Decoy sets	Nta	Lb	Evenness		npwRMSD		Psec (#firste/Zf)		RG(#firste/Zf)
			Oric	3DRd	Oric	3DRd	Oric	3DRd	Oric	3DRd
Rosetta_set	41	83	0.502	0.938	0.713	0.935	3/1.23	0/0.94	12/1.84	0/0.65
Modeller_set	20	174	0.696	0.912	0.867	0.960	11/2.23	0/0.82	2/0.91	0/0.65
I-TASSER_set	56	80	0.475	0.948	0.730	0.940	37/3.60	0/0.94	7/1.47	0/0.62
3DRobot_set	200	133	—	0.913	—	0.951	—	0/0.74	—	1/0.68

^aN_t, number of decoy sets.

^bL, average protein length in the decoy sets.

^cOri, performance of the original decoys.

^d3DR, performance of the decoys generated by 3DRobot.

^e#first, number of proteins where the native structure ranks as the first by each criterion.

^fZ, average of the absolute value of Z-scores of the native structure on each criterion.

When compared with the above-mentioned decoy sets, the evenness of the 3DRobot decoys is significantly increased, which has an Evenness score above 0.9 in all the protein sets (Table 1). The high Evenness score in the 3DRobot decoys is mainly attributed to the well-scheduled scaffold and decoy selection procedures and the restraint-free fragment assembly simulations that allow the generation of structure models of different similarity to the native.

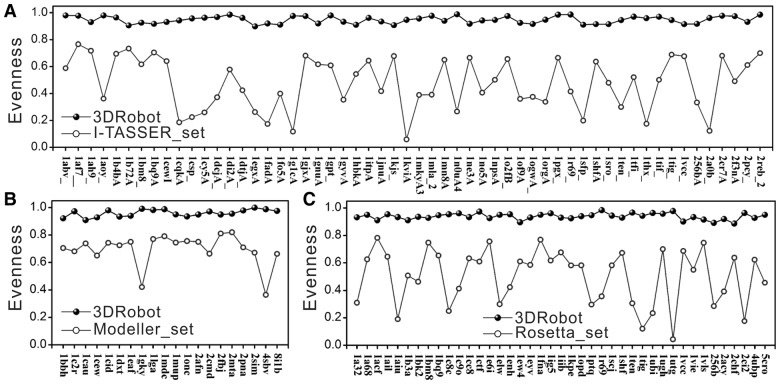
Figure 2 summarizes the evenness comparison for individual proteins of all the decoy sets. As expected, depending on the protein type and the difficulty in structure prediction, a high Evenness fluctuation is observed in all the three control decoy generators, which are rarely beyond 0.75. The Evenness scores of 3DRobot decoys are constantly above 0.85, showing the robustness of 3DRobot in generating evenly distributed decoys in the RMSD space for different type of proteins.

Fig. 2.

Comparison of 3DRobot and control decoy sets on Evenness score. (A) I-TASSER_set; (B) Modeller_set; (C) Rosetta_set

Here we note that the cutoff of RMSD used in Evenness definition and 3DRobot decoy selection is subjective. We have chosen the range of [0, 12 Å] with the purpose to maximize the comparability between 3DRobot decoys and the control sets because this is the range that most of the current structure decoy sets cover. In the 3DRobot server and the standalone program, an option has been given to allow users to choose any RMSD range in which an even distribution of structure decoys is to be created. Meanwhile, we have selected RMSD as the primary metric in 3DRobot because RMSD is the structural similarity measurement that is most widely used in the community. But it is well known that RMSD suffers from its sensitivity to local structural similarity. To address this issue, 3DRobot also has an option to select structural similarity cutoff based on TM-score that is less sensitive to the local structure fluctuation and with the physical meaning of the absolute TM-score value independent of the protein length (Zhang and Skolnick, 2004). When a TM-score cutoff is specified, the templates and decoy structures in 3DRobot will be selected to maximize the evenness distributions in the TM-score space.

3.3 Diversity of structure decoys

Structure decoys must be non-redundant from each other so that a limit number of decoys can cover a maximum conformational space for the force field evaluations. Considering that the near-native decoys have a higher opportunity to be structurally close to each other than the decoys with a high RMSD due to the geometrical constraints, we define a normalized pair-wise RMSD to assess the diversity of structure decoys:

$$\text{npwRMSD}\_30=\frac{2}{N(N-1)}{\displaystyle \sum _{i,j}^{\text{N}}\frac{{\text{RMSD}}_{i,j}}{\text{RMSD}\_{30}_n(r_i,r_j,L)}}$$ (6)

where N is the total number of decoys in the set, RMSD_i,j is the RMSD between ith and jth decoys (i ≠ j). RMSD_30n(r_i,r_j,L) is a normalization function from random structure pairs which we introduce to eliminate the dependence of pair-wise RMSD of decoys on their RMSDs to the native, where r_i and r_j are RMSD of ith and jth decoys to the native and L is the protein length. To compute RMSD_30n(r_i,r_j,L), we collected a pool of 4928 non-redundant PDB structures with a pair-wise sequence identity below 30%, which is what the names of ‘npwRMSD₃₀’ and ‘RMSD₃₀’ refer to. We first select one PDB structure as a reference structure with length L, and then calculate the average RMSD_i,j between all pairs of other proteins in the pool that have RMSD = r_i and r_j, respectively, to the reference structure. RMSD_30n(r_i,r_j,L) is then calculated as the average of RMSD_i,j for all reference proteins that has a length L. When we calculate r_i and r_j, we only count for the proteins that have a length above L, which are compared with the reference by gapless matching. The matching region with the lowest RMSD to the reference structure is then used to calculate the pair-wise RMSD_i,j. For simplicity, we only count pairs with r_i and r_j below 20 Å, which are split into 40 bins with bin-wide = 0.5 Å. In Supplementary Figure S3, we present an example of RMSD_30n(r,r,L) with the first two r_i and r_j being identical. The data clearly shows that the average RMSD between random structure pairs increases regard to both RMSD to the native and the length of proteins.

Here, although we used a specific sequence identity cutoff (30%) for creating the non-redundant structure pool, the distribution of RMSD_n(r_i,r_j,L) is actually insensitive to the cutoff selection because the majority of the randomly selected structural pairs in the PDB have the sequence identity far below 30%. In fact, we have tried to increase or reduce the sequence identity cutoff (or introduce additional structural similarity cutoff using TM-score calculated by TM-align). But we found that there is no obvious difference in the RMSD_n(r_i,r_j,L) from the data presented in Supplementary Figure S3. Thus, for the purpose of briefness, we will use ‘npwRMSD’ instead of ‘npwRMSD₃₀’ in the data presentation afterwards.

The normalized pair-wise RMSD between decoys, npwRMSD, is generally between [0, 1], with npwRMSD = 0 meaning that all decoys are identical and npwRMSD = 1 meaning that the diversity of structure decoys is comparable to that from random protein pairs. Although the necessary diversity of decoys may change depended on the method and force field that the decoys are used to train for, the npwRMSD defined sets up an objective metric to evaluate the diversity that is independent of the RMSD range and the methods that are used to generate the decoys. As shown in Column 6 of Table 1, the Modeller_set has a slightly higher diversity (0.867) than the I-TASSER_set (0.730) and Rosetta_set (0.713). But the npwRMSD in the corresponding 3DRobot decoys was increased to 0.960, 0.940 and 0.935, respectively.

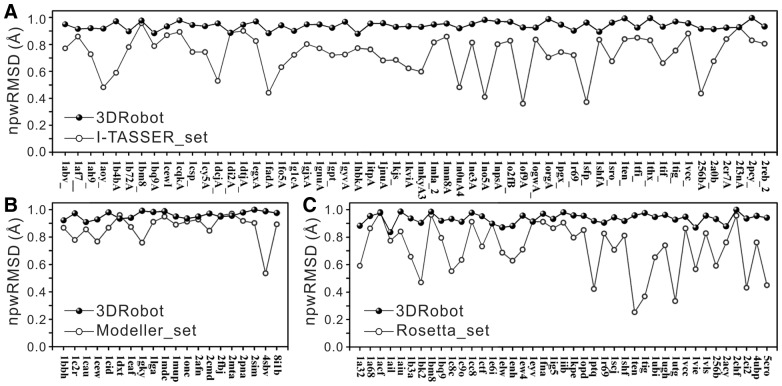
Figure 3 summarizes the npwRMSD scores for all proteins in the three decoy sets. Since Rosetta, Modeller and I-TASSER used specific ab initio and template-based modeling approaches to generate the model predictions, the diversity of the structure decoys is sensitive to the difficulty of the targets, whereby a high fluctuation is observed in all the decoys by the original simulation methods. In contrast, 3DRobot decoys have a steady and high npwRMSD score for all the proteins. The data demonstrates again the ability and robustness of 3DRobot in constructing diverged structure conformations for different type of protein folds.

Fig. 3.

Comparison of 3DRobot and control decoy sets on normalized pair-wise RMSD (npwRMSD). (A) I-TASSER_set; (B) Modeller_set; (C) Rosetta_set

3.4 Native structure recognition using trivial scoring function

Non-native structure decoys can be generated by deforming the native conformations (Park and Levitt, 1996). But brute-force deformation can break basic structure characteristics such as the hydrogen-bonding network or packing interactions. In fact, the decoys generated by many practical structure prediction methods are also prone to various unphysical structural biases, which make the native structures easily recognizable from such decoy sets (Handl et al., 2009; Park et al., 1997; Vajda et al., 2013). Since a high-quality decoy set should have the ability to ‘fool’ most of the generic scoring functions in native structure recognition (Yeh et al., 2015), here we designed two simple scores to test the decoy sets.

3.4.1 Percentage of secondary structure

Protein secondary structure elements (including alpha-helix and beta-sheet) are formed by regular arrangement of hydrogen-bonding networks of the backbone atoms. The hydrogen-bonding networks can be roughly counted by the percentage of secondary structure:

$$P_{\text{sec}}=\frac{N_{\text{sec}}}{L}\times 100$$ (7)

where N_sec is the total number of residues which are assigned as helix or strand by STRIDE (Frishman and Argos, 1995) and L is the length of protein chain.

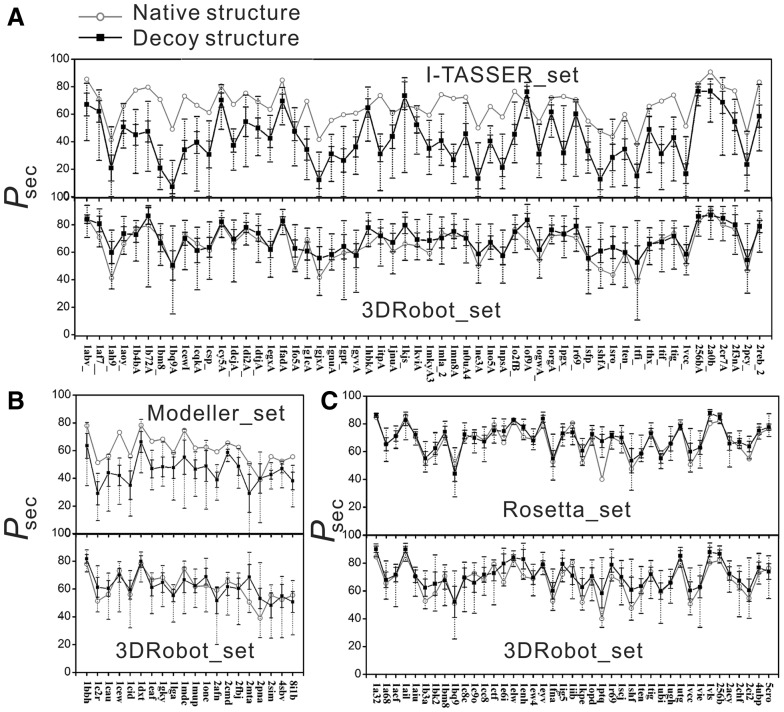
As shown in Table 1 (Column 8), the native structure in many of the control decoys can be recognized by simply counting P_sec. For example, 66% of proteins in the I-TASSER_set have the native structure with the highest P_sec. The problem is more significant for the beta-proteins since the long-range H-bonding can be easily broken in beta-sheets. Out of the 13 beta-proteins, 8 proteins have the native with the highest P_sec, while the number is only 5 in the 15 alpha-proteins. Similarly, 55% of proteins in the Modeller_set have the native structure with the highest P_sec. Rosetta_set performs much better than I-TASSER_set and Modeller_set but still has 7% of the cases that have the native structure recognizable by P_sec. In Figure 4, we listed the P_sec of decoys versus the native structures for all individual proteins in the three decoy sets. It is shown that the secondary structure of the native is clearly outside the decoy fluctuation region of the decoys for a number of proteins in the I-TASSER_set and Modeller_set, while the native is non-distinguishable from the decoys in all the 3DRobot decoys and most of the Rosetta_set.

Fig. 4.

Comparison of 3DRobot and control decoy sets on secondary structure distribution (P_sec) relative to the native structure. Open circles are P_set value for native structure and solid squares are the average P_sec for decoy conformations. The solid error bar denotes the standard deviation of P_sec for each decoy set. The dotted line with bar shows P_sec range of each decoy set. (A) I-TASSER_set; (B) Modeller_set; (C) Rosetta_set

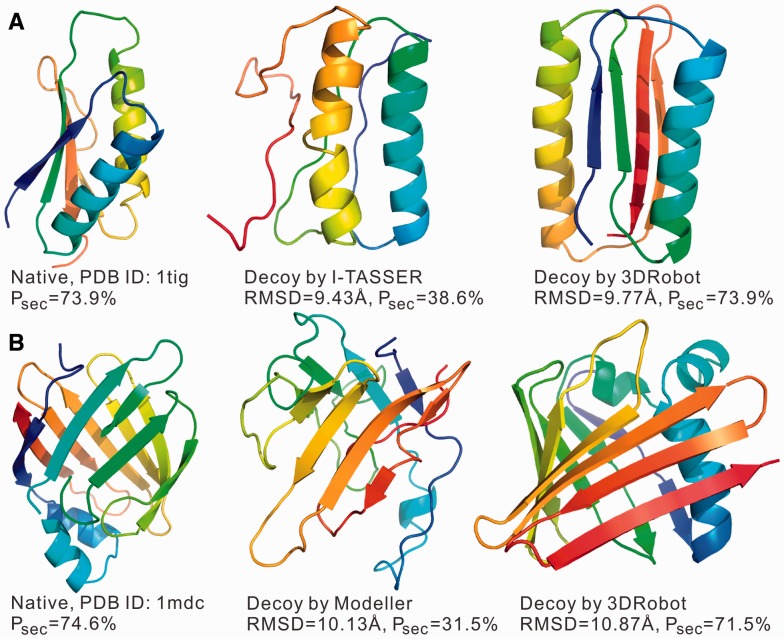
We also calculated the Z-score of P_sec, defined as the difference of the native from the mean in the unit of standard deviation, which measures how significant the P_sec of the native structure differ from the decoys. The I-TASSER_set has the highest P_sec Z-score (3.61), followed by Modeller_set (2.23) and Rosetta_set (1.23). The average Z-score of P_sec by 3DRobot is below 1.0 for all decoy sets, indicating that there is no significant difference in hydrogen bonding between 3DRobot decoys and the native structures despite the high RMS derivation. In Figure 5, we present 2 typical examples from the I-TASSER and Modeller decoy sets from the translation initiation factor (PDB ID: 1tig) and insect fatty acid binding protein (PDB ID: 1mdc), respectively. In both cases, the original decoy generators failed to generate sufficient secondary structure for a high structure deviation (RMSD > 9 Å) but 3DRobot has successfully created structure decoys with the P_sec score close to the native structure.

Fig. 5.

Typical examples of hydrogen bonding network construction for decoys with high structure deviations. (A) Comparison of decoy conformations of 1tig by I-TASSER and 3DRobot, respectively. (B) Comparison of decoy conformations for 1mdc by Modeller and 3DRobot, respectively

3.4.2 Radius of gyration

The native structure of globular proteins is usually tightly packed in cells with the radius of gyration approximately following R_G–2.2L^0.38 (Zhang et al., 2003). Column 10 of Table 1 lists the recognition results of the native structure by R_G in the three decoy sets. More than 1/4 of the proteins in the Rosetta_set can have the native structure recognized by R_G, which has an average Z-score of 1.84. The Modeller_set and I-TASSER_set only have 2 and 7 cases that have the native recognized by R_G. The average Z-score of R_G of Modeller_set and I-TASSER_set are 0.91 and 1.47, respectively, which are also lower than Rosetta_set (1.84). This is probably because Modeller and I-TASSER started from structure templates, which makes it easier to have native-like compactness than the ab initio structure folding simulations. However, we noticed that for the proteins whose compactness is notably higher or lower than that of common globular protein, the decoys by the template-based methods also tend to be significantly different from the native.

Column 11 shows the R_G recognition results for the decoys by 3DRobot. Since specific constraints to the native are considered in 3DRobot [see Equations (2–4) in Methods section), none of the native structure could be recognized by R_G in the 3DRobot decoys in the three decoy sets. There is only one target in the 3DRobot_set (PDB ID: 3ci3), which has an alpha-helix bundle fold but with two extended long tails that results in R_G higher than the decoy structures that have tails folded. The average Z-score of the 3DRobot decoys is generally below 0.70, which is lower than all the control decoy sets.

We also examined the compactness of decoys by simply counting the total number of residue pairs in contact (n_cont), with a separation > 5 residues and a Cα distance < 8 Å. A similar result to the radius of gyration were obtained, i.e. 11, 2 and 8 cases have the native structure recognized by n_cont in the Rosetta_set, Modeller_set and I-TASSER_set, respectively. But there is no native structure recognized by n_cont in the 3DRobot decoys.

Here we note that the concepts of P_sec and R_G have been introduced as criterions to assess the quality of the decoys in native structure recognition. However, these criterions should not (or cannot) be considered as restraints on structure folding simulations, because the native structure does not necessarily have the extreme P_sec and R_G scores. Meanwhile, the assessments for the decoy sets require the information of the native structure, which is not available in the structure prediction simulations.

3.5 Correlation of RMSD with simple scoring function

Instead of ranking the native structure, another approach to assess the quality of the structure decoys is to examine the Pearson correlation of the structure deviation with the simple or trivial potentials, such as percentage of secondary structure and structural compactness. However, it should be noted that the face value of the Pearson correlation is often dependent on the range of the RMSD distribution of the decoys. As shown in Supplementary Figure S4, e.g. there are no obvious correlations for the decoys in the local RMSD ranges. But a significant correlation coefficient (>0.8) can be obtained for the same decoy sets if we consider the overall RMSD range; this is often the issue for decoy sets with a low Evenness score. To reduce the bias from RMSD range, we only focus on the targets that have an Evenness score above 0.75 and calculate the Pearson correlation based on the same RMSD range (i.e. delete the decoys in the bins if the control sets have no decoy in these bins).

Table 2 lists a summary of the correlation between RMSD and the simple scoring function from the secondary structure percentage and the radius of gyration, respectively. The most noticeable correlations are the correlation between P_sec and RMSD from Modeller_set, which has a correlation coefficient of −0.739. In our unpublished data, we observed a strong correlation between RMSD and compactness for most of the decoy sets that generated by native structure perturbations. This correlation is not strong for the decoys generated by the structure simulations by the three control decoy sets. However, there are several cases where a strong RMSD-R_G correlation was observed in each of the decoy sets.

Table 2.

Pearson correlation between RMSD and secondary structure or compactness score

Decoy sets	Nta	Lb	Corr(RMSD, Psec)		Corr(RMSD, RG)
			Oric	3DRd	Oric	3DRd
Rosetta_set	7	102	−0.239	−0.253	0.335	−0.131
Modeller_set	14	148	−0.739	−0.268	0.209	0.022
I-TASSER_set	11	65	−0.287	−0.262	0.317	0.245
3DRobot_set	200	133		−0.247		0.163

^aN_t, number of decoy sets with an Evenness score above 0.75.

^bL, average protein length in the decoy sets.

^cOri, performance of the original decoys.

^d3DR, performance of the decoys generated by 3DRobot.

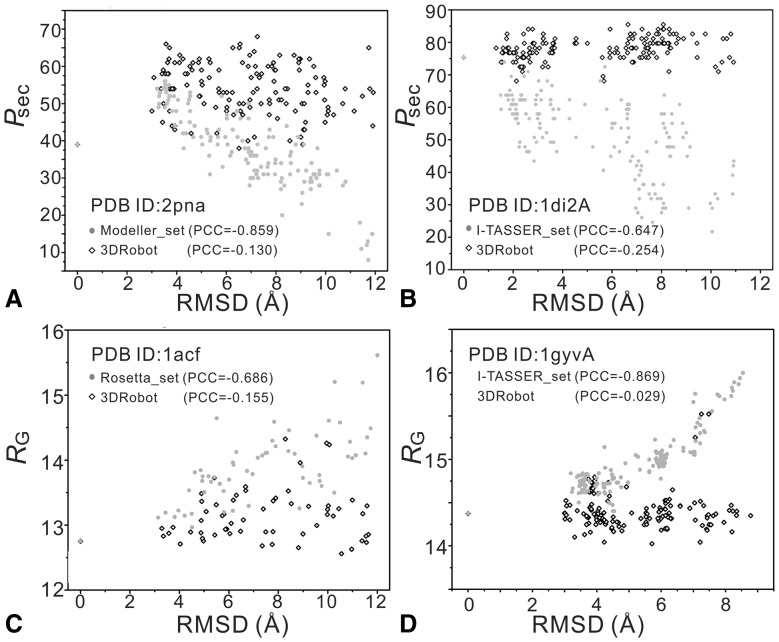
In Figure 6, we present four illustrative examples where the control decoy sets show a strong RMSD-P_sec or RMSD-R_G correlation, where 3DRobot generated decoys with a much lower correlation. The average correlation coefficients by 3DRobot are all lower than the control decoy sets, except for Rosetta_set that has a slightly lower correlation in RMSD-P_sec than 3DRobot; but Rosetta has the highest RMSD-R_G correlation (see Table 2).

Fig. 6.

Illustrative examples showing correlation of RMSD versus secondary structure (P_sec) or radius of gyrations (R_G). The gray solid circles denote the original decoys and the dark hollow diamond are the decoys by 3DRobot. (A) P_sec versus RMSD correlation from Modeller_set on 2pna; (B) P_sec versus RMSD correlation from I-TASSER_set on 1di2A; (C) R_G versus RMSD correlation from Rosetta_set on 1acf; (D) R_G versuss RMSD correlation from I-TASSER_set on 1gyvA

3.6 Native structure recognition using knowledge-based statistical potentials

In addition to the simple scoring functions, we also examined the decoys using more sophisticated knowledge-based potentials, including DFIRE (Zhou and Zhou, 2002), DOPE (Shen and Sali, 2006), KPB (Lu and Skolnick, 2001), RAPDF (Samudrala and Moult, 1998), RW (Zhang and Zhang, 2010) and SRS (Rykunov and Fiser, 2007), which have been widely used in protein model recognition studies. All these potentials were derived from the statistics of known protein structures in the PDB library based on the Boltzmann formulation but using different reference states, including ideal-gas (Zhou and Zhou, 2002), spherical non-interaction (Shen and Sali, 2006), quasi-chemical approximation (Lu and Skolnick, 2001), atomic average (Samudrala and Moult, 1998), random-walk (Zhang and Zhang, 2010) and atomic shuffling (Rykunov and Fiser, 2007). Since the original potentials were derived using different training datasets, to have a clear examination of the reference states we re-derived the potentials using the original reference formulas but based on a uniform, non-redundant set of 1022 high-resolution structures collected by PISCES server (Wang and Dunbrack, 2003). These re-derived potentials are labeled by a suffix ‘_REF’ to distinguish them from the original potentials.

In Table 3, we list the number of cases in which the native structure has the lowest energy (N_nat) and the average Z-score of the native structure when evaluated by each of the six potentials. RW-REF has on average the highest recognition rate (69%) and Z-score value (3.71) on the control decoys (Rosetta_set, Modeller_set and I-TASSER_set). But the difference between RW-REF and other potentials is not big, compared with the lowest N_nat = 59% and Z-score = 2.91 from KBP-REF, which confirm the observation made by the earlier sections and the previous studies, i.e. the native structure can be recognized by most scoring functions from the current existing decoys (Deng et al., 2012; Handl et al., 2009; Park et al., 1997; Vajda et al., 2013).

Table 3.

Native structure recognition results by six knowledge-based potentials on the 3DRobot and control decoy sets

Potentiala	Decoy sets	Nnatb		Z-scorec
		Orid	3DRe	Orid	3DRe
RAPDF-REF	Rosetta_set	2/41	0/41	2.07	0.94
	Modeller_set	19/20	1/20	3.05	1.41
	I-TASSER_set	49/56	0/56	5.28	1.67
	Average	70/1.7	1/1.7	3.47	1.34
KBP-REF	Rosetta_set	5/41	1/41	1.79	1.12
	Modeller_set	19/20	1/20	2.42	1.15
	I-TASSER_set	45/56	3/56	3.82	1.21
	Average	69/1.7	5/1.7	2.91	1.16
DFIRE-REF	Rosetta_set	6/41	0/41	2.64	1.06
	Modeller_set	19/20	3/20	2.98	1.13
	I-TASSER_set	53/56	0/56	5.08	1.25
	Average	78/1.7	3/1.7	3.57	1.15
Dope-REF	Rosetta_set	2/41	0/41	2.13	1.04
	Modeller_set	19/20	2/20	3.23	1.47
	I-TASSER_set	50/56	0/56	5.43	1.82
	Average	71/1.7	2/1.7	3.60	1.44
SRS-REF	Rosetta_set	5/41	0/41	2.27	0.96
	Modeller_set	19/20	1/20	3.18	1.40
	I-TASSER_set	49/56	0/56	5.11	1.67
	Average	73/1.7	1/1.7	3.52	1.34
RW-REF	Rosetta_set	9/41	0/41	2.74	1.07
	Modeller_set	19/20	2/20	2.94	1.16
	I-TASSER_set	53/56	0/56	5.45	1.26
	Average	81/1.7	2/1.7	3.71	1.16

^aPotential, which are reconstructed from a unified structure dataset by using different reference state models.

^bN_nat, number of proteins with the native structure ranked as first versus the total number of test proteins.

^cZ-score, average Z-score of the native structure on each potential.

^dOri, results based on the original decoy sets (Rosetta_set, Modeller_set and I-TASSER_set).

^e3DR, results based on the decoy sets generated by 3DRobot.

To clearly highlight the difference between the 3DRobot and the control decoys, in Table 4 we present the average results of N_nat and Z-score values from the six potentials. The data again show that the native structure could be recognized with high rate by the knowledge-based potentials, in particular from the decoys in the Modeller_set and I-TASSER_set, where the native structure was ranked as with the lowest energy in 95% and 89% of the cases, respectively. It is relatively more difficult to recognize the native structure from the Resetta_set, where there are on average 12% of the cases that have the native with the lower energy. The average Z-score of the native structure by the six potentials is 2.27, 2.97 and 5.03 for the Rosetta_set, Modeller_set and I-TASSER_set, respectively.

Table 4.

Summary of the native recognition results by the six knowledge-based potentials on the 3DRobot and control decoy sets

Decoy sets	Ndecoya	Nrec (%)b		Z-scorec
		Orid	3DRe	Orid	3DRe
Rosetta_set	41	4.8 (12%)	0.2 (0%)	2.27	1.03
Modeller_set	20	19.0 (95%)	1.4 (7%)	2.97	1.29
I-TASSER_set	56	49.8 (89%)	0.5 (1%)	5.03	1.48
Average	39	24.6 (63%)	1.0 (3%)	3.42	1.26

^aN_decoy, number of decoy sets.

^bN_rec, average number of cases with the native ranked as first (N_rec) and the percentage (=N_rec/N_decoy).

^cZ-score, average value of absolute Z-score of the native structure.

^dOri, results for the control decoys.

^e3DR, results for the 3DRobot decoys.

The recognition rate of the native structure in 3DRobot decoy sets is much lower than their control decoy sets, which has on average only 3% of the cases where the native has the lowest energy by the knowledge-based potentials. The average Z-score of the native structure is 1.26, which is 270% lower than the Z-score of the control decoys (3.42).

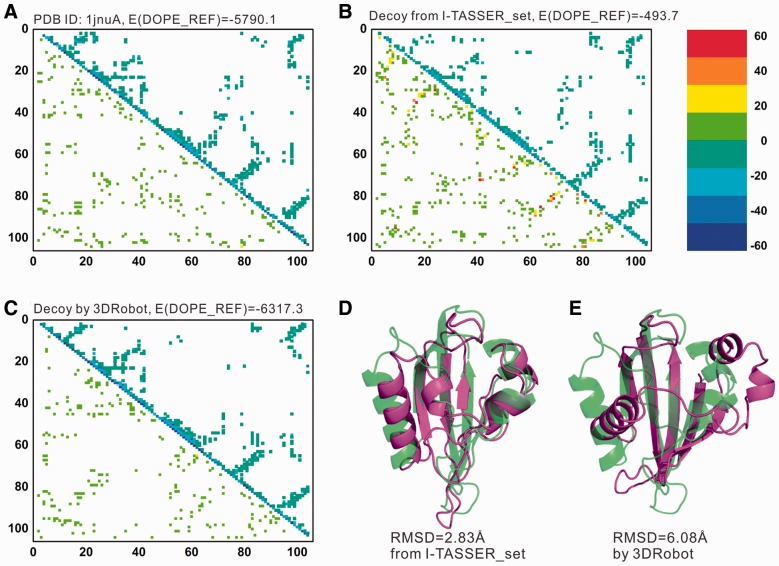
In Figure 7, we present a typical example on the plant photoreceptor domain (PDB ID: 1jnuA) from the I-TASSER_set, which has the decoys ranked by DOPE_REF potential. The first decoy generated by I-TASSER in Figure 7D has a low RMSD (2.83 Å) but there are many local sites that have energetically unfavorable contacts as highlighted by the dark dots (Fig. 7B); this results in an overall DOPE_REF energy of −493.7 that is much higher than that of the native structure (Fig. 7A). But in the decoy structure generated by 3DRobot, the high-energy spots disappear and the overall energy is −6317.3 (Fig. 7C), which is considerably lower than the native although the RMSD of the decoy is rather high (6.08 Å). Similar observation was obtained when the decoys are evaluated by other individual knowledge-based potentials. This example demonstrates the importance of the local structure packing for high quality decoy structure generations.

Fig. 7.

An illustrative example showing Dope_REF energies of the structure decoys by I-TASSER and 3DRobot. (A–C) X- and Y-axes are the residue order number. Energy for residue pair is calculated as the sum of energies of all atom pairs between the two residues. The upper triangle of each plot shows the energetically favorable residue pairs (energy<−3.0), and the lower triangle of each plot shows the energetically unfavorable residue pairs (energy > 3.0). Residue pairs with energy between −3.0 and 3.0 are not shown. Different colors are used to illustrate energy variation. (D–E) structure decoys by I-TASSER_set and 3DRobot (red) superposed on the native structure of 1jnuA (green)

4 Conclusion

Despite the central importance of structure decoys in protein folding strategy and force field developments, we found that almost all the currently used decoy sets suffer from significant issues in evenness distribution and structure diversity. Most of the existing decoy sets generate diversity by sacrificing the hydrogen-bonding networks and compactness, which render the native structures easily discriminable by simple calculations of regular secondary structure density and radius of gyration scores. The flawed decoys can result in non-protein-like bias when used for force field optimization and fold recognition training.

We developed a new decoy generation algorithm, 3DRobot, by extending the fragment assembly simulation protocol that starts from multiple structure scaffolds identified from the PDB library, with new potentials introduced to enhance the hydrogen-bonding network and compactness for high deviation conformations. 3DRobot was tested in control with three most widely used structure decoy sets generated by ab initio folding [Rosetta (Simons et al., 1997)], homology modeling [Modeller (John and Sali, 2003)] and threading assemble simulation [I-TASSER (Wu et al., 2007)]. The structure decoys generated by 3DRobot are found to have a significantly enhanced evenness and diversity score than that of control sets. This is mainly due to the fact that 3DRobot free fragment assembly simulations start from a set of optimally selected multiple templates designed with different levels of resolutions, while most of the control decoy sets were generated by the modeling simulations that aim to generate the best structure predictions; the structure distributions in these control decoy sets therefore depend on the difficulty of the target type. Here, although the decoys have been generated under the guidance of a modified I-TASSER scheme, there is no specific effort made on the decoys for I-TASSER force field refinements. In fact, a previous study has shown that decoys generated from one force field (e.g. I-TASSER) are generally more helpful for the parameter optimization of other force fields because the decoy conformations have not been overly optimized for the other force field (Zhang et al., 2003). Therefore, the fact that decoys are guided by the generalized I-TASSER potential should not necessarily affect their usefulness on testing and training of other force fields. In the meantime, appropriate combination of the decoy structures generated by other programs, such as CABS-flex (Jamroz et al., 2013), CAS-fold (Blaszczyk et al., 2013), Modeller (John and Sali, 2003), QUARK (Xu and Zhang 2012) and Rosetta (Simons et al., 1997), should help further enhance the generality and the conformational coverage of the decoys.

Further data analysis also showed that the new energy terms introduced in 3DRobot can improve the hydrogen-bonding networks and the compactness of structure decoys, which eliminate the possibility of native structure being recognized by trivial potentials as what most of the control decoy sets suffer. Finally, the decoy structures are tested by the more sophisticated knowledge-based potentials that were derived from the regularities of the high-resolution PDB structures. It was found that the native structure is more difficult to be recognized in the 3DRobot decoys than in the control decoys, where the number of cases that the native was ranked as the lowest is more than 20 times lower (or 4.8 time lower than the best Rosetta_set) in the 3DRobot decoys. Detailed analyses showed that the 3DRobot decoys have the local structures better packed, which makes the native structure more difficult to recognize. The robust decoy generations with less unphysical bias that are resistant to native recognition from trivial potential should have important usefulness and impact on designing and training protein folding force field and folding simulation methods. Here, one purpose for examining the 3DRobot decoys on the trivial (e.g. secondary structure and radius of gyration) and more sophisticated knowledge-based (e.g. Dfire and RW etc) potentials was to demonstrate the difference (or advantage) of 3DRobot from other decoy generators. It will be of interest to apply the 3DRobot decoys to test the performance of some of the more modern Model Quality Assessment Programs (MQAPs) [e.g. QMEAN4 (Benkert et al., 2008) and ProQ2 (Ray et al., 2012)] and more comprehensive potentials (Rosetta, QUARK and I-TASSER); the corresponding study is under progress and will be presented elsewhere.

Finally, we note that during the 3DRobot simulations many local structure features of the native structure (such as secondary structure and compactness) have been reinforced in order to eliminate the correlation between RMSD and the local structural characteristics and enhance the difficulty of the native structure recognition by trivial potentials. These decoy sets should find their usefulness in training the force fields for fold recognition and structure prediction that aim to identify the best final structure models. But cautions should be born when applying the decoys to training force field and models for protein folding simulations and dynamics, because the decoys have incorporated various levels of the characteristics of the native structures. Nevertheless, the force field that the nature uses to fold proteins (if such force field exists) may only favor the native secondary structure and does not necessarily have such correlation between RMSD and secondary structure. Further studies and experiments are needed to address these issues.

Funding

The work was supported in part by the National Institute of General Medical Sciences (GM083107, GM084222), the National Natural Science Foundation of China (No.11175068 and No.11474117), and China Scholarship Council (201206770004).

Conflict of Interest: none declared.