Abstract
Measurements of arterial input function (AIF) can have large systematic errors at standard contrast agent doses in dynamic contrast enhanced MRI (DCE-MRI). We compared measured AIFs from low dose (AIFLD) and standard dose (AIFSD) contrast agent injections, as well as the AIF derived from a muscle reference tissue and artery (AIFref). Twenty-two prostate cancer patients underwent DCE-MRI. Data were acquired on a 3 T scanner using an mDixon sequence. Gadobenate dimeglumine was injected twice, at doses of 0.015 and 0.085 mmol/kg. Directly measured AIFs were fitted with empirical mathematical models (EMMs) and compared to the AIF derived from a muscle reference tissue (AIFref). EMMs accurately fitted the AIFs. The 1st and 2nd pass peaks were visualized in AIFLD, but not in AIFSD, thus the peak and shape of AIFSD could not be accurately measured directly. The average scaling factor between AIFSD and AIFLD in the washout phase was only 56% of the contrast dose ratio (~6:1). The shape and magnitude of AIFref closely approximated that of AIFLD after empirically determined dose-dependent normalization. This suggests that AIFref may be a good approximation of the local AIF.
Keywords: Dynamic contrast enhanced MRI (DCE-MRI) of prostate cancer, Empirical mathematical model (EMM), Arterial input function (AIF), Contrast agent dose, First pass peak, Reference tissue method
1. Introduction
Dynamic contrast enhanced MRI (DCE-MRI) is one of the three primary components of the widely used multi-parametric prostate MRI protocol. Clinical DCE-MRI is usually acquired with a T1-weighted gradient echo sequence before and after IV bolus injection of contrast media. T1-weighted gradient echo sequences are sensitive to T1 changes due to the contrast agent, and often used for measurement of the volume transfer constant (Ktrans) and the extracellular extravascular space (ve) in prostate cancers. Aggressive prostate cancer is often associated with angiogenesis, producing tumor vasculature with higher blood flow and permeability than normal prostatic vessels [1,2]. As a result, prostate cancer typically shows earlier and more pronounced enhancement than surrounding normal prostatic tissues on DCE-MRI [3]. However, the rate of enhancement is strongly influenced by large inter-patient variations in the arterial input function (AIF) due to variability in cardiac output and systemic blood flow patterns. Therefore, precise measurement of the AIF is important for accurately, reliably, and reproducibly extracting tumor Ktrans and ve from DCE-MRI data [4,5].
In practice, the AIF is often estimated from a major artery under the assumption that this represents the exact input to the tissue [6]. However, direct measurements of the AIF from the artery are prone to partial volume effects, misregistration, inflow artifacts, etc., which can result in inaccurate AIF measurements [7]. Dose-dependent T2* and water exchange effects, in particular, were apparent even at half-dose contrast agent administration in a cardiac DCE-MRI sequence [8]. High blood concentrations of contrast agent cause an underestimation of AIF peak magnitude directly measured from the artery [9]. Therefore in practice, population AIFs are often employed in calculations of Ktrans [10]. However, the population AIF cannot take into account inter- and intra-patient physiological variations.
Accurate measurement of the AIF was the subject of several previous studies. Parker et al. measured the AIFs at 1.5 T with a temporal resolution of 4.97 s from patients' aortas or iliac arteries following a standard bolus administration of gadodiamide. They developed a functional form of a population AIF with 10 parameters that can be used when AIF measurement in each patient is impossible. Yankeelov et al. compared a reference region model of AIF with direct measurement of an AIF from Fischer-344 rat's aorta [11]. Their experiments were performed on a 1.89 T scanner with temporal resolution of 0.9 s following a bolus injection of 0.3 mmol/kg gadodiamide, and the contrast media concentration vs. time in the aorta was estimated by a combination of arterial blood sampling and phase-sensitive imaging. Kershaw et al. developed a dual-bolus technique, by splitting the contrast media dose of 0.2 mmol/kg into 20% for the pre-bolus and 80% for the main bolus, for quantitative DCE-MRI of rabbit aorta at 1.5 T [12]. They demonstrated that the AIF can be reliably measured following a low-dose pre-bolus with 0.44 s temporal resolution (using a TRICKS sequence [13]), giving the same curve as an AIF measured in the conventional way following a high-dose bolus with temporal resolution of 1.3 s. However, routine clinical DCE-MRI scans of the prostate are generally obtained at much lower temporal resolution (e.g. 3–12 s [14]).
In this study, we compared AIFs measured at 3 T after a low dose (0.015 mmol/kg) of contrast agent injected first (AIFLD), followed by a dose close to the standard dose (0.085 mmol/kg; AIFSD; referred to in this paper as the ‘standard dose’). The AIFLD measured directly from an artery is expected to approximate the true AIF, and serves as a ‘gold standard’ in this study [15]. A new empirical mathematical model (EMM) for the AIF (AIF-EMM) is introduced to fit both the first and second passes typically detected in AIFLD. A previously developed EMM was used to fit the AIFSD [16]. The AIFLD and AIFSD were compared qualitatively and quantitatively with and without an empirically determined normalization for contrast dose. The AIF derived from the contrast media concentration as a function of time (AIFref) in a muscle reference tissue and artery [17] following the standard contrast agent dose was compared with AIFLD. This reference tissue method approximates the AIFLD shape well, while being computationally simpler than earlier indirect AIF estimation methods [18,19].
2. Materials and methods
2.1. Patient recruitments
The study was compliant with the Health Insurance Portability and Accountability Act and approved by our institutional review board, and all participants provided written informed consent. Twenty-two patients (n = 22) with biopsy confirmed that prostate cancer were enrolled in this study (mean age = 57.3 years, range 43 to 70 years). A glomerular filtration rate value greater than or equal to 60 ml/min/1.73 m2 was required.
2.2. Image acquisition
All images were acquired with a Philips Achieva 3 T TX scanner using the combination of a phased array and endorectal coil. The routine clinical MRI protocol was adapted to allow AIF and tissue contrast uptake measurement, as well as a clinical reading. After other clinically required scans, two sets of axial dual-echo 3D T1-weighted (T1W) DCE-MRI data (TR/TE1/TE2 = 4.8/1.69/3.3 ms, flip angle = 10°, field of view (FOV) = 250 × 380 × 84 mm3 (AP × RL × SI extent), resolution = 1.25 × 1.75 × 3.5 mm3, reconstruction resolution = 1.0 × 1.0 × 3.5 mm3, SENSE factor = 1.67, partial Fourier factor = 0.675, temporal resolution = 8.3 s) were acquired by using a two-point modified Dixon (mDixon) method to produce the ‘water-only’ images used for analysis [20,21]. The mDixon sequence provided excellent fat-suppressed images with fewer artifacts, as compared to using fat inversion pre-pulses [22].
The total amount of contrast agent gadobenate dimeglumine (Multihance, Bracco, Minneapolis, USA) injected was a standard dose given based on patient's weight (0.1 mmol/kg). The first low dose (15% of total) of contrast agent, 0.015 mmol/kg, was injected I.V. at a speed of 0.35 ml/s, followed by a 20 ml saline flush. T1W images were acquired for a total of ~3.5 min, with 5 sets taken pre-injection and 25 sets taken post-injection of the contrast agent. The second higher dose (85% of total, but referred to as the ‘standard’ dose) of contrast agent, 0.085 mmol/kg, was injected I.V. at a speed of 2.0 ml/s, followed by a 20 ml saline flush. The speed of injection for the lower dose was calculated so that the duration of the two injections was the same. This allowed direct comparison of the concentration vs. time curve shapes. This approach is similar to that of Kershaw and Cheng, where the lower bolus dose was diluted to the same volume as the higher one, and the two doses were injected at the same speed [12]. The second scan started 5 min after the first scan finished. Subsequently, T1W images were acquired for a total of ~8.3 min with 5 sets taken before and 55 sets taken during and after the second injection.
2.3. Data analysis
2.3.1. Contrast agent concentration curves
Data analysis was performed using Matlab (MathWorks, Natick, MA) with software built in-house. Since a low concentration of contrast agent and short TR/TE were used in our DCE-MRI acquisition, the relationship between the contrast agent concentration and the enhanced MR signal was very close to linear [23]. The signal intensity of DCE-MRI was converted to contrast agent concentration using the muscle as reference tissue. For each pixel, tissue contrast agent concentration as a function of time, C(t), before and after injection was estimated by comparing the change in signal intensity, S(t) - S(0), (where S(0) and S(t) are the signal intensities before contrast injection and at a later time t), with a reference tissue (in this case muscle) with known baseline T1. Because TR ≪ T1, we can approximate signal intensity as a linear function of T1 and contrast medium concentration [24]:
| (1) |
where r1 (6.3 mM−1s−1 for gadobenate dimeglumine) [25] is the longitudinal relaxivity of the contrast agent at 3 T, T1(muscle) = 1420 ms [26], and Smuscle(0) is the muscle signal intensity before contrast injection.
2.3.2. Comparison of AIFs
The C(t) curves were averaged over the regions-of-interest (ROIs) to increase the signal-to-noise ratio (SNR). We determined the AIFs in two ways: (i) direct measurement from the artery for low and (approximately) standard dose contrast injections; and (ii) using the ‘reference tissue plus artery’ method [17] from standard dose contrast media concentration curves. For direct measurements, the AIF was determined by manually tracing ROIs to delineate cross sections of the external femoral artery on 6–10 slices perpendicular to the artery. The average (± standard deviation) number of voxels used to measure signal intensity in the artery in each patient was 73 ± 19. The directly measured AIFs were corrected to determine blood plasma concentration of contrast agent by dividing by 1-Hct, where the hematocrit (Hct) was assumed to equal 0.42.
We fit the directly measured AIFs to two different empirical mathematical models due to their different shapes. To fit AIFLD we developed a new mathematical model, AIF-EMM, with eight parameters:
| (2) |
where A and An are scaling constants, tn and σn are centers and widths of the nth Gaussian function for 1st and 2nd pass, and β is the decay constant of the exponential describing the washout of the contrast agent.
For the higher dose of contrast agent, the 1st and 2nd passes in the AIFSD were not as clearly resolved as they were with low dose AIFLD. Therefore for AIFSD, a modified empirical mathematical model (EMM) [16] with three parameters was used to fit the curve:
| (3) |
where A is the upper limit of tracer concentration, α is the rate of contrast media uptake (min−1), and γ (min−1) is the rate of contrast washout. Fits were optimized using the non-linear Levenberg–Marquardt algorithm, and evaluated by calculating the goodness-of-fit (R2). R2 is defined as the ratio of the sum of squares of the regression (SSR) and the total sum of squares (SST).
To derive AIFref, a gluteal muscle region was selected as a reference tissue on 6–10 slices and its concentration vs. time curve was analyzed. Assuming that the muscle satisfies the two-compartment model [27], Ktrans and ve of muscle were adjusted so that the AIF derived from the two compartment model matched the washout phase of the directly measured AIF (AIFSD) after the 1st pass of the contrast media bolus. AIFref was then derived from the full muscle Cm(t) for standard dose of contrast agent using Eq. (4):
| (4) |
where the Ktrans and ve for muscle were determined as described above [17].
The peak magnitudes of AIFLD, AIFSD and AIFref were compared and the coefficients of variations (CV) were calculated for all fitted parameters. The paired Student's t-test was used to test for differences between peak magnitudes of AIFLD and AIFSD. The paired Student's t-test was also used to test for differences between peak magnitudes of AIFLD and AIFref, after empirically matching AIFLD and AIFSD at 3 min post-injection. Pearson's correlation was calculated between peak magnitudes of AIFLD and AIFSD, and between AIFLD and AIFref. A p-value less than 0.05 was considered significant.
3. Results
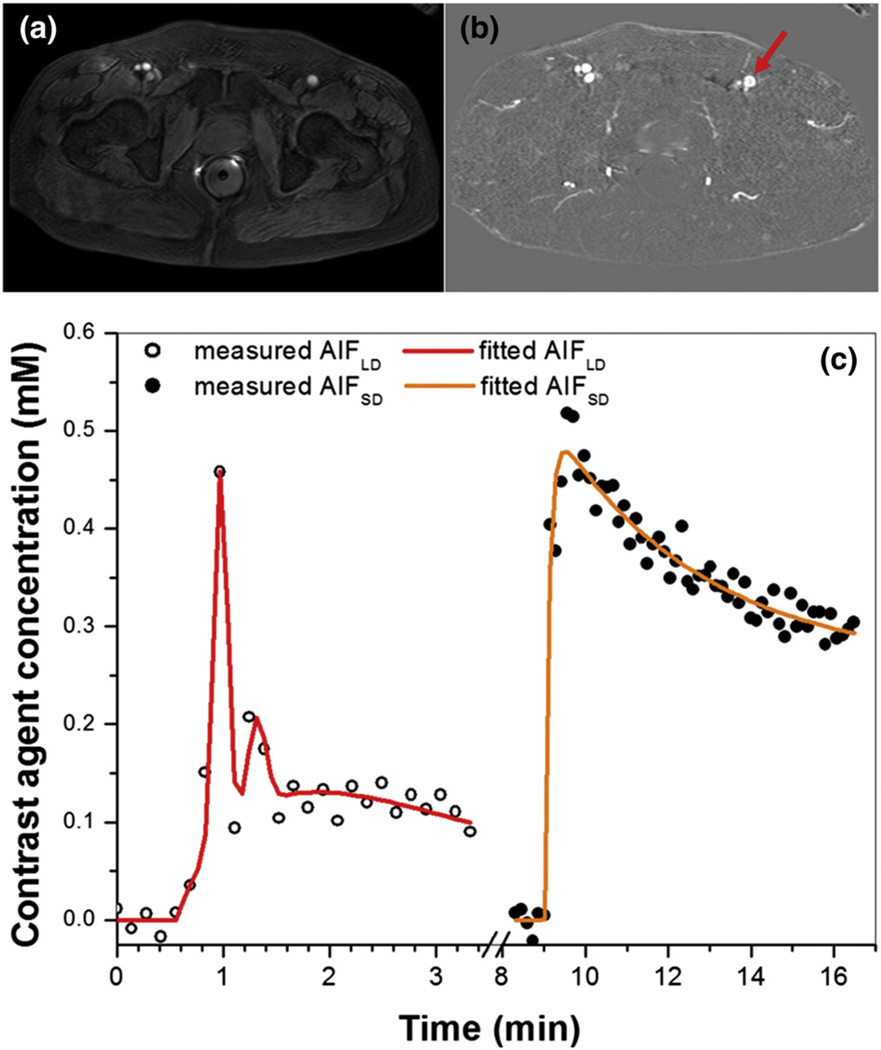
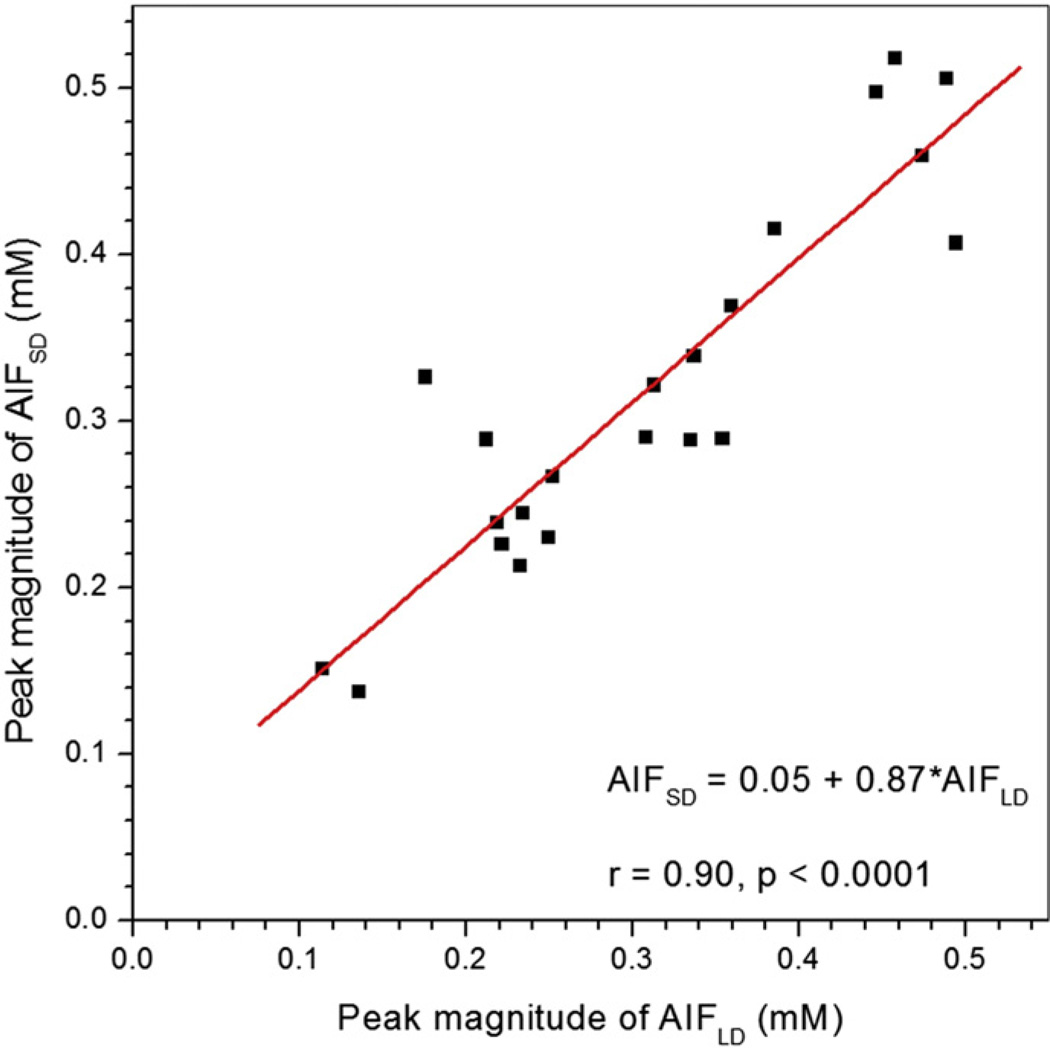
Fig. 1 shows (a) an axial slice from the pre-contrast agent (low dose) DCE-MRI series, (b) a difference image (post minus pre-contrast agent injection), and (c) the directly measured AIFLD (open circles) and AIFSD (solid circles) from the femoral artery of a typical patient (indicated by red arrow), as well as the EMM fits (red and orange lines) for the corresponding AIFs. The 1st and 2nd pass peaks of the contrast bolus can be clearly seen in AIFLD despite limited temporal resolution, while neither peak is detectable in AIFSD. Without normalizing to contrast dose, the average peak magnitudes of AIFLD (0.31 ± 0.11 mM) and AIFSD (0.32 ± 0.11 mM) calculated from the linear approximation for contrast agent concentration (Eq. (1)) did not differ (p > 0.30). Thus the average ratio of the peak magnitudes of the AIFs (approximately 1.03) is much lower than the ratio of the contrast doses (approximately 5.7). Since the peak of the AIF (in mM) should be proportional to dose, the results suggest that true peak of the AIF cannot be detected at the standard dose of contrast media. Despite the fact that the true peak of AIFSD was not detected, the correlation between the peak magnitudes of AIFLD and AIFSD was positive and very strong (r = 0.90, p < 0.0001) (Fig. 2). The peak amplitudes of both AIFLD and AIFSD varied by approximately a factor of four between maximum and minimum across the patients studied.
Fig. 1.
(a) An axial slice imaged with pre-contrast agent (low dose) injection DCE-MRI, (b) difference image between post and pre-contrast agent injection, and (c) corresponding AIFs from femoral artery (indicated by red arrow). Plots of AIFs measured from low dose (open circles) and standard dose (solid circles) contrast administration are plotted, as well as the corresponding fits by the EMM models (red and orange lines) for a representative subject. Note that AIDLD did not scale by the contrast agent dose ratio of 5.67. The plots were displayed in the order of DCE-MRI acquisition.
Fig. 2.
Scatter plot of peak magnitudes of AIFLD vs. AIFSD without scaling of AIFLD for contrast dose is shown. The red line is the linear fit through the data points. The linear relationship between AIFLD and AIFSD peak magnitudes, their correlation coefficient (r), and p value are shown on the plot.
The average ratio of the measured concentrations in the washout portions of AIFSD and AIFLD (minutes ~2.6 to ~3.3) was 3.15 ± 0.99 (based on the linear approximation for concentration). This value is approximately 56% of the contrast dose ratio (0.85 ml/kg/0.15 ml/kg = 5.67) that would be expected if contrast media concentration were accurately calculated.
Both EMM models provided good fits to AIFs (with goodness-of-fit parameters R2 > 0.90) despite AIFLD having lower SNR. The average EMM fitting parameters, their standard deviations (s.d.), and coefficients of variation (CV) are given in Tables 1 and 2. For the AIFLD, the average first pass magnitude (A1) was more than 10 times that of the average second pass magnitude (A2) and the average first pass width (σ1) was more than 1.4 times smaller than that of the second pass (σ2), reflecting the broadening of the second pass bolus. The parameters governing the 2nd pass (A2 and σ2) had larger CVs than other parameters. The average time difference (t2–t1) between the peaks of the 1st and 2nd passes was 0.41 min (25 s). For AIFSD, the parameters governing the contrast uptake and washout (α and γ) had larger CVs than the upper limit of tracer concentration (A).
Table 1.
Average AIF-EMM parameters and goodness of fit (R2), and their standard deviations (s.d.) and coefficients of variations (CV) for AIFLD (n = 22).
| A (mM) |
β (min−1) |
A1 | σ1 (min) |
t1 (min) |
A2 | σ2 (min) |
t2 (min) |
R2 | |
|---|---|---|---|---|---|---|---|---|---|
| Average | 0.31 | 0.70 | 5.84 | 0.09 | 0.20 | 0.46 | 0.12 | 0.62 | 0.95 |
| s.d. | 0.14 | 0.15 | 2.47 | 0.03 | 0.08 | 0.24 | 0.08 | 0.09 | 0.02 |
| CV | 0.44 | 0.22 | 0.42 | 0.38 | 0.40 | 0.52 | 0.65 | 0.15 | 0.02 |
Table 2.
Average EMM parameters and goodness of fit (R2), and their standard deviations (S.D.) and coefficients of variations (CV) for AIFSD (n = 22).
| A (mM) | α (min−1) | γ (min−1) | R2 | |
|---|---|---|---|---|
| Average | 0.36 | 8.93 | 0.61 | 0.93 |
| s.d. | 0.12 | 5.40 | 0.48 | 0.09 |
| CV | 0.32 | 0.61 | 0.80 | 0.09 |
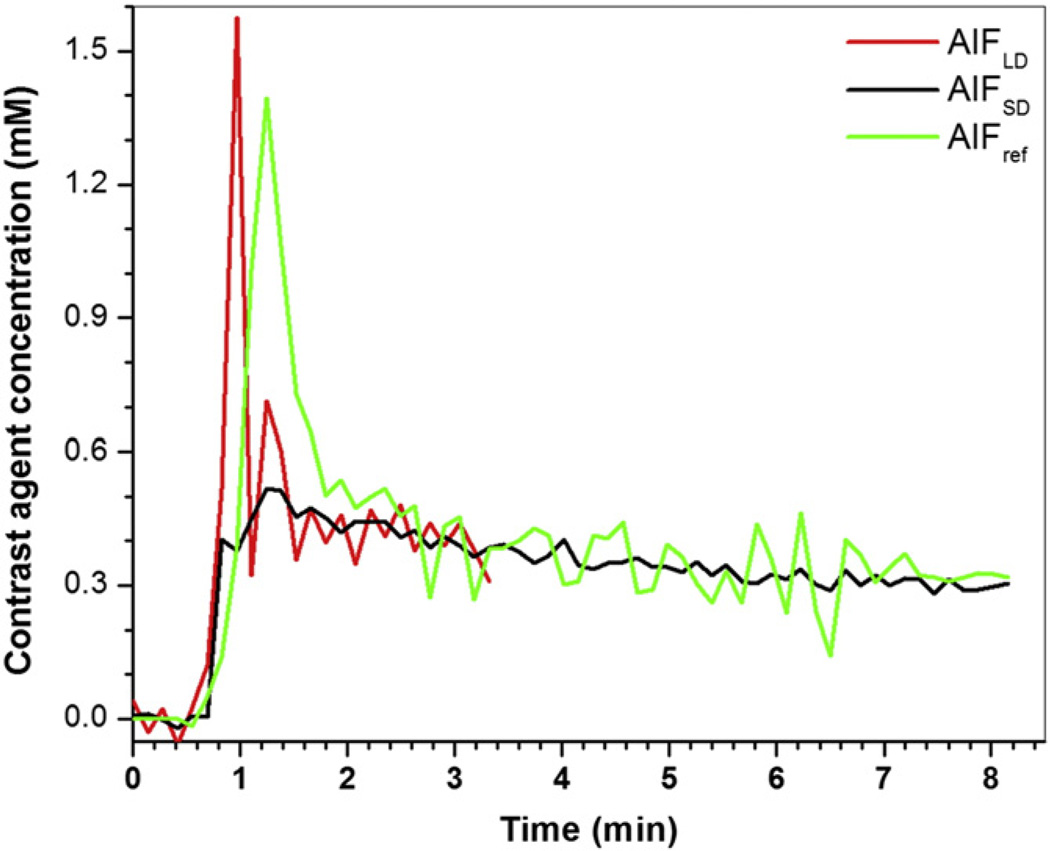
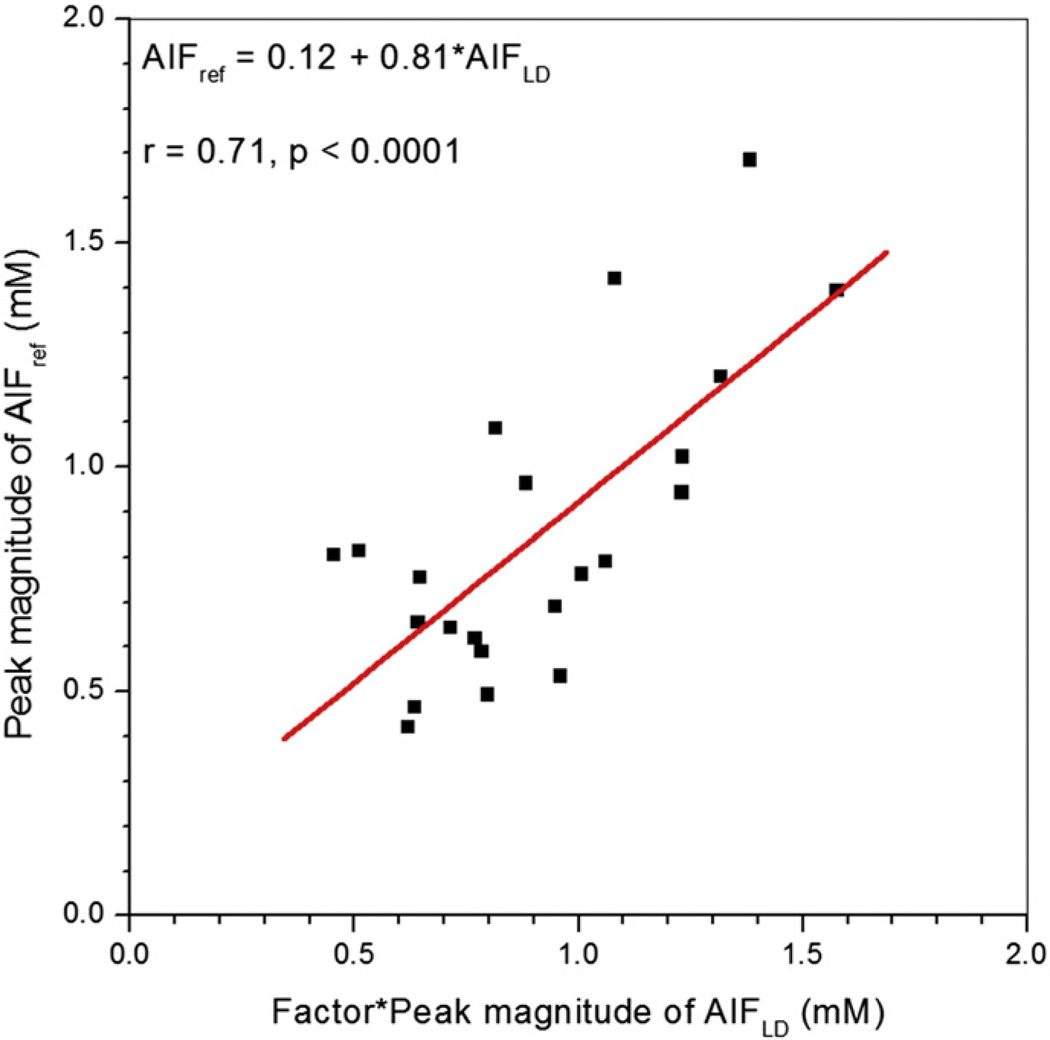
Fig. 3 shows an example of AIFref (green line) derived from the muscle contrast agent concentration vs. time curve, compared with the corresponding AIFLD (red line) and AIFSD (black line) measured in the same patient. To compare shapes directly, AIFLD was scaled using the MR-measured concentration ratio, so that the washout parts of all three curves match. Generally, the peak of AIFref was delayed and broadened when compared to directly measured AIFLD, while the peak magnitude of AIFref was close in value to peak magnitude of the scaled AIFLD. The second pass peak was generally not detected in AIFref. Fig. 4 shows a scatter plot of peak magnitudes of AIFLD multiplied by MR-measured concentration ratio vs. peak magnitudes of AIFref derived from muscle curves. The average peak magnitude of AIFLD (0.91 ± 0.30 mM) did not differ significantly (p > 0.25) from the average peak magnitude of AIFref (0.85 ± 0.34 mM). There was moderate positive correlation (r = 0.71, p < 0.0001) between these two peak magnitudes.
Fig. 3.
Plots of AIFLD (red line), AIFSD (black line), and AIFref (green line) derived from muscle reference tissue are shown for a representative subject. AIFLD was scaled by the MR-measured concentration ratio in the washout portions.
Fig. 4.
Scatter plot of peak magnitudes of AIFLD scaled by MR-measured concentration ratio vs. AIFref is shown. The red line is the linear fit through the points. The linear relationship between scaled AIFLD and AIFref peak magnitudes, their correlation coefficient (r), and p value are given on the plot.
The average values (± standard deviation) for muscle Ktrans and ve derived from the ‘reference tissue plus artery’ calculation were 0.066 ± 0.035 min−1 and 0.17 ± 0.07, respectively.
4. Discussion
The AIFs following the low and standard dose contrast agent injections were measured and compared for a total of 22 patients. The results demonstrate that the 1st and 2nd passes of contrast bolus in directly measured AIFs could be detected following the low dose of contrast agent, but not following the standard dose. This is consistent with previously published work on DCE-MRI for breast tumors [15]. The main reasons for this discrepancy were likely T2* and to a lesser degree water exchange effects [28,29] associated with the high blood concentration of contrast agent at early times for AIFSD. The low dose of contrast agent (15% of the standard dose) was expected to produce minimal T2* and negligible water exchange effects. Therefore AIFLD was expected to closely approximate the true AIF shape, and was used as ‘gold standard’.
The present results are inconsistent with those of Kershaw and Cheng [12], showing that scaled pre-bolus AIF is equivalent to the AIF from a high-dose injection measured from rabbit aorta in sagittal plane. However, they acquired data at 1.5 T, so that T2* effects were greatly reduced relative to the current study performed at 3 T. A dual-echo modified Dixon pulse sequence was used in our experiments, which may have increased T2* effects. In addition, Kershaw et al. used a view-sharing method (TRICKS) which samples the outer portion of k-space less frequently than the center of k-space [13]. Consequently this approach reduced effective temporal resolution for arteries.
Although our results show that measurements of the AIF directly from arteries are much more accurate when a low dose of contrast agent is injected, the low dose results in very weak tissue enhancement, and this will reduce the accuracy of Ktrans and ve calculations. Therefore, a low dose tissue contrast agent uptake curves should be fitted with a mathematical model prior to fitting to the pharmacokinetic model for routine clinical practice.
The lack of the first pass peak makes AIFSD unsuitable for quantitative calculation of Ktrans and ve. The necessity for this correction is demonstrated by the very large inter-patient variation in AIFLD, AIFSD, and AIFref. For example, the peak concentrations of AIFLD and AIFSD vary by more than 4-fold in the group of patients studied here. Failure to correct for variations in AIF will lead to large systematic errors in Ktrans. The correlation between peak amplitudes of AIFLD and AIFref is weaker than the correlation between AIFLD and AIFSD. This may be due to the fact that AIFref represents a local AIF derived from a muscle ROI that is some distance away from the artery. Limited SNR of the muscle reference tissue signal may also be a factor. Nevertheless, the correlation between AIFref and AIFLD is highly significant, and this suggests that reference tissue methods provide an alternative way to estimate the local AIF if it cannot be accurately measured directly.
During the washout phase the discrepancy between dose-normalized AIFLD and AIFSD is smaller than at the peak, as expected, due to the lower blood concentration of contrast media during washout. However, the scaling factor (3.15) required to match AIFLD and AIFSD in the washout phase measured by MRI is only about 56% of the dose ratio (5.67). Thus the signal enhancement produced by the standard dose is less than expected, even in the washout phase. Preliminary results (not presented here) indicate that the MR-measured concentration ratio does not change significantly with use of the full signal model in place of Eq. (1), and does not reach the value 5.67 expected from the contrast dose ratio. However, improvements in the signal model, accurate mapping of the B1 excitation field, and accurate measurements of native T1 may result in a larger MR-measured concentration ratio that corresponds to the ratio of contrast media doses during the washout phase. We are currently working to refine these calculations. While this may affect the magnitude of the measured concentration curves, it will not affect the shape differences between AIFLD and AIFSD and shape similarity between AIFLD and AIFref.
The peak magnitude of AIFref was much larger than the peak magnitude of AIFSD, and was close in value to that of AIFLD when the empirical correction for the difference in dose (multiplication by 3.15) was used. The muscle Ktrans and ve extracted from the fitting for AIFref are consistent with the results of previous studies by Padhani et al [30]. Padhani et al. found Ktrans = 0.133 ± 0.092 (min−1) and ve = 0.12 ± 0.03, providing validation for our approach. Compared to AIFLD, the first pass peaks in AIFref were slightly delayed and broadened. This is likely due to differences in timing and shape of the local AIF for gluteal muscle compared to the external femoral artery, suggesting that the reference tissue calculation is providing a good estimate of local AIF [31]. Although small differences exist, the results suggest that AIFref is a better model of the true AIF than the directly measured AIFSD obtained with the standard dose of contrast agent.
The Parker population AIF [10] was not optimal for fitting the data acquired in this study. This may have been due to the difference in field strength (1.5 T vs. 3 T) and/or the limited SNR of our data. There were also differences in contrast agent dose, the molecular structure of the contrast agents, methods used to convert the MRI signal to contrast agent concentration, location of ROIs, temporal resolutions, and MRI pulse sequences. Therefore, we developed a simpler model based on Gaussian functions with eight parameters (AIF-EMM) for the first and second pass peaks to fit AIFLD. The AIFSD was fit with a modified empirical mathematical model (EMM) with three parameters [16]; a different mathematical model was needed for AIFSD because the shapes of AIFSD and AIFLD are very different. Because different mathematical models were used to fit AIFLD and AIFSD, the fitting parameters could not be directly compared to those from previous studies. However, some of the parameters derived here can be compared to corresponding parameters measured by Parker et al. [10], because both this study and Parker et al. use Gaussian functions to describe the 1st and 2nd passes. The average widths (σ1 = 0.087, σ2 = 0.121) and centers (t1 = 0.203, t2 = 0.461) measured in our AIFLD were close to Parkers' measurements (σ1 = 0.056, σ2 = 0.132; t1 = 0.170, t2 = 0.365). The magnitude parameters measured here cannot be directly compared to the results obtained by Parker et al. due to the significant differences in protocols as discussed above. For instance, the reference tissue method used here to convert the MRI signal to contrast agent concentration could exhibit bias, even as it minimizes the error propagation from using variable flip angle measurements of T1.
There are several limitations in this study. First, the temporal resolution of the dynamic acquisitions is lower than that used in other studies of the AIF, and it is possible that the magnitude and shape of the 1st pass were not accurately assessed in AIFLD. The temporal resolution in the present study was dictated by clinical requirements. Second, the arterial ROIs used to measure the AIFs were selected far from the aorta, in order to obtain an approximately local AIF for the pelvic region. This may have resulted in relatively broad AIFs that are systematically different from AIFs reported in previous studies. Third, the AIF for the high dose did not correct for the small amount of residual contrast agent remaining from the earlier low dose injection, as this would affect the measured peak enhancement and washout rate of the contrast agent only minimally. Finally, the method used to convert the MRI signal to the contrast agent concentration may introduce errors by assuming the simple linear relationship between signal enhancement and concentration. This limitation does not affect the conclusions of our study, as the approximation was used to compare AIF shapes; the exact contrast agent concentrations and Ktrans values were not the focus of this work. In the future, a more accurate method will be developed to reduce errors and allow a more quantitative analysis of measured or derived AIFs. Any future improvements, however, will not eliminate the shape differences between AIFLD and AIFSD (presence vs. absence of first pass peak).
In summary, we compared the AIFs measured following a low dose (0.015 ml/kg) and a close-to-standard dose (0.085 ml/kg) contrast agent injection. The AIFLD is much sharper than AIFSD with a pronounced first pass peak and a peak due to the second pass of the bolus. AIFLD provides an approximate gold standard that can guide development of methods for accurately calculating the AIF following a standard dose of contrast agent. The peak and shape of the AIF was not detected accurately following the standard dose of contrast media at 3 T. This is probably due to T2* and ‘shutter speed’ effects associated with high plasma concentrations of contrast media. Direct arterial measurement of the AIF produced a significant under-estimate of peak arterial enhancement following the standard dose of contrast agent, and this would result in large systematic errors in calculations of pharmacokinetic parameters. The ‘reference tissue plus artery’ method can be used in combination with a standard dose of contrast media to more accurately derive the local AIF.
Acknowledgments
This research is supported by NIH R01 CA172801-01.
References
- 1.Bigler SA, Deering RE, Brawer MK. Comparison of microscopic vascularity in benign and malignant prostate tissue. Hum Pathol. 1993;24(2):220–226. doi: 10.1016/0046-8177(93)90304-y. [DOI] [PubMed] [Google Scholar]
- 2.Siegal JA, Yu E, Brawer MK. Topography of neovascularity in human prostate carcinoma. Cancer. 1995;75(10):2545–2551. doi: 10.1002/1097-0142(19950515)75:10<2545::aid-cncr2820751022>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- 3.Noworolski SM, Henry RG, Vigneron DB, Kurhanewicz J. Dynamic contrast-enhanced MRI in normal and abnormal prostate tissues as defined by biopsy, MRI, and 3D MRSI. Magn Reson Med. 2005;53(2):249–255. doi: 10.1002/mrm.20374. [DOI] [PubMed] [Google Scholar]
- 4.Fennessy FM, Fedorov A, Penzkofer T, Kim KW, Hirsch MS, Vangel MG, et al. Quantitative pharmacokinetic analysis of prostate cancer DCE-MRI at 3 T: comparison of two arterial input functions on cancer detection with digitized whole mount histopathological validation. Magn Reson Imaging. 2015;33(7):886–894. doi: 10.1016/j.mri.2015.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sanz-Requena R, Prats-Montalban JM, Marti-Bonmati L, Alberich-Bayarri A, Garcia-Marti G, Perez R, et al. Automatic individual arterial input functions calculated from PCA outperform manual and population-averaged approaches for the pharmacokinetic modeling of DCE-MR images. J Magn Reson Imaging. 2015;42(2):477–487. doi: 10.1002/jmri.24805. [DOI] [PubMed] [Google Scholar]
- 6.Mendichovszky IA, Cutajar M, Gordon I. Reproducibility of the aortic input function (AIF) derived from dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) of the kidneys in a volunteer study. Eur J Radiol. 2009;71(3):576–581. doi: 10.1016/j.ejrad.2008.09.025. [DOI] [PubMed] [Google Scholar]
- 7.van Osch MJ, Vonken EJ, Bakker CJ, Viergever MA. Correcting partial volume artifacts of the arterial input function in quantitative cerebral perfusion MRI. Magn Reson Med. 2001;45(3):477–485. doi: 10.1002/1522-2594(200103)45:3<477::aid-mrm1063>3.0.co;2-4. [DOI] [PubMed] [Google Scholar]
- 8.Duan Y, Loeffler RB, Song R, Tipirneni A, Spunt S, Oesingmann N, et al. A robust method for reducing inflow artifacts in the arterial input function of dynamic contrast enhanced data sets. Proc Intl Soc Mag Reson Med. 2011;19 [Google Scholar]
- 9.Gatehouse PD, Elkington AG, Ablitt NA, Yang GZ, Pennell DJ, Firmin DN. Accurate assessment of the arterial input function during high-dose myocardial perfusion cardiovascular magnetic resonance. J Magn Reson Imaging. 2004;20(1):39–45. doi: 10.1002/jmri.20054. [DOI] [PubMed] [Google Scholar]
- 10.Parker GJ, Roberts C, Macdonald A, Buonaccorsi GA, Cheung S, Buckley DL, et al. Experimentally-derived functional form for a population-averaged high-temporal-resolution arterial input function for dynamic contrast-enhanced MRI. Magn Reson Med. 2006;56(5):993–1000. doi: 10.1002/mrm.21066. [DOI] [PubMed] [Google Scholar]
- 11.Yankeelov TE, Cron GO, Addison CL, Wallace JC, Wilkins RC, Pappas BA, et al. Comparison of a reference region model with direct measurement of an AIF in the analysis of DCE-MRI data. Magn Reson Med. 2007;57(2):353–361. doi: 10.1002/mrm.21131. [DOI] [PubMed] [Google Scholar]
- 12.Kershaw LE, Cheng HL. A general dual-bolus approach for quantitative DCE-MRI. Magn Reson Imaging. 2011;29(2):160–166. doi: 10.1016/j.mri.2010.08.009. [DOI] [PubMed] [Google Scholar]
- 13.Korosec FR, Frayne R, Grist TM, Mistretta CA. Time-resolved contrast-enhanced 3D MR angiography. Magn Reson Med. 1996;36(3):345–351. doi: 10.1002/mrm.1910360304. [DOI] [PubMed] [Google Scholar]
- 14.Hansford BG, Peng Y, Jiang Y, Vannier MW, Antic T, Thomas S, et al. Dynamic contrast-enhanced MR imaging curve-type analysis: is it helpful in the differentiation of prostate cancer from healthy peripheral zone? Radiology. 2015;275(2):448–457. doi: 10.1148/radiol.14140847. [DOI] [PubMed] [Google Scholar]
- 15.Makkat S, Luypaert R, Sourbron S, Stadnik T, De Mey J. Assessment of tumor blood flow in breast tumors with T1-dynamic contrast-enhanced MR imaging: impact of dose reduction and the use of a prebolus technique on diagnostic efficacy. J Magn Reson Imaging. 2010;31(3):556–561. doi: 10.1002/jmri.22077. [DOI] [PubMed] [Google Scholar]
- 16.Fan X, Medved M, River JN, Zamora M, Corot C, Robert P, et al. New model for analysis of dynamic contrast-enhanced MRI data distinguishes metastatic from nonmetastatic transplanted rodent prostate tumors. Magn Reson Med. 2004;51(3):487–494. doi: 10.1002/mrm.10737. [DOI] [PubMed] [Google Scholar]
- 17.Fan X, Haney CR, Mustafi D, Yang C, Zamora M, Markiewicz EJ, et al. Use of a reference tissue and blood vessel to measure the arterial input function in DCEMRI. Magn Reson Med. 2010;64(6):1821–1826. doi: 10.1002/mrm.22551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fluckiger JU, Schabel MC, Dibella EV. Model-based blind estimation of kinetic parameters in dynamic contrast enhanced (DCE)-MRI. Magn Reson Med. 2009;62(6):1477–1486. doi: 10.1002/mrm.22101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yang C, Karczmar GS, Medved M, Stadler WM. Multiple reference tissue method for contrast agent arterial input function estimation. Magn Reson Med. 2007;58(6):1266–1275. doi: 10.1002/mrm.21311. [DOI] [PubMed] [Google Scholar]
- 20.Eggers H, Bornert P. Chemical shift encoding-based water-fat separation methods. J Magn Reson Imaging. 2014;40(2):251–268. doi: 10.1002/jmri.24568. [DOI] [PubMed] [Google Scholar]
- 21.Eggers H, Brendel B, Duijndam A, Herigault G. Dual-echo Dixon imaging with flexible choice of echo times. Magn Reson Med. 2011;65(1):96–107. doi: 10.1002/mrm.22578. [DOI] [PubMed] [Google Scholar]
- 22.Le Y, Dale B, Akisik F, Koons K, Lin C. Improved T, contrast concentration, and pharmacokinetic parameter quantification in the presence of fat with two-point Dixon for dynamic contrast-enhanced magnetic resonance imaging. Magn Reson Med. 2015 doi: 10.1002/mrm.25639. [DOI] [PubMed] [Google Scholar]
- 23.Walker-Samuel S, Leach MO, Collins DJ. Reference tissue quantification of DCEMRI data without a contrast agent calibration. Phys Med Biol. 2007;52(3):589–601. doi: 10.1088/0031-9155/52/3/004. [DOI] [PubMed] [Google Scholar]
- 24.Medved M, Karczmar G, Yang C, Dignam J, Gajewski TF, Kindler H, et al. Semiquantitative analysis of dynamic contrast enhanced MRI in cancer patients: variability and changes in tumor tissue over time. J Magn Reson Imaging. 2004;20(1):122–128. doi: 10.1002/jmri.20061. [DOI] [PubMed] [Google Scholar]
- 25.Pintaske J, Martirosian P, Graf H, Erb G, Lodemann KP, Claussen CD, et al. Relaxivity of Gadopentetate Dimeglumine (Magnevist), Gadobutrol (Gadovist), and Gadobenate Dimeglumine (MultiHance) in human blood plasma at 0.2, 1.5, and 3 Tesla. Invest Radiol. 2006;41(3):213–221. doi: 10.1097/01.rli.0000197668.44926.f7. [DOI] [PubMed] [Google Scholar]
- 26.Gold GE, Han E, Stainsby J, Wright G, Brittain J, Beaulieu C. Musculoskeletal MRI at 3.0 T: relaxation times and image contrast. AJR Am J Roentgenol. 2004;183(2):343–351. doi: 10.2214/ajr.183.2.1830343. [DOI] [PubMed] [Google Scholar]
- 27.Tofts PS, Brix G, Buckley DL, Evelhoch JL, Henderson E, Knopp MV, et al. Estimating kinetic parameters from dynamic contrast-enhanced T(1)-weighted MRI of a diffusable tracer: standardized quantities and symbols. J Magn Reson Imaging. 1999;10(3):223–232. doi: 10.1002/(sici)1522-2586(199909)10:3<223::aid-jmri2>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 28.Li X, Springer CS, Jr, Jerosch-Herold M. First-pass dynamic contrast-enhanced MRI with extravasating contrast reagent: evidence for human myocardial capillary recruitment in adenosine-induced hyperemia. NMR Biomed. 2009;22(2):148–157. doi: 10.1002/nbm.1293. [DOI] [PubMed] [Google Scholar]
- 29.Yankeelov TE, Rooney WD, Li X, Springer CS., Jr Variation of the relaxographic "shutter-speed" for transcytolemmal water exchange affects the CR bolus-tracking curve shape. Magn Reson Med. 2003;50(6):1151–1169. doi: 10.1002/mrm.10624. [DOI] [PubMed] [Google Scholar]
- 30.Padhani AR, Hayes C, Landau S, Leach MO. Reproducibility of quantitative dynamic MRI of normal human tissues. NMR Biomed. 2002;15(2):143–153. doi: 10.1002/nbm.732. [DOI] [PubMed] [Google Scholar]
- 31.Calamante F, Morup M, Hansen LK. Defining a local arterial input function for perfusion MRI using independent component analysis. Magn Reson Med. 2004;52(4):789–797. doi: 10.1002/mrm.20227. [DOI] [PubMed] [Google Scholar]