Arterial input functions (AIFs) measured directly from arteries with low and standard doses of contrast agent, and AIFs derived from reference tissues

Abstract

Measurements of arterial input function (AIF) can have large systematic errors at standard contrast agent doses in dynamic contrast enhanced MRI (DCE-MRI). We compared measured AIFs from low dose (AIF_LD) and standard dose (AIF_SD) contrast agent injections, as well as the AIF derived from a muscle reference tissue and artery (AIF_ref). Twenty-two prostate cancer patients underwent DCE-MRI. Data were acquired on a 3 T scanner using an mDixon sequence. Gadobenate dimeglumine was injected twice, at doses of 0.015 and 0.085 mmol/kg. Directly measured AIFs were fitted with empirical mathematical models (EMMs) and compared to the AIF derived from a muscle reference tissue (AIF_ref). EMMs accurately fitted the AIFs. The 1st and 2nd pass peaks were visualized in AIF_LD, but not in AIF_SD, thus the peak and shape of AIF_SD could not be accurately measured directly. The average scaling factor between AIF_SD and AIF_LD in the washout phase was only 56% of the contrast dose ratio (~6:1). The shape and magnitude of AIF_ref closely approximated that of AIF_LD after empirically determined dose-dependent normalization. This suggests that AIF_ref may be a good approximation of the local AIF.

1. Introduction

Dynamic contrast enhanced MRI (DCE-MRI) is one of the three primary components of the widely used multi-parametric prostate MRI protocol. Clinical DCE-MRI is usually acquired with a T1-weighted gradient echo sequence before and after IV bolus injection of contrast media. T1-weighted gradient echo sequences are sensitive to T1 changes due to the contrast agent, and often used for measurement of the volume transfer constant (K^trans) and the extracellular extravascular space (v_e) in prostate cancers. Aggressive prostate cancer is often associated with angiogenesis, producing tumor vasculature with higher blood flow and permeability than normal prostatic vessels [1,2]. As a result, prostate cancer typically shows earlier and more pronounced enhancement than surrounding normal prostatic tissues on DCE-MRI [3]. However, the rate of enhancement is strongly influenced by large inter-patient variations in the arterial input function (AIF) due to variability in cardiac output and systemic blood flow patterns. Therefore, precise measurement of the AIF is important for accurately, reliably, and reproducibly extracting tumor K^trans and v_e from DCE-MRI data [4,5].

In practice, the AIF is often estimated from a major artery under the assumption that this represents the exact input to the tissue [6]. However, direct measurements of the AIF from the artery are prone to partial volume effects, misregistration, inflow artifacts, etc., which can result in inaccurate AIF measurements [7]. Dose-dependent T2* and water exchange effects, in particular, were apparent even at half-dose contrast agent administration in a cardiac DCE-MRI sequence [8]. High blood concentrations of contrast agent cause an underestimation of AIF peak magnitude directly measured from the artery [9]. Therefore in practice, population AIFs are often employed in calculations of K^trans [10]. However, the population AIF cannot take into account inter- and intra-patient physiological variations.

Accurate measurement of the AIF was the subject of several previous studies. Parker et al. measured the AIFs at 1.5 T with a temporal resolution of 4.97 s from patients' aortas or iliac arteries following a standard bolus administration of gadodiamide. They developed a functional form of a population AIF with 10 parameters that can be used when AIF measurement in each patient is impossible. Yankeelov et al. compared a reference region model of AIF with direct measurement of an AIF from Fischer-344 rat's aorta [11]. Their experiments were performed on a 1.89 T scanner with temporal resolution of 0.9 s following a bolus injection of 0.3 mmol/kg gadodiamide, and the contrast media concentration vs. time in the aorta was estimated by a combination of arterial blood sampling and phase-sensitive imaging. Kershaw et al. developed a dual-bolus technique, by splitting the contrast media dose of 0.2 mmol/kg into 20% for the pre-bolus and 80% for the main bolus, for quantitative DCE-MRI of rabbit aorta at 1.5 T [12]. They demonstrated that the AIF can be reliably measured following a low-dose pre-bolus with 0.44 s temporal resolution (using a TRICKS sequence [13]), giving the same curve as an AIF measured in the conventional way following a high-dose bolus with temporal resolution of 1.3 s. However, routine clinical DCE-MRI scans of the prostate are generally obtained at much lower temporal resolution (e.g. 3–12 s [14]).

In this study, we compared AIFs measured at 3 T after a low dose (0.015 mmol/kg) of contrast agent injected first (AIF_LD), followed by a dose close to the standard dose (0.085 mmol/kg; AIF_SD; referred to in this paper as the ‘standard dose’). The AIF_LD measured directly from an artery is expected to approximate the true AIF, and serves as a ‘gold standard’ in this study [15]. A new empirical mathematical model (EMM) for the AIF (AIF-EMM) is introduced to fit both the first and second passes typically detected in AIF_LD. A previously developed EMM was used to fit the AIF_SD [16]. The AIF_LD and AIF_SD were compared qualitatively and quantitatively with and without an empirically determined normalization for contrast dose. The AIF derived from the contrast media concentration as a function of time (AIF_ref) in a muscle reference tissue and artery [17] following the standard contrast agent dose was compared with AIF_LD. This reference tissue method approximates the AIF_LD shape well, while being computationally simpler than earlier indirect AIF estimation methods [18,19].

2. Materials and methods

2.1. Patient recruitments

The study was compliant with the Health Insurance Portability and Accountability Act and approved by our institutional review board, and all participants provided written informed consent. Twenty-two patients (n = 22) with biopsy confirmed that prostate cancer were enrolled in this study (mean age = 57.3 years, range 43 to 70 years). A glomerular filtration rate value greater than or equal to 60 ml/min/1.73 m² was required.

2.2. Image acquisition

All images were acquired with a Philips Achieva 3 T TX scanner using the combination of a phased array and endorectal coil. The routine clinical MRI protocol was adapted to allow AIF and tissue contrast uptake measurement, as well as a clinical reading. After other clinically required scans, two sets of axial dual-echo 3D T1-weighted (T1W) DCE-MRI data (TR/TE1/TE2 = 4.8/1.69/3.3 ms, flip angle = 10°, field of view (FOV) = 250 × 380 × 84 mm³ (AP × RL × SI extent), resolution = 1.25 × 1.75 × 3.5 mm³, reconstruction resolution = 1.0 × 1.0 × 3.5 mm³, SENSE factor = 1.67, partial Fourier factor = 0.675, temporal resolution = 8.3 s) were acquired by using a two-point modified Dixon (mDixon) method to produce the ‘water-only’ images used for analysis [20,21]. The mDixon sequence provided excellent fat-suppressed images with fewer artifacts, as compared to using fat inversion pre-pulses [22].

The total amount of contrast agent gadobenate dimeglumine (Multihance, Bracco, Minneapolis, USA) injected was a standard dose given based on patient's weight (0.1 mmol/kg). The first low dose (15% of total) of contrast agent, 0.015 mmol/kg, was injected I.V. at a speed of 0.35 ml/s, followed by a 20 ml saline flush. T1W images were acquired for a total of ~3.5 min, with 5 sets taken pre-injection and 25 sets taken post-injection of the contrast agent. The second higher dose (85% of total, but referred to as the ‘standard’ dose) of contrast agent, 0.085 mmol/kg, was injected I.V. at a speed of 2.0 ml/s, followed by a 20 ml saline flush. The speed of injection for the lower dose was calculated so that the duration of the two injections was the same. This allowed direct comparison of the concentration vs. time curve shapes. This approach is similar to that of Kershaw and Cheng, where the lower bolus dose was diluted to the same volume as the higher one, and the two doses were injected at the same speed [12]. The second scan started 5 min after the first scan finished. Subsequently, T1W images were acquired for a total of ~8.3 min with 5 sets taken before and 55 sets taken during and after the second injection.

2.3. Data analysis

2.3.1. Contrast agent concentration curves

Data analysis was performed using Matlab (MathWorks, Natick, MA) with software built in-house. Since a low concentration of contrast agent and short TR/TE were used in our DCE-MRI acquisition, the relationship between the contrast agent concentration and the enhanced MR signal was very close to linear [23]. The signal intensity of DCE-MRI was converted to contrast agent concentration using the muscle as reference tissue. For each pixel, tissue contrast agent concentration as a function of time, C(t), before and after injection was estimated by comparing the change in signal intensity, S(t) - S(0), (where S(0) and S(t) are the signal intensities before contrast injection and at a later time t), with a reference tissue (in this case muscle) with known baseline T1. Because TR ≪ T1, we can approximate signal intensity as a linear function of T1 and contrast medium concentration [24]:

$$C(t)=\frac{1}{r_1·T_1(\text{muscle})}\frac{S(t)-S(0)}{S_{\text{muscle}}(0)},$$ (1)

where r₁ (6.3 mM⁻¹s⁻¹ for gadobenate dimeglumine) [25] is the longitudinal relaxivity of the contrast agent at 3 T, T₁(muscle) = 1420 ms [26], and S_muscle(0) is the muscle signal intensity before contrast injection.

2.3.2. Comparison of AIFs

The C(t) curves were averaged over the regions-of-interest (ROIs) to increase the signal-to-noise ratio (SNR). We determined the AIFs in two ways: (i) direct measurement from the artery for low and (approximately) standard dose contrast injections; and (ii) using the ‘reference tissue plus artery’ method [17] from standard dose contrast media concentration curves. For direct measurements, the AIF was determined by manually tracing ROIs to delineate cross sections of the external femoral artery on 6–10 slices perpendicular to the artery. The average (± standard deviation) number of voxels used to measure signal intensity in the artery in each patient was 73 ± 19. The directly measured AIFs were corrected to determine blood plasma concentration of contrast agent by dividing by 1-Hct, where the hematocrit (Hct) was assumed to equal 0.42.

We fit the directly measured AIFs to two different empirical mathematical models due to their different shapes. To fit AIF_LD we developed a new mathematical model, AIF-EMM, with eight parameters:

$$AI{F}_{LD}=A·\text{ln}(\mathit{1}+t)·\text{exp}(-\beta t)·(\mathit{1}+\sum _{n=\mathit{1}}^{\mathit{2}}{A}_n\text{exp}(-{(t-t_n)}^{\mathrm{2}}/\mathit{2}{\sigma }_n^{\mathit{2}}\left)\right),$$ (2)

where A and A_n are scaling constants, t_n and σ_n are centers and widths of the n^th Gaussian function for 1st and 2nd pass, and β is the decay constant of the exponential describing the washout of the contrast agent.

For the higher dose of contrast agent, the 1st and 2nd passes in the AIF_SD were not as clearly resolved as they were with low dose AIF_LD. Therefore for AIF_SD, a modified empirical mathematical model (EMM) [16] with three parameters was used to fit the curve:

$$AI{F}_{SD}=A·(1-\text{exp}(-\alpha t))·(1+\text{exp}(-\gamma t))/2,$$ (3)

where A is the upper limit of tracer concentration, α is the rate of contrast media uptake (min⁻¹), and γ (min⁻¹) is the rate of contrast washout. Fits were optimized using the non-linear Levenberg–Marquardt algorithm, and evaluated by calculating the goodness-of-fit (R²). R² is defined as the ratio of the sum of squares of the regression (SSR) and the total sum of squares (SST).

To derive AIF_ref, a gluteal muscle region was selected as a reference tissue on 6–10 slices and its concentration vs. time curve was analyzed. Assuming that the muscle satisfies the two-compartment model [27], K^trans and v_e of muscle were adjusted so that the AIF derived from the two compartment model matched the washout phase of the directly measured AIF (AIF_SD) after the 1st pass of the contrast media bolus. AIF_ref was then derived from the full muscle C_m(t) for standard dose of contrast agent using Eq. (4):

$$AI{F}_{\mathit{\text{ref}}}=\frac{1}{K^{\mathit{\text{trans}}}}\frac{d{C}_m(t)}{dt}+\frac{C_m(t)}{v_e},$$ (4)

where the K^trans and v_e for muscle were determined as described above [17].

The peak magnitudes of AIF_LD, AIF_SD and AIF_ref were compared and the coefficients of variations (CV) were calculated for all fitted parameters. The paired Student's t-test was used to test for differences between peak magnitudes of AIF_LD and AIF_SD. The paired Student's t-test was also used to test for differences between peak magnitudes of AIF_LD and AIF_ref, after empirically matching AIF_LD and AIF_SD at 3 min post-injection. Pearson's correlation was calculated between peak magnitudes of AIF_LD and AIF_SD, and between AIF_LD and AIF_ref. A p-value less than 0.05 was considered significant.

3. Results

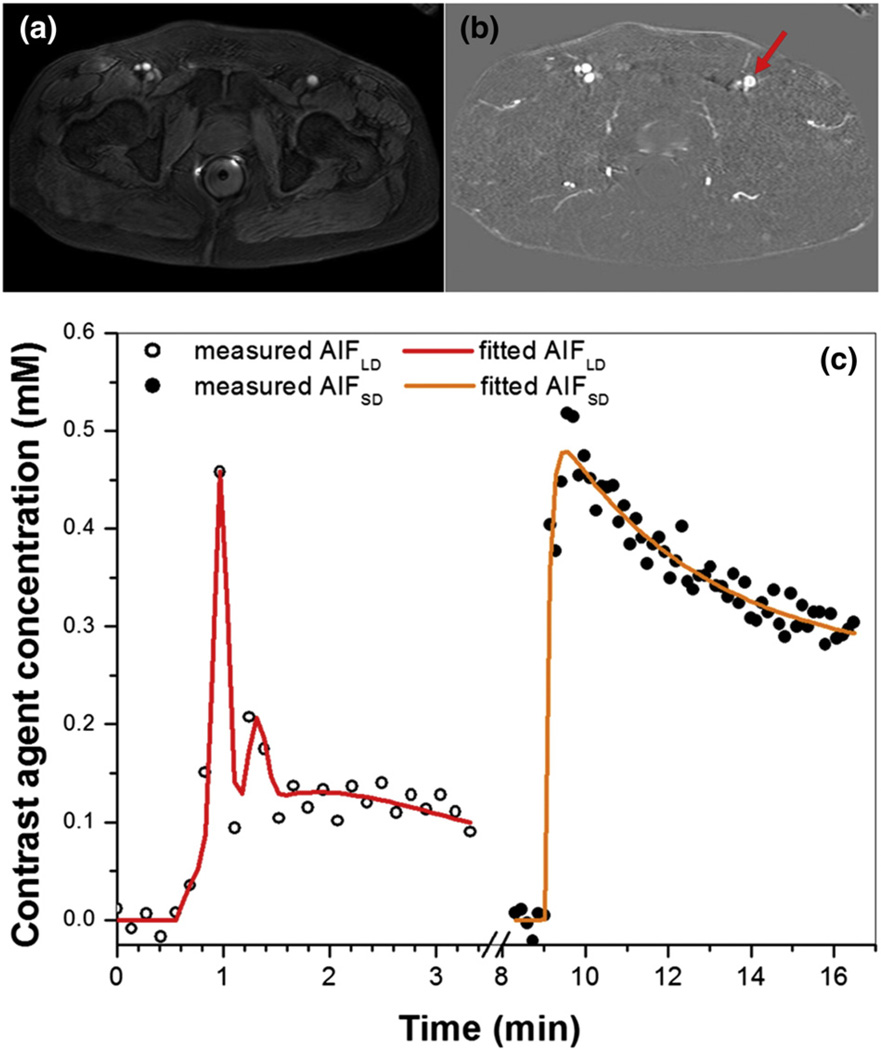
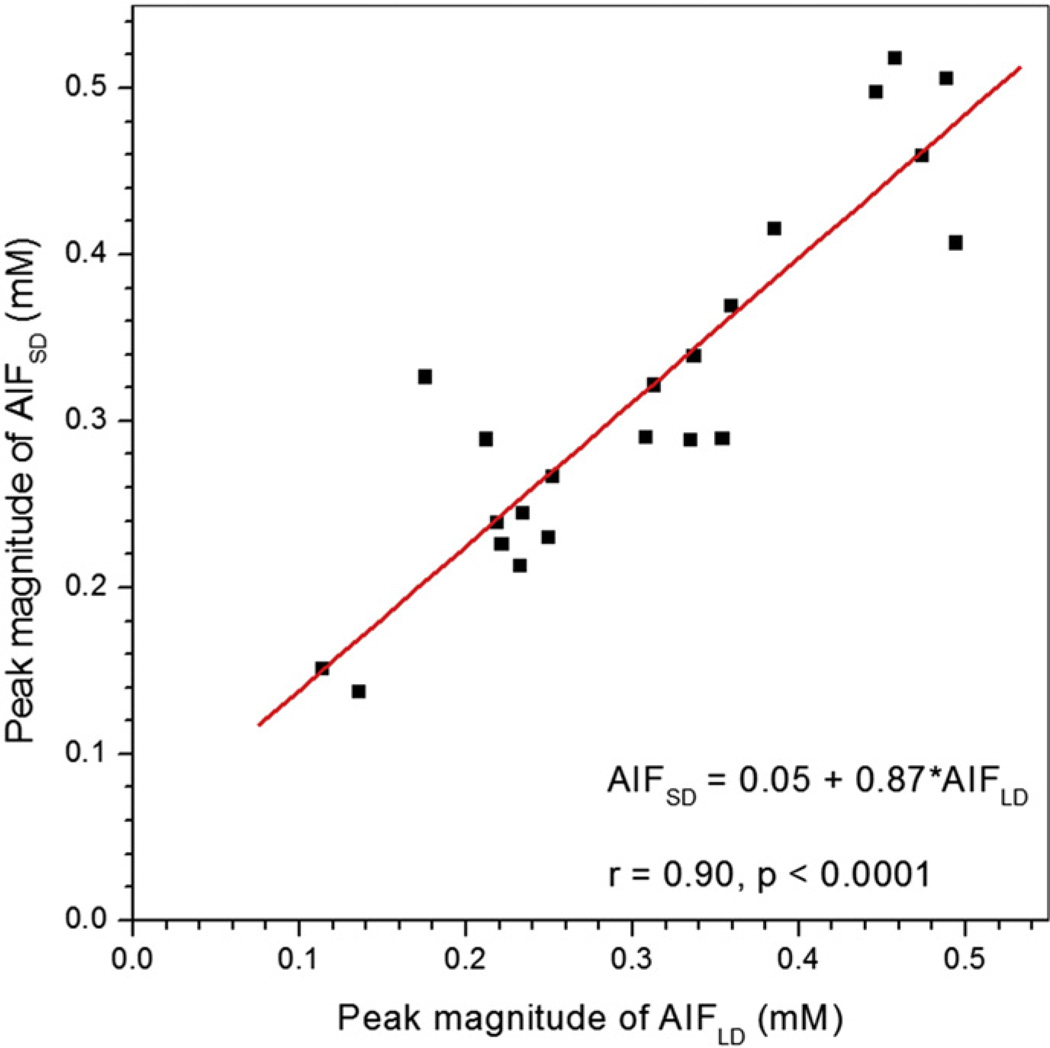
Fig. 1 shows (a) an axial slice from the pre-contrast agent (low dose) DCE-MRI series, (b) a difference image (post minus pre-contrast agent injection), and (c) the directly measured AIF_LD (open circles) and AIF_SD (solid circles) from the femoral artery of a typical patient (indicated by red arrow), as well as the EMM fits (red and orange lines) for the corresponding AIFs. The 1st and 2nd pass peaks of the contrast bolus can be clearly seen in AIF_LD despite limited temporal resolution, while neither peak is detectable in AIF_SD. Without normalizing to contrast dose, the average peak magnitudes of AIF_LD (0.31 ± 0.11 mM) and AIF_SD (0.32 ± 0.11 mM) calculated from the linear approximation for contrast agent concentration (Eq. (1)) did not differ (p > 0.30). Thus the average ratio of the peak magnitudes of the AIFs (approximately 1.03) is much lower than the ratio of the contrast doses (approximately 5.7). Since the peak of the AIF (in mM) should be proportional to dose, the results suggest that true peak of the AIF cannot be detected at the standard dose of contrast media. Despite the fact that the true peak of AIF_SD was not detected, the correlation between the peak magnitudes of AIF_LD and AIF_SD was positive and very strong (r = 0.90, p < 0.0001) (Fig. 2). The peak amplitudes of both AIF_LD and AIF_SD varied by approximately a factor of four between maximum and minimum across the patients studied.

Fig. 1.

(a) An axial slice imaged with pre-contrast agent (low dose) injection DCE-MRI, (b) difference image between post and pre-contrast agent injection, and (c) corresponding AIFs from femoral artery (indicated by red arrow). Plots of AIFs measured from low dose (open circles) and standard dose (solid circles) contrast administration are plotted, as well as the corresponding fits by the EMM models (red and orange lines) for a representative subject. Note that AID_LD did not scale by the contrast agent dose ratio of 5.67. The plots were displayed in the order of DCE-MRI acquisition.

Fig. 2.

Scatter plot of peak magnitudes of AIF_LD vs. AIF_SD without scaling of AIF_LD for contrast dose is shown. The red line is the linear fit through the data points. The linear relationship between AIF_LD and AIF_SD peak magnitudes, their correlation coefficient (r), and p value are shown on the plot.

The average ratio of the measured concentrations in the washout portions of AIF_SD and AIF_LD (minutes ~2.6 to ~3.3) was 3.15 ± 0.99 (based on the linear approximation for concentration). This value is approximately 56% of the contrast dose ratio (0.85 ml/kg/0.15 ml/kg = 5.67) that would be expected if contrast media concentration were accurately calculated.

Both EMM models provided good fits to AIFs (with goodness-of-fit parameters R² > 0.90) despite AIF_LD having lower SNR. The average EMM fitting parameters, their standard deviations (s.d.), and coefficients of variation (CV) are given in Tables 1 and 2. For the AIF_LD, the average first pass magnitude (A₁) was more than 10 times that of the average second pass magnitude (A₂) and the average first pass width (σ₁) was more than 1.4 times smaller than that of the second pass (σ₂), reflecting the broadening of the second pass bolus. The parameters governing the 2nd pass (A₂ and σ₂) had larger CVs than other parameters. The average time difference (t₂–t₁) between the peaks of the 1st and 2nd passes was 0.41 min (25 s). For AIF_SD, the parameters governing the contrast uptake and washout (α and γ) had larger CVs than the upper limit of tracer concentration (A).

Table 1.

Average AIF-EMM parameters and goodness of fit (R²), and their standard deviations (s.d.) and coefficients of variations (CV) for AIF_LD (n = 22).

	A (mM)	β (min−1)	A1	σ1 (min)	t1 (min)	A2	σ2 (min)	t2 (min)	R2
Average	0.31	0.70	5.84	0.09	0.20	0.46	0.12	0.62	0.95
s.d.	0.14	0.15	2.47	0.03	0.08	0.24	0.08	0.09	0.02
CV	0.44	0.22	0.42	0.38	0.40	0.52	0.65	0.15	0.02

Table 2.

Average EMM parameters and goodness of fit (R²), and their standard deviations (S.D.) and coefficients of variations (CV) for AIF_SD (n = 22).

	A (mM)	α (min−1)	γ (min−1)	R2
Average	0.36	8.93	0.61	0.93
s.d.	0.12	5.40	0.48	0.09
CV	0.32	0.61	0.80	0.09

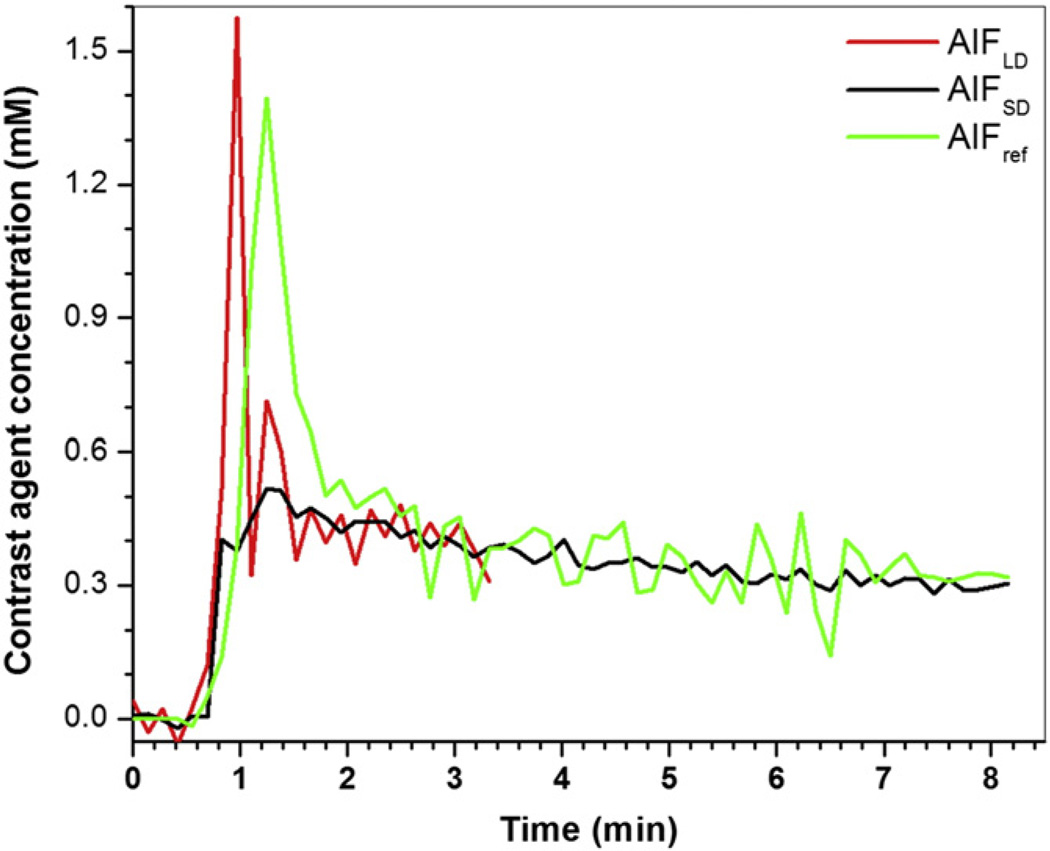
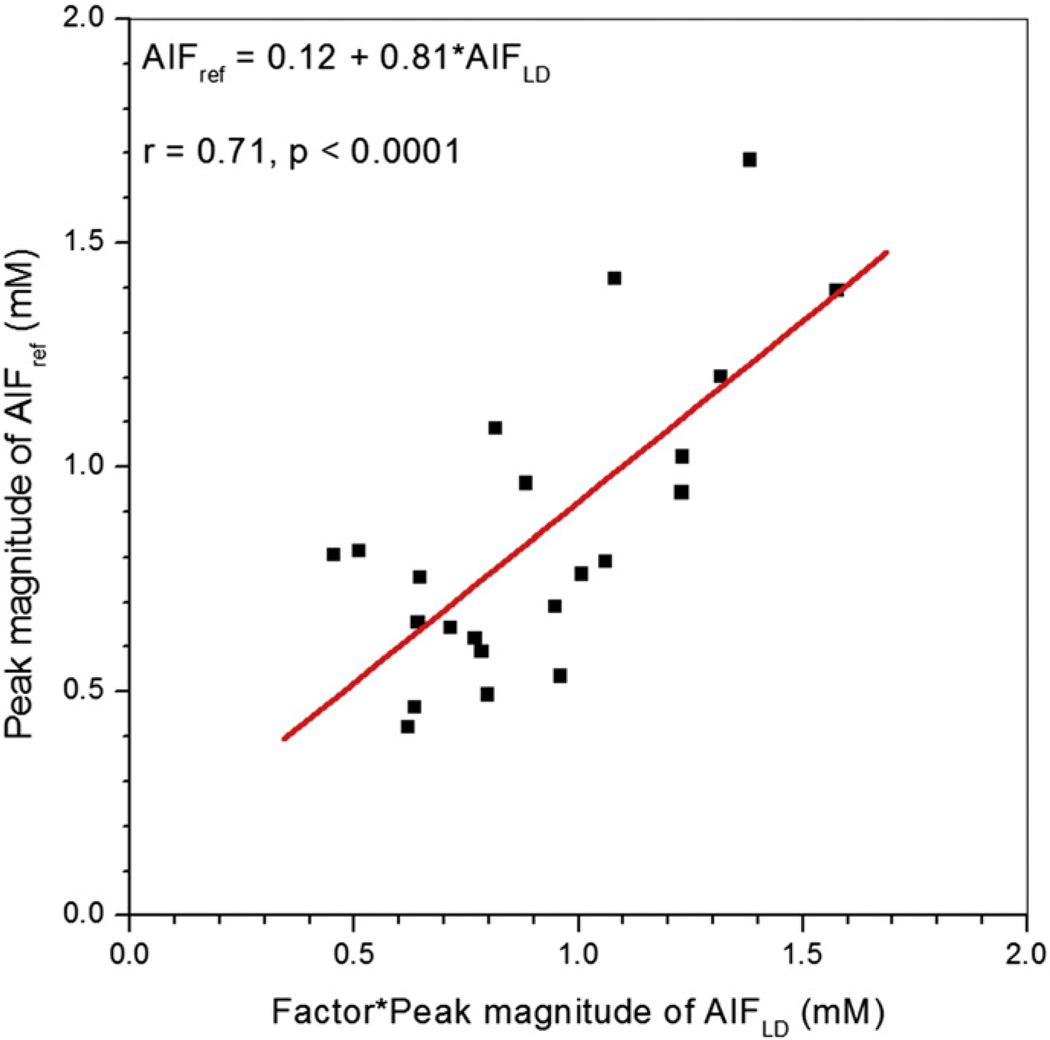
Fig. 3 shows an example of AIF_ref (green line) derived from the muscle contrast agent concentration vs. time curve, compared with the corresponding AIF_LD (red line) and AIF_SD (black line) measured in the same patient. To compare shapes directly, AIF_LD was scaled using the MR-measured concentration ratio, so that the washout parts of all three curves match. Generally, the peak of AIF_ref was delayed and broadened when compared to directly measured AIF_LD, while the peak magnitude of AIF_ref was close in value to peak magnitude of the scaled AIF_LD. The second pass peak was generally not detected in AIF_ref. Fig. 4 shows a scatter plot of peak magnitudes of AIF_LD multiplied by MR-measured concentration ratio vs. peak magnitudes of AIF_ref derived from muscle curves. The average peak magnitude of AIF_LD (0.91 ± 0.30 mM) did not differ significantly (p > 0.25) from the average peak magnitude of AIF_ref (0.85 ± 0.34 mM). There was moderate positive correlation (r = 0.71, p < 0.0001) between these two peak magnitudes.

Fig. 3.

Plots of AIF_LD (red line), AIF_SD (black line), and AIF_ref (green line) derived from muscle reference tissue are shown for a representative subject. AIF_LD was scaled by the MR-measured concentration ratio in the washout portions.

Fig. 4.

Scatter plot of peak magnitudes of AIF_LD scaled by MR-measured concentration ratio vs. AIF_ref is shown. The red line is the linear fit through the points. The linear relationship between scaled AIF_LD and AIF_ref peak magnitudes, their correlation coefficient (r), and p value are given on the plot.

The average values (± standard deviation) for muscle K^trans and v_e derived from the ‘reference tissue plus artery’ calculation were 0.066 ± 0.035 min⁻¹ and 0.17 ± 0.07, respectively.

4. Discussion

The AIFs following the low and standard dose contrast agent injections were measured and compared for a total of 22 patients. The results demonstrate that the 1st and 2nd passes of contrast bolus in directly measured AIFs could be detected following the low dose of contrast agent, but not following the standard dose. This is consistent with previously published work on DCE-MRI for breast tumors [15]. The main reasons for this discrepancy were likely T2* and to a lesser degree water exchange effects [28,29] associated with the high blood concentration of contrast agent at early times for AIF_SD. The low dose of contrast agent (15% of the standard dose) was expected to produce minimal T2* and negligible water exchange effects. Therefore AIF_LD was expected to closely approximate the true AIF shape, and was used as ‘gold standard’.

The present results are inconsistent with those of Kershaw and Cheng [12], showing that scaled pre-bolus AIF is equivalent to the AIF from a high-dose injection measured from rabbit aorta in sagittal plane. However, they acquired data at 1.5 T, so that T2* effects were greatly reduced relative to the current study performed at 3 T. A dual-echo modified Dixon pulse sequence was used in our experiments, which may have increased T2* effects. In addition, Kershaw et al. used a view-sharing method (TRICKS) which samples the outer portion of k-space less frequently than the center of k-space [13]. Consequently this approach reduced effective temporal resolution for arteries.

Although our results show that measurements of the AIF directly from arteries are much more accurate when a low dose of contrast agent is injected, the low dose results in very weak tissue enhancement, and this will reduce the accuracy of K^trans and v_e calculations. Therefore, a low dose tissue contrast agent uptake curves should be fitted with a mathematical model prior to fitting to the pharmacokinetic model for routine clinical practice.

The lack of the first pass peak makes AIF_SD unsuitable for quantitative calculation of K^trans and v_e. The necessity for this correction is demonstrated by the very large inter-patient variation in AIF_LD, AIF_SD, and AIF_ref. For example, the peak concentrations of AIF_LD and AIF_SD vary by more than 4-fold in the group of patients studied here. Failure to correct for variations in AIF will lead to large systematic errors in K^trans. The correlation between peak amplitudes of AIF_LD and AIF_ref is weaker than the correlation between AIF_LD and AIF_SD. This may be due to the fact that AIF_ref represents a local AIF derived from a muscle ROI that is some distance away from the artery. Limited SNR of the muscle reference tissue signal may also be a factor. Nevertheless, the correlation between AIF_ref and AIF_LD is highly significant, and this suggests that reference tissue methods provide an alternative way to estimate the local AIF if it cannot be accurately measured directly.

During the washout phase the discrepancy between dose-normalized AIF_LD and AIF_SD is smaller than at the peak, as expected, due to the lower blood concentration of contrast media during washout. However, the scaling factor (3.15) required to match AIF_LD and AIF_SD in the washout phase measured by MRI is only about 56% of the dose ratio (5.67). Thus the signal enhancement produced by the standard dose is less than expected, even in the washout phase. Preliminary results (not presented here) indicate that the MR-measured concentration ratio does not change significantly with use of the full signal model in place of Eq. (1), and does not reach the value 5.67 expected from the contrast dose ratio. However, improvements in the signal model, accurate mapping of the B1 excitation field, and accurate measurements of native T1 may result in a larger MR-measured concentration ratio that corresponds to the ratio of contrast media doses during the washout phase. We are currently working to refine these calculations. While this may affect the magnitude of the measured concentration curves, it will not affect the shape differences between AIF_LD and AIF_SD and shape similarity between AIF_LD and AIF_ref.

The peak magnitude of AIF_ref was much larger than the peak magnitude of AIF_SD, and was close in value to that of AIF_LD when the empirical correction for the difference in dose (multiplication by 3.15) was used. The muscle K^trans and v_e extracted from the fitting for AIF_ref are consistent with the results of previous studies by Padhani et al [30]. Padhani et al. found K^trans = 0.133 ± 0.092 (min⁻¹) and v_e = 0.12 ± 0.03, providing validation for our approach. Compared to AIF_LD, the first pass peaks in AIF_ref were slightly delayed and broadened. This is likely due to differences in timing and shape of the local AIF for gluteal muscle compared to the external femoral artery, suggesting that the reference tissue calculation is providing a good estimate of local AIF [31]. Although small differences exist, the results suggest that AIF_ref is a better model of the true AIF than the directly measured AIF_SD obtained with the standard dose of contrast agent.

The Parker population AIF [10] was not optimal for fitting the data acquired in this study. This may have been due to the difference in field strength (1.5 T vs. 3 T) and/or the limited SNR of our data. There were also differences in contrast agent dose, the molecular structure of the contrast agents, methods used to convert the MRI signal to contrast agent concentration, location of ROIs, temporal resolutions, and MRI pulse sequences. Therefore, we developed a simpler model based on Gaussian functions with eight parameters (AIF-EMM) for the first and second pass peaks to fit AIF_LD. The AIF_SD was fit with a modified empirical mathematical model (EMM) with three parameters [16]; a different mathematical model was needed for AIF_SD because the shapes of AIF_SD and AIF_LD are very different. Because different mathematical models were used to fit AIF_LD and AIF_SD, the fitting parameters could not be directly compared to those from previous studies. However, some of the parameters derived here can be compared to corresponding parameters measured by Parker et al. [10], because both this study and Parker et al. use Gaussian functions to describe the 1st and 2nd passes. The average widths (σ₁ = 0.087, σ₂ = 0.121) and centers (t₁ = 0.203, t₂ = 0.461) measured in our AIF_LD were close to Parkers' measurements (σ₁ = 0.056, σ₂ = 0.132; t₁ = 0.170, t₂ = 0.365). The magnitude parameters measured here cannot be directly compared to the results obtained by Parker et al. due to the significant differences in protocols as discussed above. For instance, the reference tissue method used here to convert the MRI signal to contrast agent concentration could exhibit bias, even as it minimizes the error propagation from using variable flip angle measurements of T1.

There are several limitations in this study. First, the temporal resolution of the dynamic acquisitions is lower than that used in other studies of the AIF, and it is possible that the magnitude and shape of the 1st pass were not accurately assessed in AIF_LD. The temporal resolution in the present study was dictated by clinical requirements. Second, the arterial ROIs used to measure the AIFs were selected far from the aorta, in order to obtain an approximately local AIF for the pelvic region. This may have resulted in relatively broad AIFs that are systematically different from AIFs reported in previous studies. Third, the AIF for the high dose did not correct for the small amount of residual contrast agent remaining from the earlier low dose injection, as this would affect the measured peak enhancement and washout rate of the contrast agent only minimally. Finally, the method used to convert the MRI signal to the contrast agent concentration may introduce errors by assuming the simple linear relationship between signal enhancement and concentration. This limitation does not affect the conclusions of our study, as the approximation was used to compare AIF shapes; the exact contrast agent concentrations and K^trans values were not the focus of this work. In the future, a more accurate method will be developed to reduce errors and allow a more quantitative analysis of measured or derived AIFs. Any future improvements, however, will not eliminate the shape differences between AIF_LD and AIF_SD (presence vs. absence of first pass peak).

In summary, we compared the AIFs measured following a low dose (0.015 ml/kg) and a close-to-standard dose (0.085 ml/kg) contrast agent injection. The AIF_LD is much sharper than AIF_SD with a pronounced first pass peak and a peak due to the second pass of the bolus. AIF_LD provides an approximate gold standard that can guide development of methods for accurately calculating the AIF following a standard dose of contrast agent. The peak and shape of the AIF was not detected accurately following the standard dose of contrast media at 3 T. This is probably due to T2* and ‘shutter speed’ effects associated with high plasma concentrations of contrast media. Direct arterial measurement of the AIF produced a significant under-estimate of peak arterial enhancement following the standard dose of contrast agent, and this would result in large systematic errors in calculations of pharmacokinetic parameters. The ‘reference tissue plus artery’ method can be used in combination with a standard dose of contrast media to more accurately derive the local AIF.