Abstract
We consider the use of randomized clinical trial (RCT) data to identify simple treatment regimes based on some subset of the covariate space, 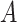 . The optimal subset,
. The optimal subset, 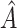 , is selected by maximizing the expected outcome under a treat-if-in-
, is selected by maximizing the expected outcome under a treat-if-in-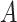 regime, and is restricted to be a simple, as it is desirable that treatment decisions be made with only a limited amount of patient information required. We consider a two-stage procedure. In stage 1, non-parametric regression is used to estimate treatment effects for each subject, and in stage 2 these treatment effect estimates are used to systematically evaluate many subgroups of a simple, prespecified form to identify
regime, and is restricted to be a simple, as it is desirable that treatment decisions be made with only a limited amount of patient information required. We consider a two-stage procedure. In stage 1, non-parametric regression is used to estimate treatment effects for each subject, and in stage 2 these treatment effect estimates are used to systematically evaluate many subgroups of a simple, prespecified form to identify 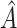 . The proposed methods were found to perform favorably compared with two existing methods in simulations, and were applied to prehypertension data from an RCT.
. The proposed methods were found to perform favorably compared with two existing methods in simulations, and were applied to prehypertension data from an RCT.
Keywords: Optimal treatment regimes, Personalized medicine, Subgroup analysis, Variable selection
1. Introduction
Although some treatments may be more widely effective than others, few, if any, work for all individuals in a target population. In many cases, a treatment may be extremely effective for some subset of a population, but mildly effective of ineffective for others. Even if a new treatment is effective, the standard of care may still be preferred for some individuals if, for example, the new treatment is very expensive and there is little difference in effectiveness between the two (Song and Pepe, 2004). Thus, it is desirable to know which subgroup(s) of a population, if any, will respond well to a particular treatment. In particular, the identification of the characteristics which lead to these individuals showing an enhanced response is of interest, as this may allow future patients to be assigned the treatment which will benefit them most.
Treatment decisions will often be made by someone who may not be comfortable with complex rules and algorithms. Thus, an issue which should be considered before employing any subgroup identification procedure is the potential interpretability of the results. A very complex subgroup, which depends on many covariates may accurately identify truly enhanced responders, but often lacks “nice” interpretability. In addition, the dependence on a large number of covariates means a large amount of information needs to be collected, which could lead to slower, more expensive, or more invasive treatment decisions than are necessary, limiting the chances of such a subgroup being used in practice. In contrast, a subgroup which depends on only one or two covariates will be easier to interpret, and in many cases, may be still able to classify enhanced responders relatively well.
If only a small number of covariates exist, or if one has specific subgroups or markers that are of interest, testing for a small number of interactions (perhaps with a correction for multiple comparisons) can be considered. However, oftentimes many covariates exist, and subgroups of interest are not know a priori, so identifying simple subgroups requires some form of variable selection. One option is to use tree-based methods (Negassa and others, 2005; Su and others, 2008, 2009; Foster and others, 2011; Lipkovich and others, 2011; Faries and others, 2013), which partition the data into subgroups of individuals who are similar with regard to the response, generally defined using only a subset of the covariates. One could also consider a more model-based approach to selecting covariates, such as penalized regression (Tibshirani, 1996; Fan and Li, 2001; Gunter and others, 2007; Zou and Zhang, 2009; Qian and Murphy, 2011; Imai and Ratkovic, 2013; Foster and others, 2013), which simultaneously estimates regression parameters and performs variable selection by shrinking some parameter estimates and forcing others to zero.
We limit our discussion to randomized clinical trial (RCT) data with a continuous outcome, two treatments and a moderate number of baseline covariates, e.g. 5–100. We consider the use of RCT data to select a treatment “regime” which, if followed by the entire population, leads to the best expected outcome (Murphy and others, 2001; Robins, 2004; Gunter and others, 2007; Brinkley and others, 2010; Qian and Murphy, 2011; Zhang and others, 2012). This expectation is sometimes referred to as the average Value (Sutton and Barto, 1998; Gunter and others, 2007; Qian and Murphy, 2011). Our potential regimes assign one treatment to individuals who are in a subgroup, 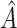 , of the population, and the other treatment to those in
, of the population, and the other treatment to those in 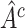 . The identification of “optimal” treatment regimes is not a new problem; however, our emphasis will be on the simple form of the regime. In particular, our goal will be to identify the best regime defined by a contiguous subsets of the covariate space of up to three dimensions, such as
. The identification of “optimal” treatment regimes is not a new problem; however, our emphasis will be on the simple form of the regime. In particular, our goal will be to identify the best regime defined by a contiguous subsets of the covariate space of up to three dimensions, such as 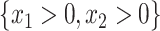 or
or 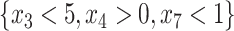 , should a worthwhile regime of this form exist. Ideally this “locally optimal” regime will give an expected outcome which is similar to that of the globally most optimal regime, but in some cases the true treatment effect may be so complex that no worthwhile simple regime exists. For example, if the truly enhanced subgroup was not contiguous, it could be difficult to capture using a contiguous region.
, should a worthwhile regime of this form exist. Ideally this “locally optimal” regime will give an expected outcome which is similar to that of the globally most optimal regime, but in some cases the true treatment effect may be so complex that no worthwhile simple regime exists. For example, if the truly enhanced subgroup was not contiguous, it could be difficult to capture using a contiguous region.
2. Identifying simple treatment regimes
Suppose that we have independent observations 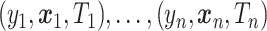 from the model
from the model
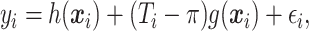 |
(2.1) |
where 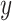 is continuous,
is continuous, 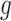 and
and 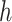 are unknown functions, with
are unknown functions, with 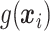 being the treatment effect for subject
being the treatment effect for subject 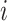 ,
, 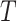 is a treatment indicator,
is a treatment indicator, 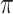 is the treatment randomization probability,
is the treatment randomization probability, 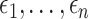 are independent and identically distributed (i.i.d.) errors with mean zero and variance
are independent and identically distributed (i.i.d.) errors with mean zero and variance 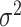 and covariates
and covariates 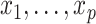 are independent, and may be continuous or categorical. Without loss of generality, assume that higher levels of
are independent, and may be continuous or categorical. Without loss of generality, assume that higher levels of 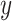 represent an improved response. This formulation was chosen because, in the linear setting (i.e.
represent an improved response. This formulation was chosen because, in the linear setting (i.e. 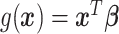 ), it was shown to be robust to misspecification of
), it was shown to be robust to misspecification of 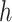 . In particular, under certain assumptions,
. In particular, under certain assumptions, 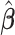 is a consistent estimate of
is a consistent estimate of 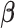 , regardless of the choice of main effect (Lu and others, 2013). To identify our treatment regime, we consider a two-stage approach where, in stage 1, we estimate
, regardless of the choice of main effect (Lu and others, 2013). To identify our treatment regime, we consider a two-stage approach where, in stage 1, we estimate 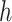 and
and 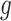 in (2.1), and in stage 2, these estimated
in (2.1), and in stage 2, these estimated 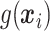 values are used to systematically evaluate many subgroups of a simple, prespecified form in order to identify our treatment regime.
values are used to systematically evaluate many subgroups of a simple, prespecified form in order to identify our treatment regime.
2.1. Non-parametric estimation of 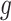 and
and 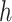
We estimate 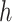 and
and 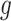 using the following iterative approach:
using the following iterative approach:
Fit the model
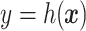 to obtain the initial estimate of
to obtain the initial estimate of 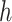 ,
, 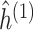 .
.Fit the model
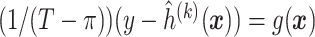 to obtain
to obtain 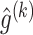 ,
, 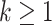 .
.Fit the model
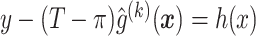 to obtain
to obtain 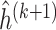 ,
, 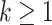 .
.Iterate between steps (ii) and (iii) until
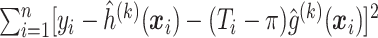 changes by less than a prespecified small number.
changes by less than a prespecified small number.
Functions 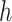 and
and 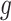 may be complex, so we use non-parametric methods, such as multivariate adaptive regression spline (MARS) (Friedman, 1991) or Random Forests (RFs) (Breiman, 2001), to estimate them. One may wish to choose the “convergence threshold” in step (iv) differently depending on which method is chosen to estimate
may be complex, so we use non-parametric methods, such as multivariate adaptive regression spline (MARS) (Friedman, 1991) or Random Forests (RFs) (Breiman, 2001), to estimate them. One may wish to choose the “convergence threshold” in step (iv) differently depending on which method is chosen to estimate 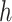 and
and 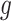 . For instance, we found a threshold of around
. For instance, we found a threshold of around 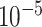 can generally be achieved within a few iterations for MARS. For RF, the amount by which the sum of squares in step (iv) changes remains somewhat constant across iterations, most likely because of the random nature of this method. Thus, in this case, we continue until 60 iterations have been performed, which we found is sufficient to obtain good estimates of
can generally be achieved within a few iterations for MARS. For RF, the amount by which the sum of squares in step (iv) changes remains somewhat constant across iterations, most likely because of the random nature of this method. Thus, in this case, we continue until 60 iterations have been performed, which we found is sufficient to obtain good estimates of 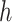 and
and 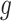 . The required number of iterations may be smaller or larger in other settings.
. The required number of iterations may be smaller or larger in other settings.
2.2. Selecting a subgroup for fixed 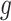 and
and 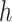
Using notation similar to Zhang and others (2012), let 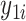 and
and 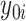 be the potential responses given that subject
be the potential responses given that subject 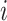 received treatment or the standard of care, respectively, so that
received treatment or the standard of care, respectively, so that 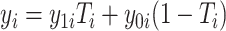 . Let
. Let 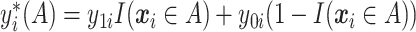 be the potential outcome for a future patient in the population under this “treat-if-in-
be the potential outcome for a future patient in the population under this “treat-if-in-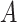 ” regime. for any
” regime. for any 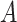 . Using simple algebra, we have
. Using simple algebra, we have
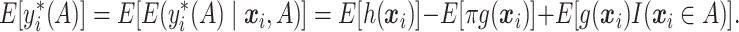 |
(2.2) |
As only the last term in (2.2) involves 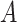 , maximizing (2.2) with respect to
, maximizing (2.2) with respect to 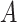 amounts to maximizing
amounts to maximizing 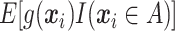 , which, given
, which, given 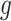 , can be estimated by
, can be estimated by 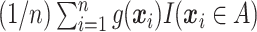 . After multiplying by
. After multiplying by 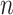 and replacing
and replacing 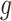 by
by 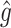 , this becomes
, this becomes
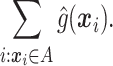 |
(2.3) |
The chosen subgroup, denoted by 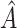 , is that which maximizes (2.3). Note that, if there were no restriction on
, is that which maximizes (2.3). Note that, if there were no restriction on 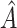 , we would choose
, we would choose 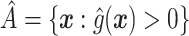 . In practice, one may wish to consider the inclusion of an offset in (2.3), as in our experience this can help to better identify truly positive responders. Specifically, one could replace (2.3) with
. In practice, one may wish to consider the inclusion of an offset in (2.3), as in our experience this can help to better identify truly positive responders. Specifically, one could replace (2.3) with 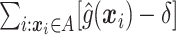 , where
, where 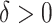 . Selection of the offset
. Selection of the offset 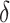 is considered below.
is considered below.
We consider 1D, 2D and 3D regions of the general form 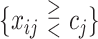 , or
, or 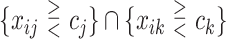 or
or 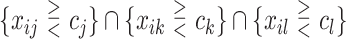 as candidates for
as candidates for 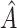 , where
, where 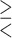 indicates either
indicates either 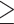 or < and covariates
or < and covariates 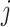 ,
, 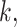 and
and 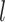 are distinct. In addition, we consider the complements of these regions. We refer to this as Simple Optimal Regime Approximation (SORA).
are distinct. In addition, we consider the complements of these regions. We refer to this as Simple Optimal Regime Approximation (SORA).
Note that for just 3D regions, there are 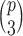 unique combinations of covariates,
unique combinations of covariates, 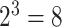 unique ways to assign directions
unique ways to assign directions  to
to 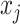 ,
, 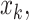 and
and 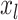 , and as many as
, and as many as 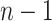 unique cutpoints for each covariate. Thus, SORA often involves the evaluation of many regions, making it computationally expensive. Therefore, we employ a modified version, in which we consider an evenly-spaced grid of 10–20 cutpoints, rather than all observed values for each covariate. Additionally, instead of considering all candidate regions simultaneously, we employ a “stepwise” approach. Let
unique cutpoints for each covariate. Thus, SORA often involves the evaluation of many regions, making it computationally expensive. Therefore, we employ a modified version, in which we consider an evenly-spaced grid of 10–20 cutpoints, rather than all observed values for each covariate. Additionally, instead of considering all candidate regions simultaneously, we employ a “stepwise” approach. Let 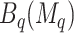 denote the set of unique covariates which define the best
denote the set of unique covariates which define the best 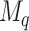 candidate regions of dimension
candidate regions of dimension 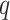 . The stepwise algorithm is as follows: (1) evaluate all candidate 1D regions, and identify
. The stepwise algorithm is as follows: (1) evaluate all candidate 1D regions, and identify 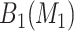 , (2) evaluate all candidate 2D regions in which one of the dimensions is defined by a member of
, (2) evaluate all candidate 2D regions in which one of the dimensions is defined by a member of 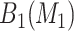 , and identify
, and identify 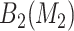 , and (3) evaluate all candidate 3D regions in which two of the dimensions are defined by a pair from
, and (3) evaluate all candidate 3D regions in which two of the dimensions are defined by a pair from 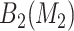 , and select the best 3D region. The best overall region is
, and select the best 3D region. The best overall region is 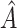 . Note that
. Note that 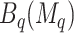 only defines which covariates are considered in the next step. All candidate directions (i.e. < or
only defines which covariates are considered in the next step. All candidate directions (i.e. < or 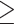 ) and cutpoints are re-considered for these covariates.
) and cutpoints are re-considered for these covariates.
2.3. Evaluation of the region 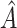
The proposed method always selects a region, so it is important to evaluate the strength of 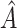 . We thus consider the metric proposed by Foster and others (2011):
. We thus consider the metric proposed by Foster and others (2011):
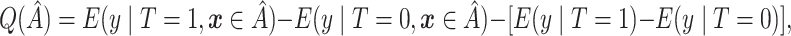 |
(2.4) |
which is a measure of the enhanced treatment effect in 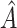 relative to the average treatment effect. Methods for estimating (2.4) are considered below.
relative to the average treatment effect. Methods for estimating (2.4) are considered below.
Resubstitution  RS
RS . Replace the four conditional expectations in (2.4) with the observed means in the data and use these obtain an estimate of
. Replace the four conditional expectations in (2.4) with the observed means in the data and use these obtain an estimate of
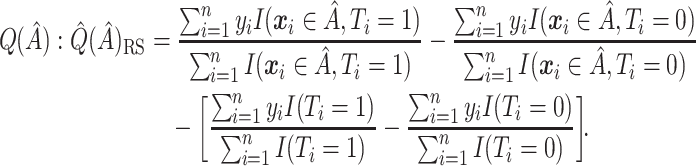 |
The RS method reuses the data which were used to identify  . It is well known that, due to overfitting, measures of a model's predictive accuracy will often be overly optimistic when obtained from the training data. It seems reasonable to assume that a similar phenomenon will occur when the training data are used to identify a subgroup and then reused to assess the enhancement of that subgroup. Thus, we expect the RS estimate to be positively biased.
. It is well known that, due to overfitting, measures of a model's predictive accuracy will often be overly optimistic when obtained from the training data. It seems reasonable to assume that a similar phenomenon will occur when the training data are used to identify a subgroup and then reused to assess the enhancement of that subgroup. Thus, we expect the RS estimate to be positively biased.
Simulate new data  SND
SND . The goal of this method is to obtain new data which “look like” the original data, but are independent of the original data, reducing the bias of the resulting estimate. This could be repeated many times, where each time
. The goal of this method is to obtain new data which “look like” the original data, but are independent of the original data, reducing the bias of the resulting estimate. This could be repeated many times, where each time  was recalculated, and the SND estimate could be found by averaging these RS estimates. We avoid actually simulating new data by instead replacing
was recalculated, and the SND estimate could be found by averaging these RS estimates. We avoid actually simulating new data by instead replacing 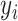 by
by 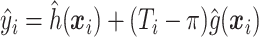 ,
, 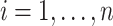 in
in 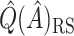 . This estimate is denoted by
. This estimate is denoted by 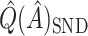 , and is generally less biased than
, and is generally less biased than 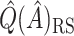 .
.
Mean 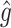 . Under (2.1), the empirical version of (2.4) is
. Under (2.1), the empirical version of (2.4) is 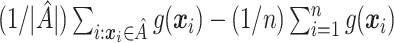 , where
, where 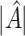 is the number of individuals in
is the number of individuals in 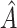 . Thus,
. Thus, 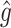 can be used to estimate (2.4):
can be used to estimate (2.4): 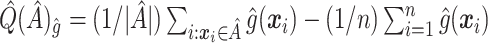 . This is similar to
. This is similar to 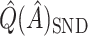 , and will generally have a similar amount of bias. In fact, if each treated observation had a corresponding identical (with respect to covariates) control observation, this would be exactly equal to
, and will generally have a similar amount of bias. In fact, if each treated observation had a corresponding identical (with respect to covariates) control observation, this would be exactly equal to 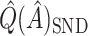 .
.
Bootstrap bias correction. We also consider the bootstrap bias correction of Foster and others (2011). The bias of 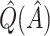 is
is 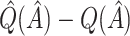 , and as discussed in Foster and others (2011), can be approximately estimated using bootstrap data. This estimated bias can then be used to adjust any of the above estimates, i.e. bias-corrected
, and as discussed in Foster and others (2011), can be approximately estimated using bootstrap data. This estimated bias can then be used to adjust any of the above estimates, i.e. bias-corrected 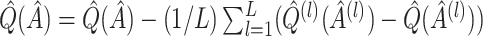 , where
, where 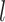 denotes a particular bootstrap sample. These adjusted RS, SND, and Mean
denotes a particular bootstrap sample. These adjusted RS, SND, and Mean 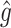 estimates are denoted by
estimates are denoted by 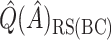 ,
, 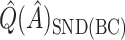 , and
, and 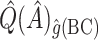 , respectively.
, respectively.
2.4. Selection of 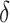
If one wishes to consider an offset, 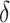 , a number of options exist. We describe two potential approaches below. In this paper, we use
, a number of options exist. We describe two potential approaches below. In this paper, we use 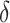 to reduce classification errors (particularly false positives) around the threshold
to reduce classification errors (particularly false positives) around the threshold 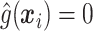 . Alternatively,
. Alternatively, 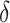 could be chosen a priori based on a meaningful treatment effect or, if one wishes for
could be chosen a priori based on a meaningful treatment effect or, if one wishes for 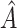 to be of a specific size,
to be of a specific size, 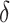 could be chosen accordingly. If one wishes to be less aggressive, an offset need not be used.
could be chosen accordingly. If one wishes to be less aggressive, an offset need not be used.
“Ad hoc” approach. True treatment effects can be broken into the following categories: (a) 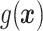 depends on the covariates, (b)
depends on the covariates, (b) 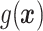 does not depend on the covariates and has a mean which is less than or equal to zero, and (c)
does not depend on the covariates and has a mean which is less than or equal to zero, and (c) 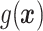 does not depend on the covariates, but has a positive mean. Factors which might be important in determining a suitable
does not depend on the covariates, but has a positive mean. Factors which might be important in determining a suitable 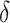 are the variability of
are the variability of 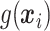 , its signal-to-noise ratio
, its signal-to-noise ratio 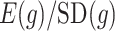 , and the amount of variability that is explained by
, and the amount of variability that is explained by 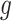 in (2.1). As we wish to identify subjects for whom
in (2.1). As we wish to identify subjects for whom 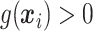 ,
, 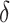 will ideally be around zero, but because the estimate
will ideally be around zero, but because the estimate 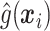 is not precise, using a small positive offset will reduce the false-positive rate. If the true treatment effect falls into category (a), then a small
is not precise, using a small positive offset will reduce the false-positive rate. If the true treatment effect falls into category (a), then a small 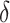 would be appropriate, unless the signal-to-noise ratio for
would be appropriate, unless the signal-to-noise ratio for 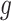 is small and
is small and 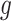 only explains a small amount of the variance. If the true treatment effect falls into category (b), we would like a modestly sized positive
only explains a small amount of the variance. If the true treatment effect falls into category (b), we would like a modestly sized positive 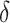 , as in this case we do not wish to identify a subgroup. If the true treatment effect falls into category (c), the ideal
, as in this case we do not wish to identify a subgroup. If the true treatment effect falls into category (c), the ideal 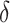 will be around zero, as in this case we essentially wish to treat everyone. Therefore, one potential
will be around zero, as in this case we essentially wish to treat everyone. Therefore, one potential 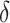 is
is
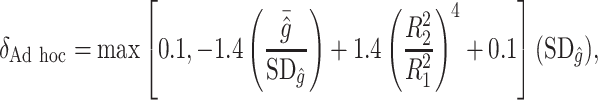 |
where 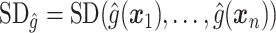 ,
, 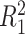 is the residual variance when model (2.1) is fit under the assumption
is the residual variance when model (2.1) is fit under the assumption 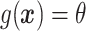 , for some constant
, for some constant 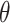 and
and 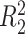 is that when model (2.1) is fit using the non-parametric procedure outlined in Section 2.1. If
is that when model (2.1) is fit using the non-parametric procedure outlined in Section 2.1. If 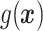 does not depend on the covariates, we expect
does not depend on the covariates, we expect 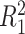 and
and 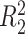 to be close, whereas if
to be close, whereas if 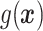 does explain more of the variability, we expect
does explain more of the variability, we expect 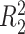 to be considerably smaller than
to be considerably smaller than 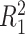 . Moreover, we expect
. Moreover, we expect 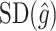 to increase as the degree to which
to increase as the degree to which 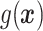 depends on the covariates increases. Thus, we expect
depends on the covariates increases. Thus, we expect 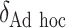 to be closer to
to be closer to 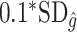 when the true treatment effect is in category (c), closer to
when the true treatment effect is in category (c), closer to 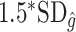 when the true treatment effect is in category (b), and between
when the true treatment effect is in category (b), and between 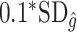 and
and 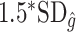 when the true treatment effect is in category (a).
when the true treatment effect is in category (a).
Augmented Inverse Probability Weighted Estimate  AIPWE
AIPWE -based approach. Recall that, if we were not interested in forcing
-based approach. Recall that, if we were not interested in forcing 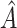 to have a simple form, we would select
to have a simple form, we would select 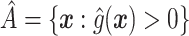 , or more generally
, or more generally 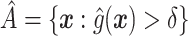 . This can be viewed as our “target group”, as our goal is essentially to identify the simple approximation that most closely captures this region. Therefore, we may select
. This can be viewed as our “target group”, as our goal is essentially to identify the simple approximation that most closely captures this region. Therefore, we may select 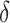 using the AIPWE of the expected response considered by Zhang and others (2012). In particular, we consider
using the AIPWE of the expected response considered by Zhang and others (2012). In particular, we consider
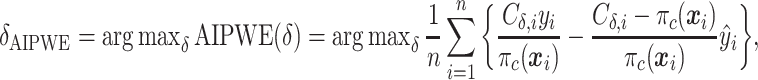 |
where 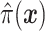 is the sample proportion assigned to the treatment group (since we consider only RCT data),
is the sample proportion assigned to the treatment group (since we consider only RCT data), 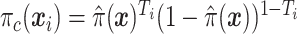 ,
, 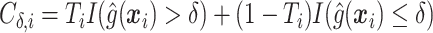 , and
, and 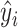 's are the predicted values from fitting (2.1).
's are the predicted values from fitting (2.1).
3. Simulations
A simulation study was undertaken, in which SORA was compared to Virtual Twins (VT) (Foster and others, 2011) and the recursive partitioning approach proposed by Su and others (2009). VT is another two-stage procedure designed to identify simple subgroups. In the first stage, 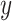 is modeled using RF, with the covariates and treatment indicator as predictors to obtain estimates of
is modeled using RF, with the covariates and treatment indicator as predictors to obtain estimates of 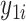 and
and 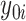 for each subject, from which estimated treatment effects are calculated. In the second stage, the estimated treatment effects are used as the outcome in a single regression tree, and the identified subgroup consists of all terminal nodes for which the estimated treatment effect from the VT tree is beyond some predefined “enhancement” threshold. The recursive partitioning approach of Su and others (2009) follows the standard classification and regression tree framework, but employs a splitting criterion which is large for strong treatment-by-covariate interactions. This can be viewed as a “one-stage” approach, as it does not require estimation of subject-specific treatment effects. We refer to this as the Tree approach. We also compare the performance of some
for each subject, from which estimated treatment effects are calculated. In the second stage, the estimated treatment effects are used as the outcome in a single regression tree, and the identified subgroup consists of all terminal nodes for which the estimated treatment effect from the VT tree is beyond some predefined “enhancement” threshold. The recursive partitioning approach of Su and others (2009) follows the standard classification and regression tree framework, but employs a splitting criterion which is large for strong treatment-by-covariate interactions. This can be viewed as a “one-stage” approach, as it does not require estimation of subject-specific treatment effects. We refer to this as the Tree approach. We also compare the performance of some 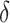 selection methods for SORA.
selection methods for SORA.
We consider eight cases:
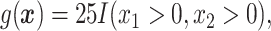
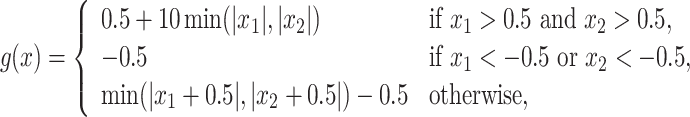
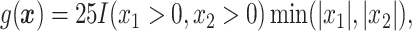
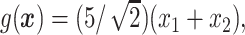
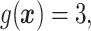
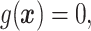
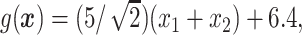
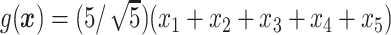 .
.
In Cases 1–7, at most two variables determine 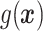 , and in Case 8, five variables determine
, and in Case 8, five variables determine 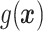 . Cases 1–3 have clearly defined enhanced individuals present. In Case 1, the treatment effect for non-responders is fixed at zero, and that for responders is a positive constant. In Case 2, there is a group of non-responders whose
. Cases 1–3 have clearly defined enhanced individuals present. In Case 1, the treatment effect for non-responders is fixed at zero, and that for responders is a positive constant. In Case 2, there is a group of non-responders whose 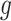 values vary slightly around zero, and a group of responders, whose values vary around some non-zero mean. Case 3 is similar to Case 2, but non-responders have a constant zero treatment effect. In Case 4, the treatment effects are symmetric about zero. Thus, there is no clearly separated “enhanced” group of individuals who are different from the rest of the population, but the treatment effect is positive for individuals with
values vary slightly around zero, and a group of responders, whose values vary around some non-zero mean. Case 3 is similar to Case 2, but non-responders have a constant zero treatment effect. In Case 4, the treatment effects are symmetric about zero. Thus, there is no clearly separated “enhanced” group of individuals who are different from the rest of the population, but the treatment effect is positive for individuals with 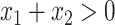 and negative for those with
and negative for those with 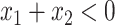 . In Case 5, the treatment effect is a positive constant for all individuals, so essentially everyone is “enhanced,” and in Case 6, the treatment effect is exactly zero for everyone. Case 7 was chosen to be analogous to the data we will analyze in Section 4. In this data set, nearly all subjects appear to respond positively to treatment, so the problem becomes identifying the small subgroup of patients who should not receive treatment. Thus, in Case 7, we generate data so that nearly all subjects have a positive treatment effect. Case 8 is similar to Case 4, but with the true treatment effect depending on five covariates instead of two. This case was chosen to assess the performance of SORA when the true treatment effect depends on more than three covariates and has a non-rectangular form. In Cases 1–3, we expect one-fourth of the population to be enhanced, in Cases 4 and 8 we expect one-half of the subjects to be enhanced, in Case 5 the true region is all individuals, in Case 6 the true region is empty, and in Case 7 we expect about 90% of the subjects to be enhanced.
. In Case 5, the treatment effect is a positive constant for all individuals, so essentially everyone is “enhanced,” and in Case 6, the treatment effect is exactly zero for everyone. Case 7 was chosen to be analogous to the data we will analyze in Section 4. In this data set, nearly all subjects appear to respond positively to treatment, so the problem becomes identifying the small subgroup of patients who should not receive treatment. Thus, in Case 7, we generate data so that nearly all subjects have a positive treatment effect. Case 8 is similar to Case 4, but with the true treatment effect depending on five covariates instead of two. This case was chosen to assess the performance of SORA when the true treatment effect depends on more than three covariates and has a non-rectangular form. In Cases 1–3, we expect one-fourth of the population to be enhanced, in Cases 4 and 8 we expect one-half of the subjects to be enhanced, in Case 5 the true region is all individuals, in Case 6 the true region is empty, and in Case 7 we expect about 90% of the subjects to be enhanced.
For each case, 500 data sets of size 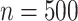 were generated from
were generated from 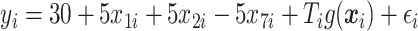 , where
, where 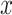 's are i.i.d.
's are i.i.d. 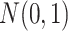 and are independent of the
and are independent of the 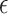 's, which are i.i.d.
's, which are i.i.d. 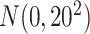 . In all cases, we consider a total of 10 variables in our analysis. To match the desired covariate balance in clinical trials and to eliminate spurious positive true
. In all cases, we consider a total of 10 variables in our analysis. To match the desired covariate balance in clinical trials and to eliminate spurious positive true 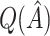 values, we used paired data, i.e. each subject in the treatment group has a “twin” in the control group with identical covariate values. This can be viewed as an approximation to a stratified trial design.
values, we used paired data, i.e. each subject in the treatment group has a “twin” in the control group with identical covariate values. This can be viewed as an approximation to a stratified trial design.
For SORA, only subgroups of size 20 or larger were considered, though this value is somewhat arbitrary. For the stepwise subgroup search, we chose  , and
, and 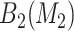 consisted of unique pairs from the top five groups of the form
consisted of unique pairs from the top five groups of the form 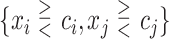 (and top five of the form
(and top five of the form 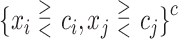 ). Candidate cutpoints for each covariate were the corresponding
). Candidate cutpoints for each covariate were the corresponding 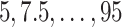 ,
, 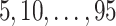 , and
, and 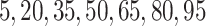 percentiles for the 1D, 2D, and 3D searches, respectively. For both SORA and VT, 20 bootstrap data sets were used to obtain the bias-corrected estimates, and for SORA,
percentiles for the 1D, 2D, and 3D searches, respectively. For both SORA and VT, 20 bootstrap data sets were used to obtain the bias-corrected estimates, and for SORA, 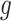 and
and 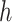 were estimated using a simple average of MARS and RF estimates, as this was found to perform better than either method alone in our simulations. These estimates were obtained using the R functions randomForest and mars with default settings. For the Tree approach, the maximum tree depth was set at 15, and terminal nodes were required to include at least 10 subjects from each treatment group. To prune initial trees for this method, a complexity parameter value of
were estimated using a simple average of MARS and RF estimates, as this was found to perform better than either method alone in our simulations. These estimates were obtained using the R functions randomForest and mars with default settings. For the Tree approach, the maximum tree depth was set at 15, and terminal nodes were required to include at least 10 subjects from each treatment group. To prune initial trees for this method, a complexity parameter value of 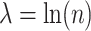 was used. Additional details can be found in Su and others (2009).
was used. Additional details can be found in Su and others (2009).
To assess the ability of the methods to identify the true underlying subgroup, we calculate the average number of individuals with a true positive treatment effect, the average 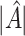 , the average sensitivity, specificity, positive and negative predictive values for
, the average sensitivity, specificity, positive and negative predictive values for 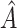 , the proportion of times the correct covariates are included in
, the proportion of times the correct covariates are included in 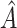 , the proportion of times
, the proportion of times 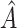 is defined using only the correct covariates. We also compute the average expected outcome if
is defined using only the correct covariates. We also compute the average expected outcome if 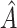 were used to assign treatment, and the average values of
were used to assign treatment, and the average values of 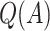 ,
, 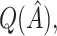 and all the estimates of
and all the estimates of 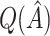 discussed in Section 2.3. Only
discussed in Section 2.3. Only 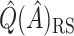 is computed for the Tree approach, as this approach does not involve the estimation of subject-specific treatment effects.
is computed for the Tree approach, as this approach does not involve the estimation of subject-specific treatment effects.
For the comparison of SORA to VT and Tree approaches, we chose 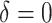 for SORA and
for SORA and
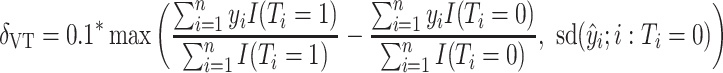 |
for VT. We considered terminal nodes with positive empirical treatment effects to be enhanced for the Tree approach. From Table 1, we can see that, though all methods are generally quite similar, SORA appears to best maximize the expected outcome. Note that this result also holds for Case 8, in which the true treatment effect depends on five covariates and is non-rectangular. In addition, when  , SORA tends to identify the largest subgroups, giving it higher sensitivity and lower specificity and positive predictive value than the other two methods. VT is the most successful at identifying regions which depend on all of the true covariates, followed by the Tree approach. Moreover, VT most frequently identifies regions which depend only on the correct covariates, though none of the methods considered performs overly well in this regard. It is worth noting that Cases 4 and 8 (for which SORA performs well) are the only scenarios in which it is truly undesirable to treat too many people. In all other cases, subjects who unnecessarily receive treatment would experience no real harm, as their true
, SORA tends to identify the largest subgroups, giving it higher sensitivity and lower specificity and positive predictive value than the other two methods. VT is the most successful at identifying regions which depend on all of the true covariates, followed by the Tree approach. Moreover, VT most frequently identifies regions which depend only on the correct covariates, though none of the methods considered performs overly well in this regard. It is worth noting that Cases 4 and 8 (for which SORA performs well) are the only scenarios in which it is truly undesirable to treat too many people. In all other cases, subjects who unnecessarily receive treatment would experience no real harm, as their true 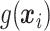 is close to zero. In Cases 5 and 7, it is important to treat a larger number of people, and SORA achieves this.
is close to zero. In Cases 5 and 7, it is important to treat a larger number of people, and SORA achieves this.
Table 1.
Simulation study results: subgroup identification performance
| Scenario | True # responders
|
Size | Sens. | Spec. | PPV | NPV | Incl. 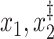
|
Only 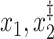
|
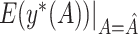 |
|---|---|---|---|---|---|---|---|---|---|
| Case 1 | |||||||||
| SORA | 125.41 | 395.71 | 0.99 | 0.28 | 0.32 | 0.99 | 0.42 | 0.01 | 36.24 |
| VT | 125.41 | 149.12 | 0.94 | 0.92 | 0.84 | 0.98 | 1.00 | 0.30 | 35.91 |
| Tree | 125.41 | 309.12 | 0.96 | 0.50 | 0.43 | 0.97 | 0.96 | 0.05 | 36.04 |
| Case 2 | |||||||||
| SORA | 125.41 | 279.90 | 0.64 | 0.47 | 0.30 | 0.80 | 0.10 | 0.002 | 30.47 |
| VT | 125.41 | 162.86 | 0.45 | 0.72 | 0.36 | 0.80 | 0.41 | 0.03 | 30.46 |
| Tree | 125.41 | 263.90 | 0.59 | 0.49 | 0.29 | 0.79 | 0.22 | 0.00 | 30.44 |
| Case 3 | |||||||||
| SORA | 125.41 | 357.02 | 0.90 | 0.35 | 0.33 | 0.92 | 0.21 | 0.004 | 32.76 |
| VT | 125.41 | 180.73 | 0.67 | 0.74 | 0.53 | 0.88 | 0.90 | 0.13 | 32.44 |
| Tree | 125.41 | 303.75 | 0.77 | 0.45 | 0.35 | 0.85 | 0.61 | 0.04 | 32.51 |
| Case 4 | |||||||||
| SORA | 250.26 | 247.76 | 0.68 | 0.68 | 0.70 | 0.70 | 0.39 | 0.01 | 31.03 |
| VT | 250.26 | 166.33 | 0.51 | 0.85 | 0.77 | 0.65 | 0.73 | 0.10 | 31.04 |
| Tree | 250.26 | 262.10 | 0.64 | 0.60 | 0.64 | 0.66 | 0.46 | 0.03 | 30.72 |
| Case 5 | |||||||||
| SORA | 500 | 391.88 | 0.78 | — | 1.00 | — | — | — | 32.36 |
| VT | 500 | 211.60 | 0.42 | — | 0.99 | — | — | — | 31.28 |
| Tree | 500 | 338.47 | 0.68 | — | 1.00 | — | — | — | 32.04 |
| Case 6 | |||||||||
| SORA | 0 | 249.83 | — | 0.50 | — | 1.00 | — | — | 30.01 |
| VT | 0 | 147.21 | — | 0.71 | — | 1.00 | — | — | 30.01 |
| Tree | 0 | 254.47 | — | 0.49 | — | 1.00 | — | — | 30.01 |
| Case 7 | |||||||||
| SORA | 449.98 | 436.08 | 0.90 | 0.39 | 0.93 | 0.32 | 0.37 | 0.01 | 36.14 |
| VT | 449.98 | 233.30 | 0.51 | 0.88 | 0.98 | 0.17 | 0.76 | 0.10 | 34.16 |
| Tree | 449.98 | 375.88 | 0.78 | 0.47 | 0.93 | 0.22 | 0.46 | 0.03 | 35.39 |
| Case 8 | |||||||||
| SORA | 250.46 | 251.30 | 0.63 | 0.63 | 0.65 | 0.65 | — | — | 30.78 |
| VT | 250.46 | 168.13 | 0.45 | 0.78 | 0.68 | 0.60 | 0.01 | 0.004 | 30.71 |
| Tree | 250.46 | 251.89 | 0.60 | 0.59 | 0.61 | 0.61 | 0.03 | 0.00 | 30.58 |
Values represent averages across 500 simulated data sets. VT failed to identify a subgroup in 3.6% of data sets for Case 2, 3.2% for Case 4, 0.8% for Case 5, 7.2% for Case 6, and 2.8% for Case 8. Tree method failed to identify a subgroup in 4.4% of data sets for Case 2, 3% for Case 4, 6.6% for Case 6, and 4.4% for Case 8.
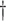 True responders defined as those with
True responders defined as those with 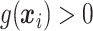 .
.
 In Case 8, these columns indicates inclusion of
In Case 8, these columns indicates inclusion of 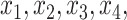 and
and 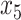 .
.
From Table 2, we can see that the VT and Tree procedures identify more enhanced regions than SORA. Again, this is a result of SORA's tendency to identify larger subgroups when 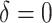 . As expected,
. As expected, 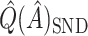 and
and 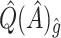 are less biased than
are less biased than 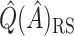 for both VT and SORA. The bias correction appears to work better for SORA, showing less of a tendency to overcorrect than with VT, though
for both VT and SORA. The bias correction appears to work better for SORA, showing less of a tendency to overcorrect than with VT, though 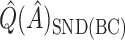 is quite poor for both approaches, and
is quite poor for both approaches, and 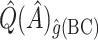 is essentially always near zero. Although none of the estimates considered is completely satisfactory,
is essentially always near zero. Although none of the estimates considered is completely satisfactory, 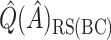 is generally the least biased for both SORA and VT.
is generally the least biased for both SORA and VT.
Table 2.
Simulation study results: 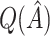 estimation performance
estimation performance
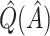 |
Bias-corrected 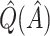 |
|||||||
|---|---|---|---|---|---|---|---|---|
| Scenario | 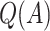 |
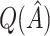 |
RS | SND | Mean 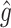
|
RS | SND | Mean 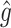
|
| Case 1 | ||||||||
| SORA | 18.73 | 1.76 | 4.15 | 2.57 | 2.94 | 2.09 | -0.33 | 0.46 |
| VT | 18.73 | 14.81 | 17.89 | 13.48 | — | 12.65 | 7.03 | — |
| Tree | 18.73 | 4.43 | 9.71 | — | — | — | — | — |
| Case 2 | ||||||||
| SORA | 3.01 | 0.31 | 6.48 | 2.59 | 3.46 | 2.67 | -2.82 | -1.25 |
| VT | 3.01 | 1.05 | 10.46 | 3.43 | — | 2.93 | -5.79 | — |
| Tree | 3.01 | 0.35 | 8.65 | — | — | — | — | — |
| Case 3 | ||||||||
| SORA | 8.75 | 1.10 | 4.50 | 2.40 | 2.88 | 1.66 | -1.61 | -0.60 |
| VT | 8.75 | 5.06 | 11.61 | 5.85 | — | 4.81 | -2.50 | — |
| Tree | 8.75 | 1.77 | 8.56 | — | — | — | — | — |
| Case 4 | ||||||||
| SORA | 3.99 | 2.27 | 7.52 | 4.26 | 5.00 | 3.73 | -1.01 | 0.45 |
| VT | 3.99 | 3.36 | 10.96 | 4.71 | — | 3.77 | -4.17 | — |
| Tree | 3.99 | 1.60 | 9.23 | — | — | — | — | — |
| Case 5 | ||||||||
| SORA | 0.00 | 0.00 | 3.44 | 1.34 | 1.81 | 0.68 | -2.56 | -1.59 |
| VT | 0.00 | 0.00 | 8.58 | 2.67 | — | 1.47 | -5.89 | — |
| Tree | 0.00 | 0.00 | 6.83 | — | — | — | — | — |
| Case 6 | ||||||||
| SORA | 0.00 | 0.00 | 7.45 | 2.75 | 3.80 | 3.33 | -3.06 | -1.25 |
| VT | 0.00 | 0.00 | 10.27 | 2.98 | — | 2.79 | -6.20 | — |
| Tree | 0.00 | 0.00 | 8.64 | — | — | — | — | — |
| Case 7 | ||||||||
| SORA | 0.98 | 0.66 | 2.63 | 1.35 | 1.64 | 0.70 | -1.25 | -0.58 |
| VT | 0.98 | 2.75 | 8.59 | 4.27 | — | 1.99 | -3.73 | — |
| Tree | 0.98 | 0.89 | 5.33 | — | — | — | — | — |
| Case 8 | ||||||||
| SORA | 3.98 | 1.71 | 7.42 | 4.00 | 4.79 | 3.57 | -1.42 | 0.10 |
| VT | 3.98 | 2.28 | 11.16 | 3.83 | — | 3.66 | -5.57 | — |
| Tree | 3.98 | 1.29 | 9.56 | — | — | — | — | — |
Values represent averages across 500 simulated data sets. VT failed to identify a subgroup in 3.6% of data sets for Case 2, 3.2% for Case 4, 0.8% for Case 5, 7.2% for Case 6, and 2.8% for Case 8. Tree method failed to identify a subgroup in 4.4% of data sets for Case 2, 3% for Case 4, 6.6% for Case 6, and 4.4% for Case 8.
SORA can be very computationally expensive. For instance, using the Biowulf Linux cluster at NIH (see website in Acknowledgments for exact specifications), the average run time for Case 8 was approximately 6 h and 22 min, whereas the VT and Tree procedures generally did not take more than a few minutes.
SORA was also implemented for Cases 1–6 using 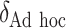 and
and 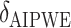 . From Tables 3 and 4, we can see that the average
. From Tables 3 and 4, we can see that the average 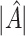 varies considerably depending on which
varies considerably depending on which 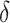 is selected, and thus so do sensitivity, specificity, positive predictive value, negative predictive value,
is selected, and thus so do sensitivity, specificity, positive predictive value, negative predictive value, 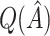 and
and 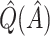 . Of the methods considered, choosing
. Of the methods considered, choosing 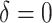 appears to lead to the best expected outcome, though all three methods are generally fairly similar in this regard. However, choosing
appears to lead to the best expected outcome, though all three methods are generally fairly similar in this regard. However, choosing 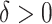 leads to smaller subgroups with a more clearly distinguishable treatment effect from the whole population.
leads to smaller subgroups with a more clearly distinguishable treatment effect from the whole population.
Table 3.
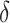 selection comparison: subgroup identification performance
selection comparison: subgroup identification performance
| Scenario | True # responders
|
Size | Sens. | Spec. | PPV | NPV | Incl. 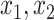
|
Only 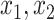
|
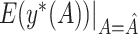 |
|---|---|---|---|---|---|---|---|---|---|
| Case 1 | |||||||||
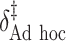
|
125.41 | 362.24 | 0.99 | 0.36 | 0.36 | 0.99 | 0.45 | 0.02 | 36.21 |
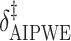
|
125.41 | 227.57 | 0.92 | 0.70 | 0.63 | 0.97 | 0.72 | 0.05 | 35.75 |
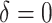
|
125.41 | 395.71 | 0.99 | 0.28 | 0.32 | 0.99 | 0.42 | 0.01 | 36.24 |
| Case 2 | |||||||||
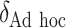
|
125.41 | 145.78 | 0.37 | 0.73 | 0.36 | 0.78 | 0.13 | 0.02 | 30.32 |
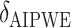
|
125.41 | 237.91 | 0.54 | 0.55 | 0.32 | 0.80 | 0.10 | 0.002 | 30.40 |
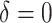
|
125.41 | 279.90 | 0.64 | 0.47 | 0.30 | 0.80 | 0.10 | 0.002 | 30.47 |
| Case 3 | |||||||||
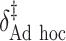
|
125.41 | 290.67 | 0.80 | 0.49 | 0.39 | 0.90 | 0.26 | 0.01 | 32.54 |
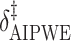
|
125.41 | 245.66 | 0.71 | 0.58 | 0.45 | 0.88 | 0.35 | 0.01 | 32.33 |
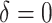
|
125.41 | 357.02 | 0.90 | 0.35 | 0.33 | 0.92 | 0.21 | 0.004 | 32.76 |
| Case 4 | |||||||||
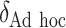
|
250.26 | 125.60 | 0.37 | 0.87 | 0.79 | 0.60 | 0.37 | 0.01 | 30.73 |
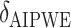
|
250.26 | 243.84 | 0.63 | 0.65 | 0.70 | 0.69 | 0.37 | 0.01 | 30.81 |
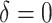
|
250.26 | 247.76 | 0.68 | 0.68 | 0.70 | 0.70 | 0.39 | 0.01 | 31.03 |
| Case 5 | |||||||||
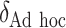
|
500 | 326.04 | 0.65 | — | 1.00 | — | — | — | 31.97 |
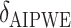
|
500 | 246.41 | 0.49 | — | 1.00 | — | — | — | 31.49 |
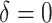
|
500 | 391.88 | 0.78 | — | 1.00 | — | — | — | 32.36 |
| Case 6 | |||||||||
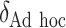
|
0 | 107.23 | — | 0.79 | — | 1.00 | — | — | 30.01 |
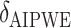
|
0 | 239.91 | — | 0.52 | — | 1.00 | — | — | 30.01 |
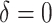
|
0 | 249.83 | — | 0.50 | — | 1.00 | — | — | 30.01 |
Values represent averages across 500 simulated data sets.
 True responders defines as those with
True responders defines as those with 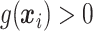 .
.
 Averages based on 497 and 499 data sets in Cases 1 and 3, respectively, due to numerical problems.
Averages based on 497 and 499 data sets in Cases 1 and 3, respectively, due to numerical problems.
Table 4.
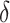 selection comparison:
selection comparison: 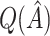 estimation performance
estimation performance
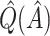 |
Bias-corrected 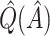 |
|||||||
|---|---|---|---|---|---|---|---|---|
| Scenario | 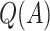 |
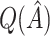 |
RS | SND | Mean 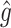
|
RS | SND | Mean 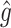
|
| Case 1 | ||||||||
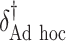
|
18.73 | 2.61 | 5.30 | 3.37 | 3.81 | 3.02 | 0.08 | 1.02 |
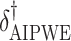
|
18.73 | 9.37 | 12.50 | 7.21 | 8.39 | 8.98 | 1.87 | 4.11 |
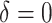
|
18.73 | 1.76 | 4.15 | 2.57 | 2.94 | 2.09 | -0.33 | 0.46 |
| Case 2 | ||||||||
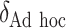
|
3.01 | 0.93 | 15.08 | 4.98 | 7.26 | 8.84 | -3.79 | -0.22 |
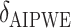
|
3.01 | 0.57 | 10.20 | 3.53 | 5.03 | 5.63 | -2.93 | -0.55 |
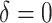
|
3.01 | 0.31 | 6.48 | 2.59 | 3.46 | 2.67 | -2.82 | -1.25 |
| Case 3 | ||||||||
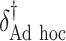
|
8.75 | 2.16 | 7.17 | 3.60 | 4.41 | 3.59 | -1.50 | 0.03 |
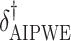
|
8.75 | 3.38 | 9.86 | 4.51 | 5.71 | 5.70 | -1.43 | 0.64 |
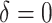
|
8.75 | 1.10 | 4.50 | 2.40 | 2.88 | 1.66 | -1.61 | -0.60 |
| Case 4 | ||||||||
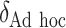
|
3.99 | 3.56 | 15.76 | 7.33 | 9.25 | 9.35 | -1.52 | 1.77 |
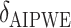
|
3.99 | 2.29 | 9.52 | 4.68 | 5.78 | 5.23 | -1.22 | 0.74 |
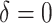
|
3.99 | 2.27 | 7.52 | 4.26 | 5.00 | 3.73 | -1.01 | 0.45 |
| Case 5 | ||||||||
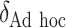
|
0.00 | 0.00 | 5.87 | 2.12 | 2.96 | 2.33 | -2.86 | -1.37 |
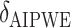
|
0.00 | 0.00 | 9.44 | 3.15 | 4.56 | 4.92 | -3.20 | -0.93 |
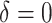
|
0.00 | 0.00 | 3.44 | 1.34 | 1.81 | 0.68 | -2.56 | -1.59 |
| Case 6 | ||||||||
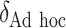
|
0.00 | 0.00 | 17.95 | 5.46 | 8.27 | 10.79 | -4.54 | -0.26 |
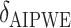
|
0.00 | 0.00 | 10.10 | 3.27 | 4.80 | 5.42 | -3.24 | -0.82 |
|
0.00 | 0.00 | 7.45 | 2.75 | 3.80 | 3.33 | -3.06 | -1.25 |
Values represent averages across 500 simulated data sets.
 Averages based on 497 and 499 data sets in Cases 1 and 3, respectively, due to numerical problems.
Averages based on 497 and 499 data sets in Cases 1 and 3, respectively, due to numerical problems.
4. Application to RCT data
The proposed methods were applied to data from the Trial of Preventing Hypertension (TROPHY) (Julius and others, 2006). This study included participants with prehypertension, i.e. either an average systolic blood pressure (SBP) of 130–139 mm Hg and diastolic blood pressure (DBP) of no more than 89 mm Hg for the three run-in visits (before randomization), or SBP of 139 mm Hg or lower and DBP between 85 and 89 mm Hg for the three run-in visits. These subjects were randomly assigned to receive either 2 years of candesartan or placebo, followed by 2 years of placebo for all subjects. Subjects had return visits at 1 and 3 months post-randomization, and approximately every 3 months thereafter. The study produced analyzable data on 772 subject (391 candesartan, 381 placebo). Baseline measurements included age, gender, race (white, black, or other), weight, body-mass index (BMI), SBP, DBP, total cholesterol, high density lipoprotein cholesterol (HDL), low density lipoprotein cholesterol (LDL), HDL:LDL ratio, triglycerides, fasting glucose, total insulin, insulin:glucose ratio, and creatinine. The insulin:glucose ratio was dropped due to extremely high correlation (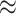 0.98) with total insulin. For our analysis, we consider SBP at 12 months post-randomization as the outcome.
0.98) with total insulin. For our analysis, we consider SBP at 12 months post-randomization as the outcome.
At 12 months post-randomization, approximately 20% of the outcome values were missing due to patient dropout and patients developing hypertension. Because hypertension was defined based only on observed blood pressure measurements, missing data due to patients experiencing the event were assumed to be missing at random. There was also a small amount of missingness in the baseline covariates, with the largest fraction for any covariate being 4.3%. All missing values were imputed using SAS PROC MI (SAS Institute, Inc., Cary, NC, USA). The imputation model included baseline measures of age, weight, BMI, total cholesterol, LDL, HDL, HDL:LDL ratio, total insulin, fasting glucose, insulin:glucose ratio, trilglycerides, and creatinine, as well as all blood pressure measurements up to 12 months post-randomization, stratified by treatment, and gender. Because the proposed methods have not yet been extended to data with missing values, only a single imputation was performed.
There are three very large and influential outliers in the covariate values. Thus, RF, rather than an average of RF and MARS, was used to estimate 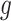 and
and 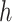 , as we found it to be less sensitive to outliers. Insulin, glucose, HDL, LDL, HDL:LDL ratio, and triglycerides were log-transformed.
, as we found it to be less sensitive to outliers. Insulin, glucose, HDL, LDL, HDL:LDL ratio, and triglycerides were log-transformed.
For SORA, all 1D and 2D regions were considered in the stepwise procedure, and 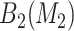 consisted of unique pairs from the top 50 2D groups (and the top 50 complement groups). Percentiles used as cutpoints in the 3D search were
consisted of unique pairs from the top 50 2D groups (and the top 50 complement groups). Percentiles used as cutpoints in the 3D search were 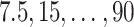 , and the RF included 2000 trees. All other settings were the same as in the simulations.
, and the RF included 2000 trees. All other settings were the same as in the simulations.
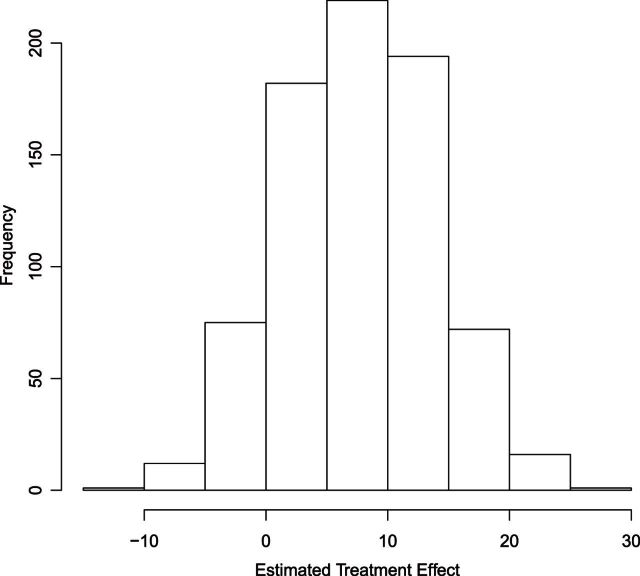
A histogram of the estimated treatment effects is given in Figure 1. The very high percentage of positive predicted treatment effects suggests that candesartan is widely effective, so in this case, it is more interesting to identify the small subgroup of individuals who should not receive treatment. As a result, we chose 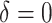 , and
, and 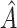 was redefined as the region which minimizes (2.3). The identified region was
was redefined as the region which minimizes (2.3). The identified region was 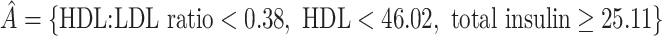 , and contained 20 subjects, suggesting a regime where these individuals receive no treatment and all others receive candesartan. These subjects also had high triglycerides, total cholesterol, and LDL, and could be described as having an elevated risk profile on lipids and a high risk of diabetes. Values of
, and contained 20 subjects, suggesting a regime where these individuals receive no treatment and all others receive candesartan. These subjects also had high triglycerides, total cholesterol, and LDL, and could be described as having an elevated risk profile on lipids and a high risk of diabetes. Values of  ,
, 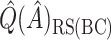 ,
, 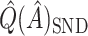 ,
, 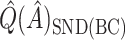 ,
, 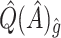 , and
, and 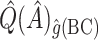 were
were  1.63, 3.92,
1.63, 3.92,  8.14, 0.35,
8.14, 0.35,  9.75, and
9.75, and  4.24, respectively. The relatively small magnitude of the bias-corrected estimates suggests that individuals in
4.24, respectively. The relatively small magnitude of the bias-corrected estimates suggests that individuals in 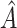 may have essentially no response to treatment, rather than a large negative response.
may have essentially no response to treatment, rather than a large negative response.
Fig. 1.
Histogram of 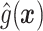 for TROPHY Data.
for TROPHY Data.
Due to the random nature of RF, results may vary slightly depending on which seed is chosen for estimating 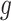 and
and 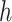 . We re-implemented SORA using a different seed, and a slightly different
. We re-implemented SORA using a different seed, and a slightly different 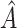 was identified; however, it was again defined using insulin and two of the cholesterol measures, and contained some, but not all of the same individuals. The above analysis was also performed without the three large outlying observations in the covariates, and again a region based on cholesterol measures and insulin was identified.
was identified; however, it was again defined using insulin and two of the cholesterol measures, and contained some, but not all of the same individuals. The above analysis was also performed without the three large outlying observations in the covariates, and again a region based on cholesterol measures and insulin was identified.
We also applied the VT and Tree procedures to the TROPHY data. For this analysis, we chose 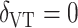 , and VT selected a tree containing HDL, total insulin, triglycerides, baseline SBP, and age, but failed to identify a subgroup, as predictions from this tree suggested that all subjects benefit from candesartan. The Tree procedure identified three disjoint subgroups, containing a total of 128 subjects:
, and VT selected a tree containing HDL, total insulin, triglycerides, baseline SBP, and age, but failed to identify a subgroup, as predictions from this tree suggested that all subjects benefit from candesartan. The Tree procedure identified three disjoint subgroups, containing a total of 128 subjects: 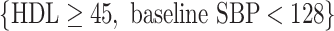 (34 subjects),
(34 subjects), 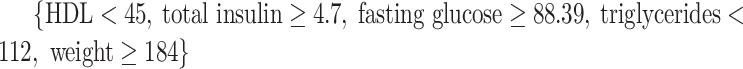 (50 subjects), and
(50 subjects), and  (44 subjects), and
(44 subjects), and 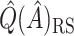 for these 128 subjects was
for these 128 subjects was  12.72. Because
12.72. Because 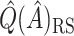 is generally strongly biased, it is difficult to assess the strength of this subgroup. However, it is possible that these individuals truly have a strong negative response to candesartan, but were not all identified by SORA because the true structure of the subgroup was too complex to be detected.
is generally strongly biased, it is difficult to assess the strength of this subgroup. However, it is possible that these individuals truly have a strong negative response to candesartan, but were not all identified by SORA because the true structure of the subgroup was too complex to be detected.
5. Discussion
We proposed a method, SORA, that uses RCT data to identify simple treatment regimes which, once properly validated, could be used to assign treatment to future patients in the population. Our simulations showed that regimes identified by SORA better maximized the expected outcome than those identified by the VT or Tree methods. Moreover, in our experience, the VT and Tree procedures have a tendency to identify subgroups which consist of two or more disjoint regions, so subgroups identified by SORA will generally be more interpretable.
The SORA method tends to select 3D regions, even when the true underlying region is of fewer dimensions. Thus, it may be interesting to consider some form of pruning, or perhaps incorporating a penalty based on the number of covariates into the objective function, which could help SORA identify regions of the correct dimension more frequently.
As illustrated in our simulations, the value of 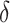 can strongly impact
can strongly impact 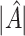 . Although we considered a few methods for selecting
. Although we considered a few methods for selecting 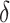 , other data-adaptive methods could be developed. There may also be logistical or cost-based reasons for preferring a non-zero
, other data-adaptive methods could be developed. There may also be logistical or cost-based reasons for preferring a non-zero 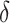 , which could be taken into account.
, which could be taken into account.
It may be of interest to consider methods for increasing computational speed. The speed of SORA as implemented in this paper does not change with 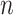 , but is heavily dependent on the number of covariates, so it may be interesting to consider a method for weeding out “useless” covariates between model estimation and subgroup identification to reduce computation time.
, but is heavily dependent on the number of covariates, so it may be interesting to consider a method for weeding out “useless” covariates between model estimation and subgroup identification to reduce computation time.
In our simulations, the bootstrap often led to an overestimate of the bias of 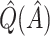 . This phenomenon was discussed by Efron and Tibshirani (1997) in the case of classification error. Although the settings are slightly different, it may be possible to improve the estimation of
. This phenomenon was discussed by Efron and Tibshirani (1997) in the case of classification error. Although the settings are slightly different, it may be possible to improve the estimation of 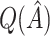 by following their same general arguments. As a rough illustration, consider
by following their same general arguments. As a rough illustration, consider 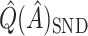 . In Table 2,
. In Table 2, 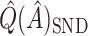 tends to overestimate
tends to overestimate 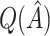 , whereas
, whereas 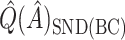 underestimates
underestimates 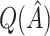 . However,
. However, 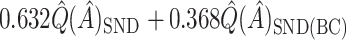 is generally very close to
is generally very close to 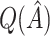 . That is, by up-weighting
. That is, by up-weighting 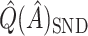 and down-weighting
and down-weighting 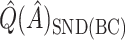 in a fashion similar to Efron and Tibshirani (1997), we can obtain a noticeably less biased estimate. It may be interesting to investigate this further. One could also potentially consider using cross-validation to obtain more honest estimates of
in a fashion similar to Efron and Tibshirani (1997), we can obtain a noticeably less biased estimate. It may be interesting to investigate this further. One could also potentially consider using cross-validation to obtain more honest estimates of 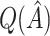 , though this was also shown by Foster and others (2011) to overestimate the bias for VT.
, though this was also shown by Foster and others (2011) to overestimate the bias for VT.
Who should and should not receive treatment are both very important and clinically meaningful questions, and considering only the primary outcome when attempting to choose the best regime may lead to less sufficient results. It may thus be useful to consider additional information when attempting to select the best regime, such as secondary outcomes, and the risks and rewards associated with each of the competing treatments for the outcome(s) considered.
6. Software
R code is available on request from the corresponding author.
Funding
This research was partially supported by a grant from Eli Lilly, grant DMS-1007590 from the National Science Foundation, grants CA083654 and AG036802 from the National Institutes of Health (NIH), and the Intramural Research Program of the NIH, Eunice Kennedy Shriver National Institute of Child Health and Human Development.
Acknowledgement
We utilized the high-performance computational capabilities of the Biowulf Linux cluster at NIH, Bethesda, MD (http://biowulf.nih.gov). We thank Xiaogang Su for sharing his R code. Conflict of Interest: None declared.
References
- Breiman L. (2001). Random forests. Machine Learning 45, 5–32. [Google Scholar]
- Brinkley J., Tsiatis A., Anstrom K. J. (2010). A generalized estimator of the attributable benefit of an optimal treatment regime. Biometrics 66(2), 512–522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B., Tibshirani R. (1997). Improvements on cross-validation: the.632 bootstrap method. Journal of the American Statistical Association 92(438), 548–560. [Google Scholar]
- Fan J., Li R. (2001). Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association 96, 1348–1360. [Google Scholar]
- Faries D., Chen Y., Lipkovich I., Zagar A., Liu X., Obenchain R. L. (2013). Local control for identifying subgroups of interest in observational research: persistence of treatment for major depressive disorder. International Journal of Methods in Psychiatric Research 22(3), 185–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster J. C., Taylor J. M. G., Nan B. (2013). Variable selection in monotone single-index models via the adaptive lasso. Statistics in Medicine 32(22), 3944–3954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster J. C., Taylor J. M. G., Ruberg S. J. (2011). Subgroup identification from randomized clinical trial data. Statistics in Medicine 30(24), 2867–2880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J. H. (1991). Multivariate adaptive regression splines. The Annals of Statistics 19(1), 1–141. [Google Scholar]
- Gunter L., Zhu J., Murphy S. (2007) . Variable selection for optimal decision making. Proceedings of the 11th conference on Artificial Intelligence in Medicine, AIME ’07. Berlin: Springer, pp. 149–154. [Google Scholar]
- Imai K., Ratkovic M. (2013). Estimating treatment effect heterogeneity in randomized program evaluation. Annals of Applied Statistics 7(1), 443–470. [Google Scholar]
- Julius S., Nesbitt S. D., Egan B. M., Weber M. A., Michelson E. L., Kaciroti N., Black H. R., Grimm R. H., Messerli F. H., Oparil S., Schork M. A. (2006). Feasibility of treating prehypertension with an angiotensin-receptor blocker. New England Journal of Medicine 354(16), 1685–1697. [DOI] [PubMed] [Google Scholar]
- Lipkovich I., Dmitrienko A., Denne J., Enas G. (2011). Subgroup identification based on differential effect search—a recursive partitioning method for establishing response to treatment in patient subpopulations. Statistics in Medicine 30(21), 2601–2621. [DOI] [PubMed] [Google Scholar]
- Lu W., Zhang H. H., Zeng D. (2013). Variable selection for optimal treatment decision. Statistical Methods in Medical Research 22(5), 493–504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy S. A., van der Laan M. J., Robbins J. M., CPPRG.(2001). Marginal Mean Models for Dynamic Regimes. Journal of the American Statistical Association 96(456), 1410–1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Negassa A., Ciampi A., Abrahamowicz M., Shapiro S., Boivin J.-F. (2005). Tree-structured subgroup analysis for censored survival data: validation of computationally inexpensive model selection criteria. Statistics and Computing 15(3), 231–239. [Google Scholar]
- Qian M., Murphy S. A. (2011). Performance guarantees for individualized treatment rules. Annals of Statistics 39(2), 1180–1210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robins J. M. (2004). Optimal structural nested models for optimal sequential decisions. Proceedings of the Second Seattle Symposium on Biostatistics. Berlin: Springer. [Google Scholar]
- Song X., Pepe M. S. (2004). Evaluating markers for selecting a patient's treatment. Biometrics 60(4), 874–883. [DOI] [PubMed] [Google Scholar]
- Su X., Tsai C.-L., Wang H., Nickerson D. M., Li B. (2008). Subgroup analysis via recursive partitioning. Journal of Machine Learning Research 10, 141–158. [Google Scholar]
- Su X., Zhou T., Yan X., Fan J., Yang S. (2009). Interaction trees with censored survival data. The International Journal of Biostatistics 4(1), 1–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton R. S., Barto A. G. (1998). Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press. [Google Scholar]
- Tibshirani R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological) 58(1), 267–288. [Google Scholar]
- Zhang B., Tsiatis A. A., Laber E. B., Davidian M. (2012). A robust method for estimating optimal treatment regimes. Biometrics 68(4), 1010–1018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H., Zhang H. H. (2009). On the adaptive elastic-net with a diverging number of parameters. Annals of Statistics 37(4), 1733–1751. [DOI] [PMC free article] [PubMed] [Google Scholar]