Mechanistic Models of Infectious Disease and Their Impact on Public Health

Abstract

From the 1930s through the 1940s, Lowell Reed and Wade Hampton Frost used mathematical models and mechanical epidemic simulators as research tools and to teach epidemic theory to students at the Johns Hopkins Bloomberg School of Public Health (then the School of Hygiene and Public Health). Since that time, modeling has become an integral part of epidemiology and public health. Models have been used for explanatory and inferential purposes, as well as in planning and implementing public health responses. In this article, we review a selection of developments in the history of modeling of infectious disease dynamics over the past 100 years. We also identify trends in model development and use and speculate as to the future use of models in infectious disease dynamics.

From the 1930s through the 1940s, Lowell Reed and Wade Hampton Frost used mathematical models and mechanical epidemic simulators as research tools and to teach epidemic theory to students at the Johns Hopkins Bloomberg School of Public Health (then the School of Hygiene and Public Health) (1, 2). Though never published by Reed and Frost (versions of the model were eventually published by their students (3, 4)), their model was one of the first mechanistic models of infectious disease transmission, and at a time long before digital computing, they may have been the first to use simulation methods to understand the epidemic process. Reed and Frost were pioneers in the study of infectious disease dynamics using mechanistic models, a field of epidemiology that has developed in parallel with the associative statistical models and methods of causal inference that dominate much of epidemiologic research. Over the past century, mechanistic models have played an essential role in shaping public health policy, the way we study interventions aimed at controlling infectious diseases, and the theory on which disease control is based.

Mechanistic models differ from traditional statistical models such as regression models because their structure makes explicit hypotheses about the biological mechanisms that drive infection dynamics. Such hypotheses range from simple representations of the time it takes to complete some part of the disease process (e.g., Sartwell's lognormal representation of the incubation period (5)) to complex agent-based models that attempt to explicitly represent social interactions of people in an entire country (6, 7) or even the world (8). Regardless of scale, approach, and complexity, these models have more of the flavor of models in physics than the statistical models that are used in other branches of epidemiology, and in many cases they can be used to predict the effectiveness of hypothetical interventions in controlling disease spread.

DISEASE CONTROL

Perhaps the first mechanistic model of infectious disease transmission used in assessing intervention strategies was a mathematical model of malaria transmission developed and refined by Ronald Ross in a series of papers published between 1908 and 1921 (9–11), pre-dating the work of Reed and Frost by decades. This model had a direct and powerful message for public health: Malaria could be controlled and even eliminated through mosquito control, even if the vector could not be completely eliminated. Ross used his theoretical framework to develop and advocate for multiple indices, including the prevalence rate and the entomological inoculation rate (12), that could effectively characterize the intensity of transmission in an area and identify goals for control. In the wake of the founding of the Global Malaria Eradication Program by the World Health Organization, George Macdonald (13) extended Ross's work in order to justify the use of insecticide as a tool for global malaria eradication (14). In particular, he showed that increasing daily mosquito mortality from 5% to 45% would be adequate to eliminate malaria even in locations with the highest transmission intensities in Africa. Mechanistic models continue to play an important role in the fight against malaria. The work of Ross and MacDonald looms large to this day, with a recent review finding that the majority of models published since 1940 depart from central hypotheses of the Ross-MacDonald model in only a few key assumptions, if any (15).

Although there are numerous instances over the past century in which mechanistic models have contributed to the control of a single disease (see Figure 1 for some examples), their larger contribution may be in our general understanding of disease control. The prime example is the concept of herd immunity and the critical vaccination threshold. Herd immunity is the indirect protection offered to members of the population susceptible to the disease (i.e., not immune and with the potential to be infected) by the immunity of surrounding individuals, and the critical vaccination threshold is the percentage of the population that must be vaccinated in order for the introduction of an infectious case to not spark an epidemic (16). To estimate the critical vaccination threshold, we must first understand one of the most critical concepts of infectious disease dynamics, the basic reproductive number, R₀. R₀ is the number of cases that a single infectious individual is expected to cause in a fully susceptible population. This concept was first introduced in demography and underwent significant development by Lotka while on a visit to the Johns Hopkins University School of Hygiene and Public Health in 1925 (see Heesterbeek (17) for a full history of the development of R₀ in infectious disease). Although this value does vary by setting, for many pathogens it is remarkably consistent across contexts and serves as a rough quantification of pathogen transmissibility. Based on dynamic models, it has been shown that if we vaccinate a proportion of the population equivalent to 1 − 1/R₀, then the pathogen will fail to spread in that population. This is the critical vaccination threshold, and it has helped to set vaccination goals for a number of diseases, particularly when elimination is the goal.

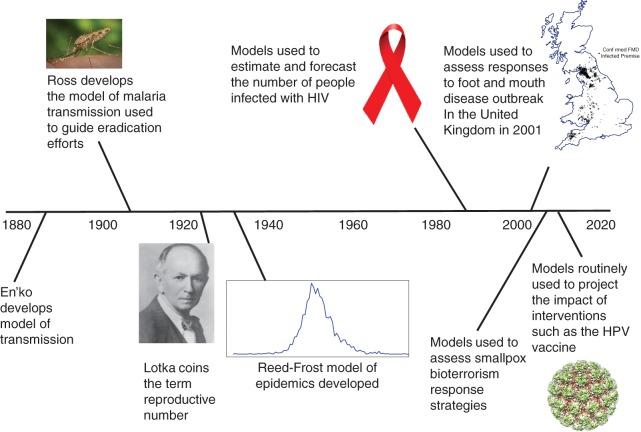
Figure 1.

Milestones in mathematical modeling and modeling to inform public policy, from En'ko's development of a model of transmission (88) to the use of models to predict the impact of interventions. FMD, foot and mouth disease; HIV, human immunodeficiency virus; HPV, human papilloma virus. Anopheles mosquito photo by James Gathany from the Centers for Disease Control and Prevention Public Health Image Library (public domain). Photo of Alfred Lotka courtesy of the Association for Information Science and Technology. HIV awareness ribbon from Wikimedia Commons (public domain). Three-dimensional structure of bovine papillomavirus (BPV) capsid; copyright N. Voss. This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.

However, the dynamics of vaccines in real populations are complex, and mechanistic models have helped us to understand what to expect after changes in vaccination policy. For instance, immediately after the introduction of a vaccine or improvement in vaccination rates, a disease may appear to be eliminated from a population. However, this long honeymoon period may be followed by a large, resurgent, outbreak that bigger than the yearly epidemics seen before the introduction of vaccination (though the cumulative number of cases is still less than what would have been seen without vaccination) (18). These results have helped public health officials to understand that initial apparent vaccine successes may not last, as well as what to expect after introducing a new vaccine. Mechanistic models have also been used to understand the optimal age range for vaccination campaigns (19, 20), how such campaigns should be timed (21), and how best to use vaccines when supplies are limited (20, 22). Models have also been used to design active response strategies for vaccine use, including ring vaccination strategies such as those implemented in the smallpox eradication campaign (23). Models were also used to assess strategies to respond to a bioterrorist release of smallpox in the early part of the 21st century and were influential in setting policy for response (24–27).

One counterintuitive prediction of mechanistic models is that in rare cases, increased population immunity from vaccination can actually increase the incidence of severe disease. The poster child for the phenomenon is congenital rubella syndrome (CRS). For most people, rubella infection causes a relatively minor infection characterized by fever and rash; however, when pregnant women are infected during the first trimester of pregnancy, it cause CRS, which results in severe complications of pregnancy including congenital disorders and death of the fetus (28). Because vaccination increases the average age of infection (by decreasing the hazard of infection), a vaccination program that does not achieve sufficient coverage can increase the number of pregnant women who are infected, thereby increasing incidence of CRS (29). This is not simply a theoretical concept; although there have been no sustained increases in the incidence of CRS (in part due to the public health response), both Costa Rica and Greece experienced transient increases in CRS burden after rubella vaccination (30, 31). In light of the threat of CRS, mechanistic models have played an important role in setting World Health Organization recommendations for the introduction of a rubella vaccine. These recommendations encourage countries to wait to introduce the vaccine until measles vaccination rates (measles and rubella vaccines are usually given together) are high enough to guarantee a reduction in CRS cases and to strongly consider vaccination campaigns in women of childbearing age before the vaccine is introduced (32).

Vaccination is only 1 of a suite of control measures. Another that is of particular importance in the control of macroparasite infections is mass drug administration. A key difference between microparasite and macroparasite dynamics is the huge variation in transmission potential of human hosts, with some individuals experiencing huge pathogen loads that contribute disproportionately to transmission within populations (33). Here, strategies have taken an eye toward reducing overall population burdens of macroparasites, including targeting those with the highest burdens. Theoretical explorations of the impact of heterogeneity in transmissibility have helped inform interventions and aided in the development of theory exploring the impact of heterogeneities in microparasites (34).

SURVEILLANCE

Over the years, mechanistic models have played an important role in the interpretation of surveillance data. In the early days of the human immunodeficiency virus (HIV) epidemic, there was massive uncertainty about how many cases of HIV actually existed because it took years, or even decades, for HIV to progress to acquired immunodeficiency syndrome (AIDS). Ron Brookmeyer (35) used the incubation period distribution of HIV to “back calculate” the number of HIV infections that must have occurred over the previous course of the epidemic and predict the number of future HIV/AIDS cases in those already infected with HIV. He thereby linked an observable quantity (the number of AIDS cases) with an unobservable one (the number of people living with HIV). Longini et al. (36) then fit a more mechanistic model of disease progression to data from HIV-infected individuals in the United States Army, achieving similar results by explicitly representing the biological process. When attempting to estimate global mortality from measles infection, Simons et al. (37) used a state-space model (i.e., a hidden Markov model) which linked an underlying model of measles epidemic dynamics (the process model) with nationally reported measles incidence via an observation model (38). They thereby were able to estimate the extent to which national reports underestimated measles cases by reconciling these reports with what was likely given birth rates and a known epidemic process.

EMERGING PATHOGENS

Planning for so called “black swans,” which are unlikely but catastrophic events, is essential to ensuring security and population health. The prime example of an infectious disease black swan is the 1918 influenza pandemic, which is estimated to have killed 50–100 million people in 2 years (39). Governments and policy makers depend on simulations built on mechanistic models to decide the extent of these threats and what can be done to confront them. For the past decade and a half, there have been ongoing concerns that one of several strains of influenza A that have been known to infect humans from domestic poultry (H5N1, H9N2, etc.), might develop the ability to transmit efficiently in humans and cause a major pandemic. H5N1 strains are seen as particularly concerning because of their high case fatality rate and the substantial increase in the number of human cases (particularly in Southeast Asia) that started in 2003 (40). Independent teams of disease modeling experts developed sophisticated agent-based models of potential emergence events to determine whether effective antiviral agents could be used to contain an emerging influenza at the source (6, 41). These models showed that under reasonable expectations of the transmissibility of an emerging influenza (i.e., R₀ in the 1.5–2.0 range), containment was possible, though perhaps not practical, as it would require the deployment of millions of courses of antiviral medication, very early detection of the disease, and rapid response. In parallel work, groups considered how the impact of a pandemic could be mitigated in the United States if the initial containment attempt was unsuccessful (42–44). The efforts of independent groups showed that something more than social-distancing measures (e.g., school closure, case isolation) would be needed to control a pandemic and that effective antivirals could help. In part on the basis of this work, the United States and other countries decided to stockpile antivirals to combat a future pandemic, a decision that has since been criticized by some (45). However, these criticisms have been focused on concerns about the efficacy of the stockpiled antiviral drugs (46) rather than the results of the modeling work itself.

The question of the probability of H5N1 influenza evolving to become transmissible in humans has itself been the focus of mechanistic modeling (47). After 2 research groups had identified 2 different sets of mutations to the H5N1 virus that would be sufficient to allow airborne transmission in a mammalian host (48, 49), Russell et al. (47) developed a mathematical model of the within host dynamics of influenza evolution. Although the authors were unable to confidently estimate the probability of the emergence of a pandemic H5N1 strain because of uncertainties about the underlying biological processes involved, they were able to identify the biological factors on which this probability would most strongly depend and recommend studies (e.g., deep sequencing of viral samples from H5N1-infected hosts) that might help to develop more precise predictions. There has been considerable debate surrounding the ethics of gain-of-function experiments for H5N1 influenza (50), but if such experiments are to be justified, they must provide us a way to have advanced warning of a coming pandemic, a task that may only be possible through mechanistic models. However, to be successful, these models will require substantial additional theoretical work on how viral evolution interacts with the distribution of immunity in the population.

In the event that an outbreak of an emerging disease does occur, mechanistic models are one of the first tools used to characterize the threat and plan a response. When a pandemic influenza strain emerged in 2009, it was critical to quickly assess whether it had the potential to cause illness with high rates of fatality, like the virus that emerged in the pandemic of 1918, or was a more mild disease, akin to what was seen in the pandemics of 1957 and 1968. Initial assessments relied heavily on dynamic models of a variety of types, including phylogenetic techniques paired with demographic models, models based on the probability of the observed number of introductions of pandemic H1N1 into populations outside of Mexico, analysis of epidemic curves, and the results of detailed investigations of early outbreaks (51, 52). Analyses by a number of groups quickly showed that the emergent pandemic H1N1 virus was behaving very much like already-circulating strains, and although it was still potentially a significant public health threat, it was unlikely to have a qualitatively different impact on mortality or morbidity than circulating influenza strains.

In addition to its role in the response to the 2009 influenza pandemic, mechanistic modeling has played a role in the response to most of the emerging disease threats of this century, from foot and mouth disease in the United Kingdom (53), to severe acute respiratory syndrome coronavirus (54), to Middle East respiratory syndrome coronavirus in Saudi Arabia (55), to Ebola in West Africa (56). The last of these shows both the power of mechanistic approaches and the dangers of its misuse. In the summer and fall of 2014, the number of Ebola cases in West Africa was continuing to grow, and it was unclear how severe the epidemic would eventually become. To address this issue, as well as the threat of spread to other countries, a number of modeling exercises were conducted (e.g., Gomes et al. (57)). Of particular note was a model released by the Centers for Disease Control and Prevention that predicted that, without further intervention, 1.4 million cases of Ebola would occur in Liberia and Sierra Leone by mid-January 2015 (58). This did not come to pass, and although the authors noted that such long-term projections were tenuous, the media and many in the public health community made much of this number. Of course interventions and behavior change did occur, but the authors had also made tenuous assumptions about how the populations of Liberia and Sierra Leone mix together, essentially treating each country as a homogenous entity. In contrast, the World Health Organization Ebola Response Team, who also made projections based on an unconstrained epidemic, declined to forecast further than 2 months into the future (56), and though theirs was a moderate overestimate of total cases, they avoided publishing any panic-inducing overestimations (they projected approximately 20,000 cases by November 2, 2014; approximately 13,000 actually were reported by that point) (59). Forecasting the course of disease spread is difficult to do well, particularly in the context of an active response. It also may be the least of what mechanistic approaches to disease epidemiology have to offer. The aforementioned work, particularly that of the World Health Organization Ebola Response Team, also characterized important aspects of Ebola's natural history and epidemiology, including its basic reproductive number (R₀), the decline in R over the course of the epidemic, the incubation period, and the serial interval, properties of the disease that will be important to understand should it re-emerge.

Mechanistic and mathematical approaches aid not only in the response to particular diseases but also in illuminating basic epidemiologic principles and important parameters that dictate whether a novel (or existing) pathogen can be controlled. In a 2004 paper, Fraser et al. (60) confronted the question of why severe acute respiratory syndrome coronavirus was successfully contained, whereas influenza, HIV, and numerous others were not. They were particularly interested in the effectiveness of the tools available when first confronting a novel pathogen: contact tracing, isolation, and quarantine. They presented evidence that a critical determinant of the controllability of a pathogen is the amount of transmission that occurs before symptom onset, expressed by their parameter θ. Pathogens that had a low proportion of all transmission occurring before symptom onset are easier to control because symptomatic individuals can be targeted with isolation or pharmaceuticals before they transmit to others.

PREDICTION/FORECASTING

Although forecasting is difficult, particularly in the response to an emerging disease threat, it remains a major goal of the disease-modeling community. Because disease reporting is often delayed, forecasting includes not only projections into the future but also “now casting” of incidence based on more readily available information. This has led to a number of approaches in which models have been used to either process a data stream that is a proxy of the data of interest but available more quickly (e.g., Google FluTrends) (61) or in analyses of ongoing outbreaks to assess (with available data) what might be the current situation given the limitations of the observation process and temporal lags in both reporting and outcomes being generated (e.g., calculating case fatality rates for the severe acute respiratory syndrome coronavirus and Middle East respiratory syndrome coronavirus outbreaks when many patients had yet to resolve) (55, 62).

At a larger time horizon, several efforts have attempted to forecast the impact of interventions on future incidence. One of the most successful was a project that forecasted the impact of respiratory syncytial virus immunization campaigns on the temporal pattern of incidence in the United States. Using mechanistic transmission models, Pitzer et al. (63, 64) made detailed predictions of the impact of vaccination on the multiannual dynamics of rotavirus, as well as the impact of the vaccine on genotype circulation. These forecasts of broad qualitative impacts of interventions are critical tests of models. Detailed prospective predictions of changes that will occur with changes in health policy, which are then validated, will provide the best evidence of the utility of mechanistic models in the future.

STUDY DESIGN AND INTERPRETATION

Dependent happenings is the term coined by Ronald Ross (10) to capture the fact that for infectious diseases, an individual's risk of infection depends on the disease status of those around them (65). This presents challenges for trial design and the interpretation of observational studies. Cluster randomization and adjustment for intra-class correlation can be used to account for this effect in some cases (66), but mechanistic models are often useful in trial design or in interpretation of results when cluster randomization is imperfect or impossible. Under these conditions, simulations studies have been used to help in study design settings, including vaccine studies (67, 68) and combination approaches to HIV prevention (69).

Mechanistic models have been particularly revealing for studies of vaccine effectiveness. For example, a naïve approach would be to consider that all vaccines acted in the same way, providing complete protection for some fraction of the population. However, in reality vaccines may be leaky and provide protection only in some dimensions (65). Vaccines may prevent infection all together (e.g., the measles vaccine) (70), offer protection against pathogenic disease but still allow individuals to become infected and transmit the disease (e.g., acellular pertussis vaccines (71)), or only prevent onward transmission of the disease (e.g., transmission-blocking vaccines for malaria (72)). In order to anticipate and assess the impact of vaccines once scaled up to widespread use, the specific actions of the vaccine in reducing infection, onward transmission, and disease must be disentangled. These specific mechanisms will contribute differently to the direct, indirect, and total effects of a vaccine. These effects are increasingly targets of inference during trials (73), and developments in infectious disease theory have driven development of both inference tools and study design to measure specific impacts (65).

SETTING PUBLIC HEALTH POLICY

In emerging outbreaks, simulation models have often been used as the framework to quickly quantitatively compare policy alternatives. The application of these models has yielded results ranging from broad information about the feasibility and potential impact of interventions to detailed recommendations about targeting of interventions. In the foot and mouth disease outbreak of 2001, models were used to determine optimal culling strategies that specified operational details of those strategies, including the timing and spatial extent of culling.

Even outside of public health crises, infectious disease models play an important role in setting public health policy. Cost-effectiveness analyses are often built on mechanistic models of disease spread (74, 75). Models can help investigators choose between different intervention strategies, determine the potential of specific interventions, and compare investments across pathogens. Infectious disease models play a critical role in incorporating indirect effects that can vary substantially across alternative programs. The design of immunization campaigns against human papillomavirus has to weigh the direct effects protecting women from human papillomavirus infection, as well as indirect protection resulting from immunization of both women and men. The tradeoffs of alternative programs in protecting individuals at risk of the most severe outcomes and those at little risk have been best evaluated in transmission models (64).

Increasingly important is the marrying of mechanistic disease models with operations research by explicitly modeling the logistical constraints on public health intervention. This approach can be key when preparing for outbreaks or bioterrorism, as speed of deployment, hospital capacity, and other logistical factors can severely impact the efficiency of disease containment and its subsequent spread (25, 76). Likewise, a logistical analysis can assess the feasibility of novel disease-control strategies, showing whether they are practical as well as efficacious; for instance, an analysis of the feasibility and potential effectiveness of passive immunotherapy in Hong Kong showed that this intervention could play an important role in controlling a mildly severe pandemic (77).

NEW OPPORTUNITIES AND THE FUTURE

As the price of computation drops and we enter the era of “big data,” the role of mechanistic models will only increase. A powerful new synergy is the combination of mechanistic models of disease spread with phylogenetic techniques outlining the evolutionary relationship between infecting pathogens. Genetic sequence data present samples of pathogens taken from a large population of pathogens both within a host and among all hosts. Understanding the impact of different selective pressures on pathogens is inherently a task of population genetics. Models of the population dynamics of pathogens have been incorporated into models in order to explain the phylogenetic structure of pathogens. Sequence data have been used to infer basic reproductive numbers of pathogens (51, 78), harkening back to Lotka's first use of the term to describe replication of organisms. In future work, we expect to see more direct integration of models with data at both population scales, as has been the tradition, and within host scales. Traversing these scales will be a key challenge to the field.

Targeted funding and the relatively new paradigm (at least for epidemiology) of sanctioning competitions to identify the best methods of disease forecasting continue to in invigorate the field. In the United States, the Models of Infectious Disease Agent Study and the recently completed Research and Policy for Infectious Disease Dynamics program have led to well over 1,000 publications and continue to invigorate research and training in the field (79, 80). Similar initiatives in the United Kingdom and other parts of Europe, such as that from the Medical Research Council's Centre for Outbreak Analysis and Modelling, have also been successful (81). Competitions such as the National Oceanic and Atmospheric Administration's Dengue Forecasting Project (82), the Defense Advanced Research Projects Agency Forecasting Chikungunya Challenge (83), and the US Center for Disease Control and Prevention's Predict the Influenza Season Challenge (84) require researchers to assess and compare the performances of their models and stand by their predictions in the face of actual events. Such initiative should serve to greatly improve the quality and number of models of infectious diseases, but this will only translate into improved public health if it is paired with greater engagement with policy and practice.

In limited space, it is impossible to cover every important contribution that mechanistic models have made over the past century, and there is much important work that we have not covered. These contributions range from work showing the potential impact of test-and-treat strategies in HIV control (85), to analyses of how to best use a limited supply of cholera vaccines to control disease (22, 86), to fundamental work on the link between demographic characteristics and disease incidence (87). These omissions should not be seen as a reflection of the quality of the work, but rather merely as the result of our need to select only a few of many good options.

The use of mechanistic models in infectious disease epidemiology has shifted over the course of 100 years. The arc of their use spans beginnings as 1 of a group of statistical and mathematical tools used by epidemiologists to understand a multitude of phenomena, to use and development by an increasingly specialized group of researchers over the course of the 20th century, to more general use by a broader group of researchers. This arc still bends. At their core, these methods provide frameworks of analysis that can be treated in the same way as other statistical tools of analysis. Refinement of methods has led to a theoretical base and application toolkit that allows nonspecialists to analyze and understand infectious disease dynamics with mechanistic models. This broader ecosystem of modelers, which includes methods-focused researchers and public health practitioners, has led to encouraging progress in tying models increasingly to data and to the most salient infectious disease problems facing global health.