An Approach for Reducing the Error Rate in Automated Lung Segmentation

Abstract

Robust lung segmentation is challenging, especially when tens of thousands of lung CT scans need to be processed, as required by large multi-center studies. The goal of this work was to develop and assess a method for the fusion of segmentation results from two different methods to generate lung segmentations that have a lower failure rate than individual input segmentations. As basis for the fusion approach, lung segmentations generated with a region growing and model-based approach were utilized. The fusion result was generated by comparing input segmentations and selectively combining them using a trained classification system. The method was evaluated on a diverse set of 204 CT scans of normal and diseased lungs. The fusion approach resulted in a Dice coefficient of 0.9855 ± 0.0106 and showed a statistically significant improvement compared to both input segmentation methods. In addition, the failure rate at different segmentation accuracy levels was assessed. For example, when requiring that lung segmentations must have a Dice coefficient of better than 0.97, the fusion approach had a failure rate of 6.13%. In contrast, the failure rate for region growing and model-based methods was 18.14% and 15.69%, respectively. Therefore, the proposed method improves the quality of the lung segmentations, which is important for subsequent quantitative analysis of lungs. Also, to enable a comparison with other methods, results on the LOLA11 challenge test set are reported.

1. Introduction

Lung segmentation is one of the first processing steps in computer-aided quantitative lung image analysis. For high throughput applications with tens of thousands of data sets to be analyzed—as required by large multi-center trials—fully automated lung segmentation approaches with high robustness and low error rate are imperative to minimize the need for human intervention (i.e., manual correction). This is especially important when segmenting lungs with lung disease.

A number of papers describing lung segmentation algorithms have been published, and a comprehensive review can be found in [1]. Basically, methods developed can be grouped into three categories given below.

1. Simple, low complexity methods like region growing [2, 3], which are based on simple assumptions (e.g., density range of lung tissue). These methods typically work well for normal lungs, but may fail in the case of diseased lungs or imaging artefacts. An advantage of such methods is the low computational complexity.

2. Advanced, more robust algorithms that try to overcome the problems of category a) and typically show higher computational complexity. Examples in this category include approaches based on registration [4], lung shape models [5, 6] and advanced threshold-based segmentations utilizing adaptive border matching [7] or texture features [8].

3. Hybrid approaches that try to use a method in category b) only if a result produced with method in category a) is classified as failed based on some heuristics (e.g., assumptions about lung volume). Representatives in this category are the work of Rikxoort et al. [9] and Mansoor et al. [10]. The main motivation behind such approaches is to take advantage of the low computational complexity of methods in category a), but with the optional performance of more advanced methods in category b). The behavior of methods in group c) depends on whether the heuristics for switching to a method in category b) work or not. Furthermore, with increasing computing power combined with lower hardware costs, hybrid methods may become less attractive, because as computational costs become less important, more advanced methods can be utilized routinely.

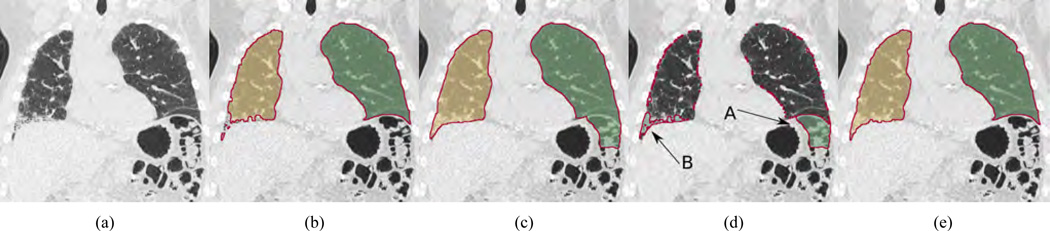
All methods in these categories have different pros and cons and are based on different design assumptions that might or might not hold. In the case of pathological lungs, it is expected that the likelihood of failure of methods in category b) is lower than for the ones in a), but despite all the efforts, they can (locally) fail too. For example, Fig. 1(a) depicts a coronal CT cross-section of a lung with idiopathic pulmonary fibrosis (IPF). Corresponding segmentations of a region growing and model-based [6] method are shown in Figs. 1(b) and 1(c), respectively. As can be seen in the difference image of both segmentations (Fig. 1(d)), both methods show local segmentation errors due to different reasons like a violation of the assumption of a specific lung density range (Fig. 1(b)) or problems with model initialization (Fig. 1(c)).

Figure 1.

Comparison of lung segmentation methods applied to a CT scan of a lung with IPF. (a) Coronal slice of the CT scan. (b) Region growing segmentation result. (c) Model-based segmentation result. (d) Difference volume between the segmentations in (b) and (c); arrows indicate components corresponding to (A) leak into colon and (B) lung tissue affected by IPF. (e) Result of the fusion approach in which component (A) is rejected and component (B) is accepted.

In this paper, we propose a segmentation fusion approach based on a classification framework, which selectively combines (components of) two independently generated lung segmentations to form a new segmentation result with no or reduced errors. The idea behind this approach is to take advantage of the strength of both methods, but without including their errors. In our case, the two segmentations are generated by a region growing and robust active shape model (RASM) based method [6] (Section 2). Compared to other lung segmentation approaches, it does not rely on a fallback method [9, 10] where a more complex segmentation approach is chosen if the output of a simple region growing method is classified as being incorrect, nor does it simply combine segmentation results with a logic OR operation [8, 10]. Instead, our approach follows a more flexible approach that can selectively combine components of both lung segmentation results, as demonstrated in Fig 1(e). We assess fusion performance on a diverse set of 204 lung CT scans and provide a comparison to the performance of both input lung segmentations. Also, the fusion method can be easily adapted to different input segmentation methods by retraining of the classification system.

2. Selecting Suitable Input Segmentation Methods and Prior Work

In this section, we discuss the general requirements for selecting suitable input methods for our segmentation fusion approach and introduce the two segmentation approaches utilized in this paper.

2.1. Considerations and requirements

The overarching assumption of deploying a fusion approach is that existing lung segmentation methods are–to a certain degree–imperfect. Thus, algorithms can and will fail, especially when applied to a large number of medical data sets, as is the case in large multi-site studies (e.g., COPDGene¹). The aim of the presented framework is to improve segmentation accuracy and reduce the failure rate by utilizing a segmentation fusion approach on two base segmentations. We assume that the base algorithms A and B are suited for lung segmentation and show already good performance, but will still fail in a number of cases. We note that such segmentation methods rarely produce complete failures (e.g., segmenting the air surrounding the patient instead of the lung). Typically, failures occur locally and are limited (e.g, leakage into colon, including the trachea, excluding a tumor, etc.). Instead of selecting method A or B, and having to deal with frequent occurring errors by time-consuming manual editing, the idea is to use both segmentation results selectively to produce a new segmentation C with no or reduced errors (i.e., lower error rate at a required accuracy level).

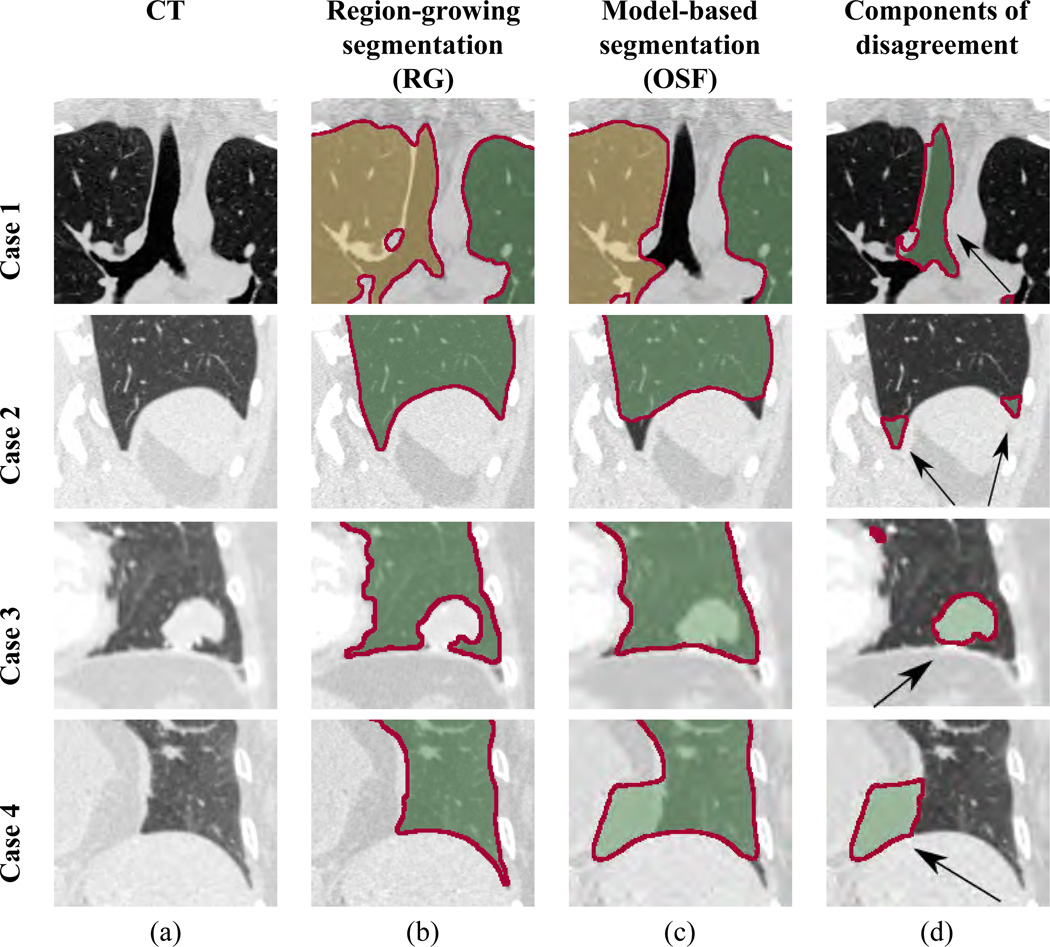
The ideal set of candidates for producing input segmentations A and B have non-overlapping weaknesses and strengths, resulting in (local) disagreement between methods. Fig. 2 provides several examples for a region growing and model-based lung segmentation approach that will be utilized in this paper. Differences in generated lung masks result in local volume components of disagreement (Fig. 2d), which can have many causes. Typically, they are caused by assumptions that methods make. As can be seen in Fig. 2, both input segmentation methods show non-overlapping weaknesses, and thus, are suited for a fusion approach.

Figure 2.

Example of the weaknesses and strengths of two different segmentation methods, leading to (local) volume components of disagreement. (a) Coronal CT slices of the lung. (b) Region growing based segmentation results. (c) Model-based segmentation results. (d) Volume components resulting from set-theoretic differences between both segmentation results. For cases 1 and 2, region-growing results without model-based results (RG \ OS F) are shown. The components of disagreement mainly represent trachea/airways and the region of the costophrenic angle, respectively. For cases 3 and 4, model-based results without region-growing results (OS F \ RG) are shown. The components of disagreement mainly represent tumor and fat tissue, respectively. Note that, while some of these components belong to the lung, others do not.

Given the results of two lung segmentation algorithms A and B, we assume that if both methods label a voxel as lung tissue, then the likelihood of the voxel representing lung is high. Therefore, it will be labeled as lung by our fusion method. For components of disagreement, a trained classifier is utilized to individually decide which components should be added to the volume of mutual agreement between both methods, resulting in the final output segmentation of the algorithm. Note that classification is performed on components of disagreement (i.e., volume chunk). Therefore, all voxels of the volume chunk will receive the same label by the classifier.

2.2. Method A - region growing based segmentation

The region growing segmentation 𝒱_RG is obtained using a threshold of −500 HU. The seeds for region growing are identified automatically as follows. Let s_x, s_y, and s_z denote the size of a CT data set in x-, y-, and z-direction, respectively. First, initial seeds are placed. For the left lung, two initial seeds are generated at $(\frac{1}{3}{S}_x,\frac{1}{2}{S}_y,\frac{2}{3}{S}_z)$ and $(\frac{1}{3}{S}_x,\frac{2}{3}{S}_y,\frac{1}{2}{S}_z)$. For the right lung, two initial seeds are placedat $(\frac{2}{3}{S}_x,\frac{1}{2}{S}_y,\frac{2}{3}{S}_z)$ and $(\frac{2}{3}{S}_x,\frac{2}{3}{S}_y,\frac{1}{2}{S}_z)$. Second, near each initial seed, the voxel with the lowest density on a 70 voxel long search line along the x-direction is identified. The search lines start at each seed location and go in distal direction. Also, to avoid leakage into airways, a pre-processing step is performed to exclude major airways from being added to the lung mask. For this purpose, the trachea and main bronchi are first found by utilizing a modified version of an airway tree segmentation method described by Bauer et al. [11]. The identified airways are dilated using a spherical form element with a radius of 2 voxels and the resulting mask is used to assign a value of 50 HU to corresponding voxels in the CT data set. To close gaps due to vessels and airways in the thresholding result, a morphological closing operation is applied. Subsequently, a marker-based watershed algorithm [3] is used to separate the result into left and right lungs.

2.3. Method B - model-based segmentation (RASM)

To generate the model-based segmentation, a point distribution model (PDM) is generated as described by Gill et al. [12], which captures the variation of lung shapes. The PDM is built separately for left and right lungs, and the following segmentation steps are done separately as well. The segmentation procedure begins with initializing the PDM by utilizing a feature-based alignment system [13]. This is followed by a robust active shape model (RASM) matching step [6] to align the PDM with the CT volume, resulting in the segmentation 𝒱_RASM. Subsequently, this segmentation is further refined using a graph-based optimal surface finding (OSF) approach [6], which allows finding a surface related to the shape prior, resulting in the final segmentation 𝒱_OSF. Note that large airways were identified as outlined in Section 2.2 to make them unattractive for 𝒱_RASM and 𝒱_OSF segmentations. In addition, instead of using original CT volume to compute RASM and OSF segmentations, we modify the CT volume using a Total Variation L¹ based texture analysis approach [14]. The modification improves the segmentation performance for lungs with interstitial lung disease (ILD), but does not affect the segmentation of normal lungs [14].

3. Methods

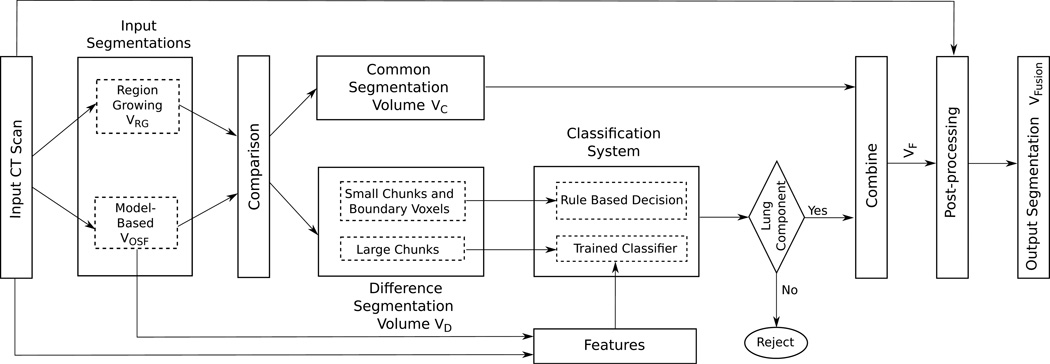
An overview of our method is given in Fig. 3. It is based on fusion of region-growing and model-based segmentation results. The segmentations are divided into two volumes: the common segmentation volume 𝒱_C = 𝒱_RG ∩ 𝒱_OSF (all voxels that belong to both segmentation volumes) and the difference segmentation volume 𝒱_D (all voxels that are in one of the segmentations but not in the other). Our fusion approach identifies components of the difference segmentation volume 𝒱_D (Section 3.1), employs a classification system (Section 3.2) to determine which components belong to lung volume, and combines them with the common segmentation volume (Section 3.3) to form a segmentation mask 𝒱_F. The resulting volume is post-processed to yield the final segmentation 𝒱_Fusion (Section 3.4).

Figure 3.

Flowchart showing the different components of our fusion system. The components of the difference segmentation volume and classification system are shown in detail.

3.1. Components of the difference segmentation volume

The volume 𝒱_D is divided into three sets of spatially distinct volume components: boundary bias region volumes, large chunks, and small chunks. The rationale behind this approach is as follows. First, consider the segmentations depicted in Figs. 4(a) and 4(b), respectively. Due to bias in boundary delineation between segmentations, the difference volume 𝒱_D may include a thin layer of voxels along the lung boundary, as shown in Fig. 4(c). The boundary voxels in volume 𝒱_B are induced by a bias of the utilized segmentation methods. With bias we refer to the preference of an algorithm where it places the lung boundary. Since this is a systematic error, this can be addressed by adjusting the base segmentation algorithm (e.g., change threshold for region growing). Therefore, voxels in 𝒱_B are not considered as a major segmentation error and are processed separately by the classification system. Second, calculating complex features for small chunks below a certain size ρ voxels will result in noisy, unpredictive features due to the low voxel count.

Figure 4.

Example of a boundary bias region. (a) Region growing segmentation result. (b) OSF segmentation result. (c) Difference volume showing the segmentation bias in the boundary region.

The following procedure is used to divide the difference volume 𝒱_D into the three subsets. First, a morphological opening operation is performed using a spherical form element with a radius of 1 mm to differentiate between chunks and boundary bias differences. Second, a connected component analysis is applied, resulting in a set of chunks Ω_C and a set of surface bias volumes Ω_B. Third, chunks in Ω_C that are smaller thanρ voxels are put into Ω_Csmall and the rest into Ω_Clarge so that classification system can process them separately. Note that in the above outlined procedure, the source (i.e., 𝒱_RG or 𝒱_OSF) of difference voxels in volume 𝒱_D is taken into account. Consequently, adjacent difference volume components that were caused by region growing and model-based segmentation will not be merged, and thus, result in separate elements in above defined sets.

The selection of ρ was performed empirically by utilizing the training data set S_train (Section 4.1), which was split into two sets S_trainA and S_trainB by means of random sampling. For ρ ∈ {100,200,300,400,500} voxels, the following procedure was performed. First, the fusion system was trained on S_trainA. Second, the classification performance of the fusion system was evaluated on S_trainB. Third, the value for ρ with the best performance was selected, yielding ρ = 200 voxels. This value was subsequently utilized in all experiments.

3.2. Classification system

The classification system (Fig. 3) comprises of two classifiers, one for classifying large chunks in set Ω_Clarge (Section 3.2.1) and one for classifying small chunks in set Ω_Csmall as well as boundary bias regions in set Ω_B (Section 3.2.3). Details are given below.

3.2.1. Classifying large chunks

A classifier is learned from a set of training CT volumes and corresponding reference lung segmentations in S_train (Section 4.1) to distinguish between chunks belonging to the lung and those not belonging to the lung. The chunks Ω_Clarge are generated by first producing region growing and model-based segmentations on the training data, followed by the processing steps given in Section 3.1. Then, a feature descriptor f_ω is computed for each chunk ω ∈ Ω_Clarge . The descriptor considers different properties that are captured by calculating the following feature volumes on the input CT scan.

1. Density: This feature volume is used to distinguish between chunks belonging to different structures in a CT volume such as air, lung tissue, fat, bones, etc. based on their Hounsfield units (HU). Density is measured after removing noise from the CT scan using a TV-L¹ filter based on the implementation proposed by Pock et al. [15] with λ=1.5.

2. Gradient magnitude: This feature volume aims to distinguish between homogeneous and non-homogeneous chunks based on density. The gradient is computed on the filtered CT volume described in i) by using a symmetric first-order derivative operator.

3. Curvature: To characterize the local shape of low density structures (e.g., lung tissue), a curvature volume, which represents the curvature in a neighborhood around each voxel, is generated. First, a threshold of −300 HU is applied to the CT volume to identify target structures. Second, the trace of the Hessian matrix is computed on this binary volume, resulting in the curvature volume. The Hessian is calculated at scale of 2 mm to produce high responses near the costophrenic angle.

4. Distance from lung boundary: This feature volume is computed to estimate how close the chunk is to the lung boundary. Also, it is used for distinguishing chunks inside the lung, such as tumors, from chunks outside the lung, such as a leak into colon. Since the model segmentation 𝒱_RASM has shown to be successful in including lung tumors [6], it is utilized to compute a signed distance transform. To compare distances across CT volumes, they are normalized by the maximum boundary distance found inside the lung.

5. Texture: This feature volume indicates which chunks are affected by ILD. It is constructed using the TV-L¹ based texture processing [14], which responds to texture patterns caused by ILD.

6. Location: To capture the relative location of chunks, two feature volumes are used to store the location of each voxel in y- (anterior-posterior axis) and z-direction (superior-inferior axis). Since the image dimensions are different across CT volumes, the location needs to be normalized so that it can be correctly compared across CT volumes. The bounding box around the model-based segmentation 𝒱_RASM is used for this purpose. The location is normalized such that it varies from 0 to 1 within the bounding box.

Histograms are computed for all chunks and all of the above described feature volumes. The number of bins for each feature histogram is determined automatically by an algorithm described in Section 3.2.2, which is applied to the the training set S_train (Section 4.1). Table 1 summarizes the number of resulting bins per feature type. All the bins of a histogram form the components of the corresponding feature vector. The resulting seven vectors are concatenated to a single feature vector per chunk. In addition, the mean and standard deviation of the density and gradient magnitude are computed for voxels inside each chunk and appended, resulting in a 37-dimensional feature descriptor f_ω for each chunk ω.

Table 1.

Histogram bins used for computing feature components (see Section 3.2.2 for details). The symbols -∞ and ∞ are used to denote the lower and upper bounds of a particular feature, respectively.

Feature type	Boundaries of histogram bins	Number of resulting feature components (bins)
Density	[−∞, −916, −496, −157, −45, 1, 40, ∞]	7
Gradient Magnitude	[0, 29, 110, 162, 542, ∞]	5
Curvature	[0, 0.18, 1]	2
Boundary Distance	[−1.0, −0.04, 0.03, 0.27, ∞]	4
Texture	[0, 0.70, 0.94, 1, ∞]	4
Y-Location	[−∞, 0.25, 0.43, 0.59, 0.79, 0.84, ∞]	6
Z-Location	[−∞, −0.03, 0.07, 0.33, 0.74, ∞]	5

For each chunk ω ∈ Ω_Clarge generated on the training data set S_train, a class label Y_ω is required to train the classification algorithm. We derive Y_ω from the corresponding reference segmentation. Because a chunk can consist of a number of voxels with different lung labels, Y_ω is computed by taking the majority class label of the chunk. We use Y_ω = 1 to indicate that the chunk belongs to the lung and Y_ω = 0 if the chunk does not. In addition, out of the pool of all chunks available for training, only the ones with 90% voxel label purity are utilized for training the classifier. While this reduces the number of utilized training examples, it also increases the quality of the trained classifier, because it can better learn the characteristics of lung and background regions.

For classification, a k-nearest neighbor (kNN) approach 𝒯 with k = 3 is utilized. The value of k=3 was determined by means of a ten-fold cross validation experiment on the training set S_train. Once trained, the following steps are performed for classifying a previously unseen large chunk. First, its feature descriptor is calculated. Second, the classifier 𝒯 is applied, resulting in a single class label for the chunk, which is assigned to all its voxels.

3.2.2. Determining histogram bins

The number of bins of the histogram determine the dimensionality of the feature descriptor. If the bins are too coarsely spaced, a potential loss of discrimination between lung and background can result. On the other hand, if the bins are finely spaced, the length of the feature descriptor increases, which can adversely impact classification performance due to the curse of dimensionality. Thus, to define the bins, we utilize the output of a decision tree classifier [16] that was trained to separate chunks in the training data according to their class labels. The rationale behind this approach is as follows. In the training phase of a decision tree classifier, a tree structure is build. In the tree, branch nodes represent simple queries regarding the value of a single feature. Each branch node has two child nodes, one for true and one for false queries, which lead to a new branch node or a leave node with an associated class label. The goal of classifier training is to build a decision tree structure such that the labels of training samples at leaves are as homogeneous as possible. Therefore, assigning the majority class label to a leave node will minimize the classification error on the training set. For our application, this means that the rules at nodes represent discriminative feature bin boundaries for use in conjunction with the kNN classifier (Section 3.2.1).

The above outlined approach was performed for each of the features separately. In addition, to better capture the preference/properties of segmentation methods that cause chunks, a more fine grain class label is used instead of the one described in Section 3.2.1. This is accomplished by also encoding the source of a chunk in addition to information whether a chunk belongs to the lung or not, resulting in four potential class labels: Ỹ_ω ∈ {0_RG, 0_OSF, 1_RG, 1_OSF}. The depth of the decision tree is limited to 5 levels to restrict the maximum number of bins. The decision rules (branches) of the decision tree directly provide the boundaries of the bins. Table 1 summarizes the resulting histogram bins and corresponding number of feature descriptor components for each of the features.

3.2.3. Classifying small chunks and boundary bias regions

As mentioned in Section 3.1, calculating complex features for small or thin chunks will result in noisy, unpredictive features due to the low voxel count. Consequently, a different classification approach is needed. Radiologists frequently use information about tissue density acquired with CT for decision making. For example, it is well established that normal lung tissue has a density range between −500 and −900 HU. We utilize this knowledge in form of a simple classification rule. However, because lung diseases (e.g., interstitial lung disease) can increase lung tissue density, we use a more relaxed threshold of −300 HU. Thus, to classify a chunk ω in Ω_B or Ω_Csmall, the average density µ_ω of chunk ω is computed, and the following rule-based classifier is utilized to determine the class label Y, indicating whether the component belongs to the lung or not:

$$ℛ({\mu }_{\omega })=\{\begin{array}{cc}1,\hfill & \text{if }{\mu }_{\omega }\le -300\text{ HU}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}.$$ (1)

3.3. Selectively combining segmentations

Given a new CT volume, the region growing based segmentation result 𝒱_RG and model-based segmentation segmentation 𝒱_OSF are computed, and the component sets Ω_Clarge, Ω_Csmall, and Ω_B are derived as described in Section 3.1. Based on the output of the classifiers 𝒯 (Section 3.2.1) and ℛ (Section 3.2.3), several sub-masks are generated with 𝒱_ω1 = {ω ∈ Ω_Clarge | 𝒯(f_ω) = 1}, 𝒱_ω2 = {ω ∈ Ω_Csmall | ℛ(μ_ω) = 1}, and 𝒱_ω3 = {ω ∈ Ω_B | ℛ(μ_ω) = 1}. The 3D fusion segmentation mask 𝒱_F is then given by

$${𝒱}_F={𝒱}_C\cup {𝒱}_{\omega 1}\cup {𝒱}_{\omega 2}\cup {𝒱}_{\omega 3}.$$ (2)

3.4. Postprocessing

The classification process may lead to small holes in the segmentation mask 𝒱_F or boundary voxels may get disconnected if adjacent chunks are classified as not belonging to the lung. Holes are filled using a morphological closing operation with a spherical element of radius 1 mm. To separate potentially connected left and right lungs, a marker based watershed approach[3] is employed, and subsequently a connected component analysis is performed to ensure a maximum of two components, resulting in lung masks for left and right lungs in the final fusion output 𝒱_Fusion.

4. Image data and independent reference standard

For training and evaluation of our segmentation fusion approach, 344 multidetector computed tomography (MDCT) thorax scans of lungs were available that consisted of five cohorts, including 65 scans with no significant abnormalities (normals), 61 scans of asthma (both severe and non-severe) patients, 61 scans of lungs with chronic obstructive pulmonary disease (COPD, GOLD1 to GOLD4), 95 scans with different lung diseases, and 62 scans with idiopathic pulmonary fibro-sis (IPF). All CT images had a matrix size of 512 × 512 elements. The number of slices varied from 205 to 781 (mean: 555.9). The in-plane resolution ranged from 0.4883 × 0.4883 to 0.9082 × 0.9082 mm (mean: 0.6508 × 0.6508 mm). The slice thickness of images ranged from 0.500 to 1.250 mm (mean: 0.5563 mm). Specifically, the unique values for slice thickness were 0.500, 0.600, 0.625, 0.630, 0.700, 1.000, and 1.250 mm, and the corresponding number of scans with these values was 234, 8, 67, 3, 24, 4, and 4, respectively.

The data was split into two disjoint sets; one for classifier training (S_train) and one for evaluation (S_test). Table 2 shows the composition of sets with respect to cohorts, and further details are given in Sections 4.1 and 4.2.

Table 2.

Number of images for each cohort per image set. See Section4 for details.

Set	Normals	Asthma	COPD	Mix	IPF	Total Number Of Scans
Strain	25	25	25	40	25	140
Stest	40	36	36	55	37	204
ALL	65	61	61	95	62	344

4.1. Training data

The utilized training data set S_train consists of the 140 CT scans (Table 2) with corresponding volumetric (3D) lung masks.

4.2. Test data

An independence reference standard was generated by an expert for all the test CT images in set S_test. First, an initial 3D segmentation was generated by using a commercial lung image analysis software package Apollo (VIDA Diagnostics Inc., Coralville, IA). Second, all segmentations were inspected and segmentation errors were manually corrected. Due to the large number of 204 test CT scans, we utilize a sampling approach to reduce the effort required for generating the reference segmentation. Thus, for every tenth axial slice, a reference segmentation was generated, resulting in a dense sampling of lung volumes. In the following sections, the different cohorts of test set S_test will be denoted by S_normal, S_asthma, S_COPD, S_mix, and S_IPF, respectively.

5. Evaluation

All reported validation experiments are performed on the complete test set S_test with 204 CT scans (Table 2), unless otherwise noted. To assess overall segmentation accuracy, the dice coefficient D [17] was utilized. Because a reference was available for every tenth axial CT slice (Section 4.2), the same sampling approach was applied to the segmentation result to be evaluated. Based on the sampled volumes, the Dice coefficient was calculated. Similarly, to enable comparison with other methods (Section 7.2), we also calculated segmentation overlap scores O (Jaccard index) [18]. For comparison, we also provide an assessment of the input segmentations generated with methods RG and OSF. All measurements are reported in mean + standard deviation format. To assess statistical significance, a paired permutation test [19] was performed.

The proposed method was designed to avoid or reduce failures. To adequately assess this ability, the failure rate F(γ) is calculated. F indicates the percentage of cases in S_test that do not meet a given quality criteria (γ) and need manual postprocessing to correct errors. For this purpose, a case is counted as a failure if its Dice coefficient is at or below the limit γ. Because selecting a suitable γ is highly application dependent, we investigated practically relevant γ values in a range from 0.92 to 0.99.

6. Results

6.1. Segmentation performance

Table 3 summarizes the Dice coefficient achieved with our fusion approach as well as region-growing and model-based input methods. On all test sets, the fusion approach delivered statistically significant improvements when compared to region-growing and model-based segmentations with p-values much smaller than 1e-03. Table 4 summarizes the failure rate F( γ) for OSF, RG, and Fusion segmentation approaches. In addition, it also provides the change in failure rate ΔF of the proposed fusion approach compared to OSF and RG, respectively. Note that an ideal method would produce a failure rate of 0%. Also, as γ approaches one, the failure rate converges to 100%, because none of the three segmentation methods produces results that are exactly the same as the reference standard.

Table 3.

Dice coefficient D for input segmentations and fusion segmentation.

Set	OSF	RG	Fusion
Snormal	0.9861 ± 0.0049	0.9882 ± 0.0052	0.9904 ± 0.0037
	p≪1e-03*	p≪1e-03*	-
Sasthma	0.9815 ± 0.0083	0.9793 ± 0.0228	0.9865 ± 0.0069
	p≪1e-03*	p≪1e-03*	-
SCOPD	0.9845 ± 0.0116	0.9890 ± 0.0048	0.9910 ± 0.0032
	p≪1e-03*	p≪1e-03*	-
Smix	0.9724 ± 0.0215	0.9662 ± 0.0588	0.9809 ± 0.0153
	p≪1e-03*	p≪1e-03*	-
SIPF	0.9744 ± 0.0106	0.9703 ± 0.0205	0.9805 ± 0.0098
	p≪1e-03*	p≪1e-03*	-
Stest (ALL)	0.9792 ± 0.0147	0.9776 ± 0.0345	0.9855 ± 0.0106
	p≪1e-03*	p≪1e-03*	-

The p-values of a paired permutation test between input segmentations and fusion segmentation is also provided. Statistically significant results are denoted by*.

Table 4.

Failure rate in dependence of segmentation accuracy (Dice coefficient) on S_test.

	Failure rate F			Change in failure rate ΔF		Change in failure rate ΔF
Dice coefficient (−)				Fusion vs. OSF		Fusion vs. RG
	OSF (%)	RG (%)	Fusion (%)	absolute (%)	relative (%)	absolute (%)	relative (%)
0.92	1.72	3.19	0.74	−0.98	−57.14	−2.45	−76.92
0.93	1.72	3.68	0.74	−0.98	−57.14	−2.94	−80.00
0.94	2.70	4.66	1.23	−1.47	−54.55	−3.43	−73.68
0.95	4.17	7.60	1.47	−2.70	−64.71	−6.13	−80.64
0.96	5.88	11.03	2.45	−3.43	−58.33	−8.58	−77.78
0.97	15.69	18.14	6.13	−9.56	−60.94	−12.01	−66.22
0.98	37.25	31.37	18.87	−18.38	−49.34	−12.50	−39.84
0.99	93.38	71.57	64.22	−29.17	−31.23	−7.35	−10.27

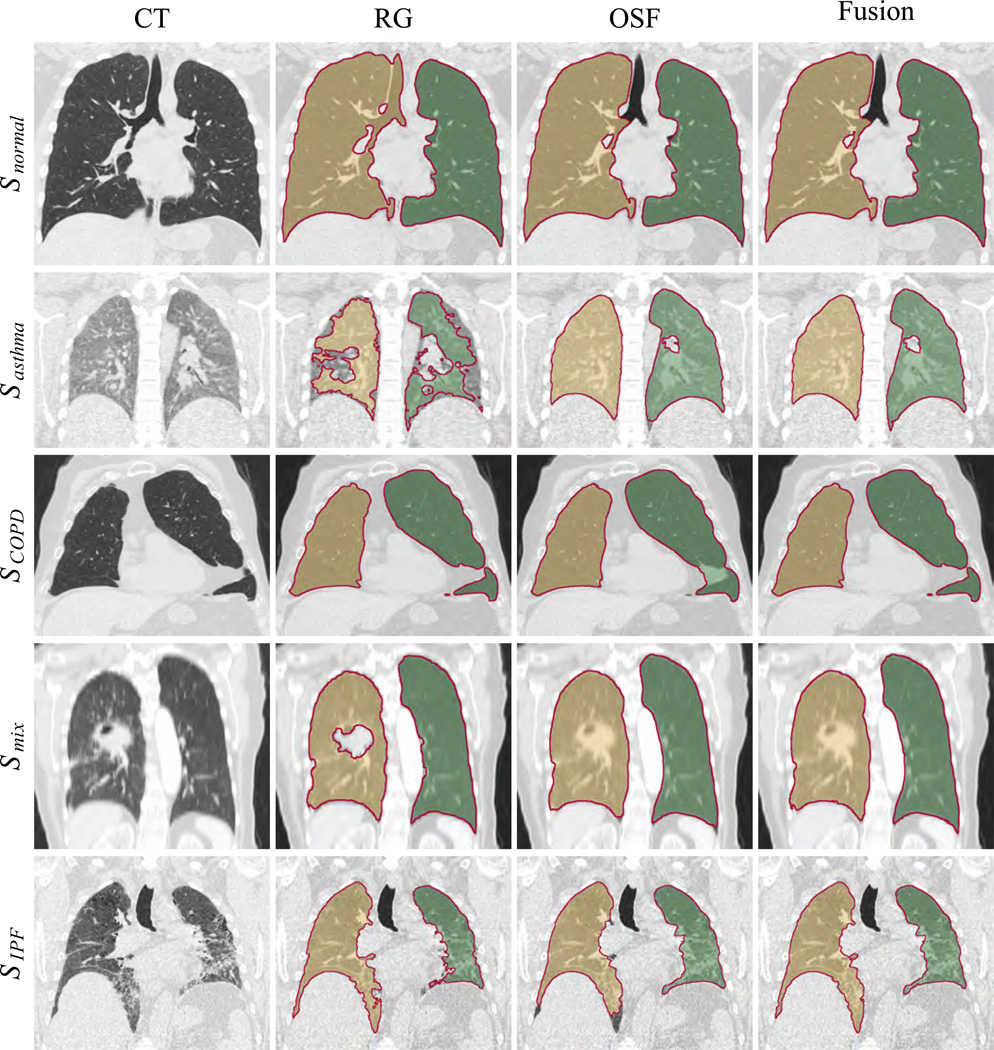
Examples of segmentation results for OSF, RG, and Fusion are given in Fig. 5. To enable a comparison with other published methods (Section 7.2), the overlap error O of the proposed fusion method is given in Table 5.

Figure 5.

Comparison of segmentation results obtained by employing region growing, model-based and fusion methods. Each row contains a new example, and the first entry on the left gives the name of the dataset from which the CT scan is taken.

Table 5.

Overlap O for different test sets for the fusion segmentation results 𝒱_Fusion.

Set	Overlap O
Snormal	0.9811 ± 0.0072
Sasthma	0.9734 ± 0.0133
SCOPD	0.9822 ± 0.0062
Smix	0.9629 ± 0.0283
SIPF	0.9620 ± 0.0186
All	0.9716 ± 0.0200

6.2. Computational complexity

Generating a segmentation with our fusion approach takes 18.17 ± 3.55 minutes. This includes 3.41 ± 0.84 minutes for region growing segmentation, 4.34 ± 0.65 minutes for model-based segmentation, and 10.41 ± 2.55 minutes for calculating features and subsequent fusion of segmentations. All experiments were performed on a PC with a 2.70 GHz CPU. Note that kNN training and classification was performed in MAT-LAB (The MathWorks, Inc., MA) and the code was not optimized for speed.

7. Discussion

7.1. Fusion performance

Each lung segmentation algorithm needs to build on certain assumptions. For example, a region growing based lung segmentation assumes that lungs have low density and a fairly homogeneous appearance, whereas a model-based approach assumes that lungs have similar shapes, which allows to build a lung model that can be used for segmentation by matching it to new image data. In practice, the assumptions of a particular segmentation method might or might not hold, and therefore, lay the groundwork for achievable segmentation accuracy as well as success in some cases and (local) failure in other cases.

The goal of this work was to develop a Fusion framework for combining the strengths of two different segmentation methods to yield a lung segmentation approach that is less likely to produce segmentation failures than its base input segmentation methods. As the analysis of the failure rate in dependence of the desired segmentation accuracy (i.e., Dice coefficient) illustrates, the fusion approach showed considerably better performance than OSF and RG approaches over all investigated accuracy levels (Table 4). For example, if segmentations with an accuracy of larger than 0.97 was required, which represents a good performance level for lung segmentation, then OSF and RG methods resulted in a failure rate of 15.69% and 18.14%, respectively (Table 4). In contrast, our fusion approach that utilizes OSF and RG as input achieved a lower failure rate of 6.13%. When compared to the performance of OSF and RG, this represents a relative reduction of 60.94% and 66.22%, respectively (Table 4). Such reductions of failures are especially relevant for applications that require computer-aided analysis of several thousand lung CT scans due to the reduced need for subsequent manual editing. The impact of our approach can be clearly seen from the examples provided in Fig. 5.

As demonstrated by the results presented in Section 6, the fusion system was found to produce statistically significant more accurate segmentations on all cohorts investigated (Table 3), showing that the fusion method doesn’t degrade overall performance. While differences were significant, the rather small change in average Dice coefficients is expected, because not all of the 204 test cases cause segmentation errors when processed with input segmentation methods OSF or RG. Consequently, the failure rate F(γ) is more relevant for assessing whether or not the fusion approach manages to reduce failures/errors, which is the main goal of our work. As Table 3 shows, the largest improvements in Dice coefficient values were achieved by the fusion approach on test sets S_mix and S_IPF, which are the most challenging to segment.

In terms of computing time, a fusion approach is more expensive than any of the input segmentation algorithms due to the need for additional processing. Despite the fact that we did not optimize the implementation of the algorithm, the increase in computational cost is manageable and opportunities for parallel implementation to run on multi-core processors exist. For many applications, the increase in automated segmentation accuracy outweighs the increase in computing time.

7.2. Comparison with other methods

To enable a comparison with other methods, we applied our fusion approach to the LObe and Lung Analysis 2011 (LOLA11) challenge data set. However, we note that the LOLA11 test set includes cases with pleural effusion, but pleural effusion cases were not present in the available training set S_train. Clearly, utilizing a fusion approach that was not properly trained is not recommended and can lead to suboptimal results. To enable a fair comparison and, at the same time, demonstrate the impact of a well adapted classification system, we processed the LOLA11 test set with two variants of our algorithm: Fusion_ST and Fusion_PE. Fusion_ST represents the standard algorithm as described in Section 3. For Fusion_PE, the following classification rule was added to the system to enable it to deal with pleural effusion cases, that could not be learned from our training data set S_train . The idea behind this rule is to reject large chunks that mainly consist of pleural fluid and constitute a large area of a lung. Therefore, a chunk ω ∈ Ω_Clarge is rejected if it’s volume is at least 20% of the volume of the model-based lung segmentation and the relative amount of pleural fluid is at or exceeds 50% of the volume of ω. Pleural fluid voxels are identified with a range-bound threshold operation, and the range [−21 32] HU was selected by combining the ranges for exudate pleural effusions and transudate effusions that were previously reported by Abramowitz et al. [20]. We note, that adding this rule had no impact on the results that were reported in Section 6 (i.e., Fusion _ST and Fusion_PE deliver the same results on S_test), confirming the selective behavior.

For performance assessment, all 55 test data sets were downloaded from the LOLA11² website, segmented with both fusion variants, and submitted to the organizers, who in return provided quantitative evaluation results based on a comparison with their undisclosed reference standard. Results for Fusion_ST and Fusion_PE on the LOLA11 test set are summarized in Table 6. In addition, the performance of an early version of our model-based (input) segmentation algorithm published by Sun et al. [23] and several other segmentation approaches is provided. By comparing the results, we can observe the following. First, both fusion methods are better performing than the early version of our model-based approach. Second, the average score of Fusion_PE is higher than the one for Fusion_ST, which is expected due to the better adapted classifier in the case of Fusion_PE. The difference between the results for Fusion_ST and Fusion_PE on LOLA11 test data demonstrates the importance of representative training data for a classification based fusion approach. Third, the proposed fusion approach is currently one of the top-performing methods (Table 6). For a quantitative comparison with results of other methods and latest results, we refer the reader to the LOLA11 website³.

Table 6.

Segmentation results on the LOLA11 test set. The results of several other methods are included for comparison. The latest results of other methods on LOLA11 data can be found at URL http://lola11.com/Results/Overview. Q1 and Q3 denote the first and third quartile. See text in Section7.2 for details.

Method	Avg. score	Lung	mean	std	min	Q1	median	Q3	max
Human (manual)	0.984	Left	0.984	0.031	0.782	0.987	0.992	0.996	0.998
		Right	0.984	0.047	0.662	0.988	0.995	0.997	0.999
UoFL Bioimaging	0.980	Left	0.986	0.022	0.874	0.987	0.992	0.995	0.999
		Right	0.974	0.128	0.052	0.991	0.995	0.996	0.998
FusionPE	0.974	Left	0.973	0.099	0.267	0.986	0.991	0.994	0.999
		Right	0.974	0.107	0.206	0.988	0.993	0.995	0.998
Frauenhofer Mevis [3]	0.973	Left	0.974	0.097	0.277	0.987	0.992	0.995	0.999
		Right	0.972	0.135	0.000	0.991	0.994	0.996	0.999
Yacta [21]	0.970	Left	0.971	0.093	0.309	0.982	0.988	0.992	0.997
		Right	0.969	0.134	0.000	0.986	0.990	0.993	0.998
SmartPaint [22]	0.969	Left	0.968	0.134	0.000	0.985	0.990	0.993	0.998
		Right	0.970	0.134	0.000	0.988	0.992	0.994	0.998
Mansoor et al. [10]	0.968	Left	0.968	0.097	0.316	0.979	0.987	0.995	0.999
		Right	0.968	0.134	0.000	0.984	0.990	0.997	0.999
FusionST	0.967	Left	0.969	0.126	0.063	0.986	0.991	0.994	0.999
		Right	0.965	0.117	0.206	0.987	0.993	0.995	0.998
NMF BI&CI Labs	0.965	Left	0.965	0.108	0.205	0.981	0.988	0.992	0.998
		Right	0.964	0.133	0.010	0.982	0.988	0.991	0.997
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
Sun et al.[23]	0.949	Left	0.939	0.173	0.039	0.979	0.990	0.994	0.997
		Right	0.959	0.122	0.167	0.985	0.990	0.994	0.998
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮

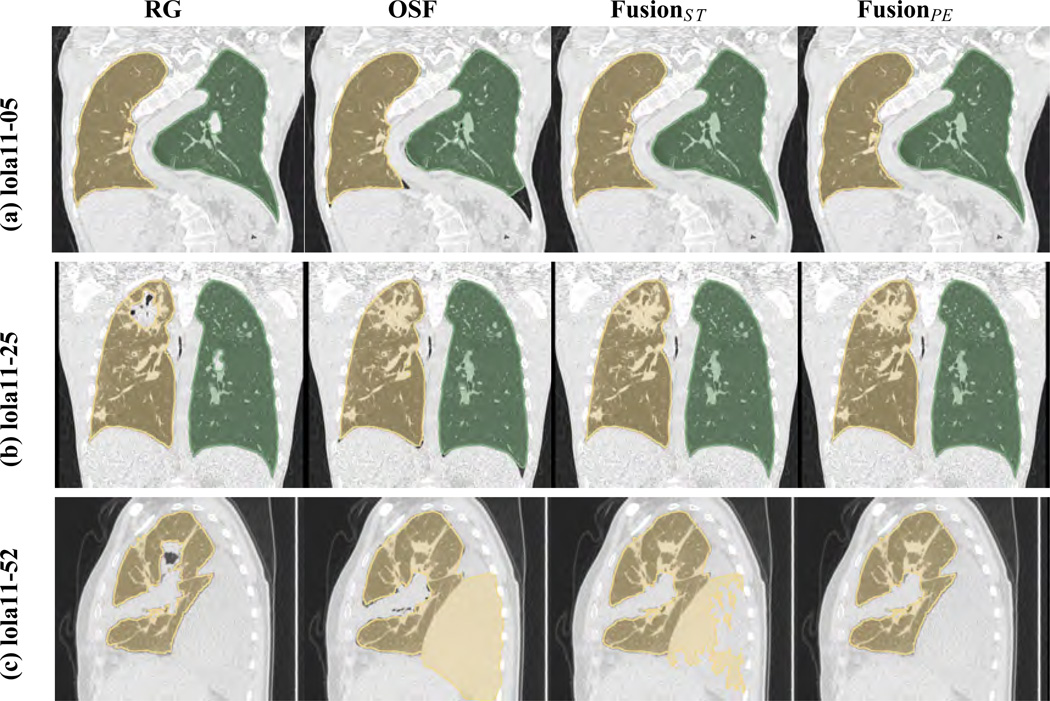
Fig. 6 provides some examples of results on LOLA11 data sets. Row (a) in Fig. 6 shows a lung CT scan of patient with scoliosis of the spine, leading to an atypical lung shape. While region-growing manages to deal with this problem, the OSF approach, which is model-based, fails to completely adapt to this abnormal lung shape. Both fusion variants correctly handle this situation. Row (b) in Fig. 6 depicts a case with a larger consolidation near the apex in one lung. As can be seen, this represents a challenge for the region-growing method, but the OSF approach includes the area of consolidation. Note that OSF produces a local segmentation error in the area of the costophrenic angle. Methods Fusion_ST and Fusion_PE manage to avoid the errors of RG and OSF, respectively. Row (c) in Fig. 6 show segmentation results on a case with a large pleural effusion. While, the region growing segmentation contains only minor errors, the OSF segmentation includes large parts of the pleu-ral effusion. Since Fusion_ST was not trained on such data, it mostly replicates the error of the OSF segmentation. In contrast, Fusion_PE better handles this difficult segmentation problem. Also, note the difference between OSF and Fusion_ST in the area of the pleural effusion, which are caused by the postprocessing (marker-based watershed) described in Section 3.4.

Figure 6.

Examples of results on the LOLA11 test set.

When comparing our LOLA11 results (Table 6) with the evaluation provided in Section 6 (Table 5), we can notice the following. The result for Fusion_PE is almost identical to our segmentation overlap results and well within the range of results reported on the different cohorts (Table 5). However, we note that our test set S _test is almost five-fold larger and is more geared towards the requirements of large clinical trials (i.e., different inclusion criteria).

7.3. Current limitations and future work

For our fusion approach, it is desirable that the union of base segmentation results include the lungs. Given the fact that both utilized base segmentation methods are optimized for lung segmentation, we found that this is the case most of the time. However, even if this is not the case, the fusion approach can still produce an improved, less erroneous lung segmentation, which might be sufficiently accurate for a given problem or require less subsequent manual editing, and therefore, is still more desirable than any of the base segmentations. In this context, if a better lung segmentation method becomes available, it can be incorporated in our fusion approach by simply replacing one of the base (input) segmentation methods. Our fusion approach can be adapted to the new configuration by simply retraining the classifier.

The fusion method assumes that if both lung segmentations label the same region as lung, the region represents true lung tissue. It is conceivable that cases exist where both methods are wrong. This issue could be addressed in two ways. One option could be to generalize the fusion system so that three or more input segmentation can be processed, which would further reduce the likelihood that all segmentation methods miss a part of the lung, but require a more fine grain processing of differences between base segmentations. Another option to address this issue is to further partition the common segmentation volume into sub-parts and develop a classification system for such “agreement” chunks.

Our fusion system computes volume chunks and accepts or rejects them based on image features. We note that in some cases a chunk might consist of a mixture of lung and other tissues. Thus, a possible future extension of the presented approach could be to further process volume chunks to split them into homogeneous volume elements (e.g., super voxels) and perform classification on them, which might help to further increase segmentation performance.

The fusion system is dependent on representative training data sets to build the classifier. One option for getting relevant new learning examples would be to implement an online learning system within a production environment. Thus, if a lung in a CT scan is not segmented satisfactory, the data set is manually processed, integrated into the training set, and the fusion classifier is retrained with the expanded training set. In this context note that a new application domain might also require new features to reach the full potential of the fusion approach.

8. Conclusions

We have presented a fusion approach to increase the robustness of automated lung segmentation by selectively combining the output of a region growing and a model-based lung segmentation method. Experiments on a diverse set of 204 CT scans have shown that the fusion method delivered statistically significant better results than the utilized individual lung segmentation algorithms, independent of the investigated cohort. In addition, the fusion approach did have a lower failure rate over a wide range of performance levels. The increased robustness make the fusion approach an attractive selection for applications requiring high volume processing like multi-site clinical trials. In addition, the algorithm can be generalized to other application domains.