Population pharmacokinetics of tenofovir and tenofovir‐diphosphate in healthy women

Abstract

The objective of this analysis was to develop and qualify a population pharmacokinetic model describing plasma tenofovir (TFV) concentrations and tenofovir‐diphosphate (TFV‐DP) concentrations in peripheral blood mononuclear cell (PBMC) in healthy women volunteers from the MTN‐001 clinical trial, an open label 3‐way crossover study of oral tenofovir disoproxil fumarate 300 mg tablet, TFV 1% vaginal gel, or both. TFV pharmacokinetics were best described by a 2‐compartment, first‐order absorption/elimination model with absorption lag time. TFV was linked to PBMC TFV‐DP by first‐order uptake with first‐order elimination. An adherence adjustment was included to account for nonadherence by explicitly modeling a bioavailability parameter on the previous day's dose. The final model included weight as a covariate on central compartment volume (V_c) with estimates as follows: absorption rate constant (Ka) 9.79 h⁻¹, absorption lag time 0.5 hours, V_c 385.71–2.16*(73‐WT(kg)), and apparent TFV clearance of 56.7 L/h ((K20 + K24)*V_c). TFV‐DP's half‐life was 53.3 hours. All diagnostic plots and bootstrap confidence intervals were acceptable. Model validation was conducted using simulations compared to data from the MTN‐001 oral + vaginal period and other clinical trial data. The resulting model closely predicted the disposition of TFV and TFV‐DP when compared to healthy participant data from another clinical trial.

Several clinical trials have demonstrated the efficacy of oral daily tenofovir disoproxil fumarate (TDF), alone or in combination with emtricitabine, for HIV pre‐exposure prophylaxis (PrEP), leading to a PrEP FDA indication for TDF in its combination formulation with emtricitibine (Truvada®).1, 2, 3, 4, 5 In these trials, the concentration of tenofovir (TFV) was significantly associated with HIV transmission as individuals with suboptimal adherence were more susceptible to contracting HIV.6 Therefore, understanding the pharmacokinetics (PK) of TDF in healthy individuals is vital.

TDF is a prodrug with rapid conversion to TFV following absorption in the gastrointestinal tract. TFV's activity is due to its uptake into CD4₊ T cells, the HIV target cells, and subsequent addition of 2 phosphate groups forming the active moiety, TFV diphosphate (TFV‐DP).7 TFV‐DP is a nucleotide reverse transcriptase inhibitor (NRTI) which prevents DNA transcription, thus, preventing productive infection.7 As TFV‐DP is the active moiety of TDF, the pharmacokinetic profile of TFV‐DP is an important determinant of therapeutic or prevention efficacy.

Population PK modeling allows determination of sources of PK parameter variation as well as their covariate relationships and can assist in trial design, dose selection, and dose timing optimization. Building a population PK model which links TFV to TFV‐DP is key to understanding the relationship between these 2 metabolites and determining resulting concentrations following a dose.

There have been several reports of the population pharmacokinetics of TFV alone8, 9, 10, 11 but fewer on both TFV and TFV‐DP. Several relationships have been used to link blood plasma TFV to peripheral blood mononuclear cell (PBMC) TFV‐DP levels. Duwal et al12 used saturable uptake for TFV‐DP formation in PBMCs whereas Baheti et al13 employed an indirect response model in which TFV concentration stimulated the formation of TFV‐DP.

While TFV PK is similar between infected patients and healthy individuals,7 TFV‐DP PK differs. Reported median 24 hour postdose concentrations of TFV‐DP in infected patients are ∼120 fmol/million cells13 whereas healthy individuals show a median ∼42 fmol/million cells.14 Thus, model estimated parameters for TFV‐DP pharmacokinetics should vary between these 2 populations. In the previously published models, parameters were estimated from either infected patients13 or a mixed group of both infected patients and healthy individuals.12 Because of the differences between TFV‐DP pharmacokinetics in patients vs. healthy volunteers—the PrEP target population—there is a need for a model built using only healthy individual data to facilitate its use for PrEP indication.

MTN‐001 is a multisite 3‐period cross‐over study which assessed pharmacokinetics and adherence/product acceptability in which healthy female participants utilized either oral TDF alone, a vaginal gel formulation of TFV, or both products together.15, 16 Trial data from MTN‐001 include both TFV and TFV‐DP concentrations and, therefore, present the opportunity to build a pharmacokinetic model for healthy individuals.

A complication to pharmacokinetic modeling of MTN‐001 is suspected suboptimal adherence.8, 12 This complicates population modeling as it may lead to biased parameter estimates.17,17, 18 Several methodologies have been described to account for nonadherence including the alternative approach based on superposition,19 the exogenous example,20 monitoring systems (MEMS) based dosing histories,21, 22 a mixture modeling approach,17 a Bayesian approach,18 a formalism of PK model including the stochastic drug intake behavior of patients,23 and a missing dose method.24

A method proposed first by Sheiner et al25 but recently described26 which uses a bioavailability adjustment to a preclinic dose was of interest to us as it was simpler to implement and has been said to be equivalent to the alternative approach and can be applied to the nonlinear models. Herein this method will be referred to as Gibiansky's method.26 Our objective was to develop and qualify a population pharmacokinetic model for plasma TFV to PBMC TFV‐DP in healthy volunteers from MTN001 trial using a method that accounts for nonadherence to facilitate unbiased parameter estimation.

Methods and Materials

Trial Design

MTN‐001 was a multisite 21‐week Phase II open label 3‐period crossover study of a daily oral TDF 300 mg tablet and/or TFV 1% vaginal gel. The full protocol is available at www.mtnstopshiv.org and results are reported elsewhere.15 Study participants received daily TDF tablet (oral period), vaginal gel (vaginal period), or both (dual period) in 3 six‐week periods separated by 1‐week washout periods. The study enrolled 168 women aged 18–45 who were HIV‐negative, sexually active, not pregnant, and using effective contraception. The final participant group included 144 participants, defined as women who were dispensed study product and completed at least 1 follow‐up visit in each period.

TFV and TFV‐DP pharmacokinetic data were collected at the midpoint and final visit of each period. At the midpoint, a single blood draw was completed to assess TFV and TFV‐DP concentrations whereas the final visit included predose concentration assessment, an observed dose followed by intensive or nonintensive postdose sampling. Intensive sites took postdose concentrations at 1, 2, 4, 6, and 8 hours whereas nonintensive sites included a single postdose level at a prespecified time point between 1 and 8 hours. Concentrations of TFV and TFV‐DP were assessed by HPLC‐MS‐MS as described elsewhere.15

Population Pharmacokinetic Model Development

Data management was conducted using R (version 3.0.1) and Microsoft Excel (Microsoft Office 2010). End visit pharmacokinetic data from the oral period were used for model building and the dual period of the trial was reserved for model validation as vaginal application of TFV does not appreciably impact plasma TFV/TFV‐DP concentrations. Dosing was in TFV equivalents (136 mg TFV/300 mg TDF) and in micromoles whereas TFV concentrations were converted to nanomoles/mL (TFV molecular weight of 288.1 g/mole). TFV‐DP was measured as femtomoles/million cells and converted to nanomoles/L using a PBMC cell volume of 282 femtoliters/cell27 (Figure S2). The volume conversion accounts for 1 million cells and modeling accounts for the amount of TFV‐DP in 1 million cells. For graphical representation, concentrations of TFV and TFV‐DP were converted back into their commonly used units of ng/mL and fm/million cells, respectively.

Population pharmacokinetic modeling was conducted with NONMEM® (ICON, Ellicott City, Maryland, version 7.2) in conjunction with a g95 (64‐bit) compiler using Perl‐Speaks NONMEM® (PSN, version 3.5.3) as an interface to run NONMEM®. R (version 3.0.1) and XPOSE4 were used for diagnostic plots. The first‐order conditional estimation with interaction (FOCEI) algorithm was used for parameter estimation.

TFV and TFV‐DP were modeled simultaneously with TFV modeled as a 2‐compartment model with an additional compartment for TFV‐DP using first‐order absorption and elimination for all compartments. Intracellular TFV‐DP were linked to TFV concentrations by a linear model which used a first‐order rate constant to connect the central TFV compartment to a PBMC TFV‐DP compartment. Parametrization was attempted using volume and clearance terms as well as micro‐rate constants using ADVAN 5 with NONMEM default settings.

Modeling of between subject variability (BSV) was performed using an exponential relationship:

$${\mathrm{\theta }}_{\mathrm{i}}={\mathrm{\theta }}_{\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}*{\mathrm{e}}^{\mathrm{\eta }\mathrm{i}}$$

where θ_i is the individual's value for the parameter, θ_typical is the population value for the parameter, and η_i the difference between θ_i and θ_typical with a mean 0 and variance ω².

Residual variability was attempted as a combined additive and proportional model as follows:

$${\mathrm{y}}_{\mathrm{i}\mathrm{j}}={\hat{\mathrm{y}}}_{\mathrm{i}\mathrm{j}}(1+{\mathrm{\epsilon }}_{1\mathrm{i}\mathrm{j}})+{\mathrm{\epsilon }}_{2\mathrm{i}\mathrm{j}}$$

where, ${\mathrm{y}}_{\mathrm{i}\mathrm{j}}$ and ${\hat{\mathrm{y}}}_{\mathrm{i}\mathrm{j}}$ represent the jth observed and predicted concentration, respectively, for the ith subject, and $\mathrm{\epsilon }$ is the residual random effect. Each $\mathrm{\epsilon }$ is assumed to be normally distributed with mean 0 and variance of σ². Reduction of the residual error model was tested during model development. Separate residual error models were included for TFV and TFV‐DP.

Nonadherence in the trial was taken into account by implementing Gibiansky's method26 in which a bioavailability parameter was applied to the previous day's dose by fixing the bioavailability parameter to 0.5 and its ω distribution to a high value, in our case 10, allowing the model to account for dose omissions or multiple doses.

$$\mathrm{F}1=0.5*{\mathrm{e}}^{\mathrm{\eta }\mathrm{i}}$$

where F1 is an individual's bioavailability on the preclinic dose. The study participants’ most recently self‐reported dose (date and time) was used to define the timing of the preclinic dose (mean 12.9 hours, range 1.95–35 hours). One participant lacked a reported dose time so a preclinic dose was imputed 12 hours prior to the in‐clinic dose based on a nominal time postdose expectation in this study.15 The preclinic dose was given as a steady‐state dose and would thus adjust for prior dose‐taking history whereas the in‐clinic dose was a transient dose and represents an average adjustment to the adherence rather than only to the single preclinic dose. The bioavailability for the in‐clinic dose was set to 1; thus all estimated parameters are apparent.

Model Selection Criteria

Model selection criteria included the likelihood ratio test to compare hierarchical models using the NONMEM objective function value (‐2LL) as well as diagnostic plots, evaluation of the clinical relevance of parameter estimates, and condition number for signifying model overparametrization. A decrease in the objective function by 3.84 (P < .05, 1 degree of freedom) units for hierarchical models was considered to be significant. All of the above elements as well as successful convergence and covariance steps were used in model selection.

General goodness‐of‐fit plots used were individual (IPRED) and population (PRED) predictions vs. observed concentrations, and conditional weighted residuals (CWRES)28 with respect to time postdose. Condition number was calculated as the ratio of highest to lowest eigenvalues calculated during the covariance step.

Covariate Model

Covariates selected for evaluation were body weight, race, and creatinine clearance and were tested using forward addition and backward elimination. Covariates were considered significant if their addition prompted a 3.84 point reduction in the objective function (P < .05, 1 degree of freedom) in forward addition and a 6.64 units (P < .01, 1 degree of freedom) increase after backward elimination. Continuous variables were assessed with either a linear or power function whereas categorical covariates were tested using a linear function.

Bootstrap

A nonparametric bootstrap (n = 2,000) was conducted on the base model and final model using PSN and was stratified based on intensively sampled sites vs. nonintensively sampled sites to preserve the blood sampling distribution. All runs were included in the calculation of 95% confidence intervals. Parameters lacking zero in the 95% confidence intervals were retained.

Internal and External Qualification by Simulation

The final model was qualified by conducting a visual predictive check (VPC),29, 30 simulation of the dual period of MTN‐001, simulation of a single dose study of tenofovir,31 and simulation of steady‐state levels of TFV‐DP after 300 mg TDF daily dosing assuming full compliance.

VPC

VPCs were conducted using a sample size of 1,000 and the resulting 90% prediction interval (PI) was compared to the observed values. Due to the inflated ω distribution on the bioavailability parameter (F1) for adherence adjustment, the Monte‐Carlo method that NONMEM uses for simulation generated a large distribution of F1 values that resulted in exaggerated prediction intervals. Therefore for VPC simulation, individual empirical Bayes estimates (EBEs) of F1 were imputed to better represent current adherence in each individual.

Simulation of the Dual Period of MTN‐001

For the dual period simulation, the parameter F1 was first estimated for each individual in the dual period and then imputed to inform the F1 value during the simulation thereby tailoring the adherence adjustment to the individual's current adherence level.

Simulation of a Single Dose Study of Tenofovir

A single dose study of oral tenofovir by Louissaint et al31 was conducted in 6 healthy premenopausal women in which they consumed a slurry of 300 mg TDF along with a radiolabeled form of the drug (¹⁴C‐TDF). Concentrations of serum TFV and PBMC TFV‐DP were assessed over the next 15 days. This study design was simulated 1,000 times and the resulting prediction interval compared to the observed data.

Simulation of Steady‐State TFV‐DP Levels After Daily 300 mg TDF Dosing

A multidose simulation (16 doses starting with the first dose, n = 1,000) was conducted with the final model (median weight of 73 kg used) using daily dosing. The resulting data were used to calculate the median trough and interquartile range (IQR) of TFV‐DP concentrations for comparison to published values from the daily dosing arm of STRAND.14

Results

Population Pharmacokinetic Model Development

Participant demographics are given in Table S1. Out of 141 participants with pharmacokinetic measurements, 101 were included in the analysis which included 476 and 399 TFV and TFV‐DP concentrations, respectively. Data that were below the limit of quantification (BQL) were excluded from our analysis as were individuals with only 1 concentration of an analyte. BQL concentrations for the oral period were 3.4% of the reported TFV concentrations and 12.9% of the TFV‐DP concentrations. The M3 method32 of accounting for BQL values was attempted, but encountered convergence issues so it was not retained. Eight reported data points were also excluded as follows: one participant's TFV‐DP concentrations were approximately 10 times higher than all other participants; therefore this patient's TFV‐DP data were excluded; another participant showed a predose concentration of TFV‐DP that was 10 times higher than the postdose concentrations and thus that data point was excluded; another participant showed a predose concentration of over 1,000 ng/mL TFV with postdose concentrations ranging from approximately 500 to 160 and thus the predose concentration was excluded.

TFV was found to be best described by a 2‐compartment, first‐order absorption/elimination model with parametrization using micro‐rate constants (Figure S2). Micro‐rate constants were used as typical Cl, V parametrization encountered numerical problems and the TFV‐DP portion of the model must be described in micro‐rate constants, thus for consistency and numerical stability, micro‐rate constants were employed. KA was held to be greater than K20 to prevent EBEs of K20 from exceeding KA EBEs. The addition of absorption lag time reduced the objective function by 192 and was thus included in the model. Mean and range for the EBEs for the preclinic dose bioavailability (F1) are shown in Table 1 and ranged from 0.015 to 4.17 with a mean of 0.98.

Table 1.

Bootstrap, Includes All Runs

	Base Model		Final Model
Parameter	Value (%RSE)	Bootstrap Median (95%CI BSV, %CV) n = 2,000	Value (%RSE)	Bootstrap Median (95%CI BSV, %CV) n = 2,000
Obj Func	2,586		2,575
Condition #	149		179
F1 *	0.98 (0.015–4.09)		0.98 (0.015–4.17)
KA (h−1)	9.81 (67.33)	10.15 (1.08–45.4)	9.79 (65.18)	10.21 (1.04–45.29)
Vc/F (L)	404.19 (15.06)	395.71 (26.02–495.50)	385.71 (14.84)	376.11 (28.5–475)
cov WT (kg) on Vc	NA	NA	−2.16 (34.52)	−1.78 (−3.37 to −0.16)
K23 (h−1)	0.604 (24.02)	0.635 (0.392–13.3)	0.631 (24.7)	0.680 (0.411–12.92)
K32 (h−1)	0.37 (24.22)	0.38 (0.229–0.923)	0.396 (23.24)	0.398 (0.238–0.848)
K20 (h−1)	0.13 (18.56)	0.14 (0.098–1.85)	0.13 (17.81)	0.14 (0.10–1.51)
K24 (h−1)	0.017 (80.36)	0.018 (0.009–0.569)	0.017 (72.48)	0.019 (0.009–0.537)
K40 (h−1)	0.013 (16.73)	0.014 (0.009–0.052)	0.013 (16.63)	0.014 (0.009–0.052)
Absorption lag (h)	0.5 (37.96)	0.5 (0.005–0.685)	0.5 (35.49)	0.5 (0.005–0.665)
BSV KA (%CV)	164.22 (170.86)	165.80 (1.64–269.79)	160.2 (169.1)	164.97 (1.60–271.83)
BSV Vc (%CV)	24.28 (36.3)	22.77 (2.45–32.18)	19.3 (45.1)	18.84 (0.19–29.11)
BSV K20 (%CV)	35.44 (41.89)	31.71 (6.43–51.84)	36.22 (33.99)	33.25 (12.09–51.68)
BSV K24 (%CV)	163.9 (74.95)	168.93 (57.51–616.05)	159.49 (69.95)	168.93 (57.51–616.05)
Proportional, TFV (%CV)	27.57 (5.12)	27.48 (22.70–31.62)	27.48 (5.24)	27.36 (22.95–31.71)
Proportional, TFV‐DP (PBMC) (%CV)	30.76 (7.42)	30.71 (27.12–35.16)	31.18 (7.21)	30.89 (27.08–35.11)

^*F1 values are the empirical Bayes estimates mean (min‐max).

It was found that parent TFV was best linked with intracellular TFV‐DP by a first‐order rate constant (K24) with TFV‐DP eliminated by a first‐order process. It was assumed that TFV‐DP kinetics were elimination rate dependent by constraining K24 to be faster than K40. Population pharmacokinetic parameters along with bootstrap estimates were provided in Table 1. The population estimate for elimination of TFV‐DP in the final model was 0.013 h⁻ which yields a half‐life of 53.3 hours. Between subject variability (BSV) was supported on KA, V_c, K20, and K24. It is important to note that both K20 and K24 are apparent clearance terms for TFV. Therefore, when assessing TFV clearance both terms were included.

Covariates that were significant include total body weight on V_c (‐11 objective function points) and CrCl on K20 (‐4 objective function points) both with linear relationships. Based on the more significant drop with the addition of weight on V_c, this relationship was added to the model followed by CrCl on K20. There was no significant drop in the objective function with the addition of CrCl on K20 and the model failed to converge. Therefore, only weight on V_c was retained in the final model. Following this addition, a 5% reduction of BSV on V_c was observed. The covariate relationship between weight and volume was linear and was centered on the median weight (73 kg) as follows:

$$\mathrm{T}\mathrm{V}\mathrm{V}=385.71-2.16*(73-\mathrm{w}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}(\mathrm{k}\mathrm{g}))$$

BSV on KA and K24 were high at 160.16% and 159.49% although they were both reduced compared to the base model values of 164.22% and 163.9%, respectively. The final model had a successful convergence and covariance step (S‐matrix calculation) with a condition number of 179. Race, defined as being either black or nonblack, on clearance was not shown to be a significant covariate and this finding was in agreement with other literature reports.8, 12 Furthermore, race was also a function of trial site as those sites in Africa included the black subjects thus confounding the variable. The final model was estimated to significant digits of 3.5 and correlations between parameters were all <0.95.

Base and final model validation plots of IPRED or PRED vs. observed concentrations showed good agreement for both TFV and TFV‐DP (Figure S3 and Figure 1) and lacked bias. CWRES vs. time (Figures S3 and 1) or vs. PRED (not shown) showed no bias.

Figure 1.

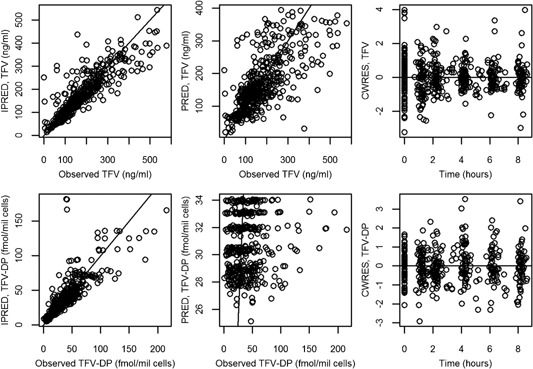
Final model diagnostic plots. Top panel shows plasma TFV and bottom panel shows intracellular TFV‐DP. Open circles indicate the observed data.

Nonparametric bootstrapping was performed for the base and final model and the 95% confidence intervals were calculated (Table 1). No parameters included 0 in their confidence interval.

Internal and External Qualification by Simulation

VPC

The VPC for both the base (Figure S4) and final model (Figure 2) showed close agreement between the predicted median and 90% prediction interval compared to the observed data.

Figure 2.

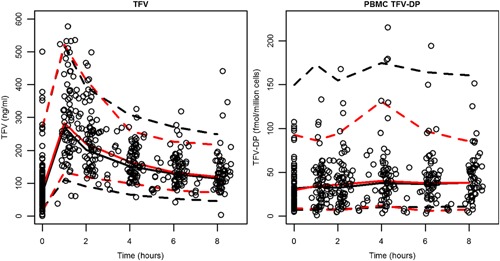
Final model VPC. Black dashed lines indicate the 90% prediction interval whereas red dashed lines show the 90% observed interval. Solid lines show the median. Open circles identify the observed data from the oral arm.

Simulation of the Dual Period of MTN‐001

Internal model qualification was conducted using data from the dual period. Both the base (Figure S5) and final (Figure 3) model yielded favorable results with the simulated medians and 90% prediction intervals matched closely with the observed dual period study data.

Figure 3.

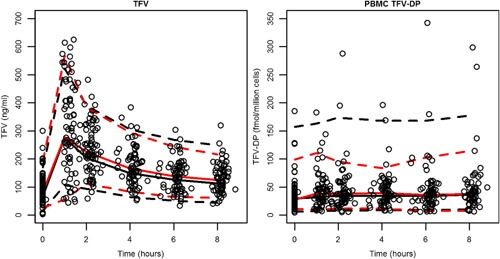
Dual arm validation, final model. Black dashed lines indicate the 90% prediction interval whereas red dashed lines show the 90% observed interval. Solid lines show the median. Open circles identify the observed data from the dual arm.

Simulation of a Single Dose Study of Tenofovir

Our model‐simulated concentrations compared well to data from a single dose study (Figure 4).31 Although most data were captured by model‐based simulations, 2 individuals, 104 and 105, were noted to have higher than predicted TFV‐DP levels for the first few data points.

Figure 4.

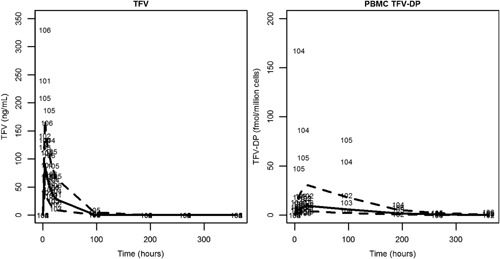
Single dose validation plot. Dashed lines indicate the 90% prediction interval. The median is shown by the solid line. Individual points are shown by ID number.

Simulation of Steady State TFV‐DP Levels After Daily 300 mg TDF Dosing

The multidose simulation data were used to calculate the median and IQR for TFV‐DP trough concentrations following achievement of steady state (after 265 hours, ∼5 TFV‐DP half‐lives based on our estimated TFV‐DP elimination rate constant). The simulated median trough at steady state was 49.9 fmole/million cells and the simulated IQR was 34.1–74.7 fmole/million cells (Figure 5).

Figure 5.

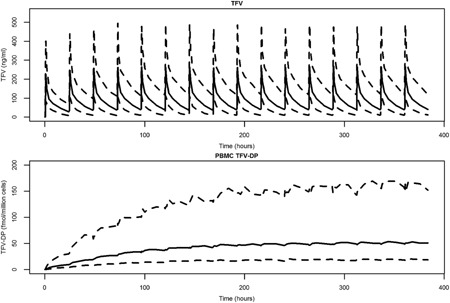
Multiple dose simulation, final model. The median subject weight of 73 kg was used for simulation to steady state. Dashed lines indicate the 90% prediction interval. The median is shown by the solid line.

Discussion

Although 2 other population PK models have been published for TFV/TFV‐DP, ours represent the first developed solely from healthy participants. Further differentiating our model from the 2 previously published models is the linear relationship used to describe TFV‐DP uptake/formation in PBMCs. While the pharmacodynamic effect is known to reach maximum clinical benefit at a dose of 300 mg TDF daily, the presence of saturating pharmacokinetics for TFV is not established especially as relates to healthy individuals. Previous modeling which used saturating kinetics to describe the relationship between TFV and TFV‐DP has modeled either mixed healthy individual data with HIV patient data or HIV patient data alone and the resulting models predicted much higher TFV‐DP, plateau level of 130 fmol/million cells12 and 128–174  fmol/million cells,13 compared to our linear model trough median of 49.9 fmol/million cells. Our model‐predicted TFV‐DP concentrations closely match study data in healthy individuals, the PrEP target population. It is possible that saturating kinetics do occur in the healthy individuals, but 300 mg TDF may not be sufficiently high to induce saturation, thus, allowing the use of the simpler linear relationship. MTN‐001 used only the clinically relevant dose of 300 mg TDF, thus, preventing us truly investigating saturating kinetics.

Although the idea of adjusting the bioavailability parameter for adherence correction was mentioned by Sheiner et al,25 systematic evaluation was recently conducted by Gibiansky et al26 and this is the first publication to use it for model development. We have experience using the alternative method4 originally published by Gupta et al19 which adjusts for nonadherence by estimating a parameter for predose concentration (C0) which arises from an unknown dosing history allowing the known in‐clinic dose to be superimposed on the temporal decline of C0. Although the alternative method uses explicit equations in NONMEM® implementation, Gibiansky's method26 takes advantage of NONMEM's PK subroutines allowing for simpler implementation. The idea is that the estimation of bioavailability for preclinic dosing is synonymous with estimation of C0, the parameter that accounts for nonadherence in the alternative method. Gibiansky's method21 fixes the between subject variability on the bioavailability parameter to a wide statistical distribution such that each individual bioavailability value can be widely altered to account for both missing doses (lower F1 value) or multiple doses taken (higher F1 value). To implement the alternative example, superposition must hold true, but Gibiansky's method26 can also be used for nonlinear kinetics. Both are suitable with a study design which has pharmacokinetic samples collected both predose and postobserved dose. Dose linearity of pharmacokinetics for TFV‐DP is not established, but a clear pharmacodynamic saturation at 300 mg QD dosing was reported where viral load was evaluated with respect to dose.7 Thus, Gibiansky's method was thought applicable for TFV‐DP kinetics as it can also handle problems which lack direct closed form of mathematical solutions. Thus, each method has their place in the arsenal of pharmacometric techniques.

Our parameter estimates for TFV were in agreement with literature values. The estimated KA was high at 9.7 h⁻¹ with a large BSV (164% in the base model and 160% in the final model) which may be due to the varied participant fasting states or lack of data points surrounding the absorption phase. Food intake was not controlled and TDF is known to be sensitive to high fat or high calorie meals causing a T_max of 2 hours vs. 1 hour in the fasted state.7 With regard to TFV clearance, although our model was parametrized in terms of rate constants, if TFV micro‐constants K20 and K24 are converted to clearance terms ((K24 + K20)*V_c), our model yields a mean total apparent clearance of 57.8 L/h for the base model and 56.7 L/h for the final model falling within the reported values we reviewed recently.8 The volume of total PBMC compared to plasma volume was reported to be small and the total amount of TFV‐DP in PBMCs was theoretically calculated to be <0.0008 mg.12 By using the linear ADVAN5 subroutine we included TFV‐DP in the mass balance equations. In addition, we modeled only 1 million PBMCs and thus the parameters were apparent in theory, but, given the small amount of TFV‐DP in PBMCs, the effect on TFV elimination parameters must be minimal or none.

The uptake of TFV into PBMCs and subsequent conversion to TFV‐DP was modeled by a single first‐order rate constant. A high level of BSV was seen which is unsurprising given the known variability in PBMC TFV‐DP concentrations seen in our data (range 0.8–215 fmol/million cells) and others.12, 13, 31 There was a high %RSE for the estimate of K24 and BSV on K24 which may be due to the variability in the data itself or potentially lack of data points in the first hour following dose administration.

The previous 2 published models12, 13 report TFV‐DP to have a long half‐life and these models are based on HIV patient data or mixed healthy individual and patient data. A single dose study in healthy individuals shows the half‐life to be shorter at 48 hours.31 Our parameter estimate for TFV‐DP elimination yields a half‐life of 53.3 hours which is in close agreement with the value for healthy individuals whereas the 2 previous publications report 85.7713 and 115.5 hours12 Interestingly, the shorter half‐life and lower trough level in healthy individuals do not correlate to in vitro data. The accumulation of TFV‐DP in resting PBMCs (expected in healthy individuals) was several folds higher and the half‐life was longer than in activated PBMCs in vitro.33, 34 Another study, however, reported no differences between TFV‐DP in resting and activated PBMCs, but found significantly more intracellular TFV in resting cells.35

We evaluated our model by simulating the dual period of MTN‐001 which served as internal validation and a separate single dose study31 which served as external validation. The preclinic F1 EBEs generated from the developed oral model would not have been appropriate as they corresponded to the adherence profile during the oral period; thus EBEs specific to the dual period were used and the resulting simulation showed similar values to the observed data.

Single dose data31 were compared by simulating the study using our model. Although the simulated 90% predication interval closely matched the majority of the data points, early time points for 2 of the 6 subjects were much higher than our predictions illustrating the variable nature of TFV‐DP kinetics. Interestingly, individual pharmacokinetic TFV‐DP profiles showed distinct biphasic patterns in the accumulation phase which was not captured by the current model. This biphasic pattern with an early and late TFV‐DP peak has been observed in another study36 but there is no explanatory evidence at this time.

We also conducted a multiple dose simulation to elucidate the model predicted trough TFV‐DP concentration following achievement of steady state. If our model simulations show similar values for TFV‐DP as the direct‐observed therapy STRAND14 trial, it indicates the adherence adjustment we employed was able to correct for bias in the estimates and reasonably predict TFV‐DP kinetics. The STRAND trial reports a median trough value (24 hours postdose) of 42 fmol/million cells while our simulations show a median value of 49.9 fmol/million cells. Furthermore, the IQR from the STRAND study versus our simulation had similar lower bounds at 31 versus 34.1 fmol/million cells and upper bounds at 47 versus 74.7 fmol/million cells respectively. Thus, our simulated trough and IQR both show good agreement with the STRAND trials results. The higher upper boundary for IQR in our simulations reflects the high level of BSV estimated in the uptake/conversion of TFV to TFV‐DP in our model. One caveat to this comparison is the difference in technique used to determine TFV‐DP concentrations in STRAND vs. MTN‐001. Concentrations in MTN‐001 for TFV‐DP were obtained from freshly lysed PBMCs whereas TFV‐DP concentrations in STRAND used viable, previously frozen PBMCs which may impact the resulting TFV‐DP concentrations. We do not feel this difference significantly impacts our ability to compare our simulations to STRAND's results.

Taken together, the 3 methods of validating our model show that the model was able to describe the pharmacokinetics of both TFV and TFV‐DP with reasonable accuracy and precision in healthy participants and indicates success of the adherence adjustment employed. This model can be used to test different dosing strategies (ie, twice weekly, every other day, etc) or could be used to find when protective concentrations of TFV‐DP are reached. It also has the potential for extension into other clinically relevant sites of TFV activity which include CD4+ cells in rectal tissue and vaginal tissue. This model could be extended into these areas should data become available but the small amount of concentration data on intracellular TFV metabolites in these sites limits incorporation at this time.

Our model has several limitations. First, our model does not incorporate saturating kinetics; therefore, if doses higher than 300 mg TDF daily were used in the PrEP setting, our model would need to be reassessed. Secondly, intracellular kinetics are simplified as follows: the rate constant linking TFV and TFV‐DP merges TFV uptake and conversion to TFV‐DP, back conversion from TFV‐DP to TFV is not accounted for, and TFV or TFV‐DP are not allowed to exit the cell. A gamma phase of TFV elimination has been observed and it has been hypothesized to be a result of cell turnover and subsequent release of TFV or TFV‐DP from cells.31, 37 These concentrations are low and may not be significant for safety or efficacy implications. Prospective validation using data from a known adherence (eg, DOT study) is warranted before clinical use of the model simulations.

In conclusion, we developed a population pharmacokinetic model for describing TFV and TFV‐DP concentrations after oral administration in healthy women. The model was qualified by internal and external clinical study data using simulation strategies and provides reasonable description of the data. No racial differences in elimination of TFV were found. The method used for adherence adjustment allowed for separation of the adherence effect from pharmacokinetics to achieve unbiased parameter estimations.

Supporting information

Additional supporting information may be found in the online version of this article at the publisher's web‐site.

Supporting Information.