Rb‐Sr resonance ionization geochronology of the Duluth Gabbro: A proof of concept for in situ dating on the Moon

Abstract

Rationale

We report new ⁸⁷Rb‐⁸⁷Sr isochron data for the Duluth Gabbro, obtained with a laser ablation resonance ionization mass spectrometer that is a prototype spaceflight instrument. The gabbro has a Rb abundance and a range of Rb/Sr ratios that are similar to those of KREEP‐rich basalts found on the nearside of the Moon. Dating of previously un‐sampled young lunar basalts, which generally have a KREEP‐rich composition, is critical for understanding the bombardment history of the Moon since 3.5 Ga, which in turn informs the chronology of the solar system. Measurements of lunar analogs like the Duluth Gabbro are a proof of concept for in situ dating of rocks on the Moon to constrain lunar history.

Methods

Using the laser ablation resonance ionization mass spectrometer we ablated hundreds of locations on a sample, and at each one measured the relative abundances of the isotopes of Rb and Sr. A delay between the resonant photoionization processes separates the elements in time, eliminating the potential interference between ⁸⁷Rb and ⁸⁷Sr. This enables the determination of ⁸⁷Rb‐⁸⁷Sr isochron ages without sophisticated sample preparation that would be impractical in a spaceflight context.

Results

We successfully dated the Duluth Gabbro to 800 ± 300 Ma using traditional isochron methods like those used in our earlier analysis of the Martian meteorite Zagami. However, we were able to improve this to 1100 ± 200 Ma, an accuracy of <1σ, using a novel normalization approach. Both these results agree with the age determined by Faure et al. in 1969, but our novel normalization improves our precision.

Conclusions

Demonstrating that this technique can be used for measurements at this level of difficulty makes ~32% of the lunar nearside amenable to in situ dating, which can complement or supplement a sample return program. Given these results and the scientific value of dating young lunar basalts, we have recently proposed a spaceflight mission called the Moon Age and Regolith Explorer (MARE). © 2015 The Authors and Southwest Research Institute. Rapid Communications in Mass Spectrometry published by John Wiley & Sons Ltd.

In this paper, we demonstrate the first radioisotopic date of a lunar analog using ⁸⁷Rb‐⁸⁷Sr resonance ionization mass spectrometry, a technique that can be made portable for use in situ on other planets. This approach offers the potential for resolving billion year discrepancies among crater‐count chronologies. The work of Robbins,1 who assembled an impactor flux model based on new crater counts using high‐resolution images from the Lunar Reconnaissance Orbiter Camera, highlights the wide variance among such chronologies. Under the 'classic' chronology of Neukum et al.2 and Ivanov,3 mare volcanism reached a volumetric maximum between 3.8 and 3.2 Ga4 and minor volcanism persisted through the recent past.5, 6, 7 However, under the alternative chronologies,^[e.g., 1, 8 ^] peak volcanism may have extended for an additional 1.1 Ga, through 2.5 Ga, which would pose a challenge for existing models of the thermal evolution of the Moon.9

In spite of large and often‐unrecognized uncertainties, crater counting nevertheless affords our best understanding of the timing of events through the majority of solar system history. However, as the lunar sample collection contains few specimens with ages younger than 3.2 Ga, the crater‐count chronology for the Moon has been extrapolated, under assumptions about the spatial distribution of impactors, to Mercury,10, 11 Venus,12, 13 Mars,14 and even Earth.15 Thus, if the alternative lunar chronologies^[e.g., 1, 8 ^] are correct, there are implications for events and processes throughout the inner solar system. For example, Mars would have undergone a longer epoch of voluminous, shield‐forming volcanism and associated mantle evolution,16, 17 as well as a longer era of abundant volatiles and hence potential habitability.18, 19, 20, 21, 22, 23, 24, 25 These alternative chronologies could even affect our understanding of the evolution of life on Earth: under the classic chronology, life is thought to have originated after the dwindling of bombardment, but under the alternative chronology, it might have appeared during heavy bombardment.^[e.g., 26, 27 ^]

Resolving the ages of young basalts on the Moon has long been assumed to require new sample return missions, due to the challenges of radioisotopic dating in general, and the difficult nature of lunar samples in particular. However, we recently demonstrated our laser ablation resonance ionization mass spectrometry (LARIMS) technique on the Martian meteorite Zagami, showing that dating of materials from the Martian surface was possible. In that paper, we presented repeated analyses of Zagami with ages in agreement with the TIMS age of 166±6 Ma28 and precision better than 200 Ma. A key finding of that work was that high‐power ablation reduced the matrix dependence of the fractionation of Rb from Sr.29 Here, we used LARIMS to determine a radioisotopic date for an analog of KREEP‐rich lunar rocks, which are thought to constitute approximately 32% of the nearside of the lunar surface.30

Background

Few of the rocks sampled by the Apollo missions are younger than 3.2 Ga, and most of those are only tenuously connected to a known geologic context. Hence, firmly establishing the correct chronology for the last ~3 Ga of solar system history requires new radioisotopic dating measurements of lunar rocks from this period with known context. While sample return is highly desirable for the range of analytical techniques that can be applied to a specimen, as well as the much greater precision that can be achieved in a geochronology experiment, in situ dating as part of a sample return mission would provide valuable triage data to inform the selection of the best samples for return to Earth. In situ dating on its own could answer many scientific questions with acceptable precision, and, without many of the costs and risks of a sample return mission, it can be more easily scaled to a campaign of missions to diverse terranes in the inner solar system. To assess the potential for in situ dating by LARIMS, we have designed and built an instrument for the resonance ionization of Rb and Sr isotopes, so as to employ the radioisotope ⁸⁷Rb as a chronometer. In this work, we tested our instrument by analyzing the Duluth Gabbro, a compositional analog for lunar basalts enriched in potassium, rare earth elements, and phosphorus, also known as KREEP terranes.31 The instrument design is consistent with portable, in situ use on future planetary missions to the Moon or Mars.

An advantage of the LARIMS technique is that a large number of spot analyses on a rock specimen can be assembled into an isochron. Unlike some kinds of analysis, isochron analysis includes built‐in self‐consistency checks: only if there is a direct spot‐to‐spot correlation between the relative abundances of radioactive parent and radiogenic daughter nuclei is an isochron age said to exist. This precludes having to make unverifiable assumptions about the initial abundance of either the parent or daughter nuclide.

One issue with ⁸⁷Rb‐⁸⁷Sr dating on lunar rocks is that the abundance of Rb in many anorthositic lunar samples is exceptionally low (<<1 ppm32), increasing the difficulty of obtaining accurate ⁸⁷Rb‐⁸⁷Sr isochrons. However, the KREEP basalts sampled by the Apollo 15 mission have 10–15 ppm Rb33 and, based on maps of potassium and thorium abundances measured by the Lunar Prospector Gamma Ray Spectrometer,34, 35 compositionally similar rocks appear to cover ~32% of the lunar nearside.30 Although the Lunar Prospector measurements did not analyze Rb directly, KREEP terrane basalts commonly exhibit a uniform Rb/Th ratio,36 and the 4–6 ppm of Th measured by Lunar Prospector34 correspond to 7–8 ppm of Rb. Our analysis of the Duluth Gabbro indicates ~4 ppm Rb (see Results section), which is at the low end of the range of Rb contents reported by Faure et al.37 for lithologies from the Duluth Gabbro Complex. A successful dating measurement with a 4 ppm Rb sample would demonstrate the technical ability to date rocks from one‐third of the lunar nearside. Strontium abundances in lunar rocks are tens to hundreds of ppm,^[e.g., 33 ^] and therefore are not a limiting challenge to ⁸⁷Rb‐⁸⁷Sr dating.

A second issue that potentially limits the precision of a ⁸⁷Rb‐⁸⁷Sr isochron age arises if the mineral‐to‐mineral range of Rb/Sr ratios within a rock is small. The ⁸⁷Rb/⁸⁶Sr ratios of mineral separates from an Apollo 17 KREEP basalt clast range from 0.016 to 0.839.38 The best indication that the Duluth Gabbro is a useful analog for KREEP basalt in this sense may come from our own analyses: none of our 310 spot analyses found ⁸⁷Rb/⁸⁶Sr ratios higher than 0.6. By contrast, our previous analyses of the Boulder Creek Granite found ⁸⁷Rb/⁸⁶Sr ratios up to ~1000,39 and for Zagami we found ⁸⁷Rb/⁸⁶Sr ratios up to ~30.29 Hence, based on the highest mineral ⁸⁷Rb/⁸⁶Sr ratios, which most strongly constrain the slope of an isochron line, the Duluth Gabbro is ~1000 times harder to date than Boulder Creek Granite, ~30 times more difficult than Zagami, and of similar difficulty to KREEP basalts.

Our sample of the Duluth Gabbro is a coarse grained anorthositic gabbro from the AS‐3 locality described by Paces and Miller,40 whose mineralogy has been described by Taylor.41 The grain size of the Duluth Gabbro is considerably larger than the grain sizes of KREEP basalts (10–250 µm42), but KREEP basalts nevertheless have many grains that are larger43 than our analytical spot size of 100 µm.

To provide useful constraints on the chronology of the Moon, any instrument must be capable of resolving the multiple potential historical hypotheses for the Moon, which span a billion year range of possibilities. Therefore, a reasonable analytical requirement is precision of ~200 Ma or better44 for rocks with ages up to 3.5 Ga. This is not a challenge for modern laboratory‐based techniques, but it is necessary to show that an in situ dating instrument can achieve such precision. The objective of our work was to date a sample of the Duluth Gabbro with 200 Ma precision. The ⁸⁷Rb‐⁸⁷Sr isochron age of the Duluth Gabbro Complex has been precisely measured by Faure et al.37 using thermal ionization mass spectrometry (TIMS); their data, once corrected for the value of the ⁸⁷Rb decay constant determined by Rotenberg et al.,45 yield an isochron age of 1096 ± 14 Ma, which is in the age range that we seek to study on the Moon.

Method

The method and instrumental approach have been fully described by Anderson et al.,29 and are only summarized here. We use laser ablation (~5 ns pulses at 213 nm into ~100 µm spots, ~0.6 GW/cm²) to vaporize a small sample of the target rock, generating ions and neutral atoms. The ions are electrostatically rejected from our time‐of‐flight mass spectrometer. About 1 µs after ablation, lasers tuned to 461 nm and 554 nm are used to excite resonances of neutral Sr in the vaporized plume, and the resulting excited atoms are photoionized with a 1064 nm laser. Resonance ionization of Rb atoms from the same ablation plume follows ~2 µs later, using lasers at 780 nm, 776 nm, and 1064 nm. This ~2 µs offset temporally separates the arrival of Sr and Rb at the time‐of‐flight detector, eliminating their isobaric interference at mass 87. For dating, we use thousands of ablation pulses to analyze each of hundreds of spots on a sample, allowing us to determine a ⁸⁷Rb‐⁸⁷Sr isochron age using isotopic data from different minerals, in a manner analogous to the 3–20 analyses normally made using TIMS.

We analyzed our sample of the Duluth Gabbro in much the same way as we analyzed the Martian meteorite Zagami.29 We calculated ratios of ⁸⁷Sr/⁸⁶Sr, ⁸⁷Rb/⁸⁶Sr, and their associated correlated errors, for every spot analysis in which ⁸⁵Rb, ⁸⁶Sr, ⁸⁷Sr, ⁸⁷Rb, and ⁸⁸Sr were all detected at greater than twice the background noise level. The isotopic ratios that we measured on a co‐analyzed standard were compared with their reference values, and we calculated multiplicative corrections to account for our instrumental fractionation. These multiplicative corrections were then applied to the Duluth Gabbro isotope ratios. Finally, we constructed the ⁸⁷Rb‐⁸⁷Sr isochron from the correlation between the ⁸⁷Rb/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios. The age of the sample was found from the slope of the best‐fitting isochron line. We stress that the isochrons we report here include all spot analyses in which the five isotopes listed above are all unambiguously detected; this is the only criterion that we presently use to filter data.

There are two noteworthy differences between this measurement and our previous work. First, whereas for Zagami we bounced the resonance ions between our twin reflectrons for five round trips before steering them onto the detector, in this experiment we used twelve round trips. The advantage of additional bounces comes from our ability to remove accidental interferences in the time‐of‐flight mass spectrum. We pulse the voltage on one of our reflectron electrodes, making it a good ion reflector for only a few µs during every ~14 µs round trip for mass 87; species with very different masses that might otherwise arrive on the detector at the same time are more efficiently suppressed after a larger number of round trips.

Second, whereas for Zagami we executed a simple raster pattern over a region of the sample, analyzing spots in a rectangular grid of points 200 µm apart, for the Duluth Gabbro we experimented with supplementing a rectangular grid with revisits to the immediate vicinities of points with particularly high Rb/Sr ratios. Analyses with especially high Rb/Sr ratios disproportionately affect the slope of the isochron line, and therefore the age. While there is no guarantee that the points with the highest Rb/Sr ratios will come from minerals whose histories are most reflective of the formation age of the rock, analyzing these doubtless helped our isochron age to converge in reasonable time (each spot analysis included 12 min of specimen conditioning to the ablation laser, and then 4 min of data acquisition; thus, the full analysis that we present here represents over 100 h of instrument operation). A posteriori, we can say that the ages determined with and without these high Rb/Sr spots are consistent with one another within their respective uncertainties.

Results

Using a traditional isochron approach (i.e., correlation of ⁸⁷Rb/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr ratios), we obtain an age for the Duluth Gabbro of 800 ± 300 Ma (Fig. 1). This agrees with the age of 1096 ± 14 Ma that one obtains from the data of Faure et al.,37 recalculated with the ⁸⁷Rb decay constant of 1.396 × 10^–11 a^–1.45 We also can estimate the whole‐rock Rb abundance in our sample of the Duluth Gabbro, by comparing the Rb signals that we observe on the sample with those that we observe on the GSD‐1G standard, which has a Rb concentration of 37 ppm.46 The standard analyses allow us to determine our analytical sensitivity to Rb and how it varied with time, and we use the inferred sensitivity to estimate the Rb concentration in each spot analysis of the Duluth Gabbro. These estimates are shown in Fig. 2; their mean is 4.4 ppm. Thus, we infer that our sample had a mean Rb concentration of ~4 ppm, which coincides with the Rb concentration reported by Faure et al.,37 for their most Rb‐poor lithologies. A similar analysis for Sr gives us an estimate of 160 ppm of Sr, compared with 69 ppm in GSD‐1G.46

Figure 1.

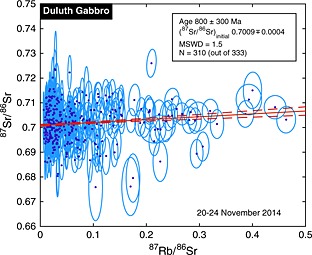
Laser Ablation Resonance Ionization Mass Spectrometry (LARIMS) isochron of lunar analog Duluth Gabbro. Each point is a ~100 µm spot analysis from within a single 1 × 1 cm sample of the Duluth Gabbro. Ellipses show the 1σ confidence intervals; all spot analyses in which ⁸⁵Rb, ⁸⁶Sr, ⁸⁷Sr, ⁸⁷Rb, and ⁸⁸Sr were detected at twice the background level are shown and included in the fit. The age, found from the slope of the best fit line, is within 1σ of previous TIMS measurements of 1096 ± 14 Ma, although the precision is only 300 Ma.37, 45

Figure 2.

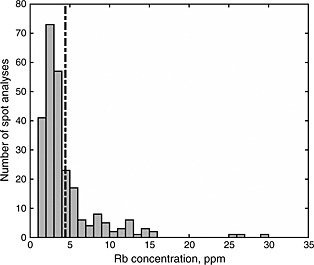
Rb concentrations inferred for spot analyses of the Duluth Gabbro. The histogram shows concentrations for only the spots analyzed during the raster of random positions on the sample; revisits to the vicinities of spots with particularly high Rb/Sr ratios are not included. The mean Rb concentration inferred for our sample is 4.4 ppm (dashed line), which is similar to the lowest Rb concentrations reported in the Duluth Gabbro by Faure et al.37

The isotope ratios conventionally plotted in an ⁸⁷Rb‐⁸⁷Sr isochron are both normalized to ⁸⁶Sr, one of the minor isotopes of Sr. If one could perfectly measure the abundances of all the Sr isotopes, it would be advantageous to normalize the isotope abundances to ⁸⁸Sr instead, simply because the higher count rate for this isotope would yield a smaller fractional uncertainty in the isotope ratios. Presumably, the convention of normalizing to ⁸⁶Sr was developed to mitigate any errors associated with slightly non‐proportional counting of the isotopes; only by comparing isotopes whose abundances are as close together as ⁸⁷Sr and ⁸⁶Sr (~30% apart in most natural materials) could one measure the isotope ratio to five or six significant figures. The precision that we obtain on individual spots, by contrast, is limited to a few percent, mostly by the shot‐to‐shot fluctuations of the ablation laser. We therefore cannot realize the extra precision that could be afforded by normalizing to the minor isotope ⁸⁶Sr.

For this measurement, we sought to learn whether we could improve our precision by normalizing to something other than a minor isotope. ⁸⁸Sr, like ⁸⁶Sr, is neither radioactive nor radiogenic and so, under the usual assumptions inherent in the isochron method, these two isotopes should be distributed in the same way throughout a specimen. ⁸⁸Sr is >8 times more abundant than ⁸⁶Sr, so it would seem a more promising candidate for normalization of the other isotope abundances. However, normalizing to the sum of ⁸⁶Sr and ⁸⁸Sr offers even better counting statistics than normalizing to either isotope alone. In principle, one might think to include ⁸⁴Sr in the normalization as well, but our low signal‐to‐noise ratio on the detection of this ~0.5% abundance isotope makes this not worthwhile. To calculate the ⁸⁷Sr/⁸⁶Sr ratio, we evaluate the ratio of ⁸⁷Sr to the sum of ⁸⁶Sr + ⁸⁸Sr, and then divide by the IUPAC recommended value for the ⁸⁶Sr/(⁸⁶Sr + ⁸⁸Sr) ratio, which is 0.1067.47 Symbolically:

$$\frac{{}^{87}\mathrm{S}\mathrm{r}}{{}^{86}\mathrm{S}\mathrm{r}}={\left(\frac{{}^{87}\mathrm{S}\mathrm{r}}{{}^{86}\mathrm{S}\mathrm{r}{+}^{88}\mathrm{S}\mathrm{r}}\right)}_{\mathrm{\text{measured}}}\cdot {\left(\frac{{}^{86}\mathrm{S}\mathrm{r}{+}^{88}\mathrm{S}\mathrm{r}}{{}^{86}\mathrm{S}\mathrm{r}}\right)}_{\mathrm{\text{known}}}$$ (1)

In introducing the ⁸⁸Sr alongside the ⁸⁶Sr in this way, we found that our instrument was fractionating these two isotopes from one another in a slightly matrix‐dependent way. Figure 3 shows the ⁸⁶Sr/(⁸⁶Sr + ⁸⁸Sr) for spot analyses on the GSD‐1G standard and the Duluth Gabbro. The error‐weighted mean of the standard analyses is 0.10863 ± 0.00005; the difference between this value and the IUPAC value is an indication of commonplace instrumental fractionation, and one reason that we analyze standards alongside our samples. However, the error‐weighted mean of the same isotope ratio for Duluth Gabbro analyses is 0.10772 ± 0.00002; because this value is ~1% lower than for the standard, applying a correction for instrumental fractionation based on the standard analyses would introduce a ~1% error. Though we have not identified the exact mechanism causing this effect in our experiment, one way that matrix dependence could arise in principle is if the ablation plume has a different velocity profile depending on the material being ablated. One might expect this effect to differ in magnitude among the mineral phases that constitute the Duluth Gabbro; however, the effect is too small for us to distinguish minerals from one another without an independent means of identification. We are presently able only to distinguish the Duluth Gabbro from the GSD‐1G standard, which is an amorphous glass. We assume that the matrix effect is mass‐dependent, so when we correct ⁸⁸Sr signals to put standards and samples on the same scale, we apply a correction half as large to the ⁸⁷Sr signals. Though 1% is much smaller than our present age resolution, it is very significant for determining the ⁸⁷Sr/⁸⁶Sr ratio of the non‐radiogenic component.

Just as we included ⁸⁸Sr to minimize uncertainty due to counting statistics, we can further improve our counting statistics by incorporating both the isotopes ⁸⁵Rb and ⁸⁷Rb which occur in a uniform proportion. To calculate the ⁸⁷Rb/⁸⁶Sr ratios for our isochrons, we first evaluate the abundance of ⁸⁷Rb by measuring the sum of ⁸⁵Rb + ⁸⁷Rb and multiplying by the IUPAC recommended ⁸⁷Rb/Rb_total ratio of 0.27835.47 We then evaluate the ⁸⁶Sr abundance by measuring the sum of ⁸⁶Sr + ⁸⁸Sr and multiplying by the IUPAC ⁸⁶Sr/(⁸⁶Sr + ⁸⁸Sr) ratio. Symbolically:

$$\frac{{}^{87}\mathrm{R}\mathrm{b}}{{}^{86}\mathrm{S}\mathrm{r}}={\left(\frac{{}^{85}\mathrm{R}\mathrm{b}{+}^{87}\mathrm{R}\mathrm{b}}{{}^{86}\mathrm{S}\mathrm{r}{+}^{88}\mathrm{S}\mathrm{r}}\right)}_{\mathrm{\text{measured}}}\cdot {\left(\frac{{}^{86}\mathrm{S}\mathrm{r}{+}^{88}\mathrm{S}\mathrm{r}}{{}^{86}\mathrm{S}\mathrm{r}}\right)}_{\mathrm{\text{known}}}\cdot {\left(\frac{{}^{87}\mathrm{R}\mathrm{b}}{{}^{85}\mathrm{R}\mathrm{b}{+}^{87}\mathrm{R}\mathrm{b}}\right)}_{\mathrm{\text{known}}}$$ (2)

As we found among Sr isotopes, we found evidence of matrix‐dependent fractionation between the Rb isotopes, and we corrected for it.

Using the sums of (⁸⁶Sr + ⁸⁸Sr) and (⁸⁵Rb + ⁸⁷Rb) allows us to represent essentially the same isochron, while including more atom counts, potentially improving uncertainty to the extent that we are limited by counting statistics. We obtain the isochron shown in Fig. 4 by evaluating the total Rb in the abscissa ratio and normalizing to the (⁸⁶Sr + ⁸⁸Sr) sum on both axes. The age estimate is 1100 ± 200 Ma, and the intercept is 0.7001 ∓ 0.0009. This age is consistent at the 1σ level with the age determined with a traditional isochron, and also coincides with the age determined by Faure et al.37 with TIMS. These considerations validate our use of total Rb and the (⁸⁶Sr + ⁸⁸Sr) sum in deriving an isochron age. The ⁸⁷Sr/⁸⁶Sr ratio of the non‐radiogenic end member in our analysis differs from the value of 0.7055 ± 0.0003 determined by Faure et al.37 by much more than our statistical uncertainty. The difference, which amounts to 0.6% of the value itself, suggests that our instrumental calibration continues to have errors of this magnitude.

Figure 4.

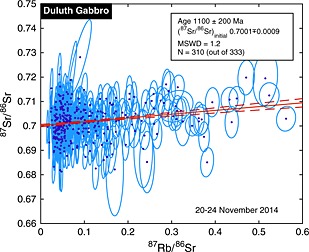
Isochron of the Duluth Gabbro using the sum of ⁸⁶Sr and ⁸⁸Sr for normalization and the total Rb as a proxy for ⁸⁷Rb, as detailed in the text. This minimizes the contribution of counting statistics to our uncertainties. Although our analyses are not primarily count‐limited, this reanalysis improves our precision to the 200 Ma specified by Barney et al.,44 and our result coincides with the TIMS measurement of 1096 ± 14 Ma.37, 45 Ellipses represent 1σ confidence contours. As in Fig. 1, all spot analyses in which ⁸⁵Rb, ⁸⁶Sr, ⁸⁷Sr, ⁸⁷Rb, and ⁸⁸Sr were detected at twice the background level are shown and included in the fit.

Figure 3.

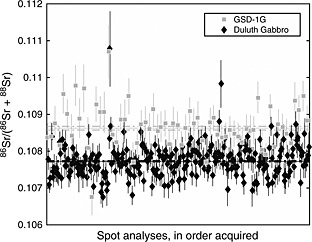
Measurements of the ratio of ⁸⁶Sr to the sum of (⁸⁶Sr + ⁸⁸Sr) in the Duluth Gabbro (black diamonds) and the GSD‐1G standard (gray squares). The IUPAC value for this ratio is 0.1067,47 although our instrumental fractionation generally favors the detection of ⁸⁶Sr over ⁸⁸Sr. The error‐weighted mean ratio for GSD‐1G (gray line) is ~1% higher than for the Duluth Gabbro (black line). These data illustrate that our instrumental fractionation is matrix‐dependent, and we correct our raw signals for this effect. Error bars on each symbol and dashed intervals around each weighted mean represent 1σ confidence intervals.

Despite the incorporation of the (⁸⁶Sr + ⁸⁸Sr) and (⁸⁵Rb + ⁸⁷Rb) sums, our age uncertainty is improved only modestly over using a traditional isochron. This implies that our measurements are not strongly counting‐limited, even on a sample with 160 ppm Sr and only 4 ppm Rb. Instead the precision of individual spot analyses is limited by shot‐to‐shot fluctuations in the pulse energy of the ablation laser, which cause fluctuations in the relative abundances of Rb and Sr in the plume of ablated neutrals. We also observe a slow drift, over tens of minutes to hours, in the instrumental fractionation of Rb from Sr.^[e.g., 29 ^] We presently account for this drift by interpolating between successive measurements of standards to estimate instrumental fractionations at the time that each spot analysis is made, but the interpolation introduces its own uncertainty of several percent. We stress, however, that in spite of this drift, we have achieved age precision on the Duluth Gabbro that meets the NASA Technology Roadmap benchmark.44

Although our measurements in this experiment are not counting‐limited, we nevertheless prefer to use the sums of (⁸⁵Rb + ⁸⁷Rb) and (⁸⁶Sr + ⁸⁸Sr) in our isochron analysis to keep the uncertainty arising from counting statistics as small as possible. To further validate this approach, we reanalyzed our Zagami data and obtained new results for our two completed measurements of 300 ± 90 Ma (N = 238) and 400 ± 200 Ma (N = 224; see Fig. 5), both within 1.5σ of the TIMS result. However, we also had two incomplete and imprecise measurements of only 35 and 85 points, respectively, on Zagami. Renormalizing data from the shorter of these short runs yielded an inaccurate isochron age.

Figure 5.

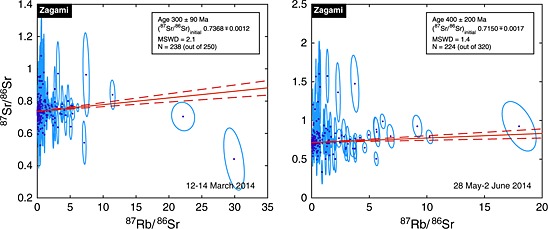
Isochrons of completed Zagami measurements from Anderson et al.,29 recalculated using the sum of ⁸⁶Sr and ⁸⁸Sr for normalization and the total Rb as a proxy for ⁸⁷Rb, as described in the text. The ages shown here are similar to those reported by Anderson et al.,29 using traditionally constructed isochrons: 280 ± 100 Ma for the March run (left) and 400 ± 200 Ma for the May–June run (right). They are also consistent at the <1.5σ level with the TIMS result of 166 ± 6 Ma from Borg et al.28 Ellipses represent 1σ confidence contours. As in Fig. 1, all spot analyses in which ⁸⁵Rb, ⁸⁶Sr, ⁸⁷Sr, ⁸⁷Rb, and ⁸⁸Sr were detected at twice the background level are shown and included in the fit.

Discussion

The analysis of the Duluth Gabbro was more technically challenging than our dating of Zagami,29 chiefly because of the smaller range of Rb/Sr ratios that we encountered in the specimen. The Rb abundances in the two samples are similar, and the Sr abundance that we find in the Duluth Gabbro is actually several times larger than in Zagami.28 The abundances of the elements of interest would therefore seem to make the Duluth Gabbro a more inviting analytical target. However, as we have seen, the uncertainty in our age determinations does not appear to be dominated by counting statistics. Instead, we appear to be limited by the mineral‐to‐mineral range of Rb/Sr ratios. A wider spread of Rb/Sr ratios essentially provides a longer lever arm to the isochron line, better constraining its slope, and thus the sample age.

For Zagami, Borg et al.28 reported a range of ⁸⁷Rb/⁸⁶Sr ratios up to ~2 in their acid leachate residues, whereas we found a few spots (<5% of all analyses) in our specimen with ⁸⁷Rb/⁸⁶Sr ratios between 5 and 25. Few of these spots yielded very high precision. However, even modest precision on such points placed considerable constraint on the slope of the isochron line. For the Duluth Gabbro, by contrast, we observed a smaller range of ⁸⁷Rb/⁸⁶Sr ratios, extending only up to 0.6. This is smaller than the range of ⁸⁷Rb/⁸⁶Sr ratios reported for the Duluth Gabbro by Faure et al.,37 although their analyses were of whole rock samples. Of greater significance for in situ dating of the Moon is that our observed range of ⁸⁷Rb/⁸⁶Sr ratios is smaller than the range reported by Shih et al.38 for mineral separates from an Apollo 17 KREEP basalt clast. In view of the limited range of ⁸⁷Rb/⁸⁶Sr ratios, it is noteworthy that we achieved similar absolute precision in dating the Duluth Gabbro to that we obtained for Zagami, and that our precision meets the technical requirement (≤200Ma) of the NASA Technology Roadmap.44

One potential concern that arose from our Zagami measurement was whether the age uncertainty that we reported, which was 100–200 Ma in our longest analytical runs, should be viewed in absolute terms or relative to the ~170 Ma absolute age of the meteorite (Borg et al.28 reported the age of Zagami as 166 ± 6 Ma). In absolute terms, an age determination with such precision is meaningful because it excludes >95% of Solar System history as the time of origin for this meteorite. However, if viewed in relative terms, an uncertainty that is nearly as large as the age of the sample would render an age determination meaningless for materials from the first half of solar system history. The present work shows that our uncertainty is, indeed, better understood in absolute terms than as a fractional error. We achieved nearly the same precision in the age of the Duluth Gabbro as we had for Zagami, in spite of the sample being six times older.

Our analysis of the Duluth Gabbro also demonstrates our instrumental capability in another way. Since each individual spot analysis that we acquire has relatively low precision, it is possible to look at our Zagami isochron and see essentially no correlation between the ⁸⁷Rb/⁸⁶Sr ratios that we measured throughout the specimen and the corresponding ⁸⁷Sr/⁸⁶Sr ratios. In fairness, since the specimen is so young, that is indeed what one would expect from a proper isochron: the extent to which the ⁸⁷Sr/⁸⁶Sr and ⁸⁷Rb/⁸⁶Sr ratios should correlate is quite small, because there has been so little time for radiogenic ⁸⁷Sr to accumulate since the formation of the specimen (i.e., the slope of the isochron line should be only 0.0025 for a 166 Ma age; Fig. 5). In other words, for a very young sample, measuring Rb and Sr isotope ratios imprecisely should show that the ⁸⁷Sr/⁸⁶Sr and ⁸⁷Rb/⁸⁶Sr ratios are nearly independent of one another. By contrast, it is quite clear from Figs. 1 and 4 that, in the case of the Duluth Gabbro, the sample is old enough for us to see a definite correlation between the ⁸⁷Sr/⁸⁶Sr and ⁸⁷Rb/⁸⁶Sr ratios. This is an expression of the precision in our age determination, which resolves the age from zero by more than 5σ.

Conclusions

Our work shows that the LARIMS technique, an approach that can be miniaturized for spaceflight, can successfully determine the age of an analog for rocks on much of the nearside of the Moon. We have successfully demonstrated a measurement of 1100 ± 200 Ma for the Duluth Gabbro, coincident with the TIMS age of 1096 ± 14 Ma,37, 45 and with the 200 Ma precision specified by Barney et al.44 These results place one‐third of the nearside of the Moon within the technical capability of LARIMS, allowing us to address major scientific questions regarding the history of the Moon and the inner solar system. Our work highlights the important role that in situ dating has to play on the Moon, Mars or other planetary bodies, whether as a standalone achievement, or to triage samples for ultimate return to Earth.

In order to resolve the science questions regarding the history of the Moon, and in light of the Duluth Gabbro results, we recently proposed a Discovery mission called MARE: The Moon Age and Regolith Explorer. We fully expect the results from MARE to: (1) revolutionize our understanding of the impact history of the inner solar system, and (2) provide new insights into the evolution and differentiation of the interiors of one‐plate planets. MARE would accomplish these goals by landing on a young, nearside lunar basalt flow southwest of Aristarchus that has a crater density corresponding to a highly uncertain absolute age, collecting >10 rock samples, and assessing their radioisotopic age, geochemistry, and mineralogy. The core of the MARE instrument suite is the LARIMS‐based Chemistry and Dating EXperiment (CDEX) instrument, which is complemented by tools that have successfully flown in space: a robotic arm similar to the arm on the Phoenix Lander,48, 49 a grinder like those aboard the Mars Exploration Rovers,50 a camera based on the Mars Science Laboratory's MAHLI,51 and an infrared spectrometer like those aboard the Mars Exploration Rovers and OSIRIS‐REX.52 These instruments would be delivered to the lunar surface by a Johnson Space Center spacecraft derived from the Morpheus lander testbed53 and outfitted with a proven Autonomous Landing and Hazard Avoidance Technology (ALHAT) precision landing system.54 The lander and ALHAT have a track record of 14 successful integrated test flights as well as fully autonomous landings with one meter landing accuracy. In conjunction with crater counts of the Aristarchus region, new dates from these young basaltic flows would redefine the chronology models forming the foundation upon which the history of the inner solar system is built. Similarly, new compositional data on young lunar basalts will clarify the evolution of thermo‐magmatic processes in the Moon, which in turn underpins the models for the internal dynamics of other one‐plate planets. Both these outcomes address explicit priorities of the most recent planetary science Decadal Survey.55

In preparation for this effort, we have miniaturized the bench‐top LARIMS system to a second prototype that is 40 cm × 50 cm × 180 cm in size, with lasers >100 times smaller than the prototype instrument used in this work. Incorporating a custom‐made mass spectrometer, electronics, and laser systems to be built specifically for flight in space, we have designed an instrument that is an additional factor of ~25 smaller, which could fit on a Mars or Moon lander. Moreover, because the spaceflight lasers have a higher repetition rate than those that we use now, the data acquisition rate of these new designs is 250 times faster than those of our current prototype.

In the future, we will continue to analyze samples of increasing difficulty and relevance to planetary science, and assess other isotopic systems that could be used for in situ radioisotopic dating on other solar system bodies.

Scott Anderson, F. , Levine, J. and Whitaker, T. J. (2015) Rb‐Sr resonance ionization geochronology of the Duluth Gabbro: A proof of concept for in situ dating on the Moon. Rapid Commun. Mass Spectrom., 29: 1457–1464. doi: 10.1002/rcm.7253.