Global patterns and controls of soil organic carbon dynamics as simulated by multiple terrestrial biosphere models: Current status and future directions

Abstract

Soil is the largest organic carbon (C) pool of terrestrial ecosystems, and C loss from soil accounts for a large proportion of land‐atmosphere C exchange. Therefore, a small change in soil organic C (SOC) can affect atmospheric carbon dioxide (CO₂) concentration and climate change. In the past decades, a wide variety of studies have been conducted to quantify global SOC stocks and soil C exchange with the atmosphere through site measurements, inventories, and empirical/process‐based modeling. However, these estimates are highly uncertain, and identifying major driving forces controlling soil C dynamics remains a key research challenge. This study has compiled century‐long (1901–2010) estimates of SOC storage and heterotrophic respiration (Rh) from 10 terrestrial biosphere models (TBMs) in the Multi‐scale Synthesis and Terrestrial Model Intercomparison Project and two observation‐based data sets. The 10 TBM ensemble shows that global SOC estimate ranges from 425 to 2111 Pg C (1 Pg = 10¹⁵ g) with a median value of 1158 Pg C in 2010. The models estimate a broad range of Rh from 35 to 69 Pg C yr⁻¹ with a median value of 51 Pg C yr⁻¹ during 2001–2010. The largest uncertainty in SOC stocks exists in the 40–65°N latitude whereas the largest cross‐model divergence in Rh are in the tropics. The modeled SOC change during 1901–2010 ranges from −70 Pg C to 86 Pg C, but in some models the SOC change has a different sign from the change of total C stock, implying very different contribution of vegetation and soil pools in determining the terrestrial C budget among models. The model ensemble‐estimated mean residence time of SOC shows a reduction of 3.4 years over the past century, which accelerate C cycling through the land biosphere. All the models agreed that climate and land use changes decreased SOC stocks, while elevated atmospheric CO₂ and nitrogen deposition over intact ecosystems increased SOC stocks—even though the responses varied significantly among models. Model representations of temperature and moisture sensitivity, nutrient limitation, and land use partially explain the divergent estimates of global SOC stocks and soil C fluxes in this study. In addition, a major source of systematic error in model estimations relates to nonmodeled SOC storage in wetlands and peatlands, as well as to old C storage in deep soil layers.

Key Points

• Simulated historical (1901–2010) SOC dynamics vary largely among models

• Ten TBMs agree that climate and land use change have reduced SOC stocks

• Rising CO₂ and N deposition are prone to increase SOC with varying magnitudes

1. Introduction

Soils contain 4.5 times the amount of carbon (C) contained in terrestrial biomass [Jobbagy and Jackson, 2000], and soil C change is one of the largest unknowns in the global C budget [Ciais et al., 2014]. The amount of soil organic carbon (SOC) represents the net balance between C inputs in the form of leaf, stem, and root litter and C outputs including the decomposition of C by soil microbes as well as C loss to downwind or downstream systems [Davidson and Janssens, 2006; Regnier et al., 2013; Tian et al., 2015]. A small change in the processes governing SOC provides feedback to atmospheric carbon dioxide (CO₂) and methane (CH₄) concentrations. In terrestrial ecosystems, SOC affects both soil physical properties such as soil structure and aggregation [Lal, 2001], thermal conductivity, soil moisture conditions, soil nutrient availability, and soil biota. Indirectly, SOC thus controls plant growth and food production [Lal, 2004]. In these ways, SOC is a key component for estimating the global C budget in the terrestrial biosphere as well as a nexus of the interactions among climate, ecosystems, and humans.

The SOC is not a homogeneous pool [Banger et al., 2010; Koarashi et al., 2009] but consists of a continuum of thousands of different C compounds from simple sugars to complex humified molecules, with mean residence times (MRT) ranging from hours to millennia. Various factors such as vegetation type and productivity [Ren et al., 2012], temperature [Davidson and Janssens, 2006], soil moisture [Ryan and Law, 2005], soil properties and nutrient [Tian et al., 2010], and disturbance regimes such as land use change [Post and Kwon, 2000] and fire [Harden et al., 2000] can affect the size of SOC pools (Figure 1). Mediated by soil microbes, heterotrophic respiration (Rh) is the dominant pathway of SOC loss. In contrast to the assumptions of conventional first‐order decomposition models [Parton et al., 1987], SOC decomposition rates should depend not only on the SOC stock size but also on the size and composition of the decomposer microbial pool [Schimel and Weintraub, 2003] as well as carbon‐mineral interactions [Six et al., 2002]. In addition, various biophysical and physiochemical factors can influence Rh, which makes it even more difficult to realistically quantify the decomposition of SOC [Davidson and Janssens, 2006]. Therefore, the magnitude and dynamics of SOC stocks and Rh across the globe are still far from certain. In the Coupled Model Intercomparison Project (CMIP5) involving 11 coupled carbon‐climate models (Earth System Models (ESMs)), Todd‐Brown et al. [2013] reported that SOC varied sixfold between ESMs, from 510 to 3040 Pg C during 1995–2005. In their study, only 6 out of 11 model estimates were within the range of the Harmonized World Soil Database (HWSD)'s estimate of 1260 Pg C (with a 95% confidence interval of 890–1660 Pg C), and spatial correlation coefficients between modeled and empirical SOC estimates at 1° resolution were <0.4, indicating that variations in the spatial distribution of SOC are not well represented by ESMs [Todd‐Brown et al., 2013].

Figure 1.

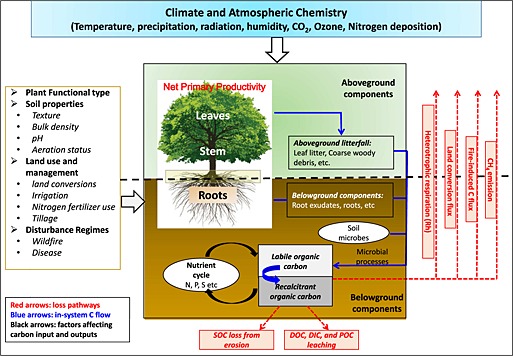
Framework of major processes and controls for soil organic carbon storage and fluxes in terrestrial ecosystems.

Uncertainties in the modeled SOC estimates may arise from model structure, parameterization, and driving data sets such as climate, soil properties, and land use. One of the major uncertainties in model structure is the representation of the belowground C processes that vary significantly in different models [Johnston et al., 2004]. In addition, nutrient limitation (nitrogen and phosphorus) of net primary production and microbial activities is another structural uncertainty but being ignored or poorly represented by most models [Zaehle et al., 2005; Thornton et al., 2009; Goll et al., 2012]. Some uncertainties come from the errors in the observations/measurements used for the parameterization and/or from scale mismatch between measured processes and the scale of global models [Zaehle et al., 2005].

Another uncertainty is derived from the climate sensitivity of soil respiration, which has been extensively studied through field experiments, laboratory incubations, and ecosystem modeling [Davidson and Janssens, 2006; Giardina and Ryan, 2000]. How changes in soil microclimate could alter SOC decomposition is still under debate. First, climate conditions can affect enzyme activity with respect to activation energy but can also influence plant primary productivity, C entering the soil pool, substrate quality and accessibility, and nitrogen mineralization [Davidson and Janssens, 2006]. Second, temperature and precipitation covary with other environmental constraints (e.g., soil aeration, soil properties, and vegetation types), which influence the litter quality and the ratio of labile and recalcitrant SOC components. The modeled climate sensitivities of SOC decomposition are highly dependent on model structure and assumptions, which may, in part, reflect complex biogeochemical processes in the real world and be able to explain different model behaviors in simulating SOC stock change.

In this study, we examined the global SOC stocks and Rh estimated by 10 terrestrial biosphere models (TBMs) with different structures, assumptions, and parameterization schemes driven by the same land use and climate forcing to explore the disagreement among models and the potential reasons responsible for model‐data mismatch. The SOC benchmark data we used include global and regional inventory‐based SOC data sets (HWSD version 1.21 [Food and Agriculture Organization/International Institute for Applied Systems Analysis/International Soil Reference and Information Centre/Institute of Soil Science‐Chinese Academy of Sciences/Joint Research Centre, 2012], Northern Circumpolar Soil Carbon Database (NCSCS) [Tarnocai et al., 2009], and the Unified North American Soil Map (UNASM) [Liu et al., 2013]). Specific objectives of this study were (1) to estimate the magnitude and dynamics of SOC stocks and Rh across the globe, (2) to identify the regions with highest uncertainties (model divergence) in the SOC stocks and Rh estimates, (3) to quantify the relative contributions of major environmental changes to SOC stock and its residence time, (4) to examine the key processes being underrepresented in models but potentially leading to divergent SOC estimates, and (5) to provide recommendations for reducing uncertainties in the SOC stock estimates in the future.

2. Methods and Data

Our analysis included modeling results from 10 TBMs that participated in the North American Carbon Program Multi‐scale synthesis and Terrestrial Model Intercomparison Project (MsTMIP) [Huntzinger et al., 2013; Wei et al., 2014b] and that were released under MsTMIP version 1 [Huntzinger et al., 2015]. The model ensemble includes Biome‐BGC [Thornton et al., 2002], CLM [Mao et al., 2012], CLM4VIC [Lei et al., 2014], DLEM [Tian et al., 2012], GTEC [Post et al., 1997], ISAM [Jain et al., 2009; El‐Masri et al., 2013], LPJ [Sitch et al., 2003], ORCHIDEE‐LSCE (ORCHIDEE thereafter[ Krinner et al., 2005]), VEGAS2.1 [Zeng et al., 2005], and VISIT [Ito, 2010]. The models were driven by the same environmental input database including climate, atmospheric CO₂ concentration, atmospheric nitrogen deposition, and land use and land cover changes during 1901–2010. Two exceptions are LPJ and VEGAS2.1 that used dynamic vegetation scheme rather than the prescribed land use maps to depict changes in natural vegetation. Global simulations were conducted at a 0.5° spatial resolution with similar forcing data, spin‐up procedure, and boundary conditions fixed across all models. In this study, model‐based estimates of SOC, Rh, and net primary productivity (NPP) were derived from each model's “best estimate” for which four models (i.e., CLM, CLM4VIC, DLEM, and ISAM) with all time‐varying driving forces “turned on” (BG1 experiment; Table 1), while the rest of the models ran in a similar mode except nitrogen deposition being “turned off” (SG3 experiment). Therefore, by following a prescribed forcing data and simulation protocol, we were able to explore the estimation uncertainties caused by differences in model structure. The model estimated SOC includes organic C stored in soil and litter pools. We assumed that Rh is the dominant pathway for carbon loss (equation (1)) and determined the MRT (equation (2)) at annual time step as the ratio of SOC stock to annual Rh, which was used in this study to assess the stability of SOC pool suggested by the MsTMIP multimodel ensemble.

$$C_{\text{loss}}=Rh=k\times \mathrm{S}\mathrm{O}\mathrm{C}$$ (1)

$$\mathrm{M}\mathrm{R}\mathrm{T}=\frac{1}{k}=\frac{\mathrm{S}\mathrm{O}\mathrm{C}}{\mathrm{R}\mathrm{h}}$$ (2)

where k is the SOC decay rate and MRT is the mean residence time across all the soil C pools and their respective residence times. In reality, the k value is affected by Rh, and other soil C loss ways such as fire emission, soil erosion, disturbance impacts on SOC as well as on dead C pools, and C export to river headstreams. However, except SOC decomposition, no other information is available in MsTMIP data products for identifying the proportions of these terrestrial C losses directly from the soils. Therefore, we assumed that Rh is the only outgoing SOC flux in all TBMs to calculate SOC residence time. The HWSD data set used in this study is modified by following the methods in Todd‐Brown et al. [2013]. Soil organic C for the topsoil and subsoil was calculated by using bulk density and organic carbon content and removing gravel content. The bulk density data from HWSD for Andosol and Histosol was replaced with data from Batjes [2009].

Table 1.

Design of MsTMIP Simulation Experiments

Name	Description	Time Period	Climate Forcing	Land Use History	Atmospheric CO2	Nitrogen Deposition
RG1	Reference	1901–2010	Constant	Constant	Constant	Constant
SG1	Climate	1901–2010	CRU + NCEPb	Constant	Constant	Constant
SG2	Climate + LUCC	1901–2010	CRU + NCEP	Time‐varying	Constant	Constant
SG3	Climate + LUCC + CO2	1901–2010	CRU + NCEP	Time‐varying	Time‐varying	Constant
BG1	Climate + LUCC + CO2 + Ndepa	1901–2010	CRU + NCEP	Time‐varying	Time‐varying	Time‐varying

^aLUCC and Ndep denote land use and cover change, and nitrogen deposition, respectively.

^bCRU is abbreviation for Climate Research Unit and NCEP is National Centers for Environmental Prediction.

We examined temporal changes of modeled global SOC stocks as difference between the year 2010 and 1901 due to small interannual variability in SOC. However, the changes of C fluxes (i.e., NPP and Rh) are quantified as the differences of decadal average value between the 2000s and 1900s given large interannual variability in C fluxes. The consistent design of model experiments made us able to distinguish and quantify the relative contributions of climate, land use, atmospheric CO₂ concentration, and nitrogen deposition to SOC and MRT changes by calculating the differences between experiments (Table 1).

We used Pearson's correlation to evaluate relationship between the modeled Rh and climate variables, and the NCAR Command Language (NCL) is used to generate the Taylor diagram.

3. Results

3.1. Modeling Estimates of Global SOC Stocks and Rh

From the 10 TBM ensembles, in the year of 2010, the global SOC stock appears to range from 425 to 2111 Pg C (1 Pg = 10¹⁵ g) with a median value of 1158 Pg C, which is close to 1255 Pg C (891–1657 Pg C) estimated by HWSD database (Table 2). The lowest SOC estimates were from CLM (643 Pg C) and CLM4VIC (425 Pg C) and the highest (2111 Pg C) by Biome‐BGC. In the 10 TBMs, Rh values ranged 35–69 Pg C yr⁻¹ with a median value of 51 Pg C yr⁻¹ during 2001–2010. Variations in the SOC and Rh resulted in a MRT range from 12 to 35 years during 2001–2010. The MRT estimates from this study were in the previously reported range (10.8–39.3 years) by 11 ESMs during 1995–2005 [Todd‐Brown et al., 2013].

Table 2.

Global SOC Estimates From Inventory Database and MsTMIP Terrestrial Biosphere Model Ensemble

Database/	Resolution	Soil Depth	No. of Soil + Litter Pools	Global Soil Carbon
Model		(m)		(Pg C)
HWSD	30 arc sec	1		1255 (891, 1657)
Updated HWSD	0.5 × 0.5	1		1400
NCSCD	0.25 × 0.25 (circumpolar permafrost)	1		495.8
		3		1024
BIOME‐BGC	0.5 × 0.5	not available (NA)	4 + 3	2111
CLM	0.5 × 0.5	NA	4 + 3	643
CLM4VIC	0.5 × 0.5	NA	4 + 3	425
DLEM	0.5 × 0.5	1	5 + 5	1023
GTEC	0.5 × 0.5	NA	4 + 0	1155
ISAM	0.5 × 0.5	3.5	4 + 4	1045
LPJ	0.5 × 0.5	1.5	3 + 0	1496
ORCHIDEE	0.5 × 0.5	2	3 + 3	1160
VEGAS	0.5 × 0.5	NA	6 + 0	1547
VISIT	0.5 × 0.5	NA	3 + 6	1488
Model range				425–2111
Model median				1158

3.2. Spatial Variation of the Modeled SOC Stock and Rh

3.2.1. Soil Organic Carbon

Median estimate of model ensembles indicate a SOC density above 10,000 g C m⁻² in the high‐latitude regions but with a cross‐model standard deviation close to or even larger than the SOC estimate itself (Figure 2 and Figure S1 in the supporting information). Tropical areas are also characterized by high SOC density with model median ranging from 6000 to 16,000 g C m⁻² and a smaller model spread compared to high‐latitude regions. Median SOC estimate from model ensembles is quite comparable to the spatial distribution of soil carbon storage indicated by the HWSD across the globe. However, compared to the NCSCD database in 1 m depth, neither HWSD nor TBM ensemble could capture the high SOC density (larger than 20,000 g C m⁻²) in high‐latitude regions (Figure 2). Spatially, SOC estimates from individual models are poorly consistent (grid to grid correlation, r < 0.4) with HWSD data at half‐degree grid level (Figure 3). A few of them show similar amplitude of variation as HWSD (i.e., normalized standard deviation, grid‐wise estimates deviated from mean value, is close to 1). However, it should be noticed that HWSD is a statistical model result so it cannot really be used to infer that modeled patterns are wrong since the geostatistical method used in HWSD could also have systematic errors.

Figure 2.

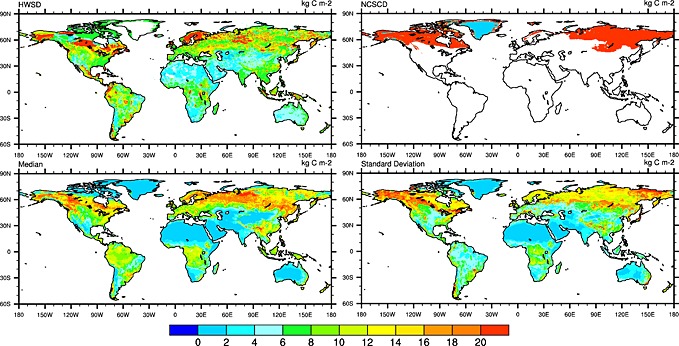
The spatial distribution of SOC density (kg C m⁻²) as estimated by Harmonized World Soil Database (HWSD), Northern Circumpolar Soil Carbon Database (NCSCS), and median and standard deviation estimated by 10 terrestrial biosphere models in 2010.

Figure 3.

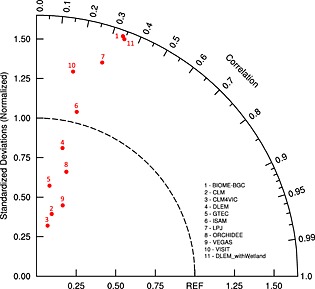
Spatial comparisons of 10 TBM estimated SOC stocks distributions with Harmonized World Soil Database (HWSD). Point 11 shows DLEM estimate considering SOC storage in wetlands and peatlands.

We examined the SOC stocks across the latitudinal gradients (Figure 4). The 10 TBM ensembles agree that SOC stock peaks in the 40–65°N band where large model divergence of SOC estimates exists, ranging from 5 to 30 Pg C per half‐degree strip. The second peak of SOC stock is in the equatorial area where the 10 TBMs show a comparatively narrower range for SOC estimates. Except for high (e.g., Biome‐BGC and LPJ) and low outliers (e.g., CLM and CLM4VIC), most TBMs obtain SOC stock estimates close to the HWSD.

Figure 4.

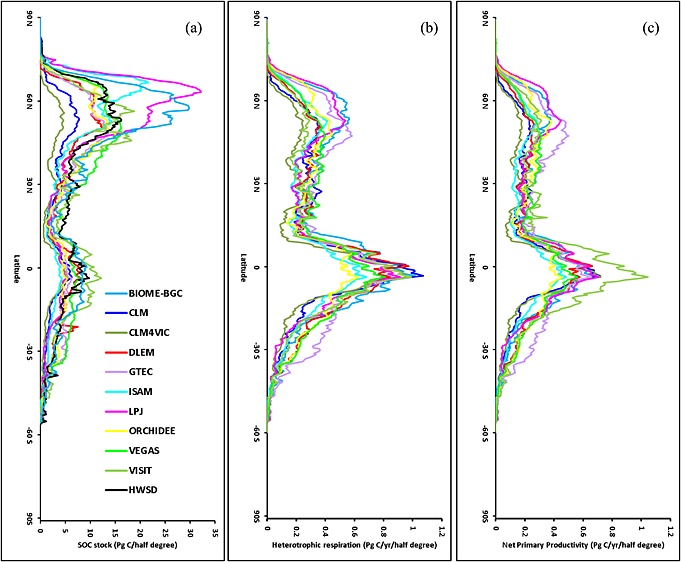
The estimated (a) SOC in the year of 2010, and (b) Rh, and (c) NPP averaged during the 2000s from 10 TBMs and Harmonized World Soil Database (HWSD) along 0.5° latitudinal band.

3.2.2. Heterotrophic Respiration

TBM ensemble median shows maximum Rh values (>1000 g C m⁻² yr⁻¹) in tropical areas including Amazon, Middle Africa, and Southeast Asia, followed by boreal regions including northern parts of Euro‐Asia and North America (Figure 5 and Figure S2 in the supporting information). The highest cross‐model divergence is found in tropical areas with standard deviation larger than 500 g C m⁻² yr⁻¹ in some areas. Along the latitudinal gradient, Rh peaks in 10°N–20°S followed by a secondary peak in 40–65°N in all the 10 TBMs (Figure 4). In general, the pattern of Rh is roughly similar to that of NPP, suggesting that SOC decomposition is primarily limited by C substrate and that Rh and NPP are colimited by biophysical conditions such as climate, soil moisture, and vegetation composition in the model ensemble.

Figure 5.

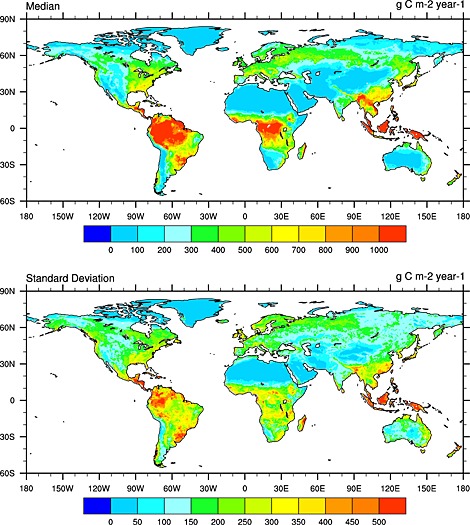
(top) The spatial distribution of median Rh (g C m⁻² yr⁻¹) in the 2000s as estimated by the 10 terrestrial biosphere models and (bottom) cross‐model standard deviation.

The median estimate of TBM ensembles shows higher SOC stability in the high‐latitude regions and Tibetan Plateau with MRT larger than 50 years (Figure 6 and Figure S3 in the supporting information). It could be explained by large SOC stocks and low Rh in cold environment. However, cross‐model divergence of MRT estimates is also very large in these areas primarily due to divergent model estimates of SOC. In contrast, most models show an agreement that tropical soils have MRT less than 20 years due to higher Rh stimulated by abundant heat and water resources. This pattern is consistent with that of ecosystem C residence time revealed by Carvalhais et al. [2014].

Figure 6.

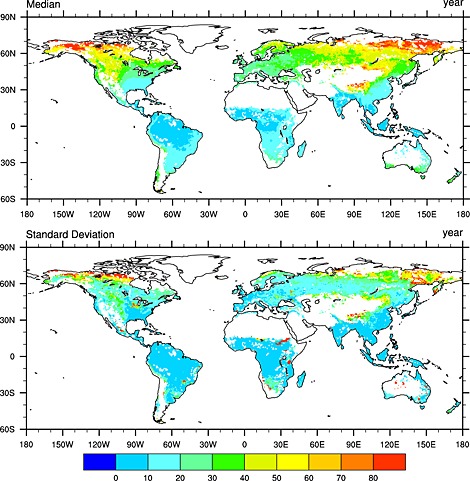
The spatial distribution of mean residence time (year) as estimated by 10 terrestrial biosphere models: (top) model ensemble median and (bottom) standard deviation.

3.3. Changes in the Modeled Global SOC Stocks and Rh During 1901–2010

During 1901–2010, the 10 TBMs indicate that terrestrial annual NPP and Rh have increased by a median value of 6.5 Pg C (range: 2.6–11.1 Pg C) and 3.2 Pg C (range: 0.2–8.0 Pg C), respectively (Table 3). The modeled SOC change during 1901–2010 ranges from −70 Pg C (GTEC) to 86 Pg C (VISIT). Five models (Biome‐BGC, GTEC, ISAM, LPJ, and VEGAS) suggest that SOC stocks have decreased by a magnitude ranging from 7 to 70 Pg C during the study period. However, the rest five models estimate an increase in SOC stock, which varies from 14 Pg C in CLM to 86 Pg C in VISIT. Overall, the model ensembles have shown that MRT has decreased by 3.4 years over past 100 years, which is driven by either increment of fast substrate availability (increase in both Rh and NPP) or reduced SOC stability in response to environmental changes (Figure 7).

Table 3.

Model‐Estimated Changes in Soil Organic Carbon (SOC) Storage, Heterotrophic Respiration (Rh), and Net Primary Production (NPP) During 1901–2010

Change	ΔSOC	ΔRha	ΔNPPa
	(Pg C)	(Pg C/yr)	(Pg C/yr)
BIOME‐BGC	−7.2	1.8	2.8
CLM	14.0	3.7	5.9
CLM4VIC	16.0	3.1	5.0
DLEM	26.7	5.1	7.0
GTEC	−70.2	2.2	8.7
ISAM	−17.2	3.2	4.1
LPJ	−18.9	1.8	7.7
ORCHIDEE	39.2	8.0	11.1
VEGAS	−37.9	0.17	2.6
VISIT	85.9	7.0	10.7
Model range	[−70.2–85.9]	[0.17–8.0]	[2.6–11.1]
Median	3.39	3.16	6.48

^aΔRh and ΔNPP are the different in Rh and NPP, respectively between the 2000s and the 1900s.

Figure 7.

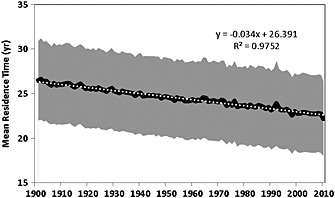
Temporal evolution of the annual mean residence time (SOC stock/Rh) estimated by 10 TBM ensemble median during 1901–2010. The model simulations used here are forced by land use, CO₂, and climate (and for models with a nitrogen cycle by N‐deposition maps). The gray area is 95% confidence interval of MRT estimate. The solid black line is the model‐ensemble median, and the white dotted line is the linear regression of annual MRT.

3.4. Modeling Attribution of Global SOC and MRT Change During 1901–2010

To further understand the underlying mechanisms for SOC changes during 1901–2010, we have quantified contributions of climate, land use, atmospheric CO₂ concentration, and nitrogen deposition to changes of SOC stock and MRT based on 10 TBMs. In general, all the models agree that climate and land use changes have decreased SOC stocks, while elevated atmospheric CO₂ and nitrogen deposition increased SOC stocks though the response varied significantly among different models (Figure 8a). Among the 10 TBMs, GTEC shows the highest decrease in SOC stocks due to climate (29 Pg C) and land use changes (92 Pg C) during 1901–2010. The highest response to rising CO₂ concentration was found in VISIT (96 Pg C) followed by ORCHIDEE (53 Pg C) and GTEC (69 Pg C). However, CLM and CLM4VIC have the smallest SOC response to climate, land use, and rising CO₂ concentration. Atmospheric nitrogen deposition stimulated SOC stocks by 14–17 Pg C over the past 110 years, close to or even larger than the impacts of rising CO₂ concentration in three models (CLM, CLM4VIC, and DLEM), which have reported the impacts of atmospheric nitrogen input in their simulation experiments. Four (i.e., CLM4VIC, DLEM, ORCHIDEE, and VISIT) out of 10 models have shown close or smaller relative contribution of land use change to SOC stocks than climate.

Figure 8.

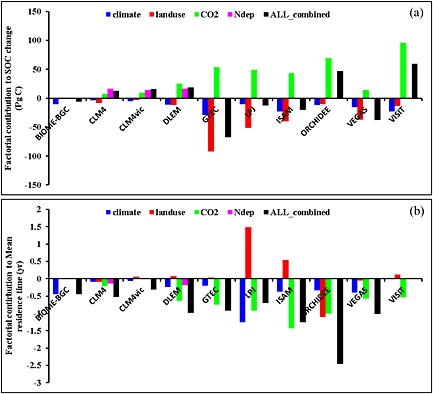
Contribution of climate, land use change, rising CO₂ concentration, and atmospheric nitrogen deposition to changes in (a) SOC stocks and (b) mean residence time (MRT) as estimated by different models during 1901–2010. Because of interaction effect, the differences between all‐combined and ∑ (climate, LUC, CO₂, and N deposition) are not zero.

All the TBMs agree that the MRT of global SOC pool decreased due to climate change and elevated atmospheric CO₂ concentration but varied in magnitude (Figure 8b). Eight models (except Biome‐BGC and CLM4VIC) from which the relative contribution of rising atmospheric CO₂ can be diagnosed showed that Rh and SOC stocks both increased under elevated CO₂ concentration. Therefore, the CO₂‐induced MRT reduction may be explained by an increment of the fast substrate (low MRT) fraction, which is supported by the model estimated NPP increase (i.e., accelerated carbon cycling), rather than by a net SOC reduction. C‐N coupled models show that nitrogen deposition tends to lead to a reduction in MRT that is likely derived from fast carbon cycling (i.e., causal increase in NPP and Rh) and/or increased soil decomposition due to nitrogen enrichment. TBMs differ in estimating impact of land use change on SOC. Six models show that land use increased MRT because NPP and Rh both decreased more than the SOC when natural ecosystems are replaced by cultivated ones, implying a decelerating C cycling. Three models (CLM, ORCHIDEE. and VEGAS) show Rh increased, while SOC decreased due to land use change, leading to a reduction in MRT. Their estimates suggest that SOC pool is less stable when land conversion took place or these models have a NPP of cultivated PFTs, which is higher than that of the natural PFTs that they replaced. Another likely reason is that they remove agriculturally harvested biomass, reducing SOC input, and thus SOC pool size in newly cultivated cropland. Overall, to better interpret SOC dynamics and their feedback to climate system, more information from both modeling group and field experimental evidence are needed to distinguish responses of labile and passive SOC pools to environmental changes.

4. Discussion

Accurate assessment of SOC stocks is essential for predicting the important ecological functions and understanding the impact of environmental changes on carbon‐climate feedback. To our knowledge, this study is the first to compare SOC and Rh from terrestrial biosphere models driven by the same land use and climate forcings, as well as constrained by uniform equilibrium standards. The global SOC stock estimated in this study (median value of 1158 Pg C with a range of 425–2111 Pg C) is slightly narrower but comparable to the estimates (median value of 1410 Pg C with a range of 510–3040 Pg C) from 11 ESMs presented in Todd‐Brown et al. [2013]. However, Todd‐Brown et al. [2013] did not examine long‐term SOC dynamics that appear to diverge among model estimations in the MsTMIP ensemble (Table 3). In this study, we have tried to identify the possible reasons responsible for different magnitude and spatiotemporal variations of SOC stock estimates from multimodel ensembles.

4.1. Major Divergences in the Modeled Initial SOC Stocks

Our analysis has shown that in the first simulation year (1901) global SOC stocks varied from 409 to 2118 Pg C while 110‐year SOC change from each model only accounted for <6% of the initial SOC stock (Table 3). Using data from the Coupled Model Intercomparison Project (CMIP5; three of the ESMs having the same land surface models as those participating to MsTMIP: IPSL‐CM5 with ORCHIDEE, CCSM4, and NorESM1 with Biome‐BGC), Exbrayat et al. [2014] demonstrated large differences in the SOC stocks existed in the initial conditions due to differences in decomposition and its response during the spin‐up procedure used by the models. Similar to their study, we also found close correlation (y = 0.98x + 24.7, R ² = 0.99; Figure 9a) in model‐specific SOC estimates between initial (1901) and contemporary (2010) periods. High correlation between preindustrial and modern SOC is derived from large cross‐model divergence in SOC estimate (e.g., 425–2111 Pg C in this study), but smaller SOC change (e.g., −70 to 86 Pg C here) relative to SOC pool size (<6%). An important result of this study is that no significant correlation was found between initial SOC stocks and modeled change of SOC during the twentieth century (Figure 9b). This suggests that the initial SOC estimate is critical to obtain an accurate estimate of modern SOC stock and that the modeled SOC sensitivity to the perturbation (CO₂, climate, land use, and nitrogen) is more responsible for SOC change estimation than the initial state.

Figure 9.

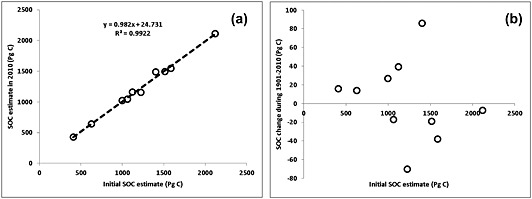
Dependence of contemporary SOC estimate in the year 2010 (a) and SOC change during 1901–2010 (b) on initial SOC estimate. Each circle denotes one model.

The modeled global NPP at the initial year varied from 34 Pg C yr⁻¹ in CLM4VIC to 65 Pg C yr⁻¹ in Biome‐BGC, and the global total NPP correlates positively (r = 0.79) with modeled global SOC stocks, thereby indicating that model to model variations of NPP are one of the major sources for modeling divergences in the initial SOC stocks. For example, four models (i.e., CLM, CLM4VIC, DLEM, and ISAM) showing the lowest SOC stocks had 28% lower total NPP (41 ± 6 Pg C yr⁻¹) than the other six models (58 ± 8 Pg C yr⁻¹) in 1901. NPP estimates from CLM and CLM4VIC are among the lowest of the models, leading to less C input to soil pools via litter pool, and therefore, these models had the lowest SOC stocks. These two models (CLM and CLM4VIC) have similar structure except hydrological parameterization in CLM4VIC, which simulates lower soil moisture and therefore has lower NPP as well as lower SOC stock for most regions [Lei et al., 2014]. In addition to the magnitude of NPP, the proportion of C allocated to litter pools and its composition appears to play an important role in determining initial SOC across the 10 TBMs. For example, using observation‐based litter‐fall data instead of model estimate in CLM4CN, Wieder et al. [2014] obtained a 49% larger global SOC stock of 746 Pg C compared to the 502 Pg C derived from the original simulation. Further, despite Bonan et al. [2013] found a higher litter decomposition rate in CLM4CN compared to Long‐term Intersite Decomposition Experiment (LIDET) observations, it may not be a general bias at global scale. Therefore, to minimize the uncertainties in the SOC stocks, a first step should be to accurately estimate NPP and litterfall using global databases as well as to validate the turnover time of vegetation compartments (e.g., leaf, stem, branch, and root), litterfall, and soil pools as Carvalhais et al. [2014] suggested.

4.2. Major Divergences in the Modeled SOC Change

The wide range of the SOC stocks and different spatial distributions from observations have been reported among the 11 CMIP5 ESMs compared during 1995–2005 [Todd‐Brown et al., 2013]. In this study, long‐term model simulations made it possible to examine the century‐long SOC change forced by more realistic climate reconstruction than the ESM climate. Yet SOC differences from model to model are still large. For example, five models (Biome‐BGC, GTEC, ISAM, LPJ, and VEGAS) showed a reduction in SOC stocks, while SOC increased in the rest models during 1901–2010 (Table 3). In the 10 TBMs, C in soil is gained mainly from litterfall input, while C loss pathways include soil erosion, land use change, crop cultivation, DOC leaching, CO₂ and methane release, and wildfire emission [Tian et al., 2012; Levis et al., 2014]. However, we have not found any relationship between the SOC change and the number of additional C loss pathways considered in models (Table 4). For example, CLM and CLM4VIC, which consider two additional soil C loss pathways (fire, and land use change), show SOC increase during 1901–2010. In contrast, Biome‐BGC and GTEC simulations indicate a decreasing SOC stock even without considering land use change. This suggests that other mechanisms such as a change in the proportion between labile and slow/passive soil C pools, and sensitivities of Rh and SOC dynamics to climate, and atmospheric composition forcings, are the major uncertainty sources in the modeling estimates of SOC stock change.

Table 4.

Model Estimates of C Fluxes and Accumulated C Storage Change in Ecosystem and Soil

Models	Rh	NPP	Rh/NPP	NCEa	Accumulated NCE (Pg C)	SOC Change (Pg C)	R SOC/∑NCE b	NCE Processesc
	(Pg C/yr)	(Pg C/yr)		(Pg C/yr)
BIOME‐BGC	60.20	66.43	91%	0.19	20.47	−7.23	−35%	F
CLM	43.67	47.35	92%	−0.64	−70.69	14.01	−20%	F/L/P/D
CLM4VIC	33.19	36.01	92%	−0.33	−36.16	15.99	−44%	F/L/P/D
DLEM	48.03	49.47	97%	0.93	102.59	26.70	26%	F/L/P
GTEC	59.87	66.92	89%	1.46	160.83	−70.19	−44%	P
ISAM	38.23	39.38	97%	−0.51	−56.62	−17.23	30%	L
LPJ	48.98	57.01	86%	−0.65	−71.08	−18.87	27%	F/L/G
ORCHIDEE	43.79	50.15	87%	0.93	101.97	39.24	38%	L/P
VEGAS	52.10	55.59	94%	0.53	58.18	−37.91	−65%	F/L/P
VISIT	64.52	66.24	97%	2.51	276.44	85.85	31%	–
Model range	[33–64]	[36–66]	[86–97%]	[−0.65–2.5]	[−71–276]	[−70–86]	[−65–38%]
Median	48.50	52.87	92%	0.36	39.32	3.39	3%

^aNCE is calculated as the residual between GPP, ecosystem respiration, and other C loss ways.

^b R _SOC/∑NCE refers to the ratio of SOC change to accumulated NCE during the study period.

^cNCE processes indicate additional variables, other than GPP and ecosystem respiration, each model used for calculating NCE. F, fire emissions; L, land use change emissions; P, product decay emissions; D, maintenance respiration deficit; and G, grazing emissions.

Among five models showing SOC decreases, LPJ and ISAM are the only two producing a global terrestrial ecosystem C source and the simulated SOC decrease during the 20th century accounts for 27%–30% of total land C storage reduction (Table 4). The other three models (Biome‐BGC, GTEC, and VEGAS) with a net SOC stock decrease (by 7 to 70 Pg C) show a net C accumulation (20 to 161 Pg C) during the past 110 years. Their estimated SOC reduction is equivalent to 35%–65% of the total C accumulation, suggesting that historical C uptake is primarily accumulated in vegetation rather than in soil pools in these models. In contrast, two models (CLM and CLM4VIC) estimate a net terrestrial C loss of 36–71 Pg C during 1901–2010, while their SOC pool increased by 14–16 Pg C, indicating an overwhelming C loss from vegetation pool. The remaining three models show SOC increase by 27–86 Pg C, accounting for 26% (DLEM) to 38% (ORCHIDEE) of the simulated net terrestrial C sequestration during 1901–2010. The above divergence suggests that model estimated net carbon exchange (NCE) should be carefully used to drive climate models since the C differently sequestered in or depleted from vegetation or soil pools may have different roles in C‐climate feedback, and thus differently affect climate projection [Ahlstrom et al., 2012; Friedlingstein et al., 2006, 2013].

4.3. Major Divergence in the Modeled SOC Responses to Driving Forces

4.3.1. Model Representation of Land Cover and Land Use Change

The modeling groups in MsTMIP project have used the same protocol to keep model initial and spin‐up procedure consistent, with TBMs sharing the same input data, spin‐up sequential climate data, and equilibrium criteria [Wei et al., 2014b; Huntzinger et al., 2013]. However, it is impossible for models to use exactly the same data sets (e.g., vegetation covers and soil properties) due to their different modeling structure and strategies. For example, some models only have one plant functional type (PFT) in one grid cell, while others adopt cohort structure containing more than one PFT per grid. Even for models with fractional coverage of different PFTs in a same grid point, their maximum PFT numbers in one grid cell vary a lot, and they have to reprocess the input data to fit their own model structure, which might have introduced uncertainties in SOC stock estimates. In addition, LPJ considers natural vegetation dynamic. Therefore, the divergences in the modeled initial SOC stocks have resulted from differences in model structures, plant, and soil distribution, as well as model parameterization methods [Exbrayat et al., 2014]. Note that modelers were not requested to output SOC and fluxes per PFT, which makes a comparison with SOC local data under a certain type of vegetation impossible.

Among the 10 TBMs, the estimated SOC change due to land use change (estimated by the difference between a simulation with land use and one without) appears to be one of the largest sources of uncertainties (Figure 8), which is possibly derived from divergent modeling scheme in estimating SOC change during land conversions. Some of them follow the bookkeeping modeling approach to estimate SOC change when natural vegetation converted to cropland and vice versa [Houghton, 1999; Houghton et al., 2012], while others treat croplands as grasslands. Tracking SOC accumulation in cultivated crops is also different among models. A few of them, such as DLEM, consider agricultural management practices including nitrogen fertilizer use and residual return to balance C and nutrient loss through harvest and product decay [Tian et al., 2011; Ren et al., 2012] while others do not.

Furthermore, changes in the SOC stocks during the study period were not related to the initial SOC stocks. This has indicated that sensitivity of SOC to environmental drivers resulted in the varied trends shown in 10 TBMs. The effects of land use change on SOC stocks, contributing to −20% to 400% of net SOC change during 1901–2010 (Figure 8a), are highly uncertain. LPJ and ISAM indicate that SOC decrease due to land use change is twofold to fourfold net SOC change, which nearly counteract SOC accumulation induced by elevated CO₂ concentration. However, GTEC and VEGAS show that land use change as compared to other factors is a predominant driver of global soil C stocks. Overall, higher differences in the contribution of land use change to SOC stocks have weakened the reliability of historical estimation and future projections. Therefore, improved model representation of SOC change related to vegetation dynamics (e.g., migration, mortality, regrowth, and recovery after disturbance) and land use change and land management (e.g., SOC changes with different conversion type and stage) is of critical significance for accurately assessing global and regional terrestrial C budget and fluxes, and most importantly, quantifying the MRT of soil C pool [Houghton et al., 2000; Post and Kwon, 2000; Guo and Gifford, 2002; Schaphoff et al., 2013; Friend et al., 2014; Wei et al., 2014a; Ciais et al., 2008]. More mechanistic processes should be taken into account in modeling studies to determine the magnitude of SOC loss and accumulation that varies with native vegetation types, soil properties, climate condition, time since conversion, and management practices [Murty et al., 2002; Wei et al., 2014a; Scharlemann et al., 2014].

4.3.2. Nitrogen Regulation

Models driven by dynamic N input have shown a direct N deposition‐induced SOC accumulation ranging from 14 to 17 Pg C over the study period, playing a similar or even more important role than elevated CO₂ in stimulating global C sequestration in soils as indicated by models including N input (Figure 8). However, those models without time series N deposition drivers all attributed SOC storage increase to rising atmospheric CO₂ concentration alone. In addition, increasing N input indirectly affects the response of terrestrial C dynamics to other environmental drivers. This study shows that cumulative impacts of rising CO₂ concentration on increasing SOC changes were significantly lower (21.32 ± 16.43 Pg C) in those models including explicit C‐N coupling mechanism (i.e., CLM, CLM4VIC, DLEM, and ISAM) than those five models without N cycle constraints (56.40 ± 29.67 Pg C) during 1901–2010 (Figure 8). Biome‐BGC is a C‐N coupled model, but its sensitivity experiments are missing in MsTMIP project. Various studies have shown that incorporation of the N cycle into the biogeochemical components of ESMs reduces the response of carbon uptake to rising CO₂ concentration [Zaehle and Dalmonech, 2011].

4.3.3. Climate Sensitivity of Rh

Our results have shown the modeled responses of SOC stocks to climate change differ among 10 TBMs, indicating uncertainties in estimating the sensitivity of both C input (e.g., NPP and litterfall) and MRT to temperature and moisture. Overall, Rh is the dominant flux causing SOC loss, that is equivalent in magnitude to 92% (86–97%) of NPP in the 10 TBMs (Table 4). During the study period, increases in the Rh range from 0.17 Pg C as estimate by VEGAS to 8.0 Pg C in ORCHIDEE, and the overall increase in Rh accounts for 8.5% (0.3–19.8%) over the initial Rh value in the 1900s.

Our analysis has shown that grid level best estimate of Rh has closer temporal correlation with temperature (r = 0.23–0.90 with median value of +0.84) than precipitation (r = 0.38–0.75 with a median value of +0.50) in most models (Figure 10). In the middle‐ and high‐latitude areas, all the models agree that both temperature and precipitation can explain the interannual variation of Rh and that Rh correlation with temperature (r values ranging from 0.50 to 0.92, p < 0.01) is above the global average and stronger than that with precipitation (r ranging from 0.34 to 0.62, p < 0.01). Interestingly, in the low‐latitude areas, LPJ and VEGAS exceptionally show a negative correlation between temperature and Rh (although it is insignificant for LPJ, r = −0.12, p = 0.20), but a significant positive correlation between precipitation and Rh. One possible reason is that simulated Rh is more sensitive in this latitude band (i.e., higher slope) to soil moisture rather than temperature, which is true for VEGAS. Besides, both LPJ and VEGAS considered vegetation dynamics during simulations. The simulated changes in vegetation composition and growth constrained by warming‐induced drought could be another reason as suggested by a wide variety of field evidence [Barber et al., 2000; Wilmking et al., 2004]. In their simulations, warming and drought may suppress tropical plant growth or increase forest mortality and thereby reduce C entering into soil pool and SOC decomposition rate compared to the early twentieth century. Therefore, the SOC response is not only determined by SOC decomposition sensitivity represented by different models but also by the simulated vegetation dynamics that can potentially alter C input via NPP and litterfall.

Figure 10.

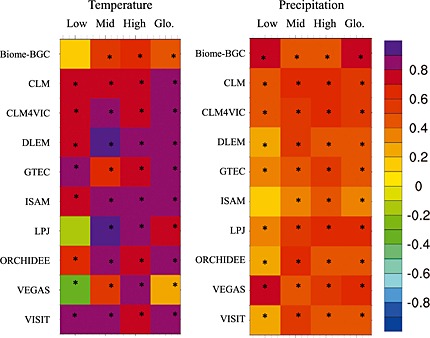
Temporal correlation of the modeled Rh with (left) temperature and (right) precipitation in low‐ (30°S–30°N), middle‐ (30°N–60°N and 30°S–60°S), and high‐ (60°N–90°N and 60°S–90°S) latitude areas and global during 1901–2010. The asterisk denotes that the correlation is significant (p < 0.05).

We find that the effect of climate and CO₂ on SOC change opposes each other, but with varied magnitude among models (Figure 8a). CO₂ increase alone should increase NPP and thus increase SOC. But climate change can both increase NPP in some regions or decrease it in other regions (making the sign of soil input change uncertain) and increase Rh in most regions. Therefore, SOC changes in response to climate depend upon regional differences of climate effect on input versus respiration. These differences could be analyzed more deeply for instance by prescribing to model a climate‐dependent NPP but a climate‐independent decomposition (and vice versa), which was not done in MsTMIP.

4.4. Modeling Divergence Due to Lack of Wetlands and Peatlands

In the MsTMIP protocol, vegetation covers do not include wetlands and peatlands, which have high SOC density and slow turnover rate, especially in high‐latitude regions [Raich and Schlesinger, 1992; Tarnocai et al., 2009; Page et al., 2011]. We believe that nonmodeled wetlands and peatlands are a major uncertainty sources for modeling the spatial distribution and magnitude of SOC. In this study, we have shown that when wetland and peatland distribution is considered, in one model (DLEM) global SOC estimate goes up from 1023 Pg C to 1428 Pg C, being enhanced by 40% (Figure 11). The spatial correlation coefficient between DLEM‐Peatland estimate and HWSD (point 11 in Figure 3), showing how closely this model's estimate matches observation pattern in the spatial context, is enhanced from 0.21 to 0.35. However, the normalized amplitude of spatial variation as estimated by the DLEM‐Peatland is shown to be far from HWSD since high‐latitude SOC density is not well represented in HWSD data. In the arctic region, model estimation indicates SOC density higher than 40,000 g C m⁻², which is closer to NCSCD and UNASMC. Therefore, inclusion of wetlands and peatlands could to a large extent improve global SOC modeling estimation.

Figure 11.

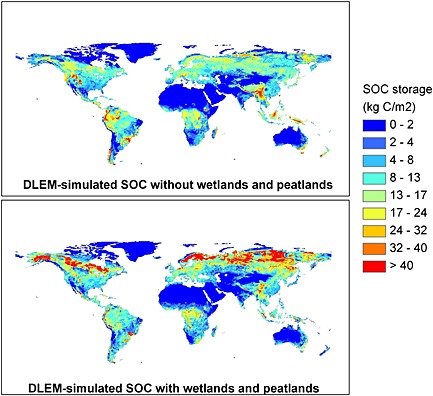
Comparison of two versions of Dynamic Land Ecosystem Model (DLEM)‐simulated SOC storage with and without consideration of wetlands and peatlands.

The NCSCD data indicated that in the northern circumpolar permafrost region alone 496 Pg organic C are contained in 1 m soil column, 1024 Pg C in 0–3 m depth, and 1672 Pg C in soil layers deeper than 3 m [Tarnocai et al., 2009]. SOC stocks in deep soil layers have been overlooked or underestimated in some soil survey‐based SOC estimates (e.g., HWSD) and ecosystem modeling. Most TBMs divide SOC into several pools (e.g., structural and metabolic, labile, slow, and passive C pools) with different turnover rates. However, few of them consider the vertical distribution of SOC [Jobbagy and Jackson, 2000] and the different SOC stability between shallow and deep soil layers when facing climate change. Incorporating vertical distribution of SOC into the LPJmL model, a recent study [Koven et al., 2011; Schaphoff et al., 2013] predicted that large amount of old soil C may be released, exceeding the stimulated C uptake owing to global warming. However, in this study, only 2 out of 10 TBMs (LPJ and BIOME‐BGC) have shown large SOC stocks north of 60°N, but their estimates of Rh in those areas are very close to other models. Therefore, inclusion of vertical soil dimension and characterizing soil C dynamics along with depth (e.g., depth of active soil layer in permafrost regions) and accordingly changes in soil properties is an important step for modeling studies to improve the global SOC stock estimation as well as to better understand belowground C dynamics in response to changes in climate and other environmental constraints.

5. Recommendations and Outlook

Through a multimodel intercomparison project, MsTMIP, this study provides the state‐of‐the‐art estimates of global SOC storage and Rh at a spatial resolution of 0.5° × 0.5° during 1901–2010. Large divergence is revealed in initial modeling estimates, the simulated dynamics in SOC and Rh, impacts of environmental drivers on net SOC change, and soil C sensitivity to variations in temperature and precipitation among different regions. Therefore, reducing uncertainties in the MRT via extensive validations of model simulated C fate (e.g., NPP, allocation, and Rh) against field observations should be an important step toward accurately estimating global SOC dynamics.

From the modeling perspective, divergent model estimates of SOC dynamics informed us of cautiously interpreting current model estimates of terrestrial C budget change and its feedback to climate system. How to improve and validate model performance in simulating long‐term SOC and Rh dynamics is an even bigger challenge than to accurately estimate magnitude of SOC and Rh. To improve TBM estimation of SOC, major recommendations derived from this study include the following: (1) the estimation of initial NPP as well as its partition into various litter and belowground components with different residence time and responses to climate and atmospheric forcings is one of the biggest uncertainties in the initial SOC stocks in 10 TBMs and needs to be improved. (2) To address nutrient limitation that affects NPP, biomass formation, litterfall, and SOC decomposition is of critical significance for accurately estimating historical SOC stocks as well as future projections. (3) TBM models ought to have better representation of litter composition, decay, and net nitrogen mineralization by comparing model performance against site level observations (e.g., Long‐term Intersite Decomposition Experiment (LIDET) used in Bonan et al. [2013]). (4) Wetland/peatlands and their functional traits should be included to increase SOC in high‐latitude band and improve SOC stock estimation especially in the permafrost region. (5) The lateral (subgrid) and vertical heterogeneities of SOC should be considered in modeling extrapolation from small scale to large scale. (6) Spatially explicit characterization of soil thickness and model representation of deep soil C dynamics are crucial for mimicking high‐latitude SOC dynamics. (7) In future model intercomparison project, we recommend to output PFT‐specific SOC estimate in each grid cell to make real “data‐model” comparison possible (i.e., compare to raw data instead of interpolated fields, which are also modeling estimates).

From the field experiment side, we anticipate the following efforts to facilitate future modeling estimation of SOC. (1) Given that cross‐model divergence in SOC estimates is much larger than SOC change in each model, it is critical to converge our estimation of initial conditions that will allow us to reject models that do not fall within acceptable limits of uncertainty and reduce cross‐model deviations. (2) Network of long‐term, large‐scale field experiments are needed to reduce scaling uncertainty especially for SOC at high latitudes and Rh in the tropics where larger uncertainties are found in the model ensembles. (3) A set of benchmarking data harmonizing regional and global SOC inventories would be greatly helpful to reconcile large differences among current data we used (e.g., HWSD and NCSCD) and provide solid observational evidence for modeling groups. (4) More efforts are needed to distinguish Rh that is commonly monitored as a confounded component of either soil respiration or ecosystem respiration to benchmark modeling estimates. (5) In addition to measure magnitude and distribution of SOC and Rh across a wide variety of ecosystems, we call for extensive manipulated experiments to examine how SOC and Rh respond to changes in climate, land use, and atmospheric compositions over long time period, which could serve as functional benchmark data to reduce modeling uncertainty.

Supporting information

Figures S1–S3

Tian, H. , Lu C., Yang J., Banger K., Huntzinger D. N., Schwalm C. R., Michalak A. M., Cook R., Ciais P., Hayes D., et al. (2015), Global patterns and controls of soil organic carbon dynamics as simulated by multiple terrestrial biosphere models: Current status and future directions, Global Biogeochem. Cycles, 29, 775–792. doi:10.1002/2014GB005021.