Basic and Advanced Numerical Performances Relate to Mathematical Expertise but Are Fully Mediated by Visuospatial Skills

Abstract

Recent studies have highlighted the potential role of basic numerical processing in the acquisition of numerical and mathematical competences. However, it is debated whether high-level numerical skills and mathematics depends specifically on basic numerical representations. In this study mathematicians and nonmathematicians performed a basic number line task, which required mapping positive and negative numbers on a physical horizontal line, and has been shown to correlate with more advanced numerical abilities and mathematical achievement. We found that mathematicians were more accurate compared with nonmathematicians when mapping positive, but not negative numbers, which are considered numerical primitives and cultural artifacts, respectively. Moreover, performance on positive number mapping could predict whether one is a mathematician or not, and was mediated by more advanced mathematical skills. This finding might suggest a link between basic and advanced mathematical skills. However, when we included visuospatial skills, as measured by block design subtest, the mediation analysis revealed that the relation between the performance in the number line task and the group membership was explained by non-numerical visuospatial skills. These results demonstrate that relation between basic, even specific, numerical skills and advanced mathematical achievement can be artifactual and explained by visuospatial processing.

An extensive body of research has focused on highlighting the contribution that cognitive processes and other academic skills can have on the acquisition of mathematical competences. The evidence that humans are born equipped with the innate ability to discriminate between numerical quantities (Antell & Keating, 1983; Izard, Sann, Spelke, & Streri, 2009; Xu & Spelke, 2000) has provided strong support for the dominant theory that the acquisition of formal mathematical competences may rely on early nonsymbolic numerical representations (Feigenson, Dehaene, & Spelke, 2004; Piazza, 2010), and what has been termed as the “number sense” (Berch, 2005). In this regard, several studies have found a significant correlation between nonsymbolic numerical skills and math achievement (Halberda, Mazzocco, & Feigenson, 2008; Mazzocco, Feigenson, & Halberda, 2011; Nosworthy, Bugden, Archibald, Evans, & Ansari, 2013; Pinheiro-Chagas et al., 2014; Schleifer & Landerl, 2011; Sella, Lanfranchi, & Zorzi, 2013; Starr, Libertus, & Brannon, 2013; for a different interpretation see Gilmore et al., 2013). However, the representation of symbolic quantities may play a crucial role in the development of mathematical skills (Butterworth, 2010; Reeve, Reynolds, Humberstone, & Butterworth, 2012). For instance, the performance in comparing digits has been found to correlate with mathematical achievement in children (Brankaer, Ghesquière, & De Smedt, 2014; Bugden & Ansari, 2011; Holloway & Ansari, 2009; Lyons, Price, Vaessen, Blomert, & Ansari, 2014; Mussolin, Mejias, & Noël, 2010). In line with this results, Rousselle and Noël (2007) showed that children with developmental dyscalculia (i.e., a clinical condition characterized by an extremely poor mathematical achievement) displayed a deficit in comparing symbolic quantities (i.e., digits), whereas the ability to compare nonsymbolic quantities seemed to be preserved. Besides the distinction between basic symbolic and nonsymbolic numerical skills (for a review see De Smedt, Noël, Gilmore, & Ansari, 2013), other authors have suggested that domain-general processes are primarily related to mathematical learning rather than domain-specific (basic numerical) skills (Passolunghi, Cargnelutti, & Pastore, 2014; Soltész, Szűcs, & Szűcs, 2010; Szűcs, Devine, Soltész, Nobes, & Gabriel, 2014). For example, Szűcs, Devine, Soltész, Nobes, and Gabriel (2014) recently highlighted the role of an “executive memory function centric model” in the development of mathematical competences in primary school children. Other studies have also demonstrated that domain-general cognitive abilities (e.g., working memory) and intelligence can explain a consistent amount of variance in mathematical performance (Deary, Strand, Smith, & Fernandes, 2007; Spinath, Spinath, Harlaar, & Plomin, 2006). Nevertheless, both domain-general and domain-specific cognitive processes may contribute to the acquisition of advanced mathematical skills (Fuchs et al., 2010; Passolunghi & Lanfranchi, 2012; Träff, 2013). Finally, language related abilities, such as phonological awareness and reading skills, have also been found to contribute to the development of mathematical competences (Koponen, Aunola, Ahonen, & Nurmi, 2007; Lee, Ng, Ng, & Lim, 2004). In summary, mathematical learning appears to be the linked to both domain-specific and domain-general cognitive processes as well as to other academic skills (e.g., reading).

Much research in this field has primarily focused on explaining the interindividual differences in mathematical achievement in children belonging to different age groups. Conversely, few studies have been conducted on individuals with a wide mathematical expertise, such those who are attending or have already completed a degree in mathematics.

Professional mathematicians usually display high intelligence and good reasoning skills, whereas their calculation skills might be above the average but not necessarily exceptional (Pesenti, 2005). In fact, exceptional calculation skills might be the consequence of an intensive and protract drill, which may become an obsessive–compulsive behavior as in clinical conditions such as Asperger and savant syndrome (Fehr, Weber, Willmes, & Herrmann, 2010). In one of the first studies exploring mathematicians’ numerical skills, Dowker (1992) asked a group of professional mathematicians to perform a computational estimation task. In such a task, participants were presented with arithmetical problems (e.g., a complex multiplication with two-digit numbers) and were asked to estimate plausible answers without actually calculating the correct solutions. Mathematicians displayed accurate estimates along with a vast repertoire of appropriate arithmetical strategies (e.g., rounding one or two numbers, use of fractions). In a subsequent study, Dowker, Flood, Griffiths, Harriss, and Hook (1996) administered a computational estimation task to mathematicians, accountants, psychology students, and English students. In line with previous results, mathematicians displayed more accurate estimates compared to accountants and psychology students, whereas English students had the lowest performance. Again, mathematicians adopted appropriate arithmetical strategies when providing estimates to the proposed arithmetical problems. Therefore, mathematicians possess excellent computational estimation skills compared to highly educated people with expertise in different academic and professional fields. In fact, as Levine (1982) originally observed, American college students (with no mathematics majors) displayed imprecise estimations and a reduced repertoire of strategies. Interestingly, the accuracy in estimating was related to calculation abilities, thereby suggesting a link between computational estimation and exact calculation skills. Accordingly, college students’ estimation skills have been found to correlate with the mathematics subscale scores of the Scholastic Assessment Test (College Board, 1999; Hanson & Hogan, 2000).

Regarding basic numerical skills, Castronovo and Göbel (2012) asked undergraduates and postgraduates from the faculties of mathematics and psychology to complete symbolic and nonsymbolic numerical tasks. Participants with expertise in mathematics displayed a better performance in estimating nonsymbolic numerosity and in comparing two-digit numbers. Conversely, the two groups showed a similar performance when comparing nonsymbolic numerosities (i.e., sets of dots). Therefore, the intentional processing of symbolic quantities (i.e., Arabic numbers) seems to be linked to advanced mathematical skills. In a recent study, Cipora and colleagues (2015) used a digit parity judgment task to verify whether the Spatial-Numerical Association Response Code effect (i.e., faster responses with the right hand for larger numbers and faster responses with left hand for smaller numbers; Dehaene, Bossini, & Giraux, 1993; van Dijck, Gevers, & Fias, 2009) varied depending on participants’ mathematical expertise. The authors found that mathematicians lacked the automatic spatial-number association, which was instead found in professionals who used mathematics for their job (e.g., engineers) but were not mathematicians. The authors concluded that mathematicians may possess a more flexible representation of symbolic numbers, which lacks a rooted spatial connotation.

In summary, mathematicians usually display advanced calculation skills with a flexible and strategic use of their arithmetical knowledge. Basic domain-specific numerical skills have been to some extent linked to superior mathematical competences but it remained unclear whether this connection can be mediated by cognitive processes from different domain (e.g., visuospatial skills). For instance, Wei, Yuan, Chen, and Zhou (2012) investigated the contribution of basic numerical, complex numerical, spatial, language, and general cognitive processes to advanced mathematical performance in a sample of university students. The authors used an extensive cognitive battery composed of several tasks to assess specific skills (e.g., digit comparison, computation, mental rotation, word rhyming, progressive matrices, etc.), which have been found to differently contribute to advanced mathematics. The authors also directly compared basic numerical processing and spatial processing to verify which component was more relevant for advance mathematical achievement. Spatial skills remained significantly correlated with advanced mathematical abilities even when the effect of other factors (basic numerical, language, and general cognitive) was statistically controlled. Conversely, no one of the tasks assessing basic numerical competences displayed a significant partial correlation. Therefore, spatial abilities, as measured by mental rotation, spatial working memory, and figure analysis, explained a significant amount of variability of advanced mathematical competences in nonmathematicians. However, advanced mathematical abilities were solely assessed using a task related to the acquisition of new advanced mathematical concepts and the solving of mathematical problems. Moreover, participants were adults without an advanced expertise in mathematics (Wei et al., 2012). Therefore, it remains unclear the effect that basic domain-specific numerical processes and domain-general processes can have on advanced mathematical abilities, especially in those individuals with a vast expertise in mathematics (i.e., mathematicians).

In the present study, we investigated whether basic numerical skills are connected to more complex arithmetical abilities in a group of mathematicians in comparison with highly educated nonmathematicians.

For the assessment of basic symbolic skills, the administered tasks should be designed to reduce the confounding involvement of domain-general cognitive processes (e.g., verbal working memory), thereby lessening their influence on the outcome measure. Moreover, when accomplishing the task, more emphasis should be put on accuracy rather than reaction times (RTs) in order to minimize the influence of speed of processing. In this regard, the number line task (NL; Siegler & Opfer, 2003) can be considered an excellent tool to compare basic intentional numerical skills in mathematicians and nonmathematicians. In this task, participants are asked to place target numbers (e.g., 25) on a horizontal line comprising a specific numerical interval (e.g., from 0 to 100). Siegler and Opfer (2003) originally observed that, in the number line from 0 to100, first graders overestimated the magnitude of small numbers and slightly underestimated the magnitude of large numbers, thereby yielding a biased log-like pattern of estimates which is consistent with the notion of a logarithmically compressed mental number line (Dehaene, 2003; Dehaene, Izard, Spelke, & Pica, 2008). Conversely, on the same 0–100 interval, third graders displayed an accurate linear mapping. Although this developmental shift from a logarithmic to a linear representation has been repeatedly observed in different contexts (Berteletti, Lucangeli, & Zorzi, 2012; Sella, Berteletti, Lucangeli, & Zorzi, 2015; Siegler, Thompson, & Opfer, 2009), some authors have suggested that the NL task lacks any assessment of the internal representation of numbers (Karolis, Iuculano, & Butterworth, 2011). Furthermore, the biased pattern estimates can be also fit by other functions (e.g., bilinear, power function) and thus explained by adopting different theoretical perspectives (Barth & Paladino, 2011; Bouwmeester & Verkoeijen, 2012; Cohen & Sarnecka, 2014; Ebersbach, Luwel, Frick, Onghena, & Verschaffel, 2008; Moeller, Pixner, Kaufmann, & Nuerk, 2009; Opfer, Siegler, & Young, 2011; Slusser, Santiago, & Barth, 2013). Beyond this theoretical debate, and more importantly, the accuracy in placing numbers on the line has been repeatedly correlated with the performance in other numerical tasks, as well as with children mathematical achievement (Berteletti, Lucangeli, Piazza, Dehaene, & Zorzi, 2010; Booth & Siegler, 2006, 2008; Geary, 2011; Sasanguie, De Smedt, Defever, & Reynvoet, 2012). Accordingly, children with mathematical difficulties show a less accurate mapping of numbers compared with typically developing children (Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Landerl, Bevan, & Butterworth, 2004; Landerl, 2013; Sella, Berteletti, Brazzolotto, Lucangeli, & Zorzi, 2014). In short, the adoption of the NL with familiar target numbers should ensure a valid measure of basic symbolic skills in both mathematicians and nonmathematicians.

Another issue regarding the basic symbolic representations is understanding whether they are numerical primitives or cultural artifacts (Kallai & Tzelgov, 2009; Pinhas & Tzelgov, 2012; Tzelgov, Ganor-Stern, & Maymon-Schreiber, 2009). The term “primitives” refers to numbers that can be automatically and holistically retrieved from memory. For example, the magnitude of single digit numbers is automatically accessed when the task does not require processing the numerical meaning (parity judgment; Dehaene et al., 1993). Conversely, “cultural artifacts” denotes those numbers whose magnitude representation is generated online in order to perform a specific task (Kallai & Tzelgov, 2009; Pinhas & Tzelgov, 2012; Tzelgov et al., 2009). For example, the processing of multidigit numbers appears to be less automatic and related to the separate processing of number components (i.e., decade, unit) rather than to a direct magnitude retrieved from long term memory (for a detailed review see, Tzelgov, Ganor-stern, Kallai, & Pinhas, 2015). It has been suggested that positive integers constitute the primitive of the numerical system, while negative integers are a cultural artifacts (Tzelgov et al., 2015, 2009). Indeed, children’s progressive experience with positive numbers leads them to automatically access their numerical magnitude (Girelli, Lucangeli, & Butterworth, 2000; Rubinsten, Henik, Berger, & Shahar-Shalev, 2002). Conversely, negative numbers are learned lately in the development, lack immediate physical reference, and are less likely to be used in everyday life. In this regard, the processing of positive numbers should be familiar to the vast majority of population, whereas only expert individuals (i.e., mathematicians) may demonstrate a more accurate and automatic processing of negative numbers. Alternatively, mathematicians might have a more refined representation of number primitives. The impact of numerical/mathematical expertise on the processing of positive numbers remains unknown.

In our study, mathematicians and nonmathematicians completed the NL task mapping positive and negative numbers in order to examine the nature of numerical symbolic processing as a function of expertise. Indeed, the processing of negative numbers, which may be considered as nonprimitive cultural artifacts, may be strongly linked to high-level numerical skills. Conversely, the numerical expertise may be associated with the ability to process better positive numbers, which based on theories outlined earlier, serve the building block for more advanced numerical skills. Participants also completed two additional tasks to evaluate their advanced arithmetical skills: a computational estimation task (adapted from Levine, 1982) in which they had to provide approximate results for arithmetical problems; and a numerical agility task to evaluate their flexible use of arithmetic operations. Finally, a numerical Stroop task was proposed as control task to assess whether mathematicians performed generally better on basic numerical tasks, beside the NL, that involved numbers but an automatic and not intentional numerical processing (Bugden & Ansari, 2011; Cohen Kadosh, Henik, & Rubinsten, 2008; Girelli et al., 2000; Rousselle & Noël, 2008; Rubinsten & Henik, 2005; Tzelgov, Meyer, & Henik, 1992).

We expected mathematicians to outperform nonmathematicians in the computational estimation and in the numerical agility tasks. The groups might differ in their performance on the NL task, and this can depend on the number’s polarity. Moreover, a detailed analysis of the NL task may reveal whether negative and positive numbers are mapped differently and whether their processing is related to the level of numerical expertise. Finally, we assessed how basic numerical processing, as indicated in the NL task, is linked to advanced numerical skills and group membership (mathematicians vs. nonmathematicians) via mediation analysis. We further examined whether such a relationship can be explained by non-numerical cognitive abilities (visuospatial skills, as measured by block design subtest).

Method

Participants

Thirty-eight right-handed academics (doctoral-level students and postdoctoral fellows) from the Department of Mathematics (n = 19), and their peers from the Humanities Division (n = 19), were recruited from the University of Oxford (see Table 1). Participants were reimbursed at £10 per hour. The study was approved by the Berkshire Research Ethics Committee.

Table 1. Group Comparison for Age and IQ Scores.

	Nonmathematicians	Mathematicians
Measures	Mean (SD)	Mean (SD)	t(36)	p	d
Age (in years)	26.28 (2.46)	25.66 (1.57)	.93	.36	.3
Full scale IQ	125 (6)	128 (10)	1.27	.214	.41
Verbal IQ	130 (5)	124 (13)	1.85	.073	.6
Performance IQ	115 (8)	126 (6)	4.71	<.001	1.53
Block design (t score)	61 (5)	67 (3)	4.02	<.001	1.30
Matrix reasoning (t score)	57 (5)	61 (9)	1.84	.075	.6

Stimuli, Procedure, and Design

Participants completed the following tasks.

The number line task (Siegler & Opfer, 2003)

This task requires spatial positioning of a given number on a horizontal continuum where only the extremes of the line are labeled. Stimuli were displayed on a 19-inch Dell monitor at a distance of 55 cm (Thompson, Nuerk, Moeller, & Cohen Kadosh, 2013). On each trial, participants were presented with a blue, horizontal line (approximately 40 cm long) stretching from left to right. The line was centered vertically on a black background and labeled with an anchor number on each end, with the numerically smaller anchor always on the left. To avoid center- or side-bias, target numbers were displayed in both the upper-left and upper-right corners above the numerical anchors (−1,000 and 1,000). To differentiate between target and anchor numbers, target numbers appeared in yellow. The participants completed 30 trials of the task (15 positive numbers: 85, 127, 216, 265, 372, 415, 482, 521, 612, 689, 770, 809, 872, 910, 966; and 15 negative numbers: −67, −98, −152, −223, −275, −356, −427, −493, −576, −623, −691, −727, −865, −889, −955, administered in a mixed order which differed for each participant).¹ The participants gave a mouse click on the number line where they believed the given target number should be mapped. Each trial was presented immediately following the mouse click of the previous trial. Trials were not restricted in terms of time, but participants were instructed to respond as fast as possible while maintaining high accuracy. We calculated the absolute deviation between the target number and the estimated number following this formula:² |estimate-target number|. Better performance on this task is reflected in a smaller difference between the estimated mapping and the objective location of the number on the axis.

Numerical Stroop task (Henik & Tzelgov, 1982)

We used this task to assess whether mathematicians performed generally better on basic numerical tasks that involved numbers, or whether this was limited to the NL task. Subjects were presented with pairs of digits that could differ in both their numerical value and physical size. These stimuli could be either incongruent (the physically larger digit is numerically smaller, e.g., 2 4), neutral (the stimuli differ only in the physical size, e.g., 2 2), or congruent (the physically larger digit is also numerically larger, e.g., 2 4). Participants were asked to choose the physically larger stimulus on the screen, while ignoring the numerical value. Both accuracy and RTs were measured. A congruity effect reflects conflict between task demands and automatic numerical processing, and is indicated by longer RTs for incongruent trials in comparison to congruent trials. Such an effect with symbolic numbers characterizes numerical competence (Cohen Kadosh, Soskic, Iuculano, Kanai, & Walsh, 2010; Girelli, Lucangeli, & Butterworth, 2000; Rubinsten & Henik, 2005, 2006; Rubinsten, Henik, Berger, & Shahar-Shalev, 2002). We calculated a single score for this task by calculating the numerical Stroop ratio using the following equation:

$$NumericalStroopRatio=(IncongruentRT-CongruentRT)/NeutralRT$$

This analysis takes into account the general response speed as indicated by the neutral condition, which could augment the congruity effect when RTs are slow (Schwarz & Ischebeck, 2003).

The computational estimation task (Dowker, Flood, Griffiths, Harriss, & Hook, 1996; Levine, 1982)

Ten multiplication and division problems were chosen from Levine’s original paper: 76 × 89, 145 × 37, 64.6 × 0.16, 12.5 × 11.4, 0.47 × 0.26, 4645 ÷ 18, 648.9 ÷ 22.4, 546 ÷ 33.5, 66 ÷ 0.86, 0.76 ÷ 0.89. The participants were asked to give their best estimation of these 10 multiplication and division problems within 10 min. They did not have a pen and paper for this task, and were explicitly told to estimate, and not calculate, the exact answer, and to provide their strategy after each item. None of their answers provided the exact answer. For each item, we calculate the proportion of the absolute deviation from the actual answer (|estimate-target number|/target number), and used the median of the calculated proportions as their global score.

The numerical agility task

Participants were asked to repeatedly generate the number 24 from four presented numbers. Five problems were presented in total (see Appendix 1). The problems were administered in order of difficulty, and for the earlier items, hints (such as the structure of the answer) were provided. There was a 2-min time limit for each item. The instructions made it clear that only the four basic operations (×, /, +, −) were allowed, such that any individual having completed secondary school should be able to solve these problems. For each item, 2 points were awarded if the correct answer was achieved within 1 min, 1 point was awarded if it was achieved within 2 min, and no points were awarded otherwise.

Wechsler Abbreviated Scale of Intelligence, WASI-II (Wechsler & Chou, 2011)

Participants completed two verbal subtests (i.e., vocabulary and similarities) and two performance subtests (i.e., block design and matrix reasoning) of the intelligence scale, which allows an estimation of verbal and performance IQ as well as the full scale IQ. In the vocabulary subtest, participants defined the meaning of visually and verbally presented words. This subtest is designed to assess words knowledge and verbal concepts construction. In the similarities subtest, participants have to describe how two objects or concepts are similar, thereby assessing verbal concepts formation and reasoning skills. The block design subtest requires participants to assemble red and white cubes to reproduce a model figure within a given time limit. This task assesses the ability to analyze and spatially manipulate visual stimuli. Finally, in the matrix reasoning subtest, an incomplete matrix is presented and the participant has to select from available images the one that completes the series. This subtest is widely considered a measure of fluid intelligence, perceptual organization, and reasoning.

Results

Groups Matching

The two groups were perfectly matched for gender, handedness, and academic status (14 males and five females, all right-handed, 17 PhDs and two Postdocs in each group). Both groups had a similar age, verbal IQ, and full scale IQ (see Table 1). Conversely, mathematicians displayed a higher performance IQ compared with nonmathematicians. A deeper analysis revealed that mathematicians displayed better performance in the block design subtest compared with nonmathematicians, whereas the two groups had a similar performance in the matrix reasoning subtest.

Numerical Tasks

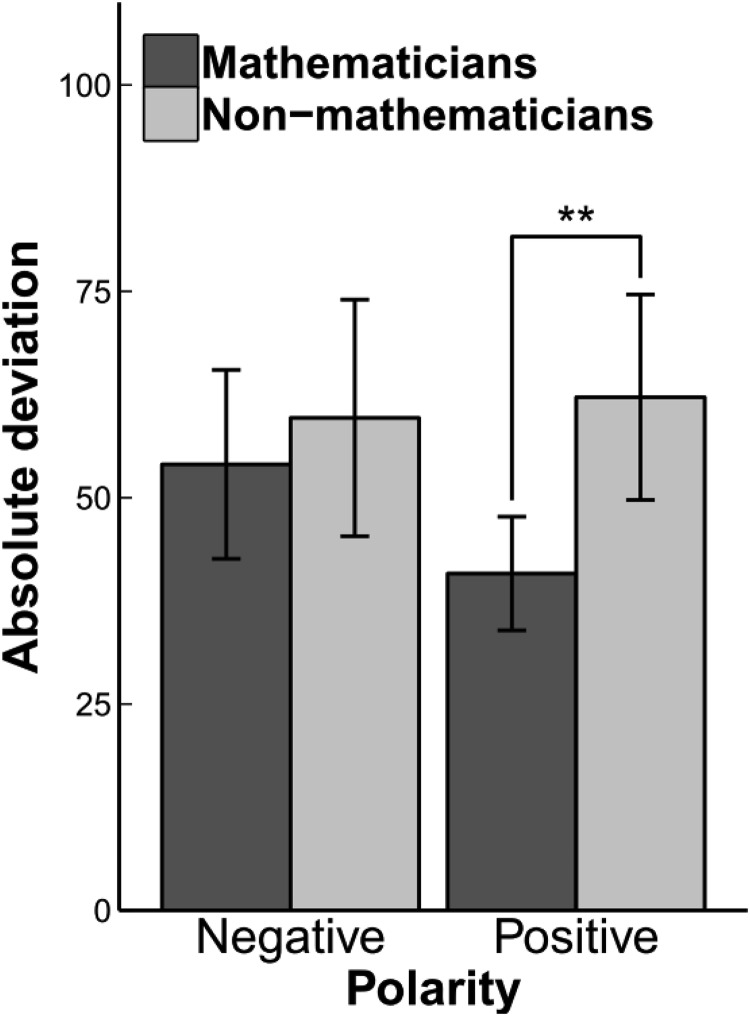
For the NL task, we first excluded from the analysis responses involving polarity errors, which is placing positive numbers on the left side of the line or placing negative numbers on the right part of the line (2% of trials). Thereafter, we analyzed the absolute deviation of estimates in a mixed ANOVA with Polarity (Positive, Negative) as within-subjects factor and Group (Mathematicians, Nonmathematicians) as between-subjects factor. The interaction between Group × Polarity was significant, F(1, 36) = 7.17, MSE = 164, p < .01, η_p² = .17 (Figure 1). Further analyses indicated that mathematicians were more accurate compared to nonmathematicians at mapping positive, but not negative, numbers (Table 2 and Figure 2). Interestingly, only mathematicians showed a better performance in mapping positive numbers compared to negative numbers, t(18) = 3.2, p = .005. As expected, mathematicians also showed better performance compared with nonmathematicians on both the numerical agility task and the computational estimation task. In contrast, no group differences were observed in the Numerical Stroop task (see Table 2).

Figure 1.

An interaction between numerical polarity and group, indicating selectively improved performance in mapping positive numbers among mathematicians compared with nonmathematicians. The values on the y-axis indicate the absolute deviation from the target numbers in integers (Error bars represent 95% CI). ** p < .01.

Table 2. Descriptive Statistics for the Administered Numerical Tasks.

	Nonmathematicians	Mathematicians
Measures	Mean (SD)	Mean (SD)	t	p	d
Note. NL = number line.
* One nonmathematician did not complete the task.
NL task (absolute deviation)
Positive numbers	62 (26)	41 (14)	3.16	.003	1.02
Negative numbers	60 (30)	54 (24)	.64	.52	.21
Computational estimation task	.21 (.21)	.04 (.03)	3.5	.001	1.14
Numerical agility task	1.84 (2.32)	5.74 (1.33)	6.36	<.001	2.07
Numerical Stroop*	.1 (.08)	.1 (.04)	.04	.96	.01

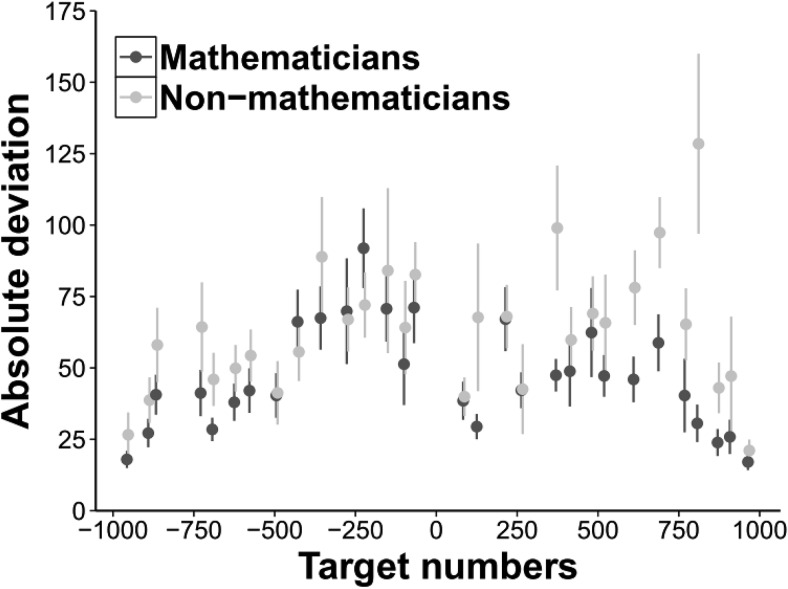
Figure 2.

Mean absolute deviation for each target numbers separately for mathematician and nonmathematicians (bars represent SEM).

The interested reader can view the correlations between the numerical tasks for the entire sample as well as separately for mathematicians and nonmathematicians in Table 3.

Table 3. Pearson’s Correlation Matrix for the Administered Numerical Tasks for the Entire Sample as Well as Separately for Mathematicians and Nonmathematician.

Group	Measures	1	2	3	4	5
Note. NL = number line.
* p < .05. ** p < .01. *** p < .001.
All sample	1 NL task—Positive numbers	—	.701**	.475**	−.503***	.094
	2 NL task—Negative numbers		—	.325*	−.218	−.011
	3 Computational estimation			—	−.486**	−.077
	4 Numerical agility				—	−.202
	5 Numerical Stroop					—
Mathematicians	1 NL task—Positive numbers	—	.654**	−.107	.188	−.015
	2 NL task—Negative numbers		—	−.039	.061	.087
	3 Computational estimation			—	−.419	.178
	4 Numerical agility				—	−.001
	5 Numerical Stroop					—
Nonmathematicians	1 NL task—Positive numbers	—	.794**	.371	−.417	.147
	2 NL task—Negative numbers		—	.413	−.332	−.051
	3 Computational estimation			—	−.199	−.109
	4 Numerical agility				—	−.389
	5 Numerical Stroop					—

NL Advanced Analyses

Problem size effect on absolute deviation

From the visual inspection of the Figure 2, it seemed that the absolute deviation tended to increase as a function of target magnitude from left (negative numbers) to right (positive numbers). We verified whether the absolute deviation tended to increase from left to right by running, for each participant, a series of regression analyses on individual absolute deviations as a function of target numbers leaving one estimate out each time (i.e., leave-one-out). Therefore, for each participant, we used the median of the obtained distribution of standardized beta coefficients (i.e., positive values = increasing absolute deviation as a function of target size; negative values = decreasing absolute deviation as a function of target size) as a robust index of the tendency to provide worse (or better) estimates when target numbers increased. Mathematicians displayed a lower mean of beta coefficient (M = −0.05, SD = 0.13) compared with nonmathematicians (M = 0.1, SD = 0.17), t(34) = 2.94, p = .006, d = 0.98. Interestingly, the mean of beta coefficients was significantly different from zero only for Nonmathematicians, t(18) = 2.54, p = .02, whereas this was not the case for mathematicians, t(16) = 1.61, p = .126. Nonmathematicians displayed more absolute deviation moving from left to right on the visual line.

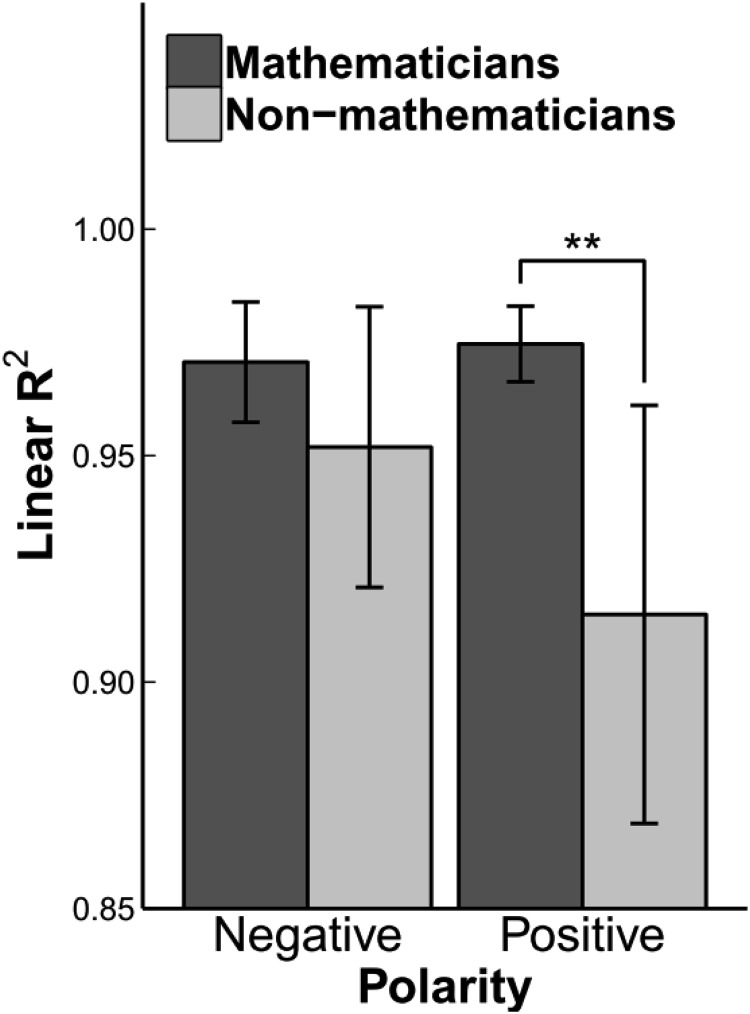
R² of the linear fit

To further investigate the performance in the NL task, we fit the linear and logarithmic model on individual estimates as a function of target numbers separately for positive and negative polarity. Due to a computer backup problem, the raw estimates of two mathematicians were lost. As for the analysis of mean absolute deviation, we excluded additional responses involving polarity errors (1.72% of trials). We compared the absolute residuals of the linear and logarithmic fit with a paired t test (Siegler & Opfer, 2003).³ We analyzed the individual linear R² in a mixed ANOVA with Polarity (Positive, Negative) as a within-subjects factor and Group (Mathematicians, Nonmathematicians) as a between-subjects factor (see Figure 2). The main effect of polarity was not significant, F(1, 34) = 2.87, MSE = 0.002, p = .10, η_p² = .078, whereas the main effect of group reached significance F(1, 34) = 4.78, MSE = 0.006, p = .036, η_p² = .123. The interaction Polarity × Group also reached significance, F(1, 34) = 4.44, MSE = 0.002, p = .043, η_p² = .115. Planned comparisons revealed that mathematicians showed a significantly higher R² compared with the nonmathematicians only when mapping positive numbers, t(34) = 2.53, p = .016, d = 0.85.

The position of the zero

In the NL task, participants possibly used the perceived position of the zero (i.e., the central point on the line) as landmark to anchor other estimates. In this regard, the perceived position of the number zero possibly influenced the whole mapping performance. The position of the zero can be inferred as the intercept of the regression line interpolating all the estimates as a function of the target numbers. In this case, the intercept literally represents the estimated value on the y-axis when the value on x-axis is zero. We used a robust leave-one-out analysis to estimate the perceived position of the number zero: For each participant, we ran a series of regression analyses on individual estimates as a function of target numbers separately for positive and negative polarity leaving one estimate out at time. Therefore, for each participant, we used the median of the obtained distribution of intercepts as a robust estimation of the position of the zero on the line. We analyzed the obtained medians of intercept in a mixed ANOVA with Polarity (Positive, Negative) as within-subjects factor and Group (Mathematicians, Nonmathematicians) as between-subjects factor. The main effect of polarity was the only significant one, F(1, 34) = 48.05, MSE = 3513, p < .001, η_p² = .59. Indeed, the mean estimated zero point was 10 (SD = 61) for positive numbers and −87 (SD = 62) for negative numbers. Importantly, neither the main effect of the group, F(1, 34) = 0.59, MSE = 4082, p = .447, η_p² = .02, nor the interaction Polarity × Group were significant, F(1, 34) = 0.62, MSE = 3513, p = .437, η_p² = .02, thereby suggesting that the two groups had a similar perception of the position of the number zero on the line.

Confidence in mapping numbers

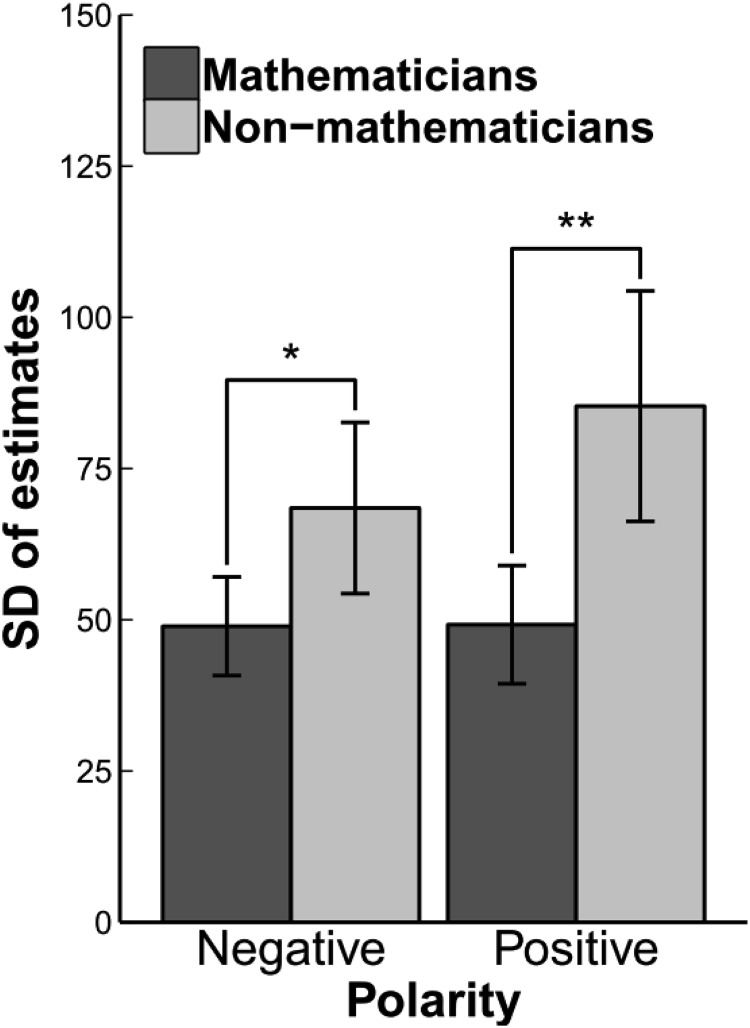
To further investigate mapping strategy, we calculated for each target number the standard deviation of estimates separately for mathematicians and nonmathematicians. A large SD across target numbers means that a group displayed more variability in placing numbers independently from the accuracy of the positioning. Note that, in this analysis, the target numbers are treated as cases. Both negative and positive target numbers showed less variability when estimated by mathematicians (negative: M = 49, SD = 15; positive: M = 49, SD = 18) compared with nonmathematicians (negative: M = 68, SD = 26; positive: M = 85, SD = 34), t(28) = 2.57, p < .016, d = 0.94, and t(28) = 3.62, p < .001, d = 1.32, respectively (see Figure 3).

Figure 3.

Mean R² of the linear fit of estimates as a function of negative and positive target numbers in mathematicians and nonmathematicians (Error bars represent 95% CI). * p < .05.

RT analysis

We analyzed the median RTs in a mixed ANOVA with Polarity (Positive, Negative) as a within-subjects factor and Group (Mathematicians, Nonmathematicians) as a between-subjects factor. The main effects of group (p = .25) and polarity (p = .71) and the interaction Group × Polarity (p = .37) did not reach significance. Therefore, no differences emerged in term of response speed for the polarity or between groups.

Mediation Analyses Between Basic and Advanced Numerical Skills

We ran two path analyses to see if the ability to map respectively positive and negative numbers was associated with a higher chance of being a mathematician and if this relationship was mediated by computational estimation and/or arithmetic agility. We used the PROCESS module in SPSS (Hayes, 2013; IBM Corp., 2013) to run the mediation analyses (all one-tailed p values) and to estimate the bootstrapped (10,000 resamples) 95% confidence intervals for the specific indirect effects. The mediation analysis verified whether the effect of an independent variable (X) on a dependent variable (Y), denominated c path, is mediated by one or more variable(s) called mediator(s) (Ms). The c path corresponds to the beta regression coefficient of the linear regression with Y as dependent variable and X as predictor. The connections between the independent variable (X) and the mediators (Ms) are denominated a paths, whereas the connections between the mediators (Ms) and the dependent variable (Y) are denominated b paths. Each a path corresponds to the beta coefficient of the linear regression with the mediator (M) as outcome variable and the independent variable (X) as predictor. Each b path, instead, corresponds to the beta coefficient of the linear regression with the dependent variable (Y) as outcome and the mediator (M) as predictor when also the independent variable (X) is inserted in the model. In the case of a dichotomous outcome variable (Y), the logistic regression is implemented to assess the regression coefficients for the b and the c paths. The product of a and b paths represents the indirect effect of the independent variable (X) on the dependent variable (Y) through the mediator(s) (Ms) and its significance is evaluated adopting a resampling technique to obtain a bootstrapped distribution of ab products. Despite the a and b paths may be themselves statistically significant, a robust way to establish a specific indirect effect of the independent variable (X) on the dependent variable (Y) through the mediators (Ms) is to observe whether the 95% of the bootstrapped distribution of the ab products does not overlap zero (Hayes, 2013; Hayes & Scharkow, 2013).

Mapping of positive numbers in the NL task

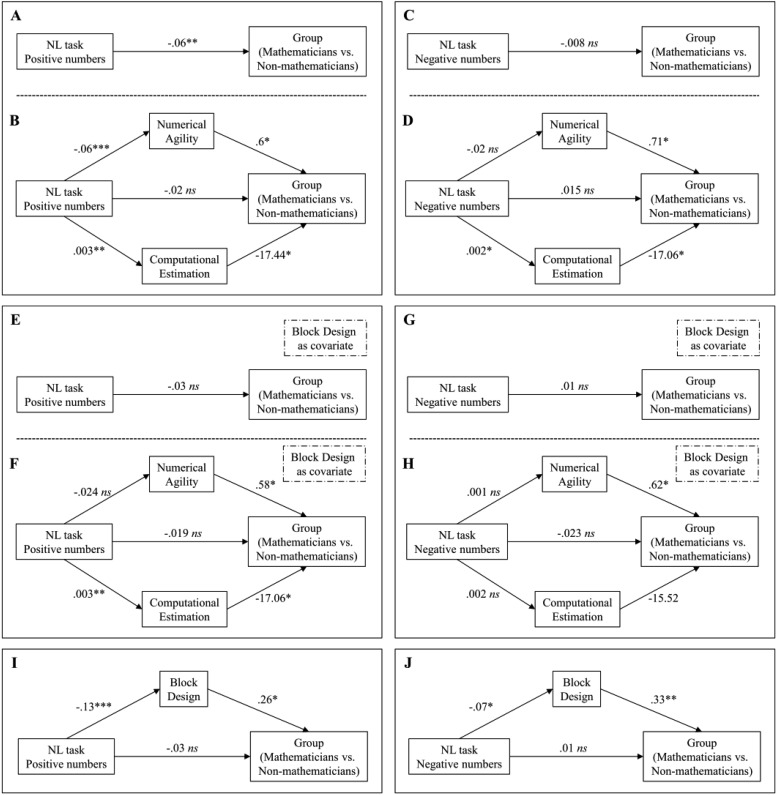
Regressing participant group onto the positive numbers absolute deviation resulted in a significant association between the variables (b = −.06, SE = .023, p = .007; Figure 5, panel A), indicating that individuals who were more accurate at mapping positive integers in the NL task were more likely to be mathematicians, which is consistent with the ANOVA results. We then entered the two mediators, numerical agility and computational estimation scores into the model. The mapping of positive numbers in the NL task was significantly associated with the score in numerical agility task (b = −.059, SE = 0.017, p < .001) and in the computational estimation task (b = .003, SE = .001, p = .001). Both scores in the numerical agility task (b = 0.6, SE = .31, p = .027) and in the computational estimation task (b = −17.44, SE = 10.19, p = .043) were, in turn, significantly associated with group. Once the mediators were entered into the model, the direct association between the mapping of positive integers in the NL task and group became nonsignificant (b = −.022, SE = .032, p = .24; Figure 5, panel B). Bias-corrected bootstrapped confidence intervals for the specific indirect effects of the mapping of positive numbers on group membership through computational estimation task (−0.6, 95% CI [−0.23, −0.001]) and numerical agility task (−0.35, 95% CI [−0.17, −0.002]) were both below zero. This result supports an indirect effect of the mapping of positive numbers on group through the scores in the numerical agility and in the computational estimation task.

Figure 5.

Bivariate regression analyses between the mapping of positive (panel A) and negative (panel C) numbers in the number line (NL) task and group. The full mediation models for positive (panel B) and negative numbers (panel D) in the NL task. Bivariate regression analyses between the mapping of positive (panel E) and negative (panel G) numbers in the NL task and group with block design as covariate. The full mediation models for positive (panel F) and negative numbers (panel H) in the NL task with block design as covariate. Mediation models in which the relation between the mapping of positive (panel I) and negative (panel J) numbers in the NL task and the group is mediated by block design. Unstandardized regression coefficients are reported. All p values are one-tailed. * p < .05. ** p < .01. *** p < .001.

Mapping of negative numbers in the NL task

Previous researchers call into question the necessity of first showing a direct effect between the independent variable and dependent variable before testing for an indirect effect (Alwin & Hauser, 1975; Hayes, 2009; Kenny, 2008; Mathieu & Taylor, 2006; Rucker, Preacher, Tormala, & Petty, 2011; Zhao, Lynch, & Chen, 2010). An independent variable may very well influence a dependent variable only through indirect means; finding such an effect would have important implications regarding theory surrounding the effects. It is quite possible that good performance on mapping of negative numbers in the NL task might not directly affect whether someone belongs to the mathematician group, but it may be possible that this relation is still mediated advanced numerical tasks. Missing such an indirect effect would equate to committing a Type II error. Indeed, MacKinnon, Lockwood, Hoffman, West, and Sheets (2002), in comparing 14 methods of mediational analysis, showed that Baron and Kenny’s (1986) requirement that a relationship between the independent and dependent variable exists before testing for a mediated effect led to the most Type II errors.

We therefore ran the same mediation analysis as specified above with negative, rather than positive, numbers in the NL task. Consistent with the ANOVA results, regressing group onto the mapping of negative numbers in the NL task resulted in a nonsignificant association (b = −.008, SE = .013, p = .26; Figure 5, panel C). We next entered the mediators into the path analysis. The absolute deviation in mapping negative numbers in the NL task was not associated with score in the numerical agility task (b = −.02, SE = .016, p = .09) whereas it was associated with the scores in the computational estimation task (b = .002, SE = .001, p = .023). The scores in the numerical agility and in the computational estimation task were significantly associated with group (b = .71, SE = .31, p = .01 and b = −17.06, SE = 9.18, p = .03; Figure 5, panel D). Bias-corrected bootstrapped confidence intervals for the specific indirect effects of the mapping of negative numbers on group membership through computational estimation task (−0.35, 95% CI [−0.167, 0.013]) and numerical agility task (−0.016, 95% CI [−0.092, 0.017]) overlapped zero. This result also fails to support an indirect effect of the mapping of negative numbers on group through the scores in the numerical agility and in the computational estimation task.

Number-Space Mapping and Visuospatial Skill: A Mediation Analysis

The results of the mediation analysis suggest that the connection between basic numerical skills (i.e., mapping of positive numbers) and mathematical expertise is fully mediated by advanced numerical skills. While these results cannot provide a causal inference of the role of basic numerical skills in mathematical expertise, they are in line with the theoretical view that formal mathematical competences may rely on basic numerical representations (De Smedt et al., 2013; Feigenson, Libertus, & Halberda, 2013; Halberda et al., 2008). Moreover, they also support the view that numerical polarity is dissociable (for a detailed review see, Tzelgov et al., 2015) and therefore plays a role in the link between numerical skills and whether a given participant is mathematician.

However, these results might be in turn mediated by different cognitive process. In fact, despite a fine matching between the two groups on several dimensions, we observed that mathematicians outperformed nonmathematicians at visuospatial abilities as indexed by the scores in the block design subtest (Groth-Marnat & Teal, 2000). To clarify this issue, we verified whether the scores in the block design subtest influenced the performance in the NL task. Thus, we run an ANCOVA with absolute deviation of positive numbers as dependent variable, group as independent variable, and block design scores as covariate. The effect of the group was no longer significant, F(1, 35) = 1.51, MSE = 357, p = .23, η_p² = .04, thereby suggesting that the difference between mathematicians and nonmathematicians in mapping positive numbers disappeared when visuospatial skills are taken into account. Following this reasoning, we reran the mediation model in which the association between mapping positive integers in the NL task and belonging to the group of mathematicians is mediated by the scores on the numerical agility task and the computational estimation task, this time adding the scores in the block design as covariate. Regressing participant group onto the positive numbers absolute deviation resulted in a nonsignificant association between the variables (b = −.03, SE = .024, p = .10; Figure 5, panel E), which is consistent with the ANCOVA results. We then entered the two mediators, numerical agility and computational estimation into the model. The mapping of positive numbers in the NL task was still associated with the scores in the computational estimation task (b = .003, SE = .001, p = .008), but not with the scores in the numerical agility task (b = −.024, SE = .019, p = .10). Both scores in the numerical agility task (b = 0.58, SE = .33, p = .038) and in the computational estimation task (b = −17.06, SE = 10.41, p = .05) were, in turn, significantly associated with group. After the mediation, the direct association between the mapping of positive integers in the NL task and group remained nonsignificant (b = −.019, SE = .036, p = .30; Figure 5, panel F). Bias-corrected bootstrapped confidence intervals for the specific indirect effects of the mapping of positive numbers on group membership through computational estimation task (−0.058, 95% CI [−0.297, 0.045]) and numerical agility task (−0.014, 95% CI [−0.12, 0.013]) overlapped zero, when the performance in the block design subtest was used as covariate. Therefore, this result failed to support the presence of an indirect effect of the mapping of positive numbers on group through the scores in advanced numerical tasks when the scores in block design subtest were added as covariate. The inclusion of block design subtest scores as covariate compromised the link between the ability to map positive numbers and advanced numerical skills. Similar results were observed when we repeated the analysis with negative, instead of positive, numbers (Figure 4, panel G-H).

Figure 4.

SD of estimates in the NL task for negative and positive numbers in mathematicians and nonmathematicians (Error bars represent 95% CI). * p < .05. ** p < .01.

To further investigate the relation between spatial mapping and visuospatial abilities, we ran two mediation models to see if numerical polarity (positive or negative) was associated with a higher chance of being a mathematician when this relation was mediated by the performance in the block design subtest.

As for the previous mediation model, we regressed participant group onto the absolute deviation of positive numbers variable, which yielded a significant association between the variables (b = −.06, SE = .023, p = .007). We then entered the block design performance as mediator into the model. The absolute deviation for positive numbers in the NL task was significantly associated with block design (b = −.13, SE = 0.03, p < .001), which in turn was associated to the belonging to the mathematicians group (b = .26, SE = 0.12, p = .013). Once the mediator was entered into the model, the direct association between the mapping of positive numbers in the NL task and group became nonsignificant (b = −.03, SE = .024, p = .10; Figure 5, panel I). A bias-corrected bootstrap confidence interval for the specific indirect effect of mapping of positive numbers on group membership through block design was entirely below zero (−0.035, 95% CI [−0.116, −0.006]). This result supports an indirect effect of the mapping of positive numbers on group through the scores in the block design subtest. Interestingly, when substituting the group dichotomous variable with the scores in the numerical agility task, the pattern of results remained the same with block design scores mediating the relation between the accuracy in mapping positive numbers and the performance in the numerical agility task.

We then run the same mediation analysis entering into the model the mapping of negative numbers as independent variable. Regressing group onto the mapping of negative integers in the NL task resulted in a nonsignificant association (b = −.008, SE = .01, p = .26). We next entered the block design as mediator into the model. The absolute deviation for negative numbers in the NL task was significantly associated with block design (b = −.07, SE = 0.03, p = .012), which in turn was associated to the belonging to the mathematicians group (b = .33, SE = 0.11, p = .001). Once the mediator was entered into the model, the direct association between the mapping of negative numbers in the NL task and group remained nonsignificant (b = .01, SE = .02, p = .29; Figure 5, panel J). Despite the significant association between the mapping of negative numbers and, in turn, the significant association between block design and group membership in the mediation analysis, a bias-corrected bootstrap confidence interval for the specific indirect effect of the mapping of negative numbers on group membership through block design overlapped zero (−0.024, 95% CI [−0.075, 0.001]). This result fails to support an indirect effect of the mapping of negative numbers on group through the scores in the block design subtest. However, when substituting the group dichotomous variable with the scores in the numerical agility task, the pattern of results highlights the block design scores mediating the relation between the accuracy in mapping negative numbers and the scores in the numerical agility task.

Discussion

In the present study, mathematicians and nonmathematicians completed basic and advanced numerical tasks in order to verify how low and high numerical skills are related to advanced mathematical expertise. Both groups displayed a similar performance on the numerical Stroop task, thereby suggesting that a simple task involving the automatic numerical processing might not be linked to superior mathematical competences. However, we do not exclude that other numerical tasks exploring the automatic processing of numbers may highlight significant differences in individuals with different level of math expertise (Cipora et al., 2015). Regarding advanced numerical tasks, in line with previous results, mathematicians outperformed nonmathematicians in computational estimation and in the flexible use of arithmetical operations (Dowker et al., 1996; Hanson & Hogan, 2000; Levine, 1982). In addition, mathematicians showed better performance on the numerical agility task. Crucially, mathematicians displayed a more accurate spatial mapping of positive numbers, whereas no difference emerged for negative numbers. Therefore, the attainment of advanced mathematical expertise in this study appears to be primarily and specifically related to a basic numerical skill, such as the spatial mapping of positive integers. Nevertheless, the relation between basic and advanced numerical skills became nonsignificant when visuospatial abilities were taken into account. As corroborated by a mediation model, the relation between the spatial mapping of numbers and superior mathematical competences was mediated by visuospatial abilities. This result strongly suggests that while basic numerical domain-specific processes are likely to be linked more advanced mathematical skills, this relation is fully mediated by a different domain process such as visuospatial processing.

A detailed analysis of the NL provided an accurate description of the mapping performance for mathematicians and nonmathematicians. Mathematicians displayed a more linear pattern in the positioning of positive numbers, which perfectly coupled with their more accurate mapping. Interestingly, mathematicians, irrespectively from the accuracy of the positioning, were also more coherent as group when placing both positive and negative numbers. This result might suggest that mathematicians were more likely to use similar (and possibly more efficient) mapping strategies, whereas among nonmathematicians there was less agreement on the strategy to be adopted. Given that the number line entailed the interval from −1,000 to 1,000, some participants probably estimated the position of the number zero on the line as a reference anchoring point for calibrating other estimates. We adopted a robust resampling technique to infer the position of the number zero on the line as indexed by the intercept of the regression line interpolating all the estimates as a function of the target numbers. Crucially, the two groups displayed a similar estimation of the number zero on the line, which varied only between the two polarity conditions. Therefore, the observed differences in spatial mapping performance are unlikely related to the estimation of the number zero on the line.

Mathematicians outperformed nonmathematicians only in the mapping of positive numbers, which are considered as “primitives” of numerical representation. Moreover, it is worth noting that mathematicians actually showed a better performance in mapping positive numbers compared to negative numbers, whereas nonmathematicians displayed a similar performance in both polarity conditions. On the one hand, it might be possible that mathematicians displayed a better spatial mapping of numerical “primitives” (i.e., positive numbers) because, with advanced expertise, the spatial representation of these numbers becomes more accurate and automatized compared to more artifactual numbers (i.e., negative). On the other hand, it might be possible that positive numbers were more likely to elicit in expert individuals the application of advanced mapping strategies (e.g., segmentation of the line to find reference points, anchoring) compared with negative numbers. It is worth noting that nonmathematicians displayed less accurate estimates as a function of target size moving from left (negative numbers) to right (positive numbers). In particular, the estimation of large positive numbers (e.g., 521, 612, 689, 770, 809, and 872) appeared to be particularly difficult for nonmathematicians, whereas mathematicians displayed an accurate performance also for those numbers. Mathematicians could possibly use advance anchoring points (i.e., 750) to adjust their estimates whereas nonmathematicians may have used a more inconsistent strategy.

The ability to map positive numbers appears to be connected to visuospatial skills (measured by block design in our study) which in turn predicted the likelihood to belong to the group of mathematician as well as the performance in the numerical agility task. More importantly, this link can fully explain the relation between basic numerical skills and advanced mathematical achievement. Previous studies have highlighted the relation between block design performance and mathematical achievement. In particular, block design scores and, more broadly, visuospatial skills, have been correlated with math problem solving skills (Hale, Fiorello, Bertin, & Sherman, 2003; van Garderen, 2006) as well as with spatial components of calculation such as borrowing and carrying (Rourke, 1993; Venneri, Cornoldi, & Garuti, 2003). Therefore, it is not surprising that mathematicians displayed a better performance in the block design subtest compared with nonmathematicians. However, what is the relation between block design performance and NL task? A possible explanation is that an accurate placing of numbers may require participants to maintain and actively transform different spatial locations in their memory (e.g., landmarks) while moving the mouse cursor to select the desired position on the line. The ability to maintain and transform spatial information online is similarly required by the block design subtest in which red and white cubes have to be spatially manipulated in order to realize the given target image. The spatial manipulation component of the two tasks could also explain the previously observed relation between mental rotation skills and number line estimation in adults (Thompson, Nuerk, Moeller, & Cohen Kadosh, 2013). Nevertheless, we reiterate that alternative explanations can be formulated and then constitute empirical hypotheses for future studies.

The results of the present study pose important theoretical questions for future research. First, we observed that both mathematicians and nonmathematicians displayed an evident linear mapping for both positive and negative numbers; nevertheless, the mathematicians outperformed the nonmathematicians only in placing positive numbers, and this performance was fully mediated by visuospatial skills. How and at what developmental stage does the relationship between positive numbers and visuospatial skills emerge, and what is the contribution of formal education? Which cognitive function is the driving force in this link, and whether the theoretical framework of numerical primitives and cultural artifacts for positive and negative numbers, respectively, can shed light on the potential cognitive mechanisms?

Another crucial question for future research is to clarify what is specific in domain-specific processes. In our study, the adoption of the mediation analysis allowed us to demonstrate that the prediction of group membership by the NL task is fully mediated by the block design subtest scores, thereby suggesting that the link between the NL task and group membership is crucially influence by different (non-numerical) domain processes. Accordingly, another study has pointed out the association between the NL performance and mental rotation skills, thus reinforcing the role of visuospatial abilities in the accomplishment of the number mapping task (Thompson et al., 2013). Crucially, in the present study, the visuospatial abilities mediated the relation between NL task performance and math expertise.

In sum, we highlighted that mathematicians were more accurate compared with nonmathematicians when it comes to mapping numbers. However, this ability was specific to positive, but not negative numbers, as indicated by different types of analyses that yielded the same conclusion. Moreover, the ability to map positive, but not negative, numbers on the line appeared to be related to advanced mathematical expertise. While such a result could have led to a strong theoretical support for the domain-specific advocates, a mediation analysis revealed that the relation between the performance in the NL task and the mathematical expertise was fully mediated by visuospatial skills. Therefore, the relationship between basic numerical domain-specific processes and more advanced mathematical skills can be attributed to a different domain process such as visuospatial skills.

The Numerical Agility Task

The instructions for the numerical agility task were: “Create the number 24 using the numbers provided. You may add, subtract, multiply, and divide. You may use parentheses and fractions. You must use each digit exactly once. You may not glue digits together (e.g., 14). Powers and decimals are not allowed.”

Example: Create the number 24 using 1, 5, 5, 5.

$$24=25-1=5\times 5-1=5\left(5-\frac{1}{5}\right)$$

Item 1

Create the number 24 using 7, 5, 5, 4.

Keep in mind that 24 = 6 × 4 and that the answer will be of the form displayed below:

$$.\; .\; .\left(.\; .\; .-\frac{.\; .\; .}{.\; .\; .}\right)$$

Item 2

Create the number 24 using 3, 3, 8, 8.

Keep in mind that:

$$24=8\times 3=\frac{8}{\left(\frac{1}{3}\right)}$$

The answer will be of the form shown below:

$$\frac{.\; .\; .}{\left(.\; .\; .-\frac{.\; .\; .}{.\; .\; .}\right)}$$

Item 3

Create the number 24 using 1, 3, 4, 6.

Keep in mind that 24 = 6 × 4 and that the answer will be of the form shown below:

$$\frac{.\; .\; .}{\left(.\; .\; .-\frac{.\; .\; .}{.\; .\; .}\right)}$$

Item 4

Create the number 24 using 3, 3, 7, 7.

Keep in mind that 24 = 21 + 3.

(Note that no clue was provided for this problem.)

Item 5

Create the number 24 using 2, 3, 10, 10.

(Note that no clue was provided for this problem.)