Classification-based data mining for identification of risk patterns associated with hypertension in Middle Eastern population

Supplemental Digital Content is available in the text

Abstract

Hypertension is a critical public health concern worldwide. Identification of risk factors using traditional multivariable models has been a field of active research. The present study was undertaken to identify risk patterns associated with hypertension incidence using data mining methods in a cohort of Iranian adult population.

Data on 6205 participants (44% men) age > 20 years, free from hypertension at baseline with no history of cardiovascular disease, were used to develop a series of prediction models by 3 types of decision tree (DT) algorithms. The performances of all classifiers were evaluated on the testing data set.

The Quick Unbiased Efficient Statistical Tree algorithm among men and women and Classification and Regression Tree among the total population had the best performance. The C-statistic and sensitivity for the prediction models were (0.70 and 71%) in men, (0.79 and 71%) in women, and (0.78 and 72%) in total population, respectively. In DT models, systolic blood pressure (SBP), diastolic blood pressure, age, and waist circumference significantly contributed to the risk of incident hypertension in both genders and total population, wrist circumference and 2-h postchallenge plasma glucose among women and fasting plasma glucose among men. In men, the highest hypertension risk was seen in those with SBP > 115 mm Hg and age > 30 years. In women those with SBP > 114 mm Hg and age > 33 years had the highest risk for hypertension. For the total population, higher risk was observed in those with SBP > 114 mm Hg and age > 38 years.

Our study emphasizes the utility of DTs for prediction of hypertension and exploring interaction between predictors. DT models used the easily available variables to identify homogeneous subgroups with different risk pattern for the hypertension.

1. Introduction

Hypertension is today a critical health concern worldwide.^[1] Globally, the overall prevalence of hypertension in adults age ≥ 25 years was around 40% in 2008 and the number of people with elevated blood pressure (systolic blood pressure [SBP] ≥ 140 mm Hg or diastolic blood pressure [DBP] ≥ 90 mm Hg) had increased from 600 million in 1980 to a billion in 2008.^[2] A national survey, conducted in 2005, showed that approximately 25% or 6.6 million Iranians, age 25 to 64 years had hypertension and 46% or 12 million Iranians, age 25 to 64 years, had prehypertension. This survey also showed that among patients with hypertensive, only 34% were aware of their elevated blood pressure.^[3] Worldwide, raised blood pressure is estimated to cause 51% of stroke deaths and 45% of coronary heart disease deaths,^[2] and around 13% of all deaths.^[4] Recently, we reported that systolic–diastolic hypertension increased the risk of cardiovascular disease (CVD) and mortality outcomes among both middle aged and elderly Iranian populations followed for over 10 years of follow-up.^[5]

Evidence from prospective cohort studies suggests that several factors, such as age, body mass index (BMI), blood pressure, smoking, family history of hypertension, and physical inactivity can determine the risk for progression to hypertension.^[4] Therefore, combining these known risk factors into a multivariable model to identify populations at higher risk for hypertension incidence has been a field of active researches.^[4,6–9] Several prediction models for hypertension have been derived using traditional methods such as Cox regression, logistic regressions, and Weibull regression,^[4] statistical methods which require that 1 or more assumptions be met; when these assumptions are violated the results of the analysis can be misleading.^[10,11] In addition, assessment of interactions using these models requires prespecification of the interaction terms, for example, in a linear model involving outcome Y, and 2 predictor variables (x₁ and x₂), the product term x₁x₂ is the common representation of the 2-way interaction effect. As the number of variables in the model increases, the number of possible interactions that can be investigated is large and leads to a complicated model that can be difficult to fit and interpret.^[11,12] Decision trees (DT) are nonparametric regressions introduced in 1963 and many variants and extensions of the tree methods have been developed in the last 50 years, and are widely used in many fields such as machine learning, data mining, and pattern recognition.^[13] The trees provide a very flexible framework without prespecifying the interactions, and the investigator can instead assess interactions after trees are grown. This method makes fewer modeling assumptions which can be used as an explorative method to partition objects in a dataset into groups with a similar outcome.^[12,13]

DT uses a flowchart-like graph which breaks down a complex decision-making process into a collection of simpler decisions, thus providing a solution, which is often easier to interpret by users who are not too much familiar with statistical methods.^[14] Interactions or nonlinear relationship between the predictors and the outcome variable can be captured automatically by DTs. These methods are not sensitive to outliers and missing data and are useful when a dataset has more categorical variables.^[15,16]

In the present study, 3 types of DT algorithms (C5.0, Classification and Regression Tree [CART], and Quick Unbiased Efficient Statistical Tree [QUEST]) were applied for construction of the models to identify relative importance of factors contributing to incidence of hypertension, and detecting the subgroups with different risk patterns based on related covariates.

To our knowledge, this is the first report describing application of DT methods for prediction of hypertension based on a cohort dataset.

2. Methods

2.1. Study population

The Tehran Lipid and Glucose Study running to determine the risk factors for noncommunicable diseases among a population of Iran's capital city, Tehran. The rationale and design of the study have been described elsewhere.^[17] Briefly, the baseline study (phase 1) was performed from 1999 to 2001, which more than 15,000 people, age > 3 years, were selected and followed in 3 consecutive phases, that is, 2002 to 2005 (phase 2), 2005 to 2008 (phase 3), and the last 2009 to 2012 (phase 4). In the second phase, 3550 new people entered and were followed in the next 2 phases (phases 3 and 4). Subjects were categorized into the cohort and intervention groups, the latter to be educated for implementation of life style modifications. In our study, subjects age ≥ 20 years (n = 12,808) from the first and second phases were selected. From this population, we excluded subjects with prevalent hypertension (n = 2660) at baseline, those with missing data on blood pressure (n = 311) and participants if they self-reported CVD (n = 609). We also excluded pregnant women and subjects if they were on antihypertensive drugs. After excluding those lost to follow-up (n = 2905), the remaining 6205 subjects (2763 men and 3442 women), representing 68% of those eligible, were followed from the date of enrollment through to the end of phase 4, for the incidence of the hypertension (see Supplementary Fig. 1, which shows the flow diagram for the selection of study subjects). All participants signed informed consent forms, and study protocol was approved by the ethical committee of the Research Institute for Endocrine Sciences of Shahid Beheshti University of Medical Sciences, Tehran, Iran.

2.2. Measurements

The baseline examination included data collection on demographic characteristics, anthropometric indices, biochemical parameters, smoking status, physical activity, and past medical and drug history. For women, information on previous pregnancy history, menstruation status, interventions to prevent pregnancy, and history of hyperglycemia or hypertension in previous pregnancies was collected. Weight, height, waist circumference (WC), and wrist circumference were measured in accordance with standard protocols.^[17] BMI was calculated as weight in kilograms divided by the square of the height in meters squared (kg/m²).

After a 15-minute rest in the sitting position, 2 measurements of blood pressure were taken, on the right arm, using a standardized mercury sphygmomanometer (calibrated by the Iranian Institute of Standards and Industrial Researches), and the mean of the 2 measurements was considered as the participant's blood pressure. Fasting plasma glucose (FPG), 2-h postchallenge plasma glucose (2h-PCPG), triglycerides, total cholesterol (TC), and high-density lipoprotein cholesterol were measured using previously reported methods.^[18] Estimated glomerular filtration rate (eGFR) was obtained using an equation derived from the Modification of Diet in Renal Disease study.^[19] All measurements were conducted by the same methods at the baseline and follow-up examinations.

2.3. Definition of variables and outcomes

Education level was categorized to 4 levels as illiterate, 1 to 9, 9 to 12, and over 12 years of schooling. A current smoker was defined as a person who smokes cigarettes daily or occasionally. The family history of premature CVD was considered as any experience of fatal or nonfatal myocardial infarction, stroke or sudden cardiac arrest in first-degree relatives, if it occurred before 55 years of age in male relatives and before 65 years of age in female relatives. Family history of diabetes was defined as having type 2 diabetes in first-degree relatives. On the basis of their self-reported levels of leisure time physical activity, participants were categorized into 2 groups in which “inactive” were those doing exercise or labor <3 times a week or performing activities achieving a metabolic equivalent value below 600. Participants were also grouped in 2 categories based on participating in the life style intervention. Women were categorized into 3 groups on the basis of their menstruation status; having normal or menstruating by taking medication, normal menopause, early menopause because of surgery or other reasons. Women were also categorized to 7 levels considering pregnancy prevention methods; use of hormonal contraceptive drugs, intrauterine devices, using condoms, withdrawal method, tubectomy/vasectomy, and not applicable. Incidence of hypertension was defined based on SBP ≥ 140 mm Hg or DBP ≥ 90 mm Hg or taking antihypertensive medications in all phases of the study.

2.4. Statistical analysis

Participants’ baseline characteristics were compared between hypertensive and normotensive subjects across the men, women, and total population. Continuous baseline characteristics were compared between followed-up versus nonfollowed up participants. Differences were tested by t test and chi-squared and, 2-tailed P values < 0.05 were considered statistically significant throughout.

2.4.1. DT models building

2.4.1.1. Data preparation

The final data included total population dataset (6205 subjects and 30 variables), dataset of male participants (2763 subjects and 30 variables), and dataset of female participants (3442 subjects and 35 variables). Missing data were imputed using the CART algorithm,^[20] separately for the female and male datasets. In order to identify the best subset of variables to include in models building process, we applied the multivariate filter approach.^[21] All prediction models were developed using 70% of the each dataset and evaluated on the remaining (30%). Because data in our study were imbalanced, we applied a method called Synthetic Minority Oversampling Technique for balancing the train datasets.^[22,23] (The detailed methods of data preparation are provided as a Supplemental Content 1.)

2.4.1.2. Classification methods

Classification or DT is a nonparametric methodology that creates a flowchart-like structure based on some predictors and their interactions which are most important in determining the outcome. A tree is a set of nodes and branches; the topmost node in a tree is the root node. Growth of the tree starts from root which split into child nodes based on predictors that produce maximum separation among the generated child nodes. Some statistical tests (splitting criteria) are used to select the variable that best partitions the root node into distinct classes (positive/negative). The partitioning repeated iteratively for each internal node until following stopping criteria is satisfied: if the cases in a node are all of the same class, then that node becomes a leaf node and is labeled by the class. There are no remaining variable on which the cases may be further partitioned; in this case, that node is labeled by the most common class.^[16] Each path from the root node through a leaf node represents an “if-then” rule. For example, “if condition 1 and condition 2 and condition k occur, then outcome j occurs.” Different algorithms have been developed for learning DT that are variations of a core algorithm described above. These algorithms are distinguished by splitting criteria (e.g., Gini Index, Gain Ratio, and Entropy) and pruning method (removal of branches that do not provide general information to the model).^[13] We applied 3 types of DT algorithm for all 3 datasets; the algorithm with the best performance was selected as a final prediction model. These algorithms are briefly explained in Supplemental Content 1.

2.4.1.3. Evaluation and selection of the models

Overall performance of the models was assessed using the accuracy and the Brier score.^[24] To indicate the discriminative ability of models, we used C-statistic or the area under the curve (AUC), sensitivity, specificity, positive predictive value (PPV), negative predictive value, F-measure (the weighted harmonic mean of specificity and PPV),^[25] and the geometric mean (G-mean).^[26] To select the best models in 3 datasets, we applied the ROC Convex Hull (ROCCH) method^[27,28] (see Supplemental Content 1, which provides further explanation).

3. Results

3.1. Characteristics of participants

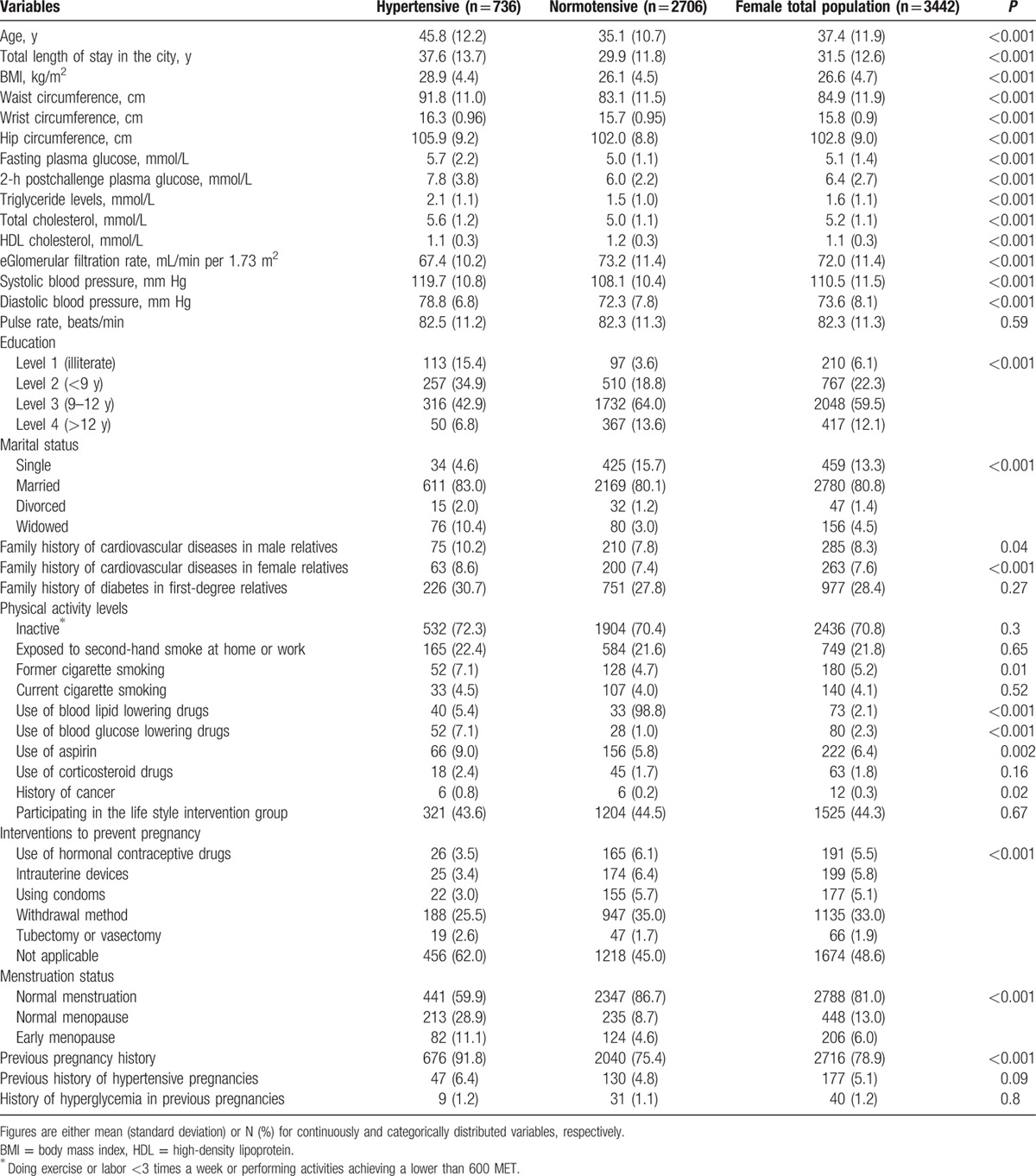
Baseline characteristics of populations are presented in Tables 1 and 2 and Supplementary Table 1. The mean age was 40.1, 37.4, and 38.6 years in the men, women, and total population, respectively. Comparison of continuous baseline variables between the followed and nonfollowed participants showed that the former had lower FPG (5.2 vs 5.3 mmol/L) and eGFR (76.4 vs 77.3 mL/min per 1.73 m²); among the women, only eGFR was lower in the followed, compared to the nonfollowed (72.1 vs 73.4 mL/min per 1.73 m²). During a median 8.7-year follow-up (interquartile range: 8.5–10.6 years), hypertension developed in 1467 subjects (731 men), with cumulative incidence rate of 25.8 per 1000 person-years in the total population.

Table 1.

Baseline characteristics of male population: Tehran Lipid and Glucose Study (1999–2012).

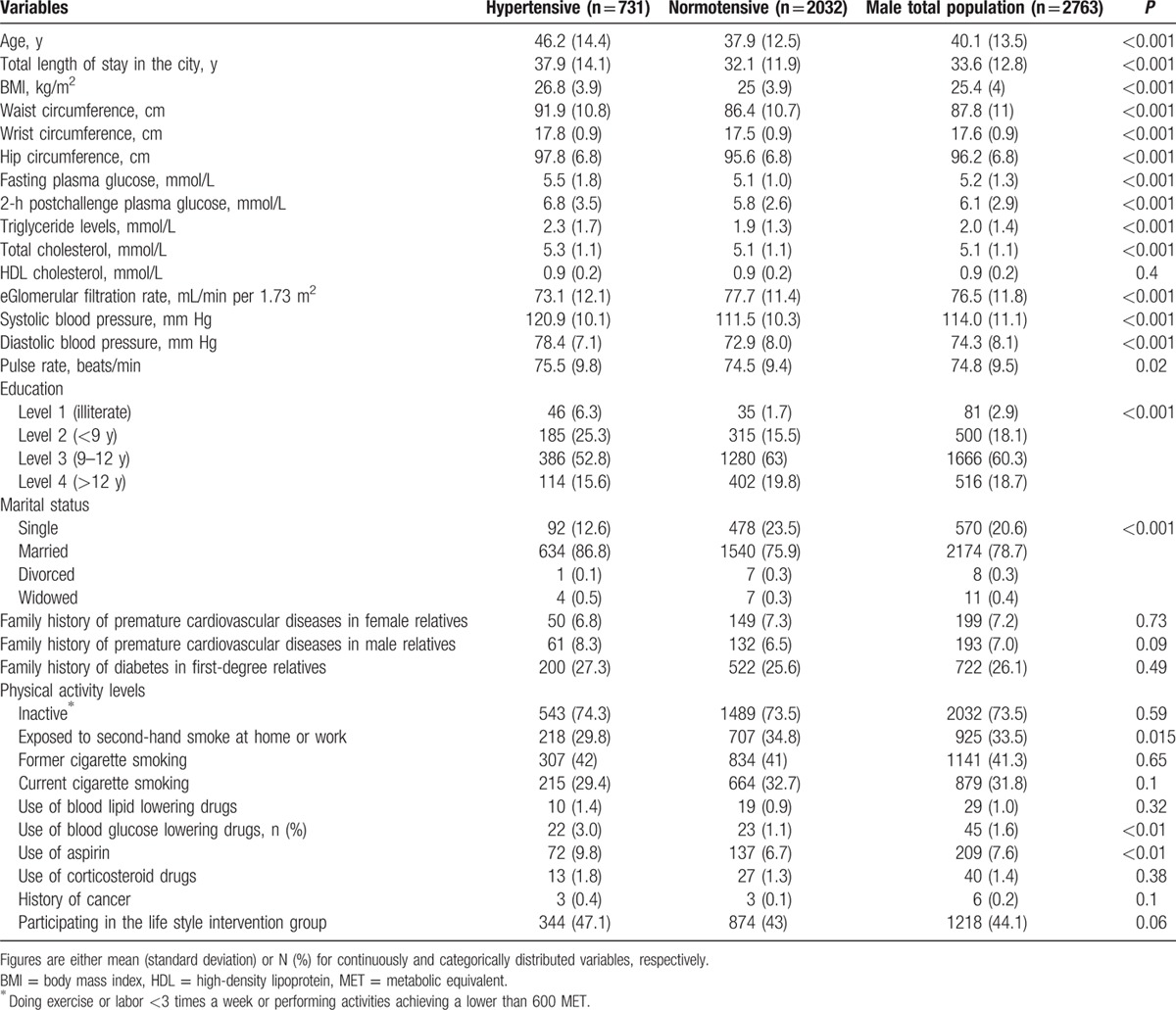
Table 2.

Baseline characteristics of female population: Tehran Lipid and Glucose Study (1999–2012).

3.2. Selected variables

There were 4 subsets of variables selected using a combination of the 2 search strategies and 2 evaluation criteria. To arrive at the final set, the 4 subsets were reviewed to choose the variables that were observed at least in 2 subsets; therefore, 20, 13, and 20 variables were selected to include in the model building process for men, women, and the total population, respectively (see Supplementary Table 2, which shows the list of selected variables for model building).

3.3. Performance of prediction models

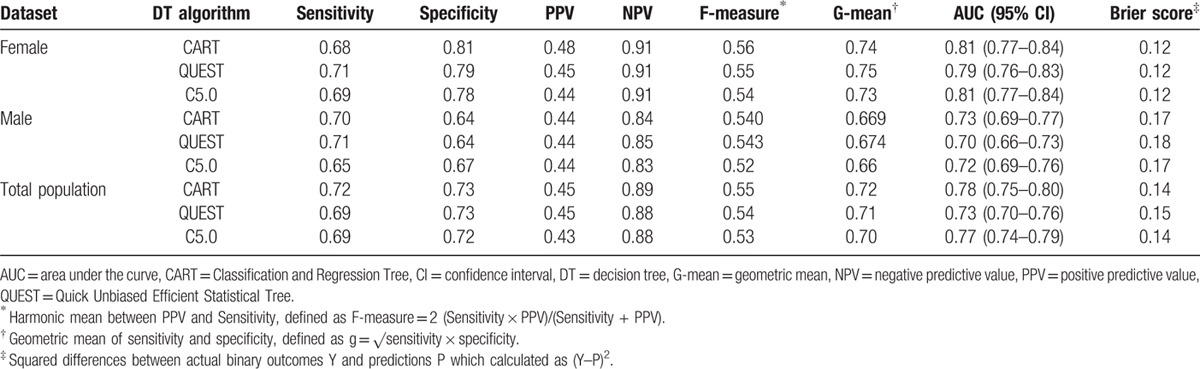
The performances of the 3 types of DT algorithms on the testing datasets have been shown in Table 3. The QUEST achieved the best sensitivity and G-mean, (71% for both) in men and (67% and 75%) in women, respectively. For the total population the CART algorithm had the highest sensitivity and G-mean (72% for both). All models achieved an acceptable discrimination (an AUC > 0.70) in the all datasets. The Brier score in all datasets and all models was <0.25 with range of 0.12 to 0.18, demonstrates the acceptable level of overall performance for all the models.^[24]

Table 3.

Performance of the models in the male, female, and total population: Tehran Lipid and Glucose Study (1999–2012).

3.4. Comparison and choosing the best model

The receiver operating characteristics curve for the models on the 3 testing datasets is shown in Fig. 1. The AUC for women is higher than those for men and the total population. We drew ROCCH for 3 testing datasets (Fig. 1), which shows that in men and women QUEST and CART are optimal models and for total population CART and QUEST are optimal. Considering the 2 performance measures (sensitivity and G-mean) and ROCCH curve, we chose the QUEST as the best model in men and women and the CART for total population.

Figure 1.

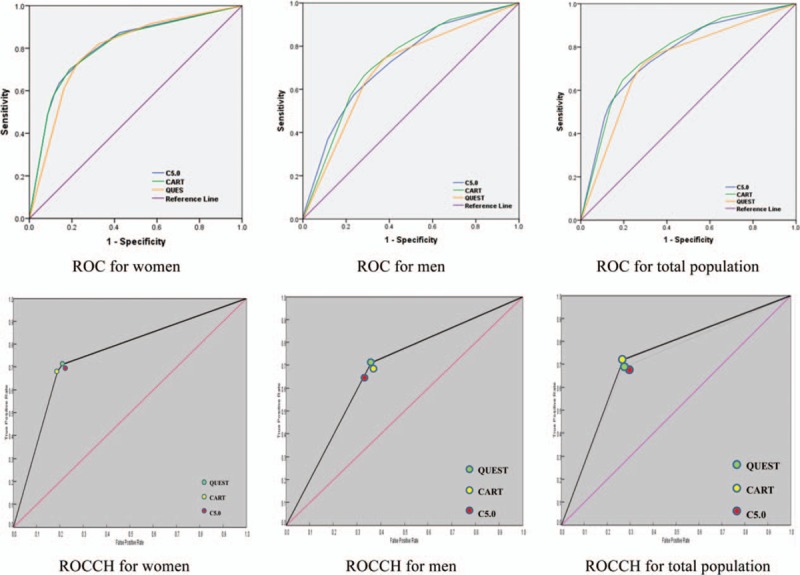
ROC curves and ROCCH for the 3 classifiers on 3 testing datasets, Tehran Lipid and Glucose Study (1999–2012). ROC = receiver operating characteristics, ROCCH = ROC Convex Hull.

3.5. Classification tree models

Figure 2A shows the DT based on the QUEST methodology in the female training dataset. As we described in the results, 13 variables for females were selected for including in the DT analysis (Supplementary Table 2). In the first step, the QUEST algorithm examines all variable to find out which variable has the strongest effects on the outcome. The 1-way analysis of variance and Pearson chi-squared test are performed for continuous and categorical predictor, respectively, and the predictor with the smallest P value is selected.^[29] From Fig. 2A, we note that the most important predictor in women is the SBP. The next step is to determine a cutoff point for the selected predictor. Again, algorithm searches over all possible cut-points, and selects the best one using statistical tests. As Fig. 2A shows, cut-point of 114 mm Hg was found for SBP by the algorithm; therefore, the root node was divided into 2 child nodes by the cut-point. The algorithm recursively is applied for every child node, so that all samples in 1 node are from the same class (normotensive/hypertensive), or other stopping rules reaches to the predefined value.

Figure 2.

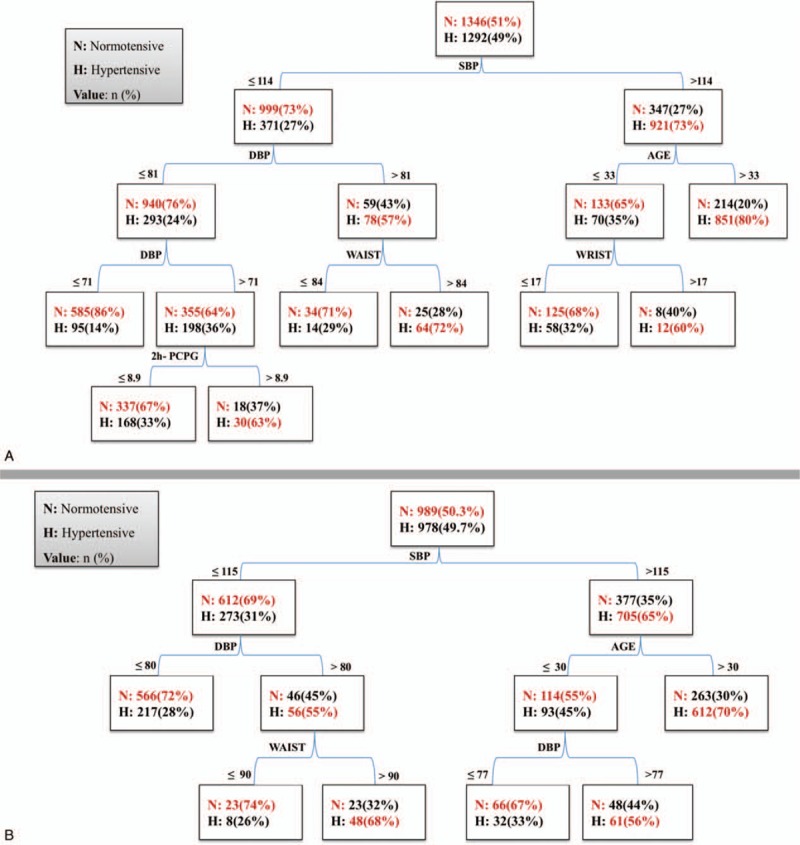
Decision tree models for prediction of hypertension derived from training dataset: (A) female population and (B) male population. Tehran Lipid and Glucose Study (1999–2012). 2h-PCPG = 2-h postchallenge plasma glucose (mmol/L), DBP = diastolic blood pressure (mm Hg), SBP = systolic blood pressure (mm Hg), WAIST = waist circumference (cm).

The QUEST algorithm found 6 variables for prediction of hypertension incidence and generated 8 terminal nodes in women. As we described above, the tree started with SBP with cut-point of 114 mm Hg. Two nodes or subgroups were identified: a subgroup of 1268 persons (73% incidence) with SBP > 114 mm Hg and a subgroup of 1370 persons (27% incidence) with SBP < 114 mm Hg. Women with SBP > 114 mm Hg were further partitioned with respect to age with split point of 33 years. Women with SBP > 114 mm Hg and age > 33 years had the most probability for incidence of hypertension (80%), and there was no other predictor for subdivision of these subgroup. In contrary, women with SBP > 114 mm Hg and age ≤ 33 years were further subdivided based on wrist circumference. In a group of women with SBP > 114 mm Hg, age ≤ 33 years and wrist circumference > 17 cm, the incidence of hypertension was 60%.

In the left side of the tree, among women with SBP ≤ 114 mm Hg, other predictors (DBP, WC, and 2h-PCPG) were found by the algorithm. Those women with DBP > 81 mm Hg and WC > 84 cm had a significant risk of hypertension (72%); those with DBP of 71 to 81 mm Hg had a high risk of hypertension, depending on their level of 2h-PCPG: women with 2h-PCPG > 8.9 mmol/L had higher incidence risk (63%).

Figure 2B shows that the DT for men was based on QUEST algorithm; it used 4 variables for prediction of hypertension incidence and generated 6 terminal nodes (subgroups). The first variable was SBP which divided the male population into 2 subgroups; those with SBP > 115 and those with SBP ≤ 115 mm Hg. The tree shows that the risk of hypertension in men with SBP > 115 mm Hg depends on age; that is, men > 30 years had a higher risk (70%), while, among men with age ≤ 30 years, the risk depends on DBP. In left side of the tree, a subgroup with SBP ≤ 115 mm Hg, those with DBP > 80 mm Hg and WC > 90 cm had higher risk (68%).

The DT for the total population based on CART algorithm is shown in Fig. 3; it used 5 variables for construction of prediction model and generated 8 terminal nodes (subgroups). The most important predictor was SBP, which divided the total population into 2 segments; in the right side of the tree, in those with SBP > 114 mm Hg, the risk of hypertension depended on age and DBP: those with age > 38 years had higher risk (81%), while in those with age ≤ 38 years, the risk of hypertension increases with DBP > 82 mm Hg. In the second segment (left side of the tree), in those with SBP ≤ 114 mm Hg the risk depended on the DBP, WC and FPG levels: those with DBP > 70 mm Hg, WC > 83 cm, and FBS > 5 mmol/L had higher risk (60%).

Figure 3.

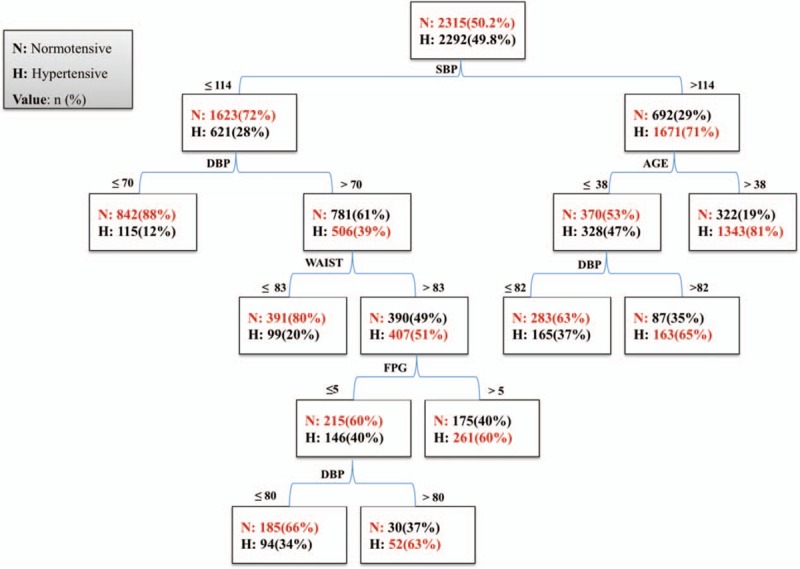
Decision tree models for prediction of hypertension in entire population derived from training dataset: Tehran Lipid and Glucose Study (1999–2012). DBP = diastolic blood pressure (mm Hg), FPG = fasting plasma glucose (mmol/L), SBP = systolic blood pressure (mm Hg), WAIST = waist circumference (cm).

4. Discussion

In the present study, we developed models to predict hypertension incidence for a cohort population using data mining approaches, performed for male, female, and the total population, separately. The results of the present study showed that QUEST and CART were the optimal classifiers for predicting hypertension. The QUEST was the best model in men and women, whereas, for the total population the CART was the best. The common predictors for both genders and the total population were SBP, age, DBP, and WC. For women additional variables (wrist circumference and 2h-PCPG) were found for the prediction model. For the total population, FPG was found by the CART algorithm, in addition to the 4 common predictors.

Our DT models have acceptable discriminative power with C-statistics in range of 0.70 to 0.79. The existing risk models developed using traditional statistical methods have C-statistics in the range of 0.71 to 0.81.^[4] The Brier scores (0.12–0.18) and G-means (0.67–0.75) show the overall good performance of the models.^[24,30]

A systematic review on 13 existing prediction models has shown that age, sex, BMI, SBP, and DBP, parental history of hypertension and cigarette smoking were the most frequently predictors in the final risk models.^[4] Although some of the predictors in our study had been previously identified as risk factors, DT analysis provided a deeper insight into their relative importance in risk prediction and how these risk factors interact to increase risk of hypertension.

Each path from root node to the terminal nodes in top-down fashion is a decision rule which is a combination of several predictors (3 or 4). Each decision rule defines an interaction between a subset of variables. Such a 3- or 4-way interaction term would almost never be detected by traditional methods. For example, DT in our study identified interaction between age and SBP and also, by generating optimal cut-points showed that how these 2 variables interact, for example, in the total population, those who have SBP > 114 mm Hg and age > 38 years have higher risk of hypertension than those with age < 38 years (81% vs 47%). It shows a nonlinear relationship between SBP and risk of hypertension; that is, the association between SBP and hypertension risk differs with level of age. In traditional regression models, the users need to have a powerful prior knowledge about which interactions may be important or which main effects may be statistically significant before fitting the model.^[11,31] Of 13 existing risk models, only 2 models have so far included a predefined interaction term between age and blood pressure.^[4,7] Application of logistic regression models among healthcare providers who may not be familiar with complex mathematical formulas requires converting the logistic equations to a point scoring system^[4]; for example, we previously developed a point scoring system, using traditional multivariable technique for prediction of the 6-year risk of incident hypertension, and categorized age into 10-year groups and divided SBP into 5 mm Hg categories to assess interaction between age and SBP.^[7] Although point-scoring format of risk estimation might facilitate the use of these tools among healthcare providers, performance of the point-scoring format may be lower than that of the original model.^[4] Second, categorization of continuous variables prior to construct a point-scoring model is a potential drawback that may have affected model performance.^[4]

In addition, DTs permit some individuals to be classified based on only 1 or at most a few variable, whereas, the traditional models require that all variables be available.^[16]

An interesting finding in our study was the predictability wrist circumference in women for hypertension risk estimation that has not yet been observed in current risk prediction models.^[4] We recently evaluated the effect of wrist circumference on risk of incident hypertension in women age ≥ 30 years, using Cox proportional hazard regression and found a significant interaction between WC and wrist circumference in risk prediction of hypertension (demonstrating that in women with WC < 95 cm increase in wrist circumference was independently associated with hypertension).^[32] Our study shows that wrist circumference > 17 cm increases the risk for hypertension only among women with SBP > 114 mm Hg and age ≤ 33 years. Therefore, we found an interaction between wrist circumference, age, and SBP in women for risk prediction.

The present study also determined the predictability of 2h-PCPG for hypertension incidence in women. Even though 2h-PCPG was included in all models, it was found only in women as a predictor: those women with SBP ≤ 114 and DBP between 71 and 81 mm Hg had increased risk when 2h-PCPG level was > 8.9 mmol/L. As increased level of 2h-PCPG is a surrogate of insulin resistance,^[33] results of the present study are consistent with our previous findings that homeostasis model assessment of insulin resistance, an indicator of insulin resistance, was associated with incident hypertension only among women,^[34] which may be explained by the fact that WC in men is more influenced by visceral fat, whereas it is composed mostly of subcutaneous adipose tissue in women.^[35] Compared to the subcutaneous abdominal fat, visceral abdominal fat contributes considerably to insulin resistance^[35]; hence, in the DT model of men, it appears that the effect of WC per se does not permit the emergence of other predictors, in this case, 2h-PCPG; on the contrary, in women, it seems that 2h-PCPG (a measure of insulin resistance) and WC are independent predictors for hypertension. As decision rules in Fig. 2A show, each of these predictors has been observed in 2 different rules. Among the current risk models, 2h-PCPG has not been included as a predictor in the final model,^[4] 1 reason for which is that most of the risk models excluded diabetic subjects from the study^[4]; another explanation may be that those studies did not include 2h-PCPG in the list of candidate predictors. As an ancillary analysis for developing a practical model in clinical decision making or healthcare systems, we excluded 2h-PCPG from the predictor lists, and repeated the analysis with the same previous parameters (for women). We observed a reduction in sensitivity (from 0.71 to 0.69) and an increase in specificity (from 0.79 to 0.80) of the models; it found 5 variables for prediction of hypertension incidence and generated 6 subgroups (Supplementary Fig. 2). Generally, DT models in our study showed that in all 3 final models, SBP was the most important predictor following age, DBP, and WC. The importance of WC in predicting cardio-metabolic risk factors such as elevated blood pressure has been examined in many large epidemiological studies,^[7,9,36] which report that selection of the most appropriate cut-points for WC is a complex process because it is influenced by sex, race/ethnicity, age, BMI, and other factors.^[36] The DT in our study revealed interactions between WC and other factors and identified optimal cut-points for WC; in men (90 cm), in women (84 cm), and in the total population (83 cm), all of which were associated with increased risk of hypertension when combined with other risk factors such as elevated SBP and DBP. An Iranian national cross-sectional survey with more than 70,000 participants, age 25 to 64 years, showed that optimal cut-points of WC for detecting of hypertension were about 90 and 94 cm in men and women, respectively.^[37] Our study identified lower cut-points for WC in women (84 cm); this difference may be related to the cross-sectional design of the national survey study.

It is also important to note that the identified risk groups in the DTs do not mean that there is no predictive ability for other variables within those groups. What the risk groups do is define a limited set of characteristics that are the most meaningful for grouping patients based on risk of hypertension. When a DT is grown to full depth, many other variables may be involved in prediction; however, growing trees to full depth leads to over-fitting.^[15,16] For example, when the number of levels below the root node in DT increased from 3 to 6, in men data, other variables such as eGFR and FPG were allowed to be selected in the 6th level. However, sensitivity of the DT decreased from 71% to 63% (data are available on request).

The strengths of our study are that we used data from a large population sample, which allowed us to develop and validate separate prediction models for men, women, and the total population; we also included people with diabetes in our study because, according to the Eighth Joint National Committee, the cut-point of 140/90 mm Hg is defined as the threshold of treatment in patient with diabetic^[38]; therefore, our models are applicable to this segment of population. We used a broad range of variables such as medical history and drug use and applied multivariable filter approaches to identify the best subset among those variables to include in the model building. Missing data were analyzed, and CART algorithm was applied for imputation of missing data. We used graphical techniques in addition to the scale metric for evaluation and comparing the models performance. The overall performance of our models to predict the 10-year incidence of hypertension is as good as that of other current models, but with greater ease of use in clinical practice. To find the probability of risk for a person, it is enough to determine to which path of the tree the person belongs; then, the probability will be the value of the terminal nodes in that path. For example, translation of the right-most paths in DT for whole population (Fig. 3) is as follow: If a person has SBP > 114 mm Hg and age of >38 years, then, he has 81% risk of hypertension in next 10 years. Additionally, DTs’ models can be used in the screening programs for identification of different risk groups (e.g., from Fig. 3), a group of people with SBP ≤ 114 mm Hg and DBP ≤ 70 mm Hg have lowest risk (12%) for hypertension in the next 10 years. As, there will never be enough resources to implement every program for all target groups, health policy makers prefer interventions that target high-risk groups.^[39] Therefore, using DTs’ models, they can implement specific interventions for each group according their risk probabilities (low-risk, moderate-risk, and high-risk groups). Moreover, the DT models like any other statistical prediction models can be used to develop a user-friendly and interactive web-based tool or simple medical calculator on mobile devices^[40] that calculates 10-year hypertension risk predictions.

4.1. Limitations of this study

Limitations of our study include first, about 32% of participants were lost to follow-up. A number of authors have proposed a value of 30% to 50% as acceptable level of loss to follow rates.^[41] The statistically, but not clinically, important differences were between the followed versus nonfollowed population in some baseline variables. The followed population had higher values for most of the continuous variables; as these factors were associated with hypertension, the results may be biased toward an overestimation of the incidence of hypertension. Second, we did not examine the effect of dietary intake in the analysis. Recently, a study on a representative adult population of Iran has shown that the amount of urinary excretion of sodium was >8 g/d, hence, it was estimated that the equivalent salt intake was between 9 and 11.8 g/d.^[42] Different relations between predictors might have been revealed if we had included dietary intake in our study. Third, in the present study, we used hold-out validation strategy to obtain independent training and validation datasets. The reduced data can result in an enlarged variance; although this method is reasonable in our study because the sample size is large,^[15,16] other validation strategies such as external validation in other settings and an independent population may achieve more accurate performance estimation.^[24,40] Finally, we used single DTs which may have high variance or bias in small sample size. Some “black box” model such as Random Forests (ensemble of DTs) attempts to mitigate the problems of high variance and high bias. But, Random Forests which measures variable importance is used for prediction purpose; it is impractical to present a flowchart diagram or interpret a Forest.^[12,13] Therefore, due to large sample size in our study, we developed single trees for exploration of risk factors and their interactions related to incidence of hypertension.

5. Conclusion

In summary, we successfully used a data mining classification method to develop 3 prediction models separately, in male, female, and the total population for incidence of hypertension. DT models used 5 easily available variables to identify a small number of homogeneous subgroups among men and women with different risk pattern related to incidence of hypertension. These models can ultimately guide interventions and improve clinical decision making.

Acknowledgments

The authors wish to acknowledge Ms Niloofar Shiva for critical editing of English grammar and syntax of the manuscript.