Functional connectome fingerprinting: Identifying individuals based on patterns of brain connectivity

Abstract

While fMRI studies typically collapse data from many subjects, brain functional organization varies between individuals. Here, we establish that this individual variability is both robust and reliable, using data from the Human Connectome Project to demonstrate that functional connectivity profiles act as a “fingerprint” that can accurately identify subjects from a large group. Identification was successful across scan sessions and even between task and rest conditions, indicating that an individual’s connectivity profile is intrinsic, and can be used to distinguish that individual regardless of how the brain is engaged during imaging. Characteristic connectivity patterns were distributed throughout the brain, but notably, the frontoparietal network emerged as most distinctive. Furthermore, we show that connectivity profiles predict levels of fluid intelligence; the same networks that were most discriminating of individuals were also most predictive of cognitive behavior. Results indicate the potential to draw inferences about single subjects based on functional connectivity fMRI.

Introduction

We are all unique individuals. Nevertheless, human neuroimaging studies have traditionally collapsed data from many subjects to draw inferences about general patterns of brain activity that are common across people. Studies that contrast two populations—such as patients and healthy controls—typically ignore the considerable heterogeneity within each group.

Despite the predominance of such population-level inferences, researchers have long recognized that even among the neurologically healthy, brain structure^1–3 and function^4–6 show high individual variability. In terms of function, variability is found in activation patterns during cognitive tasks^4–6 as well as intrinsic organization as measured by functional connectivity analyses of data acquired while subjects are simply resting⁷. Recently, the Human Connectome Project (HCP) set out to map the connections in the human brain by acquiring high-quality structural and functional MRI scans from a large number of healthy subjects⁸. Many of the early analyses of HCP data have focused on elucidating the general blueprint for brain connectivity that is shared across people. Yet despite the gross similarities, there is reason to believe that a substantial portion of the brain connectome is unique to each individual⁹.

An open question is whether this uniqueness is sufficiently observable by fMRI to enable a transition from population-level studies to investigations of single subjects. Here, we show that functional connectivity profiles act as an identifying “fingerprint,” proving that individual variability in connectivity is both substantial and reproducible. Using HCP data from 126 subjects, each scanned during six separate sessions across two days, we demonstrate that a functional connectivity profile obtained from one session can be used to uniquely identify a given individual from the set of profiles obtained from the second session. We show that identification is successful between rest sessions, task sessions and even across rest and task. Results indicate that while changes in brain state may modulate connectivity patterns to some degree, an individual’s underlying intrinsic functional architecture is reliable enough across sessions and distinct enough from that of other individuals to identify him or her from the group regardless of how the brain is engaged during imaging.

Furthermore, we establish the relevance of these connectivity profiles to behavior by demonstrating, in a fully cross-validated analysis, that functional connectivity profiles can be used to predict the fundamental cognitive trait of fluid intelligence in novel subjects. These results provide a critical foundation for future work to begin to test inferences about single subjects, to reveal how individual functional brain organization relates to distinct behavioral phenotypes.

Results

Data for this study consisted of scans from 126 subjects provided in the Q2 data release of the Human Connectome Project⁸. Each subject was scanned over a period of two days. Here, we used data from six separate imaging conditions: two rest sessions (one on each of the two days) and four task sessions (working memory, emotion, motor and language; two on each day). Functional connectivity was assessed using a functional brain atlas¹⁰ consisting of 268 nodes covering the whole brain; this atlas was defined based on a separate population of healthy subjects (see Online Methods for Yale dataset description). The Pearson correlation coefficient between the timecourses of each possible pair of nodes was calculated and used to construct 268×268 symmetrical connectivity matrices where each element represents a connection strength, or edge, between two nodes. This was done for each subject for each condition separately, such that each subject had a total of six matrices reflecting connectivity patterns during each of the different scan sessions.

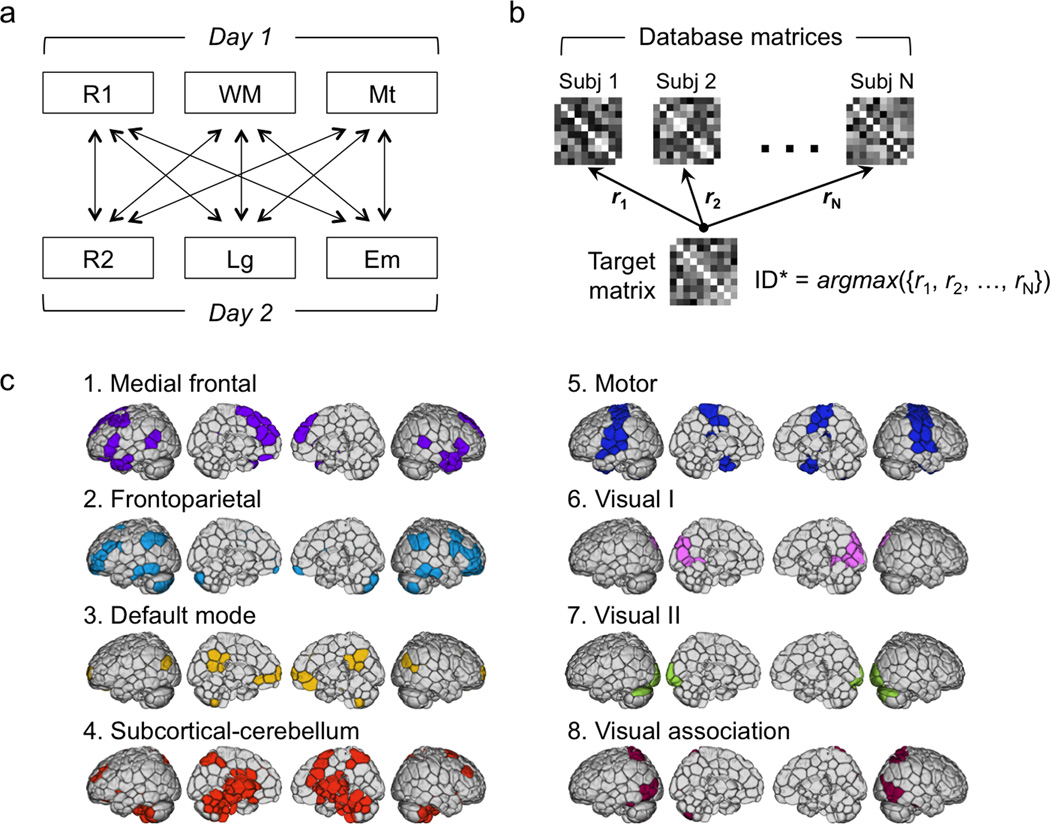
Identification was performed across pairs of scans consisting of one “target” and one “database” session, with the requirement that the target and database sessions be taken from different days: for example, day 1 rest matrices were used as the target and compared to a database of day 2 rest matrices (see Fig. 1a for a schematic). In an iterative process, one individual’s connectivity matrix was selected from the target set and compared against each of the connectivity matrices in the database to find the matrix that was maximally similar (Fig. 1b). Similarity was defined as the Pearson correlation coefficient between vectors of edge values taken from the target matrix and each of the database matrices. Once an identity had been predicted, the true identity of the target matrix was decoded and that iteration was scored 1 if the predicted identity matched the true identity, 0 if it did not. Within a target-database pair, each individual target connectivity matrix was tested against the database in an independent trial.

Figure 1. Identification analysis procedure and network definitions.

a) Database and target design. Each subject had six sessions of fMRI data: a resting-state session (R1), a working memory task (WM) and a motor task (Mt) on day 1, and a resting-state session (R2), a language task (Lg) and an emotion task (Em) onday2. For identification, we used a set of connectivity matrices from one session for the database, and connectivity matrices from a second session acquired on a different day as the target set. All possible combinations of database and target sessions are indicated by the arrows connecting session pairs. b) Identification procedure. Given a query connectivity matrix from the target set, we computed the correlations between this matrix and all the connectivity matrices in the database. The predicted identity (ID*) is the one with the highest correlation coefficient. c) Node and network definitions. We used a 268-node functional atlas defined on an independent dataset of healthy control subjects using a group-wise spectral clustering algorithm. Nodes were further grouped into eight networks using the same clustering algorithm, and these networks were named according to their correspondence to other existing resting-state network definitions.

Identification was tested across all the various pairs of scan sessions (Fig. 1a; nine pairs, each with two possible configurations created by exchanging the roles of target and database session). In each case, the success rate was measured as the percentage of subjects whose identity was correctly predicted out of the total number of subjects.

Connectivity-based identification of individual subjects

Whole-brain identification

As a first pass, identification was performed using the whole-brain connectivity matrix (268 nodes; 35,778 edges), with no a priori network definitions. The success rate was 117/126 (92.9%) and 119/126 (94.4%) based on a target-to-database of Rest1-to-Rest2 and the reverse Rest2-to-Rest1, respectively. The success rate ranged from68/126 (54.0%) to110/126 (87.3%) based on other database and target pairs including rest-to-task and task-to-task comparisons (see Fig. 2a, rightmost bar in each graph).

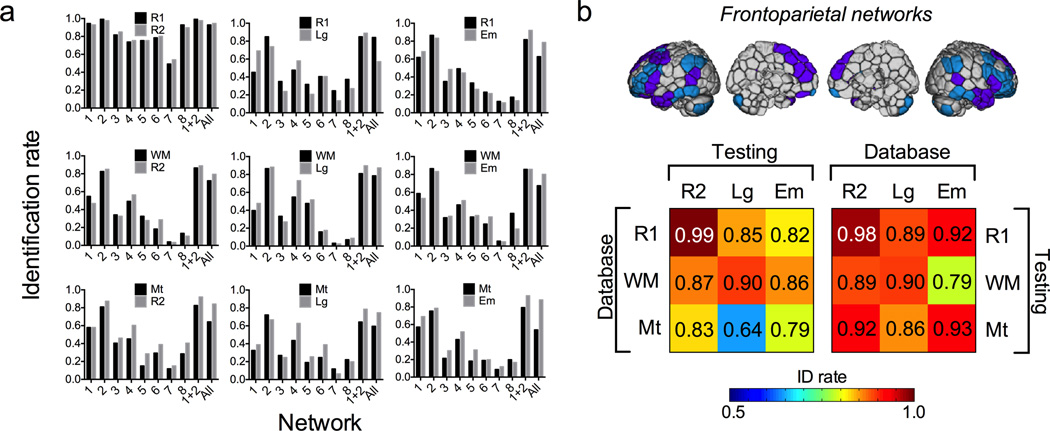
Figure 2. Identification accuracy across session pairs and networks.

a) Identification accuracy based on all nine database and target pairs, where each row has the same database session and each column has the same target session. Each graph shows accuracy based on each individual network as well as a combination of networks 1 and 2 (the frontoparietal networks) and the whole brain (“All”). Bar shading (black or gray) indicates which session was used as the database (with the other session serving as the target). b) Identification results from the combined frontoparietal networks (top) are highlighted in color-coded matrices (bottom) to more readily compare accuracy across rest-rest, rest-task and task-task session pairs. Identification was most successful between the rest-rest pair, with a slight drop in accuracy for both rest-task and task-task pairs.

Given that the 126 identification trials are not independent from one another, we performed non-parametric permutation testing to assess the statistical significance of these results (see Online Methods). Across 1,000 iterations, the highest success rate achieved was 6/126, or roughly 5%. Thus the p value associated with obtaining at least 68 correct identifications (the minimum rate achieved above) is 0.

Network-based identification

We next tested identification accuracy based on each of eight specific functional networks to test the hypothesis that certain brain networks contribute more to individual subject discriminability than others. These networks were derived from the same set of healthy subjects used to define the 268-node atlas (Fig. 1c). Two networks emerged as the most successful in individual subject identification; these were the medial frontal (network 1) and frontoparietal network (network 2), both comprised of higher-order association cortices in the frontal, parietal and temporal lobes. A combination of these two networks was also tested to determine if this combination might afford even higher predictive power than each network on its own. Figure 2a shows identification rates based on each network separately, the combination of networks 1 and 2 as well as the whole brain for each of the nine database and target pairs. We also highlight identification based on the combination of networks 1 and 2, referred to for convenience as the frontoparietal networks, in Fig. 2b. Frontoparietal-based identification was extremely high between Rest1 and Rest2 (98–99%). Accuracy dropped slightly when identification was performed between rest and task, or between two task conditions, but remained highly significant (80–90% for most condition pairs). The combination of these two frontoparietal networks significantly outperformed either network on its own, as well as the whole brain, across all 18 database-to-target pairs (one-tailed paired t-test versus network 1: t₁₇ = 10.4, p < 10e⁻⁹; versus network 2: t₁₇ = 1.97, p = 0.03; versus whole brain: t₁₇ = 5.1, p < 10e⁻⁵).

Factors affecting identification accuracy

We next explored several factors affecting identification accuracy, including quantifying contributions of individual edges to subject discriminability, varying the length of the timecourses used to calculate connectivity matrices, expanding the database set from one matrix to two, comparing different node and network schemes, and ruling out potential confounds (motion and anatomic differences).

Quantifying edgewise contributions to identification

To quantify the extent to which different edges contribute to subject identification, we derived two measures: the differential power (DP) and the group consistency (Φ). DP reflects each edge’s ability to distinguish an individual subject by quantifying how “characteristic” that edge tends to be, such that edges with a high DP tend to have similar values within an individual across conditions, but different values across individuals regardless of condition. Φ quantifies the consistency of a connection within a subject and across the group (see Online Methods for details of how DP and Φ were calculated).

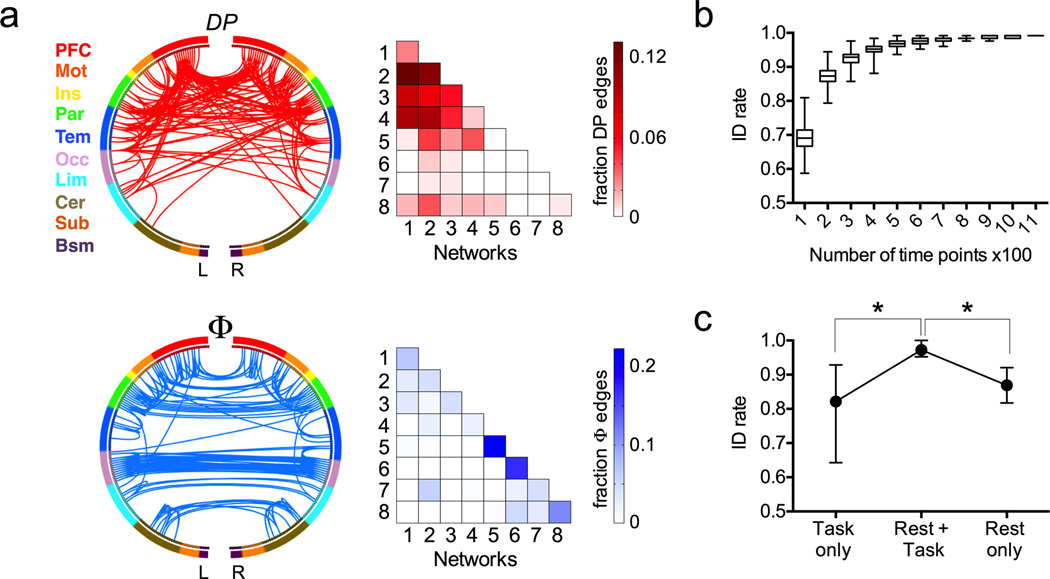
Restricting analysis to the two rest sessions, DP and Φ were calculated for all edges in the brain, and edges in the 99.5 percentile of DP and Φ are visualized in Figure 3a. The majority of high-DP edges are in the frontal, temporal, and parietal lobes and involve nodes in the frontoparietal networks (1 and 2) or default mode (network 3). (This result was stable across percentile thresholds; see Supplementary Table 1.) This data-driven mathematical definition of characteristic edges recapitulates the results of our network-based analysis, showing that in general, connections involving higher-order association cortices are the most discriminating of subjects. Approximately 28% of the edges with high DP were within and between the two frontoparietal networks. Another 48% were edges linking these two networks to other networks (Fig. 3a, top right), suggesting that levels of interaction and integration between the frontoparietal networks and the rest of the brain are also highly discriminating.

Figure 3. Factors affecting identification accuracy.

a) Highly unique (DP, top row, red) and highly consistent (Φ, bottom row, blue) edges in individual connectivity profiles. For visualization, both sets of edges were thresholded at the 99.5 percentile. In the circle plots (left), the 268 nodes (inner circle) are organized into a lobe scheme (outer circle) roughly reflecting brain anatomy from anterior (top of circle) to posterior (bottom of circle), and split into left and right hemispheres; lines indicate edges. In the colored matrices (right), the same data are plotted as percentage of edges within and between each pair of networks; a darkly shaded cell indicates a relative over-representation of that network pair in the DP (top) or Φ (bottom) masks. PFC, prefrontal; Mot, motor; Ins, insula; Par, parietal; Tem, temporal; Occ, occipital; Lim, limbic (including cingulate cortex, amygdala and hippocampus); Cer, cerebellum; Sub, subcortical (including thalamus and striatum); Bsm, brainstem; L, left hemisphere; R, right hemisphere. b) Longer timeseries improve identification accuracy. To control for the fact that task sessions contained fewer time points than rest sessions, we recalculated rest connectivity matrices using truncated timeseries containing between 100 and 1,100 time points. Results shown are from 500 randomizations using Rest1 and Rest2 as the database and target sessions, respectively. Box represents median with 25 and 75^th percentiles; whiskers represent range. c) Use of a two-matrix database improves identification rate relative to a single matrix (task or rest). Dots and error bars represent mean and range of identification rate across all possible database and target pairs, where the target matrix was always from a task session and the database consisted of a rest-task pair (n = 8 combinations), task only (n = 8) or rest only (n = 4). *p < 0.01, Mann Whitney U test.

Conversely, the majority of high-Φ edges connect cross-hemisphere homologsin the occipital and parietal lobes (Fig. 3a, bottom left). Many of these edges were within the motor network (network 5) or the primary visual network (network 6; Fig. 3a, bottom right). These edges are highly consistent both within and across subjects, and thus do not contribute substantially to individual subject identification.

Identification using shorter timecourses

Scan sessions differed in duration, meaning that the amount of data used to compute the connectivity profiles varied between sessions. The two rest sessions contained two runs of 1,200 brain volumes (time points) each, which is substantially longer than the working memory scan (two runs with 405 time points), the language scan (316), the motor scan (284), or the emotion scan (176). To investigate the effect of the number of time points on identification power, we performed frontoparietal-based identification between the two rest sessions while varying the number of time points used to calculate connectivity matrices between 100 and 1,100. Results indicate that longer timecourses are preferable in preserving individual characteristics in connectivity profiles (Fig. 3b), and that temporal variability in the connectivity profiles degrades identification based on shorter timecourses, especially those under approximately 500 time points.

Identification based on two-matrix database

Results in Fig.2 indicate, as expected, that individual identification is more challenging when performed across connectivity matrices obtained from different task conditions, or across task and rest (even after taking into account the fact that task runs contain fewer timepoints). It is well known that connectivity patterns can be modulated by different imaging conditions^11–13, and such modulation contributes to the intra-subject variation, making identification more difficult. In an effort to capture the intra-subject variation, we performed identification using an expanded database that included two connectivity matrices per subject (one rest session and one task session from the same day, with the target matrix from a task session on the other day; the frontoparietal networks were used for this analysis). In all cases, accuracy was improved using the two-matrix database over a database of either the rest or task session alone (Mann Whitney U test, versus rest alone: rank sum = 68, two-sided p = 0.004; versus task alone: rank sum = 100, two-sided p = 0.0002). The average success rate increased to 97.2%, with a maximum rate of 100% (compare to an average rate of 82.1% using a task-only database, and 86.9% using a rest-only database; see Fig. 3c). This suggests that the within-subject variability is well captured by a linear model that includes a baseline (connectivity at rest) and a deviation introduced by an independent task (connectivity during task).

Effects of parcellation scheme

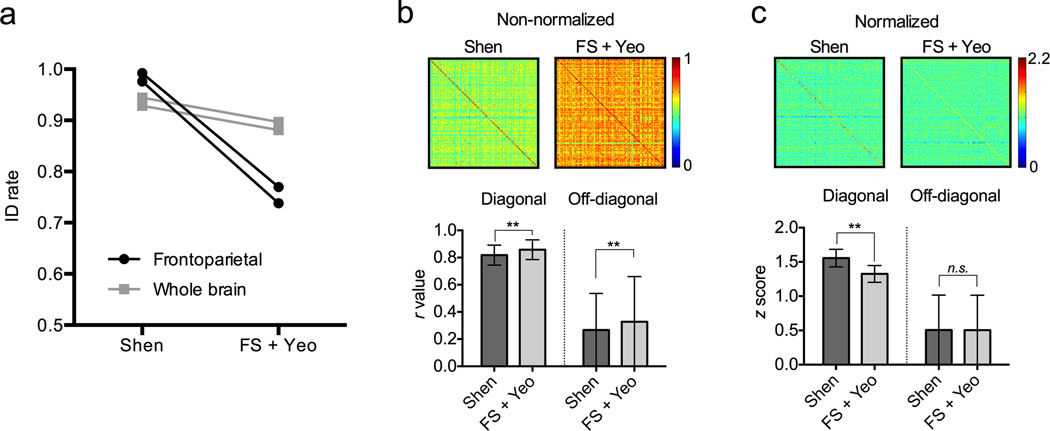
To investigate the sensitivity of identification to the specific choice of parcellation atlas and network definitions, we repeated the identification experiments using connectivity matrices calculated from the 68-node FreeSurfer atlas¹⁴, grouped into seven networks based on Yeo et al.’s network scheme¹⁵ (where networks 3, 4 and 6 represent the frontoparietal networks). Between the two rest sessions, the identification rate based on this atlas was about 89% using the whole brain, and about 75% using the frontoparietal networks (Fig. 4a). Reduction in identification accuracy compared to our 268-node functional parcellation and corresponding network definitions, especially in the case of frontoparietal-based identification, suggests that a relatively high-resolution parcellation contributes to the detection of individual variability and boosts identification rate.

Figure 4. Effect of node and network scheme on identification accuracy.

a) Comparison of identification accuracy using the Shen node atlas and network definitions (left) versus the FreeSurfer (FS) node atlas and Yeo network definitions (right). Accuracy is numerically higher using the Shen scheme; the difference is exaggerated when using just the frontoparietal networks (black lines) relative to the whole brain (gray lines). b) Raw 126×126 cross-subject correlations of frontoparietal connectivity patterns from Rest 1 and Rest 2 (top; scale bar indicates r value). Row and column subject order is symmetric; thus, diagonal elements are correlation scores from matched subjects. Mean correlation coefficients for both diagonal (matched) and off-diagonal (unmatched) elements are shown in the bar graph at bottom (error bars represent ± s.d.). The overall correlation coefficients are higher using the FS+Yeo scheme, for both diagonal elements (n = 126) and off-diagonal elements (n = 15,876). **p < 10⁻⁵, two-tailed t-test. c) Cross-subject correlation matrices after z score normalization (top; scale bar indicates z score). The global difference in correlation values is eliminated since there is no significant difference in the off-diagonal z scores. However, correlations between diagonal elements are significantly higher using the Shen scheme than the FS+Yeo scheme (bottom; error bars represent ± s.d.), which helps account for the increase in identification accuracy using the Shen scheme. **p < 10⁻⁵, two-tailed t-test.

To further investigate the difference in identification accuracy, correlations between connectivity matrices of all 126 subjects from Rest1 and Rest2 were calculated based on our atlas and network scheme and based on the FreeSurfer and Yeo scheme. Figure 4b compares the raw cross-subject correlation coefficients for the frontoparietal networks. The diagonal elements in Figure 4b represent correlation coefficients between matched subjects, while the off-diagonal elements are from unmatched subjects. Successful individual identification requires the diagonal elements to be the largest. The comparison shows that using the FreeSurfer and Yeo scheme, the raw coefficients are larger for both diagonal (t₂₅₀ = −4.3, p < 10e⁻⁵) and off-diagonal (t_31,750 = −18.0, p < 10e⁻⁷²) elements (Fig. 4b, bottom), which is uninformative in explaining the difference in identification accuracy. To control for equal global distribution of correlation coefficients, we normalized both matrices (Fig. 4c). After normalization, there was no difference between schemes in off-diagonal elements (t_31,750 = 0.27, p = 0.79), however using our parcellation and network scheme, the diagonal elements were significantly larger than using the FreeSurfer and Yeo scheme (t₂₅₀ = 14.6, p < 10e⁻³⁵), underpinning the increase in identification rate. In Fig.4c (top), the diagonal line is visually more prominent in the matrix on the left compared to the matrix on the right.

Effects of head motion

As head motion is a known confound of connectivity analyses¹⁶, we tested if subjects could be identified based on their distribution of frame-to-frame motion during functional scans (see Online Methods). Identification based on each subject’s motion distribution had an average success rate of 2.4%, which is well below the identification accuracy achieved using connectivity profiles. Thus it is unlikely that identification power is based on idiosyncratic patterns related to motion in the scanner.

Effects of anatomic differences

HCP provides functional data that has been normalized to a common space. Despite this, the influence of individual brain anatomy is hard to eliminate completely from functional data and may contribute to individual identification, for example via registration conferring a preference between the same subject on two different days. Nonetheless any such influence from anatomy should remain largely static, and should not be modulated by task conditions.

To confirm that identification power came from true differences in functional connectivity rather than anatomic idiosyncrasies, we recalculated connectivity matrices using different smoothing kernels for the BOLD data (4 mm, 6 mm and 8 mm). With larger smoothing kernels, the registration advantages for the same brain compared to a different brain should be vastly reduced or eliminated. Yet we saw only a very slight drop in identification power: based on Rest1/Rest2 pairs, identification using the frontoparietal networks remained above 96% for all three smoothing levels (see Supplementary Table 2).

We also investigated whether individuals could be identified by BOLD signal variance in each node (see Online Methods). While BOLD variance likely reflects metabolic function to a substantial degree, it could also be influenced by anatomic factors such as differing number of gray-matter voxels per node across subjects. This identification was successful—ranging from 48–87% across different combinations of database and target sessions—but in all cases, it was less successful than connectivity-based identification (see Supplementary Table 3, compare to Fig. 2b). Crucially, if BOLD variance were driven mostly by anatomic properties, it should be fairly constant regardless of how the brain is engaged during imaging, and thus the accuracy of variance-based identification should not differ according to brain state. That there was considerable variability with brain state further suggests that functional rather than anatomic features are responsible for the high degree of identification accuracy observed.

Connectivity profiles predict cognitive behavior

To determine whether individual differences in functional connectivity are relevant to individual differences in behavior, we tested whether connectivity profiles could be used to predict subjects’ level of fluid intelligence. Fluid intelligence (gF) is the capacity for on-the-spot reasoning to discern patterns and solve problems, independent of acquired knowledge¹⁷. Levels of gF vary widely in the population¹⁸ and correlate with many other cognitive abilities and life outcomes^19–22; investigating the biological basis of gF is of interest since it is considered to reflect intrinsic cognitive ability. In the HCP protocol, fluid intelligence (gF) was assessed using a form of Raven’s progressive matrices with 24 items²³ (scores are integers indicating number of correct items).

We used leave-one-subject-out cross-validation to demonstrate that gF can be predicted based solely on the connectivity profile of a previously unseen individual. In this iterative process, data from one subject is set aside as the test set, and data from the remaining n−1 subjects is used as the training set. Each iteration consisted of three steps: (1) feature selection, in which edges with a significant relationship to gF are identified in the training set and separated into two tails according to sign (positive and negative); (2) model building, in which training data is used to fit two simple linear regressions between gF and a summary statistic of connectivity strength in the positive- and negative-feature network, respectively; and (3) prediction, in which data from the excluded subject is input into each model to generate a predicted gF score (see Online Methods for further details). Following all iterations, we assessed the predictive power of each model by correlating predicted and observed gF scores across all subjects. Data from the day 1 rest session was used here.

Similar to the identification analysis, as a first pass, we tested whether whole-brain connectivity could predict gF in novel subjects. Based on a feature-selection threshold of p < 0.01, the correlation between predicted and observed gF scores was r = 0.50 (p < 10e⁻⁹) for the positive-feature model (Fig. 5a) and r = 0.26 (p = 0.005) for the negative-feature model. While both models generated significant predictions, the positive model was more accurate than the negative model (z = 2.15, two-tailed p = 0.03). Prediction was significant across all three feature-selection thresholds tested: all r > 0.29, p ≤ 0.001 for the positive tail; all r > 0.22, p ≤ 0.01 for the negative tail. (Note, though, that the predicted range is narrower than the observed range in Fig. 5a; thus the model is most successful at generating predictions of gF level relative to other subjects.)

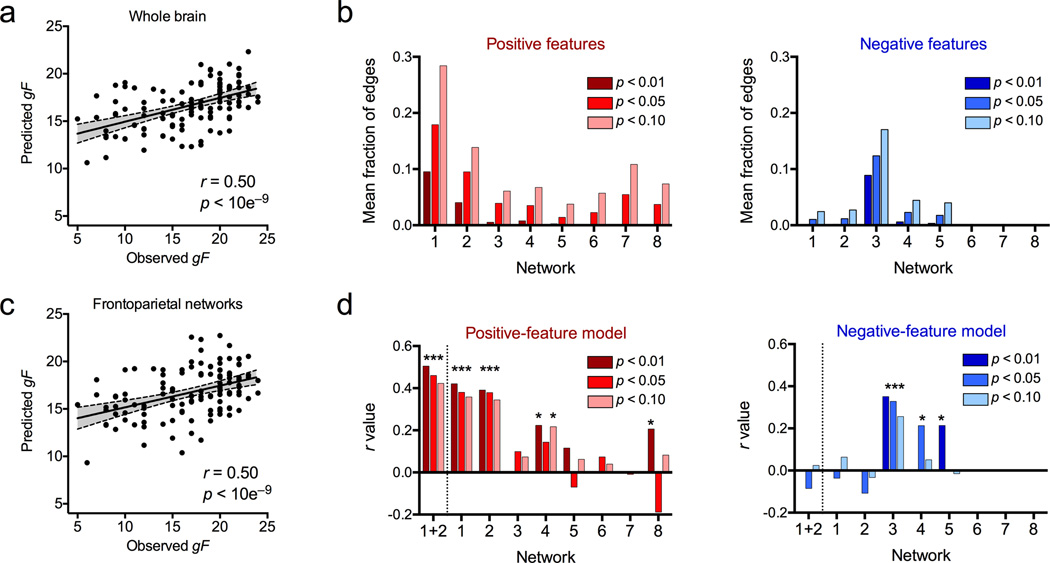
Figure 5. Individual connectivity profiles predict cognitive behavior.

a) Results from a leave-one-subject-out cross-validation (LOOCV) analysis comparing predicted and observed fluid intelligence (gF) scores (n = 118 subjects). Scatter plot shows predictions based on the whole brain in the positive-feature network at a feature-selection threshold of p < 0.01. Each dot is one subject; gray area represents 95% confidence interval for best-fit line, used to assess predictive power of the model. b) Mean fraction of within-network edges selected in the whole-brain positive-feature (left, red) and negative-feature (right, blue) models, shown at a range of statistical thresholds for feature selection. Y-axis indicates mean fraction of edges selected across all LOOCV iterations; x-axis indicates network label (see Fig. 1c). c) Results from a LOOCV analysis in which feature selection was restricted to within-network edges in the frontoparietal networks (1 and 2), at a feature-selection threshold of p < 0.01. As in (a), each dot is one subject; gray area represents 95% confidence interval for best-fit line. d) Results from nine separate LOOCV analyses in which feature selection was restricted to within-network edges in each of the eight networks plus a combination of networks 1 and 2. Y-axis indicates correlation between predicted and observed gF scores; x-axis indicates network label. Asterisks indicate correlations significant at p < 0.05 (uncorrected). Results based on a range of feature-selection thresholds (p-values) are shown to demonstrate consistency across thresholds. Note that for some networks, no features passed the statistical thresholding step, and thus it was not possible to generate predictions; this is reflected by missing bars.

Due to the nature of our cross-validated approach, a slightly different set of edges was selected in each iteration. To explore which networks contributed the most predictive power, for each of the eight networks, we calculated the average number of within-network edges selected across all iterations and normalized by the total number of within-network edges (to control for differences in overall network sizes). Networks 1 and 2 contributed the highest fraction of edges to the positive model, while network 3 contributed the highest fraction of edges to the negative model; this was consistent across statistical thresholds for feature selection (Fig. 5b). Thus, edges that show a consistent positive correlation with gF are disproportionately located in the frontoparietal networks, and edges that show a consistent negative correlation with gF are mostly in the default-mode network.

As a second-pass analysis, we directly tested whether predictive power varied across the different networks; specifically, whether the networks that performed best for identification (the frontoparietal networks) also performed best for predicting cognitive behavior. To do this, we repeated the leave-one-subject-out cross-validated procedure described above, this time restricting the feature selection step to features (within-network edges) from each of the eight networks in turn. We also tested a combination of networks 1 and 2. Thus, nine sets of predicted gF scores were generated. Each of these was correlated with observed gF scores to assess the predictive power of each network or network combination. Results are shown in Figure5c and 5d.

As hypothesized, predictive power based on the positive features was highest for the frontoparietal networks (at a feature-selection threshold of p < 0.01: r = 0.42, p < 10e⁻⁶ and r = 0.39, p = < 10e⁻⁵ for networks 1 and 2 respectively, r = 0.50, p < 10e⁻⁹ for the combination of the two networks; this pattern was consistent across different statistical thresholds used for feature selection). The subcortical-cerebellar network (network 4) also had significant predictive power at a feature-selection threshold of p < 0.01 (r = 0.22, p = 0.01, though this result was less consistent across feature-selection thresholds). Based on the negative features, only the default mode (network 3) had significant predictive power (r = 0.35, p < 10e⁻⁵ at p < 0.01; this result was consistent across feature-selection thresholds).

These results reinforce the functional relevance of our identification analyses, in that the networks most discriminating of individuals are also the most relevant to individual differences in behavior. Crucially, the relationship between connectivity and cognitive ability is sufficiently robust to generalize to previously unseen subjects.

Discussion

Here we show that an individual’s functional brain connectivity profile is both unique and reliable, analogous to a fingerprint. We demonstrate that it is possible, with near-perfect accuracy, to identify individuals from a large group of subjects based solely on their connectivity matrix. While inter-individual consistency in functional brain networks has been well characterized across both task and rest conditions^24,25, and even across states of consciousness²⁶, the remarkable intra-individual reliability observed here suggests that while the general blueprint may be shared, functional organization within individual subjects is idiosyncratic, relatively robust to changes in brain state, and provides meaningful information above and beyond the common template²⁷.

We also demonstrate that this individual variability is relevant to individual differences in behavior, in that connectivity profiles can be used to predict the fundamental cognitive trait of fluid intelligence in novel subjects. These results underscore the potential to discover fMRI-based connectivity “neuromarkers” of present or future behavior that may eventually be used to personalize educational and clinical practices, improving outcomes^28–30.

Anatomic loci of distinguishing connectivity features

Although identification based on the whole-brain connectivity matrix was highly successful, performance was best using a combination of the two frontoparietal networks. These networks are comprised of higher-order association cortices rather than primary sensory regions; these cortical regions are also the most evolutionarily recent³¹ and show the highest inter-subject variance^7,32,33.

That the frontoparietal networks were most distinguishing of individuals—and the most predictive of behavior—is consistent with the role these networks play in cognition. Nodes in these networks tend to act as flexible hubs, switching connectivity patterns according to task demands³⁴. Additionally, broadly distributed across-network connectivity has been reported in these same regions³⁵, suggesting a role in large-scale coordination of brain activity. Although the frontoparietal network is particularly active in tasks requiring a high degree of cognitive control, here we show that it can identify individuals regardless of whether the data is collected during task or at rest. Training cross-subject classifiers based on frontoparietal connectivity to predict which task a subject is performing yields classification accuracy that is statistically significant but still quite low³⁴; the present findings of high inter-individual variability may help explain these results. In light of this, future work might use within-subject classification to explore how the frontoparietal networks reorganize according to task demands in individual subjects.

Similarly, the frontoparietal networks emerged as most predictive of gF, which is consistent with previous reports that structural and functional properties of these networks relate to intelligence^36–38. Also of interest, aberrant functional connectivity in the frontoparietal networks has been linked to a variety of neuropsychiatric illnesses^39,40. The work presented here, while focused on healthy subjects, suggests that sensitivity may be compromised in studies of disease if inferences are drawn only at the group level. New insights into neuropsychiatric illnesses may be gained from an approach that links individual functional connectivity profiles to a spectrum of behavioral and symptom measures rather than a single diagnosis^41,42.

Additional considerations

Note that the discriminating power of connectivity profiles here is a result of integrating over a relatively long period of time (i.e., runs that last several minutes). There is a growing body of literature⁴³ showing that in the resting state, functional connectivity is dynamic and varies considerably over short periods of time (i.e., intervals less than one minute). Future work may seek to characterize individuals based on properties of these dynamic fluctuations, however, the current results indicate that single measures of time-averaged functional connectivity, based on relatively long scan sessions, provide meaningful information about individuals.

Note also that the cross-session identification performed here was between sessions separated by a single day; it remains unclear to what degree individual connectivity profiles are consistent across the lifespan. Cross-sectional studies have shown changes in functional connectivity with age^44–46, but future work should employ longitudinal designs to test the stability or evolution of the functional connectivity “fingerprint” over the course of months or years rather than days.

From a methodological perspective, the scale of the node atlas appears to influence identification accuracy. The parcellation used in our primary analysis consisted of 268 nodes across the whole brain, with each node optimized to contain voxels with similar resting-state timecourses¹⁰. This number is consistent with the range postulated by other groups^47,48, but represents a more fine-grained scheme than other atlases such as the automatic anatomic labeling atlas (90 nodes)⁴⁹ or the FreeSurfer atlas (68 nodes). In a comparison of identification rates, network definitions based on our high-resolution parcellation outperformed networks based on the FreeSurfer atlas; the coarser node size of the latter likely diminishes accuracy by averaging out individual variability.

Conclusion

Together, these advances suggest that analysis of individual fMRI data is possible, and indeed, desirable. Given this foundation, human neuroimaging studies have an opportunity to move beyond population-level inferences, in which general networks are derived from the whole sample, to inferences about single subjects, examining how individuals’ networks are functionally organized in unique ways and relating this functional organization to behavioral phenotypes in both health and disease.

Online Methods

Subject information

The primary dataset used in this work is from the Human Connectome Project (HCP). A second dataset, acquired at Yale, was used for node and network definitions. These two datasets are described in turn below.

HCP data

We used the Q2 HCP data release, which was all the HCP data publicly available at the time that this project was begun. The full Q2 release contains 142 healthy subjects; we restricted our analysis to subjects for whom all six fMRI sessions were available (n = 126; 40 males, age 22 to 35). This represents a relatively large sample size compared to most neuroimaging studies and has the advantage of being an open-source dataset, facilitating replication and extension of this work by other researchers. Note that most subjects have at least one blood relative in the group, with many sets of twins. A more heterogeneous population should make the identification problem easier, and therefore the high accuracy rate observed here, despite the homogeneity of the sample, underscores the power of functional connectivity-based identification.

The resting-state runs (rfMRI_REST1 and rfMRI_REST2) were acquired in separate sessions on two different days. Task runs included the following: working memory (tfMRI_WM), motor (tfMRI_MOTOR), language (tfMRI_LANGUAGE, including both a story listening and arithmetic task) and emotion (tfMRI_EMOTION). The working memory task and motor task were acquired on the first day, and the language task and emotion task were acquired on the second day. In total, there were six conditions: day 1 rest, day 2 rest, working memory, motor, language, and emotion. The HCP scanning protocol was approved by the local Institutional Review Board at Washington University in St. Louis. For all sessions, data from both the left-right (LR) and right-left (RL) phase-encoding runs were used to calculate connectivity matrices. Full details on the HCP dataset can be found elsewhere⁸.

Yale data

This dataset consisted of 45 healthy subjects scanned on a Siemens 3T Tim Trio at Yale University (28 males; age= 31 ± 7.3, range 19–50). Resting-state fMRI data was acquired using a multiband gradient echo EPI sequence with similar parameters to the HCP acquisition (FOV = 210 mm, matrix size 84 × 84, TR = 0.956 ms, TE = 30 ms, resolution = 2.5 mm³). Eight 5.6 minute runs were acquired, totaling 45 minutes of data. Additionally, an MPRAGE image (TR = 2530 ms, TE = 2.77 ms, TI = 1,100 ms, flip angle = 7 degrees, resolution = 1 mm³) and a two-dimensional anatomical T1 image (TR = 285 ms, TE = 2.61 ms, resolution = 2.5 mm³) were acquired for registration purposes. All participants provided written informed consent in accordance with a protocol approved by the Human Research Protection Program of Yale University.

Preprocessing

The HCP minimal preprocessing pipeline was used⁵⁰ for the HCP dataset. This pipeline includes artifact removal, motion correction, and registration to standard space. For the Yale dataset, images were motion corrected using SPM8 and were warped to common space using a series of linear and non-linear transformations as previously described¹⁰.

For both the HCP and Yale datasets, standard preprocessing procedures were applied to the fMRI data, including removing linear components related to the six motion parameters (Yale data) or 12 motion parameters (HCP data; these include first derivatives, given as Movement_Regressors_dt.txt), regressing the mean time courses of the white matter and cerebro-spinal fluid as well as the global signal, removing the linear trend, and low-pass filtering. For the HCP dataset, we investigated a range of spatial smoothing Gaussian kernel sizes—from no smoothing to a full-width half-max (FWHM) of 4 mm, 6 mm or 8 mm—and found that smoothing level had essentially no effect on identification accuracy (see Supplementary Table 2); thus results based on data with no spatial smoothing are presented in the main text. (Note that our node-based analysis, in contrast to a voxel-wise analysis, contains a considerable degree of inherent smoothing because the timecourses of many contiguous voxels are averaged into a single node.)

Image preprocessing and calculation of connectivity matrices was done using BioImage Suite software⁵¹. Pearson correlation coefficients between pairs of node timecourses were calculated and normalized to z scores using the Fisher transformation, resulting in a 268 × 268 symmetric connectivity matrix for each session for each subject. Connectivity matrices were not thresholded or binarized in any way.

Functional parcellation and network definition

Using the 45 subjects in the Yale dataset, a 268-node functional atlas was constructed using a group-wise spectral clustering algorithm¹⁰. The two hemispheres were segmented separately into a target number of 150 regions. The final parcellation was examined to ensure each node contained a reasonable number of voxels. Note that this single whole-brain parcellation atlas was defined in MNI space, and was applied to all subjects in the HCP dataset via traditional registration techniques. The parcellation image is publicly available on the BioImage Suite NITRC page (https://www.nitrc.org/frs/?group_id=51).

In addition to parcellating the brain into 268 functionally coherent nodes, we further clustered these nodes into large-scale networks. To define the networks, the same group-wise spectral clustering algorithm was applied to connectivity matrices from the45 Yale subjects to group the 268 nodes into eight networks¹⁰. The eight networks were evaluated and compared visually to existing definitions of resting-state networks published by other groups^15,25. Despite the fact that we included subcortical regions and cerebellum, whereas other definitions excluded these regions, our network configuration matched well with these other network definitions. Our eight clusters represent approximately the following networks: 1) medial frontal, 2) frontoparietal, 3) default mode, 4) subcortical/cerebellum, 5) motor, 6) visual I, 7) visual II, 8) visual association (see Fig. 1c).

Identification analysis

Fig. 1b illustrates the prediction procedure. First, a database was created that consisted of all the individual subjects’ connectivity matrices from a single condition, D = [X_i, i = 1, …, 126], where X_i is a 268 × 268 correlation matrix and the subscript i denotes subject. In the identification step, the identity of the target matrix was predicted using a correlation matrix obtained from a different session. To predict the subject identity, the similarity between the current target matrix Y_i and all other matrices in D was computed, and the predicted identity was that with the maximal similarity score. Similarity was defined as the Pearson correlation between two vectors of edge values taken from the target matrix and each of the database matrices. Note that we performed prediction with replacement, such that the algorithm was not forced to predict a unique subject on each iteration within a condition.

To assess the statistical significance of identification accuracy, we performed non-parametric permutation testing. In each iteration, we first randomly selected one condition from day 1 to serve as the database set, and a second condition from day 2 to serve as the target set. Next, subject identity was permuted—such that each subject in the target set was assigned a “correct” identity corresponding to a different subject in the database set—and identification performed. Then the roles of database and target sets were reversed. This procedure was repeated 1,000 times.

To investigate the contributions of individual networks (as described above) to identification accuracy, a sub-matrix was used corresponding to a single network or combination of networks. If we denote the set of nodes belonging to network j as V_j = [v_jk, k = 1, …, K_j], where K_j is the total number of nodes in network j, the sub-matrix of network j is X(V_j, V_j), thus only connections within the selected network(s) are included.

Quantifying edgewise contributions to identification

Edge-based analyses were performed to determine if specific edges contribute more to individual identification than other edges. When performing subject identification, the Pearson correlation coefficients were computed between the target connectivity pattern and all connectivity patterns in the database, and the subject identity was chosen to be the one that had the largest correlation coefficient. Computationally, the Pearson correlation of two vectors is the sum of element-wise products, given that the two vectors are z-score normalized (zero-mean with unit standard deviation). Therefore, this score can be broken down to quantify the individual amount contributed from each entry in the vector, where some edges contribute positively to the total coefficient and others contribute negatively.

Given two sets of connectivity matrices $[X_i^{R1}],[X_i^{R2}]$ obtained from Rest1 and Rest2 runs after z-score normalization, we computed the corresponding edge-wise product vector (φ_i),

$${\phi }_i(e)=X_i^{R1}(e)*X_i^{R2}(e),e=1,\dots ,M,$$

Where i indexes subject, e indexes edge and M is the total number of edges in the selected network (or the whole brain). The sum of φ_i over all edges ∑_eφ_i(e) is the correlation between $X_i^{R1}$ and $X_i^{R2}$. The group consistency measure (Φ) was computed as the mean of φ_i across all subjects. Large positive entries in Φ are edges that are consistent both within a subject and across the group.

In the same way, we can calculate φ_i between patterns from different subjects, e.g.:

$${\phi }_{ij}(e)=X_i^{R1}(e)*X_j^{R2}(e),i\ne j.$$

It is possible that an edge e is equally correlated within the same subject and between different subjects. In other words, φ_ij(e) (when subject subscript is not matched) and φ_ii(e) (when subject subscript is matched) are of similar value. Therefore, such an edge will not contribute to distinguishing an individual from the other subjects.

For an edge to be truly helpful in individual identification, the following property must hold,

$${\phi }_{ii}(e)>{\phi }_{ij}(e),\mathit{\text{and}}{\phi }_{ii}(e)>{\phi }_{ji}(e),i\ne j.$$

In this way, the particular edge contributes to maximize the correlation between connectivity patterns from matched subjects. To quantify the differential power of an edge for the purpose of subject identification, we computed an empirical probability, P_i(e),

$$P_i(e)=P[{\phi }_{ji}(e)>{\phi }_{ii}(e)\mathit{\text{or}}{\phi }_{ij}(e)>{\phi }_{ii}(e)]=([{\phi }_{ji}(e)>{\phi }_{ii}(e)]+[{\phi }_{ij}(e)>{\phi }_{ii}(e)])/2(N-1),N=126.$$

We defined P_i(e) in this way so that it can be interpreted similarly as the p value in a standard statistical test. The smaller the P_i(e)value the better differential power the edge has to identify a single subject i. The overall differential power of an edge across all subjects is then defined by the differential power measure (DP),

$$DP(e)=\sum _i\{-\text{ln}(P_i(e)\left)\right\}$$

The results of these edgewise analyses are visualized in Fig. 3a.

Identification using shorter timecourses

Scan sessions differed in duration: rest sessions were substantially longer than task sessions, and thus the discrepancy in amount of data could at least partially account for the differences in identification accuracy between rest-rest, rest-task and task-task pairs. To explore this possibility, we tested frontoparietal-based identification between the two rest sessions while varying the number of time points used to calculate connectivity matrices between 100 and 1,100 in increments of 100. For each number of time points n, identification accuracy was tested for each of 500 randomizations; these randomizations were generated by choosing among 50 starting points for each of the two rest runs and using n brain volumes beginning with that starting point to calculate matrices. Results based on a database and target of Rest1 and Rest2, respectively, are shown in Fig. 3b; results based on reversing the database and target were extremely similar.

Identification based on two-matrix database

We also tested a database design option where two matrices were included for each subject. The current design of the database and target set makes identification challenging because the two sets of data were not only acquired on separate days, but also under different conditions (except for the Rest1 and Rest2 pair) with the brain engaged in a different cognitive task. Inputting additional information about the difference between task and rest could potentially improve identification performance. Therefore, we created a database that included a connectivity matrix obtained from a resting-state session and another matrix obtained from a task session acquired on the same day: $\mathit{D}=[(X_i^R,X_i^T),i=1,\dots ,126]$. For identification, we always required that the target matrix be obtained on a different day. To predict the subject identity, we projected the current target matrix Y_i to the subspace spanned by the pair $[X_i^R,X_i^T]$, to obtain a projection Ỹ_i, and then computed the similarity between Ỹ_i and Y_i to find the best match. Results are shown in Fig. 3c.

Effects of parcellation scheme

To investigate the effect of brain parcellation and network assignment on identification accuracy, we also computed correlation matrices based on the 68-node FreeSurfer atlas included as part of the HCP data. We used Yeo et al.’s previously published seven-network definition¹⁵ which included the following networks: 1) visual, 2) motor, 3) pre-motor/parietal (dorsal attention), 4) ventral attention, 5) ventromedial prefrontal, 6) frontal-parietal control, 7) default mode. These networks do not include subcortical structures or cerebellum. Network labels were assigned to each node in the FreeSurfer atlas as follows. Given a node, we counted the number of voxels belonging to each of the seven networks. The network with the largest number of voxels is assigned as the primary network label for the given node. Because the 68-node parcellation is created independently from the seven networks, their boundaries do not align in a one-to-one manner. Therefore, we also allowed a secondary network association for a node when the number of voxels in this network ranked second and the proportion to the total number of voxels in the node exceeded 30 percent. All 68 nodes have at least one primary network association. When defining a sub-matrix that represents a single network, we included nodes for which the target network was either the primary or secondary label.

Comparisons of identification accuracy between the Shen and FreeSurfer and Yeo schemes are shown in Fig. 4.

Effects of head motion

In order to rule out the possibility that successful identification was driven simply by characteristic movement patterns leading to predictable motion artifacts, we performed prediction using motion estimates only. HCP data collection provides an estimate of frame-to-frame displacement for each run (Movement_RelativeRMS.txt). This data was used to generate a discrete motion distribution vector from each of the six Relative RMS vectors (from the six conditions, using data from the left-right phase encoding run). We computed the mean and standard deviation of the Relative RMS across all conditions and subjects. We then specified 60 bins that spanned three standard deviations below and above the grand mean, and the motion distribution vectors were calculated accordingly. The motion distribution vectors were then used in the same way as the correlation matrices for individual identity prediction purposes.

Effects of anatomic differences

While connectivity calculations are based on functional BOLD data, subtle effects of anatomic variability could potentially confer a preference between the same subject on two different days when it comes to applying the 268-node parcellation, defined in standard space, to each individual subject. To help rule out confounds of anatomy introduced at the registration step, we recalculated connectivity matrices based on BOLD data smoothed with three different kernel sizes (4 mm, 6 mm and 8 mm, keeping all other preprocessing steps the same), and re-performed the identification analysis; at higher levels of smoothing, any registration advantage for the same brain relative to a different brain should be eliminated or vastly reduced. The resulting identification accuracies are presented in Supplementary Table 2.

We also performed a second analysis to help rule out the possibility that identification is driven mainly by anatomic rather than functional differences between subjects. Rather than connectivity between pairs of nodes, we tested whether individuals could be identified based simply on a measure of BOLD variance in each node (calculation described below). In theory, while BOLD variance likely reflects baseline metabolic function to a substantial degree, it could also be influenced by anatomic factors such as partial volume effects introduced by the gray/white-matter segmentation and/or differing numbers of gray-matter voxels per node due to underlying variation in regional tissue volumes and gyral folding patterns. This analysis helps to address these potential confounds. BOLD variance was calculated and identification performed as follows:

1. Within each node, we computed the mean BOLD signal in each frame. This yields an N×268 matrix of node-wise mean BOLD intensities for each subject for each condition, where N is the number of frames (1,200 for the resting-state runs and fewer for the task runs). (This is identical to the first step in calculating connectivity matrices. Note that the mean across the time dimension is zero because of the drift removal and band-pass steps.)

2. For each node, using its N×1 timecourse vector, we compute its variance as follows:

   $$\mathit{\text{variance}}=\mathit{\text{sum}}(\mathit{\text{mean timecourse}}.^\mathit{2})/N$$

   This results in a single 1 × 268 vector of node-wise BOLD variances for each brain state for each subject. In signal processing terms, this variance is also known as “mean energy.”

3. We then performed identification by computing the correlation between these mean BOLD variance vectors across the different conditions (states) and sessions (days).

The results of this analysis are presented in Supplementary Table 3.

Behavioral prediction

In the HCP protocol, fluid intelligence (gF) was assessed using a form of Raven’s progressive matrices with 24 items²³ (scores are integers indicating number of correct items; mean = 16.8, s.d. = 4.7, median = 18, mode = 20, range 5–24; HCP: PMAT24_A_CR).

In light of evidence that head motion is a substantial confound in functional connectivity analyses, we first checked for any correlation between head motion and gF score. In the full sample of n = 126, this correlation was trending toward significance (r = −0.15, p = 0.09). Upon further examination, we found that this relationship was driven by a small number of individuals with both high head motion and low gF score. Thus, for purposes of the behavioral analysis, we excluded subjects with particularly high motion during the Rest1 run; specifically, eight subjects with > 0.14 frame-to-frame head motion estimate (averaged across both day 1 rest runs; HCP: Movement_RelativeRMS_mean) were excluded. There was no correlation between head motion and gF in the remaining set of n = 118 subjects (r = −0.05, p = 0.55).

Leave-one-subject-out cross-validation was used for the prediction analysis. In this iterative analysis, features are selected and a predictive model is built based on n−1 subjects (the training set) and the model is then tested on the remaining subject (the test set). Each subject is left out once. Each iteration consisted of 1) feature selection, 2) model building, and 3) prediction, described in turn below.

In the feature-selection step, Pearson correlation was performed between each edge in in the connectivity matrices andgF score across subjects in the training set. (Note that it is not necessary to correct for multiple comparisons in this step because the nature of a predictive analysis includes a built-in guard against false positives: if the proportion of false positives in the feature-selection step is high, the model should not generalize well to independent data.) Based on the signs of the resulting correlation values, edges were separated into two tails: those positively correlated with gF and those inversely correlated with gF. Edges were then thresholded based on the statistical significance of their correlation with gF, resulting in two sets of features (positive and negative). Because the choice of statistical threshold at this step is somewhat arbitrary, a range of thresholds was tested — p < 0.01, 0.05, 0.10 — to ensure that results were consistent.

In the model-building step, we first defined a single-subject summary statistic, “network strength,” by summing values of all edges in each feature set in individual connectivity matrices. In graph-theoretic terms, this statistic can be thought of as a type of weighted degree for each feature network⁵². This summary statistic can be represented as follows:

$${[\text{Positive feature network strength}]}_s=\sum _{i,j}{c}_{ij}{m}_{ij}^{(+)}$$

$${[\text{Negative feature network strength}]}_s=\sum _{i,j}{c}_{ij}{m}_{ij}^{(-)}$$

Where c is an individual s’s connectivity matrix, and m⁽⁺⁾ and m^(-) are binary matrices indexing the edges (i,j) that are significantly positively or negatively correlated with gF, respectively.

After obtaining network strength for each subject in the training set, simple linear regression was used to model the relationship between network strength (the explanatory variable) and gF (the dependent variable). Two models were built: one based on strength in the positive-feature network, and a second based on strength in the negative-feature network. Each model—positive and negative—consisted of a first-degree polynomial that fit the training data best in a least-squares sense:

$${[\text{Predicted}gF\text{score}]}^{\text{pos}}=\mathrm{a}*{(\text{Network strength})}^{\text{pos}}+\mathrm{b}$$

$${[\text{Predicted}gF\text{score}]}^{\text{neg}}=\mathrm{a}*{(\text{Network strength})}^{\text{neg}}+\mathrm{b}$$

Finally, in the prediction step, positive and negative network strengths from the excluded subject were calculated and input into each of the two respective models to generate predicted gF scores for that subject.

These three steps were repeated iteratively such that each subject was excluded once. Finally, we assessed predictive power of both models by correlating observed versus predicted gF scores across all subjects. Results are shown in Fig. 5.