Statistical assessment of bi-exponential diffusion weighted imaging signal characteristics induced by intravoxel incoherent motion in malignant breast tumors

Abstract

Background

The purpose of this study is to statistically assess whether bi-exponential intravoxel incoherent motion (IVIM) model better characterizes diffusion weighted imaging (DWI) signal of malignant breast tumor than mono-exponential Gaussian diffusion model.

Methods

3 T DWI data of 29 malignant breast tumors were retrospectively included. Linear least-square mono-exponential fitting and segmented least-square bi-exponential fitting were used for apparent diffusion coefficient (ADC) and IVIM parameter quantification, respectively. F-test and Akaike Information Criterion (AIC) were used to statistically assess the preference of mono-exponential and bi-exponential model using region-of-interests (ROI)-averaged and voxel-wise analysis.

Results

For ROI-averaged analysis, 15 tumors were significantly better fitted by bi-exponential function and 14 tumors exhibited mono-exponential behavior. The calculated ADC, D (true diffusion coefficient) and f (pseudo-diffusion fraction) showed no significant differences between mono-exponential and bi-exponential preferable tumors. Voxel-wise analysis revealed that 27 tumors contained more voxels exhibiting mono-exponential DWI decay while only 2 tumors presented more bi-exponential decay voxels. ADC was consistently and significantly larger than D for both ROI-averaged and voxel-wise analysis.

Conclusions

Although the presence of IVIM effect in malignant breast tumors could be suggested, statistical assessment shows that bi-exponential fitting does not necessarily better represent the DWI signal decay in breast cancer under clinically typical acquisition protocol and signal-to-noise ratio (SNR). Our study indicates the importance to statistically examine the breast cancer DWI signal characteristics in practice.

Introduction

Angiogenesis plays a vital role in tumor growth, and is an independent prognostic factor in breast cancer (1-5). New anti-angiogenetic therapy concepts for breast cancer treatment have being introduced (6,7). Dynamic-contrast enhanced (DCE) magnetic resonance imaging (MRI) is a valuable clinical tool to investigate angiogenesis of breast cancer in vivo (8-11). However, DCE-MRI requires contrast agent administration (12) and is associated with long-term risk of renal failure (13). As such, non-invasive assessment of breast cancer angiogenesis is desirable.

Intravoxel incoherent motion (IVIM) MRI (12) offers such a non-invasive means for simultaneous assessment of tumor diffusivity and vascularity in breast cancer (14,15). According to IVIM principle, diffusion weighted imaging (DWI) signal is not only influenced by true water diffusion in tissue due to the thermal Brownian motion, but also affected by micro-circulation of blood in the randomly structured capillary network, named pseudo-diffusion effect. As such, a bi-exponential mathematical model is proposed to quantify IVIM effect beyond the mono-exponential diffusion model, which only quantifies Brownian diffusion using apparent diffusion coefficient (ADC). By applying appropriate b-factor sets including both low and high b values, DWI signal is sensitive to both true water diffusion and pseudo-diffusion. IVIM parameters of pseudo-diffusion coefficient (D*), true diffusion coefficient (D) and pseudo-diffusion fraction (f) can be determined by fitting DWI signal decay with b-factors to a bi-exponential function. In a number of studies, it has been observed that diffusion signal decay in breast tumors is better fitted by bi-exponential function with smaller residual errors (14-16).

IVIM-MRI is postulated to provide additional tumor vascularity information potentially for better tumor characterization (17), while this postulation could be hindered by some limitations of IVIM quantification. First, simply applying a more complex model with more parameters (bi-exponential model here) for least-square fitting would always yield smaller residual errors. As such, the commonly used goodness-of-fit measured by coefficient of determination (R²) to evaluate fitting quality would introduce bias and thus always prefer the bi-exponential model (18). The higher R² value does not necessarily mean that bi-exponential model better describes the observed data but rather reflects the flexibility of the more complex model to match the observed data (19). Furthermore, fitting with a more complex model may sometimes overly capture the observed data variation contaminated by noise and motion, hence leads to the problem of overfitting (18). Although the use of adjusted R² could partially penalize the statistic when extra variables are added to the model, it is still inadequate to determine whether the complex model significantly better fit the observed data (19). In addition, accurate and precise bi-exponential quantification is mathematically difficult, particularly for f and D* in situations of low signal-to-noise ratio (SNR) and limited data points (20,21). As such, the obtained IVIM parameter values may associate with bias, inaccuracy, high uncertainty and poor reproducibility (22-24). Although advanced estimation methods other than least-square fitting have also been proposed, such as Bayesian analysis (25), bootstrapping (26,27) and maximum likelihood estimation (28), their use in clinical practice is still sparse and yet to be further evaluated. Last, although mono-exponential function is nested within bi-exponential function, the fitting to bi-exponential function does not always yield the fitting result of f=0, which makes bi-exponential model equivalent to mono-exponential one, even in the absence of IVIM effect (29,30), as the fitting procedure is subject to local minima, much dependent on the fitting method (31).

In consequence, the use of bi-exponential fitting to study IVIM effect should be carefully examined in a statistical point of view. In this study, we focus on malignant breast tumors in which higher micro-vascularity and hence pronounced IVIM effect could be presumed. We prompt to statistically assess whether bi-exponential function better fits the DWI signal decay of malignant breast tumors obtained with typical acquisition protocol for clinical scans through two statistical approaches, F-test (32) and Akaike information criterion (AIC) (33). We also prompt to examine whether the DWI model preference could be influenced by analysis means, i.e., region-of-interests (ROI)-averaged signal fitting or voxel-wise signal fitting.

Methods

Patient information and MRI protocol

This retrospective study was approved by the local Institutional Review Board with a waiver of informed consent. Consecutive patients were considered in this study if they underwent 3 T bilateral breast MRI and had DWI scan performed with eight b values appropriate for IVIM quantification. A cohort of 29 tumors in 29 patients was generated, including 22 invasive ductal carcinoma (IDC), 3 invasive lobular carcinoma (ILC), and 4 pure ductal carcinoma in situ (DCIS).

MRI protocol

All patients received MRI scan in a prone position on a 3.0 T clinical scanner (Magnetom Trio; Siemens Healthcare, Erlangen, Germany) with a dedicated 4-channel breast array coil. DWI was performed in axial views that covered the entire bilateral breasts prior to the contrast agent administration using a fat-saturated single-shot spin-echo type echo-planar imaging sequence. Major imaging parameters included: FOV =350 mm, matrix size = 192×192, voxel size =1.82×1.82 mm², slices =40, slice thickness/gap =3/0 mm, TE/TR=102/5,800 ms, number of signal averages (NSA) =4, SENSE factor =2. DW images at eight b-factors of 0, 50, 100, 150, 200, 400, 600, 1,000 s/mm² were acquired. The DWI scan time was about 3 minutes.

Image analysis and statistical analysis

Curve fittings of DW signal decay with regard to b-factor, based on Gaussian diffusion model and IVIM model, were conducted using in-house developed Matlab programs (The MathWorks, Inc., Natick, MA, USA).

Gaussian diffusion model was given in a mono-exponential function as shown in Eq. [1]:

$$S(b)=S_0{e}^{-b\cdot ADC}$$ [1]

where S(b) and S₀ are the DW image intensities obtained with the b-factor value of b and zero, respectively. ADC is the apparent diffusion coefficient.

IVIM model was given in a bi-exponential decay function as shown in Eq. [2]:

$$S(b)=S_0\left(f\cdot e^{-b\cdot D^{•}}+(1-f)\cdot e^{-b\cdot D}\right)$$ [2]

where D* and D respectively denote the pseudo-diffusion coefficient and the true water diffusion coefficient, and f is the unitless perfusion fraction. S(b) and S₀ have the same meaning as in Eq. [1].

DWI images were first rigidly registered on console to the baseline image with b=0 s/mm². The registration performance was visually inspected to make sure there was no apparent observable displacement of the lesion. ROIs of tumors were drawn manually on the slice of high-b DW images in which the tumor had the largest cross sectional area by referring to the DCE-MRI images. Two types of analyses were utilized. The first type, termed ROI-averaged analysis, calculated the average of DW image intensity for all voxels within the ROI and then this ROI-averaged intensity decay with regard to b-factor was fitted to mono- and bi-exponential function respectively to calculate ADC and IVIM parameters. For the other type, termed voxel-wise analysis, DW image intensity decay of each voxel within the ROI was fitted to mono- and bi-exponential function to obtain the voxel-wise value of ADC and IVIM parameters.

For both mono- and bi-exponential fitting, DW image intensities were first normalized to S₀ and then logarithmized. The logarithmized DW signal decay with regard to all eight b-factors was least-square fitted to a linear function, and the slope of the best fitted linear curve was the estimated ADC. Bi-exponential fitting was conducted using the segmented fitting method, which was reported as an improved fitting method for IVIM quantification in particular at sufficiently high SNR (20,34-36). In detail, D was obtained similarly as ADC in mono-exponential through least-square linear fitting but only using the logarithmized DW signal at the b values of 200 s/mm² and above. The fitted linear curve was then extrapolated to obtain an intercept at b=0. The ratio between this intercept and the DW signal at b=0 gave an estimate of f. Finally, the obtained D and f were substituted into the logarithmized Eq. [2] and non-linear least-square fitted against all b-factors to estimate D*. The start point for D* fitting was set as 10×10⁻³ mm²/s. By taking account of the reasonable physiological values, the lower limits of 0.0.01×10⁻³ and 1×10⁻³ mm²/s, and the upper limits of 1.5×10⁻³ and 500×10⁻³ mm²/s, were set for f, D and D* fitting respectively. D was constrained to be smaller than D*.

To statistically assess which model better fit the DW signal of breast tumors, two approaches, i.e., F-test (32) and AIC (19,33), were utilized and implemented in customized Matlab programs. F-test and AIC select model based on different but independent criteria. F-test is a null-hypothesis test applicable for nested models, but has the limitation to tend to choose the simpler model (34). In comparison, AIC is not a statistical hypothesis test so has no null hypothesis and P value. Instead, AIC provides a relative estimate of the information lost when a given model is used to describe the observed data, and is applicable to both nested and non-nested models. F-test and AIC were used in this study to complement each other and strengthen the confidence of the model preference results.

The null hypothesis of F-test is that the simpler model with fewer parameters, mono-exponential model here, is preferable. An F-ratio (F) was calculated to test whether the sum of squared deviations was sufficiently reduced to justify fitting with additional parameters by using the more complex bi-exponential model according to Eq. [3]:

$$F=\frac{S{S}_{mono}-S{S}_{bi}}{S{S}_{bi}}\cdot \frac{D{F}_{bi}}{D{F}_{mono}-D{F}_{bi}},\mathrm{where},DF=N-n$$ [3]

In Eq. [3], the subscripts mono and bi represent the mono-exponential and bi-exponential models, respectively. SS is the residual sum-of-squares. DF is degrees of freedom, which can be calculated by the subtraction of the number of model parameters n (n=3 for bi-exponential and n=1 for mono-exponential model) from the number of measured data points N. The P value associated with the F-ratio was then calculated based on F-distribution. If the P value associated with F-ratio was smaller than a significance level of 0.05, bi-exponential model was preferable. Otherwise, mono-exponential model was preferable in a statistical point of view.

AIC is not a statistical hypothesis test so has no null hypothesis and P value. Instead, it provides a relative estimate of the information lost when a given model is used to represent the observed data. We calculated the finite sample size corrected AIC values (AICc) first using Eq. [4]:

$$AICc=Nln(SS)+2n+\frac{2n(n+1)}{N-n-1}$$ [4]

where all parameters have the same meaning as in Eq. [3]. The preferred model is the one with the smaller AICc value. Based on the calculated AICc values for two models, relative likelihood of bi-exponential model (RLbi) was calculated as Eq. [5]:

$$R{L}_{bi}=e^{(ATC{c}_{mono}-AIC{c}_{bi})/2}$$ [5]

In general, if RL_bi value was larger than 1, bi-exponential model was preferable, and the larger RL_bi value implies that the mono-exponential model is more probable to result in a loss of information relative to the bi-exponential model. Conversely, mono-exponential was preferable if RL_bi value was smaller than 1, and the preference was more strengthened with the smaller RL_bi value.

For voxel-wise analysis using both F-test and AIC, if there were more voxels preferred bi-exponential model than mono-exponential one in a tumor ROI, this tumor was considered bi-exponential preferable. Otherwise, it was considered mono-exponential preferable.

The calculated ADC values were compared to D values (reported in mean ± SD) for all tumors, mono-exponential preferable tumors and bi-exponential preferable tumors for both ROI averaged analysis and voxel-wise analysis using Wilcoxon-signed rank test. For ROI-averaged analysis, the mean ADC, D and f values of the mono-exponential preferable tumors were compared to their corresponding counterparts of the bi-exponential preferable tumors using Mann-Whitney U-test. A significant level of 0.05 was used for all comparisons. Considering the unreliability of D* quantification in bi-exponential fitting (26), particularly when SNR was limited, comparison of D*, was still conducted but without further interpretation between mono-exponential and bi-exponential preferable tumor groups.

Results

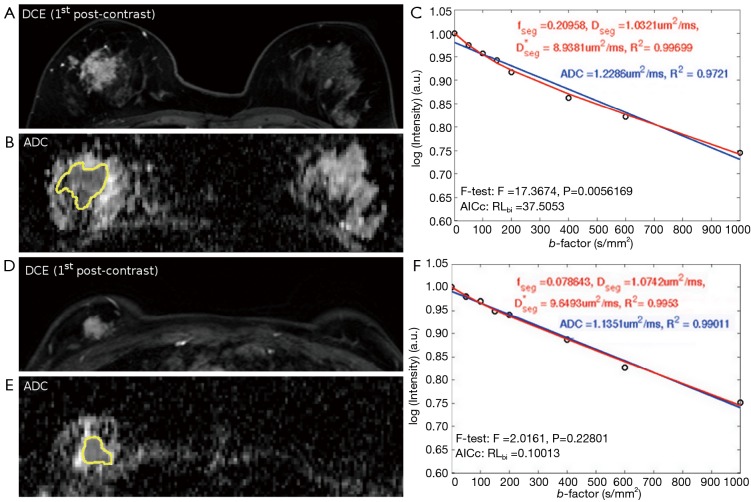
No observable displacement was observed in lesions after registration. All lesions were still well visible even at the highest b value of 1,000 s/mm², without dropping to the background image intensity level. Excellent R² value was achieved in all tumors by fitting the ROI-averaged DWI signal to both mono-exponential (all R²>0.91) and bi-exponential models (all R²>0.97). Regarding the ROI-averaged analysis using F-test, 15 tumors were significantly better described by bi-exponential model, including 12 IDCs, 1 DCIS and 2 ILCs. In other 14 tumors, bi-exponential model was not significantly better than mono-exponential model, including 10 IDCs, 3 DCISs and 1 ILC. Regarding the ROI-averaged analysis using AIC, the preference results were well agreed with those using F-test. Figure 1 illustrates the 1^st post-contrast DCE-MRI image and its corresponding ADC map of an IDC (Figure 1A,B) in which bi-exponential fitting is preferred (Figure 1C), and a DCIS (Figure 1D,E) in which mono-exponential fitting is preferred (Figure 1F).

Figure 1.

The illustration of ROI-averaged analysis. (A-C) the DWI signal of an IDC is significantly better fitted by bi-exponential fitting; (D-F) the DWI signal of a DCIS is not significantly better fitted by bi-exponential fitting. DWI, diffusion weighted imaging; IDC, invasive ductal carcinoma; DCIS, ductal carcinoma in situ; ROI, region-of-interests.

For ROI-averaged analysis, the mean D of total 29 tumors (0.92±0.25×10⁻³ mm²/s) was significantly smaller (P<0.001) than the mean ADC (1.04±0.29×10⁻³ mm²/s) (Figure 2). The values (mean ± SD) of f and D* for the whole cohort (n=29) were 13.4%±7.7% and 13.8±15.4×10⁻³ mm²/s, respectively. For those bi-exponential preferred tumors based on the F-test results, the mean ADC of total 15 tumors (0.97±0.24×10⁻³ mm²/s) was significantly larger (P<0.001) than the mean D (0.86±0.22×10⁻³ mm²/s). For the remaining 14 mono-exponential preferred tumors, the mean ADC was 1.11±0.32×10⁻³ mm²/s, still (but less) significantly larger (P<0.001) than the corresponding mean D of 0.98±0.27×10⁻³ mm²/s (Figure 2). Meanwhile, ADC, D, and f were not significantly different between the mono-exponential and bi-exponential preferable cohorts (Table 1). Although the D* value difference between the two cohorts appeared to be significant, the further interpretation should be made with caution by taking account of the higher uncertainty of D* quantification via bi-exponential fitting.

Figure 2.

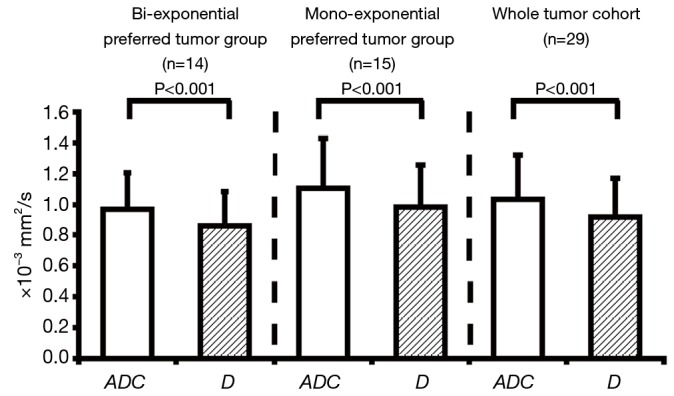
The statistical comparison of ADC and D for bi-exponential preferred tumor group, mono-exponential preferred tumor group and whole tumor cohort (n=29) based on ROI-averaged F-test. ADC, apparent diffusion coefficient; ROI, region-of-interests.

Table 1. The comparison of mean ADC, D and f (mean ± SD) between the bi-exponential preferable and mono-exponential preferable tumor cohorts according to ROI-averaged F-test.

ROI-averaged analysis	ADC (×10-3 mm2/s)	D (×10-3 mm2/s)	D* (×10-3 mm2/s)	f
Bi-preferred	0.97±0.24	0.86±0.22	11.78±2.81	0.14±0.04
Mono-preferred	1.11±0.32	0.98±0.27	15.97±22.22	0.13±0.10
P values	0.1437	0.1112	0.0121	0.6468

Note, the P values are calculated using Mann-Whitney U-test. ADC, apparent diffusion coefficient; ROI, region-of-interests.

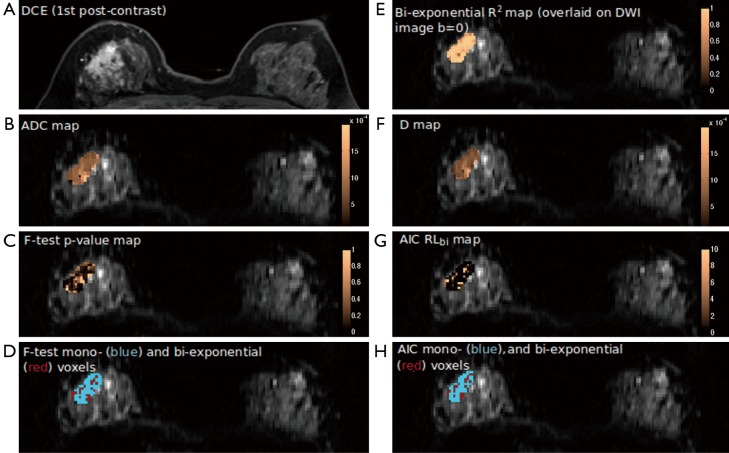
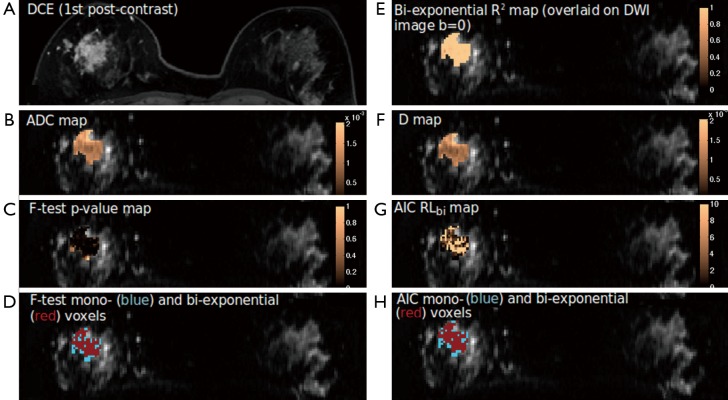
Heterogeneity of parameter values was found in all tumors by using voxel-wise mono-exponential and bi-exponential mapping. The voxel-wise R² ranged from 0.75 to over 0.95, indicating the heterogeneous SNR within voxels. Regarding the voxel-wise analysis results using F-test and AIC, in sharp contrast to ROI-averaged analysis, all tumors except for two IDCs exhibited over half of all voxels presenting apparent mono-exponential DWI signal decay rather than bi-exponential decay (Figure 3). For the remaining two IDCs (Figure 4), more voxels within the tumor were significantly better fitted by bi-exponential function (ROI-averaged analysis also revealed bi-exponential preference). In terms of voxel fractions for each tumor subtype, voxel-wise F-test revealed that 23%±21% of voxels within the ROI exhibited bi-exponential signal decay for IDC, and 23%±12% for ILC, higher than the fraction of 10%±11% for DCIS (P=0.35 and P=0.23, respectively).

Figure 3.

The DCE post-contrast image (A) and parametric maps (B-H) of an ILC tumor containing more mono-exponential preferred voxels. DCE, dynamic-contrast enhanced; ILC, invasive lobular carcinoma.

Figure 4.

The DCE post-contrast image (A) and parametric maps (B-H) an IDC tumor exhibiting more bi-exponential preferred voxels. DCE, dynamic-contrast enhanced; IDC, invasive ductal carcinoma.

Similar to ROI-averaged analysis, the mean ADC (1.02±0.28×10⁻³ and 1.03±0.29×10⁻³ mm²/s for entire tumor cohort and the mono-exponential preferred cohort, respectively) was systematically and significantly (P<0.001) larger than the mean D (0.97±0.28×10⁻³ and 0.97±0.28×10⁻³ mm²/s, respectively) for the entire tumor cohort and the mono-exponential preferred cohort (Figure 5). Due to the extremely limited sample size of bi-exponential preferred cohort (n=2), the mean ADC (0.97±0.18×10⁻³ mm²/s) and D (0.88±0.11×10⁻³ mm²/s) showed no significant difference (P>0.05), although the mean ADC was still larger than D (Figure 5).

Figure 5.

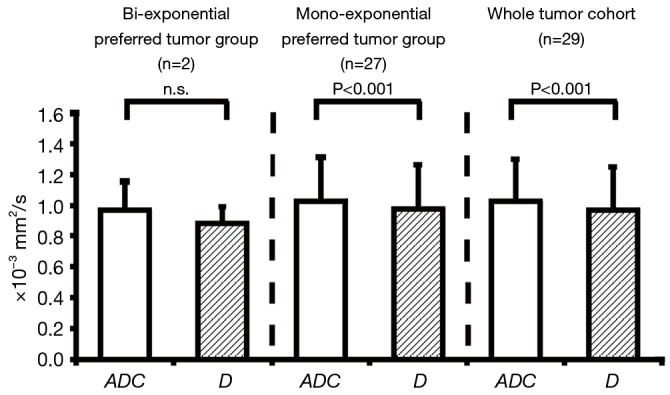
The statistical comparison between ADC and D for bi-exponential preferred tumor group, mono-exponential prefer group and whole tumor cohort (n=29) based on voxel-wise F-test. ADC, apparent diffusion coefficient.

Discussion

IVIM-MRI has been gaining increased attention in clinical applications of various organs, including breast (14,34,37-41). Sigmund et al. (14) first demonstrated the feasibility of using IVIM model in breast lesions. In a cohort of cancerous breast lesion including different subtypes (n=24), the segmented-fitting estimated ADC, D, f, and D* (mean ± SD) from a spin echo based DWI acquisition at 3 T were 1.34±0.39×10⁻³, 1.15±0.35×10⁻³ mm²/s, 9.8%±4.8% and 15.1±10.4×10⁻³ mm²/s, respectively. Subsequent studies showed that IVIM parameters of f and D were helpful to better differentiate malignant and benign breast tumors than ADC (15,42). In the work of Bokacheva et al., the estimated ADC, D, f, and D* (mean ± SD) of 26 malignant breast lesions acquired by an EPI-DWI sequence at 3 T were 1.40±0.30×10⁻³, 1.29±0.28×10⁻³ mm²/s, 6.4%±3.1% and 21.7±11.0×10⁻³ mm²/s, respectively (15). In the work of Liu et al., EPI-DWI were obtained at 1.5 T on 40 malignant breast lesions, the median values of ADC, D, f, and D* were reported as 0.95×10⁻³, 0.85×10⁻³ mm²/s, 10.34% and 94.71×10⁻³ mm²/s, respectively (42). In terms of IVIM quantification in breast, Cho et al. (36) compared fitting methods and sampling strategies, then proposed an optimized b-factor combination for improved IVIM parameters estimation in breast cancer. Their reported IVIM parameters of malignant lesions (n=24) estimated from an optimized b-factor combination and segmented fitting at 3 T were 1.195±0.471×10⁻³ mm²/s, 13.183%±6.529% and 16.83±9.06×10⁻³ mm²/s, for D, f, and D* respectively. Suo et al. (43) also compared three different curve-fitting methods for IVIM analysis in a cohort of 12 IDC tumors obtained at 3 T using an EPI sequence with 7 b-factors. The reported D, f, and D* values estimated by the similar segmented fitting as our approach were 0.83±0.19×10⁻³ mm²/s, 6.10%±3.19% and 159.50±90.32×10⁻³ mm²/s, respectively. By comparing the ADC and IVIM parameters values obtained in our study to those in the literatures, variabilities of the estimated values were found for all parameters, which could be attributed to the heterogeneities of tumor cohorts, acquisition sequences, b values and quantification methods. In particular, the largest discrepancy (>1,000% difference) was found in D*, and the second largest (up to 276% difference) in f, indicating the high uncertainty of f and D* via bi-exponential fitting approach, even when the optimized method was applied. In contrast, the discrepancies on the estimated ADC (up to ~47% difference) and D (up to ~52% difference) between different studies were much smaller compared to D* and f. However, none of previous studies examined whether IVIM analysis provides significantly better fit of DWI signal decay in breast cancer in a statistical view.

In this study, we statistically compared the segmented bi-exponential fitting and mono-exponential fitting f of DWI signal decay in malignant breast tumors. Despite that F-test is known to tend to choose the simpler model in comparison to AIC (44), the model preference results derived from both F-test and AIC in our study were consistent. In total 29 breast tumors, 15 tumors were significantly better fitted by bi-exponential function while other 14 tumors were not by using ROI-averaged analysis. More advanced invasive tumors of IDC (12:10) and ILC (2:1) while fewer precursor tumors of DCIS (1:3) were better fitted by bi-exponential model as found in ROI-averaged analysis. Regardless of model preference and tumor subtypes, ADC value was significantly larger than D. On the other hand, there was no significant difference in the value of ADC, D, and f between the mono-exponential preferred cohort and the bi-exponential preferred cohort.

The significantly better fitting to bi-exponential function by ROI-averaged analysis in over half tumors strongly suggested the presence of IVIM effect in these tumors. The exhibition of bi-exponential DWI signal in more advanced invasive tumors might indicate the increased micro-vascularity in the invasive tumors compared to the precursor tumor in situ (i.e., DCIS), while yet to be further verified. On the other hand, a number of advanced invasive tumors apparently exhibited mono-exponential DWI signal decay. This may be interpreted by either the absence of IVIM effect, or the undetectability of IVIM effect restricted by the limited SNR under the scan protocol (16). These two possibilities cannot be further delineated based on the current study. Presuming the presence of IVIM effect, the detectability of bi-exponential DWI signal could theoretically be improved by using more and optimized b-factors, higher NSA and better estimation methods. Nevertheless, as 8 b-factors and NSA of 4 were applied for acquisition and the segmented bi-exponential fitting was used for IVIM analysis, our data represented a typical clinically applicable protocol with reasonably high SNR, so it is believed that the model preference was not biased by the scan protocol and fitting method. The significantly larger value of ADC than D in all tumors suggests that the DWI signal at low b-factors does affect most likely overestimate the tumor diffusivity (45), regardless of fitting model preference. In consequence, D may be used as a more accurate parameter to reveal tissue diffusivity than ADC. The insignificant difference in the calculated f between the mono-exponential preferred cohort and the bi-exponential preferred cohort was a bit out of expectation, which might be majorly explained by the relatively lower micro-vascularity and hence the small value of underlying f (generally reported as <15% in literatures) in breast cancers. It has been suggested that small f could be associated with higher estimation uncertainty, which was also reflected by the larger SD of f in the mono-exponential preferable cohort (Table 1). It is plausible that this larger SD resulted from the f estimation uncertainty may obscure the difference of f between the mono-exponential and bi-exponential cohorts. On the other hand, the relatively small sample size might also contribute to the insignificant difference, so should be increased in future studies for better delineation.

Quite different from the ROI-averaged analysis, the voxel-wise analysis reveals that most tumors (n=27) presented more voxels exhibiting mono-exponential diffusion behavior than bi-exponential type, implying the heterogeneous but relatively small microvascularity in breast cancer. In addition, this difference may be explained by that ROI-averaged analysis could remarkably increase the DWI signal SNR and thus enhance the detectability of macroscopic IVIM effect (46,47). It has been recognized that the noise of magnitude MR image acquired by a single coil has Rician distribution rather than Gaussian distribution (48). At extremely low SNR below three, Rician distribution can be considerably deviates from Gaussian distribution, and results in the non-zero positive mean of the noise. In this study, all images were acquired by an array coil. Although the magnitude image noise pattern could be complicated, the voxel-wise fitting, in particular at high b values was carefully examined in this study to avoid the possible bias introduced by noise. In all cases, flattening of the DWI decay at high b-factors was not observed, and the image intensities within the lesion ROIs were still well above the background noise level even at the highest b value of 1,000 s/mm². In the presence of tumor heterogeneity revealed by voxel-wise analysis, it is interesting to find that the average bi-exponential preferable voxel fraction (23%) was higher in advanced IDC and ILC tumors than the voxel fraction (10%) in precursor DCIS tumors, indicating the increased micro-vascularity in advanced breast tumors. Nevertheless, this has to be thoroughly further validated. Similar to the ROI-averaged analysis result, the calculated mean ADC in voxel-wise analysis was significantly larger than the corresponding mean D. One advantage of voxel-wise analysis over ROI-averaged analysis is the capability of revealing tumor heterogeneity. However, considering the relatively lower SNR compared to ROI-averaged analysis, f and D* should be used and interpreted with caution due to the possible inaccuracy and high uncertainty induced by quantification (23,36).

It is interesting to compare the DWI model preference results in breast cancer as found by this study to those in other tissues. Wittsack et al. reported that bi-exponential model better described the DWI signal decay of the healthy kidney at 3 T even for voxel-wise analysis, while was less robust to noise than mono-exponential model (49). In another study, Quentin et al. (44) found that mono-exponential model was most preferable in prostate cancers compared to other advanced diffusion models including bi-exponential IVIM, and bi-exponential model was best to describe DWI signal in healthy prostates of young volunteers. These model preference differences from our results in breast cancer could be explained by the intrinsic properties of different tissues, such as diffusivity and capillary density, as well as the different acquisition protocols used. It is speculated that the capillary density in kidney might be much higher (mean f=0.44 in Wittsack’s study) than that in breast, which makes the bi-exponential DWI behavior more easily to be detected. Meanwhile, breast and prostate DWI is suspected to suffer from lower SNR and more pronounced artifact than kidney DWI, which might also obscure the underlying bi-exponential DWI under a typical clinical acquisition protocol. It is also noticed that the averaged f in prostate cancer was reported as 0.29 in Quentin’s study (44) while mono-exponential was still preferable. This also supports the more frequent mono-exponential model preference as found by our study in breast cancer since the f value was even lower (<0.15).

This study is majorly limited in its small sample size, in particularly of DCIS and ILC. We only focused on malignant breast tumors in which more pronounced IVIM effect could be presumed. The discrimination of normal tissue, precursor and advanced breast tumors using IVIM parameters (15,42) is beyond the study purpose. We did not correlate the IVIM parameters to pathology or clinical outcome either because of the retrospective nature of this study. To further enhance the clinical impact, these investigations are warranted in the future and some promising results have been reported in other tissues in literatures (50,51). It is worth noting that DWI signal model preference and the calculated parameter values are dependent on scan protocol and fitting method. Although high NSA and segmented fitting were applied, our results just applied to the specific acquisition protocol and fitting method, representing a typical situation under clinically practical and achievable protocol, which might not be the most optimized one. It is also recognized that the number of b-factors used in our study, i.e., 8, was relatively small. As such, the statistical power of F-test and AIC might need to be further strengthened by applying even more b-factors, but at the cost of the longer scan time. Meanwhile, the pre-processing for fitting in this study might have some pitfalls. For example, performing linear least-square fits to logarithmic forms of the mono-exponential function, although is frequently adopted in many studies to simplify computation, this logarithmization operation might potentially affect the noise distribution pattern of the image and hence the fitting result, in particular at low SNRs. The optimization of IVIM acquisition and quantification is definitely worth being further exploited, whereas is also beyond the purpose of this study, and needs to be conducted in a prospective study design in the future.

Conclusions

In conclusion, although the presence of IVIM effect could be strongly suggested in some malignant breast tumors, our results show that bi-exponential fitting does not necessarily better represent the DWI signal decay in breast cancer in a statistical view under a clinically typical acquisition protocol and SNR as the microvascularity in breast cancer might be generally small. Although the IVIM detectability and quantification in breast cancer are much dependent on many factors such as acquisition protocol, fitting algorithm and analysis method, our study indicates the importance to statistically examine the breast cancer DWI signal characteristics in practice so as to select the appropriate model to interpret the quantification result in DWI analysis.

Ethical Statement: The study was approved by the local Institutional Review Board with a waiver of informed consent.