Active sensing without efference copy: referent control of perception

The notions of direct neural preprogramming of the motor outcome and the use of a copy of commands to muscles (efference copy) to control our senses conflict with basic physiological and physical principles. Instead, the brain predetermines where, in the spatial domain, muscles can work whereas commands to muscles emerge in this domain due to the interaction of the neuromuscular system with the environment, thus solving several problems in action and perception.

Abstract

Although action and perception are different behaviors, they are likely to be interrelated, as implied by the notions of perception-action coupling and active sensing. Traditionally, it has been assumed that the nervous system directly preprograms motor commands required for actions and uses a copy of them called efference copy (EC) to also influence our senses. This review offers a critical analysis of the EC concept by identifying its limitations. An alternative to the EC concept is based on the experimentally confirmed notion that sensory signals from receptors are perceived relative to referent signals specified by the brain. These referents also underlie the control of motor actions by predetermining where, in the spatial domain, muscles can work without preprogramming how they should work in terms of motor commands or EC. This approach helps solve several problems of action and explain several sensory experiences, including position sense and the sense that the world remains stationary despite changes in its retinal image during eye or body motion (visual space constancy). The phantom limb phenomenon and other kinesthetic illusions are also explained within this framework.

NEW & NOTEWORTHY

The notions of direct neural preprogramming of the motor outcome and the use of a copy of commands to muscles (efference copy) to control our senses conflict with basic physiological and physical principles. Instead, the brain predetermines where, in the spatial domain, muscles can work whereas commands to muscles emerge in this domain due to the interaction of the neuromuscular system with the environment, thus solving several problems in action and perception.

active sensing is the well-established notion suggesting that sensory impressions are not directly represented in signals from receptors but are formed with the participation of the brain. It has also been recognized that although action and perception are mediated by different pathways, they are somehow interrelated, as implied by the notion of perception-action coupling (Dayan et al. 2007; Goodale and Humphrey 1998; November and Keller 2014; Rizzolati and Craighero 2004; Sperry 1950, 1952; von Holst and Mittelstaedt 1950; Warren 1990; Warren et al. 2001). Therefore, to progress in the understanding of active sensing, we need to answer the question of how motor actions are controlled by the nervous system. The answer to this question is not as clear as it might seem.

Historically, contemporary views explaining the unique ability of animals to control motor actions began to emerge several centuries ago. After Newton, it became clear that physical actions of biological systems are not an exception in obeying the laws of mechanics and are therefore naturally described in terms of kinematic and kinetic variables characterizing the motor outcome of actions. Neurophysiological data were then limited and, focusing on the mechanical output of actions, it seemed natural to assume that the brain is able to prepare in advance (“preprogram,” in modern terms) the desired motor outcome and specify the requisite motor commands to muscles (i.e., the motoneuronal output or EMG patterns). It is this conviction that motivated the notion that a copy of predicted motor commands—efference copy (EC)—fed back to sensory processing areas of the brain is responsible for active sensing. Therefore, the notion of EC-based active sensing will be evaluated together with the precursor notion that the brain preprograms motor commands for actions. These notions will be compared with alternative views originating about 50 years ago. Specifically, starting from studies by Matthews (1959) and Asatryan and Feldman (1965), it was found that, to produce intentional motor actions, the nervous system changes specific neurophysiological parameters, the spatial thresholds at which muscles begin to be activated. When changed, these parameters shift the equilibrium state in the interaction between the organism and environment. Motor commands to muscles and the resulting motor action emerge, without preprogramming, due to the cooperative tendency of neuromuscular elements to reach the shifted equilibrium state. If the emerging action is unsatisfactory, the system adjusts these parameters to eventually reach the motor goal. They can also be considered as the origin or referent points of spatial frames of reference in which neuromuscular elements are ordained to work. This theoretical framework was initially called the equilibrium-point hypothesis, then gradually developed into the theory of referent control of action and perception (Feldman 2015).

Compared with previous publications (Feldman 2009; Feldman 2015; Feldman and Latash 1982a), further examples of referent control of perception and action are considered in this review. In particular, in addition to perception of the body schema, perception of body location in the environment and body orientation with respect to the direction of gravity is also considered. Moreover, in contrast to the usual assumption that position-related information conveyed by proprioceptive and cutaneous afferents is sufficient for sensing passive movements (Gritsenko et al. 2007; Paillard and Brouchon 1968), it will be shown that active participation of the brain is necessary to adequately sense even these movements. Therefore, the term active sensing refers to any movement. This review further elaborates on the previously discussed issue of referent control of eye movements and visual space constancy.

Efference Copy (EC) in the Context of the Posture-Movement Problem

The EC concept (Efferenzkopie) was introduced by von Holst (von Holst and Mittelstaedt 1950; von Holst 1954). Long before von Holst, concepts similar to EC were used by other, especially German scientists who were influential at the time (Helmholtz 1866; Steinbuch 1811; Uexküll 1926). Later, a similar concept was used by Bell (1981). Sperry (1950, 1952) introduced the term “corollary discharge” that implies that EC is formed based on the anticipated sensory outcome of a motor action. With this reservation, the term corollary discharge is used on parity with the EC concept.

Helmholtz (1866), a physicist, proposed that the nervous system uses a copy of motor commands (a copy of “innervation” in his terminology) to oculomotor muscles (EOMs) to compensate for shifts of the retinal image of the world during eye rotation in order to perceive the world as motionless (visual space constancy). He also suggested that sense of effort (Willensanstrengung) may represent an EC-like signal.

EC is a central concept in the “reafference principle” proposed by von Holst (von Holst and Mittelstaedt 1950; von Holst 1954) to explain how posture and movement are controlled and perceived. As many researchers before him, von Holst did not question the notion that neural control centers predict and specify motor commands required for active (self-initiated) movements, but noticed that there is a problem associated with this notion. Von Holst was aware that the stretch reflex is a postural stabilizer and emphasized that attempts to execute predicted motor commands to move away from a stable posture would be met with resistance of this reflex. Based on current knowledge, one can say that stability is maintained by the position- and velocity-dependent stretch reflex reactions (usually associated with stiffness and damping, respectively) as well as by reflexes that mediate intermuscular interaction, such as Ia reciprocal interaction between flexor and extensor muscles (Hultborn and Nielsen 2007). Intrinsic muscle properties also contribute to postural stability. Moreover, reactions to perturbations may involve spinal and descending systems that initiate transitions to another stable posture if perturbation exceeds certain limits, forcing, for example, a step to be taken to prevent falling. Postural stabilization is therefore a dynamic process. Taken together, mechanisms contributing to postural stability, including those that restore balance at a new posture, will be called “posture-stabilizing mechanisms.”

The problem of preventing resistance of posture-stabilizing mechanisms to self-initiated movements considered by von Holst can be recognized as the classical “posture-movement problem” (Stuart 2005). Von Holst assumed that, while sending motor commands (efference in Fig. 1) to initiate a movement, control centers simultaneously send EC to sensory levels to compensate for the influence of movement-related afferent feedback (reafference) on the central motor program and thus prevent resistance of posture-stabilizing mechanisms to self-initiated motion. In other words, von Holst thought that reflexes underlying postural stabilization are incompatible with and should be neutralized during active motion.

Fig. 1.

Von Holst's reference principle for control of action and perception. It suggests that each self-initiated action results from preprogrammed motor commands (efference). The influence of afferent signals (reafference) on the central program is prevented by a copy of these commands (EC). If present, the residual afferent signal (exafference) is perceived as elicited by external forces (perturbation).

The reference principle was also used to explain how the system perceives the difference between self-initiated and passive (involuntary) movements. Afferent signals elicited by external forces (perturbations) during such movements were called exafference (Fig. 1). It was assumed that if afferent feedback is fully suppressed by EC, the system would recognize such movement as self-initiated motion. In contrast, afferent signals remaining after subtraction of EC would be identified as exafference and perceived as elicited by external perturbation. Von Holst also applied the EC concept to optomotor behavior in fish and insects (von Holst and Mittelstaedt 1950; von Holst 1954).

The EC concept became central to various theories of action and perception. Most well-known is the theory suggesting that, in addition to other remarkable properties, the brain can function like a computer to predict and specify action and perception (Fodor 1975). Interestingly, some ideas preceding this theory originated long before the invention of computers (Uexküll 1926). Motivated by methods mainly developed in robotics, some scientists pointed out that the required computations can only be made with the help of internal models, i.e., neural emulators of mechanical and other properties of the organism interacting with the environment (Hollerbach 1982; Wolpert et al. 1998). To be functional, internal models must imitate mechanical and other physical laws, but in so doing, must invert cause-effect relationships inherent in these laws (so-called inverse-dynamic problem) (Ostry and Feldman 2003). Other computational models focus on optimality of motor actions by assuming that motor commands to muscles (also called control signals) are precomputed based on some cost function (e.g., Kuo 1995; Todorov and Jordan 2002). They may not require inverse-dynamic transformations of mechanical laws, but, like other computational approaches, have hidden inverse-dynamic problems at the stage when the computed motor commands should be converted into a physiological action. The question of how these commands are converted to physiologically meaningful synaptic inputs to motoneurons has not been addressed in computational approaches. As a consequence, the computational approach combined with internal models and/or optimality criteria have not gone beyond the boundaries of thinking in mechanical terms about motor control: it has retained the notion of preprogramming of motor outcome and using EC for perception. In fact, EC is central to many schemes of action and perception (e.g., Cullen 2004; Scott 2008; Wolpert et al. 1995).

Some researchers have suggested that the nervous system focuses on anticipated sensory outcome, rather than on or in addition to motor commands in action production (Adams et al. 2013; Powers 1973; Sperry 1950, 1952). However, afferent signals depend on many mechanical variables, including muscle forces. Therefore, to predict sensory outcome, the nervous system still needs to preprogram motor commands, a major attribute of EC. In other words, the idea of preprogramming of sensory outcome of motor actions does not leave the tenets of the mechanical framework within which the EC concept originated.

Challenging the Idea of Preprograming of Motor Outcome Underlying the EC Concept

Not all researchers have accepted the EC concept and the related notion that motor commands are programmable. In particular, Gibson (1966) suggested that the sense that the external world is not moving is based on the invariant topological structure of the motionless world and is recognized regardless of motion of its retinal images, making compensation of retinal shifts with EC unnecessary. Bridgeman (2007) who initially supported the EC concept later identified its limitations in solving the problem of visual space constancy. Recently, his team offered an alternative solution to this problem (Bridgeman 2010; Deubel et al. 2010) (see Visual space constancy). The notions of preprograming of motor outcome and EC underlying von Holst's reafference principle will be critically evaluated based on the current knowledge of physiological mechanisms underlying the control of posture and movement.

Coactivation of α- and γ-motoneurons (MNs) during active movements is a regular phenomenon (α-γ-linkage; Granit 1955; Matthews 1972; Prochazka 2015). This means that the activity of agonist muscles responsible for acceleration as well as the activity of antagonist muscles responsible for deceleration of intentional movement is supported by γ-MNs that increase discharges of muscle spindle afferents. Therefore, reafference is mostly enhanced, rather than suppressed, during intentional movements, invalidating von Holst's proposal that the posture-movement problem is solved due to cancellation of reafference.

There is an important aspect of the posture-movement problem not addressed in the reafference principle. Postural stability is associated with the ability of neuromuscular systems (reflexes) to automatically generate both position- and velocity-dependent afferent signals responsible for resistance to deviations from the stabilized posture (see above). Fast unopposed arm movements are produced by generating a triburst EMG pattern that terminates with the movement offset (Gottlieb et al. 1992). Being transient, EC could only temporarily suppress the position-dependent component of reafference, and the problem would remain: restored after the end of motion, the accumulated position-dependent resistance would drive the body segments back to the initial position. Therefore, to solve the posture-movement problem it is necessary to explain how the system transfers stability from one posture to another to prevent movement reversal.

The assumption that the nervous system preprograms and specifies motor commands to achieve the desired motor outcome is also inconsistent with several physical and physiological principles. In particular, in deafferented subjects, EMG levels are not affected by loading or unloading of preloaded muscles (Figure 5 of Levin et al. 1995). This implies that, in normal conditions, afferent feedback is responsible for the EMG-force relationship (Bigland and Lippold 1954; De Luca 1997). Specifically, during muscle stretching, the number of recruited motor units increases resulting in greater EMG activity and muscle force. In this way, afferent feedback works optimally to minimize situations when, for example, a strong external force is confronted by a small number of active motor units, which may cause overstretching and damage of sarcomeres. Therefore, motor commands are low-level variables, direct central specification of which would interfere with normal functioning of afferent feedback, causing new problems.

Fig. 5.

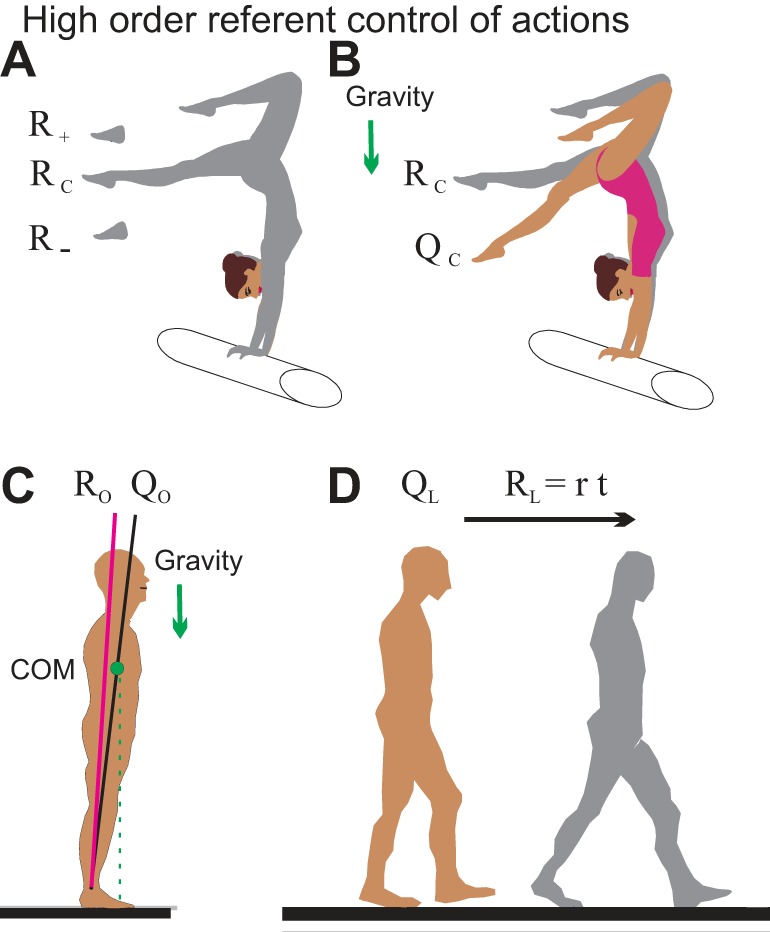
Global factors in the control of actions. A: referent control of the body configuration (R_C) and spatial zone of muscle coactivation (R₋, R_C, R₊) that increases body stability. B: at a subconscious level, the athlete learns to specify a referent body configuration (R_C). Under the influence of gravity, the body moves away from R_C until increasing muscle resistance begins to balances gravitational torques at some actual body configuration (Q_C). If this body posture is not satisfactory, it is corrected by changing the referent body configuration. C: referent body orientation (R_O) in the control of body leaning in gravitational field. D: locomotion results from shifting the referent body localization (R_L) at which body balance can be reached in the environment. [A and B reproduced with permission from Feldman 2011. Copyrights 2011 John Wiley and Sons.]

Strange as it may seem, the notion of preprogramming of motor commands implies that the nervous system is able to invert the causalities inherent in physical and physiological laws. To clarify, suppose the system predetermined motor commands required for an action. The problem is that internal models directly compute motor commands. Such motor commands represent output signals of MNs and muscles (i.e., forces) instead of physiological signals such as synaptic inputs to MNs. Therefore, in order to physically execute the computed commands, the system would need to invert causality by converting MN output to input. Such an inversion is not physiologically feasible because of the fundamental irreversibility of input-output relationships of MNs (e.g., threshold properties, self-supporting spike generation) in addition to the associated tremendous number of redundancy problems (Foisy and Feldman 2006). The inverse-dynamic problem is inherent in all computational theories of motor control and is not recognized or considered (e.g., Kuo 1995; Todorov and Jordan 2002).

Computational theories of motor control are based on the assumption that afferent feedback directly transmits information about kinematic variables, thus conflicting with the notion of active sensing for kinesthesia (see below).

The greatest challenge to the notions of preprogramming of motor commands and EC comes from inconsistency of these notions with a physical principle regarding the determinants of equilibrium states considered in thermodynamics and applied to any natural system (Glansdorf and Prigogine 1971). In its application to neural control of posture and movement, this principle declares that although muscle and external torques tend to be balanced at any chosen equilibrium position, the specific body position at which balance can be achieved is not defined by torques. This becomes obvious in the cases of arm motion against a constant external torque. In such an isotonic condition, subjects are free to establish different stable arm positions at any of which muscle torques may be the same. More generally, variables comprising and therefore constrained by physical laws cannot be determinants of equilibrium states. Constrained by mechanical laws, torques and forces are not determinants of such states. Moreover, variables related to those that are constrained by physical laws also cannot be responsible for positions at which a stable equilibrium is achieved. For example, EMG levels (motor commands) are closely related to law-constrained muscle forces (Bigland and Lippold 1954; De Luca 1997). Therefore, EMG levels, like torques, cannot predetermine where, in space, an equilibrium state can be achieved. This is apparent from findings that, in certain conditions, tonic EMG levels of arm muscles can be similar at different positions (Feldman and Latash 2005; Ostry and Feldman 2003; Raptis et al. 2010).

In contrast, according to the physical principle, the equilibrium position is defined by system parameters that are constant and others that can be changed independently of law-constrained variables typically used in biomechanical studies. Parameters characterize the hidden, intrinsic system state influencing the external, mechanical equilibrium that the system tends to reach if stability requirements are met.

The same physical principle governs how motor actions can be controlled. In particular, to produce motion from one stable position to another, the nervous system must change system parameters. In response to parametric control, EMG signals, muscle forces, and kinematics will emerge automatically, without any preprogramming. These emergent forces bring the body from one stable posture to another without any posture-movement problem.

The failure to solve the problems of perception and action considered by von Holst illustrates the well-known saying by Albert Einstein that problems cannot be solved in the same conceptual framework within which they are encountered. The problems considered by von Holst were encountered in the framework associated with the belief in preprogramming of motor commands. Therefore, to find solutions to these problems, we need to abandon this framework. This conclusion also refers to computational theories in which control signals underlying actions are identified with motor commands to muscles.

I will briefly describe methods and results of the initial study (Asatryan and Feldman 1965) in which neurophysiological parameters underlying the control of motor actions in humans have empirically been identified, thus refuting the notions of preprogramming of motor commands and EC-based active sensing. Subsequent results related to parametric control will be summarized by citing relevant experimental and theoretical studies.

Referent Control of Arm Actions

Parametric control of arm movements was revealed by analyzing three motor tasks: involuntary motion of the arm elicited by sudden unloading of preloaded muscles (the unloading reflex); intentional changes in arm position; and passive arm motion produced by the experimenter during full muscle relaxation (Asatryan and Feldman 1965).

In unloading experiments, subjects placed the forearm on a horizontal manipulandum and grasped a handle. They established an initial elbow angle by producing a flexor torque to balance a load torque acting horizontally on the manipulandum. In the absence of a torque motor during this study in Moscow, the initial torque was created by suspended weights that acted on the manipulandum via pulleys and small electromagnetic locks. The combination of elbow angle and torque was called the initial equilibrium point (EP). It was presented as a dot on the screen of an oscilloscope in front of subjects (point a in Fig. 2).

Fig. 2.

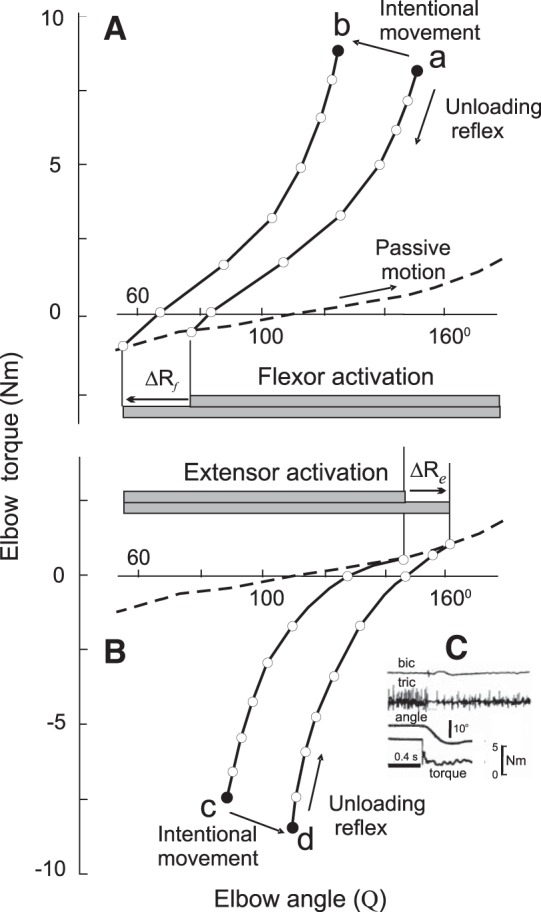
Threshold control of the unloading reflex, intentional movements and muscle relaxation. Families of static torque-angle characteristics (solid curves) of elbow flexors (A) and extensors (B) were obtained in unloading experiments. Filled circles (a–d): initial equilibrium points (EPs). Open circles: final EPs established after unloading. For each characteristic, the tonic EMG activity decreased with the decreasing load, as exemplified for the elbow extensors (triceps brachii) in C. Dashed curves in A and B: passive torque-angle characteristic obtained by slow passive rotation of the manipulandum with the forearm on it when the subject fully relaxed arm muscles. Each solid curve in A and B bifurcated from the characteristic of passive muscles at a specific position-threshold joint angle (R) that changed (ΔR) when the subject made intentional movements from a to b or from c to d. In contrast, the threshold remained invariant during unloading reflexes. Full muscle relaxation was achieved by setting activation threshold outside the biomechanical range of elbow angle. [Reproduced with permission from Feldman (2011). Copyright 2011 John Wiley and Sons.]

When subjects established the initial EP, they closed their eyes, and the experimenter pressed a button to deactivate electromagnet locks and drop weights in a bucket with a pillow inside, thus producing sudden unloading of the arm. Unloading of the arm could be partial or complete without the subjects' knowledge. In response, the arm involuntary moved to another EP, the unloading reflex. The final EP was dependent on the residual load (open dots in Fig. 2). Subjects were instructed to abstain from intentional corrections of unloading effects (“do not intervene voluntarily”). At the beginning of each trial, the initial load was restored. Subjects established the same initial EP, and unloading was repeated by diminishing the load by the same or a different amount. The experiment yielded a monotonic nonlinear torque-angle curve, a characteristic of the unloading reflex.

Mathematically, this characteristic represents a one-dimensional set of EPs associated with some hidden invariant, a neurophysiological parameter that, according to the above definition, is independent of mechanical variables. Apparently, the elbow angle, muscle torque and its derivative, muscle stiffness (the slope of the characteristic at different EPs), were not invariants of the unloading behavior. Moreover, the tonic EMG activity of elbow flexor muscles at different EPs was different and was modulated according to the level of residual muscle torque (Fig. 2C). Therefore, EMG levels were not invariants of the unloading behavior.

To identify the hidden invariant, we asked subjects to intentionally change the elbow angle while compensating another load torque, and the unloading procedure was repeated with a new initial EP (point b in Fig. 2). Indeed, we got another torque-angle characteristic (curve starting from point b). We also took into account that such characteristics include some passive elbow torque. We asked subjects to completely relax elbow muscles and recorded a torque-angle characteristic of passive elbow muscles when the experimenter rotated the manipulandum (dashed curve in Fig. 2).

The two characteristics of the unloading reflex (starting from points a and b) bifurcated from the characteristic of passive muscles at different joint angles. These bifurcation points indicate the specific joint angles at which elbow flexors began to generate active muscle torque. These threshold angles were different for different unloading characteristics. In other words, intentional motion from point a to point b was associated with a shift (ΔR) in the threshold joint angle at which active muscle torque began to be generated. By recording EMG activity of elbow muscles, we confirmed that intentional motion from point a to point b was associated with a shift in the threshold angle at which elbow flexor muscles began to be recruited.

Anatomically, each threshold angle (R) corresponds to the threshold lengths (λ) at which flexor muscles begin to be recruited. Thus physiological parameters (R and λ) that the nervous system shifted (“reset”) to produce intentional arm movement were identified. In the unloading reflex, neural control levels maintain these parameters invariant. To produce muscle relaxation in the entire biomechanical range of muscle length, the threshold muscle length is increased to a value exceeding the upper limit of this range.

By the above definition, parameters characterize the intrinsic state of neural circuitry involved in the control of motor actions. As a consequence, parameters affect but remain independent of mechanical variables and motor commands. Reflecting an intrinsic state of the nervous system, these parameters always change in a feedforward way, i.e., in advance of changes in the EMG patterns, muscle forces, and kinematics. The understanding of the nature of parameters R and λ helps explain how movements are controlled without any preprogramming of motor commands and without posture-movement problems. It is also essential that these parameters do not predetermine the targeted position: Central signals to α-MNs specify the origin (referent) point in the spatial frame in which these MNs are predetermined to function. Given this interpretation, threshold control is also called referent control, and the two terms will be used synonymously.

Solving the Posture-Movement Problem: Converting Posture-Stabilizing to Action-Producing Mechanisms

In is necessary to explain why a change in parameter R is sufficient to elicit motion without any posture-movement problem. For simplicity, the explanation below uses only one, albeit major, R command underlying action production. Other commands (one of them is called the referent coactivation, C, command) will be defined later in this review.

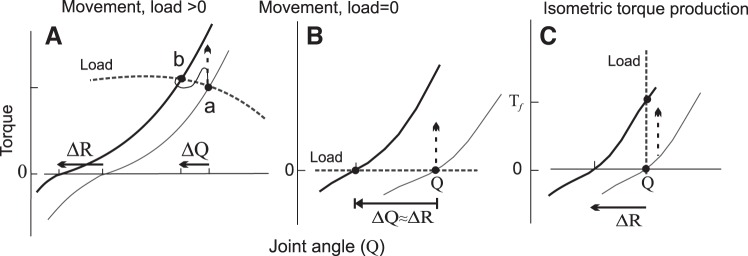
Consider first elbow flexion associated with transition from the initial EP (a) to the final EP (b) in experiments shown in Fig. 2A. These EPs are reproduced in Fig. 3A together with the torque-angle characteristics that can be considered as characteristics of the tonic stretch reflex. Each of these characteristics represents an important property of posture-stabilizing mechanisms—muscles gradually oppose lengthening and yield to shortening. Indeed, in dynamics, the activation threshold and muscle torque are velocity-dependent. We should take into account that flexor muscles interacted with a load have some torque-angle characteristic (dashed curve in Fig. 3A). The initial EP, a, is the crossing point of the respective muscle and load characteristics since only at this point were the muscle and load torques balanced.

Fig. 3.

Referent control of motor actions. A: a qualitative explanation of intentional motion from equilibrium point a to b in experiments shown in Fig. 2. Referent control (ΔR) results from a shift in the intrinsic (threshold) state of the neuromuscular system, also shifting the torque-angle characteristic. For each characteristic, the tonic level of muscle activation increases with increasing active muscle torque. Therefore, at the initial arm position, the shift results in an increase in the muscle activation and torque (vertical arrow) eliciting arm motion (ΔQ) to a new equilibrium point, b, along a dynamic trajectory (curved). B: if the external load (L) is zero, the initial arm position (Q) is close to the threshold one (R). A decrease in the R results in flexor activation and torque (vertical arrow). The emerging movement is ended at the new EP (left circle). C: if the movement is blocked, shifts in the R result in transition to a final EP (top circle) at which an isometric muscle torque is generated. [Reproduced with permission from Feldman (2015). Copyright 2015 Springer.]

Consider, qualitatively, electromyographic and mechanical consequences of a central shift in R (ΔR in Fig. 3A) together with the torque-angle characteristic. According to the shifted characteristic, the EMG activity of flexor muscles at the initial position will increase (vertical arrow), producing additional torque that will begin to drive the arm toward a new stable EP, b. This process also signifies an increase in the joint range in which flexor posture-stabilizing mechanisms are destined to work. With the motion of the elbow to EP b, flexor muscles will be shortened and their activation and torque will start decreasing to a level below the load curve. The load toque exceeding the muscle torque will decelerates motion to the final EP, b. The curve from a to b shows, in a qualitative way, the trajectory of motion between these points on the torque-angle plane. Intentional elbow flexion in the absence of an external load can be explained similarly (Fig. 3B). In this case, it is necessary to take into account that the R command shifts the torque-angle characteristic of all muscles in the flexion direction, resulting in an increase in the activation of agonist muscles (vertical arrow in Fig. 3B). With motion of the elbow to the final EP (left filled circle), flexor activation and force responsible for movement acceleration will be diminished due to muscle shortening, while extensor muscles will be stretched and reactivated, thus decelerating the elbow to the new EP. A dynamic model confirms this qualitative explanation (Pilon and Feldman 2006; Zhang et al. 2016).

Note that in the case of referent control, posture-stabilizing mechanisms are not suppressed. When the common threshold position is shifted, it is the initial arm position that becomes deviated from the new stable EP. As a result, the same posture-stabilizing mechanisms, instead of resisting intentional motion, actively drive the arm to the final position, without any posture-movement problem. In other words, referent control allows the nervous system to convert posture-stabilizing to movement-producing mechanisms. It also automatically transfers stability from the initial position to the final one due to the shift in the torque-angle characteristic. Contrary to von Holst's assumption (Fig. 1), suppression of reafference would be detrimental to motor action: reafference is essential both for postural and movement stability. Nor is preprogramming of motor commands necessary in the referent control strategy: these commands emerge automatically, depending on the difference between the actual and the velocity-dependent threshold arm positions.

Referent control underlies not only motion but also isometric torque production when, say, the arm pushes against a wall. On the torque vs. angle plane, the isometric condition is characterized by a vertical line since the arm position remains the same regardless of muscle force applied to the wall (Fig. 3C). As in other cases, the EP of the system is the point of intersection between the load and muscle characteristics. Thus, if the movement is blocked, shifts in the R result in transition to a new final EP due to the change of isotonic to isometric load, without efforts of neural control levels (see Fig. 5C, top circle). Isometric muscle torque increases until the new EP is reached.

Spatial (Referent) Control of Motoneurons

To my knowledge, the study by Asatryan and Feldman (1965) was the first to show that threshold (referent) control underlies intentional motion in humans. Before that, it was Matthews (1959) who found in decerebrate cats that the spatial activation thresholds can be modified by γ-MNs or by changing reflex intermuscular interaction. Confirming his findings, Feldman and Orlovsky (1972) additionally showed that vestibulo-, reticulo-, corticospinal and, according to Nichols and Steeves (1986), rubrospinal systems are involved in setting and resetting spatial thresholds of muscle activation. Muscle activation thresholds can be changed by both post- and presynaptic influences on α-MNs (Capaday 1995). Recent studies confirmed that the corticospinal system in humans specifies spatial activation thresholds in task-specific ways without directly stipulating motor commands to muscles (Ilmane et al. 2013; Raptis et al. 2010; Sangani et al. 2011). These, as well as other findings (Feldman 2015), provide experimental evidence for referent control of posture and movements.

Knowledge of how the motoneuronal pool functions is important for any theory of action and perception, and the finding of threshold control is an essential part of this knowledge. However, in order to proceed further in the understanding of how the motoneuronal pool is controlled we need to take into account additional physiological data. Figure 4A schematically summarizes the network associated with afferent and central influences on MNs. It includes muscle and α-MNs that receive pre- or/and postsynaptic mono- or polysynaptic afferent inputs from proprioceptive and cutaneous receptors that are sensitive to muscle stretching and shortening. The network also includes central spinal and supraspinal influences transmitted to α-MNs directly or indirectly via γ-MNs or interneurons (INs) that mediate intermuscular interaction, in particular, via Ia interneurons of reciprocal inhibition between agonist and antagonist muscles. Indeed, additional, dynamic properties of MNs should be taken into account to address the question of how MNs are controlled. To do so, we need first to answer the question of how central influences on α-MNs of an electrochemical nature are transformed into changes in parameters R and λ that have a spatial dimension—the threshold joint angle or muscle length at which α-MNs begin to be recruited. By producing this transformation, the nervous system places our motor actions in FRs associated with our body and/or environment.

Fig. 4.

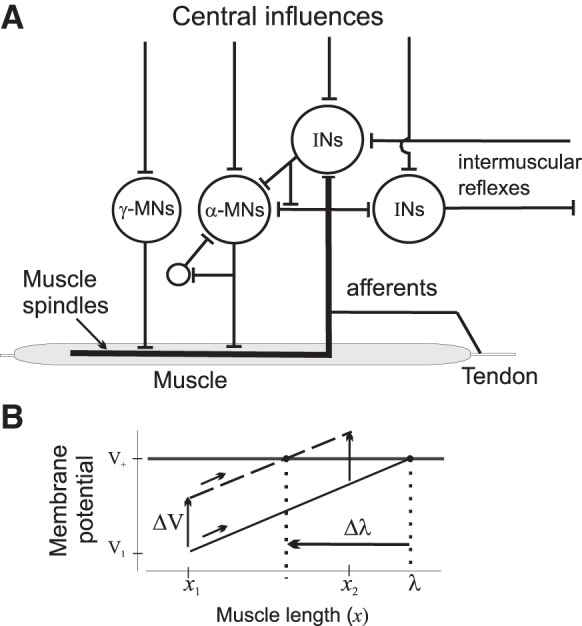
Physiological origin of spatial recruitment of motoneurons. A: simplified neuromuscular network underlying the control of threshold muscle length at which motor units begin to be recruited. B: shift in the threshold length (Δλ) as an integral spatial measure of electrochemical central influences (ΔV) on α- and γ-MNs. For details see text.

It is important that α-MNs have an electrical threshold for recruitment. Consider the smallest α-MN in the motoneuronal pool under a constant, tonic influence of descending systems (Fig. 4B). At an initial muscle length, x₁, the MN is in a subthreshold state. With slow passive muscle lengthening, the motoneuronal membrane potential increases (low diagonal line) due to predominantly facilitatory afferent feedback, and reaches the electrical threshold (V₊) at which the α-MN is recruited. This occurs at a threshold muscle length, λ. With further stretching, other α-MNs will gradually be recruited according to their individual threshold lengths, as occurs during a stretch reflex. The membrane potential can be enhanced (ΔV, top diagonal line) via direct or indirect central influences on the α-MN (left vertical arrows). As a consequence, the spatial recruitment threshold will be diminished by Δλ. Thus in the presence of afferent feedback, central spinal or supraspinal facilitation or inhibition have an integral, spatial measure, a shift in the threshold length at which α-MNs begin to be recruited.

Taken together, anatomical and neurophysiological data justify the following condition of muscle activation: If x is the current muscle length, then the muscle is active if

$$x-\lambda \ast >0$$ (1)

where λ* is the dynamic threshold muscle length

$$\lambda \ast =\lambda -\mu \text{v}+\rho$$ (2)

which means that λ* decreases with stretch velocity (v > 0 for muscle stretching and v < 0 for shortening); μ is the sensitivity of the threshold to velocity that possibly can be controlled by dynamic γ-MNs; and ρ is a combined measure of the influence of the intermuscular interaction and history-dependent intrinsic state of MNs (e.g., associated with plateau potentials). In the suprathreshold range, recruitment of motor units and active muscle force increases with the difference between the actual and threshold muscle lengths. Threshold λ* defines the range of muscle lengths in which active muscle force can be generated.

These formulas account for different ways by which muscles can be activated or deactivated. In particular, the threshold length (λ*) can be considered as the threshold of the stretch reflex. This does not mean that this reflex is the only way of activating muscle: the initially silent muscle can be activated centrally, by decreasing the activation threshold. The initially silent muscle can also be activated transiently, by brief rapid stretching, as occurs during the knee jerk reflex. On the other hand, a rapid transient shortening of initially active muscle can elicit a silent period in its EMG activity (Fig. 2C). This phasic reaction as well as the knee jerk reflex indicates that the activation threshold is velocity-dependent (Eq. 2). Responses to muscle stretches can be prevented by increasing the spatial threshold (Turpin et al. 2016). Thereby, with increasing the threshold, the stretch reflex is not suppressed as such; it remains fully functional but at higher muscle lengths. Therefore, gating of reflexes should be considered as an emergent property caused by shifts in spatial thresholds, rather than by direct timing of reflexes by central generators, as is usually assumed in physiological studies. Only if the threshold is shifted beyond the upper biomechanical limit of the range of muscle lengths, the muscle will be relaxed within the entire biomechanical range and can only be activated by stretching at a high speed, as occurs during the knee jerk reflex. The muscle can be activated at the biomechanically shortest length by setting the threshold below that length. Taken together, these properties imply that the normal range of the central regulation of the threshold length (λ₋, λ₊) exceeds the biomechanical range of the actual muscle length (x₋, x₊) in the organism. This rule may be violated by neurological lesions, resulting in spasticity, weakness, and movement incoordination (Levin et al. 2000; Mullick et al. 2013).

Some descending systems can shift the electrical threshold, V₊, of α-MNs (Fedirchuk and Dai 2004; Heckman et al. 2008; Krawitz et al. 2001). A testable prediction is that this might be an additional mechanism of central changes in the spatial threshold, λ. It is also possible that, compared with low-fatigable motor units, fast-fatigable motor units have greater dynamic sensitivity (μ). As a consequence, with increasing speed of stretch, these motor units can be recruited before low-fatigable motor units (recruitment reversal), which may also be tested.

Note that von Holst thought that efferent innervation of proprioceptors is a part of EC (see figure 3.9 in von Holst and Mittelstaedt 1950). This view persists despite several studies, starting from that by Matthews (1959), showing that the activity of γ-MNs is part of the central mechanism that sets the spatial threshold (R) at which the muscle begins to be activated.

High-Order Referent Control of Actions

The scheme in Fig. 4B can be applied to other neurons in the following way. Suppose a group of neurons receives afferent inputs continuously dependent on some sensory variable. By substituting x with this variable, one can conclude that independent central inputs to these neurons will predetermine the threshold value of this variable at which they begin to be recruited. This generalization has been used to define different forms of referent control that, in particular, allow the nervous system to control multiple muscles as coherent units (Feldman 2015).

Consider neurons that receive afferent inputs depending on the body configuration (i.e., on positions of body segments). Then, independent central inputs to these neurons predetermine the threshold body configuration (R_C) at which these neurons begin to be recruited (Fig. 5A). If projections of these neurons to MNs are organized appropriately, then these neurons will specify the referent body configuration at which all muscles reach their threshold lengths. In other words, these neurons can specify a common threshold configuration of the body at which muscles are silent but become activated depending on the deflection of the actual body configuration (Q_C) from the R_C (Fig. 5B). The common threshold, R_C, can be shifted by reciprocal central influences on MNs of flexor and extensor muscles.

Referent control can also be used to control muscle coactivation. Physiologically, this can be done by central cofacilitation of flexors and extensor MNs. Because of differences in the anatomical arrangements, the central cofacilitation splits the common threshold, R_C, in the opposite directions for flexors and extensors. Muscles become coactivated in a spatial zone (R₋, R_C, R₊) that surrounds the R_C. (Fig. 5A). The extent of this zone is defined by the degree of cofacilitation of MNs. This central process is called the referent coactivation command. During active movement produced by shifting the R_C, the zone is shifted together with R_C. In the presence of coactivation, muscle activity depends not only on the deviation of Q_C from R_C but also on the extent of the coactivation zone. The activity also depends on the speed (rate) of changes in this deviation.

In the example shown in Fig. 5B, the athlete's nervous system presumably specifies a referent body configuration R_C, possibly with some level of coactivation of muscles due to a C command. Due to gravity, the body is deflected to position Q_C at which muscles begin to balance gravitational torque.

On the earth, body posture and movements are oriented relative to the direction of gravity. Suppose that neurons receive afferent inputs from vestibular receptors sensitive to the direction of gravity. Then independent central inputs to these neurons predetermine the referent orientation (R_O) of the body at which these neurons begin to be recruited. In addition to the factors described above, the recruitment of muscles will depend on the deviation of the actual body orientation (Q_O) from R_O (Fig. 5C). Suppose that initially a subject was quietly standing almost vertically such that muscle and gravitational torques were balanced. Leaning involves a small inclination of the referent body orientation forward. This will result in a decrease in the activity of antigravity muscles. The unbalanced gravitational torque will begin to lean the body forward until balance is restored at a new body posture.

Yet another group of neurons can receive sensory information that depends on the actual localization (Q_L) of the entire body in the environment. Then, according to the general rule, central inputs to these neurons will define the referent body localization (R_L) at which these neurons are recruited. Muscles will be activated depending on the difference between Q_L and R_L, forcing the body to walk from the initial position to the referent position in the environment (Fig. 5D). With increasing rate of shifts in R_L, walking will be transformed into running. It has been confirmed that shifts in R_L underlie the control of body steering in the environment (Feldman et al. 2013; Krasovsky et al. 2013).

Referent Control of Eye Movements: Similarity with Control of Arm Movements

It is apparent that the choice between different gaze directions can be made intentionally, i.e., to certain limits independently of optic stimuli. A physical rule described in the section on posture-movement problem restricts the ways in which such a choice can be made. In reference to the eye system, the rule stipulates that the choice between different gaze directions, i.e., equilibrium positions of the eyes in the orbit, is not defined by mechanical variables or variables dependent on them. It is defined by variables that influence but are specified independently of eye position and movement, i.e., technically speaking, in an open-loop way. In physics, such variables are called modifiable parameters. They characterize the intrinsic state of the system, rather than its external, motor outcome.

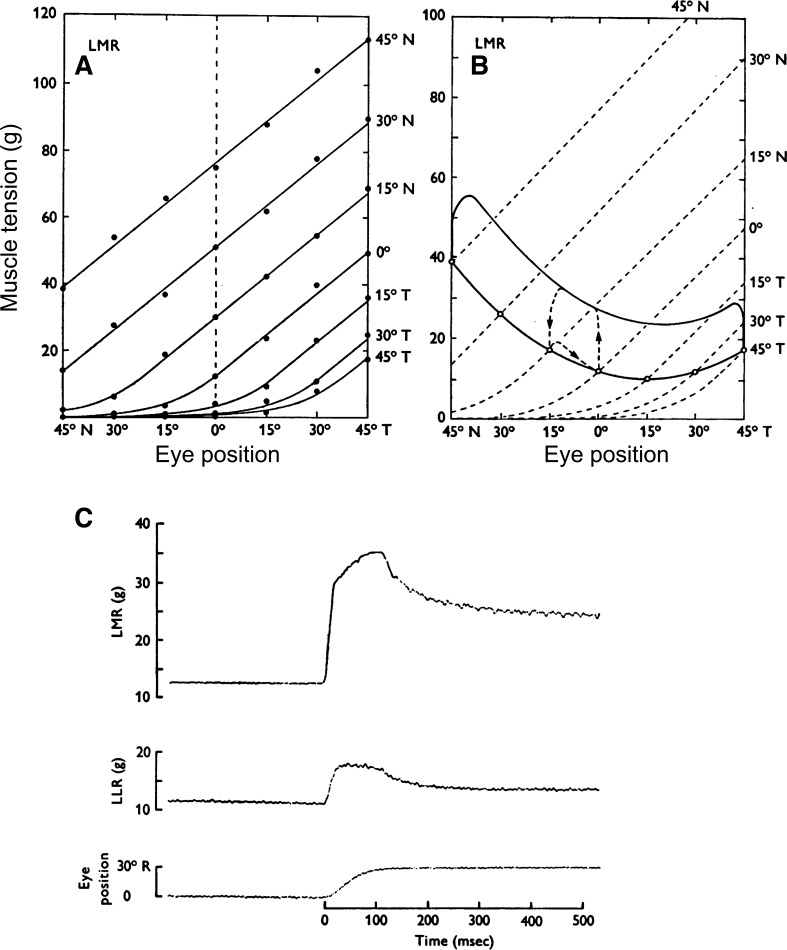
Based on this definition, can we say that motor commands to EOMs or its copy, EC, belong to the set of such parameters? Indeed, motor commands influence motor outcome but can these commands be specified in an open-loop way, i.e., independently of motor outcome? The answer appears to be negative since, as in limb muscles, the number and firing frequency of recruited motor units of EOMs increase with increasing muscle force (Björk and Kugelberg 1953; Lennerstrand 2007), implying that recruitment of MNs of EOMs is regulated by proprioceptive feedback. In other words, being related to muscle forces, motor commands or EC are not responsible for the choice of the equilibrium position to which the eyes move. Motor commands just move the eyes to the position predetermined by system parameters. We need thus to indicate adjustable parameters that are responsible for shifts in the equilibrium state of the oculomotor plant. The unique study by Collins et al. (1975) is helpful in identifying such parameters (Fig. 6).

Fig. 6.

Data (Collins et al. 1975) that were used to suggest that referent control is inherent in eye movements in humans. A: family of tension-extension characteristics of EOMs for different direction of gaze fixation in a human subject (N nasal and T temporal gaze directions) B: dynamic tension-extension diagrams during saccades (top curve) and pursuits (bottom curve). C: an example of agonist (top trace) and antagonist tension during a single saccade (bottom curve). [Reproduced with permission from Collins et al. (1975). Copyright John Wiley and Sons.]

Before a surgery to correct for strabismus in several subjects, Collins et al. (1975) attached a small force transducer in series with tendons of horizontal rectus muscles detached from their points of insertion on the eye globe. While subjects maintained the same gaze direction with the nonoperated eye, the experimenters stretched EOMs on the operated side to measure their tension-extension characteristics. They found that each gaze direction is associated with specific tension-extension characteristics of EOMs and these characteristics are shifted with changes in the gaze direction (Fig. 6A). A similar control process called the referent command, R, underlies intentional changes in the position of body segments (Fig. 2). EMG activity was not recorded during stretching EOMs but the finding that EMG activity in EOMs scales with muscle tension (Björk and Kugelberg 1953; Lennerstrand 2007) indicates that motor commands (tonic EMG levels) increased with the muscle force for each tension-extension curve and were reduced to zero when muscle force became zero at a specific eye position characteristic of each gaze direction. This justifies the conclusion that shifts in the referent (R) eye position related to the thresholds at which EOMs begin to be activated underlie the control of gaze. Also note that the family of EOM characteristics qualitatively resembles the family of characteristics of elbow muscles in humans for different intentionally specified arm positions (Fig. 2), which also motivates the conclusion about referent control of arm motor actions.

There is a persistent argument that afferent feedback (proprioceptive reflexes) is essential in limb muscles for adjusting motor commands to reach the motor goal in different external force fields but this feedback is not needed for eye movements produced in a relatively stationary external force field. This argument does not take into account the multifaceted role of afferent feedback. In particular, afferent feedback and the stretch reflex associated with it are fundamental for the stability of position and movement, which is equally important for EOMs and skeletal muscles. Only comparatively recently the opinion about a minor role of afferent feedback in eye movements was questioned by the finding that deafferentation of EOMs results in substantial deficits of eye movements and gaze instability, not to mention that deafferentation elicits malfunctioning of the vestibulo-ocular reflex (Donaldson 2000; Hayman and Donaldson 1995). Distinctive stretch reflexes were observed in semi-awake squirrel monkeys during passive eye rotations (Dancause et al. 2007). Although muscle spindles are absent in EOMs of these animals, EOMs have receptors called palisades that probably have a similar structure, including efferent innervation (Steinbach 2000).

Additional results obtained by Collins et al. (1975) indicate that the R command is combined with another command during saccades. After attaching the tendons to the globe, Collins et al. (1975) recorded tension-extension diagrams during saccades and pursuits (Fig. 6B). At the onset of a saccade, tension in the agonist increased almost isometrically (Fig. 6C). Then, as the eye moved, tension levels paralleled those of fixation but with an isotonic increment of 15–25 g. At the end of the saccadic movement, tension fell essentially isometrically to the new fixation level. Tensions recorded during smooth pursuits just slightly exceeded those of fixation. These findings suggest that shifts in the tension-extension characteristics during saccades by the R command are combined with additional shifts in thresholds responsible for coactivation of agonist and antagonist EOMs during saccades and that this coactivation recedes with the offset of saccade. Based on the dynamic diagram, one can suggest that a command similar to the referent coactivation (C) command in fast arm motion is also used during saccades.

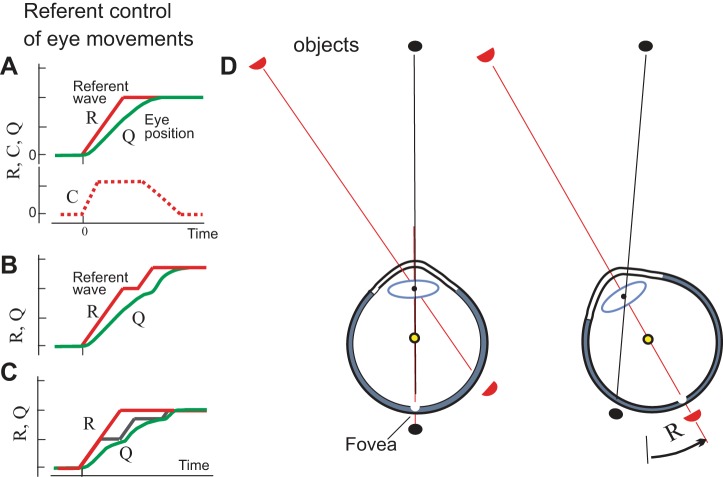
To summarize, based on data by Collins et al. (1975), one can suggest that a bicomponential referent R-C control underlies eye motion (Fig. 7A). Like for limb movements, the R command can be produced by changing spatial thresholds at which MNs of EOMs begin to be recruited, thus shifting the tension-extension characteristics of EOMs. Physiologically, such shifts result from central depolarization of agonist MNs in combination with hyperpolarization of antagonist MNs (reciprocal pattern). Changes in the referent eye position are accomplished at a certain rate specified according to the type of eye movement (saccade or pursuit). The rate and duration of referent shifts predetermine the total shift in gaze, required for saccades to bring the retinal image of the object of interest to the fovea. The referent gaze shift can thus be represented as a ramp-shaped function in time (Fig. 7A). Neurologically, it can be associated with propagation of excitation along a neuronal ensemble (referent wave). Reflecting the intrinsic state of the neural mechanism responsible for referent eye movements, the referent wave leads the activation of EOMs and eye motion. EOM activation emerges depending on the difference between the emergent actual position and centrally specified referent position of the eyes.

Fig. 7.

Referent control of eye motion and visual space constancy. A: saccadic motion results from appropriate shifts in the tension-extension characteristic of EOMs shown in Fig. 6. As in arm muscles, these shifts result from a combination of referent reciprocal (R) and referent coactivation (C) commands, both producing changes in the eye threshold position at which EOMs begin to generate active tension. When an object of interest is defined, saccadic referent eye rotation is initiated that virtually brings the object image to the fovea. Actual eye rotation (Q) follows. Q lags behind the changes in R because of eye inertia, gradual muscle activation and force generation as well as of passive resistance of connective tissue in the orbit. Because of transient discrepancy in R and Q, to avoid misperception, vision is blocked until the eyes come to the final referent position. The C command contributes to saccade speed and can be minimized in pursuit. Shifts in R can be associated with wave propagation along a neural ensemble (referent wave). EOMs generate activity depending on the difference between the actual and the referent position of the eyes. B: if necessary, a second saccade can be initiated even before the end of the first saccade. C: the R can predetermine a total shift in gaze, but at a lower, executive level this shift can be produced in several saccadic steps. D: referent eye rotation (R) symbolizes transition to a new spatial frame of reference in which retinal images are considered such that the external world is perceived as stationary despite retinal shifts in its images. [D reproduced from Feldman 2015 with permission from Springer. Copyrights Springer.]

A good candidate for the structure that generates referent waves for eye movements is the superior colliculus in which propagation of excitation has been identified by Guitton's team (Munoz et al. 1991). Propagation of excitation has been found in other neural circuits (e.g., Takahashi et al. 2011; Zanos et al. 2015) but it remains to be seen whether or not it can be considered as a referent wave in the sense described above.

The R command alone is likely sufficient for visual pursuit behavior. The capacity of speeding eye movement by increasing the rate of the R command is probably limited, and in order to produce very rapid, saccadic eye movements, another referent, C command is added. This command is produced by facilitation of agonist and antagonist MNs, thus shifting their activation thresholds from those specified by the R command. The referent position thus becomes surrounded with a range of eye positions at which agonist and antagonist EOMs can be coactivated (the C zone). The R and C commands are combined to produce saccades (Q in Fig. 7A). Since the localization of the C zone is defined by the R command, the former is shifted with the latter. As a result, the C command increases shifts of agonist tension-extension characteristic, thus additionally accelerating eye motion. Without such shifts, the C command would coactivate and stiffen agonist/antagonist EOMs at the initial position, thus impeding eye movement. As shown in a model, by shifting the C zone by the R command, the system not only increases acceleration but also deceleration of motion, minimizing terminal oscillations (Pilon and Feldman 2006). The C command is only necessary to speed up eye motion and being unnecessary at the final eye position, gradually recedes with the movement offset, which is consistent with the dynamic tension-extension diagram by Collins et al. (1975), showing an almost isometric drop in net torque at the end of saccade (Fig. 6C).

It is interesting to compare the bicomponential R-C referent pattern presumably underlying eye motion with the pulse-step pattern for control of saccades (Clark and Stark 1975). These patterns have some common features but differ in fundamentals. In both patterns, there is a transient command terminated with eye movement offset (C and pulse) and a long-duration command (R and step, respectively) maintained at the final eye position. In both patterns, the transient command is used to speed up eye motion, whereas the long-duration command holds the eye at the final position. However, as a presumed pattern of motor commands to eye muscles, the pulse-step model misses the important point that the system must shift the tension-extension characteristics in the spatial domain to transfer balance to the final eye position of the oculomotor plant. The R-C pattern shifts such characteristics without direct specification of motor commands to EOMs.

It is known that direct muscle activation changes the slope (stiffness) of the muscle characteristic whereas data by Collins et al. (1975) show parallel shifts in the characteristic (Fig. 6A). In contrast, by shifting the activation threshold, the R-C commands just change the position at which regular recruitment of motor units starts without much influence on the shape of the characteristic. In the presence of the stretch reflex, direct specification of motor commands to MNs of EOMs in the pulse-step model would be impeded by this reflex, complicating the reaching of the final eye position (the posture-movement problem). Compared with the step command, the gradual, ramp-shaped R command has the advantage of allowing the system to influence eye movement speed and distance accomplished through changing the rate and duration of the R ramp. The C command expands the capacity of the R command in speeding up eye movement. A similar function of the step command associated with direct motor commands to EOMs would be complicated by the posture-movement problem described in the beginning of this review. Finally, in contrast to the pulse-step pattern implying that a saccade can be performed by agonist EOMs alone, the R and C commands control saccades by coordinated influences on agonist and antagonist MNs.

In summary, the suggested R-C pattern for eye movements is qualitatively similar to that underlying arm movement (Pilon and Feldman 2006). The R command plays a major role in the control of eye and arm motion: in both cases, it converts position-stabilizing to movement-producing mechanisms, thus transferring stability from the initial to the final position of the plant. In both cases, a referent coactivation command is presumably employed. In referent control, muscle coactivation is not direct but emerges in the centrally specified spatial zone. The localization of this zone in the angular coordinates of the plant is defined by the R command. Therefore, the coactivation zone is shifted with the R command during active movements. Due to this subordination, the referent coactivation command initially contributes to movement acceleration and then to movement deceleration (Feldman 2015). At movement offset, muscle coactivation is unnecessary and gradually recedes (Fig. 7A). In contrast, direct coactivation of muscles would result in resistance to motion, thus recreating the posture-movement problem. In both cases, the C command, unlike the R command, is transient: it is employed to contribute to the speed of eye motion and is attenuated at movement offset. In slow movements, the C command can be minimized.

Sensing the Body Schema and Positions of Body Segments

The notion of referent control does not reject but rather strengthens the idea of perception-action coupling. Active position sensing based on referent control of motor action was originally proposed several decades ago (Feldman and Latash 1982a,b) and gradually updated (Feldman 2009, 2011, 2015). This process continues in the present paper.

Position sense rule.

Threshold control implies that spinal and supraspinal excitation and inhibition eventually influencing α-MNs via-pre-, post-, mono- and polysynaptic inputs as well as γ-MNs, have an integral, spatial measure, R, associated either with a threshold position of body segments at which muscles begin to be activated (in the absence of the coactivation command) or, otherwise, with a position at which muscles generate net zero torques. In other words, the integral measure of central influences on α-MNs has a positional (spatial) dimension. Naturally, such a measure of central influences on the neuromuscular periphery would be essential in forming position sense. This is an unforeseen conclusion from the simple unloading experiments described above (Fig. 2). Another important conclusion is related to the notion that all motor actions can be considered as reactions to the deviation of the actual position of the body from the referent position specified by the nervous system in task-specific ways. Sensory information about this deviation would be essential for determining the actual position of the body. Therefore, it seems natural to suggest that afferent feedback delivers relative, rather than absolute, positional information. These notions are integrated in the position sense (PS) rule.

External forces or loads deflect the arm position from position R to an actual arm position Q. How can the system get information about the actual position, if afferent signals do not deliver such information? Experimental data are consistent with the assumption that these signals transmit relative positional information, i.e., information about the deflection, P, of the arm from its referent position. In this case, the brain can determine the actual arm position, Q, by summating R and P (Fig. 8A):

$$\text{Q}=\text{R}+\text{P}$$ (3)

Fig. 8.

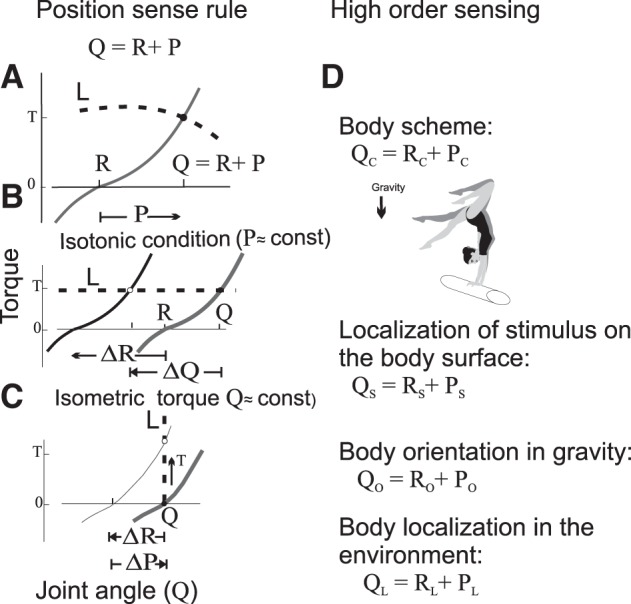
The positional sense rule. Application to different cases of sensing. [Modified from Feldman 2015 with permission from Springer. Copyright 2015 Springer.]

One can also say that, to form PS, afferent feedback is interpreted in the spatial frame of reference in which action is produced.

The PS rule is similar to the physical process of measuring the position of an object in space: its position is always determined with respect to a referent position. For example, the position of a cup on a table is determined by the distances of the cup from one of the table corners. The table corner thus plays the role of a referent point in the identification of the cup position.

Active sensing of involuntary and passive movements: kinesthetic illusions.

The PS rule refers not only to active, self-initiated but also to passive movements elicited by external forces. To clarify, afferent signals from muscle spindles and cutaneous receptors are very sensitive to passive changes in the muscle length or position of body segments (Edin and Johansson 1995; Matthews 1972; Windhorst 2007). However, being electrical by nature, position-sensitive afferent signals do not carry information about specific, actual values of the muscle lengths or positions traversed during passive movements. A referent, central signal is needed to identify that a given afferent activity occurs, say, at 140° of elbow extension. For comparison, to calibrate an electrical goniometer in angular units it is not sufficient to determine the sensitivity (gain) of the electrical signal to changes in the angle. The person who calibrates the goniometer should choose a referent value of the electrical signal for a specific value of the angle such that all other electrical signals can be read directly in angular units. The PS rule shows that, although usually constant, the active referent component, R, is necessary for PS during every passive movement. In fact, the PS rule is formulated by assuming that the arm is passively deflected by an external force (load) from the referent position.

Consider the unloading reflex as an example of involuntary action. Recently, it was shown that the corticospinal and other descending systems maintain the referent position of the wrist during unloading (Ilmane et al. 2013), thus allowing the neuromuscular periphery, under tonic central “supervision,” to change motor commands and the wrist position in response to unloading. If the R remains constant (ΔR = 0), then changes in the joint angle elicited by unloading are perceived from afferent feedback: ΔQ = ΔP. Although invariant, the central component R is essential for perceiving the actual position, e.g., before and after unloading. With increasing the amount of unloading, arm excursion increases but the sense of effort decreases according to the residual load. Therefore, the unloading reflex shows that PS is independent of sense of effort.

An important point raised by Sherrington (1900) was that we are fully aware of the position of our relaxed limb, when the “sensation of innervation” (i.e., EC) mechanism is not operating. In terms of referent control, full muscle relaxation is achieved by shifting the muscle activation threshold beyond the upper biomechanical limit of the muscle length. Muscle spindle afferents have background activity and are sensitive to passive stretching even below the muscle activation threshold (Proske and Gandevia 2012). The PS rule shows that changes in position can be perceived from changes in the afferent activity alone. However, absolute values of position during passive motion can be sensed only if the active, referent signal, R, is present, although during muscle relaxation it is set outside the biomechanical range of the joint. In other words, even during full muscle relaxation, PS is an active process.

Consider kinesthetic illusions elicited by tonic vibration of the tendon of an elbow flexor, biceps (Eklund 1972; Goodwin et al. 1972). Vibration enhances the activity of flexor spindle afferents, eliciting an illusion of elbow extension, as if elbow flexors were stretched. In terms of the PS rule, this illusion results from an increase in the afferent component, P, while the central component, R, remains unaffected by vibration. Sometimes, however, the direction of the illusory motion is inverted (Feldman and Latash 1982a,b; Roll et al. 1980), which can be explained by the influence of vibration on the central component R of PS. Moreover, flexor vibration can elicit an actual elbow flexion but in the absence of vision of the arm, subjects do not feel that their arm is moving (Feldman et al. 2013). Such a “no-motion illusion” can also be explained by the influence of vibration predominantly on the component R of PS if the resulting actual motion does not reach a conscious level.

Position sense is independent of sense of effort.

Activity of muscle spindle afferents is minimally different at different actively established finger positions (Hulliger et al. 1982), but subjects have no difficulty in recognizing the change in the finger position. On the other hand, in isometric conditions, discharges of muscle spindle afferents increase with increasing muscle torque at the elbow joint, but subjects feel that the arm is stationary (Vallbo 1974). These examples show that during active motor actions, adequate positional information can only be obtained with an active participation of the brain. They also show that position sense and sense of effort are different senses. The difference results from differences in central processing of sensory information. The PS rule helps clarify these conclusions.

To make active elbow flexion in isotonic conditions, the system diminishes the threshold R (Fig. 8B). During slow movement, the afferent component, P, may remain constant (Hulliger et al. 1982), but changes in the arm position will be adequately perceived due to changes in the central component of position sense: ΔQ = ΔR. Thereby, during slow motion, the sense of effort hardly changes, confirming, once again, that PS and sense of effort are different senses, invalidating the proposal by Helmholtz (1866) that effort-like EC can be used in perception of motion.

To generate flexor torque in isometric condition (e.g., by pushing with the arm against a wall), the nervous system should also diminish the threshold angle, R. Flexor muscles will generate EMG activity and isometric torque in proportion to the difference between position Q at which isometric torque is produced and the threshold angle, R. Figure 8C shows that in isometric conditions, changes in R and P cancel each other (ΔP = −ΔR) and the arm is adequately perceived as motionless: ΔQ ≈ 0. Indeed, the sense of effort increases with increasing isometric torque. This is another example that, contrary to the proposal by Helmholtz (1866), an effort-like EC cannot be used to feel that the arm is motionless.

These examples show that although referent control underlies both isotonic and isometric tasks, position sense and sense of effort are different senses because of differences in processing of afferent information delivered to the brain: change in R in isotonic conditions in the absence of changes of afferent component, P, is perceived as motion, but changes in R with compensatory changes in the afferent component of PS are perceived as an increase in effort without motion.

Phantom motion.

Several researchers (McCloskey 1981; Proske and Gandevia 2009, 2012) assumed that active position sensing is based on EC. Like Helmholtz (1866), Proske and Gandevia (2009, 2012) also assumed that, as a copy of motor commands, EC is related to muscle forces and, as a consequence, to the sense of effort. They thus hypothesized that the sense of effort plays an important role in PS. Indeed, in some motor tasks (e.g., during arm motion against a spring), these two senses can change in parallel, but they are obviously dissociated in isometric and isotonic tasks. Moreover, during the unloading reflex and motion against a spring, these senses are inversely correlated. These examples show that position sense is independent of sense of effort. Nevertheless, Proske and Gandevia (2009, 2012) suggested that position sense and sense of effort are related, which was tested in an elegant experiment. Subjects were trained to produce different isometric forces associated with different efforts. After ischemic deafferentation of the arm, subjects reproduced these efforts. Although the deafferented arm remained motionless, these efforts produced the feeling of arm motion (phantom motion).

Proske and Gandevia (2009, 2012) concluded that the two senses are related. We need to provide an explanation of their findings that would be consistent with the apparent examples of independence of PS from sense of effort. The PS rule is helpful in this case. Specifically, before deafferentation, subjects were trained to change the referent arm position (ΔR) to specify the required torque levels. In isometric conditions, the central component of PS is compensated by the changes in the afferent component, so that the arm is perceived as motionless (ΔQ = 0), although the sense of effort increases. After deafferentation, the reproduced changes in the R were not accompanied by afferent feedback (ΔP = 0) and, according to the PS rule, were perceived as arm motion (ΔQ = ΔR), as observed in the experiment. In other words, the experiment shows that the same control process can elicit different sensations depending on conditions. Thus the observation of phantom motion illustrates that both senses are controlled by a similar, referent mechanism but cannot be considered as evidence that PS is coupled with the sense of effort.

The PS rule refers to subconscious processing of signals that should reach a conscious level to be perceived. Experiments show that by artificially interfering at this level, one can elicit, for example, motion of the arm (ΔQ ≠ 0) of which the subject may not be aware. In particular, long-term tendon vibration or electrical stimulation of some brain areas can elicit arm motion that the subject may not feel (“no-motion illusion”; Desmurget et al. 2009; Feldman et al. 2013). Conversely, electrical stimulation of some brain areas can elicit the sensation of movement in the absence of actual motion of the arm (Desmurget et al. 2009).

Body schema, phantom limb phenomenon, and out-of-body sensation.

The position sense rule is generalized to the whole body by considering R as the referent body configuration and Q as the actual body configuration (Fig. 8D). Then the rule implies that the actual body configuration (body schema, Q_C) results from summation of referent body configuration (R_C) with the deflection from it elicited by external forces and delivered by sensory feedback (P_C).

Inclusion of the skin surface to the body schema could be provided by a convergence of cutaneous afferent inputs to proprioceptive neurons that form the referent body configuration. A cutaneous stimulus (touching, pain, heat, etc.) would generate a change in the membrane potential of the subpopulation of such neurons. According to the general rule (Fig. 4B), this increment in the potential will be sensed as localized in the respective locus of the body schema (Fig. 8D).

The PS rule also helps explain the phantom limb phenomenon—the feeling that an amputated limb is still attached to the body (Melzack et al. 1997; Mitchell 1871; Ramachandran and Hirstein 1998). Although the afferent component (P_C) of position sense vanishes or is much distorted after amputation, and the central, R_C component still remains present for some time, producing the illusory feeling that the limb is still attached to the body, it takes time for neural plastic changes to correct the body schema. In the absence of adequate afferent information after amputation, the R can be sensed as being in an awkward position (twisted knee or elbow), which might be perceived as painful (phantom limb pain; Melzack et al. 1997). The PS rule suggests that the perceived position of the phantom can be corrected by using some afferent feedback, e.g., ipsilateral projections from the intact contralateral limb, explaining the success of mirror therapy in treating phantom limb pain (Chan et al. 2007).

By artificially interfering in the process of the formation of the body schema by electrical stimulation of some brain areas (the right angular gyrus), one can elicit the feeling of the body being sensed outside the person, the phantom body (Arzy et al. 2006; Blanke at al. 2002). Although the “out-of-body” experience was primarily observed in neurological subjects (epileptics), the PS rule suggests that it may also be observed in healthy subjects.

Sensing the body orientation in gravity and body localization in the environment.

The perception of the orientation in the body in the gravitational field can be formed by combining the centrally specified referent body orientation with afferent information that reflects the deflection of the body by external forces from the referent orientation (Fig. 8D). Neurons that receive input from vestibular receptors sensitive to the direction of gravity (vestibulospinal neurons) could be a major center of such integration, although these neurons can also receive inputs from foot afferent and visual inputs.

Similarly, the localization of the body in the environment can be detected with respect to centrally specified referent body localization (Fig. 8D). By shifting the referent localization, the nervous system can transfer body balance in the environment, eliciting locomotion (Feldman et al. 2011; Krasovsky et al. 2013).

Experimental verification of high-order forms of referent control has been done in several studies (reviewed in Feldman 2015). Further testing of this rule would be desirable to verify, in particular, the hypothesis that ascending tracts transmit sensory deflections from respective referents, rather than ECs, to the brain (cf. Arshavsky et al. 1978).

Visual Space Constancy Without Compensation of Shifts in Retinal Images

How is referent control of saccadic eye motion related to the perception of the visual scene? Referent shifts are feed-forward, starting before the onset and ending before the offset of the saccade (Fig. 7A). By producing a referent eye rotation, R, the system anticipates that the retinal image of the world will be rotated as well, such that the image of the target, if it is motionless, will appear in the fovea (Fig. 7D). If the object is moving, there is always the option to make additional saccades or pursue the object. One can also say that while producing a saccade, the system simultaneously rotates the spatial frame of reference in which we perceive the same stationary world, which we also do by photographing the same visual landscape from different viewpoints. This suggestion is similar to the general suggestion motivated by the position sense rule that sensory information is interpreted in the spatial frame of reference in which action is produced. Anyway, contrary to the suggestion by Helmholtz (1866), compensations of shifts of retinal images would be not only unnecessary but also be counterproductive to sensing world stationarity.

In dynamics, the actual (Q) and referent (R) eye positions during saccades are temporarily different (Fig. 7A) and to minimize the influence of the previous visual scene on the current perception of the visual world, referent shifts are produced in an open-loop way, i.e., independently of the current shifts in retinal images during saccades. The same purpose is achieved by blocking visual perception during saccades (Bridgeman et al. 1975; Matin 1974). Saccades in this case are used to simply bring the object of interest to the fovea: It will be there if the object is motionless; otherwise it will be recognized as moving relative to the stationary environment. In a dark or featureless environment, the frame of reference relative to which the position of an object can be identified as absent, explaining the autokinetic effect in which a stationary, small point of light in such environment appears to move (Adams 1912).

It seems that referent control of eye motion is consistent with the ideas about visual perception by Gibson (1966, p. 256) who also questioned the necessity of EC for perception of world stability. According to Gibson (1966, p. 261), despite motion of retinal images, we perceive the same world as stable by recognizing that the visual scene remains topologically invariant in time (in the terminology of Gibson) which means that the majority of objects in the world are motionless with respect to each other despite motion of retinal images. The notion of referent control helps clarify this idea by Gibson: transitions to a new frame of reference with motion of eye, head, or whole body allow us to perceive the same stationary world despite shifts in retinal images caused by saccades, locomotion, or even by an optical deformation of retinal images elicited by pressing on one of the eyes with a finger.

It is also interesting to compare the above explanation of world stability perception with that offered by Bridgeman and co-workers (Bridgeman 2010; Deubel et al. 2010). They rejected the long-held belief that EC plays an essential role in perception of world stability and suggested, instead, that some world landmarks are preserved in trans-saccadic memory despite suppression of visual perception during the saccade. These landmarks are presumably responsible for the sense that after the saccade, the world continues to be stable. This implies some extraretinal comparison of the landmarks before and after the saccade. Such a comparison seems unnecessary in referent control: by producing referent shifts in gaze, the system predetermines how the invariant world structure will be presented after the saccade. In other words, the images of the motionless world before and after the saccade are optically different and it would be inappropriate to sense them as identical. The referent eye rotation symbolizes the transition from one image of the same stationary world to another during the saccade. Although the interpretation of visual space constancy based on referent control is somewhat different from that offered by Bridgeman's group, these interpretations are similar in terms of rejection of the EC concept, and their validity can be tested in future experiments.

As in fast arm movements, referent shifts during saccades are ceased before the end of eye motion (Fig. 7A). Therefore, the system can, if necessary, produce an additional referent shift to initiate a new saccade and quickly correct an error in the final eye position, often occurring in large eye movements. Moreover, one can additionally suggest that referent shifts predetermine a total shift in gaze whereas, at an executive level, the referent process can be split into several steps, resulting in several saccades (Fig. 7C), which is consistent with findings of the multiple saccades during continuous propagation of excitation in the superior colliculus (Bergeron et al. 2003). Such referent control is also appropriate for arm movements, allowing the system to generate rapid sequences of discrete arm movements without waiting for the end of each (the phenomenon of coarticulation, often observed in piano playing as well as during speech production).

Summary and Conclusions

There are many physiological and physical reasons for considering referent control of action and perception as an alternative to traditional beliefs that the nervous system directly preprograms motor actions and uses EC to actively control our senses. Based on the notion of referent control, the position sense rule explains many cases of active sensing, including the phantom limb phenomenon and offers some ideas of experimental testing. Indeed, the PS rule mainly focuses on the initial steps in processing of efferent and afferent signals for sensing, without considering higher levels of operational control, such as feelings and consciousness. Referent control also shows that in order to perceive the world as stationary, no compensation of shifts in retinal images resulting from eye or/and body motion is necessary. The system perceives these images relative to referent signals underlying the control of eyes and/or body motion.

It is understandable that traditionally many researchers in behavioral neuroscience appreciate the EC concept and, to preserve it, they might consider referent variables as a form of motor commands. This would be incorrect, since it would rearrange cause and effect in the control of motor actions. Referent variables are not “motor” per se; they just predetermine where, in spatial frames of reference, the neuromuscular periphery can generate commands to muscles. These commands emerge without any preprogramming due to the cooperative interaction of the neuromuscular system with the environment in the spatial frames of reference predetermined by referent variables. It is in this meaning that these variables become responsible for action and perception of not only self-initiated but also passive and involuntary movements.

Some may also claim that the validity of the EC concept for perception and action has been confirmed in many studies and therefore the EC concept can hardly be questioned. Given the inconsistencies of the EC concept with physical and physiological fundamentals revealed in this review, such studies should be revisited and critically reevaluated having in mind the alternative referent-control hypothesis, as exemplified by the analysis of the reafference principle by von Holst (von Holst 1954) in the present review. The notion of referent control also affects the understanding of the role of reflexes in action and perception. In particular, central control of reflexes is usually interpreted as a modulation of gain (change in EMG response per unit of muscle stretch) or as reflex gating—phase-dependent inhibition and facilitation of reflex pathways to α-MNs by central generators, as is often observed during locomotion (Duysens et al. 1990; Evarts and Tanji 1974; Sillar 1991). From these observations one could conclude that reflexes are suppressed at certain phases of motion. However, knowing that reflexes are controlled by shifting their spatial thresholds, one can conclude that afferent feedback (reafference) is not suppressed as such but is transferred to evolving body postures at which it remains fully functional (Turpin et al. 2016). Reflex gating or changes in reflex gain can thus be considered as secondary, emergent effects of referent control manifested by changes in the spatial thresholds for muscle activation. Findings of afferent suppression at some phases of motion are therefore insufficient to claim the validity of EC-based schemes of motor control and active sensing. Theories of sensing based on prediction of sensory consequences of motor actions derived from computations with the help of internal models and optimality criteria should also be reexamined.

GRANTS

This review was supported by the National Science and Engineering Research Council and Heart and Stroke Foundation, Canada.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

A.G.F. conception and design of research; A.G.F. performed experiments; A.G.F. analyzed data; A.G.F. interpreted results of experiments; A.G.F. prepared figures; A.G.F. drafted manuscript; A.G.F. edited and revised manuscript; A.G.F. approved final version of manuscript.