WebDISCO: a web service for distributed cox model learning without patient-level data sharing

Abstract

Objective The Cox proportional hazards model is a widely used method for analyzing survival data. To achieve sufficient statistical power in a survival analysis, it usually requires a large amount of data. Data sharing across institutions could be a potential workaround for providing this added power.

Methods and materials The authors develop a web service for distributed Cox model learning (WebDISCO), which focuses on the proof-of-concept and algorithm development for federated survival analysis. The sensitive patient-level data can be processed locally and only the less-sensitive intermediate statistics are exchanged to build a global Cox model. Mathematical derivation shows that the proposed distributed algorithm is identical to the centralized Cox model.

Results The authors evaluated the proposed framework at the University of California, San Diego (UCSD), Emory, and Duke. The experimental results show that both distributed and centralized models result in near-identical model coefficients with differences in the range ${10}^{-15}$ to ${10}^{-12}$ . The results confirm the mathematical derivation and show that the implementation of the distributed model can achieve the same results as the centralized implementation.

Limitation The proposed method serves as a proof of concept, in which a publicly available dataset was used to evaluate the performance. The authors do not intend to suggest that this method can resolve policy and engineering issues related to the federated use of institutional data, but they should serve as evidence of the technical feasibility of the proposed approach.

Conclusions WebDISCO (Web-based Distributed Cox Regression Model; https://webdisco.ucsd-dbmi.org:8443/cox/ ) provides a proof-of-concept web service that implements a distributed algorithm to conduct distributed survival analysis without sharing patient level data.

BACKGROUND AND SIGNIFICANCE

Survival analysis ¹ is widely used in biomedical informatics to study time-to-event data, where a typical binary event might be, for example, the development of a symptom, disease, relapse, or death. Survival analysis can help researchers compare the effect of treatments on mortality or other outcomes of interest. ² Lundin developed and evaluated several models for prognostication in oncology and has built an online resource for displaying survival curves for patient strata. ^3,4 Hagar et al. ^5,6 proposed using Bayesian multiresolution hazard model in chronic kidney disease based on electronic health record (EHR) data. EHR data mining including survival analysis was also studied in. ⁷ Finprog ⁸ is an early work for predicting survival curves using a Kaplan-Meier (KM) approach, which belongs to population-level time-to-event analyses. In a KM-based approach, if a patient does not fit into a group, a curve cannot be generated. The Cox proportional hazards model ⁹ (aka, Cox model), which was primarily developed to determine the importance of predictors in survival, can make use of covariate information to make individual predictions. ^10,11 This is one of the most popular survival analysis models and the focus of this study.

The main problem we are trying to address is how to build a survival analysis model using patient data that are distributed across several sites, without moving those data to a central site. This is important because of multiple factors, which can include concerns about individual privacy, ¹² practical considerations related to data transmission (e.g., data size), and institutional policies. Institutional policies for nondisclosure of data to other parties may be motivated by several factors, including business interests, concerns about reputation and perception of service quality, loss of control, etc. The Health Insurance Portability and Accountability Act (HIPAA) Safe Harbor ¹³ defines explicit rules for healthcare data de-identification. The risk depends on the nature and amount of shared data, as well as on the external information that an attacker may use. Not having to share patient-level data is convenient and helps overcome several barriers. For example, institutional- and country-wide policies ¹⁴ and legislation ¹⁵ may restrict the hosting of patient data outside predetermined geographical boundaries. For example, covered entities can host patient data in HIPAA-compliant environments, ¹⁵ and they need to ensure data confidentiality by not disclosing patient data to unauthorized third parties. The Data Protection Act in the UK ¹⁶ requires that all clinical data that have not been explicitly consented by patients for secondary uses remain in servers that are physically located in European Union countries. The recently released Genome Data Sharing policy ¹⁴ also states that genome data cannot be submitted to databases without the informed consent of participants. Another problem researchers are facing when comparing multi-site patient records is database heterogeneity. ¹⁷ Multi-site collaborative analyses following the same experimental protocol could reduce the bias caused by different data capture processes or different source populations. Analyses involving large sample sizes may improve the confidence in estimation results. Our methodology can be used by large data consortia like Observational Health Data Sciences and Informatics (OHDSI), ¹⁸ or the patient-centered Scalable National Network for Effectiveness Research, ¹⁹ a clinical data research network involving nine health systems, by promoting interdisciplinary collaboration while minimizing data sharing through distributed analysis. An advantage is that the computation time to complete the analysis may be decreased, as each site can perform the calculations in parallel.

Related Work

We propose an approach so that biomedical researchers can build and use a model without having to share patient-level data. The system is deployed as a web service, through which researchers can conduct distributed survival analysis within their web browser directly. In this article, we consider horizontally partitioned data ^20–23 —that is, each participant has a subset of records with the same variables, as opposed to vertically partitioned data in which a patient has records distributed across sites. This work is based on recently developed approaches for horizontally partitioned distributed data, including Grid Logistic Regression (GLORE) ²⁴ and its Bayesian extension EXPLORER (Expectation Propagation Logistic Regression: Distributed Privacy-Preserving Online Model Learning). ²⁵ GLORE developed binary logistic regression in a distributed manner, allowing researchers to share models without necessarily sharing patient data. EXPLORER alleviated the synchronized communication requirement of GLORE and enabled online learning for efficiently handling incremental data. Two recent publications consider a distributed Cox model. Yu et al .²⁶ introduced a dimensionality reduction method that is not reversible. This approach may be used to make predictions but cannot estimate parameters to assess the importance of different covariates. Moreover, the low-dimensional projection used in this method will result in information loss and inaccurate predictions. Another approach suggested by O’Keefe et al. ²⁷ discusses how to obtain survival analysis outputs from a remote database in a confidential manner (i.e., protecting covariate values from being disclosed). Their model avoids patient-level data exchange, but does not perform distributed learning. Therefore, it is important to develop accurate distributed computational algorithms to enable accurate survival model learning across multiple sites. The proposed method is specifically designed to handle the problem of building a shared accurate Cox model without sharing patient-level data.

MATERIALS AND METHODS

Cox Model

The hazard function in a Cox model, ⁹ which represents the hazard at time $t$ , takes the form

$$\lambda (t|\mathbf{Z})={\lambda }_0(t)\text{exp}({\mathit{\beta }}^T\mathbf{Z})={\lambda }_0(t)\text{exp}({\beta }_1{Z}_1+\mathrm{...}+{\beta }_p{Z}_p).$$ (1)

Here, ${\lambda }_0(t)$ is the baseline hazard function; $\mathbf{Z}=\{Z_1,Z_2,\cdots ,Z_p\}$ and $\mathit{\beta }=\{{\beta }_1,{\beta }_2,\cdots ,{\beta }_p\}$ are $p$ dimensional vectors of explanatory variables and model parameters, respectively. The ratio between $\lambda \left(t\text{|}\mathbf{Z}\right)$ and ${\lambda }_0\left(t\right)$ can be calculated from the data even if ${\lambda }_0(t)$ is not specified explicitly, since it is based on survival at each time point i . For this reason, $\mathit{\beta }$ helps estimate a proportional hazard, not an absolute hazard. In practice, many partial likelihood based methods ^28,29 are widely used for estimating $\mathit{\beta }$ . Breslow et al .²⁹ introduced an approximate partial likelihood function to handle the situation with tied event times. Breslow’s partial likelihood function can be expressed as follows:

$$L(\mathit{\beta })={\displaystyle \prod }_{i=1}^D\frac{\text{exp}\left({\mathit{\beta }}^T{{\displaystyle \sum }}_{l\in {\mathcal{D}}_i}{z}^l\right)}{{\left[{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i}\text{exp}\left({\mathit{\beta }}^T{z}^l\right)\right]}^{d_i}},$$ (2)

where $D$ is the total number of distinct event times; ${\mathcal{D}}_i$ and ${\mathcal{R}}_i$ are the index sets of subjects with observed events (e.g., death) and at risk for the event, respectively, at the $i$ -th distinct event time with $i=1,\mathrm{...},D$ ; $d_i=|{\mathcal{D}}_i|$ is the count of tied survival times at event time i . $z^l=\{z_1^l,z_2^l,\cdots ,z_p^l\}$ is the realization of the $p$ dimensional explanatory variable $\mathbf{Z}$ for a subject indicated by the superscript $l$ .

Based on the partial likelihood function in (2) , the log likelihood $l(\mathit{\beta })$ , its first order derivative $l_r^{\text{'}}(\mathit{\beta })=\frac{\partial l(\mathit{\beta })}{\partial {\beta }_r}$ , and its second order derivative $l_{r,q}^{″}(\mathit{\beta })=\frac{{\partial }^{2}l(\mathit{\beta })}{\partial {\beta }_r\partial {\beta }_q}$ , where $r\text{ and }q=1,2,\cdots ,p$ are the indices of the $r$ -th and $q$ -th element in the parameter vector $\mathit{\beta }$ , respectively, can be calculated as follows:

$$l(\mathit{\beta })={\displaystyle \sum }_{i=1}^D\left\{{\mathit{\beta }}^T{\displaystyle \sum }_{l\in {\mathcal{D}}_i}{z}^l-d_i\text{log}\left[{\displaystyle \sum }_{l\in {\mathcal{R}}_i}\text{exp}({\mathit{\beta }}^T{z}^l)\right]\right\}$$ (3)

$$l_r^{\prime }(\mathit{\beta })={\displaystyle \sum }_{i=1}^D\left\{{\displaystyle \sum }_{l\in {\mathcal{D}}_i}{z}_r^l-d_i\frac{{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i}{z}_r^l\text{exp}({\mathit{\beta }}^T{z}^l)}{{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i}\text{exp}({\mathit{\beta }}^T{z}^l)}\right\}$$ (4)

$$l_{r,q}^{″}\left(\mathit{\beta }\right)=-{\displaystyle \sum }_{i=1}^D{d}_i\left\{\frac{{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i}{z}_r^l{z}_q^l\exp \left({\mathit{\beta }}^T{z}^l\right)}{{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i}\exp \left({\mathit{\beta }}^T{z}^l\right)} –\frac{{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i}{z}_r^l\exp \left({\mathit{\beta }}^T{z}^l\right)}{{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i}\exp \left({\mathit{\beta }}^T{z}^l\right)}\frac{{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i}{z}_q^l\exp \left({\mathit{\beta }}^T{z}^l\right)}{{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i}\exp \left({\mathit{\beta }}^T{z}^l\right)}\right\}.$$ (5)

Using the Newton-Raphson algorithm, ²⁸ the parameters ${\mathit{\beta }}^{\tau }$ that maximize the likelihood function at the $\tau$ -th iteration can be updated until convergence as

$${\mathit{\beta }}^{\tau }={\mathit{\beta }}^{\tau -1}-{[l^{″}\left({\mathit{\beta }}^{\tau -1}\right)]}^{-1}{l}^{\prime }({\mathit{\beta }}^{\tau -1}).$$ (6)

Furthermore, the baseline hazard function in Breslow’s approach ² is defined as

$${\lambda }_0(t_i)=\frac{1}{{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i}\text{exp}({\widehat{\mathit{\beta }}}^T{z}^l)},$$ (7)

where $t_i$ is $i$ -th distinct event time, and $\widehat{\mathit{\beta }}$ is the best estimate learned in (6) that maximizes the likelihood function.

The survival function of the subpopulation with explanatory variable $\mathbf{Z}$ is given by

$$S(t|\mathbf{Z})={\left[\text{exp}\left(-{\displaystyle \sum }_{i:t_i<t}\frac{d_i}{{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i}\text{exp}({\widehat{\mathit{\beta }}}^T{z}^l)}\right)\right]}^{\text{exp}({\widehat{\mathit{\beta }}}^T\mathbf{Z})},$$ (8)

which can be used to generate a survival curve and test predictions.

Distributed Cox Model

As mentioned above, the traditional Cox model requires that data be gathered in a central repository. In this section, we propose a distributed Cox model. Specifically, each participant from different data repositories is able to upload aggregated statistics without revealing patient-level data at each iteration (i.e., each update of coefficients), and the model parameters trained at the global server can generate the same model outputs (i.e., estimated parameters) as those would have been generated in a centralized model. Some authors ³⁰ showed that the order of aggregation of the population may have impact on mutual information calculations, but this is not the case for the proposed algorithm because the decomposition is done at each iteration and is mathematically equivalent to performing updates using centralized data. In this section, the mathematical derivation demonstrates that the distributed Cox model under the Breslow likelihood assumption is mathematically equivalent to the centralized Cox model.

Suppose that there are $M$ participant sites in a survival study. Then, the first and the second order derivatives $l^{\text{'}}\left(\beta \right)$ and $l^{″}\left(\beta \right)$ can be rewritten as

$$l_r^{\prime }(\mathit{\beta })={\displaystyle \sum }_{k=1}^M{\displaystyle \sum }_{i=1}^D{\displaystyle \sum }_{l\in {\mathcal{D}}_i^k}{z}_r^l-{\displaystyle \sum }_{i=1}^D\left({\displaystyle \sum }_{k=1}^M|{\mathcal{D}}_i^k|\right)\frac{{{\displaystyle \sum }}_{k=1}^M{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i^k}{z}_r^l\text{exp}({\mathit{\beta }}^T{z}^l)}{{{\displaystyle \sum }}_{k=1}^M{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i^k}\text{exp}({\mathit{\beta }}^T{z}^l)}.$$ (9)

and

$$\begin{array}{c}{l}_{r,q}^{″}(\mathit{\beta })=-{\displaystyle \sum }_{i=1}^D\left({\displaystyle \sum }_{k=1}^M|{\mathcal{D}}_i^k|\right)\{\frac{{{\displaystyle \sum }}_{k=1}^M{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i^k}{z}_r^l{z}_q^l\exp \left({\mathit{\beta }}^T{z}^l\right)}{{{\displaystyle \sum }}_{k=1}^M{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i^k}\exp \left({\mathit{\beta }}^T{z}^l\right)} \\ -\frac{{{\displaystyle \sum }}_{k=1}^M{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i^k}{z}_r^l\exp \left({\mathit{\beta }}^T{z}^l\right)}{{{\displaystyle \sum }}_{k=1}^M{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i^k}\exp \left({\mathit{\beta }}^T{z}^l\right)}\frac{{{\displaystyle \sum }}_{k=1}^M{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i^k}{z}_q^l\exp \left({\mathit{\beta }}^T{z}^l\right)}{{{\displaystyle \sum }}_{k=1}^M{{\displaystyle \sum }}_{l\in {\mathcal{R}}_i^k}\exp \left({\mathit{\beta }}^T{z}^l\right)}\},\end{array}$$ (10)

where ${\mathcal{D}}_i^k$ and ${\mathcal{R}}_i^k$ are subsets of ${\mathcal{D}}_i$ and ${\mathcal{R}}_i$ denoting subjects from the $k$ -th participant site, and $k=1,2,\cdots ,M$ . In (10) , the count $d_i$ is replaced by $d_i=\sum _{k=1}^M|{\mathcal{D}}_i^k|$ , so that it can be aggregated from distributed sites. According to (9) and (10) , the derivatives of the log likelihood function are naturally decomposed by computing and sharing locally aggregated values such as $\sum _{i=1}^D\sum _{l\in {\mathcal{D}}_i^k}{z}_r^l$ , $|{\mathcal{D}}_i^k|$ , $\sum _{l\in {\mathcal{R}}_i^k}\text{exp}({\mathit{\beta }}^T{z}^l)$ , $\sum _{l\in {\mathcal{R}}_i^k}{z}_q^l\text{exp}({\mathit{\beta }}^T{z}^l)$ , and $\sum _{l\in {\mathcal{R}}_i^k}{z}_r^l{z}_q^l\text{exp}({\mathit{\beta }}^T{z}^l)$ from each site $k$ . This decomposition guarantees that sum of derivatives learned from distributed sites is exactly the same as the derivative calculated from a central repository that is used in the traditional, centralized Cox model.

The details of the proposed distributed Cox model are listed in Algorithm 1 (A1). The inter-site update in the distributed Cox model starts with the local and global initialization steps (A1: lines 1–3), where the local index subsets ${\mathcal{R}}_i^k$ and ${\mathcal{D}}_i^k$ , local aggregation $\sum _{i=1}^D\sum _{l\in {\mathcal{D}}_i^k}{z}_r^l$ , initial model parameter ${\mathit{\beta }}^0$ are calculated. We can iteratively update the model parameter ${\mathit{\beta }}^{\tau }$ until it converges through (A1: lines 4–12). Finally, the converged model parameters will be reported and sent to each client to allow survival predictions.

Algorithm 1:

Inter-site update in the distributed Cox model

1:	Local initialization for all sites:
2:	Each site initializes index subsets ${\mathcal{R}}_i^k$ and ${\mathcal{D}}_i^k$ based on their local data. Each site sends the aggregated statistic $\sum _{i=1}^D\sum _{l\in {\mathcal{D}}_i^k}{z}_r^l$ to the global server to avoid additional communication overhead, as this value is unchanged during the whole learning process.
3:	Global initialization:
	The global server requests distinct event times from each site to initialize the parameters $D$ and $|{\mathcal{D}}_i^k|$ . Additionally, the global server aggregates the incoming statistics from all sites as ${\widehat{z}}_r=\sum _{k=1}^M\sum _{i=1}^D\sum _{l\in {\mathcal{D}}_i^k}{z}_r^l$ based on (10) . The server initializes ${\mathit{\beta }}^0$ and disseminates it to each site.
4:	Repeat
5:	For all sites (parallel update)
6:	Receive an updated ${\mathit{\beta }}^{\tau }$ from the global server.
7:	Calculate the following aggregated statistics:     $\sum _{l\in {\mathcal{R}}_i^k}\text{exp}({\mathit{\beta }}^T{z}^l)$ , $\sum _{l\in {\mathcal{R}}_i^k}{z}_q^l\text{exp}({\mathit{\beta }}^T{z}^l)$ and $\sum _{l\in {\mathcal{R}}_i^k}{z}_r^l{z}_q^l\text{exp}({\mathit{\beta }}^T{z}^l)$ .
8:	Send these statistics back to the global server
9:	end for
10:	Calculate the first and second derivatives of the likelihood function using the statistics received from each site according to (10) and (11).
11:	Update ${\mathit{\beta }}^{\tau +1}$ using the Newton-Raphson algorithm as shown in (6) and send the updated ${\mathit{\beta }}^{\tau +1}$ back to each site.
12:	Until parameters converge
13:	Send the converged model parameters to each site.

Implementation

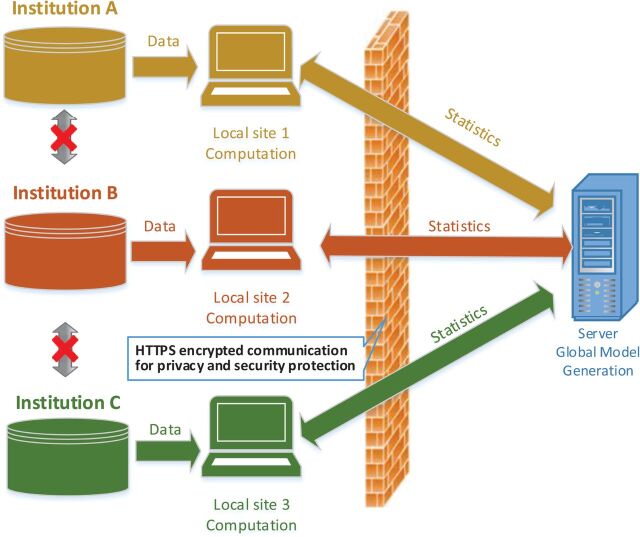
In this section, we focus on the development of the Web-based Distributed Cox Regression Model (WebDISCO). WebDISCO enables iterative optimization of model parameters in real time among different participants on a network, as illustrated in the diagram shown in Figure 1 .

Figure 1:

Datasets from different institutions are locally aggregated into intermediate statistics, which are combined in the server to estimate global model parameters for each iteration. The server sends the re-calculated parameters to the clients at each iteration. All information exchanges are protected by HTTPS encrypted communication. The learning process is terminated when the model parameters converge or after a pre-defined number of iterations are completed.

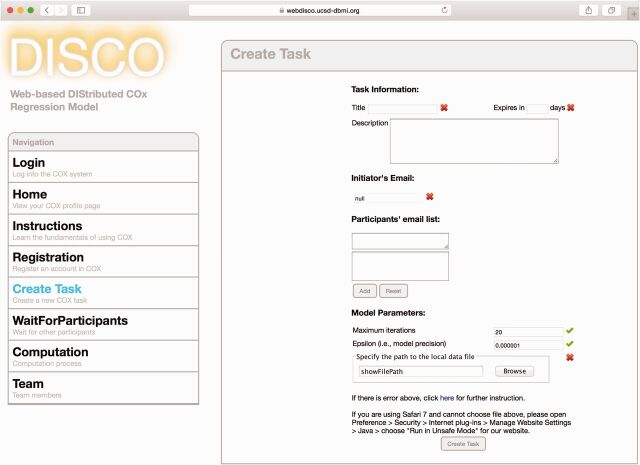
Procedure: When entering WebDISCO, the user can choose to log into the system, register, read instructions, or directly create a new task via an anonymous login (see Figure 2 as an example). The registration step requires the following information: user name, email address, and password. The input information is checked by the system. To minimize user burden, anyone can use WebDISCO without registration. Only a registered user has the ability to access his/her study analysis history.

Figure 2:

Snapshot of task creation page in WebDISCO. To create a task, a task initiator needs to provide the following information: task title, expiration day, email address for participants, maximum number of iterations, criterion for terminating the process, and location of input data. The initiator has the administrator role after login. The input data need to have the same format across participants.

When a user initializes a task, he/she needs to specify the following parameters: task title, expiration day, email address for participants, maximum number of iterations, and criterion for terminating the process and location of input data. The description of the data is an optional field. The create button is disallowed until all the information has been checked and validated. To ensure consistency, the training set used by each participant is required to be in exactly the same format.

Once a task is created, both the task creator and invited participants are informed by emails originated by the WebDISCO service. A unique link hashed with the task name and the participant’s email is provided in each email. All the participants can specify the path of their local training data in WebDISCO.

When triggered by the task creator, the server starts interacting with the clients. First, the clients send their survival times to the server, and the server responds with a list of unique survival times (i.e., time points in which at least one event occurred at any of the sites) to synchronize all the clients. Then, the global server will collaborate with all clients to start the computation based on Algorithm 1. During the computation, the web page will show the progress in learning parameter estimates. After the computation, the user can obtain globally learned model parameters. The user can also click on the test button to evaluate the local data based the globally learned survival function.

2) Software : HTML5 standards make it possible to build self-contained applications for modern browsers without knowing the specific server side language used to serve pages containing the application. Although such applications are cutting edge, there are strong limitations. Due to the constraint of keeping data locally, the majority of the computation task will need to take place in client side web browser rather than on server side, which is in conflict with the heavy-server light-client architecture and limits the duration of the iteration to that of the slowest web browser among all the sites.

To address this challenge and ensure wide accessibility, we developed a signed communication between Servlets and Applets based on Java technology, which is deployable in a variety of host environments. The Applets are embedded in webpages to handle local computation so that original data are never sent to the server. Since only signed Applets can execute and communicate with Servlets, we can easily check the validity of inputs from participants on the server side. Based on the Java backbone, the front-end consists of Ajax webpages supported by JavaServer Pages (JSP), which dynamically reflect user and task status. Safari, Firefox, and Chrome browsers currently support WebDISCO. Note that other implementations of distributed algorithms are possible, but we wanted to illustrate a simple one in which there is no need to download any particular software.

RESULT

The dataset used in our experiment is publicly available in the UMASS Aids Research Unit (UARU) IMPACT study. ^31,32 The purpose of the study was to investigate how different treatment programs affect the drug abuse reduction and high-risk HIV behavior prevention. The original UARU dataset contained 628 observations, where 574 records were kept after missing data removal and 8 variables were used in this study: age, Beck depression score, heroin/cocaine use, IV drug use, number of prior drug treatments, race, length of the treatment, and treatment site. Moreover, we introduced dummy variables to convert nonbinary categorical variables into binary indicators as summarized in Table 1 .

Table 1:

Summary of features in the UARU dataset ^31,32 used in our experiments, where the categorical variable, IV drug use history, is converted into binary covariates based on dummy coding. ³³ We included the following 10 covariates in our experiment

Feature	Description
AAE	Age at enrollment (years)
BDS	Beck depression score (0–54)
HU	Heroin use during 3 months prior to admission
CU	Cocaine use during 3 months prior to admission
IVDUPN	IV drug use history: previous vs never
IVDURN	IV drug use history: recent vs never
NPDT	Number of prior drug treatments (0–40)
RACE	Subject’s race: White vs Non-white
TREAT	Treatment assignment: short vs long
SITE	Treatment Site: A vs B

We split the UARU dataset of 574 records into a training dataset with 295 records and a test dataset with 279 records for prediction purposes. Furthermore, the training dataset was split into 2 subsets with 244 and 51 records based on the treatment site (i.e., site A or B as listed in Table 1 ), respectively. Table 2 shows the estimated parameters for the proposed WebDISCO service with 1-site and 2-site settings, where we observed identical results at the precision of ${10}^{-12}$ . The coefficient differences between centralized R and WebDISCO implementations are also compared in Table 2 , and range from ${10}^{-15}$ to ${10}^{-12}$ . The response time for distributed model learning using the proposed WebDISCO website is very short (5–10 s) to support a real-time web service, as shown in Table 3 , based on the average over 10 trials. The experiments were conducted by the authors from three geographically different sites (i.e., UCSD, Emory, and Duke), where two training subdatasets with 244 and 51 records were used between each of 2 sites (i.e., UCSD and Emory, UCSD and Duke, Emory and Duke). Safari browsers on Apple Mac OS X 10.10 were used at Duke and Emory. A Chrome browser on Microsoft Windows 8 64-bits machine was used at UCSD during the experiments. All sites were using Java Runtime Environment with version 1.8.0. For each pair sites test, one site initiated the experiments through the WebDISCO service; the other site joined the experiments when they received the automatic email notification sent by the WebDISCO service. Based on the experimental results in Table 3 , we can see that the response time is <10 s among all participant sites.

Table 2:

Comparison of estimated parameters between distributed and centralized R implementations

Features	$\beta$ learned in WebDISCO		Differences	Other feature statistics
	1 site	2 sites		Se( $\beta$ )	z	P
AAE	−0.035664309	−0.035664309	5.06E-13	0.0118	−3.023	.0025
BDS	0.017800253	0.017800253	8.30E-15	0.0068	2.617	.0089
HU	0.053507037	0.053507037	9.21E-12	0.1704	0.314	.75
CU	-0.051884396	−0.051884396	6.68E-13	0.1349	−0.385	.7
IVDUPN	0.299188008	0.299188008	2.78E-12	0.2249	1.33	.18
IVDURN	0.251226316	0.251226316	5.09E-12	0.2047	1.227	.22
NPDT	0.025211755	0.025211755	4.47E-12	0.0102	2.46	.014
RACE	-0.455673981	−0.455673981	2.87E-12	0.1678	−2.716	.0066
TREAT	-0.275508156	−0.275508156	2.16E-12	0.1366	−2.017	.044
SITE	-0.621506977	−0.621506977	8.81E-12	0.2111	−2.944	.0032

We use R to implement both the centralized (i.e., 1 site) Cox model and the WebDISCO distributed (2 sites) Cox model. Both experiments were based on the same training dataset, where we split training dataset between 2 sites for WebDISCO based on the attribute: treatment site. The results show that both models resulted in near-identical model coefficients with differences in the range ${10}^{-15}$ to ${10}^{-12}$ . We also included other feature statistics learned from WebDISCO.

Table 3:

Comparison of response time according to dataset size and number of participant sites

Average Response Time (seconds)
UCSD and Emory	UCSD and Duke	Emory and Duke
5.50	9.25	9.33

We evaluated WebDISCO among geographically different sites (UCSD, Emory, and Duke). We used the same training datasets as in Table 2 , 2 subsets with 244 and 51 records based on the treatment site, respectively. The table presents average response time from 10 trials according to different pairs of sites, which shows that WebDISCO provides robust real-time service given all average response time <10 s.

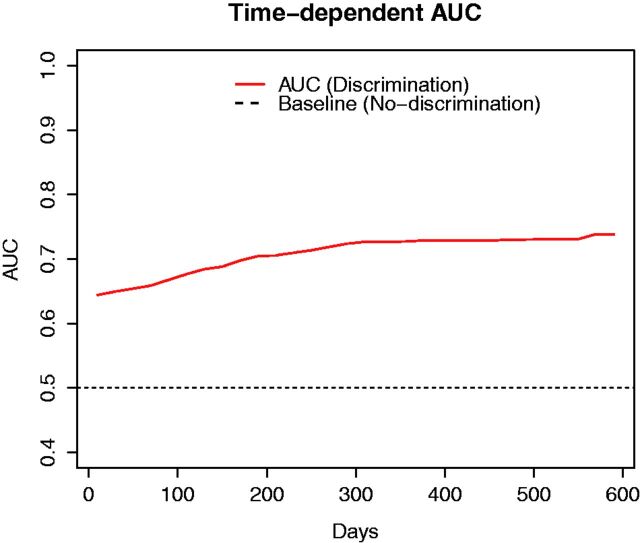
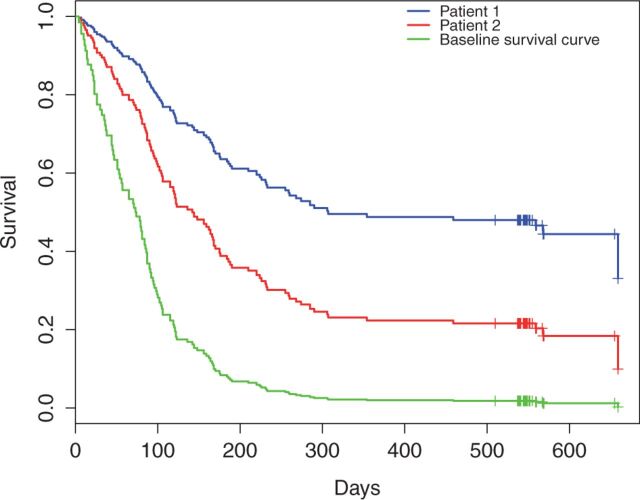
Given the model parameters learned in WebDISCO, Figure 3 depicts the time-dependent Area Under Curve (AUC) to measure discrimination based on the method proposed by Chambless and Diao ³⁴ using a test dataset with 279 records. When comparing the “baseline” (no-discrimination) performance in Figure 3 , the learned Cox model resulted in AUCs ranging from 0.64 to 0.75 for different time points. Finally, Figure 4 illustrates survival curves resulting from the application of the global model (i.e., the model learned in a distributed manner) to 2 randomly selected patient records from site A (in blue) and site B (in red). We illustrate different individual survival curves produced from the model that used information from both sites (without transmitting patient-level data across sites) to provide improved personalized predictions. The red and blue survival curves correspond to applying the global model (learned in a distributed manner) to 2 randomly selected patient records from site A and site B (test data), respectively, using the baseline survival estimated using Breslow’s approach. Figure 4 illustrates that survival curves of individual patients can be obtained without exchanging patient level data across sites. Table 4 lists the attribute values of two randomly selected patients for readers’ reference.

Figure 3:

Time-dependent AUC based on method proposed by Chambless and Diao, ³⁴ where the solid and dashed lines depict the AUC and random chance, respectively. The AUC increases with the number of days and ranges from 0.64 to 0.75, which indicates that our distributed Cox model works properly for prediction (AUC > 0.5) by estimating parameters $\mathit{\beta }$ .

Figure 4:

Individualized survival curve from a randomly selected patient from Site A (patient 1, illustrated in blue) and a randomly selected patient from Site B (patient 2, illustrated in red). Survival curves of individual patients were obtained by using model estimates and a baseline survival curve, without exchanging patient level data across sites.

Table 4:

Attribute values of two randomly selected patients from Sites A and B

	AAE	BDS	HU	CU	IVDUPN	IVDURN	NPDT	RACE	TREAT	SITE	Time	Censor
P1	32	4	1	1	0	0	4	1	1	0	313	1
P2	24	15	0	1	1	0	0	0	0	1	238	1

LIMITATIONS AND DISCUSSION

The proposed study just scratches the surface in terms of distributed computing on sensitive data. It addresses the algorithm aspects by showing that it is mathematically sound to decompose the Cox model by sites, and illustrates a simple proof-of-concept implementation that suggests that technical barriers are addressable. The study has some important limitations. First, a public dataset ^31,32 was used to evaluate the accuracy of federated survival analysis. Using real data generated by partnering institutions would be indeed better to test whether our proposed solution would be acceptable to health system leaders, but it would require cross-institutional review board approval for a specific study with named investigators, which would make it hard for external users to check the results. Federated use of institutional data involves multiple aspects, such as distributed algorithm development, secure and practical engineering implementation, and adherence to policy. The proposed solution limits its focus on the algorithm development with a proof-of-concept web service implementation and does not imply that it would be readily adopted by health systems. The current implementation of WebDISCO has an important limitation in handling high dimensional data. L1-norm regularization ³⁵ provides a way to select a small number of features as well as achieve high model accuracy for high-dimensional data. As this paper mainly focuses on the development of a web interface to enable distributed Cox model learning, we have not focused on the developing a L1 regularized distributed Cox model but plan to do this in future work. Finally, WebDISCO does not implement sophisticated privacy methods such as differential privacy ³⁶ that guarantee that the risk of re-identification via inspection of aggregate statistics would rest below a certain value. We will investigate the utilization of differential privacy algorithms, secure multi-party computation, and encryption to protect such information in the future.

WebDISCO is a proof-of-concept web service for biomedical researchers to collaborate and build a global Cox regression model without sharing patient-level data. It does not preclude the need for partners to trust each other in terms of modifying local Java settings, submitting truthful aggregate statistics, and obtaining patient consent as needed, but addresses the problem of partners not being able to transmit patient-level data to another site. The WebDISCO framework relies on a distributed Newton-Raphson algorithm and an HTTPS interface, where the local statistics among participating institutions are aggregated. This is useful to enable collaboration among institutions that are not allowed to transmit patient-level data to an outside server. WebDISCO is the first web service for distributed Cox model learning in which global model parameters can be iteratively optimized in real time among distributed collaborators of a network. We expect that the utilization of distributed computation such as the one illustrated in WebDISCO could help lower some barriers for collaboration and can potentially accelerate research. WebDISCO might fit the work of large multi-national data analysis projects, such as the OHDSI. ¹⁹ In future work, the proposed WebDISCO framework will need to accommodate its Common Data Model and be released as production-level software for OHDSI. Our ultimate goal is to contribute to the large-scale distributed data analysis project with WebDISCO and other distributed statistical models. This article’s goal is to serve primarily as a proof of concept for the decomposition algorithm we developed for distributed Cox regression analyses.

CONCLUSION

We introduced WebDISCO, a proof-of-concept web service to provide federated Cox model learning without transmitting patient-level data over the network. WebDISCO has an interactive user interface so that nonstatisticians can use the system without difficulty. When several institutions participate, the analysis employs all datasets to produce reliable results that are expected to be more generalizable than those produced by a single institution. The proposed framework demonstrated the feasibility of a federated survival analysis algorithm to facilitate collaboration across different institutions. However, the proposed framework is limited as it does not deal with the policy and engineering concerns related to federated use of institutional data. We envision that additional distributed models will continue to be added to the arsenal of distributed statistical methods that can now be easily available to investigators worldwide.

FUNDING

This work was funded in part by NIH grants R00LM011392, K99HG008175, R21LM012060, U54 HL108460 and Patient-Centered Outcomes Research Institute (PCORI) contract CDRN-1306-04819.

CONTRIBUTORS

First authors C.L.L. and S.W. contributed the majority of the writing and conducted major parts of the experiments. Z.J. conducted some experiments and produced the tables. Y.W. and X.J. contributed significant portions to the methodology. L.Xiong provided helpful comments on both methods and presentation. L.O.-M. provided the motivation for this work, detailed edits, and critical suggestions.