Precursory changes in seismic velocity for the spectrum of earthquake failure modes

Abstract

Temporal changes in seismic velocity during the earthquake cycle have the potential to illuminate physical processes associated with fault weakening and connections between the range of fault slip behaviors including slow earthquakes, tremor and low frequency earthquakes¹. Laboratory and theoretical studies predict changes in seismic velocity prior to earthquake failure², however tectonic faults fail in a spectrum of modes and little is known about precursors for those modes³. Here we show that precursory changes of wave speed occur in laboratory faults for the complete spectrum of failure modes observed for tectonic faults. We systematically altered the stiffness of the loading system to reproduce the transition from slow to fast stick-slip and monitored ultrasonic wave speed during frictional sliding. We find systematic variations of elastic properties during the seismic cycle for both slow and fast earthquakes indicating similar physical mechanisms during rupture nucleation. Our data show that accelerated fault creep causes reduction of seismic velocity and elastic moduli during the preparatory phase preceding failure, which suggests that real time monitoring of active faults may be a means to detect earthquake precursors.

Earthquake prediction was considered an attainable goal in the early 1970s, based on laboratory and seismic observations showing complementary variations in elastic wave speed prior to rock failure and earthquakes¹. While the excitement attendant with these predictions waned unfulfilled in the following decades, recent works provide accumulating evidence for changes in elastic wave speed associated with a range of fault slip behaviors, including earthquakes^4,5, slow fault slip⁶, landslides⁷, and laboratory stick-slip failure events^2,3. For the most part, these data document changes during and after failure, although in a few cases premonitory changes are known⁴.

The detection and characterization of the physical processes during earthquake nucleation^8,9 via remote acoustic techniques could provide fundamental insights into fault weakening mechanisms that precede failure. Laboratory studies have related variations in seismic velocities to the magnitude of applied stress via the existence of networks of microcracks that alter the elastic properties of rocks¹⁰. Moreover, it has been shown that acoustic transmissivity of faults is intimately related with the evolution of shear strength via the load-bearing population of asperity contacts^2,11, and laboratory studies show clear precursors to earthquake-like, frictional failure. However, the question of whether such changes in elastic properties can be imaged in the vicinity of earthquake fault and used to forecast failure remains unanswered.

Tectonic faults accommodate plate motion via a spectrum of slip behaviors ranging from steady aseismic creep, at mm/yr, to quasi-dynamic transients such as slow earthquakes, with fault slip velocities of ~10^-7-10^-3 m/s, and dynamic rupture with slip velocities of ≥1 m/s during powerful earthquakes^12,13. The wide range of environments within which these behaviors have been documented^12–17 and the observation that large earthquakes are often preceded by slow slip^16,18,19 suggest commonalities in the physical mechanisms of slow and fast rupture. Yet, we neither know if a given fault patch can host both slow slip and dynamic rupture²⁰, nor do we understand the physical properties that dictate rupture speed for slow earthquakes.

Here, we use measurements of P-wave velocity linked with mechanical data to illuminate the physical processes that dictate fault weakening and slick-slip frictional failure. We evaluate changes in elastic wave speed during the seismic cycle of slow and fast slip events and find clear precursors to failure that extend across the whole spectrum of slip behaviors.

The mechanics of frictional stick-slip can be evaluated for a 1-D fault obeying rate-and-state friction²¹ by considering the elastic stiffness around the fault, k, and the fault frictional properties, which can be written in terms of a critical rheologic stiffness, k_c (see methods). In this context, the ratio K=k/k_c describes the stability boundary between stable, K>1, and unstable, K<1, behavior. Numerical studies²¹ and limited laboratory data^22–24 suggest that the transition from stable to unstable behavior involves a region of oscillatory, quasi-dynamic sliding, near K=1. However, the implications of this region for tectonic faulting have not been explored.

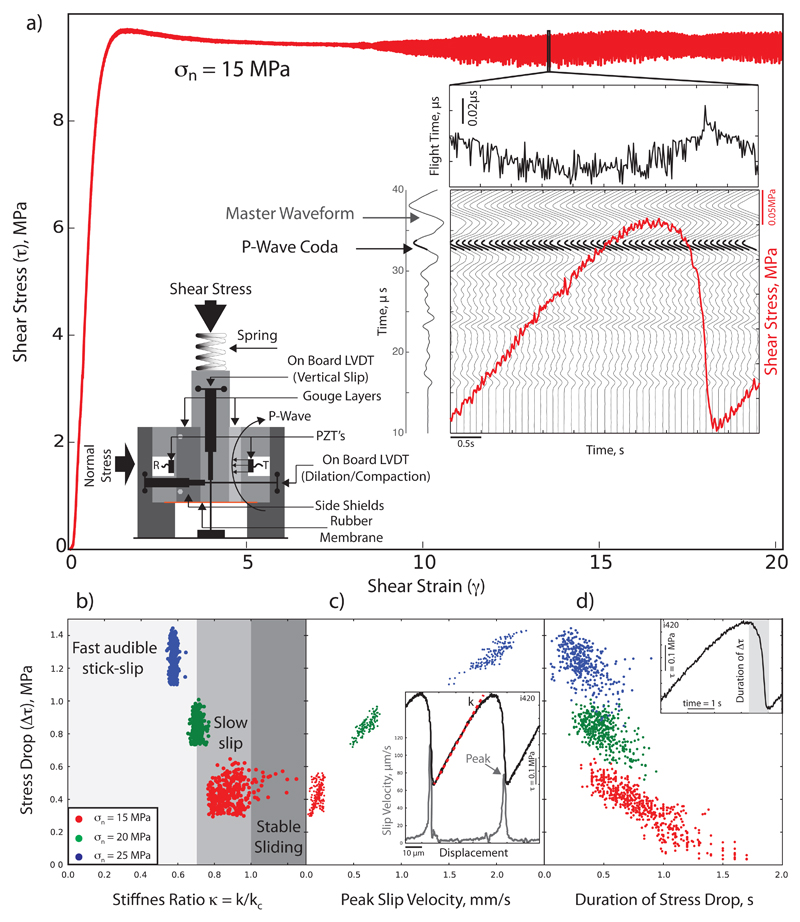
We report on laboratory experiments designed to investigate the spectrum of fault slip modes from stable creep, slow-slip to fast stick-slip (see methods). We observe a spectrum of slip behaviors as a function of K (ref. 21,23,24) (Figs. 1, Supplementary 1,2). Our experiments document an initial stage of stable sliding, followed by a spontaneous evolution to oscillatory stick-slip and creep-slip behavior with accumulated strain (Fig. 1a and Supplementary 1). We systematically vary K and document a transition from fast, dynamic stick-slip, accompanied by audible energy radiation, to silent slow-slip events (Figs. Supplementary 1,2). For each event we measured the loading stiffness k, peak slip velocity, and stress drop duration (Fig. 1). Slow slip events show peak slip velocity of ≤100 μm/s resulting in small stress drop events lasting up to 1-2 seconds (Fig. 1). At lower stiffness (K~0.6), dynamic stick-slip instabilities occurred with a larger stress drop (≥1 MPa), higher slip velocity (≥2 mm/s) and shorter slip duration (≤0.2 s). The strong negative correlation between stress drop and event duration is consistent with observations from tectonic faults, where slow earthquakes have systematically lower stress drop than regular earthquakes¹².

Figure 1. The spectrum of fault slip behaviour for laboratory faults.

(a) Representative experiment at σ_n=15 MPa. Left inset shows the double direct shear configuration. Right inset shows details for a slow-slip event (red) with associated recorded seismic waveforms (grey) and the corresponding variations in flight time (top). The stiffness ratio, K, controls the transition from slow to fast stick-slip as mapped in the stability phase diagram (b), the peak slip velocity (c), and the slip event duration (d). Inset in panel (c) shows the linear fit (red dashed line) to the shear stress-displacement curves (black) used to obtain k, and slip velocity (grey). Inset in panel (d) shows a failure event and the duration of the stress drop.

The laboratory slip events exhibit a range of slip velocities that mimic those observed in nature^13,19, with peak slip velocities during slow slip events of ~100 µm/s and much higher slip rates for fast stick-slip events. We note that our laboratory work focused on the slow end of the spectrum, and did not fully explore faster stick-slip velocities (≥1 m/s) appropriate for regular earthquakes, resulting in a smaller range of slip velocities than that observed in nature.

Near the stability boundary, at K~1, we observe complex behavior including period doubling and long-period modulation of the stress drop, consistent with theory²¹ (Fig. Supplementary 2). In this framework, the high slip velocity and large stress drop events represent laboratory analogues for regular earthquakes²⁵, whereas the slow, long duration, and small stress drop events are like slow earthquakes.

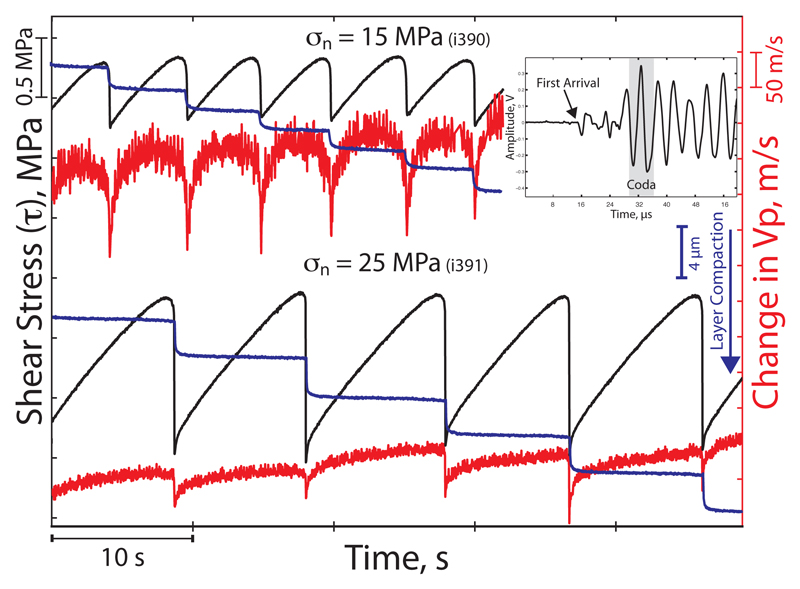
To shed light on the microphysical processes during slow- and fast- stick-slip events, we measured P-wave velocity (V_p), from the P-coda, throughout stick-slip cycles (Fig. 1a inset and method). Wave speed evolves systematically as the fault approaches failure, characterized by an initial increase during elastic loading, followed by a plateau, and a decrease prior to failure (Figs. 2 and 3). The reduction in P-wave velocity during stick-slip events is coincident with layer compaction, indicating that wave speed is more sensitive to grain contact stiffness and coordination number than bulk layer density.

Figure 2. Mechanical and P-wave velocity measurements during slow-slip (top) and fast-slip cycles (lower curves).

Data showing the evolution of shear stress (black), layer thickness (blue) and changes in P-wave velocity (V_p) (red) during slow (top set of curves) and fast (lower curves) stick-slip events. Inset shows a typical waveform with the P-wave arrival and the P-coda used to calculate V_p (see Fig. Supplementary 4 and methods for additional details). Note the consistency in the V_p evolution during the slow and fast stick-slip cycles, mimicking the evolution of shear stress.

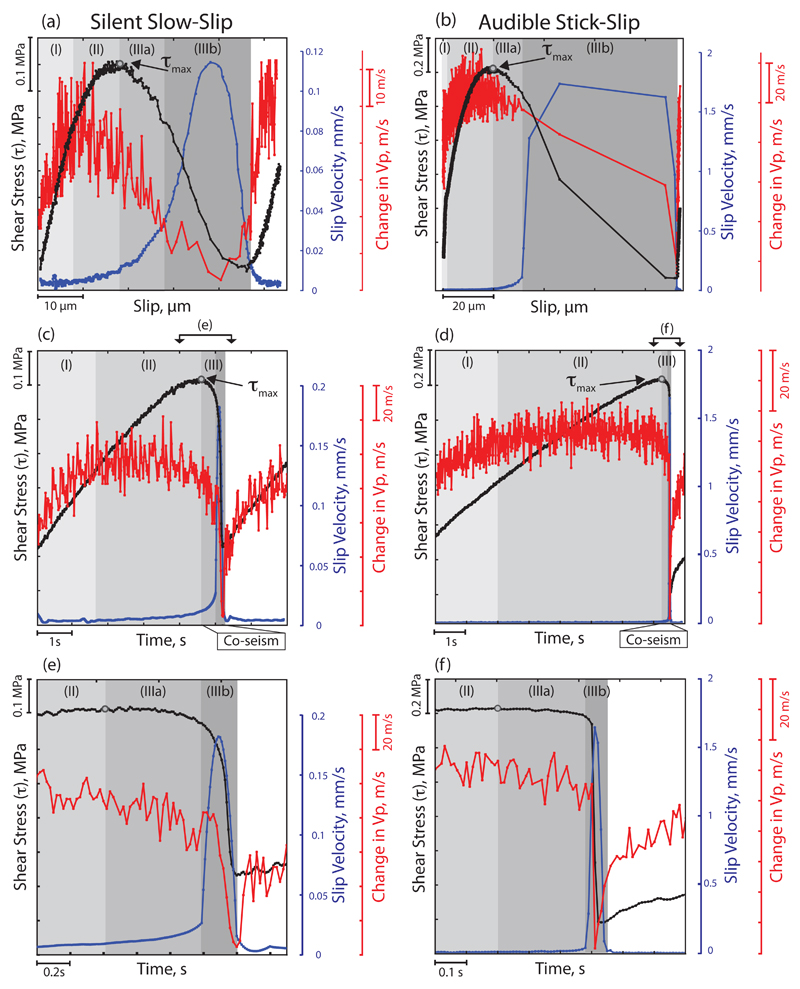
Figure 3. Comparison between slow slip and fast stick-slip cycles.

Details of slow (left column) and fast (right column) stick-slip events. (a, b) Representative slip events taken at shear displacement of 25 mm, and (c, d, e, f) at displacement of 30 mm. The evolution of shear stress (black), slip velocity (blue) and P-wave velocity (red) is shown as a function of: (a, b) fault slip and (c, d, e, f) time. The grey shaded boxes indicate the three phases of the seismic cycle: (I) inter-seismic, (II) pre-seismic and (III) co-seismic, as described in the text.

The combination of frictional properties and acoustic data provide a comprehensive view of fault strength evolution during the seismic cycle (Fig. 3). We find that both slow and fast stick-slip events can be divided into three distinct phases: (I) inter-seismic, described by linear elastic loading; (II) pre-seismic, which begins at the onset of inelastic deformation; and (III) co-seismic, defined by rapid slip acceleration and measured from the peak stress to the residual shear stress after failure. The co-seismic phase can be further divided into a preparatory stage, where the shear stress decreases slowly and fault motion accelerates (IIIa) followed by a failure stage, where dynamic stress drop occurs (IIIb) (Fig. 3a, b).

For both slow and fast slip events, the inter-seismic phase is associated with elastic loading, near zero fault sliding velocity, and increasing Vp (Fig. 3). In this phase the fault is considered locked and the increase in Vp represents contact aging and particle interlocking, consistent with laboratory³ and seismological observations along natural faults^26,27 (Fig. 4).

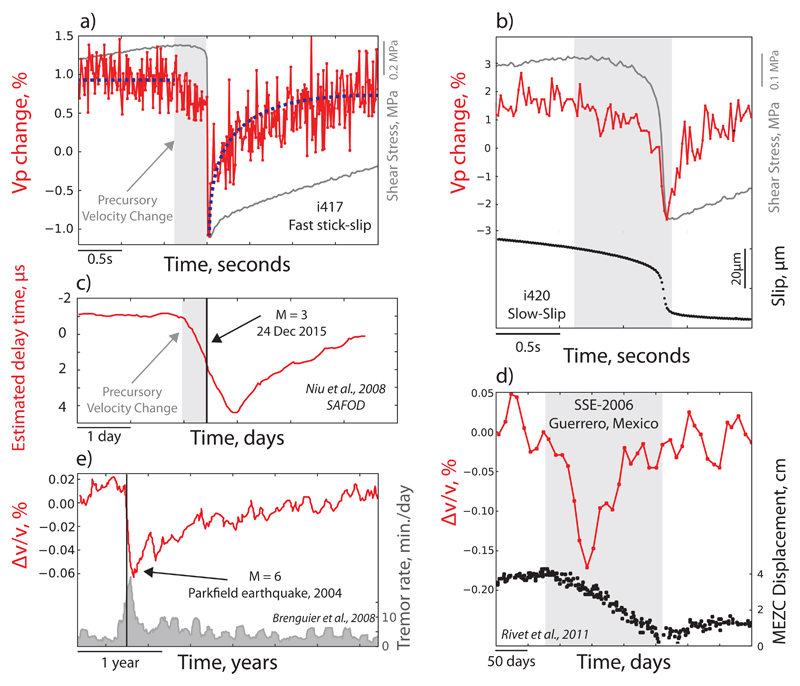
Figure 4. Comparison between laboratory and natural variation in seismic velocity.

Seismic velocity changes during the earthquake cycle for fast (a) and slow (b) laboratory earthquakes and fault slip events in nature ranging from typical earthquakes (c and e) to slow-slip events (d). Grey shaded bands in (b) and (d) represent slow-slip events in the lab and in nature.

In the pre-seismic phase (II), creep begins to accelerate and deformation is inelastic. Acceleration in slip velocity coincides with maximum Vp, which generally plateaus during phase II (Fig. 3c, d). For fast stick-slip events, the fault slip velocity is still nearly zero in phase II. Shear stress decreases slowly at the beginning of phase III (Fig. 3) and in this preparatory stage of failure (phase IIIa) accelerated creep coincides with a reduction in Vp of ~1%, which is comparable although larger to seismic observations prior to earthquake failure (Fig. 4). During phase IIIb we observe an abrupt increase in slip velocity followed immediately by a rapid stress drop. The maximum slip velocity is attained during phase IIIb, as expected for dynamic rupture. The P-wave velocity shows a marked decrease of ~2-3% coinciding with abrupt acceleration and stress drop (Fig. 3).

Our data show that accelerated creep marks the onset of non-linear elastic deformation (i.e. phase II in Fig. 3a, b) and a peak in Vp. This transition is not attendant with macroscopic layer dilation (Fig. 2). Fault creep and the reduction in Vp indicate that asperity contacts within the fault zone begin to fail prior to macroscopic frictional sliding. The onset of creep is likely accommodated by grain boundary sliding, particle rolling, and microcracking, which lead to reduction of elastic wave speed prior to failure. Note that the onset of wave speed reduction and creep occur at similar stages of the loading cycle for slow and fast failure events (Fig. 3), suggesting that the microphysical processes of fault weakening may share key features for slow and fast earthquake rupture (Fig. 4).

Our data indicate that earthquake nucleation and slip is controlled by the interaction between fault frictional rheology and local elastic properties of the fault zone and wall rock. Previous works suggest that the major factors dictating the mode of fault slip are frictional properties, effective normal stress, and elastic stiffness of the fault zone^{14,15,28–30}. Fault zone width and maturity may also play a role because they affect friction constitutive parameters, and elastic stiffness (Fig. Supplementary 3). Our observations suggest that the stiffness ratio K incorporates the key parameters for slip stability as applied to tectonic faults and may provide a general mechanism for the spectrum of tectonic fault slip behaviors²⁴, possibly acting in concert with dilatancy hardening or other mechanisms to limit rupture speed^3,28–30. The systematic relationship that we observe between shear stress, fault slip rate and Vp during the seismic cycle for slow and fast slip events suggests commonalities in the nucleation and rupture processes for the observed spectrum of slip behaviors²⁰. These data together with existing field observations⁴ suggest that seismic velocity precursors may occur during the preparatory phase preceding earthquakes, even if only within a limited region.

To address the question of how our data may apply to tectonic faults, we note that active seismic surveys and analysis of ambient seismic noise have documented systematic changes in elastic wave speed associated with earthquakes^4–6,27. In both the laboratory and nature, seismic wave speed decreases during coseismic slip and increases during the interseismic period (Fig. 4). In nature, the most obvious changes occur after earthquake rupture; wave speed drops abruptly coseismically and then increases with log-time, consistent with fault re-strengthening due to healing mechanisms^26,27. A coseismic reduction in wave speed has been documented for a number of major earthquakes (M>6)⁵. Additionally, in special cases where high resolution monitoring was carried out, precursory changes in seismic wave speed have been observed prior to a M3 earthquake⁴ (Fig 4c). Similar observations of velocity reduction have been reported during slow earthquakes⁶, where the maximum seismic velocity perturbation was observed at the time of maximum strain change (Fig. 4d). Although fault dimensions and wave frequencies in natural and laboratory studies differ, and a more comprehensive discussion is required, the similarities between natural observations and our results, suggest the applicability of our findings to natural faults (Fig. 4).

Our data show that the state of stress on a fault can be monitored by P-wave velocity changes during the seismic cycle. In particular, we document fault creep and a reduction in Vp during a preparatory phase (IIIa) preceding failure (IIIb). Recent works show that large earthquakes are often preceded by slow slip during a preparatory phase^16,18, which is consistent with our observations. In summary, our data illuminate: 1) key connections in the underlying physics of slow and fast earthquake rupture nucleation, and 2) precursory changes in seismic velocity that may be a promising avenue for the detection of earthquake precursors.

Methods

Friction experiments

All experiments were performed in a double direct shear configuration using a biaxial loading frame (Brittle Rock deformAtion Versatile Apparatus, BRAVA, at HP-HT laboratory INGV, Rome)³¹. Two fast-acting servo-hydraulic rams are used to apply horizontal and vertical load. The applied load was measured via strain gauge load cells (accuracy ±0.03kN) positioned at the extremity of the rams in contact with the sample assembly. Horizontal and vertical displacements were measured by Linear Variable Displacement Transformers (LVDTs), with an accuracy of ±0.1μm, referenced at the load frame and the upper side of the ram. Additionally, two Direct Current Displacement Transducers (DCDTs), with an accuracy of ±0.1μm, were mounted directly on the sample assembly (Fig. 1a inset). The first DCDT was positioned in the horizontal direction and used to accurately resolve details of sample compaction/dilation, avoiding unlikely artifacts from the remote measurement of the LVDT positioned on the ram. The second DCDT was mounted at the top of the shearing block and referenced at the end-platen, to measure the true fault slip.

The sample assembly consisted of two layers of simulated fault gouge sandwiched between three steel forcing blocks equipped with grooves (0.8 mm high and 1 mm spacing) to couple the gouge and eliminate boundary shear. We used granular quartz powder as simulated fault gouge. The powder is (Min-U-Sil 40, U.S. Silica Co.), 99.5% SiO₂ with traces of metal oxides and a median grain diameter of 10.5 μm. We chose granular quartz because it is a common mineral in natural fault gouge and a well studied material with reproducible frictional behavior²⁴. Gouge layers were prepared using leveling gigs to achieve a constant initial layer thickness of 3 mm and a nominal frictional contact area of 5 x 5 cm. All experiments were performed at room temperature and under 100% relative humidity.

We conducted two types of experiments. (1) Stiff experiments were used to determine rate- and state-friction parameters (a-b) and D_c to directly calculate k_c (Fig. Supplementary 3 and Table Supplementary 1). In these experiments a normal load of 15 or 25 MPa was applied and maintained constant throughout the experiment via a force-feedback servo control. Gouge layers were allowed to compact under load prior to shear to allow compaction and densification. Shear was induced by driving the vertical ram at constant displacement rate of 10 μm/s measured at the top of the central forcing block in the double direct shear arrangement (Fig. 1a inset). Once a steady state coefficient of friction was achieved (usually after 5 mm of shear) a series of velocity steps, from 10 – 1 – 3 to 10 μm/s were performed. The sequence was repeated throughout these experiments until a shear displacement of ~25 mm was achieved. (2) Experiments with lower shear stiffness were performed by placing a spring (k = 29.63 MPa/mm, for our sample size) in series between the vertical ram and the central forcing block. In these experiments the normal load was varied from 13 to 25 MPa and the shear velocity was maintained constant (10 μm/s) throughout the experiments until a displacement of ~30 mm was achieved.

In the context of frictional stability²¹, when sliding velocity is still slow, the threshold between stable sliding and stick-slip is defined by the interaction between the stiffness of the elastic surroundings, k, and a rheologic critical stiffness k_c:

$$k<k_c=\frac{({\sigma }_n-P_f)(b-a)}{D_c}$$ (1)

where σ_n is the normal stress, P_f is the pore fluid pressure, (b-a) is the friction rate parameter, and D_c is the critical slip distance. Equation 1 represents simplified elastic and frictional conditions, but it is consistent with more complex models of earthquake nucleation^28–30 and applicable to the slow, early stages of slip nucleation²⁴. If the stiffness of the loading system (k) is less than the critical stiffness (i.e. k < k_c), instability occurs because the fault weakening rate, given by k_c, exceeds the rate of elastic unloading, resulting in a force imbalance and acceleration. For stiffer systems, in which elastic unloading outpaces frictional weakening, k > k_c, sliding is stable.

To investigate the full spectrum of frictional slip behaviors, we altered the effective stiffness of the loading system, k’ [μm^-1] = k/σ_n, to the desired values (i.e. to be greater, less or equal to k_c) following the methods described by Leeman et al. 2016. To determine the rate- and state-friction parameters, (a-b) and D_c, from the stiff experiments (Fig. Supplementary 3b, c), we modeled each velocity step using an iterative singular value decomposition technique, which solves the rate- and state-friction equations using the Ruina evolution law coupled with the elastic interaction of the testing machine^32–34 (Fig. Supplementary 3a). Direct calculation of k_c yields a threshold value of 8x10^-4 [μm^-1] (Fig. Supplementary 3d). For experiments with reduced stiffness, k is given by the summation, in series, of the stiffness of the loading apparatus and the spring. We further altered the effective stiffness by varying the normal stress (Table Supplementary 1). We measured k_ev (representing the stiffness of the loading system and gouge layers) from the linear elastic portion of each stick-slip event using a least-square linear fit to the friction vs. displacement curves. We find that k_ev increases as normal load is decreased and at the transition between unstable to stable behavior we obtain values of k_ev ~ 0.001 [μm^-1] (Fig. Supplementary 3e). Comparing our direct (k_c =8x10^-4 [μm^-1]) and empirical (k_ev = 0.001 [μm^-1]) measurements of k_c we note that the values are quite similar. The stiffness ratio K reported in Figure 1b is then calculated as the ratio between the k_ev measured for each stick-slip cycle and an averaged k_c = 0.0009 [μm^-1].

Ultrasonic Measurements

Elastic properties were measured with two, 20-mm diameter, 2-mm thick, barium-titanate P-type Piezoelectric transducers (PZT), with a central frequency of 1MHz (PI Sensor PIC255). PZTs were embedded into cavities within each of the side forcing blocks and positioned at a distance of 13.5 mm from the fault gouge boundary (Fig. 1a inset and Supplementary 4a). One PZT (Transmitter) is excited by a high voltage (900V) and very short (~0.8 μs) pulse at a repetition rate between 50 and 100Hz, using a custom-made pulse generator. Each waveform was received by the PZT (Receiver) at the opposite side of the sample assembly after passing through the gouge layers and forcing blocks. We recorded the output signal with an eight channel, 14-bit, fast AD converter (ADLink PXIe-9848) at sampling rates up to 100MHz. For these experiments we configured the board for finite acquisition at 50MHz with a capture duration of 200μs (10000 points per signal). Each waveform is synchronized in real-time during the experiment with the mechanical data.

To calculate P-wave velocity we used cross correlation to pick P-wave first arrival as well as P-coda. The cross-correlation procedure followed standard techniques where, for a time interval of the experiment, a specific pattern of a master waveform is compared to other seismograms to identify a time-shift in the selected wave pattern (Fig. 1a inset). One benefit of cross correlation is that it can offer up to a tenfold increase in temporal resolution compared to the data sampling rate. Thus, we subsampled each master wave and seismogram with a 50x spline fit. The arrival time of a wave pattern is called “flight time” and is defined as the time required to go from the source to the receiver. To obtain the absolute P-wave velocity for our experiments, we performed calibration experiments where we loaded the empty assembly (side + central steel blocks) at normal loads between 5 and 25 MPa. This calibration returned an average flight time t₀ = 13.6 μs which correspond to a P-wave velocity of 5421.2 ±5.2 m/s.

For our experiments with gouge layers, the P-wave velocity can be computed as:

$$v_p(t)=\frac{2*h(t)}{T(t)-t_0}$$ (2)

where h(t) is the thickness of one gouge layer, T(t) is the flight time of the P-wave first arrival and t₀ is the calibration time (which is constant all over the experiments) (Fig. Supplementary 4 data coded in green). Generally, the first arrival was quite noisy and for this reason we focused on the P-wave coda, consistent with previous work³.

We developed a new approach to retrieve the absolute value of the P-wave velocity by using coda waves (Fig. Supplementary 4). We consider a simplified propagation model with linear ray path, following Snell`s theory, with rays that reflect at the interfaces of our sample assembly with an incidence angle equal to zero (Fig. Supplementary 4a red and blue paths). In this context the definition of “coda waves” correspond to all the excitations due to the summation of constructive or destructive effects of reflected or transmitted rays that are recorded after the first arrival. We modified Eq. 2 as follow:

$$v_p(t)=\frac{(N_{g1}+N_{g2})*h(t)}{T(t)-[(N_{e1}+N_{e2})*t_e+N_c*t_c]}$$ (3)

where T(t) is the P-coda flight time, t_e and t_c are the P-wave flight times along the two side blocks and the central block respectively, calculated from the calibration; the coefficients N_g1,N_g2 represent the number of reflections within the gouge layers; N_e1, N_e2, N_c represent the number of reflections within the side steel forcing blocks and the central forcing block respectively; and h(t) is the layer thickness. Eq. 3 reduces to Eq. 2 when the first arrival is considered. In Figure Supplementary 4 we show an example of the P-wave velocity calculated using the first arrival (green), and two P-codas (red and blue). Note that by using the P-coda we sensibly decrease the noise in the data without changing the absolute P-wave velocity (compare green and blue curves).

Data Availability

All the data that support the findings of this work were collected using the BRAVA apparatus at HP-HT Laboratory at the Istituto Nazionale di Geofisica e Vulcanologia (INGV), Rome. Source data files that generated the mechanical curves and all the waveforms shown in this study are available upon request by contacting the corresponding author MMS.