An analysis of patient-sharing physician networks and implantable cardioverter defibrillator therapy

Abstract

The application of social network analysis to the organization of healthcare delivery is a relatively new area of research that may not be familiar to health services statisticians and other methodologists. We present a methodological introduction to social network analysis with a case study of physicians’ adherence to clinical guidelines regarding use of implantable cardioverter defibrillators (ICDs) for the prevention of sudden cardiac death. We focus on two hospital referral regions (HRRs) in Indiana, Gary and South Bend, characterized by different rates of evidence-based ICD use (86% and 66%, respectively). Using Medicare Part B claims, we construct a network of physicians who care for cardiovascular disease patients based on patient-sharing relationships. Approaches for weighting physician dyads and aggregating physician dyads by hospital are discussed. Then, we obtain a set of weighted network statistics for the positions of hospitals in their referral region, global statistics for the physician network within each hospital, and of the network positions of individual physicians within hospitals, providing the mathematical specification and sociological intuition underlying each measure. We find that adjusting for network measures can reduce the observed differences between referral regions for evidence-based ICD therapy. This study supports previous reports on how variation in physician network structure relates to utilization of care, and motivates future work using physician network measures to examine variation in evidence-based medicine.

1 Introduction

A network is a graph that consists of a set of entities, called the nodes, and the relationships between them, called edges. In a social network, the edges between two individuals represent sociological relationships and can imply communication, influence, trust, or affiliation (Wasserman and Faust 1994). The application of social network analysis to health care, particularly with respect to its organization, is relatively new among health services researchers (Luke 2007; O'Malley 2013). It has been demonstrated empirically that professional relationships between physicians influence clinical outcomes, including prescribing behavior, diffusion of technology, and quality and cost of care (Barnett et al. 2012; Bridewell and Das 2011; Fattore et al. 2009; Pollack et al. 2015). For example, physician networks with higher density have greater levels of Medicare spending (Barnett et al. 2012).

In this work, we employ social network methodology to examine the structure of patient-sharing relationships among physicians and hospitals within two adjacent hospital referral regions (HRRs) (Wennberg and Cooper 1999) with disparate adherence to clinical guidelines regarding patient selection for implantable cardioverter defibrillator (ICD) therapy. ICDs have been proven effective for the prevention of sudden cardiac death in patients with advanced systolic heart failure (Bardy et al. 2005; Kadish et al. 2004; Moss et al. 2002). Patient selection for ICD surgery is an example of a clinical situation in which guidelines for evidence-based care exist, and yet there remains variation among hospitals’ rate of adherence to these guidelines (Al-Khatib et al. 2011; Matlock et al. 2011; Mehra et al. 2009). Adherence to guidelines can be influenced by several factors, such as physician awareness, familiarity, or agreement with the guidelines, inertia of previous practices, and other external barriers (Cabana et al. 1999). These factors are potentially reinforced or modified by the professional network of a physician.

We used Medicare claims data to construct a network of physicians who care for beneficiaries with cardiovascular disease, a subset of whom received ICD therapy. To address the complexity of inferring the strength and type of relationships among physicians using claims-based data to quantify patient-sharing, we discuss approaches for weighting the relationships between physicians and for aggregating patient-sharing information by hospital. The patient-sharing physician networks we constructed reveal features of the organizational structure of the hospitals the physicians are fully or primarily affiliated with (Bynum et al. 2007) and of the positions of key physicians within these hospitals. The motivation for using a case study approach was to visualize and quantify these complex networks in ways that were feasible, informative, and comprehensible at both the aggregated physician-level and hospital-level, which can be obscured with larger, more complex data, such as that for the entire United States. An in-depth case-study is an underrated way of detecting logical and data flaws that could threaten “big data” statistical analysis. We calculated several classic and modern network measures and investigated their association with evidence-based ICD use in the HRRs. This methodology can be applied generally to any situation where data is available on the relationships between all pairs of individuals within an organization or region. We take a novel approach to describing variation in the practice of evidence-based use of ICDs by constructing networks of physicians and hospitals and applying network analysis methodology. Thus, this paper serves as a methodological contribution to the meaningful and practical analysis of health systems.

2 Methods

We first detail the clinical problem that motivates the use of social network analysis (Section 2.1) and then describe the social network analyses, the summary network measures they yield (Sections 2.2 and 2.3), and the subsequent statistical methodology that combines the various inputs in models of ICD utilization (Section 2.4).

2.1 Methodology related to clinical case study

2.1.1 Classification of evidence-based ICD implantations

Information from the National Cardiovascular Data Registry's (NCDR's) ICD Registry was used to determine the number of ICDs and rate of evidence-based ICDs that occurred among Medicare beneficiaries. We were interested in those ICD therapies prescribed for primary prevention in patients with heart failure. Thus, patients must be indicated as having heart failure in the registry to contribute to the number and rates of ICD therapy. Following the Class I recommendations in The American College of Cardiology Foundation (ACCF) guidelines, we considered an ICD therapy to be evidence-based in patients with a left ventricular ejection fraction (LVEF) ≤ 35% who have NYHA class II or III symptoms (Russo et al. 2013). Any hospital or physician-level aggregation of ICD surgery counts between 1 and 11 are indicated as “Not Reportable” to protect patient confidentiality.

2.1.2 Selection of HRRs for case study

We aimed to investigate two HRRs that had differences in adherence to guidelines in their selection of patients who received ICDs. The proportion of patients with implanted ICDs that adhere to the guidelines in each of the 306 HRRs ranged from 0.47 to 1, with a median of 0.84 and a mean of 0.83. In order to minimize differences driven by location and size, we limited our comparisons to HRRs that were within the same state, of similar population size, and with similar counts of ICD surgeries. After applying these criteria to the 306 HRRs in the United States, two geographically adjacent HRRs in Indiana, Gary and South Bend, which had rates of evidence-based ICDs of 0.86 and 0.66, respectively, were chosen for the case study.

2.1.3 Assigning physicians to hospitals and HRRs

Physicians were empirically assigned to hospitals using the physician hospital network (PHN) methodology described by Bynum (2007). Briefly, this approach determines the hospital at which a physician submitted the most Medicare claims (inpatient or outpatient physician services) or, if the physician did not submit any claims for inpatient services either for specific services (Part B) or as the attending physician, they were assigned to the hospital at which the plurality of their assigned patients were admitted. The geographic location (zipcode) of the physician's hospital determines the HRR to which each physician is assigned, both of which serve as attributes of the physician nodes in the patient-sharing networks described below.

2.2 Bipartite network formation

A bipartite network is a network in which two distinct social entities make up the node set and direct relational ties exist only between nodes from different social entities (Iacobucci and Wasserman 1990). For example, in this work the two social entities that informed our bipartite network were patients and physicians, and we inferred ties between them by extracting Evaluation and Management (E&M) claims related to cardiac care from the 2008 Medicare Physician/Supplier Part B claims file. We excluded claims associated with mid-level practitioners (e.g., physician assistants and nurse practitioners).

2.2.1 Defining a relevant population of patients

We considered a cohort of beneficiaries who are 65 years or older on January 1, 2008, had full Parts A and B coverage (12 months or until death), and who did not have Medicare Advantage. In addition to this, we also restricted our network to include only patients with certain cardiovascular diagnoses who are at increased risk for requiring an ICD (Curtis et al. 2007). They must have had two or more visits for one of the following diagnoses (ICD-9 diagnosis codes in parentheses): arrhythmia (427.1, 427.41, 427.42, 427.5, 427.9), congestive heart failure (425.4, 428, 428.0, 428.1, 428.2, 428.20, 428.21), coronary heart disease (410.xx, 411.xx, 414.xx, 429.2), or peripheral vascular disease (440.xx, 443.89, 443.9), where “.xx” ⊆ {.00, .01, .02....,.99} represents a superset of sub-diagnoses in existence that will vary depending on the condition being diagnosed. To avoid falsely classifying patients into this category, we required patients to have two claims separated by at least 7 days.

2.2.2 Constructing a patient-sharing network of physicians

The Part B claims were used to identify our population of cardiovascular patients and the physicians who treated them. From this we were able to construct a bipartite network between the physicians and patients, where a tie between the two social entities existed if a patient had at least one claim with the physician listed as the provider during 2008 (Fig. 1). A common approach to studying bipartite networks is to reduce the dimension and complexity by focusing on a unipartite network inferred from the bipartite relationship (Porter et al. 2007; Borgatti et al., 2011). A benefit to this approach is that one can apply the myriad methods developed for unipartite network analyses. To form an undirected unipartite network among physicians, edges were created between physicians who shared at least one patient. A “dyad” in this network refers to a pair of physicians. Although patient-sharing is not a direct measure of a relationship, it has been used previously to determine physician ties (Barnett et al. 2012; Landon et al. 2012).

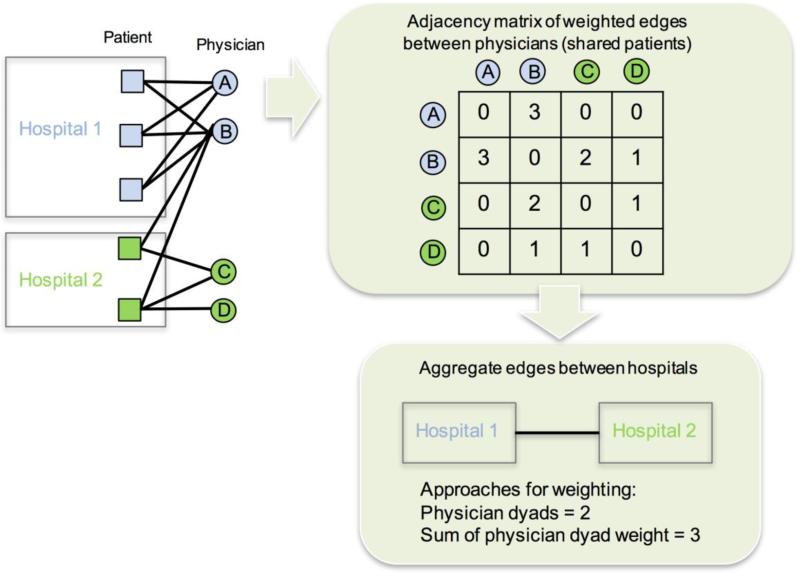
Fig. 1.

Diagram depicting construction of the bipartite network. Physicians who share patients are tied to each other to create a unipartite network of physicians. Physicians are assigned to a hospital based on where the majority of patients they submit claims for receive their care. Ties between hospitals are formed by aggregating physician-level dyads

2.2.3. Weighting and aggregating patient-sharing networks

Patient-sharing relationships between physicians constructed with Medicare data can be made potentially more informative than simply existing or not-existing by quantifying the extent of the physicians’ patient overlap and incorporating this information in the form of network edge-weights. Weights we computed and considered include: number of shared patients, volume of visits with shared patients, or volume of billable procedures attributed to their shared patients quantified by the procedure's relative value unit, or RVU, for example. Weighting network edges by the number of shared patients may lend itself more easily to studies for which each patient episode of care is considered equally informative to a physician's practice irrespective of the number of visits entailed. However, to account for the wide range in number of clinical visits patients may have with their physicians, we also computed the geometric mean of shared visits across the common patients of each pair of physicians and summed these to form more refined edge-weights. Alternatively, we note that weighting edges by the geometric mean of the RVUs from the claims involving all shared patients may be ideal for studies interested in investigating variation in cost or total utilization of care. In the results reported herein, the physician dyads were weighted by the summed geometric means of the number of shared visits.

Our analyses also rely on the aggregation of physicians up to their hospital. One approach to creating an edge between a pair of hospitals involves summing the edge weights over each pair of physicians bridging the two hospitals. A second approach would be to weight the edges between hospitals by the number of unique patients who had clinical encounters at both hospitals. This approach is likely less favorable for studies aiming to interpret each connected physician dyad as an independent potential path for communication or influence. Finally, one could count the number of connected physician dyads that span two hospitals, assuming equal weights. This approach is a logical aggregation of a binary network. As we weighted the edges between physicians by the number of shared visits, we chose to weight edges between hospitals by summing these weights of the physician dyads that span each pair of hospitals.

2.3 Network metrics and definitions

All networks considered were undirected in the sense that all ties representing the relationship between nodes have no directionality associated with them. We note these network measures typically have straight-forward generalizations for directed networks (Wasserman and Faust 1994; O'Malley and Marsden 2008; O'Malley and Onnela 2015). The graph is denoted by G = (V, E) where V is the set of nodes (or vertices) and E is the set of edges between any pair of nodes. The network can also be represented in the form of a symmetric adjacency matrix A = [A]_ij where a_ij = a_ji = 1 for all i and j that are connected in the network and is 0 otherwise. To distinguish value-weighted edges from the mere existence of the edge itself, we introduce the weighted adjacency matrix W, where w_ij represents the weight of the tie between nodes i and j.

The size of a network is the number of nodes, or in other words the cardinality of V, and is denoted by N. The size of a patient-sharing physician network within a hospital is equal to the number of physicians in the network. The total number of dyads in an undirected network is then $\left(\begin{array}{c}\hfill N\hfill \\ \hfill 2\hfill \end{array}\right)=N(N-1)∕2$. The overall density of a network, μ, is typically expressed as the ratio of the number of edges (the cardinality of E) divided by the maximum possible number of edges:

$$\mu =\frac{2{\sum }_{i<j}^N{a}_{ij}}{N(N-1)}$$

Density ranges from μ = 0 (no edges) for an empty network to μ = 1 for a complete network (all possible edges).

2.3.1 Node-level metrics and definitions

Generally speaking, centrality is a measure of the prominence of a node in the network. For graphs including weighted edges between pairs of nodes, weighted centrality measures can be calculated.

The node with the greatest number of ties, which is known as its degree, may be considered the most important or influential node in a network if it is felt that importance or influence manifests in terms of the number of direct connections to other nodes. Degree ranges from 0 to N – 1, and is given by:

$$d_i={\sum }_{j\ne i}{a}_{ij}.$$

It follows that

$$\mu =\frac{{\sum }_{i=1}^N{d}_i}{N(N-1)}=\frac{\stackrel{‒}{d}}{N-1}$$

where d̄ is the average degree of the nodes. The degree of a node has been extended to weighted networks by summing the weights of adjacent ties, a term known as node strength (Barrat et al. 2004), formalized as follows:

$$d_i^w={\sum }_{j\ne i}{w}_{ij}.$$

A deficiency of degree and node strength is that they do not take into account the extent to which the node is in a structurally important position in the network in ways other than those reflected in a node's direct connections.

An array of centrality measures aims to address additional aspects of positional importance in a network. The basis of several of them is the network distance between a pair of nodes, typically calculated as the minimum number of edges from one node to the other and referred to as the “geodesic distance.” We denote the geodesic distance between nodes i and j as g_ij with g_ii = 0. The geodesic distance between any two nodes can be easily determined from the ij'th element of the matrices A^k for k = 1, 2, ..., N – 1 due to the fact that [A^k]_ij contains the number of paths of length k between nodes i and j. Therefore, for i ≠ j,

$$g_{ij}={\min }_k\{k:{\left[A^k\right]}_{ij}>0\}.$$

If the network contains multiple components, or disparate groups of nodes with no edges linking them, then it is possible that no path exists between a pair of nodes. In this case, we let g_ij = ∞.

Geodesic distance can also be generalized to weighted networks (Opsahl et al. 2010). Newman (2001) and Brandes (2001) proposed to invert the edge weights, therefore converting their interpretation to the cost of the tie. By implementing Dijkstra's algorithm (Dijkstra 1959), they defined the “cost” of a path as the sum of the inverted edge weights and this the minimum cost path as:

$$g_{ij}^w=\min (\frac{1}{w_{ih}}+\cdots +\frac{1}{w_{hj}})$$

This calculation of shortest path in weighted networks is used to calculate several centrality measures, such as weighted closeness and betweenness centralities. Briefly, the weighted closeness centrality is the inverse of the total weighted geodesic distance from a node to all other nodes in the network. The weighted betweenness centrality measures the relative frequency with which node i appears on the weighted geodesic path between all pairs of nodes (j,k). Descriptions for centrality measures in weighted networks can be reviewed in Opsahl et al. 2010, and detailed statistical descriptions for the measures in this study, including weighted closeness, betweenness, and eigenvector centrality (Newman 2004), and clustering coefficient, can be found in Appendix 1.

2.3.2 Exponential-family random graph modeling

Exponential-family random graph models (ERGMs) are probability models that summarize the general structure of graphs in terms of the frequency of various subnetworks or configurations (e.g., dyads, triads, nodes of particular degrees or types) and as such can be a flexible approach for handling the complex dependence structure of network graphs (Robins et al. 2007). ERGMs are based on exponential-family theory for specifying the probability distribution for a set of random graphs or networks to describe the local selection forces that shape the global structure of the network (Hunter 2008). One selection force is homophily, which is the tendency of actors in the network to form ties with similar others. In practice, this methodology can be employed to investigate functions of network statistics, such as degree distribution, triad configuration, or homophily on nodal attributes, that may be more or less common than expected in a simple random graph consisting of a set of n isolated vertices where edges between them are added at random and all ties have equal probability (Goodreau 2007). ERGMs are most often used to analyze single networks. The existence of multiple networks in our data set (e.g., for each hospital within each HRR) allow us to estimate separate ERGMs on each hospital to obtain a vector of network measures adjusted for the other terms in the ERGM. As seen in the general form for an ERGM presented below, its fundamental feature is that multiple network features of any form and other variables may included as determinants of the network:

$$\mathrm{Pr}(Y=y)=\left(\frac{1}{\kappa }\right)\exp \left\{{\Sigma }_A{\eta }_A{g}_A\left(y\right)\right\}$$

where g_A(y) represents any possible network statistic. A indexes the multiple statistics included in the model vector g(y), and η_A represents the coefficients for these terms. κ represents the normalizing constant, the sum of exp(Σ_Aη_Ag_A(y)) over all possible networks with n actors (Goodreau 2007). ERGMs provide a means to supplement the standalone descriptive measures described in Section 2.3.1 with adjusted counterparts that extract the independent contribution of each feature of the structure of the network. For example, the interpretation of the homophily coefficient is the change in the log-odds of the tie if the actors have the trait in common (homophilic dyad) compared to if they do not have the trait in common, conditioned on the rest of the network. The ERGMs in this study include k-star statistics, which is equivalent to the exponentially weighted degree statistic, and helps to obtain estimated coefficients of other terms that are free of confounding by the degrees of the actors. A configuration (i, j₁,...,j_k) is called a k-star if i is tied to each of j₁, j₂, up to j_k (Snijders et al. 2006). An edge is a one-star. We used the alternating k-star, ‘altkstar’, term as a predictor, which is equivalent to the exponentially weighted degree term, as an approximate way of accounting for the degree distribution without encountering the numerical problems from including a list of individual k-star terms.

A large number of network features have been incorporated as predictors in software for ERGMs. However, as more subtle features of a network are included as predictors in ERGMs, substantial computational challenges are encountered (Handcock 2003a, Rinaldo 2009). The clustering in our network is higher than would be expected by a random graph because it is a projection of the bipartite network between patients and physicians. Consequently, we found that ERGMs do not converge or yield plausible estimates for our physician network when including dyad dependent model terms such as the frequency of triad configurations or even the new alternating k-triangle or geometric weighted edgewise shared-partner network statistics (Goodreau 2007, Hunter 2007) designed to overcome degeneracy, under these conditions. Thus, we limited the scope of our ERGM's adjustment for non-homophily terms to the edges (i.e., density) and k-star statistics (i.e., actor degrees) using the ERGM library (Hunter et al. 2008) in the statnet package (Handcock et al. 2003b) in R (R Development Core Team 2008). This allows differences between the hospital networks in the estimated homophily coefficients, representing the extent to which homophily on various characteristics is a determinant of network ties adjusting for the network's density and degree distribution, to be used as predictors of the likelihood of an ICD recipient receiving guideline consistent care.

2.3.3 Computing network measures and visualizing networks

The igraph package in R was used to calculated weighted centrality measures of physicians and hospitals (Csardi and Nepusz 2006). Gephi version 0.9.1 was used to visualize the networks (Bastian et al. 2009). The network with hospital-level nodes was visualized with the GeoLayout plugin to yield their true geographic locations (as given by latitude and longitude coordinates) while physician-level networks were visualized with the Force Atlas 2 layout.

2.4 Mixed-effects logistic regression of guideline-supported ICD implantation

Questions such as whether a patient's quality of care is more affected by the physician who attends to them or the institution at which they receive care has long been debated. A novel contribution of this paper is that the model of individual patient outcomes combined with the novel compendium of network-based predictors allows us to estimate the effects of predictors reflecting a physician's position in their hospital network, the features of the hospital network, and the position of the hospital in the network of hospitals within their HRR as well as patient characteristics in a model of a patient utilization outcome (guideline consistency of ICD implantation). The logistic model to address the above question and in general determine which network-based and other factors are most associated with the outcome is given by

$$\mathrm{Pr}(y_{ijkl}=1\mid {\theta }_{ij},{\delta }_i)={\mathrm{logit}}^{-1}({\beta }_0+{\beta }_{1}HR{R}_l+{\beta }_{2}Hos{p}_{il}+{\beta }_{3}Phy{s}_{ijl}+{\beta }_{4}Pa{t}_{ijkl}+{\delta }_i+{\theta }_{ij})$$ (1)

where Y_ijkl is a binary indicator of evidence-based ICD therapy for patient k who received surgery from physician j at hospital i in HRR l (= 1 for South Bend, = 0 for Gary). Patient level covariates (age, sex, and race) are depicted by Pat, the network characteristics particular to a given physician are depicted by Phys, the descriptors of the hospital network and of a hospital's position in their HRR network are depicted by Hosp, and the effect of HRR (South Bend versus Gary) is represented by β₁. Random effects for physician and hospital are depicted as θ_ij and δ_i, respectively. The effects of particular interest are (i) the individual centrality of providers within their hospital network (included in Phys), (ii) the centrality of a hospital within the HRR (included in Hosp), and (iii) the adjusted homophily of provider specialty over and above the network's degree distribution (included in Hosp). While the bipartite nature of our data constrains the list of structural characteristics whose effects can be estimated, in general any network feature whose coefficient is estimable under an ERGM may be included in Hosp.

We began by modeling the effect of HRR (β₁) adjusting only for patient level covariates, with physician and hospital as random effects, as depicted in Equation 2:

$$\mathrm{Pr}(y_{ijkl}=1\mid {\theta }_{ij},{\delta }_i)={\mathrm{logit}}^{-1}({\beta }_0+{\beta }_{1}HR{R}_l+{\beta }_{4}Pa{t}_{ijkl}+{\delta }_i+{\theta }_{ij})$$ (2)

Then, Hosp and Phys covariates were added to determine whether adjusting for hospital or physician network measures reduces the impact due to geography observed between the two HRRs in the study, respectively, as follows:

$$\mathrm{Pr}(y_{ijkl}=1\mid {\theta }_{ij},{\delta }_i)={\mathrm{logit}}^{-1}({\beta }_0+{\beta }_{1}HR{R}_l+{\beta }_{2}Hos{p}_{il}+{\beta }_{4}Pa{t}_{ijkl}+{\delta }_i+{\theta }_{ij})$$ (3)

$$\mathrm{Pr}(y_{ijkl}=1\mid {\theta }_{ij},{\delta }_i)={\mathrm{logit}}^{-1}({\beta }_0+{\beta }_{1}HR{R}_l+{\beta }_{3}Phy{s}_{ijl}+{\beta }_{4}Pa{t}_{ijkl}+{\delta }_i+{\theta }_{ij})$$ (4)

before finally combining all the predictors as depicted in (1). We used the glmer function in the lme4 package (Bates et al. 2015) in R to estimate each model in (1) - (4) above.

3 Results

3.1 Centrality of hospitals within an HRR

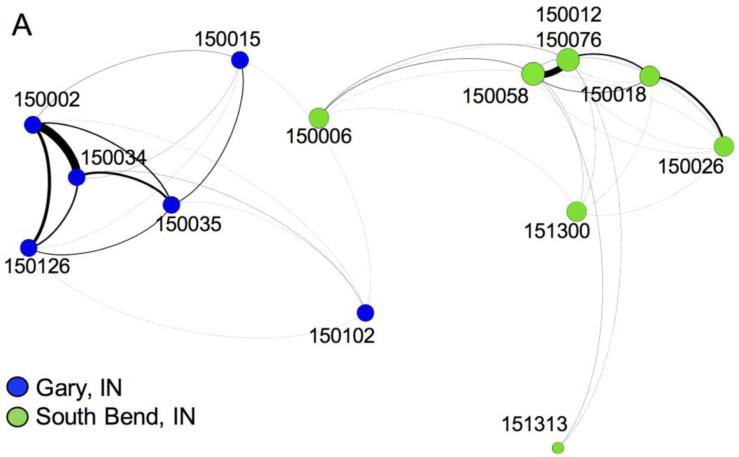
Gary, IN included 10,350 cardiovascular patients who had clinical encounters with 481 physicians, and South Bend, IN included 9,653 cardiovascular patients who had clinical encounters with 639 physicians. Fig. 2 illustrates the aggregated hospital-level network, with edges weighted by summing the weights of the physician dyads spanning each pair of hospitals. Gary, IN (blue nodes) includes 6 hospitals, and ICD implantations occurred at 3 of them (herein referred to as “ICD capable hospitals”). South Bend, IN (green nodes) includes 8 hospitals, 5 of which are ICD capable. The hospitals in Gary had high rates of evidence-based ICD implantations (86% of ICDs qualified as evidence-based) compared with South Bend (66% of ICDs qualified as evidence-based). Receiving care in the South Bend HRR was a significant negative predictor of evidence-based ICD utilization in the model specified by Equation 2 (β₁ = −1.09, p < 0.0001).

Fig. 2.

Network aggregated to hospital-level nodes. Patient-sharing ties for hospitals in Gary, IN (blue) and South Bend, IN (green) are shown. Nodes are placed based on their latitude and longitude coordinates to show patient-sharing patterns across geographic space. The nodes are sized by degree and the edges are weighted by the number of physician pairs spanning the hospitals

Table 2 reports the weighted centrality measures of the hospitals in each HRR network. The location and ties of a hospital may indicate paths of influence or communication between hospitals. Betweenness centrality is a measure of how frequently the hospital appears on the geodesic path between all other hospital pairs, and indicates potential influence of a hospital over the flow of communication in the network (Freeman 1979). Closeness centrality is the inverse of the sum of the geodesic paths from the focal hospital to all other hospitals in the network. In this setting it is hypothesized to capture a hospital's efficiency of diffusion and is motivated by the belief that the hospital disseminates knowledge to its ties, which then disseminate the knowledge to their ties, and so on until all hospitals in the network receive the knowledge (Freeman 1979). Eigenvector centrality indicates the centrality or influence of the adjacent ties of a hospital. Employing the model specified in Equation 3, we found no statistically significant associations between hospital centrality and evidence-based ICD use for patients in these HRRs, but hospital closeness centrality had a positive association and was approaching significance (p=0.06). However, the effect of receiving care at South Bend compared with Gary remained a statistically significant negative predictor of evidence-based ICD use (β₁ = −1.334, p < 0.0001).

Table 2.

Network characteristics of hospitals.

		Centrality measure
Hospital	HRR	Degree	Node strength	Betweenness (weighted)	Closeness (weighted)	Eigenvector (weighted)
150034	Gary	5	40367	0	0.0003	0.64
150035	Gary	5	17562	0	0.0005	0.26
150002	Gary	5	42569	0	0.0005	0.65
150015	Gary	5	4522	4	0.0008	0.05
150102	Gary	5	1174	9	0.0009	0.02
150126	Gary	5	18080	0	0.0009	0.32
150058	SB	7	25995	0	0.0005	0.67
150018	SB	6	13608	0	0.0015	0.23
150012	SB	7	28276	0	0.0007	0.69
150026	SB	6	7862	13	0.0016	0.10
150076	SB	7	2524	13	0.0016	0.07
150006	SB	6	2552	0	0.0012	0.07
151300	SB	6	898	0	0.0013	0.02
151313	SB	3	822	5	0.0009	0.02

Note: Edges between hospitals are weighted by summing the weighted physician dyads that span each pair of hospitals. SB = South Bend.

3.2 Physician networks within hospitals

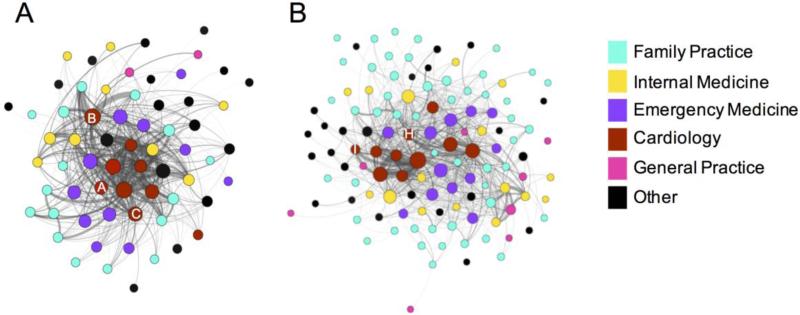
The following sections focus on network descriptors for the structure of physician ties within each hospital. The hospital that performed the highest number of ICD implants among hospitals in each HRR is visualized in Fig. 3. St. Mary Medical Center (hospital ID: 150034) performed the largest number of ICD surgeries in Gary, where 85 patients received ICDs and 83.5% were evidence-based. The hospital with the highest number of ICD implants among hospitals in South Bend was Memorial Hospital of South Bend (hospital ID: 150058), where 60 patients received ICDs and 58% were evidence-based. The density of St. Mary Medical Center was 0.41 and the average degree of all of the physicians within this hospital was 30. The density of Memorial Hospital was 0.19 and the average degree of all physicians within this hospital was 30. These metrics demonstrate that, on average, physicians share at least one patient with a relevant cardiovascular diagnosis with 30 other physicians in their hospital. This supports the observation that a larger network does not necessarily lead to an increase in the average degree of physicians, certainly not a linear increasing trend. Thus, larger networks tend to have lower density.

Fig. 3.

(A-B) Network of physicians at ICD hub hospitals. The patient-sharing practices of physicians at St. Mary Medical Center (A) and Memorial Hospital (B) are shown. Nodes represent physicians and are colored by specialty and sized by degree. Edges are weighted by the number of shared patient visits between the physicians. For a cleaner graph, edges with a weight of one were not visualized. (C-D) The correlations, presented as percentages to conserve space, between centrality measures calculated from the within-hospital or the broader within-HRR networks for physicians at St. Mary Medical Center (C) and Memorial Hospital (D) are shown

Homophily by attributes describes the tendency of individuals to form ties with those who are similar to them. ERGMs were used to examine differential homophily of physicians by specialty within each hospital adjusting for the network's density (e.g., edges) and degree distribution (e.g., altkstar). For doctors assigned to St. Mary Medical Center, pairs of physicians were more likely to be tied if their specialties were cardiology (est = 2.772, p < 0.0001) or emergency medicine (est = 1.702, p < 0.0001) and less likely to be tied if the specialties were family practice (est = −1.834, p < 0.0001) (Table 3). The pairs of physicians in Memorial Hospital were more likely to be tied if their specialties were cardiology (est = 2.662, p < 0.0001) or emergency medicine (est = 3.084, p < 0.0001), and less likely to be tied if their specialties were family practice (est = −1.547, p < 0.0001) (Table 3). The set of ERGM adjusted homophily coefficients were specified by Hosp in Equation 3 and were not found to be statistically associated with evidence-based ICD use. The effect of receiving care in South Bend remained a negative predictor of evidence-based ICD therapy (β₁ = −1.099, p = 0.022).

Table 3.

ERGM adjusted homophily effects within St. Mary Medical Center and Memorial Hospital.

	St. Mary Medical Center (150034), Gary			Memorial Hospital (150058), South Bend
	Estimate	Std Err	p-value	Estimate	Std Err	p-value
Edges	−23.030	2.088	<0.001	−20.298	0.889	<0.001
Altkstar	3.876	0.351	<0.001	3.286	0.150	<0.001
Cardiology	2.772	1.026	0.007	2.662	0.475	<0.001
Family Practice	−1.834	0.255	<0.001	−1.547	0.096	<0.001
Internal Medicine	−0.398	0.339	0.241	0.208	0.182	0.255
Emergency Medicine	1.702	0.408	<0.001	3.084	0.466	<0.001
Other specialty	−1.004	0.142	<0.001	−1.245	0.129	<0.001

Note. ERGM adjusted coefficients for the network's density (edges), degree distribution (altkstar), and homophily effects by specialty are listed for the two ICD hub hospitals. Specialties included in the “other” category did not achieve an estimable effect when included as an independent specialty. The set of ERGM adjusted homophily by specialty estimates in these models were included in Equation 3 as hospital-level covariates.

3.3 Centrality of physicians within hospitals

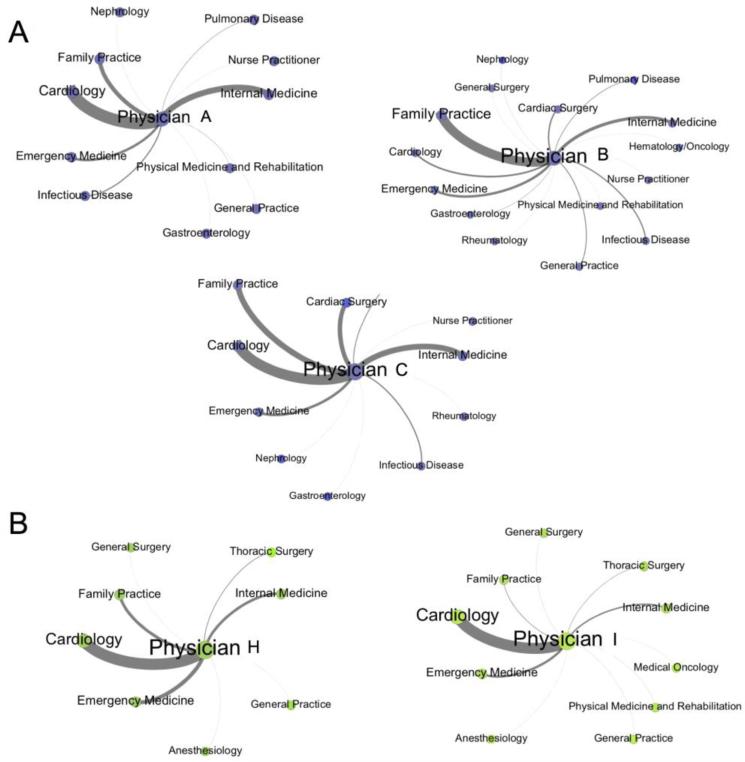
We are interested in examining whether the network position and direct connections of the cardiologists who implanted at least one ICD in 2008, herein referred to as “ICD capable physicians”, is associated with rates of evidence-based ICD use, as they are likely key determinants in the decision of whether or not a patient is selected for ICD surgery. These physicians were identified as the corresponding physician indicated on the associated claims/files: those with CPT code 33249 in Medicare Part B/outpatient or those with the ICD-9 codes 222-227 in the inpatient/Medpar files. There were a total of 14 physicians identified to be ICD capable in these two HRRs (Table 1). St. Mary Medical Center had 3 ICD capable physicians, and Memorial Hospital had 2 ICD capable physicians. The ICD capable physicians in each of these hospitals are labeled with letters (Fig. 3). ICD capable physicians tended to have strongly weighted ties with cardiology and cardiac surgery, consistent with the high estimated homophily effects of cardiologists obtained from the ERGMs (Fig. 4). Next, we calculated the centrality measures for the physicians within each network. The ICD capable physicians in St. Mary Medical Center and Memorial Hospital were in the top quartile for degree and node strength (Table 4), indicating that they are central in the patient-sharing network in terms of the number and strength of direct connections to other physicians in both hospitals.

Table 1.

Evidence-based ICD implantation in the two HRRs.

Hospital	HRR	No. Providers in Network	No. ICD capable physicians (labels)	No. ICD procedures	Rate of evidence-based ICD implantation
150034	Gary	74	3 (A,B,C)	85	0.84
150035	Gary	111	1(D,E)	27	0.85
150002	Gary	133	2 (F)	Not reportable	Not reportable
150015	Gary	61	0	0	0
150102	Gary	14	0	0	0
150126	Gary	88	2 (G)	0	0
150058	SB	155	2 (H,I)	60	0.58
150018	SB	126	2 (J,K)	15	0.73
150012	SB	163	1 (L)	Not reportable	Not reportable
150026	SB	70	1(M)	Not reportable	Not reportable
150076	SB	30	0	Not reportable	Not reportable
150006	SB	76	0	0	0
151300	SB	6	0	0	0
151313	SB	13	0	0	0

Note: A physician can perform ICD surgeries at more than one hospital, and thus some hospitals without an assigned ICD capable physician will have a count for ICD surgeries. The letters A-M represent the ICD capable physician assigned to that hospital. SB: South Bend, IN. Hospitals with between 1 and 10 ICD procedures are not reportable to protect patient confidentiality.

Fig. 4.

Ego-centric graphs of ICD capable physicians. The ICD capable physicians at St. Mary Medical Center (A) and Memorial Hospital (B) are shown. The physicians tied to each ICD capable physician are aggregated by specialty. The nodes are sized by the number of physicians within each specialty, and the edges are weighted based on the number of shared patient visits between the physicians

Table 4.

Network measures of ICD capable physicians in hub hospitals.

	St. Mary Medical Center (150034), Gary				Memorial Hospital (150058), South Bend
	A	B	C	hospital average (1st Qu, 3rd Qu)	H	I	hospital average (1st Qu, 3rd Qu)
Degree	58	58	54	30 (16, 46)	83	77	30 (17, 227)
Node strength	2194	2195	1345	651 (74, 782)	605	1149	297 (16, 337)
Betweenness (weighted)	32.5	9.5	8.5	56.3 (4, 94)	796.9	337.3	123 (4, 173)
Closeness (weighted)	0.004	0.003	0.004	0.004 (0.004, 0.004)	0.002	0.002	0.002 (0.002, 0.002)
Eigenvector (weighted)	0.23	0.16	0.14	0.07 (0.007, 0.09)	0.03	0.22	0.03 (0.001, 0.03)
Clustering Coefficient (weighted)	0.56	0.56	0.61	0.79 (0.67, 0.90)	0.41	0.46	0.73 (0.62, 0.86)
% ICDs that are evidence-based	82	100	84	84	73	55	58

Note: Network measures for each ICD capable physician and the average, 1^st, and 3^rd quartile of all physicians in the ICD hub networks are shown. Physicians A, B, and C are from St. Mary Medical Center (83.5% evidence-based ICD implantation) and Physicians H and I are from the Memorial Hospital (58% evidence-based ICD-implantation).

We analyzed the effects of node strength and closeness, betweenness, and eigenvector centrality measures of ICD capable physicians on evidence-based ICD use (Equation 4) and found adjusting for these network measures reduced the effect of receiving care in the South Bend HRR on evidence-based ICD use (β₁ = −0.275, p = 0.67). The node strength of ICD capable physicians was the only physician centrality measure to show a statistically significant (positive) association with evidence-based ICD therapy (est = 0.001, p < 0.05). The significance of node strength was dependent upon the inclusion of weighted closeness centrality in the model.

Finally, we estimated combined models which included predictors reflecting physician's position in their hospital network, the features of the hospital network, and the position of the hospital in the network of hospitals within their HRR in a model of evidence-based ICD implantation as specified by Equation 1 (Box 2). First, we found that adjusting for ICD capable physician centrality and hospital closeness centrality reduced the effect due to HRR (β₁ = −0.677, p = 0.17) (Table 5). Second, we found that including as a covariate the hospital ERGM adjusted homophily coefficient that had the largest estimate for evidence-based ICD use (family practice) in addition to physician and hospital centrality reduced the effect of HRR on evidence-based ICD use (Table 5). Overall, including ICD capable physician node strength and closeness centrality as covariates without hospital-level centrality measures in the patient-level analysis had the largest impact on reducing the HRR effect on evidence-based ICD therapy, suggesting that differences in ICD capable physician centrality between HRRs may be an explanatory factor for the variation in guideline-supported care delivery.

Table 5.

Models of association between HRR and evidence-based ICD use with various adjustments for network centrality and network other measures.

	Estimate	Std. err.	p-value
HRR (South Bend) without adjusting for network measures	−1.09	0.306	<0.0001

	Estimate	Std. err.	p-value
HRR (South Bend)	−0.677	0.494	0.171
Physician node strength	0.005	0.003	0.050
Physician weighted closeness centrality	0.157	0.264	0.551
Hospital weighted closeness centrality	0.384	0.286	0.178

	Estimate	Std. err.	p-value
HRR (South Bend)	−0.825	0.618	0.182
Physician node strength	0.005	0.003	0.096
Physician weighted closeness centrality	0.136	0.307	0.656
Hospital weighted closeness centrality	0.637	0.713	0.372
Family practice homophily	−0.252	0.410	0.539

Note: The model estimates, standard errors (std. err.) and p-values for models adjusting only for patient characteristics (top), and then also for physician and hospital centrality (middle) and physician and hospital centrality and family practice homophily (bottom) are shown.

4 Discussion

This work provides an illustrative example of how classic and modern network analyses can be used to describe the organization of physicians and hospitals within geographic regions, and how they may influence evidence-based ICD implantation. With this case study, we ascertained the structure of complex networks by performing detailed contextual analyses. We showed how edges at varying levels of aggregation, namely, between physicians and between hospitals can represent two distinct but related aspects of patient sharing practices within an HRR. By generating centrality measures of hospitals within their HRR, estimates of homophily by specialty within hospitals, and centrality of physicians within their hospital network, we were able to examine whether these various summaries of network structure were associated with evidence-based ICD therapy. Our results suggest that differences in evidence-based ICD use observed between the two HRRs may be driven by differences in physician network structure, specifically node strength and closeness centrality of the ICD capable physicians, a finding and line of inquiry which has not yet been investigated in the literature. A diminished effect of the HRR demonstrates that previously unobserved measures that relate to the positions of providers within their hospital networks may account for some of the variation in evidence-based ICD therapy observed across the geographic regions.

In this work, we chose the simplest approach for characterizing within-guideline ICD therapy by selecting those heart failure patients with NYHA Class II or III symptoms and LVEF ≤ 35%. In using these rules, we are more conservative than previous studies that place more requirements on within-guideline patients, for example that they had been diagnosed with CHF for at least 3 months. (Al-Khatib et al. 2011). We recognize that under certain clinical conditions, it may be appropriate to prescribe ICD therapy to a patient who is out-of-guidelines (for example if they are getting a replacement ICD but in the meantime their health has improved), so our out-of-guideline measure is not the clinical gold standard. However, it is unlikely that the wide differences we observe between our two sample regions can be explained by such differences.

It is not yet well understood whether patients’ quality of care is more affected by the physicians who attend to them or the institutions at which they receive care. Here we develop and describe a multi-faceted statistical design and methodology for addressing whether the answer to this question is provided by physician networks. The case study demonstrates that network structure, and measures of relationships between physicians, may be a driving factor for differences in care observed between geographic regions. The influence of node strength, or increased patient sharing with a higher number of physicians in the networks, of ICD capable physicians on greater adherence to ICD guidelines warrants further study. One hypothesis of interest is whether ICD capable physicians who have more clinical encounters with a greater number of patients receiving care from their connections in the network are more discriminating in which patients receive the surgery out of necessity and therefore are more likely to follow clinical guidelines.

This work also provides an example of approaches to weighting edges between actors in a network and how centrality measures are calculated for weighted networks. It is important for researchers constructing physician networks to consider how they are planning to interpret edges between physicians, which will help guide their strategy regarding if and how they weight edges or aggregate dyads. Aggregating dyads by hospital results in loss of information regarding physician-level variation in network measures, but it has the advantage of reducing the total number of nodes in the network, making visualization of the entire network more feasible and interpretable. This approach would be useful for illustrating the implementation and diffusion of a new practice or technology across a network of hospitals.

In conclusion, this novel compendium of methods for network construction and applications of network methodology has the potential to yield insights about latent phenomena, such as organizational traits of hospitals and structural importance of physicians, for which we do not have direct observations (Lurie et al. 2009). This approach holds promise in identifying new aspects of regional differences in health care delivery and diffusion of appropriate (or inappropriate) application of new technologies and health care practices. Network measures have widespread application across disciplines that relate to the diffusion of knowledge. For example, eigenvector centrality measured by Google PageRank, is a tool that has had a substantial influence on the information most readily available through a web-based search (Brin and Page 1998). By providing precise mathematical definitions, graphical illustration, and supporting intuition, we hope to have provided a similar starting point for future work in network analysis, to help policy-makers better understand the complex networks of hospitals and physicians, and help investigators to better target interventions.

Box 1.

Approaches to weighting and aggregating dyads in complex patient-sharing physician networks.

Problem	Approach
Weighting edges between physicians	Number of shared patients
	Volume of shared patient visits
	Volume of shared relative value units
Aggregating edges between hospitals	Sum of all physician dyads weights spanning pairs of hospitals
	Volume of unique patients with clinical encounters at each pair of hospitals
	Sum of physician dyads bridging pairs of hospitals

Note: Each approach for weighting and aggregating may be more or less appropriate depending upon the study design and research questions. In this work, edges between physicians were weighted by the volume of shared patient visits, and edges between hospitals were aggregated by summing the physician dyad weights spanning each pair of hospitals.

Box 2.

Physician and hospital network metrics included in combined model for predicting evidence-based ICD utilization.

Unit	Metric	Interpretation
Hospital	Closeness centrality	The efficiency at which patient-sharing ties connect the hospital to all other hospitals in their network
	Homophily coefficient by family practice	The likelihood of sharing patients among family practice physicians
ICD capable physician	Node strength	The number of clinical encounters a provider has with patients who are cared for by his/her patient-sharing connections in the hospital network
	Closeness centrality	The efficiency at which patient-sharing ties connect the ICD capable physician to all other providers in the hospital network

Note: The network metric(s) that had the largest effect within each category (even if it did not reach statistical significance of p<0.05) was included in the combined model to demonstrate how various network metrics can be used as predictors in models of evidence-based care.

Appendix

The centrality measures discussed herein can be calculated for unweighted and weighted networks. We specify the descriptions for weighted networks to reflect our use of a weighted network. Unweighted counterparts can be derived by simplifying the weighted measures in the case when all the weights equal 1. The unweighted measures are presented or described explicitly below when they have a particularly intuitively interpretable form.

The weighted closeness centrality (C^wc) is the inverse of the total weighted geodesic distance from a node to all other nodes in the network. Thus, if $g_{ij}^w$ denotes the weighted geodesic distance from node i to node j, it follows that

$$C_i^{wc}=\frac{1}{{\sum }_{j=1}^N{g}_{ij}^w}$$

Closeness centrality measures both the direct and indirect connections of node i to quantify its closeness to all other nodes in the network. Therefore, if node i has smaller geodesic distances than all other nodes, it is considered most central in the network and subsequently will have a larger centrality measure. Multiplying $C_i^{wc}$ by N – 1 yields the inverse of the average geodesic distance of node i to the other nodes and is the measure used herein. If $g_{ij}^w=\infty$ for any nodes j ≠ i then $C_i^{wc}=0$. For studies interested in computing closeness centrality for a network containing multiple components, or subnetworks of nodes with no connecting dyads between them, a common practice is to use the largest connected component of the network (the set of nodes for which a finite length path exists between every pair of nodes) to compute closeness centrality and other network measures that depend on distance measures between nodes.

The weighted betweenness centrality (C^wb) measures the relative frequency with which node i appears on the weighted geodesic path between all two pairs of nodes (j, k) such that j ≠ i and k ≠ i. A standardized measure of betweenness centrality is obtained by dividing the relative frequency by the total number of geodesic paths that could have included the focal node, yielding the measure:

$$C_i^{wb}=\frac{2{\sum }_{i<j}^N{\sigma }_{jk\left(i\right)}∕{\sigma }_{jk}}{(N-1)(N-2)}$$

where 0 ≤ σ_jk(i)/σ_jk ≤ 1 is the sum of the weights along the weighted geodesic paths between nodes j and k that pass through node i, denoted σ_jk(i), divided by the sum of the weights along all of the weighted geodesic paths between nodes j and k, denoted σ_jk. If there is a unique weighted geodesic path between nodes j and k then ${\sigma }_{jk}=g_{jk}^w$ and the numerator of $C_i^{wb}$ reduces to a binary indicator variable.

Eigenvector centrality (C^e) represents the importance of a node based on the importance of the nodes it shares edges with. Let C denote a vector of centrality values defined such that the centrality of node i, denoted, $C_i^e$ is proportional to a linear combination of the centrality of the nodes with whom node i is directly connected, implying the mathematical relation

$$C_i^e\propto {\sum }_{j=1}^N{W}_{ij}{C}_j\text{for}i=1,\dots ,N,$$

where W is the weighted adjacency matrix (equal to A for binary networks). Therefore, the eigenvector centrality measure satisfies the matrix equation WC = λC, which is immediately recognized as being equivalent to the characteristic equation whose solution yields the eigenvalues and eigenvectors of W. Intuitively, the solution that best discriminates between the nodes’ positions in the network is the eigenvector associated with the principal (largest) eigenvalue of W, representing the axis along which most of the variability in W occurs. Furthermore, because A is real-valued and square, the Perron-Frobenius theorem implies that the eigenvector associated with the largest unique eigenvalue of W contains only positive elements thereby yielding a quantity suitable for use as a centrality measure (Ruhnau 2000). Weighted eigenvector centrality $W{C}_i^e$ for node i is therefore defined as the ith element of the vector WC^e that solves the equation:

$$W{C}^e={\lambda }_{max}{C}^e,\text{where}{\lambda }_{max}=ma{x}_{\lambda }\{\lambda :W{C}^e=\lambda C^e\}.$$

The generalization of eigenvector centrality to a weighted network is still the leading eigenvector of the adjacency matrix, but ties that are valued at twice the weight will contribute twice as much to the vertex's eigenvector centrality (Newman 2004). Compared with closeness and betweenness centrality measures, eigenvector centrality is more informative for binary-valued networks when centrality is driven by differences in degree, and it is more informative in situations where a high degree node is tied to many low degree nodes or vice versa (Bonarich 2007).

Another important network measure is network clustering. The clustering coefficient is a measure of how complete the neighborhood of the node is (Latapy et al. 2008) and does not directly involve the focal node nor its edges. The igraph package uses the weighted clustering coefficient as defined by Barrat (2004):

$$ClustCoe{f}_i^w=\frac{1}{d_i^w(d_i-1)}\sum _{j,k}\frac{(w_{ij}+w_{ik})}{2}{a}_{ij}{a}_{ik}{a}_{jk}\left(\text{for weighted networks}\right)$$

where $d_i^w$ is the strength of node i, d_i is the degree of node i, w_ij is the weight of the edge between nodes i and j, and a_ij are elements of the adjacency matrix. The unweighted counterpart to this can be calculated intuitively with the following definition:

$$ClustCoe{f}_i=\frac{t_i}{d_i(d_i-1)}\left(\text{for binary networks}\right)$$

In the case of a binary-valued network, the clustering coefficient reduces to the ratio of the number of triangles (or closed triads) involving node i, denoted t_i, divided by the number of two-paths with node i at the apex (a “two-star”), denoted d_i(d_i – 1). In other words, ClustCoef_i is the ratio of the sum of the weighted products over the closed triads to the sum of the weighted products over all open or closed triads with respect to node i (the weighted products reduce to binary indicators in the case of binary networks). A network with a high level of clustering implies if nodes i and j have highly weighted edges to node k, it is more likely i and j will also have highly weighted edges (or have ties in a binary network) than in a network with little clustering.