Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Apr 12;120(17):9276–9281. doi: 10.1021/acs.jpcc.6b01659

Free Energy of Ligand Removal in the Metal–Organic Framework UiO-66

Jessica K Bristow †, Katrine L Svane †, Davide Tiana †, Jonathan M Skelton †, Julian D Gale ‡,*, Aron Walsh †,∥,*
PMCID: PMC5010357  PMID: 27610208

Abstract

graphic file with name jp-2016-016595_0005.jpg

We report an investigation of the “missing-linker phenomenon” in the Zr-based metal–organic framework UiO-66 using atomistic force field and quantum chemical methods. For a vacant benzene dicarboxylate ligand, the lowest energy charge-capping mechanism involves acetic acid or Cl–/H2O. The calculated defect free energy of formation is remarkably low, consistent with the high defect concentrations reported experimentally. A dynamic structural instability is identified for certain higher defect concentrations. In addition to the changes in material properties upon defect formation, we assess the formation of molecular aggregates, which provide an additional driving force for ligand loss. These results are expected to be of relevance to a wide range of metal–organic frameworks.

Introduction

Metal–organic frameworks (MOFs) are materials formed via the coordination of metal centers and organic linkers in three dimensions. The varied chemical compositions and structural topologies of MOFs make them suitable for a broad range of applications including gas storage and separation, solar energy conversion, and heterogeneous catalysis.1−6

One MOF that has attracted particular attention is UiO-66 (Figure 1), which was first synthesized by Cavka et al.7 This material features a high coordination of 12 benzene-1,4-dicarboxylate (BDC) ligands around each ZrIV node and is thermally stable up to 813 K.8 The internal surface area (800 m2 g–1) is large with the structure containing both tetrahedral and octahedral cages. Each octahedral cage is edge-sharing with eight tetrahedral cages and face-sharing with eight octahedral cages.9 The inner-sphere coordination of Zr in UiO-66 is 6, but additional face-sharing oxide and hydroxide ligands lead to an outer-sphere coordination of 12.

Figure 1.

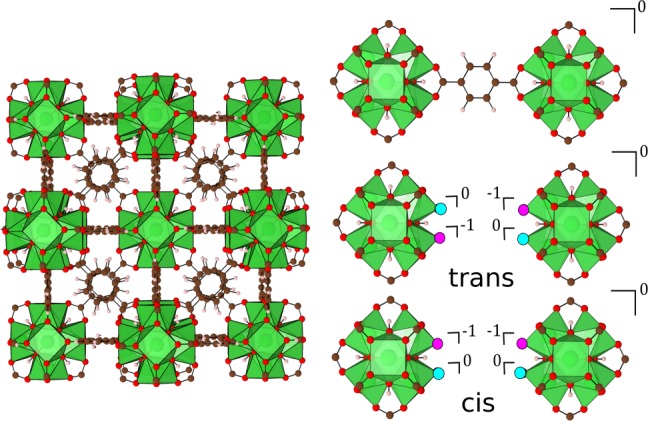
Figure 1

Open in a new tab

Crystal structure of UiO-66 (left) and locations on the metal node where charge compensating or neutral molecules can bind following BDC linker removal (right). The locations of charge compensating molecules are highlighted in maroon and neutral molecule locations are highlighted in black. Top right shows the BDC linker connection between Zr-metal nodes prior to removal. Centre and bottom right shows the locations considered for charge compensating molecules following linker removal.

Wu et al. and Vermoortele et al. reported a significant internal surface area increase for UiO-66 synthesized with an acidic modulator such as acetic or hydrochloric acid.10,11 This phenomenon, leading to increased gas storage capabilities with little stability loss, has been attributed to a missing BDC linker from the unit-cell, with a subsequent reduction in coordination of the Zr metal.9,12,13 The acid modulator has been shown to promote linker removal.10 Recent reports have focused on the charge-capping mechanism following the removal of the linker. Experimental evidence, such as quantum tunnelling peaks in inelastic neutron scattering, associated with terminating methyl groups, suggest acetic acid becomes incorporated into the framework.11 The incorporation of Cl– ions when using HCl has also been suggested.14 Considering that an excess of ZrCl4 is often used during synthesis and that experimental conditions do not completely exclude water, there is an abundance of potential charge-capping ions.

NU-100015 is a structurally similar Zr-containing MOF, which is often compared to UiO-66. The Zr node in NU-1000 has the formula [Zr6(η3-O)4(η3- OH)4(OH)4(H2O)4]8+ and in UiO-66 has the formula [Zr6(η3-O)4(η3–OH)4]12+. The additional incorporation of four hydroxide and four water molecules in NU-1000 is due to the use of ZrOCl2 as the Zr precursor source, as opposed to the ZrCl4 precursor used to synthesize UiO-66.15−17

The fraction of BDC linkers missing from UiO-66 is highly debated. Reports vary from 1–4 vacancies per metal node depending on synthesis conditions; however, all measurements are indirect (e.g., thermogravimetric analysis) and usually yield an average over a large sample volume. Regardless of the method employed, it is clear that the defect concentrations are high and beyond those typically found in crystalline materials.

In this paper, we investigate the free energy of formation of missing ligand defects in UiO-66 using a combination of first-principles and molecular mechanics computational techniques. We consider a range of charge compensating schemes involving commonly used species. The results validate recent experimental observations of high defect concentrations and reveal a thermodynamic driving force for defect aggregation in the UiO-66 system.

Methodology

The predictive power of computational chemistry applied to metal–organic frameworks is well established.18−23 Here, we combine empirical and first-principle methods. The analytical force field calculations allow us to probe large and complex defect structures including vibrations and hence calculate the Gibbs free energy of ligand removal. The higher-level density functional theory calculations provide a means of validation, while also giving an estimation of solvation and cluster energies for reaction products that are challenging to compute using empirical interatomic potentials.

Force-Field Calculations

We have considered the cubic unit cell of UiO-66, which contains 24 linkers and 4 metal nodes. Force-field calculations were performed with GULP.24,25 Parametrisation of the interatomic potential was conducted to recreate the structural and material properties of nondefective UiO-66, including bond lengths, bond angles, phonon frequencies, bulk modulus, and elastic constants. The details of the force field and a comparison of the predicted structure of UiO-66 against experimental data is given in the Supporting Information (SI). The bulk and defective structures were first optimized with respect to the internal energy, and then the free energy of the final structure was calculated including the vibrational entropy. For all defect reactions considered, reactants and products were optimized at constant external pressure, thus providing the Gibbs free energy (ΔG) of reaction.

Density Functional Theory Calculations

Reference solid-state density functional theory (DFT) calculations on the pristine and defective structures of UiO-66 were performed using VASP.26 These periodic DFT calculations were to provide high-quality fitting data for the force field and to validate the defect structures. The PBEsol functional27 was used with a plane-wave cutoff of 600 eV and wave functions were calculated at the Γ-point of the Brillouin zone. Projector augmented wave potentials were used to model the interaction between valence and core of all atoms with 4d25s2 as the valence configuration of Zr. Internal forces were converged to less than 0.005 eV/Å. The optimized unit-cell parameters from PBEsol/DFT (a = 20.80 Å and α = 90.0°) reproduce the experimental structure (a = 20.98 Å and α = 90.0°) of UiO-66 to within 1%. Comparisons of the crystal structures produced by DFT and force field methods are given in the SI.

Free energies of solvation for molecular fragments in DMF (dimethylformamide) were calculated with the continuum solvation model, COSMO, in NWChem28 (cc-pVTZ basis set).29,30 The self-consistent field energy convergence was set to 10–6 Ha and the M06-2X functional,31,32 which is known to produce accurate thermodynamic properties, was used to obtain geometries. In the solvation model, we used the temperature-dependent experimental dielectric constant of DMF, as reported by Bass et al.33 Other thermodynamic quantities, such as the energy of protonation of BDC, were taken from the NIST database.34 Finally, molecular cluster binding energies were calculated with the B3LYP functional.35 This approach gives a good description of hydrogen bonding interactions at low computational cost. The dielectric constant of DMF at 300 K was used. A single point counterpoise correction for the basis set superposition error (BSSE)36 was calculated on the converged cluster geometries.

Results

Charge-Capping Mechanism

For a balanced defect reaction, conservation of charge and mass is required. Acetic acid (CH3COOH) and/or HCl are commonly used as acidic modulators to promote linker removal from the structure. In addition, the commonly used solvent, DMF, and also H2O can be incorporated. The removal of one BDC linker results in a system with an overall +2 charge and reduces the coordination sphere of 4 Zr centers from 12 to 11. We consider seven capping mechanisms for charge compensation and stabilizing the structure by saturating the coordination of each metal center with a neutral molecule (Table 1).

Table 1. Charge Compensation Models for a Missing Linker from UiO-66a.

  charged
  
model precursor anion neutral
1 HCl Cl–  
2 HCl Cl– H2O
3 CH3COOH CH3COO–  
4 H2O OH–  
5 H2O OH– H2O
6 H2O OH– DMF
7 HCl Cl– DMF
Open in a new tab
a

Given are the charge compensating molecules coordinated onto the two Zr centers, the precursors, and the neutral molecules included in some models to saturate the Zr coordination spheres.

There are two choices for adding the charge-capping and neutral molecules into the structure, labeled as trans and cis in Figure 1. We find the lowest energy arrangement for trans substitution, which can be understood from simple electrostatics, as it maximizes the distance between the charge-capping species, and also steric effects. All results refer to the most stable (trans) configuration.

Defect Formation Energies

The defect free energies as a function of temperature, calculated using mass and charged balanced chemical reactions, are given in Figure 2. The charge compensating models are detailed in Table 1 and full reactions are listed in the SI. The reaction energy is sensitive to the charge compensation model. The inclusion of OH– as a binding ligand is particularly unfavorable. The higher calculated defect energy associated with OH– is due to the energy required to split its precursor (water) in DMF as a solvent.

Figure 2.

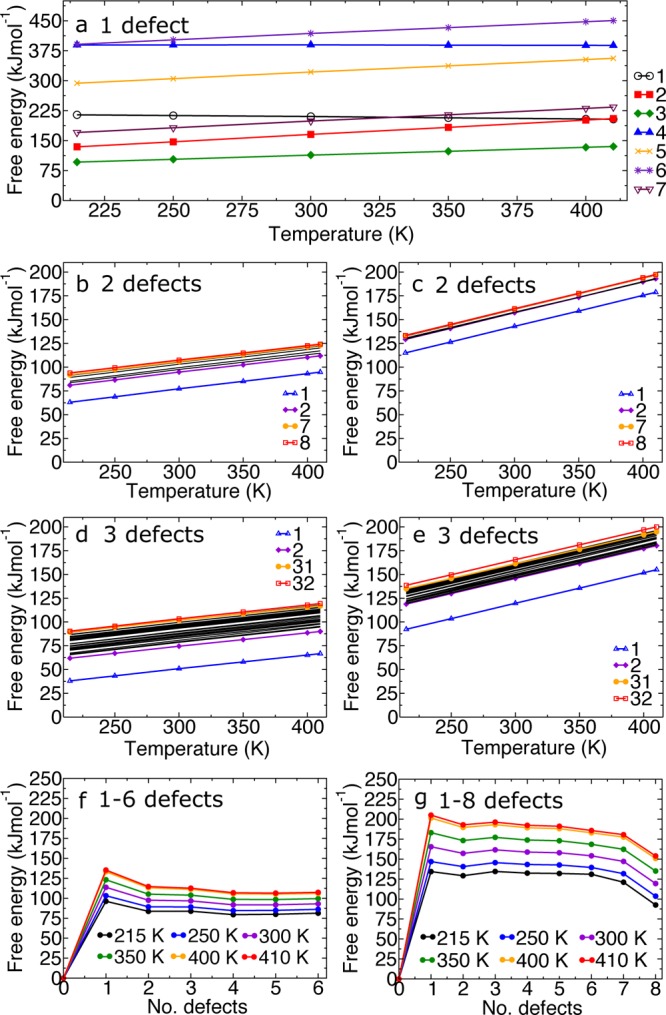
Figure 2

Open in a new tab

Free energy of defect formation for (a) a single vacancy with a range of capping models (labeled 1–7 corresponding to Table 1). (b,c) Two vacancies with acetate and Cl–/H2O capping models. Highlighted are the two lowest and highest energy configurations, all other configurations are shown as black lines. (d,e) Three vacancies with acetate and Cl–/H2O capping models. (f,g) removal of 1–8 ligands for the CH3COO– and Cl–/H2O charge-capping models toward the formation of the ordered vacancy NU-1000 type configuration. All energies are presented per defect and include contributions from the vibrational internal energy and entropy.

The charge-capping mechanisms that had the lowest associated formation free energy were with acetic acid and Cl–/H2O. The acetic acid cap was optimized from multiple initial configurations. In each case, the CH3COO– ligand converged to a structure with bidentate coordination and identical bond lengths. Little structural distortion or loss of symmetry occurs to the framework of UiO-66 with the incorporation of acetic acid due to it possessing an identical headgroup to BDC. Slight losses of symmetry calculated when using CH3COO– as the charge-capping ion are due to the loss of a mirror plane from the introduction of the methyl group. It is therefore the similarity between the chemical structure and solvation energies of the BDC and acetate head groups that makes acetic acid the lowest energy charge-capping mechanism in UiO-66.

Interestingly, we found that binding a Cl– ion with a neutral molecule had a much lower energy than binding only Cl– ions. Following the insertion of a monodentate charge-capping ion alone we observed it bridging between two neighboring Zr centers. When water/DMF were introduced, such that the Zr centers remained fully coordinated, the defect energy was lowered. This confirms, as expected, that an undercoordinated metal center is energetically unfavorable. Our findings also suggest that a small concentration of water during synthesis may increase the number of linker vacancies within the material. We found the effect of coordinating DMF as a neutral molecule to have little influence on the defect energy. It can be seen that when comparing the energies for single Cl– and Cl–/DMF substitution, DMF, as a neutral coordinating molecule, lowers the defect energy of removing one BDC linker. Note that between 350–400 K, the energies of the respective charge-capping mechanisms cross and the single Cl– model becomes more favorable than the Cl–/DMF model, suggesting DMF coordination to be unfavorable at high temperatures.

Multiple Ligand Vacancies

Taking the lowest energy charge-capping mechanisms (CH3COO– and Cl–/H2O), as identified in Figure 2a, we further investigated the defect energies associated with the removal of additional BDC ligands. We present the defect energies for each of the symmetry unique locations of 2 BDC removals in Figure 2b,c. The details of these configurations are given in the SI. The lowest energy configurations are identified to occur when removing linkers from the faces of the same tetrahedral cage, which also form the vertices of the central octahedral cage. The most favorable position renders one metal node as 10 coordinate and two other metal nodes as 11 coordinate.

For the removal of three BDC linkers, we calculate 32 symmetry unique configurations in a single unit cell. We have calculated the defect formation energy of all configurations for the lowest energy charge-capping mechanisms (CH3COO– and Cl–/H2O), Figure 2d,e. Each configuration is numbered in order of increasing magnitude of the defect energy, (i.e., configuration 1 has the lowest energy and configuration 32 has the highest). We find a broader distribution of defect energies for the acetate capping than for Cl–/H2O. We observe the short-range structural disorder in the acetate configurations, where the acetate molecule points into the pore and does not stay in planar alignment, to be larger with clustered defects due to local interactions and a loss of symmetry. Configuration 1 has the lowest defect energy by 23.8 and 26.5 kJmol–1 for the acetate and Cl–/H2O capping, respectively, when compared to configuration 2. This configuration corresponds to three BDC linkers being removed from the same tetrahedral cage within the structure with strong local interactions between the defects. In contrast, the highest energy configurations feature parallel vacancies that create a long-range structural instability.

Beyond three ligands, there is a combinatorial explosion and we become limited by our simulation cell size. However, we have considered some representative configurations. For acetic acid, removing four ligands equating to two BDC linkers per metal node has no significant energy penalty (Figure 2f). This result agrees, at least qualitatively, with experiment in that a large increase in surface area can be obtained by using acetic acid as a modulator to remove linkers from the structure. The removal of five and six linkers from the unit cell results in a small increase in defect energy per linker removal before phonon stability and therefore structural integrity is lost with the removal of 7–8 linkers for acetic acid compensation. For Cl–/H2O (Figure 2g), there is a reduction in energy per defect when removing 7 and 8 BDC linkers (i.e., 3.5–4 linkers per metal node), together with a phase change from cubic to monoclinic symmetry, which occurs in a similar manner to the breathing motion of “winerack” MOFs. There is also an increased structural flexibility due to the high number of vacant ligand sites. The predicted phase change occurs at a very high concentration of defects and so may not be experimentally observable. Simulated powder X-ray spectra are given in the SI.37 The symmetry reduction to monoclinic does not happen in the case of the acetic acid charge cap, because this is a bidentate ligand and the structural integrity of the cubic phase is maintained.

A Boltzmann distribution for two and three linker vacancies shows that 99% of defects will be clustered at 300 K for the acetate and Cl–/H2O, respectively. Under equilibrium conditions, a distribution of isolated vacancies is unlikely and a dominant preference for clustered vacancy motifs would be expected, which is consistent with recent X-ray scattering analysis.38 Furthermore, the dynamic nature of charge capping, including rapid proton transfer has been suggested from very recent simulation studies.500

Ordered Defect Structure

A further simulation was performed for the OH–/H2O charge-capping system with 8 linkers missing from the cubic unit cell. This corresponds to the node structure of NU-1000, a MOF synthesized from a different Zr precursor. As an analysis of the energy required to form this structure, we repeat the removal of 1–8 linkers in the same manner as previously performed but instead for the OH–/H2O charge capping. The final structure is equivalent to NU-1000 and was constructed along the highest symmetry path (the same path as was followed for the acetate and Cl–/H2O charge capping). Interestingly, we do not see the same phase change as was observed with the Cl–/H2O capping; instead hydrogen bonding between the hydroxyl groups and water maintains the cubic symmetry with only small structural distortions. The defect energy associated with the formation of this structure (8 vacant linkers from the cubic unit cell) is similar to the cost of a single defect (see SI), highlighting the unusual tolerance of UiO-66 for high defect concentrations. We note that the defect energy for this charge capping considers the OH– capping source to be from the splitting of water. Synthesis methods for NU-1000 involve the use of a Zr–OH precursor, which offers an alternative OH– source. We therefore highlight the observed trend as being of interest rather than the specific energetics of ligand removal for making a NU-1000 type structure.

Molecular Association in Solution

Because of the high concentration of defects predicted for UiO-66, we should consider processes beyond the typical dilute limit of noninteracting defects. Cluster formation following the removal and subsequent protonation of BDC may occur both in the framework but also between the removed species in the solvent. Possible clusters that may form in solution are depicted in Figure 3. A strong binding energy of −104.7 kJmol–1 between two acetic acid molecules and one BDC-H2 linker has been calculated (Figure 3f).

Figure 3.

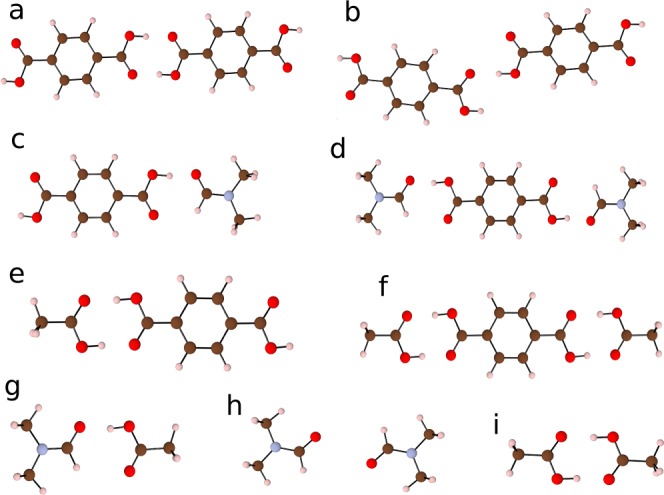
Figure 3

Open in a new tab

Equilibrium geometries of molecular clusters for which binding energies are given in Table 2.

Formation of molecular clusters in solution may provide an additional driving force for BDC linker to leave the UiO-66 framework when this acid is used as a modulator. Other clusters considered are shown to have a weaker binding energy between components (Table 2). Experimental evidence has been reported that even when synthesized without an acidic modulator UiO-66 can possess the missing linker defect at a low concentration. A contributing factor may be the strong calculated binding energy (−75.3 kJmol–1) between DMF and BDC-H2 (Figure 3d). The formation of this cluster can provide a thermodynamic driving force for a reduced number of linkers to be incorporated into the framework during the formation of UiO-66. The values reported are qualitative because hydrogen bonding between the solvent and molecule is not described in a continuum model. An explicit solvent model could provide a more accurate description of aggregate formation in future studies.

Table 2. Binding Energies (after BSSE Correction) of Molecular Clusters Shown in Figure 3 Formed Following Linker Removal from UiO-66 at 300 K (in DMF Solvent).

cluster       ΔE (kJmol–1)
a BDC BDC   –47.6
b BDC BDC   –22.5
c BDC DMF   –29.5
d BDC DMF DMF –75.3
e BDC CH3OOH   –52.8
f BDC CH3OOH CH3OOH –104.7
g CH3OOH DMF   –38.3
h DMF DMF   –4.7
i CH3OOH CH3OOH   –56.1
Open in a new tab

Spectroscopic Signatures

The volume of the crystal lattice is found to increase and bulk modulus to decrease for the majority of capping models (see Table 3). The single anion capping (Cl– and OH–) is an exception as the anion effectively bridges between two metal centers, taking less physical space than BDC, and the lattice volume decreases. The bulk moduli are all lower for the defect structures but remain within 5 GPa of pristine UiO-66.

Table 3. Structural and Mechanical Properties of Pristine and Defective UiO-66 with Different Capping Mechanisms Following the Removal of a Single BDC Ligand.

capping volume (Å3) bulk modulus (GPa)
UiO-66 9120 23.04
Cl– 9074 20.03
Cl–/H2O 9126 20.77
Cl–/DMF 9132 21.15
OH– 9092 20.19
OH–/H2O 9137 20.67
OH–/DMF 9138 19.98
CH3COO– 9148 20.60
Open in a new tab

A key question is whether the missing ligands have an observable spectroscopic signature. The simulated infrared (IR) spectra of 1–4 missing linkers for the two lowest energy charge-capping mechanisms (acetate and Cl–/H2O) are presented in Figure 4. We highlight several important features for the identification of either charge cap. First, for the acetate capping acetate peaks are evident at 1463 cm–1 and between 1583–1586 cm–1 due to the asymmetric and symmetric stretching of the C–O carboxylate bonds, respectively, which can be distinguished from the C–O carboxylate stretch of BDC, occurring between 1617 and 1650 cm–1. The C–H bond stretch of acetate occurs at 2900 cm–1, and the BDC C–H stretch at 2947 cm–1. Additional peaks between 720–994 cm–1 are associated with bending and twisting of the Zr node. Shoulder peaks are associated with the loss of symmetry at the Zr node, but are difficult to distinguish. For the Cl–/H2O charge cap, allocating specific frequencies is more difficult. As was the case for acetate, additional peaks between 500–900 cm–1 are present due to the reduction in symmetry of the Zr node (as evident for eight missing linkers in Figure 4). The Zr–Cl stretch is difficult to assign to one specific mode but occurs in the same frequency range as the Zr–O stretches between 582–612 cm–1. The most obvious difference for this system is the O–H bond stretch of water at 3378 cm–1 (see SI for the full spectral range and associated Raman spectra). The results suggest that high-resolution vibrational spectroscopy may provide the means to assign the local charge-capping mechanism and give insights into defect concentrations.

Figure 4.

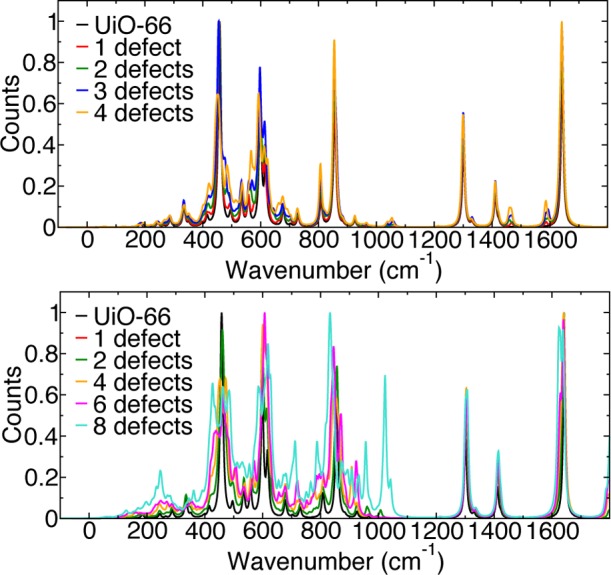
Figure 4

Open in a new tab

Simulated IR spectra for pristine and defective UiO-66 with acetate (1–4 missing BDC linkers) (top) and Cl–/H2O (1, 2, 4, 6, and 8 missing BDC linkers) (bottom) as the charge-capping mechanism. IR spectra are plotted between −200–1800 cm–1. A broadening factor of 10 cm–1 was applied.

Conclusion

From an analysis of the defect chemistry of linker removal in UiO-66, we conclude that the lowest energy processes are for acetate and Cl–/H2O charge-capping mechanisms. We show that H2O capping at high concentrations results in an ordered-defect structure consistent with the NU-1000 framework. A cluster between two acetic acid molecules and a protonated BDC linker is found to have a strong binding affinity and is a candidate product of ligand loss. The results are expected to be transferable to other UiO frameworks with relevance to a wider range of hybrid organic–inorganic solids.

Acknowledgments

J.K.B is funded by the EPSRC (EP/G03768X/1). J.D.G thanks the Australian Research Council for funding under the Discovery Program, as well as the Pawsey Supercomputing Centre and NCI for the provision of computing resources. A.W. acknowledges support from the Royal Society. D.T. and K.L.S. are funded under ERC Starting Grant 277757 and J.M.S is funded under EPSRC Grant EP/K004956/1. Access to the ARCHER supercomputer was facilitated through membership of the HPC Materials Chemistry Consortium (EP/L000202). Data access statement: the parameter files and input configurations used in this work are available from http://dx.doi.org/10.4225/06/570D936A4B86F.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.6b01659.

  • Further methodological and computational details including a full breakdown of the defect free energies, IR and Raman spectra, and force field parameters. (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp6b01659_si_001.pdf (3.9MB, pdf)

References

  1. Ma L.; Abney C.; Lin W. Enantioselective Catalysis with Homochiral Metal-Organic Frameworks. Chem. Soc. Rev. 2009, 38, 1248–1256. 10.1039/b807083k. [DOI] [PubMed] [Google Scholar]
  2. Liu J.; Zhou W.; Liu J.; Howard I.; Kilibarda G.; Schlabach S.; Coupry D.; Addicoat M.; Yoneda S.; Tsutsui Y. Photo-induced Charge-Carrier Generation in Epitaxial MOF Thin Films: High Efficiency as a Result of an Indirect Electronic Band Gap?. Angew. Chem., Int. Ed. 2015, 54, 7441–7445. 10.1002/anie.201501862. [DOI] [PubMed] [Google Scholar]
  3. Arstad B.; Fjellvåg H.; Kongshaug K. O.; Swang O.; Blom R. Amine Functionalised Metal-Organic Frameworks (MOFs) as Adsorbents for Carbon Dioxide. Adsorption 2008, 14, 755–762. 10.1007/s10450-008-9137-6. [DOI] [Google Scholar]
  4. Alvaro M.; Carbonell E.; Ferrer B.; Llabrés i Xamena F. X.; Garcia H. Semiconductor Behavior of a Metal-Organic Framework (MOF). Chem. - Eur. J. 2007, 13, 5106–5112. 10.1002/chem.200601003. [DOI] [PubMed] [Google Scholar]
  5. Hwang Y. K.; Hong D.-Y.; Chang J.-S.; Jhung S. H.; Seo Y.-K.; Kim J.; Vimont A.; Daturi M.; Serre C.; Férey G. Amine Grafting on Coordinatively Unsaturated Metal Centers of MOFs: Consequences for Catalysis and Metal Encapsulation. Angew. Chem., Int. Ed. 2008, 47, 4144–4148. 10.1002/anie.200705998. [DOI] [PubMed] [Google Scholar]
  6. Liu Y.; Eubank J. F.; Cairns A. J.; Eckert J.; Kravtsov V. C.; Luebke R.; Eddaoudi M. Assembly of Metal-Organic Frameworks (MOFs) Based on Indium-Trimer Building Blocks: A Porous MOF with soc Topology and High Hydrogen Storage. Angew. Chem., Int. Ed. 2007, 46, 3278–3283. 10.1002/anie.200604306. [DOI] [PubMed] [Google Scholar]
  7. Cavka J. H.; Jakobsen S.; Olsbye U.; Guillou N.; Lamberti C.; Bordiga S.; Lillerud K. P. A New Zirconium Inorganic Building Brick Forming Metal-Organic Frameworks with Exceptional Stability. J. Am. Chem. Soc. 2008, 130, 13850–13851. 10.1021/ja8057953. [DOI] [PubMed] [Google Scholar]
  8. Valenzano L.; Civalleri B.; Chavan S.; Bordiga S.; Nilsen M. H.; Jakobsen S.; Lillerud K. P.; Lamberti C. Disclosing the Complex Structure of UiO-66 Metal-Organic Framework: A Synergic Combination of Experiment and Theory. Chem. Mater. 2011, 23, 1700–1718. 10.1021/cm1022882. [DOI] [Google Scholar]
  9. Katz M. J.; Brown Z. J.; Colón Y. J.; Siu P. W.; Scheidt K. A.; Snurr R. Q.; Hupp J. T.; Farha O. K. A Facile Synthesis of UiO-66, UiO-67 and their Derivatives. Chem. Commun. 2013, 49, 9449–9451. 10.1039/c3cc46105j. [DOI] [PubMed] [Google Scholar]
  10. Vermoortele F.; Bueken B.; Le Bars G.; Van de Voorde B.; Vandichel M.; Houthoofd K.; Vimont A.; Daturi M.; Waroquier M.; Van Speybroeck V. Synthesis Modulation as a Tool To Increase the Catalytic Activity of Metal-Organic Frameworks: The Unique Case of UiO-66 (Zr). J. Am. Chem. Soc. 2013, 135, 11465–11468. 10.1021/ja405078u. [DOI] [PubMed] [Google Scholar]
  11. Wu H.; Chua Y. S.; Krungleviciute V.; Tyagi M.; Chen P.; Yildirim T.; Zhou W. Unusual and Highly Tunable Missing-Linker Defects in Zirconium Metal-Organic Framework UiO-66 and Their Important Effects on Gas Adsorption. J. Am. Chem. Soc. 2013, 135, 10525–10532. 10.1021/ja404514r. [DOI] [PubMed] [Google Scholar]
  12. Van de Voorde B.; Stassen I.; Bueken B.; Vermoortele F.; De Vos D.; Ameloot R.; Tan J.-C.; Bennett T. D. Improving the Mechanical Stability of Zirconium-based Metal-Organic Frameworks by Incorporation of Acidic Modulators. J. Mater. Chem. A 2015, 3, 1737–1742. 10.1039/C4TA06396A. [DOI] [Google Scholar]
  13. Barin G.; Krungleviciute V.; Gutov O.; Hupp J. T.; Yildirim T.; Farha O. K. Defect Creation by Linker Fragmentation in Metal-Organic Frameworks and its Effects on Gas Uptake Properties. Inorg. Chem. 2014, 53, 6914–6919. 10.1021/ic500722n. [DOI] [PubMed] [Google Scholar]
  14. Shearer G. C.; Chavan S.; Ethiraj J.; Vitillo J. G.; Svelle S.; Olsbye U.; Lamberti C.; Bordiga S.; Lillerud K. P. Tuned to Perfection: Ironing Out the Defects in Metal-Organic Framework UiO-66. Chem. Mater. 2014, 26, 4068–4071. 10.1021/cm501859p. [DOI] [Google Scholar]
  15. Planas N.; Mondloch J. E.; Tussupbayev S.; Borycz J.; Gagliardi L.; Hupp J. T.; Farha O. K.; Cramer C. J. Defining the Proton Topology of the Zr6-Based Metal-Organic Framework NU-1000. J. Phys. Chem. Lett. 2014, 5, 3716–3723. 10.1021/jz501899j. [DOI] [PubMed] [Google Scholar]
  16. Hod I.; Bury W.; Karlin D. M.; Deria P.; Kung C.-W.; Katz M. J.; So M.; Klahr B.; Jin D.; Chung Y.-W. Directed Growth of Electroactive Metal-Organic Framework Thin Films Using Electrophoretic Deposition. Adv. Mater. 2014, 26, 6295–6300. 10.1002/adma.201401940. [DOI] [PubMed] [Google Scholar]
  17. Yang D.; Odoh S. O.; Wang T. C.; Farha O. K.; Hupp J. T.; Cramer C. J.; Gagliardi L.; Gates B. C. Metal-Organic Framework Nodes as Nearly Ideal Supports for Molecular Catalysts: NU-1000-and UiO-66-Supported Iridium Complexes. J. Am. Chem. Soc. 2015, 137, 7391–7396. 10.1021/jacs.5b02956. [DOI] [PubMed] [Google Scholar]
  18. Cadman L. K.; Bristow J. K.; Stubbs N. E.; Tiana D.; Mahon M. F.; Walsh A.; Burrows A. D. Compositional Control of Pore Geometry in Multivariate Metal-Organic Frameworks: An Experimental and Computational Study. Dalton Trans. 2016, 45, 4316–4326. 10.1039/C5DT04045K. [DOI] [PubMed] [Google Scholar]
  19. Bristow J. K.; Tiana D.; Walsh A. Transferable Force Field for Metal-Organic Frameworks from First-Principles: BTW-FF. J. Chem. Theory Comput. 2014, 10, 4644–4652. 10.1021/ct500515h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Butler K. T.; Hendon C. H.; Walsh A. Electronic Chemical Potentials of Porous Metal-Organic Frameworks. J. Am. Chem. Soc. 2014, 136, 2703–2706. 10.1021/ja4110073. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Fuentes-Cabrera M.; Nicholson D. M.; Sumpter B. G.; Widom M. Electronic Structure and Properties of Isoreticular Metal-Organic Frameworks: The Case of M-IRMOF1 (M= Zn, Cd, Be, Mg, and Ca). J. Chem. Phys. 2005, 123, 124713. 10.1063/1.2037587. [DOI] [PubMed] [Google Scholar]
  22. Torrisi A.; Bell R. G.; Mellot-Draznieks C. Predicting the Impact of Functionalized Ligands on CO2 adsorption in MOFs: A combined DFT and Grand Canonical Monte Carlo Study. Microporous Mesoporous Mater. 2013, 168, 225–238. 10.1016/j.micromeso.2012.10.002. [DOI] [Google Scholar]
  23. Devautour-Vinot S.; Maurin G.; Serre C.; Horcajada P.; Paula da Cunha D.; Guillerm V.; de Souza Costa E.; Taulelle F.; Martineau C. Structure and Dynamics of the Functionalized MOF Type UiO-66 (Zr): NMR and Dielectric Relaxation Spectroscopies Coupled with DFT Calculations. Chem. Mater. 2012, 24, 2168–2177. 10.1021/cm300863c. [DOI] [Google Scholar]
  24. Gale J. D.; Rohl A. L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. 10.1080/0892702031000104887. [DOI] [Google Scholar]
  25. Gale J. D. GULP: A Computer Program for the Symmetry-Adapted Simulation of Solids. J. Chem. Soc., Faraday Trans. 1997, 93, 629–637. 10.1039/a606455h. [DOI] [Google Scholar]
  26. Kresse G.; Hafner J. Ab initio Molecular Dynamics for Liquid Metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 558. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  27. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  28. Valiev M.; Bylaska E. J.; Govind N.; Kowalski K.; Straatsma T. P.; Van Dam H. J.; Wang D.; Nieplocha J.; Apra E.; Windus T. L. NWChem: A Comprehensive and Scalable Open-Source Solution for Large Scale Molecular Simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. 10.1016/j.cpc.2010.04.018. [DOI] [Google Scholar]
  29. Dunning T. H. Jr Gaussian Basis Sets for use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  30. Woon D. E.; Dunning T. H. Jr Gaussian Basis sets for use in Correlated Molecular Calculations. III. The Atoms Aluminum through Argon. J. Chem. Phys. 1993, 98, 1358–1371. 10.1063/1.464303. [DOI] [Google Scholar]
  31. Zhao Y.; Truhlar D. G. The M06 Suite of Density Functionals. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
  32. Zhao Y.; Truhlar D. G. Density Functionals with Broad Applicability in Chemistry. Acc. Chem. Res. 2008, 41, 157–167. 10.1021/ar700111a. [DOI] [PubMed] [Google Scholar]
  33. Bass S.; Nathan W.; Meighan R.; Cole R. Dielectric Properties of Alkyl Amides. II. Liquid Dielectric Constant and Loss. J. Phys. Chem. 1964, 68, 509–515. 10.1021/j100785a011. [DOI] [Google Scholar]
  34. Lemmon E. W.; Huber M. L.; McLinden M. O.. NIST Standard Reference Database 23; 2003.
  35. Becke A. D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  36. Xantheas S. S. On the Importance of the Fragment Relaxation Energy Terms in the Estimation of the Basis Set Superposition Error Correction to the Intermolecular Interaction Energy. J. Chem. Phys. 1996, 104, 8821–8824. 10.1063/1.471605. [DOI] [Google Scholar]
  37. Fleming S.; Rohl A. GDIS: A Visualization Program for Molecular and Periodic systems. Z. Kristallogr. - Cryst. Mater. 2005, 220, 580–584. 10.1524/zkri.220.5.580.65071. [DOI] [Google Scholar]
  38. Cliffe M. J.; Wan W.; Zou X.; Chater P. A.; Kleppe A. K.; Tucker M. G.; Wilhelm H.; Funnell N. P.; Coudert F.-X.; Goodwin A. L. Correlated Defect Nanoregions in a Metal-Organic Framework. Nat. Commun. 2014, 5, 4176. 10.1038/ncomms5176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Ling S.; Slater B.. Dynamic Acidity in Defective UiO-66. Chem. Sci. 2016, DOI: 10.1039/C5SC04953A. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp6b01659_si_001.pdf (3.9MB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES