A hybrid agent-based model of the developing mammary terminal end bud

Abstract

Mammary gland ductal elongation is spearheaded by terminal end buds (TEBs), where populations of highly proliferative cells are maintained throughout post-pubertal organogenesis in virgin mice until the mammary fat pad is filled by a mature ductal tree. We have developed a hybrid multiscale agent-based model to study how cellular differentiation pathways, cellular proliferation capacity, and endocrine and paracrine signaling play a role during development of the mammary gland. A simplified cellular phenotypic hierarchy that includes stem, progenitor, and fully differentiated cells within the TEB was implemented. Model analysis finds that mammary gland development was highly sensitive to proliferation events within the TEB, with progenitors likely undergoing 2–3 proliferation cycles before transitioning to a non-proliferative phenotype, and this result is in agreement with our previous experimental work. Endocrine and paracrine signaling were found to provide reliable ductal elongation rate regulation, while variations in the probability a new daughter cell will be of a proliferative phenotype were seen to have minimal effects on ductal elongation rates. Moreover, the distribution of cellular phenotypes within the TEB was highly heterogeneous, demonstrating significant allowable plasticity in possible phenotypic distributions while maintaining biologically relevant growth behavior. Finally, simulation results indicate ductal elongation rates due to cellular proliferation within the TEB may have a greater sensitivity to upstream endocrine signaling than endothelial to stromal paracrine signaling within the TEB. This model provides a useful tool to gain quantitative insights into cellular population dynamics and the effects of endocrine and paracrine signaling within the pubertal terminal end bud.

1. Introduction

Development of the mammary gland begins in the embryo but occurs primarily postnatally, subsequent to pubertal expansion of the fat pad. The rudimentary mammary ductal tree present at birth remains relatively dormant until puberty, when estrogen receptor positive (ER+) progenitor cells respond to estrogen signaling upregulation, in part, by proliferating and increasing local membrane-bound amphiregulin (AREG) cleavage into the extracellular space; AREG serves as a paracrine signal that promotes proliferation of estrogen receptor negative (ER−)/epidermal growth factor receptor positive (EGFR+) neighbors (Dontu et al., 2004). During pubertal gland development, each actively growing branch is terminated with and advanced by a terminal end bud (TEB), a bulbous structure composed primarily of progenitor cells. A TEB is capped with a layer rich in stem and regenerative cells, although it has been demonstrated that stem cells are not exclusively at the tip of the TEB (Visvader and Stingl, 2014).

Stem cells within the TEB are fundamental in mammary gland development through maintenance of the progenitor population. Work by Shackleton et al. demonstrated that a fully functional mammary gland could be developed from a single Lin⁻CD29^hiCD24⁺ highly proliferative mammary stem cell (MaSc) (Shackleton et al., 2006), which was isolated from a stem cell population later determined to be ER− (Asselin-Labat et al., 2006). More recent studies into the stem cell population within the TEB have indicated that the stem cell niche in the TEB is composed of cells with different proliferation potentials, where stem cells can be either multipotent (able to give rise to daughters of all phenotypes found within the TEB) or unipotent (able to give rise to only one daughter phenotype (Visvader and Lindeman, 2011; Visvader and Stingl, 2014). MaScs are able to divide symmetrically, resulting in two phenotypically similar daughters, or to divide asymmetrically giving rise to one stem and one progenitor daughter, both of which can proliferate symmetrically or differentiate towards a more lineage-restricted phenotype (Dontu et al., 2004; LaMarca and Rosen, 2007), together giving rise to luminal and myoepithelial lineages. This provides a mechanism for maintenance of stem and progenitor cell populations within a population of rapidly developing mature, differentiated cells during organogenesis. Furthermore, the dynamics of symmetric vs. asymmetric divisions within the progenitor population (where a mitosis event results in both mother and daughter having the same phenotype (either proliferative or differentiated; symmetric division) or the mother retains a proliferative phenotype while giving rise to a terminally differentiated daughter (asymmetric division)) plays a critical role in proper organogenesis, and is likely involved in mammary ductal elongation rates during this process. Efforts to quantify the rates of symmetric vs. asymmetric proliferation of stem cells indicate that they proliferate primarily asymmetrically. Investigations of stem cell symmetric division probability have shown 16% symmetric division in mammalian epithelial cells in vivo (Clayton et al., 2007), 25% symmetric division in CD34⁺CD39^lo human severe combined immunodeficiency mouse-repopulating cells in vivo (McKenzie et al., 2006), and 13% symmetric division in primitive human hematopoietic stem cells in vitro (Giebel et al., 2006), which are in agreement with mathematical modeling studies as well (Clayton et al., 2007; Yatabe et al., 2001). Daughter phenotypes resulting from progenitor proliferation are more uncertain where symmetric proliferation has been reported from 10–70% (Bultje et al., 2009; Kim et al., 2015; Li et al., 2003; Noctor et al., 2004; Nomura et al., 2013; Osawa et al., 1996; Takano et al., 2004). Specific to the mammary gland, cell cycle time in MCF-10A immortalized human mammary epithelial cells in the presence of epidermal growth factor has been reported as approximately 15.5 hours (Brummer et al., 2006).

It is well-established that AREG production increases in response to binding of ER alpha in the TEB epithelium (Ciarloni et al., 2007a), that ER− mice fail to initiate pubertal mammary gland development in response to hormonal signaling at the onset of puberty (Mallepell et al., 2006), and that loss of AREG results in gross stunting in pubertal mammary gland development (Ciarloni et al., 2007a; Luetteke et al., 1999). AREG is involved in epithelial to stromal paracrine signaling through its interaction with EGFR (Sternlicht et al., 2005), is connected to cellular differentiation and carcinogenesis in the mammary gland (LaMarca and Rosen, 2007), and has been demonstrated to play a required role in development of TEBs, epithelial growth, and ductal elongation in the pubertal murine mammary gland (Ciarloni et al., 2007b).

We note that pubertal mammary gland development, and the resulting glandular architecture, is induced and regulated by a complex network of endocrine, paracrine, and autocrine signaling pathways (Gjorevski and Nelson, 2011). The complexity of these signaling networks is beyond the scope of this work, and in fact remains partially uncharacterized, both in terms of all molecular players involved and in terms of quantification of molecular signaling thresholds necessary for upregulation of cellular proliferation. Accordingly, we have chosen to focus on only a small portion of the signaling network, namely endocrine system estrogen signaling and subsequent epithelial to stromal AREG signaling, as shown in Figure 1. For an excellent review of the more complete known signaling regulation pathways in development of the mammary gland, the reader is referred to (Gjorevski and Nelson, 2011).

Figure 1.

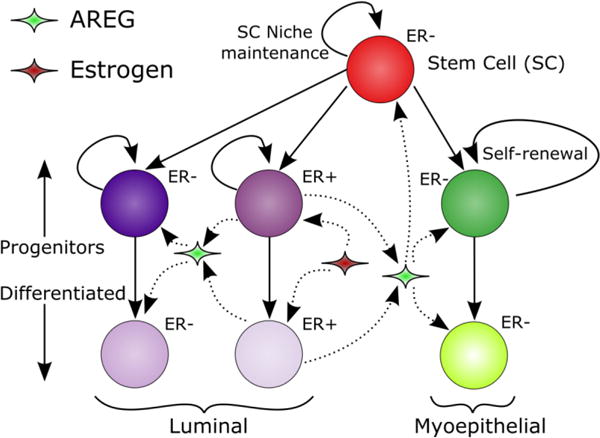
Cellular phenotypic hierarchy and signaling pathways. Stem cells may be unipotent or multipotent, and may self-renew or contribute to the myoepithelial or luminal progenitor populations when undergoing proliferation events. Progenitor populations are maintained primarily through symmetric progenitor proliferations. Progenitors may also give rise to differentiated daughters, and may differentiate upon reaching the proliferation cycle threshold. ER+ cells are stimulated to proliferate and produce AREG by upregulation of estrogen endocrine signaling, while AREG stimulates downstream proliferation of ER−/EGFR+ cells.

While signaling events are responsible for induction and maintenance of gland development (as described above), gland growth is also a direct result of stem and progenitor population’s proliferation within the TEBs. In addition, progenitor population size, distribution, and proliferation capacity play key roles in glandular development, phenotypic distribution within the mature duct, and ductal elongation rates. Hence, in this work, we examine how cellular phenotypic distribution and behavior within the TEB, as well as pubertal estrogen upregulation to stimulate ER+ cellular proliferation, in collaboration with downstream AREG paracrine signaling to ER− cells, affect cellular proliferation, as well as how these signaling pathways play a role in overall cellular proliferation within the TEB during active pubertal mammary ductwork development.

Mathematical modeling and computer simulation have emerged as promising tools to help understand cellular phenotypic transitions and molecular signaling kinetics at different stages of tissue development. In study of the mammary gland, mathematical modeling has made impressive strides, often with a focus on ductal carcinoma in situ (DCIS), the most common noninvasive cancer of the breast. In some mathematical studies of DCIS, the tumor is modeled as a continuum, allowing for calculation of estimated tumor size based on diffusion and mitotic/apoptotic indices (Edgerton et al., 2011) and examination of DCIS growth tendencies (Xu and Gilbert, 2009). In other models, each cell is represented as a unique entity, an approach known as agent-based modeling (ABM) (Anderson et al., 2007; Walker and Southgate, 2009; Wang et al., 2015), which allows for information such as individual phenotype, cellular state, and cell-cell interactions to be included in the model. ABM has provided valuable insight into the apoptosis mechanisms that are known to play an instrumental role in mammary gland lumen formation (Giebel et al., 2006; Tang et al., 2011), and how the morphologies of DCIS can be influenced by cellular proliferation and apoptosis (Boghaert et al., 2014). Other modeling approaches include aspects from both continuum and ABM methods to form hybrid models (Deisboeck et al., 2011; Lowengrub et al., 2010). Hybrid methods allow interaction and feedback between the different scales, with cells responding to the surrounding environment and modifying it. For example, the tumor environment is known to be hypoxic, low in pH, and have high glycolytic rates associated with high cellular proliferation (for more information the reader is referred to (Vander Heiden et al., 2009)), where limited concentration of available molecular resources can result in cell-cell competition and selection of more aggressive phenotypes. These phenomena are often incorporated into hybrid models, with feedback between the agents and the continuum solutions that account for both time-dependent movement of relevant molecules and their cellular uptake or production. In fact, hybrid models of DCIS have been used to provide insight into contact inhibition in the formation of the four morphologies of DCIS (Shumate and El-Shenawee, 2009), and examine how acidosis and hypoxia influence phenotypic selection (Gatenby et al., 2007). Furthermore, recent advances in modeling capabilities have resulted in highly complex, patient calibrated models of DCIS (Hyun and Macklin, 2013; Macklin et al., 2012).

While modeling has helped elucidate mechanisms involved in several mammary gland related processes, much has focused on formation of and transition to DCIS in a fully formed duct, instead of the behavior of the normal TEB and mammary gland ductal development. Recently, an experimentally-validated population-based continuum model to study mammary ductal elongation during pubertal development has been presented (Paine et al., 2016). While this baseline model presents the first work on modeling ductal elongation using actual experimental data, it lacks a description of spatial heterogeneity, specific cell type localizations, cell-cell interactions and signaling. Here, we have implemented a hybrid ABM to study how endocrine and paracrine signaling within the normal TEB environment is involved in cellular proliferation and differentiation during pubertal development of the mammary gland, and how apoptosis events are involved in the formation of the lumen and influence ductal elongation rates. By gaining a more complete picture of how the healthy TEB functions, we are able to quantitatively examine how cellular phenotypic distribution, population size, proliferation and differentiation potentials, and the influence of endocrine and paracrine signaling systems and their effects on observed ductal elongation rates. Here, we describe methods for developing the model and provide biological insights we have observed. In the future, we plan to use this model to study how perturbations in endocrine and paracrine signaling and cellular phenotype proliferation and differentiation probabilities may contribute to developmental abnormalities observed in the pubertal mammary gland.

2. Hybrid Modeling Methods

We have developed a framework for multiscale hybrid modeling in C++ through implementation of a hybrid of partial differential equations (PDEs) and ABM. PDEs are solved with the finite element method (FEM), and used to model biologically relevant molecular distributions, including diffusion of important molecules from the surrounding tissue (oxygen and estrogen) and diffusion of growth factor (i.e., AREG) produced in the TEB by cells. Agents represent cells discretely, and have the capability to model many aspects of cellular function, including proliferation, migration, differentiation, apoptosis, and cell-cell signaling. Agents also modify the environment around them; for example, agents probe the oxygen concentration at their physical location from the FEM solution, and either undergo hypoxia induced necrosis (if oxygen concentration is insufficient to maintain cellular function; however, in our mammary gland model, necrosis does not occur (or is very rare) because all possible locations a cell may occupy within the TEB are well within the Krogh length from the oxygen supply at the TEB outer boundary) or consume some of the available oxygen as necessary to maintain homeostasis, modifying the FEM solution at their location accordingly. Figure 2 describes the computational domain, with TEB geometry based on measurements from murine models (Paine et al., 2016).

Figure 2.

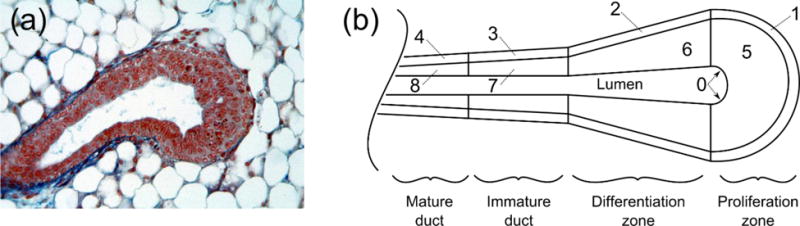
TEB and schematic of computational domain. (a) Microscopic view of the TEB (courtesy of Dr. Helen Hathaway, University of New Mexico). (b) Schematic of regions within the TEB. Regions 1–4 compose the myoepithelium, 5–8 compose the lumen, and 0 is the lumen-formation region. Definition of the regions was adapted from (Paine et al., 2016).

2.1 Continuum partial differential equation component

Small molecule movement within the computational domain is described according to the reaction-diffusion equation form:

$$\frac{\partial u}{\partial t}=D{\nabla }^{2}u+R(u),$$ (1)

where u is a substrate concentration normalized by its maximum/saturation level, D is the diffusion coefficient of the molecule of interest and R(u) = U(u)−L(u) is a reaction term to account for molecular production/consumption U(u) and degradation L(u). The diffusion coefficient of oxygen in tissue has been reported over a wide range, from 10⁻⁴ to 10⁻⁸ cm²/s (Macdougall and McCabe, 1967). In light of this large reported range, we take the somewhat central value of 2.57*10⁻⁶ cm²/s from (Sidell, 1998) in our specific model. Diffusion coefficients of estrogen and AREG are estimated (as corresponding data are not available in the literature) from reported diffusion coefficients of similar molecules (see Table 1). Briefly, AREG diffusion coefficient was estimated relative to published values for similar molecules (i.e. EGFR), while estrogen diffusion coefficient was estimated using both Graham’s law and linear interpolation, as these methods gave estimates that were reasonable relative to other values. We note that these estimated values, while estimates, are taken to be reasonable relative to the large reported range of diffusion coefficient for oxygen. For the reaction term R(u), we assume negligible molecular degradation comparing to the primary molecular production/consumption by cells, i.e., |L(u)|≪|U(u)|. More specifically,

$$\mathrm{R}(\mathrm{x},\mathrm{u})=\mathrm{U}(\mathrm{x},\mathrm{u})-\mathrm{L}(\mathrm{u})=\pm {\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{\lambda }}_{\mathrm{i}}{\mathrm{H}(\mathrm{r}}_{\mathrm{i}}-\left|\mathrm{x}-{\mathrm{a}}_{\mathrm{i}}\right|)\mathrm{u}-\mathrm{L}(\mathrm{u}),$$ (2)

where a_i and r_i are the central position and radius of cell i, respectively, H(x) is the Heaviside function, and is a defined consumption or production per-volume rate of the substrate by cell. The positive sign represents production, and the negative sign consumption. In the current model implementation, we have made the assumption that all cells of similar phenotypes have the same λ values for each molecule of interest (i.e. all ER+ cells uptake estrogen at the same volume rate, and all cells have the same per volume oxygen consumption). In future modeling efforts, this assumption will be relaxed in order to study the effects of cell heterogeneity and the loss of function within healthy cells to study the effects of changes in signaling intensity in the transition to a cancerous disease state.

Table 1.

Baseline values of key model parameters. When not available in the literature, diffusion constants are interpolated from values from structurally similar molecules (^*) or estimated from known values based on relative molecular weights (^**). Other uncited values were determined from model calibration. Stem cell symmetric proliferation rate has been reduced 1% from the value reported in (Giebel et al., 2006).

Model Parameter	Baseline Value	Reference
Necrosis threshold (normalized)	0.2
Doxygen	2.5 × 10−6cm2s−1	(Sidell, 1998)
Destrogen	2.45 × 10−6cm2s−1	*
DAREG	3.18 × 10−7cm2s−1	(Thorne et al., 2004)**
Proliferation rate	≤ 1 per 16 hours
Cell cycle time	16 hours	(Brummer et al., 2006)
(Cell death + lysis) time	< 16 hours	(Shimizu et al., 1996)
Progenitor symmetric proliferation (regions 2, 6)	30%
Proliferation cycles before differentiation	2–3
Stem cell symmetric proliferation probability	12%	(Giebel et al., 2006)
Spontaneous differentiation probability	0.01%
Apoptosis probability, proximal to lumen	14.5%	(Humphreys et al., 1996)
Apoptosis probability, distal to lumen	7.9%	(Humphreys et al., 1996)

Biologically, L(u) represents molecular sinks separate from molecular consumption in routine cellular functionality, i.e. unconsumed molecules in/on cells lost to apoptotic processes or molecular consumption by receptors/pathways other than the primary pathways in the model. We include L(u) in the model for completeness of the mathematical description of the biological process and for future considerations where the primary consumption pathway may possibly be blocked. Molecular concentration profiles are also modified locally by agents due to molecular production or consumption, which are imposed discretely on the solution (as described in Eq. 3 below), as determined separately from the reaction term. For externally supplied molecules (i.e. oxygen and estrogen), we assume constant and homogeneous saturated concentrations in the surrounding tissue through blood. These molecules enter the computational domain through imposition of Dirichlet boundary conditions (u = 1) at the outer boundary of the TEB. On the other hand, we assume that molecules produced by agents within the TEB (i.e., AREG) are free to diffuse throughout the simulated domain based on the conditions specified in the associated reaction-diffusion equation. Hence, far-field homogeneous Neumann boundary conditions have been implemented in this case, and molecular concentration attenuates towards a steady-level at the far field.

Time-dependent solutions for diffusion profiles of oxygen, AREG, and estrogen are obtained numerically using FEM. FEM solutions are obtained with Sundance (Long et al., 2010), a finite element solver available as part of the Trilinos Project developed by Sandia National Laboratory. Solutions are obtained in two dimensions on a triangular mesh generated with Telis meshing software. The Dirichlet and Neumann boundary conditions are implemented as essential and natural boundary conditions in FEM, respectively. Continuum FEM solutions are modified discretely based on local agent consumption or production of the corresponding molecule across the computational domain. Molecular consumption and production by the whole volume of an agent are assigned to its center of mass and quantified phenomenologically (when unavailable from the literature) in normalized units. This hybridization of contributions from the discrete component into the continuum solutions is accomplished numerically by imposing Dirac delta modifications to the continuum solution profile at the mesh nodes. The magnitude of node modifications is determined by sorting agents in a Voronoi tessellation (a method of sorting where all agents that are closer to a node than any other node are associated with that node, and noting that the entire cytoplasmic volume of each agent is assigned to the Voronoi cell that contains the agent’s center of mass) around the node and then averaging the FEM modification magnitude (calculated as a per volume rate) of each agent nearest to that node, as described in the following equation:

$$\mathrm{U}(\mathrm{u})=\frac{{\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{\lambda }}_{\mathrm{i}}\mathrm{u}{\displaystyle {\int }_{-\infty }^{\infty }\mathrm{\delta }(\mathrm{x}-{\mathrm{a}}_{\mathrm{i}})\mathrm{dx}}}}{\mathrm{n}},$$ (3)

where n is the number of agents in a Voronoi cell. Here we assume that the agents equally divide the Voronoi volume, and thus contributions from agents (cells) of different phenotypes in the same Voronoi cell are averaged. The computational domain was discretized in the same order of magnitude as agent radius, as the simple TEB geometry (which does not vary much over time and from animals to humans (Gusterson and Stein, 2012; Manni, 1999)) does not possess any features requiring local mesh refinement, while both numerical and ABM time step discretization are equal (set to be 30 minutes of simulated time in all results shown; at each time step, the PDE is solved first; thus we integrate the hybrid model using a semi-implicit method by lagging the cell positions). A separate FEM solution is obtained for each molecule of interest.

2.2 Discrete agent-based modeling component

Agent distribution is lattice-based in a hexagonal close packed conformation in two dimensions. Growth within the TEB is proliferation-driven, where proliferating agents must displace their neighbors to create room for the new daughter (if there is not already room to divide left by an agent that has undergone apoptosis). To keep our focus on the TEB, we describe the model on a moving frame that moves at the same speed as the duct elongation. Hence, our computational domain contains a fixed section of the TEB, as illustrated in Figure 2b. Cells exit through the open end of the mature duct and out of the modeled domain but are counted to estimate the duct elongation rate. Moreover, as our primary goal is to understand the longitudinal cell distribution and the ductal elongation resulting from endocrine and paracrine signal mediated cell proliferation, we reduce the full three-dimensional structure of a TEB to its two-dimensional cross-section by assuming cylindrical symmetry. When a cellular proliferation event occurs, the daughter cell is placed at a neighbor position of the mother within the appropriate region of the TEB. If the selected position is already occupied, the occupant is displaced to make room, and in turn further displaces one of its neighbors. Cells are assumed infinitely compliant to displacement, so the process continues until an agent is displaced either into an unoccupied position previously cleared by apoptosis or out of the computational domain. Because we do not currently model the entire mammary gland, any agents displaced out of the computational domain are counted by phenotype and removed from the simulation.

Apoptosis within the TEB model occurs stochastically, with higher apoptosis percentages (14.5% per cell cycle) proximal to the lumen-formation region (region 0 in Figure 2b) and lower apoptosis percentages (7.9% per cell cycle) distal to the lumen-formation region, based on apoptotic populations observed in the murine mammary gland (Humphreys et al., 1996). Here, we use the reported percentage of cells undergoing apoptosis at a snapshot as the apoptosis percentage in one cell cycle, based on the observation that apoptosis and subsequent clearance by macrophages is a rapid process (Hochreiter-Hufford and Ravichandran, 2013); accordingly we take clearance of apoptotic cells time to be roughly the same as or less than our cell cycle time (see Table 1). Positions freed by an apoptosis event may be filled by agents displaced from a proliferation event elsewhere in the TEB or at a later time step. Agents extract the values of molecular concentrations at their location for every time step and use these values to make decisions, and also modify molecular concentrations as a result of molecular uptake or production. Myoepithelial cells are ER−, while cells in the lumen may be ER+ or ER−. ER+ cells uptake estrogen, reducing the concentration at their locations, and respond to estrogen stimulation by proliferating and producing AREG, increasing local AREG supply. ER− cells may be stimulated into proliferation if the concentration of AREG satisfies a proliferation threshold. For both ER+ and ER− phenotypes, proliferation may only occur if they are not entering necrosis or apoptosis. Progenitor cells may also differentiate due to extended quiescence (as is commonly accomplished in confluent cells in vitro).

Cellular proliferation rates are bounded by cell cycle duration, which has been demonstrated to be in the 16 hour range in the case of mammary gland (Brummer et al., 2006). To satisfy this proliferation threshold, agents count the time since their last mitosis event, and may not proliferate again until at least 16 hours of simulated time has passed. Both the molecular signaling thresholds (AREG for ER− and estrogen for ER+) and the cell cycle time threshold are implemented as binary step functions, where the proliferation of an agent is disallowed below the threshold. Upon satisfaction of the thresholds, an agent with a stem or progenitor phenotype may proliferate with a given probability. This proliferation probability is set to 100% for this study, as we focus our investigation on the effects of phenotypic distribution and AREG and estrogen thresholds. In future development, this probability can be regulated by various incorporated microenvironment conditions, such as the oxygen concentration, or to include the effects of abnormal behavior from perturbation from a healthy to a disease state. Subsequent to a proliferation event, the new daughter cell displaces one of the agents around the mother cell according to the cellular displacement algorithm described above, moving the TEB forward. The phenotype of the daughter is determined stochastically and is based on mother type and partially on mother location.

To quantify the probability of the cell fate, we divide the TEB into proliferative, differentiation, immature, and mature ductal zones ((Paine et al., 2016) also see Figure 2b), based on a commonly adopted hypothesis. The proliferative zone is thought to be composed of proliferative body cells (region 5) and myoepithelial progenitors (region 1), and is capped with cap cells. These are followed by regions with increasing number of differentiated cells as cells become farther away from the TEB tip (Gjorevski and Nelson, 2011). Progenitors in the proliferation zone always proliferate symmetrically, while progenitors in the differentiation zone have a reduced symmetric proliferation probability (see Table 1), which is further reduced 25% (arbitrarily) after the mother moves out of the differentiation zone. Baseline symmetric proliferation probabilities are shown in Table 1. A more complete description of agent decision pathways is shown in Figure 3. In our model, stem cells may be either multipotent or unipotent, as determined by their location within the TEB. To maintain phenotypic separation between the lumen and myoepithelium, stem cells within these regions are restricted to unipotent phenotype, where they may only give rise to the surrounding phenotype. Stem cells at the leading cap of the TEB tip are allowed to be multipotent, giving rise to either unipotent stem or progenitor daughters, as determined by which region the daughter is placed into. We note that for the purpose of simplifying visualization output, we show both multipotent and unipotent stem cells using the same color (Figures 1, 4 and 9).

Figure 3.

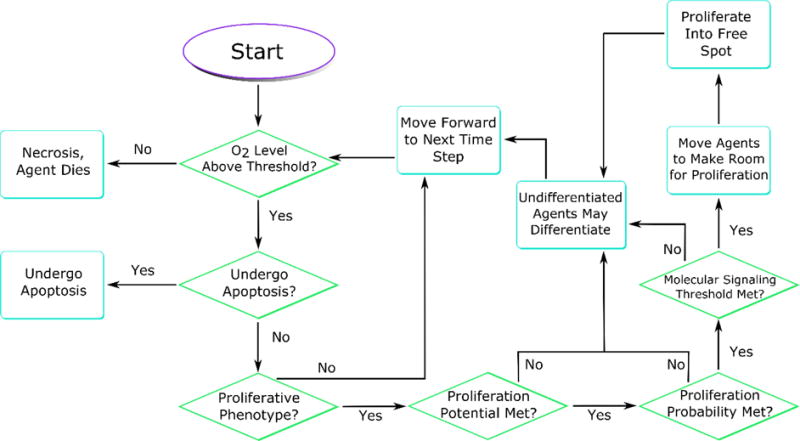
Agent phenotype decision flowchart. At each time step, agents query their environment to find the values of molecular concentrations of interest. If (i) agents do not enter necrosis, (ii) are not chosen to under apoptosis, (iii) they are progenitors, and (iv) it has been at least one cell cycle since they have proliferated, then they may proliferate, provided that a stochastic proliferation probability and molecular signaling thresholds are met. Agents that are not progenitors or do not meet the proliferation criteria wait for the next time step. Proliferation events displace surrounding agents to make room for the daughter, either filling a location freed by an apoptosis event or displacing an agent out of the computational domain as the TEB moves forward.

Figure 4.

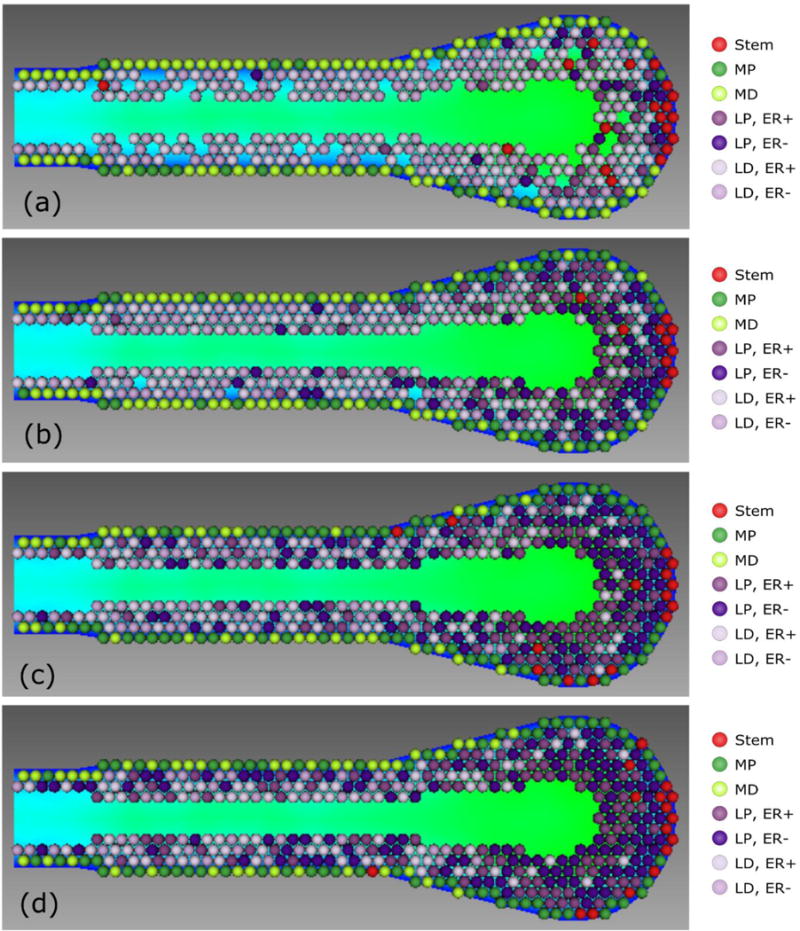
Effects of proliferation cycles before differentiation. (a) One cycle before differentiation results in progenitor depletion, and apoptosis events overtake proliferation, disrupting TEB morphology, seen here as numerous holes disrupting confluency in the TEB. Morphology disruption shown is after three simulated cell cycles. (b) Two cell cycles before differentiation maintains TEB homeostasis, with noticeable differentiated population within the proliferation zones. (c) Three cycles before differentiation reduces differentiated population in the proliferation zone and results in increased progenitor population within the differentiation zone. (d) Four cycles before differentiation; the proliferation zone is now mostly free of differentiated agents. Background colors within the TEB show a graphical representation of the numerical solution of oxygen concentration, with blue corresponding to higher normalized concentration (up to 1.0) around the boundary and green corresponding to the lower concentration. See the online version of this article for better distinction of the phenotypic color codes.

Figure 9.

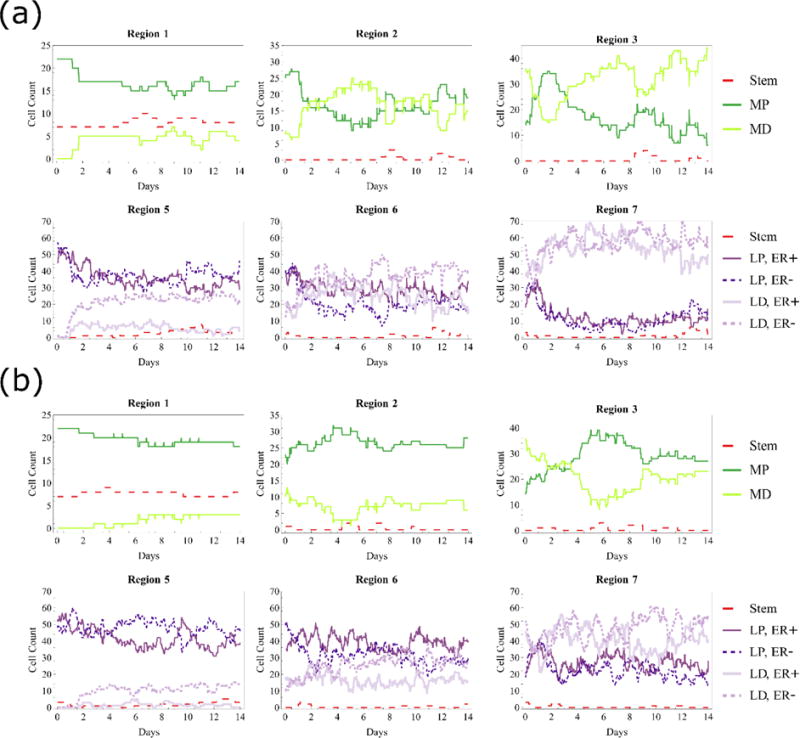
Cell types in each region for (a) two cycles before differentiation and (b) three cycles before differentiation (cell counts in the mature duct not shown). Data shown in both cases are taken from one sample simulation with baseline molecular signaling thresholds in effect, and myoepithelial plot colors correspond to cellular phenotype coloration shown in Figure 1, while the luminal color scheme has been simplified to increase readability. Regions closer to the TEB tip contain primarily progenitors with some differentiated agents that have hit the proliferation threshold limit, while regions farther from the TEB tip have increased differentiated populations. More proliferation cycles before differentiation maintain larger progenitor populations in all regions.

3. Results

We have enlisted, to our best knowledge, literature-supported values into our model studies whenever possible. When these values were not available, we sought to determine a baseline value for the model parameter that result in model behavior in agreement with physically verifiable values. In brief, baseline values must result in biologically relevant ductal elongation rates (previously reported at 500 μm per day (Hinck and Silberstein, 2005; Williams and Daniel, 1983)), cellular distributions, and reasonable phenotypic transition from the highly proliferative zone within the TEB to the mature, mostly differentiated duct. The chosen baseline values as quantified from the literature or quantified in agreement with literature-supported values are summarized in Table 1 (we note that normalized and/or phenomenologically determined values are not included, as they are not directly translatable to biologically measured values). In all simulations described, any model parameter not explicitly varied was assigned the baseline value.

3.1 Cell cycles before differentiation

Within the TEB, myoepithelial and luminal progenitors are restricted in the number of mitosis cycles they may undergo before differentiation into a non-progenitor phenotype, while stem cells are allowed to proliferate indefinitely. In our model, if progenitor cells were only allowed to proliferate once before differentiation, it was insufficient to maintain a progenitor population, resulting in growth arrest and loss of confluency in the TEB (Figure 4a). Without a sufficient progenitor population, apoptosis events dominated and the TEB cellular population was diminished, with greatly arrested ductal elongation rates and disruption of correct organ structure. Conversely, in the case of four proliferation cycles before differentiation (Figure 4d), many progenitors did not remain in the TEB for sufficient cell cycles to differentiate, resulting in mature duct with a biologically irrelevantly large progenitor cell population. Reduction to three proliferation cycles before differentiation (Figure 4c) reduced this number, with fewer than 30% of cells entering the mature duct with progenitive phenotype, and reduction to two proliferation cycles before differentiation (Figure 4b) further reduced the percentage of progenitor cells in the mature ductal zone to around the 10% range. This result is in good accordance with the literature, where percentages of progenitor cells within the mature mammary gland are found to be under 10% (or slightly over 10% for the nulliparous gland) (Chepko and Smith, 1997). Accordingly, we identify 2–3 (2×–3×) cycles before differentiation (a quantity we will henceforth refer to as the proliferation cycle threshold) as the most likely to be biologically relevant, and this is also in agreement with experimental measurements as well (Paine et al., 2016). Together, we have determined that TEB growth is highly dependent on the number of progenitor proliferation cycles before differentiation. Note that because we only model the TEB, we do not consider differentiation events that may occur after cells enter the mature duct.

3.2 Symmetric vs. asymmetric division

The phenotypic fate of daughter cells has been reported to contain high heterogeneity amongst different tissues and developmental stages. Our model allowed us to specify the stochastic probability that a progenitor will divide symmetrically (increasing the progenitor population) or divide asymmetrically, giving rise to a differentiated daughter. We have made the assumption that, at the onset of mammary gland pubertal growth, all progenitors may undergo the maximum allowed number of proliferations before differentiation. This resulted in initially increasing numbers of progenitors as new cells generated from symmetric proliferation events displace differentiated cells that were initially seeded at the beginning of the simulation until the proliferation cycle threshold was reached (see Figure 5). Subsequent to reaching this threshold, differentiation events reduced progenitor population and the entire cell population transitioned towards progenitor/differentiated homeostasis.

Figure 5.

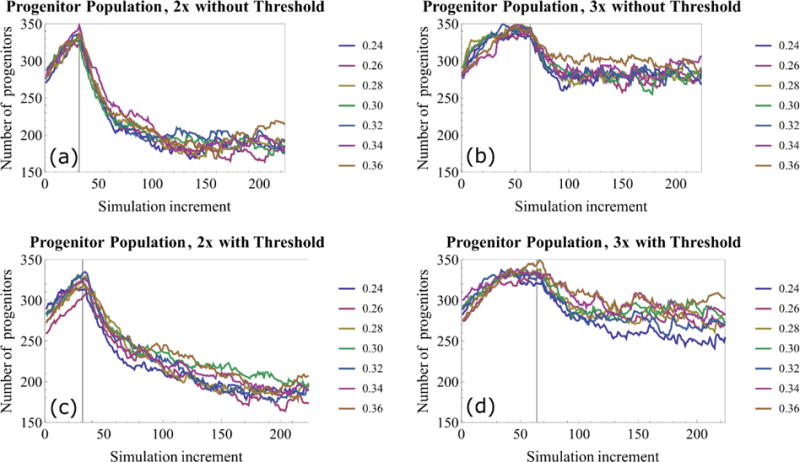
Progenitor population within the TEB with different symmetric proliferation probabilities (1.0 = 100% symmetric proliferation). (a,b) Progenitor population vs. simulation iteration without signaling threshold in place. (c,d) Progenitor population after incorporation of signaling thresholds. 3× proliferation events maintains a larger progenitor population within the TEB relative to 2×. In each case, progenitor population is seen to increase until differentiation events start (indicated by vertical lines), reducing the progenitor population until it reaches homeostasis. Each curve represents one simulation, and each simulation step corresponds to 30 minutes of simulated time, thus 32 simulation increments correspond to one simulated cell cycle.

In the model, cell agents differentiate immediately upon hitting their proliferation cycle threshold. In the case of no signaling threshold, proliferation events were more frequent relative to the signaling limited case, with progenitors always proliferating as soon as they had waited one cell cycle (provided all other conditions were met). Increased proliferation events also led to an increase in differentiation events as cells reached the proliferation threshold, and thus a faster transition to population homeostasis (Figure 5a,b), resulting in reduced temporal fluctuation of total progenitor population count in subsequent cell cycles. As expected, higher percentages of symmetric proliferations resulted in higher total percentage of progenitors in the TEB (Figure 5). Ductal elongation rates were lower for two proliferation cycles relative to the three proliferation cycle case (Figure 6a,b) because increased proliferation cycles maintain a larger progenitor population, allowing for more proliferation events per cell cycle.

Figure 6.

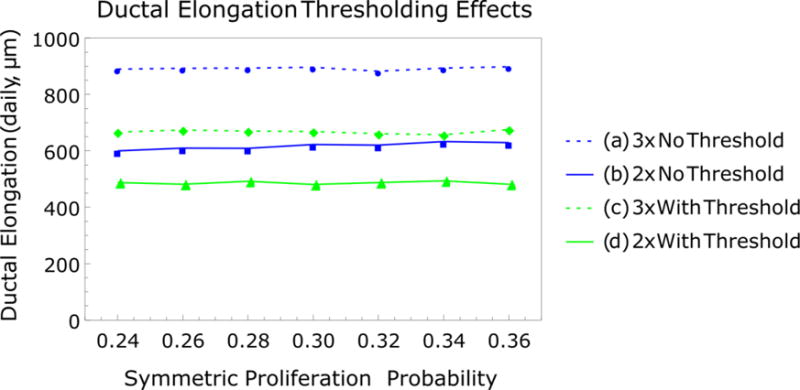
Ductal elongation growth rates with 2× and 3× proliferation cycles before differentiation with symmetric proliferation probability perturbation (1.0 = 100% symmetric proliferation). (a,b) Daily elongation rates without molecular signaling threshold and (c,d) daily elongation rates with molecular signaling threshold. In both cases, higher elongation rates are observed with 3× proliferation cycles before differentiation, and molecular signaling thresholds reduce elongation rates relative to the unregulated, purely proliferative case. All plots show elongation rates observed over 7 simulated cell cycles.

3.3 Signaling thresholds

Perturbation simulations of the percentage of symmetric proliferation events were then repeated with molecular signaling threshold restrictions in effect (Figure 6c, d), where baseline signaling thresholds were set equal to continuum molecular concentration (set with the same normalized value for all simulations at time t=0; molecular perturbation values are relative to this initial concentration). Interestingly, varying progenitor symmetric proliferation percentages did not have an impact on elongation rates, as observed from the uniform simulated elongation rates for each parameter variation case (Figure 6a–d). The number of cycles before differentiation still influenced elongation rates, as higher progenitor populations allowed for more proliferation events both in the presence and absence of a molecular signaling threshold.

We then sought to gain insight on the effects of specific perturbations in molecular parameters (i.e., thresholds for estrogen and AREG) on model output (i.e., ductal elongation rate). Initially, thresholds for both molecular parameters were varied together (Figure 7). Signaling threshold was found to closely control simulated ductal elongation rates. Figure 7 reveals how the threshold affects ductal elongation rates. An increase of as little as 7–10% above the baseline led to a 60–80% reduction in ductal elongation rate (from 423.75 to 80.25 μm/day for 2× before differentiation, and from 582.2 to 226.9 μm/day for 3×), which is low compared to the established level in literature, where pubertal ductal elongation rates have been reported to be around 500 μm /day (Hinck and Silberstein, 2005).

Figure 7.

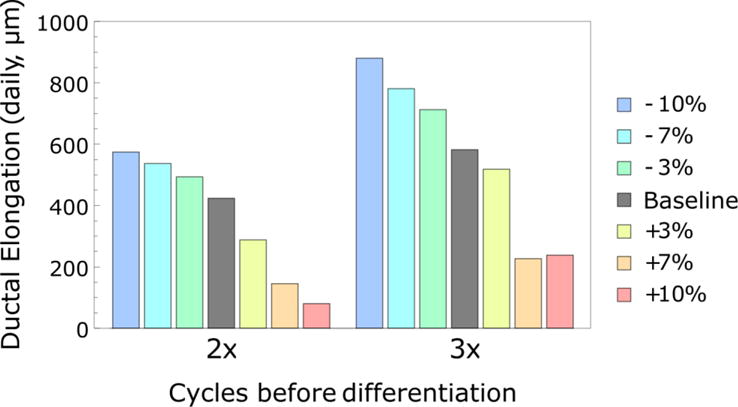
Effects of synchronized ±10% estrogen and AREG signaling threshold variation on ductal elongation rates. Proliferation events are sensitive to molecular signaling thresholds when both estrogen and AREG thresholds are perturbed in unison (shown here). Higher (+) thresholds inhibit proliferation events, stunting ductal elongation rates, while lower (−) thresholds are less restrictive, resulting in more proliferation events and higher elongation rates. All plots show elongation rates observed over 7 simulated cell cycles.

Simulations were then conducted with independent perturbation of each individual molecular threshold (±10% signaling threshold; Figure 8). One threshold was subjected to ±10% perturbation, while the other remained fixed at the baseline value (see Table 1). Ductal elongation rates were reduced at higher thresholds for both cases, with greater reduction in the case of high estrogen thresholds relative to high AREG thresholds. Linear best-fit curves were generated for the ductal elongation rate data to provide quantification of threshold growth arrest effects. Then, the magnitude of the slope of each regression line was used as a measure to estimate the rate of change of output for one unit of change in input; the greater the magnitude of the slope, the greater the rate of change, and thus the bigger impact the parameter has on model output. As a result, for both cases, estrogen signaling was found to have more impact on ductal elongation rate than AREG signaling (slope magnitude (AREG vs. estrogen perturbation) increased from 804.36 to 1933.98 for the 2× case, and from 1242.10 to 2442.78 for the 3× case). In the case of high AREG thresholds, ER− cells show significant population decrease (due to reduced proliferation events), while ER+ cells proliferate uninhibited at their baseline threshold (data not shown). Imposition of high estrogen thresholds, however, resulted in reduction of proliferation events in both ER+ and ER− phenotypes.

Figure 8.

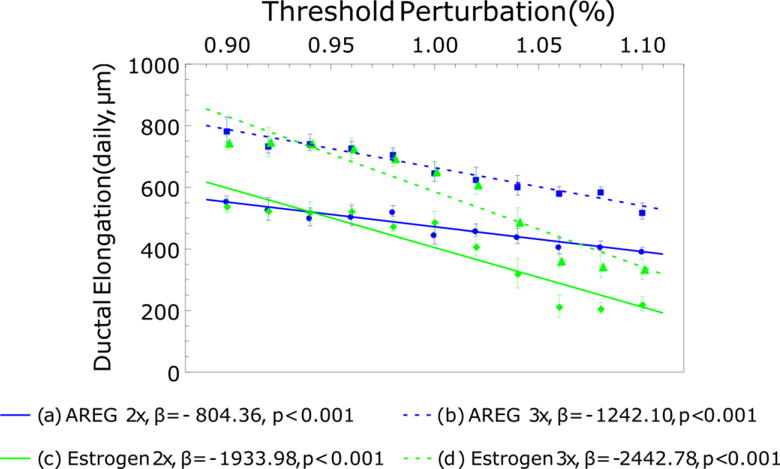
Effects of independent ±10% signaling threshold variation on ductal elongation rates. AREG restricted growth (a, b) shows reduced daily elongation reduction relative to estrogen restricted ductal elongation. Estrogen restricted growth resulted in more than twice the ductal elongation reduction relative to the AREG restricted case. Each data point represents the mean of 5 simulations with standard deviations; linear best-fit curves are shown as dashed lines. β: the slope of a regression line.

3.4 Cell types in each region

We have quantified the types of cells in each region (see Figure 2b for region definitions) through longer simulation runs (two weeks of simulated growth) using baseline values as identified in Table 1. At the end of each simulation step, agents of each type were counted across the computational domain. Simulation results are shown in Figure 9. Regions closer to the TEB tip (i.e., regions 1 and 5) maintained larger populations of progenitors than differentiated agents, with 3× proliferation before differentiation maintaining larger total progenitor populations relative to the 2× case. In the 2× before differentiation case (Figure 9a), differentiated population quickly overtook progenitor population in regions 2 and 6. In regions 3 and 7 cellular population was primarily differentiated. For the 3× proliferation before differentiation case (Figure 9b), increased proliferation events slowed the transition from progenitor dominated to differentiated dominated populations, as differentiated populations did not overtake progenitors until regions 3 and 7. In both cases, phenotypic population was volatile in the short portion of mature duct that we model (i.e., regions 4 and 8), and many of the cells that move into this region move out of the computational domain before they are counted; accordingly cell counts in these regions are not shown. Note that because counts were taken at the end of each simulation step, it is possible that an agent may have passed through a region in the simulation step and accordingly not been counted during its short residence that region.

4. Discussion

Through a hybrid multiscale ABM, we have explored the contribution of cellular phenotypic hierarchy, phenotypic distribution, and the effects of endocrine and paracrine signaling on ductal elongation rates within the developing mammary gland. We examined the effects of proliferation cycles before differentiation, symmetric vs. asymmetric proliferation probabilities, and the influence of molecular signaling threshold on elongation rates and phenotypic populations within the TEB. Under our assumption that all daughters within the proliferation zone will be progenitors, we demonstrate that elongation rates were driven primarily by proliferating population renewal within the proliferation zone. Molecular signaling thresholds were found to provide consistent ductal elongation rate regulation, with elongation rates shown to be sensitive to molecular signaling intensity. The model also demonstrated that 2–3× cell proliferation cycles before differentiation accurately reproduced biologically relevant ductal elongation rates and cellular phenotypic distributions within the TEB; this result confirms previous experimental data as well (Paine et al., 2016). Achieving a primarily differentiated population within the mature mammary gland necessitates rapid phenotypic transition from primarily progenitor phenotypes within a short residence time in the TEB. We find that reduction of symmetric proliferation events in the differentiation zone in combination with the proliferation cycle threshold was sufficient to induce this phenotypic transition, in agreement with literature reported values (Chepko and Smith, 1997).

In our simplified model of cellular phenotypic hierarchy within the TEB (Figure 1), we observed that the number of proliferation cycles before differentiation in progenitor cells plays an important role on simulated replication of biologically correct TEB growth and functionality. Inadequate proliferation cycles before differentiation (Figure 4a) resulted in a TEB that rapidly exhausts its supply of progenitors, all but halting mammary gland growth and disrupting proper TEB structure as the few remaining progenitors and stem cells competed with apoptosis events to maintain the proper gland structure. This ultimately resulted in loss of confluency, and is seen as holes that have developed throughout the TEB in Figure 4a. Conversely, greater than 3 proliferation cycles before differentiation (Figure 4d) prevented adequate time for many progenitors to differentiate prior to exiting the TEB, resulting in biologically unrealistic numbers of progenitors in the mature duct. Our results show that 2–3 proliferation cycles before differentiation (Figure 4b,c) resulted in mammary gland growth which is in good agreement with the literature, both in terms of ductal elongation rates (Hinck and Silberstein, 2005; Williams and Daniel, 1983) and phenotypic populations within the mature gland (Chepko and Smith, 1997). While it is likely that the number of proliferation cycles will vary from cell to cell in vivo, we demonstrate evidence that the distribution is likely centered around the 2–3 proliferation cycles range.

Effects from changing the stochastic probability of symmetric divisions was found to be minimal, likely due to short cellular residence times within the TEB (see Figure 6). At 2×, cells average three cell cycles in the TEB before being displaced into the mature duct and out of the computational domain, while average residence time is reduced to two cycles in the 3× case. In both cases, residence time in the TEB is shorter than or equal to the number of cycles necessary for a cell to differentiate due to hitting the proliferation threshold, thus minimizing the effects of different symmetric proliferation probabilities. Ductal elongation rates were consistently higher in the 3× case due to larger progenitor populations, with increased symmetric proliferation events contributing only minimally to the higher elongation rates.

Our results demonstrate that imposition of signaling molecule thresholds onto the proliferation with apoptosis model resulted in reliable TEB cellular proliferation and mammary gland ductal elongation rate regulation. The ductal elongation rates were lower than the unrestricted case of pure proliferation in the absence of any signaling threshold (Figure 6c, d). This indicates that signaling thresholds may act as an elongation rate regulation mechanism in the pubertal mammary gland by reducing the cellular proliferation rates. The observed reduction of proliferation events and ductal elongation rates due to molecular threshold effects implies that the mammary gland has the potential to elongate at faster rates than reported in the literature (Hinck and Silberstein, 2005) if molecular signaling is increased in intensity, and this can occur with a proliferation cycle threshold as low as two cycles before differentiation. It should be noted that molecular production rates and boundary values, uptake rates, diffusion constants, and signaling threshold are not independent. All have a direct influence on and contribution to the time dependent solutions of the molecular profiles. Unfortunately, we have not been able to obtain literature-based quantified values for all parameters; thus, we have calibrated a set of parameter baseline values that gave rise to biologically realistic elongation rates and phenotypic distributions.

Ductal elongation rates were found to be consistently reduced with higher proliferation thresholds, and, under the conditions implemented in the simulations presented here, cellular proliferation rates exhibited higher sensitivity to increased estrogen-mediated proliferation than in the AREG-mediated case. When cellular proliferation events within the ER− phenotype were restricted by the AREG threshold, ER+ phenotype cells were able to proliferate as normal, as estrogen signaling is not affected by downstream signaling events. However, restriction of proliferation events of the ER+ phenotype due to higher estrogen thresholds constituted an upstream interruption in the signaling pathway, and lead to interruption of downstream AREG mediated proliferation in the ER− population. Initially, estrogen-mediated reduction in ER+ proliferation events resulted in increased ER− population within the TEB as the ER+ proliferation events decreased. This population shift lead to a change in AREG signaling effectiveness, as AREG production decreased concurrently with an increase in AREG consumption. Ultimately, this resulted in reduced ER− proliferation events due to upstream reduction of ER+ proliferation and AREG production. Thus, our results indicate that, under simulation conditions as presented here, mammary gland ductal elongation is more sensitive to disruptions in estrogen signaling than AREG signaling, as estrogen signaling disruption ultimately decreases proliferation in both ER+ and ER− phenotypes, while AREG signaling disruption only affects the ER− population. Ductal elongation rates were also observed to be more sensitive to estrogen signaling in the 2× case relative to the 3× case. It is likely that the larger progenitor population maintained by the greater number of proliferation cycles is able to offset some of the cellular proliferation restriction effects of reduced signaling molecule intensity.

Cell types in each region were found to be variable, with stochastic events resulting in population shifts over time. However, trends can clearly be seen, with progenitor population consistently decreasing farther away from the TEB tip, primarily due to differentiation events after progenitors reach their maximum cycle before differentiation, and with differentiated population also subsidized from decreased symmetric proliferation events as progenitors are distanced from the TEB tip. Increased proliferation cycles before differentiation resulted in larger progenitor populations in each region of the TEB, including greater percentages of progenitors left behind in the mature duct trailing the TEB. While two proliferation cycles before differentiation resulted in progenitor populations in the mature duct closer to values reported in the literature, this likely does not elucidate the full picture, as additional differentiation events after agents enter the mature duct may have downstream effects on cellular population distribution in the fully formed mature gland.

It should be noted that ductal elongation rates predicted with a two-dimensional model may be lower than elongation rates possible in the three-dimensional case, as in the 3D case the ratio of progenitors in the TEB to number of cells necessary to elongate the duct is higher. Similarly, under identical boundary, diffusion, and molecular uptake conditions, internal molecular concentrations would also be higher in a 3D model. However, this simplified case sheds valuable insights onto the effects cellular differentiation pathways and phenotypic transition decisions play in the morphological development of the mammary gland. Future development of the model will transition to a three-dimensional computational domain and remove the restriction of on-grid agent movement. A model of healthy organogenesis can also provide a jumping-off point for transition to disease state. In future computational experiments, we will incorporate another type of stem cell into the model (alveolar stem cells) and then break the rules that maintain homeostasis to seek insight into the signaling and phenotypic transitions involved in disruption of normal mammary gland development.

HIGHLIGHTS.

• Presents an agent-based model of mammary terminal end bud

• Implemented cellular hierarchy based, proliferation-driven growth model

• Rapid duct elongation rates are achievable in only two progenitor proliferation cycles

• Cell differentiation is necessary for proper phenotypic transition to mature the duct