Abstract
Do parents invest more in higher quality children, or do they compensate for lower quality by giving more to children with lower endowments? We answer this question in the context of a large-scale iodine supplementation programme in Tanzania. We find that children with higher programme exposure were more likely to receive necessary vaccines and were breastfed for longer. Siblings of treated children were also more likely to be immunised. Fertility behavior and investments at the time of birth were unaffected.
Keywords: endowments, parental investments, intra-household resource allocation, child health, Tanzania
A growing body of recent work provides evidence that children’s “endowments” in early life, for example in health or cognitive ability, and interventions that change these endowments, can have large effects on later-life health and economic outcomes that, in some cases, persist even into adulthood (see Doug Almond and Janet Currie (2011) for a synthesis of this literature).1 Given the size and persistence of these endowment effects, it is natural to ask how household behaviors–particularly as relate to resource allocation among children–respond to shifts in endowments. The sign and magnitude of these behavioral responses indicate whether–and by how much–parents’ investments magnify or dampen the baseline effects of early-life interventions.2
In this study, we estimate the impact of shifts in childhood endowments (primarily cognitive ability) on health investments in children. We exploit variation in in utero exposure to a large-scale iodine supplementation programme in Tanzania. The program, an effort begun in the 1980s by the Tanzanian government to curb the high national rate of iodine deficiency, distributed iodised oil capsules in at-risk districts, primarily targeting mothers of childbearing age and young children. We focus on the effects of in utero exposure to iodine because fetal iodine is crucial to the cognitive development during pregnancy. We measure exposure using a procedure developed by Field, Robles and Torero (2009, hereafter FRT), who find that the same intervention had significant effects on schooling attainment for pre-teens.3 We regress available health investment measures (vaccination coverage, breastfeeding duration, and at-birth investments) on the programme exposure measure. We find that children exposed to the iodine supplementation programme while in utero are more likely to receive necessary vaccines and are breastfed for longer.
On the other hand, we find that the quantity and spacing of births, as well as investments made at the time of birth, are not significantly affected by treatment exposure. Similarly, physical health at birth is not affected, though availability of data is limited. We interpret these results as consistent with the notion that parents responded once improvements in cognitive functioning were observed, and that expectations prior to birth and perceptions of endowments at birth appear to have been unaffected. While we cannot conclusively rule out impacts on at-birth health and investments, investments in infancy respond strongly and robustly. Magnitudes of these impacts are small relative to mean investment levels, but treatment exposure explains a sizable fraction of the variation in investments (i.e. a one standard deviation increase in treatment exposure leads to a roughly 0.2 standard deviation increase in vaccination doses)
Finally, we ask whether programme exposure, and the resulting investment responses we measure, have spillover effects onto siblings of the treated child. Spillovers may work through a variety of mechanisms–for example, resource reallocations among children; epidemiological externalities; behavioral peer effects; parental learning about the effects of health inputs; and economies of scale in investments. These spillovers have potentially large implications for interventions that target specific groups of children, say, school-age children or girls. For example, if households strongly reinforce early-life interventions but hold fixed the total level of investment in their children, welfare gains to one child may be offset by losses in the welfare of his siblings. On the other hand, if parents’ preferences are such that equity among children is valued, it is possible that a policy that increases one child’s endowment may spur increases in resource allocations to all children.
To test for resource allocation spillovers across siblings, we include siblings’ (cumulative) treatment exposure in the regression described above–that is, we regress health investments on own and siblings’ treatment exposure. Across vaccination categories, we consistently find that the siblings of children exposed to treatment are also more likely to be immunised. This pattern of own- and sibling-investment responses is consistent with a model of intra-household resource allocation in which parents are averse to inequity among their children.
Our study makes three contributions. First, it is meant to increase our understanding of the impacts of early-life events on long-run outcomes. A small but expanding subset of this literature has recently stressed the potentially important role investments play in reinforcing or compensating for the initial effects of early-life shocks and interventions.4 We show that, in the case of interventions that improve cognitive functioning, health investments are reinforcing. Moreover, it bears mention that our study is in a low-income country context, in which resource constraints on investments in children are likely more binding than in high-income countries. The natural next step is to compare reinforcement or compensation behavior in a variety of countries across the per capita income distribution.
Second, we build on the use of sibling fixed effects estimators in studies on the impacts of early-life events. Sibling fixed effects are frequently used to control for unobserved household- or mother-level confounders like preferences and household resources.5 If treatment spillovers across siblings are large enough, the fixed effect estimate will not purely reflect the investment response to own endowment changes, but rather will reflect the investment response relative to the responses of other siblings.. Since the sign of this cross-sibling response is a priori indeterminate, we cannot sign the bias. Our strategy, under the assumption that programme exposure was exogenous, allows us to identify effects on both own investments as well as sibling investments. Moreover, sibling fixed effects estimators rely on households with multiple children, whereas our strategy is able to include single-child households (in our sample, this amounts to more than a quarter of households).
Finally, we contribute to the discussion on proxy variables for child endowments. The difficulty in finding exogenous variation in the endowment is that outcomes at birth (e.g., birth weight, APGAR scores) or in infancy (e.g., health shocks, cognitive ability) are in part determined by prenatal investments. Studies using comparisons within twin pairs have circumvented this problem (Behrman and Rosenzweig 2004; Rosenzweig and Zhang 2009; Datar et al. 2010; Bharadwaj et al. 2013), but those that estimate investment responses must contend with the same difficulties outlined above regarding sibling fixed effects estimators. Our strategy adds to this discussion. Iodised oil capsule distribution is advantageous for the purposes of our study, in the sense that the intervention has its effect prior to conception, but this effect is not readily perceptible until some time after the child’s birth. The benefit of this timing is that our measure of treatment exposure does not fall prey to the criticism levied on the studies mentioned above. The drawback is that we do not use a direct measure of cognitive ability. We contend that the insights gained from the analysis of programme exposure effects are nevertheless useful, because they help answer the policy-relevant question: do iodine supplementation programs change parents’ investment behaviors?
The remainder of the paper is structured as follows. Section 1 describes the iodine supplementation programme in Tanzania. Section 2 describes the data. Section 3 explains the empirical strategy. Section 4 presents the results and provides evidence related to the potential mechanisms of impact. Section 5 interprets the results of sibling spillovers in the context of a simple model of optimal intrahousehold allocations. Last, section 6 concludes.
1 Iodine Supplementation Program
In this section, we describe the relevant aspects of the iodine supplementation programme in Tanzania. The programme was developed by the Tanzanian government as a stopgap measure to curb iodine deficiency disorder (IDD), which, prior to programme roll-out, was rampant (FRT quote a figure of approximately 25 percent of the Tanzanian population) (F. van der Haar, P. Kavishe, and M.G. Medhin 1988). Pre-programme measurements of visible goiter rate among school children were taken in 1984. Districts with a goiter rate above 10 percent were enrolled in the program. Stefan Peterson et al. (1999) estimate that the population in these districts totaled about 25 percent of the national population.
Iodine supplementation, via 380mg iodised oil capsules (IOC), was targeted towards women of child-bearing age in programme districts. Remaining supplies were distributed, in declining order of importance, to children 1–5, older children, and adult men 15–45. Priority was given to adult women because of the importance of iodine in fetal brain development.
Dissemination of the capsules began in 1986 and was slotted to take place every two years. The goal of the campaign was to visit each district every two years, but administrative problems prevented this from happening; as a result, districts were visited between 1 and 5 times during the programme years (Peterson et al. 1999). Nevertheless, when the programme ended in 1994, approximately 5 million individuals, most of them women and children, had received IOC supplementation. Table A.1 in the Appendix (reproduced from FRT) lists the programme districts and the years in which the programme visited each district.
Table A.1.
Program Years
| Region | District | Year 1 | Coverage 1 | Year 2 | Coverage 2 | Year 3 | Coverage 3 | Year 4 | Coverage 4 | Year 5 | Coverage 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Dodoma | Mpwapwa | 1990 | 0.65 | 1992 | 0.58 | ||||||
| Arusha | Monduli | 1992 | 0.71 | ||||||||
| Arusha | Arumeru | 1991 | 0.89 | ||||||||
| Kilimanjaro | Rombo | 1990 | 0.68 | ||||||||
| Morogoro | Ulanga | 1988 | 0.73 | 1991 | 0.61 | 1992 | 0.34 | ||||
| Ruvuma | Songea Rural | 1987 | 0.91 | 1991 | 0.74 | 1995 | 0.85 | ||||
| Ruvuma | Mbinga | 1995 | 0.92 | ||||||||
| Iringa | Mufindi | 1986 | 0.41 | 1991 | 0.63 | 1995 | 0.54 | ||||
| Iringa | Makete | 1986 | 0.2 | 1991 | 0.62 | 1993 | 0.62 | 1996 | 0.49 | ||
| Iringa | Njombe | 1989 | 0.76 | 1992 | 0.68 | 1995 | 0.64 | ||||
| Iringa | Ludewa | 1989 | 0.59 | 1992 | 0.62 | 1995 | 0.47 | ||||
| Mbeya | Chunya | 1990 | 0.49 | ||||||||
| Mbeya | Mbeya Rural | 1986 | 0.44 | 1989 | 0.84 | 1990 | 0.9 | 1993 | 0.53 | 1997 | 0.53 |
| Mbeya | Kyela | 1989 | 0.91 | 1993 | 0.57 | ||||||
| Mbeya | Rungwe | 1986 | 0.35 | 1990 | 0.73 | 1993 | 0.49 | ||||
| Mbeya | Ileje | 1989 | 0.94 | 1992 | 0.71 | ||||||
| Mbeya | Mbozi | 1989 | 0.67 | 1991 | 0.63 | ||||||
| Rukwa | Mpanda | 1987 | 0.79 | 1991 | 0.6 | 1993 | 0.72 | ||||
| Rukwa | Sumbawanga | 1987 | 0.76 | 1990 | 0.89 | 1993 | 0.72 | 1996 | 0.51 | ||
| Rukwa | Nkansi | 1987 | 0.89 | 1991 | 0.49 | ||||||
| Kigoma | Kibondo | 1989 | 0.73 | 1992 | 0.75 | 1996 | |||||
| Kigoma | Kasulu | 1987 | 0.5 | 1990 | 0.66 | 1996 | 0.49 | ||||
| Kigoma | Kigoma Rural | 1991 | 0.91 | ||||||||
| Kagera | Karagwe | 1990 | 0.96 | 1994 | 0.85 | ||||||
| Kagera | Bukoba Rural | 1994 | 0.78 | ||||||||
| Kagera | Biharamulo | 1990 | 0.96 | 1994 | 0.38 | ||||||
| Kagera | Ngara | 1989 | 0.29 | 1994 | 0.51 |
Notes: Taken from Field et al. (2009)
Peterson (2000) evaluated the short-term impact of this programme in three programme districts in 1991, and found that visible goiter rate and total goiter rate had declined significantly among children who received IOC supplementation directly. FRT point out that, given the medical evidence on the importance of fetal iodine, the potential programme impact on children affected while in utero is much higher. They produce the first evidence of the long-run impact of the program, documenting significant improvements in educational attainment for treated children.
2 Data
In this section, we provide details on the data; variables used in analysis and their construction; and the matching procedure used to identify residence in treatment districts.
2.1 The 1999 Tanzania Demographic and Health Survey (DHS)
We use the 1999 round of the Tanzania DHS. As described below, many of the early-life investment variables, such as receipt of vaccinations and duration of breast-feeding for example, are only recorded for children under five years old. Thus, our main sample is the sample of live children under five in 1999. There are 456 such children in 1999.
Note that we are restricting attention to only those children living in districts that were visited at least once during the supplementation program. This is because programme districts were not chosen randomly, but rather selected on the basis of visible goiter rates. In this sense, comparison between districts visited at least once during the programme and those excluded from programme participation is rendered invalid.
The DHS collects information on demographic characteristics of all household members. We use the following demographic variables: child’s age (month and year of birth), gender, and birth order; mother’s age and educational attainment in years; and household’s total size, number of children, and urban/rural status. Means and standard deviations of these variables are reported in Table Ia by sample.
Table 1. Summary Statistics.
Demographic Characteristics, IOC Exposure, and Health Investments
| Children Aged Under 5 in 1999 DHS | ||||||
|---|---|---|---|---|---|---|
| Whole Sample | Own Treatment Exposure >=.75 |
Own Treatment Exposure <.75 |
||||
| Number of children: | 456 | 156 | 300 | |||
| Mean | SD | Mean | SD | Mean | SD | |
| Children | ||||||
| Age | 1.860 | 1.393 | 2.064 | 1.263 | 1.753 | 1.447 |
| Female | 0.478 | 0.500 | 0.513 | 0.501 | 0.460 | 0.499 |
| Birth Order | 3.123 | 2.065 | 2.942 | 1.750 | 3.217 | 2.209 |
| Mothers | ||||||
| Age | 28.502 | 6.987 | 28.737 | 6.555 | 28.380 | 7.209 |
| Years of Completed Educ. | 5.024 | 3.137 | 4.974 | 3.261 | 5.050 | 3.076 |
| Households | ||||||
| Number of Children | 3.559 | 2.261 | 3.410 | 2.000 | 3.637 | 2.385 |
| Household Size | 6.568 | 3.215 | 6.295 | 2.890 | 6.710 | 3.368 |
| Urban | 0.086 | 0.280 | 0.103 | 0.304 | 0.077 | 0.267 |
| Program Exposure | ||||||
| Own IOC Treatment Exposure | 0.437 | 0.425 | 0.955 | 0.071 | 0.168 | 0.246 |
| Siblings' IOC Treatment Exposure | 0.631 | 0.751 | 0.623 | 0.755 | 0.636 | 0.749 |
| Vaccinations | ||||||
| Number of polio doses (max = 3) | 2.645 | 0.842 | 2.795 | 0.660 | 2.567 | 0.914 |
| Number of DPT doses (max = 3) | 2.629 | 0.897 | 2.808 | 0.673 | 2.537 | 0.982 |
| Measles | 0.756 | 0.430 | 0.833 | 0.374 | 0.715 | 0.452 |
| Number of total vaccinations (max = 7) | 6.026 | 2.006 | 6.436 | 1.512 | 5.812 | 2.194 |
| Nutritional Investments | ||||||
| Mos. Breastfeeding | 16.223 | 8.281 | 18.255 | 6.953 | 15.184 | 8.713 |
| Mos. Breastfeeding >6 | 0.872 | 0.334 | 0.974 | 0.160 | 0.819 | 0.385 |
| Neonatal Investments | ||||||
| Formal Sector Delivery | 0.447 | 0.498 | 0.494 | 0.502 | 0.423 | 0.495 |
| Attended Delivery | 0.947 | 0.224 | 0.949 | 0.221 | 0.947 | 0.225 |
| Polio 0 Dose | 0.445 | 0.498 | 0.429 | 0.497 | 0.453 | 0.499 |
| BCG | 0.941 | 0.236 | 0.955 | 0.208 | 0.933 | 0.250 |
| Has Health Card | 0.958 | 0.200 | 0.981 | 0.138 | 0.947 | 0.225 |
The first two columns of Table 1 present means and standard deviations of child, mother, and household level covariates included in the analysis. Columns 3–6 show the same summary statistics for two subsamples: children with treatment probability of 0.75 and above and children with treatment probability below 0.75.6 The treatment probability is largely determined by month and year of birth and so we might expect to find a difference in the mean of age across these two subsamples. This, of course, motivates the inclusion of age and related variables as covariates in the specifications. We conduct all of our analysis using fixed effects for the child’s age in years to avoid any issues deriving from this systematic relationship between timing of birth and treatment probability.7 Indeed, we see that there exists a difference in mean age of the child across the two subsamples. Otherwise, the means of the remaining covariates show no statistical differences across the two subsamples.
Apart from demographic information, the DHS contains detailed information on early-life health investments for all children under five in surveyed households. We use the following investment variables:
Count of the number of polio vaccine doses administered (maximum 3);
Count of number of DPT (diphtheria, pertussis and tetanus combination) vaccine doses administered (maximum 3);
Receipt of measles, BCG and polio 0 vaccines;
Formal-sector delivery and attended delivery;
Possession of a health card, which tracks vaccinations;
Duration of breastfeeding in months;
Perceived average size at birth (scale of 1–5);
Birth weight (only recorded for the most recent birth of the household, 205 out of 456 children under 5 in our sample).
Means and standard deviations of these variables are reported in Table 1. Own treatment exposure is, by definition, substantially higher in the “treatment group” (column 3). Note that sibling treatment exposure is not significantly different across the two groups, lending credence to our assumption that own and sibling treatment are not systematically related.
In terms of the outcomes, the general pattern observed in Table 1 is that children who were more exposed to treatment received more vaccinations and were breastfed for longer, but do not have substantially different means in terms of neonatal investments. This preliminary evidence is corroborated using a more rigorous econometric specification in the sections that follow.
2.2 IOC Supplementation Programme Data
The DHS also includes, upon request, geocode data for the sampling clusters. Coordinates are skewed using a random skewing algorithm which skews the coordinates by a distance drawn from a uniformly distributed probability area with radius of 15km around the actual coordinate pair. To identify which households live in intervention districts, we superimposed geocode data on the latitude and longitude of each cluster in 1999 onto a raster map of Tanzania with district borders. We used this mapping to identify which clusters fell inside treatment districts (with a very small random probability of misclassification due to geocode skewing by DHS). We obtained data on the names of intervention districts and programme years from FRT (Table A.1). As described in the following section, we use these data to construct (following FRT) a measure of programme participation.8
3 Empirical Strategy
In this section, we define programme participation, present our empirical specification, and discuss threats to validity.
3.1 Definition of Programme Participation
We define an exposure-to-treatment variable that reflects the extent to which an individual was exposed to IOC supplementation while in utero. We generally follow the procedure outlined in FRT, and note where our procedure differs from theirs. To construct the treatment indicator, we combine information on the following:
the month and year of birth of the child;
the district of the mother’s residence at time of survey;
years in which the programme was rolled out in each district;
and the biological properties of iodine within the body.
Suppose we knew exactly when each mother received IOC supplementation. If this were true, we could calculate how long after receiving supplementation the woman was pregnant, and thus we could determine (after making some assumptions on the rate of decay of iodine in the body) the exact amount of exposure for the fetus.
However, we do not know the date of supplementation (nor, in fact, whether a given mother received the IOC at all). Thus, as in FRT, we must instead calculate the probability with which an individual was treated with IOC while in utero. FRT begins by assuming, using administrative records from the programme roll-out, that each roll-out took three months, and that the timing of this three-month period was uniformly distributed over the roll-out year.
FRT then couples this probability with information on the birth month and birth year of the child and the biological properties of iodine within the body to arrive at a final probability of treatment for each individual. IOC supplementation allows for normal development of neural networks of fetuses in the first trimester of pregnancy, but not thereafter. Thus, the intervention can only be effective if iodine from the IOC is present in the body during the first trimester.
To approximate how much iodine is present at various times, FRT use information pertaining to the decay of iodine in the body. 85 percent of the iodine is extracted immediately through urination, and the rest is assumed to follow a hyperbolic decay pattern. Additionally, a lower cutoff level is assumed, after which there is too little iodine left in the body for adequate protection against fetal iodine deficiency disorder. These values, as well as the half-life formula derived from the assumed hyperbolic iodine depletion, are detailed in FRT’s Web Appendix.
The procedure described above generates a positive probability of treatment for each month following a roll-out for four years after a roll-out year (after which the probability is uniformly 0). These probabilities are reported in Appendix Table A.2 (replicated from FRT). Coupling data on the birth month and birth year of each child with data on programme roll-out years in each intervention district, we can assign each individual in our data a probability of treatment.9 Since programme roll-outs happened up to five times in a given district, individuals may have multiple instances of exposure to IOC. In these cases, we use the maximum of the multiple assigned probabilities for that individual.
Table A.2.
Treatment Probabilities
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Program Year | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.028 | 0.083 | 0.167 | 0.250 | 0.333 |
| 1st Year After Program | 0.417 | 0.500 | 0.583 | 0.667 | 0.750 | 0.833 | 0.917 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 2nd Year After Program | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.998 | 0.991 | 0.977 |
| 3rd Year After Program | 0.955 | 0.927 | 0.891 | 0.849 | 0.802 | 0.749 | 0.690 | 0.627 | 0.559 | 0.488 | 0.419 | 0.353 |
| 4th Year After Program | 0.292 | 0.237 | 0.189 | 0.148 | 0.112 | 0.082 | 0.057 | 0.037 | 0.022 | 0.011 | 0.004 | 0.001 |
Notes: Taken from Field et al. (2009)
To estimate the effects of siblings’ treatment probabilities on the individual, we add up the treatment probabilities of the two immediately older siblings and the two immediately younger siblings in the child’s household (which may include siblings from a different mother) to generate a total sibling probability of treatment. If the child has, in fact, less than two older and/or two younger siblings, zeros are imputed for the treatment probabilities of these non-existent siblings. In this way, we may compare children with a differing number of siblings on the basis of total treatment within the household (we flexibly control for number of siblings in all specifications). Treatment probabilities of siblings more than two spaces ahead or behind the child in the birth order are ignored, under the notion that, for example, decisions of whether to vaccinate two children of vastly different ages are not made contemporaneously.10
3.2 Empirical Specification
We now turn to estimation of the effects of IOC supplementation on early-life health investments, using the programme exposure measure whose construction is described in the previous section. Denote the investment (e.g. vaccinations, length of breastfeeding, etc.) as I; programme exposure as To; i as child (which is the level of observation); j as household; k as district; a as age of the child; and X as child-and household-level controls. We estimate models with the following specification:
| (1) |
We focus attention on two important sets of controls: district fixed effects (μk) and (integer) age fixed effects (ζa). The district fixed effects capture time-invariant elements of districts which may be correlated with demand- and supply-side factors governing adoption of health investments, as well as with treatment intensity. For example, districts with low access to vaccinations may also have been targeted more intensively for IOC supplementation due to a higher level of observed IDD (via visible goiter rates, as described in Section IIC, on programme targeting, in FRT).
The age fixed effects restrict our treatment comparisons to children of the same integer age who have different treatment probabilities (either because they were born in different districts, or in separate months). Since variation in To, own treatment probability, is entirely determined by an interaction of district of birth and age in months, we must be careful to empirically distinguish between age-related trends in health investments and the true endowment effects we seek to estimate. Integer age fixed effects are thus essential, as they flexibly absorb variation in health investments related to age.
In later analysis, we also estimate the following slightly modified specification, in which cumulative sibling programme exposure (Ts) is added to the regression:
| (2) |
Note that Ts, cumulative sibling programme exposure, potentially varies at the individual level within the household (though, as described earlier, we need not rely on this variation for identification), since sibling treatment is only defined for the four closest siblings in terms of birth order (two older and two younger).
3.2.1 Controls
In addition to integer age and district fixed effects discussed above, we control for characteristics of the child (i), his mother, and his siblings and household (j). Included are a female dummy, number of girl siblings, fixed effects for the number of younger and of older siblings, the sum of age across siblings, the minimum and maximum ages of siblings, and dummies for the median age of children in the household. Finally, X includes various additional child-, mother-, and household-level controls. Included are an urban dummy; a rainy season dummy11; fixed effects for within-gender birth order12; and decile fixed effects for each of the following: household size, number of females in the household, mother’s age, and mother’s education in years.
3.2.2 Sample Restrictions
Our main sample is all children in the data born between 1986 and 1999 (inclusive) in intervention districts (i.e. districts which were targeted for IOC supplementation at least once). We focus on these years of birth because this is the maximum range within which children were potentially exposed to the programme with positive probability. Outside of this birth year range (and obviously outside of intervention districts), the treatment probability is uniformly zero. Our analysis is run on the sample of children under five years old (i.e. with a maximum age of 59 months) in 1999 for whom data on vaccinations and breastfeeding are available.
4 Results
4.1 Main Results
In this section, we present the main results. Table 2 presents results of regressions of various health investments on IOC programme exposure. Recall that “IOC Treatment Exposure” ranges from 0 to 1, reflecting the extent of exposure to IOC supplementation. Columns 1–4 present results for recommended vaccinations during infancy, namely, polio (3 doses), DPT (3 doses), and measles. We use count variables for the number of polio doses and number of DPT doses, a dummy for receipt of measles vaccine, and a count variable for total number vaccinations (maximum 7). We use linear probability specifications for all variables. In column 5, we regress a dummy that equals 1 if the child was breastfed for more than 6 months (the WHO-recommended minimum length of breastfeeding) on own and sibling treatment exposure.
Table 2. Healthcare Investments in Infancy.
Effects of IOC Treatment on Vaccinations and Breastfeeding Behavior
| Vaccinations | |||||
|---|---|---|---|---|---|
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
Breastfed for more than 6 mos. |
|
| IOC Treatment Exposure | 0.373** (0.139) |
0.427*** (0.154) |
0.103* (0.0543) |
0.900*** (0.327) |
0.0818* (0.0407) |
| 1(Female) | 0.103 (0.0665) |
0.128** (0.0618) |
0.0306 (0.0310) |
0.270* (0.145) |
0.0116 (0.0227) |
| 1(Age 1) | 0.859*** (0.185) |
0.858*** (0.194) |
0.656*** (0.0872) |
2.392*** (0.433) |
0.629*** (0.0636) |
| 1(Age 2) | 1.023*** (0.228) |
1.001*** (0.242) |
0.747*** (0.121) |
2.762*** (0.532) |
0.647*** (0.0684) |
| 1(Age 3) | 1.040*** (0.270) |
1.088*** (0.278) |
0.741*** (0.128) |
2.867*** (0.614) |
0.601*** (0.0756) |
| 1(Age 4) | 1.029*** (0.280) |
1.032*** (0.312) |
0.764*** (0.151) |
2.811*** (0.674) |
0.644*** (0.0774) |
| Observations | 456 | 456 | 454 | 454 | 453 |
| Mean of Dependent Variable | 2.645 | 2.629 | 0.756 | 6.026 | 0.872 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1), clustered at the level of DHS cluster (primary sampling unit). Treatment exposure calculated using month and year of birth, and years in which the program was rolled out in each district (see Table A1). Specifications also control for: district fixed effects; urban dummy; rainy season dummy; percent of household's salt that is iodized (0, 25, 50, 75, or 100); minimum and maximum sibling ages; dummies for median sibling age; household size (deciles); number of females in household (quintiles); gender-specific birth order dummies; dummies for number of younger and older siblings; dummies for mother's integer age; and dummies for mother's years of completed schooling. Sample is restricted to households with at least 1 child < 5 years in 1999 DHS.
The results from all columns show that IOC programme exposure significantly increases the number of vaccinations received and the duration of breastfeeding in infancy. Increasing programme exposure by one standard deviation (0.43) increases the number of polio and DPT doses by 0.16 and 0.18, respectively; the probability of receiving the measles vaccine by 4.5 points; and the number of total vaccinations received by 0.38. A one standard deviation increase in IOC programme exposure yields a 3.5 point increase in probability of having been breastfed for the recommended period of time.
These effects on investments are somewhat small as compared to the means. For example, the mean numbers of polio and DPT doses received by children in our sample are 2.65 and 2.63, respectively. However, there is a great deal of variation in these vaccination numbers (e.g. standard deviations in polio and DPT doses are 0.84 and 0.90, respectively). A one standard deviation increase in IOC treatment exposure leads to a roughly 0.2 standard deviation increase in both polio and DPT doses received, as well as in total vaccinations. The results on breastfeeding amount to roughly a tenth of a standard deviation rise in the probability of being breastfed for at least 6 months in response to a one standard deviation rise in IOC treatment exposure. We interpret these results as small to moderate in magnitude, but statistically significant and very robust, as demonstrated in the Appendix.
4.2 Potential Mechanisms of Impact
In what follows, we explore impacts of IOC treatment exposure on other investments and at-birth measures of health. We then discuss these results in the context of potential mechanisms of impact of IOC treatment on investments.
4.2.1 Formal sector deliveries and investments at birth
We might expect, since vaccinations and breastfeeding behavior respond strongly the type of delivery and other at-birth investments respond as well. In Table 3, we test whether this is indeed the case, by presenting results from regressions of neonatal investments on IOC treatment exposure. Columns 1 and 2 of Table 3 report estimates of effects on dummy variables for whether the child was delivered in a formal-sector facility, and whether he had an attended delivery, respectively. We find insignificant and fairly small effects compared with the effects we observe on health investments in infancy.
Table 3. Healthcare Investments at Birth.
Effects of IOC Treatment on Neonatal Investments
| Delivery | Vaccinations | ||||
|---|---|---|---|---|---|
| Formal Sector | Attended | Polio 0 Dose | BCG | Health Card | |
| IOC Treatment Exposure | 0.0283 (0.0740) |
0.0245 (0.0366) |
0.0294 (0.0594) |
0.0261 (0.0426) |
0.0176 (0.0216) |
| 1(Female) | −0.0499 (0.0419) |
−0.0298 (0.0201) |
−0.0437 (0.0559) |
0.0212 (0.0261) |
−0.0170 (0.0191) |
| 1(Age 1) | 0.0645 (0.0969) |
0.0645 (0.0396) |
0.178* (0.0994) |
0.143** (0.0534) |
0.137** (0.0565) |
| 1(Age 2) | −0.140 (0.111) |
−0.0211 (0.0519) |
0.180 (0.132) |
0.179** (0.0696) |
0.141** (0.0559) |
| 1(Age 3) | −0.165 (0.137) |
−0.0314 (0.0626) |
0.325* (0.191) |
0.180** (0.0792) |
0.158** (0.0692) |
| 1(Age 4) | −0.181 (0.172) |
0.0454 (0.0800) |
0.381 (0.231) |
0.165** (0.0796) |
0.148* (0.0754) |
| Observations | 456 | 456 | 456 | 456 | 456 |
| Mean of Dependent Variable | 0.447 | 0.947 | 0.445 | 0.941 | 0.958 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1), clustered at the level of DHS cluster (primary sampling unit). Treatment exposure calculated using month and year of birth, and years in which the program was rolled out in each district (see Table A1). Specifications also control for: district fixed effects; urban dummy; rainy season dummy; percent of household's salt that is iodized (0, 25, 50, 75, or 100); minimum and maximum sibling ages; dummies for median sibling age; household size (deciles); number of females in household (quintiles); gender-specific birth order dummies; dummies for number of younger and older siblings; dummies for mother's integer age; and dummies for mother's years of completed schooling. Sample is restricted to households with at least 1 child < 5 years in 1999 DHS.
Column 3 reports estimates of the effects on the initial dose of the polio vaccine, which is recommended to be administered at the time of birth, and column 4 corresponds to a regression of receipt of the BCG vaccine, recommended from 0–6 weeks, on IOC treatment exposure. In both columns, we find small effect estimates that are not significantly different from 0. In column 5, estimates from a regression of a dummy for whether the child has a health card on treatment exposure are reported. A health card is used to keep track of which vaccinations the child has received and is usually issued very early in the child’s life. Here again the point estimates are small and not significantly different from 0.
We interpret this evidence as consistent with the notion that parents appear to be responding to observed improvements in endowments later in infancy rather than to expected improvements in birth endowments or observed endowments at birth. That is, if parents’ expectations regarding their child’s endowments were impacted by the programme before realised endowments were observed, their investment decisions might reflect these amended expectations as well as amended realised endowments; however, expectations alone can impact at-birth investments, where as both expectations and realised endowments might impact investments later in infancy.
Nevertheless, while it is interesting to see that investments in infancy respond to treatment exposure when neonatal investments do not, we refrain from strongly interpreting these results as conclusive evidence of investments responding only to observed improvements in endowments after the child’s birth. Data limitations prevent us from ruling out the possibility that programme exposure impacted expectations regarding child endowments, which in turn impacted investment responses. Specifically, we do not have data on expectations or perceptions of cognitive endowments. We do, however, have some data on perceived physical endowments at birth.
4.2.2 Health at birth
We next test whether the child’s health at birth is affected by the program, either through direct biological impacts of iodine or as a result of prenatal investment responses to information and/or expectations regarding endowments. We regress dummies for perceived size of the child (below- and above-average size dummies), as well as the actual birth weight (for last birth only), on IOC treatment exposure, using the same baseline specification as employed for the main results on vaccinations. Table 4 reports the results of these regressions. We find that treatment exposure is not clearly and consistently related to perceived size or birth weight. In general, the coefficients are small and, at most, weakly significant.
Table 4. Effects on Health At Birth.
Effects of Treatment on Perceived and Measured At−Birth Health of Child
| Perceived | Measured | |||
|---|---|---|---|---|
| Size at Birth (ordered, 5 categories) |
1(Below Avg. Size) |
1(Above Avg. Size) |
Birth Weight (g) (last birth only) |
|
| IOC Treatment Exposure | 0.0345 | 0.000802 | −0.0722* | 209.7* |
| (0.120) | (0.0659) | (0.0373) | (123.9) | |
| 1(Female) | −0.323** | −0.0881* | 0.0320 | −136.8 |
| (0.155) | (0.0480) | (0.0264) | (113.8) | |
| 1(Age 1) | 0.0934 | 0.0609 | 0.0648 | −16.17 |
| (0.254) | (0.0907) | (0.0536) | (233.9) | |
| 1(Age 2) | −0.184 | 0.0133 | 0.0866 | 69.26 |
| (0.233) | (0.106) | (0.0907) | (393.7) | |
| 1(Age 3) | 0.173 | 0.125 | 0.0661 | 380.0 |
| (0.345) | (0.140) | (0.127) | (580.4) | |
| 1(Age 4) | 0.0702 | 0.0588 | 0.0611 | 103.3 |
| (0.404) | (0.180) | (0.147) | (658.4) | |
| Observations | 455 | 454 | 454 | 205 |
| Mean of Dependent Variable | 0.110 | 0.165 | 0.0881 | 3071 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1), clustered at the level of DHS cluster (primary sampling unit). Treatment exposure calculated using month and year of birth, and years in which the program was rolled out in each district (see Table A1). Perceived size at birth (column 1) normalized to 0 (categories are −2, −1, 0, 1, 2); ordered probit model used. Below average size is dummy for smallest 2 categories of 5: ";smaller than average" and "very small." Specifications also control for: district fixed effects; urban dummy; rainy season dummy; percent of household's salt that is iodized (0, 25, 50, 75, or 100); minimum and maximum sibling ages; dummies for median sibling age; household size (deciles); number of females in household (quintiles); gender-specific birth order dummies; dummies for number of younger and older siblings; dummies for mother's integer age; and dummies for mother's years of completed schooling. Sample is restricted to households with at least 1 child < 5 years in 1999 DHS.
In Table 4, we find no consistent evidence of an impact of programme exposure on size at birth. That is, columns 1 and 2 show no evidence of an impact on categorical size or below average size. Column 3 shows a weakly significant, negative impact on the probability of above average size; while column 4 shows a weakly significant, positive impact on measured birthweight of the last born child. Overall, we find no consistent evidence that health at birth was affected by in utero programme exposure.
We interpret this evidence as suggestive that indirect programme effects on prenatal investments, if they existed at all, were indeed not substantial.13 Nevertheless, we should note that data on perceptions of size at birth and measured birthweight for a subsample of children are not ideal measures for studying programme impacts on physical health at birth, expected endowments, and prenatal or neonatal investment responses. Accordingly, while these results are consistent with our notion that parental investments responded to observed improvements in cognitive endowments later in infancy, we cannot provide conclusive evidence against impacts on physical endowments and responses in prenatal or neonatal investments.14
Though the evidence of the impact of in utero iodine availability on observable physical health endowments at birth (e.g., birth weight) is mixed, it is possible that parents perceived or expected to observe improvements in the physical health of their children and adjusted their investment decisions in response. Given that the primary empirical contribution of this study is to estimate parental investment responses to endowments, the validity of the results in Table 2 is unaffected by whether parents respond to perceived shifts in physical or cognitive endowments.
4.2.3 Can Mothers Perceive the Cognitive Endowments of Their Infant Children?
The main class of investments we examine is vaccinations, which infant children are supposed to receive between 6 and 12 months of age (depending, of course, on the particular vaccination and number of doses). Although, as discussed above, investments might respond to some combination of expected endowment shifts and perceived shifts in both physical and cognitive endowments, for cognitive endowments to play any role, parents must indeed be able to perceive the cognitive endowments of their infant children. In what follows we cite a collection of medical studies on the plausibility of this notion.
The ability of mothers to identify behaviors in newborns is well documented. T. Berry Brazelton’s (1984) seminal work on the Neonatal Behavior Assessment Scale has documented significant variation in observable behaviors even at 7 days after birth; the scale is often used by mothers to catalog their infant’s level of cognitive and physical activity. Further, a long literature on pre-linguistic communication has demonstrated that the infants’ cognitive abilities become apparent through their demonstration of coordinated actions. For instance, Bullowa (1979) writes that “infants master the difficulties of relating objects and situations to themselves and predict consequences, not merely in hidden cognitive processes but in manifest, intelligible actions” (Bullowa 322). Infants as young as 1 day old begin to imitate the facial gestures of their mothers, and that this imitation is the root of later social cognition (Meltzoff and Moore 1983, 1997). Maternal sensitivity to infants’ signals indeed feeds back into the understanding of relationships and attachment security in adulthood (Susman-Stillman et al. 1996; Beckwith et al. 1999). Overall, the evidence from the medical literature supports the notion that mothers are able to recognise, assess, and react to signals of cognition in their infant children from very early ages.
4.2.4 In Utero Exposure v. Mother’s IOC exposure
While the main purpose of the Tanzanian IOC distribution campaign was to establish protection for children during the crucial in utero period of brain development, iodine supplementation also has direct, contemporaneous effects on energy and cognition for mothers (Peter Laurberg et al. 2001). This fact poses a threat to the validity of our interpretation that changes in investments occurred because of changes in the child’s endowment. If direct exposure matters, part of the estimated effects of the child’s IOC exposure might reflect changes in the mother’s health.
We present two arguments against this critique. First, if in utero IOC exposure had a large enough effect on mothers’ energy levels to impact immunization and breastfeeding behaviors up to a year after the child’s birth, we would expect that investments at birth (closer to the time of supplementation) would respond as well, analogously to the argument in the previous section. But as the results in Tables 3 and 4 show, these investments do not respond significantly.
Second, we control directly for whether the mother was exposed an additional time to the IOC campaign after the birth of the child, since contemporaneous exposure would boost energy levels for mothers at the time when vaccination and breastfeeding choices are being made. We report the results of this estimation in Table 5. Across all dependent variables, we find that controlling for mother’s subsequent exposure (“Additional programme roll-out after child’s birth”) does not affect the magnitude or precision of the estimates on the impact of IOC treatment exposure.
Table 5. Does IOC Affect Investments Via Mother's Exposure?
Effects of IOC Treatment Conditional on Number of Program Roll-outs Since Child's Birth
| Vaccinations | |||||
|---|---|---|---|---|---|
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
Breastfed for more than 6 mos. |
|
| IOC Treatment Exposure | 0.404** (0.154) |
0.465*** (0.169) |
0.116* (0.0583) |
0.984** (0.361) |
0.0727* (0.0403) |
| 1(Additional Program Roll-out After Child's Birth) |
0.199 (0.161) |
0.240 (0.166) |
0.0796 (0.0671) |
0.532 (0.374) |
−0.0601 (0.0383) |
| 1(Female) | 0.101 (0.0655) |
0.125** (0.0611) |
0.0298 (0.0305) |
0.263* (0.142) |
0.0116 (0.0225) |
| 1(Age 1) | 0.859*** (0.186) |
0.858*** (0.195) |
0.655*** (0.0871) |
2.394*** (0.436) |
0.628*** (0.0632) |
| 1(Age 2) | 1.017*** (0.229) |
0.993*** (0.244) |
0.743*** (0.120) |
2.746*** (0.534) |
0.648*** (0.0679) |
| 1(Age 3) | 1.030*** (0.270) |
1.076*** (0.280) |
0.734*** (0.125) |
2.840*** (0.615) |
0.602*** (0.0759) |
| 1(Age 4) | 0.978*** (0.284) |
0.969*** (0.319) |
0.738*** (0.148) |
2.668*** (0.690) |
0.656*** (0.0777) |
| Observations | 456 | 456 | 454 | 454 | 453 |
| Mean of Dependent Variable | 2.645 | 2.629 | 0.756 | 6.026 | 0.872 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1), clustered at the level of DHS cluster (primary sampling unit). Treatment exposure calculated using month and year of birth, and years in which the program was rolled out in each district (see Table A1). Specifications also control for: district fixed effects; urban dummy; rainy season dummy; percent of household's salt that is iodized (0, 25, 50, 75, or 100); minimum and maximum sibling ages; dummies for median sibling age; household size (deciles); number of females in household (quintiles); gender-specific birth order dummies; dummies for number of younger and older siblings; dummies for mother's integer age; and dummies for mother's years of completed schooling. Sample is restricted to households with at least 1 child < 5 years in 1999 DHS.
4.2.5 Endogenous Fertility Determination
Next we address the potential threat posed by the endogenous determination of fertility. If some households (or mothers) time their fertility so as to optimise the gains from IOC supplementation, then the realised programme exposure would be larger for these households. If these same households, who may hold a high preference for their children’s health, make health investments more frequently, then the coefficient on IOC programme exposure would be an upward-biased estimate of the true endowment effect. Moreover, programme exposure might itself change fertility patterns via the quantity-quality tradeoff. That is, households may adjust their completed fertility or the spacing of births after a high-endowment child is born.
Timing of Births
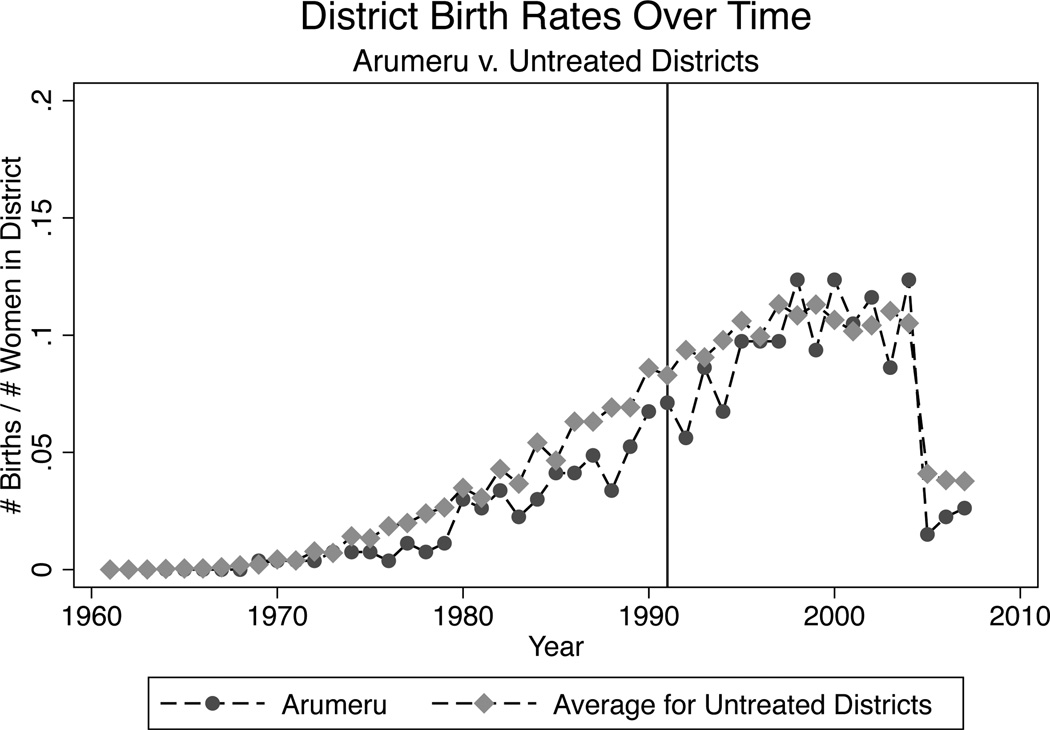
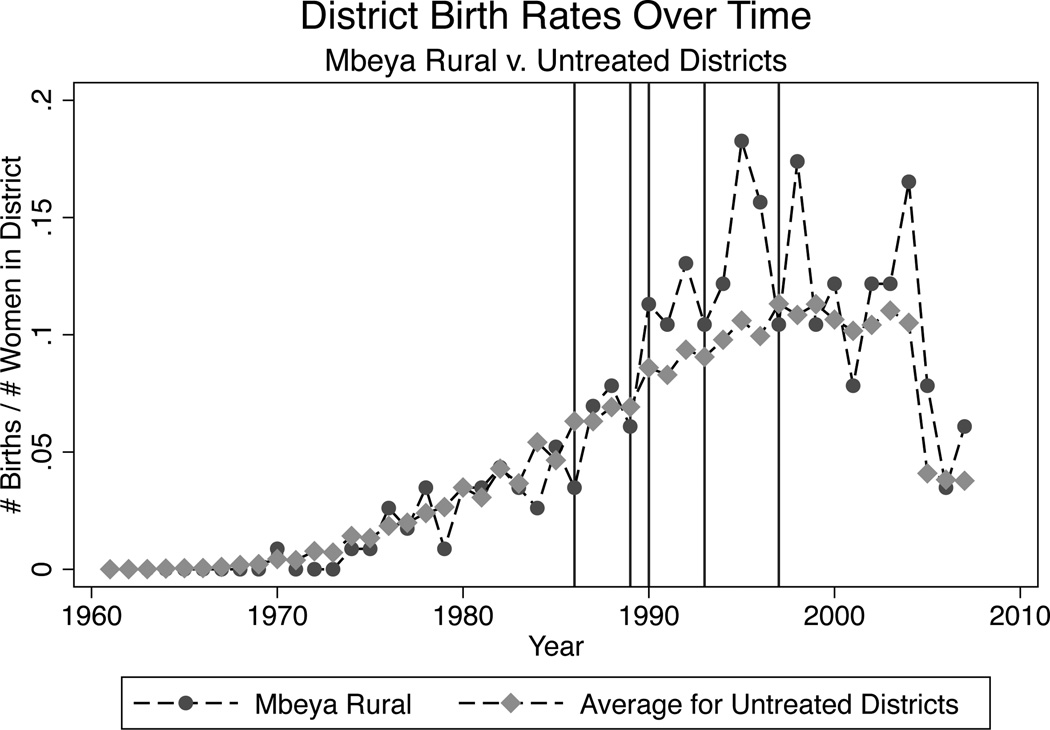
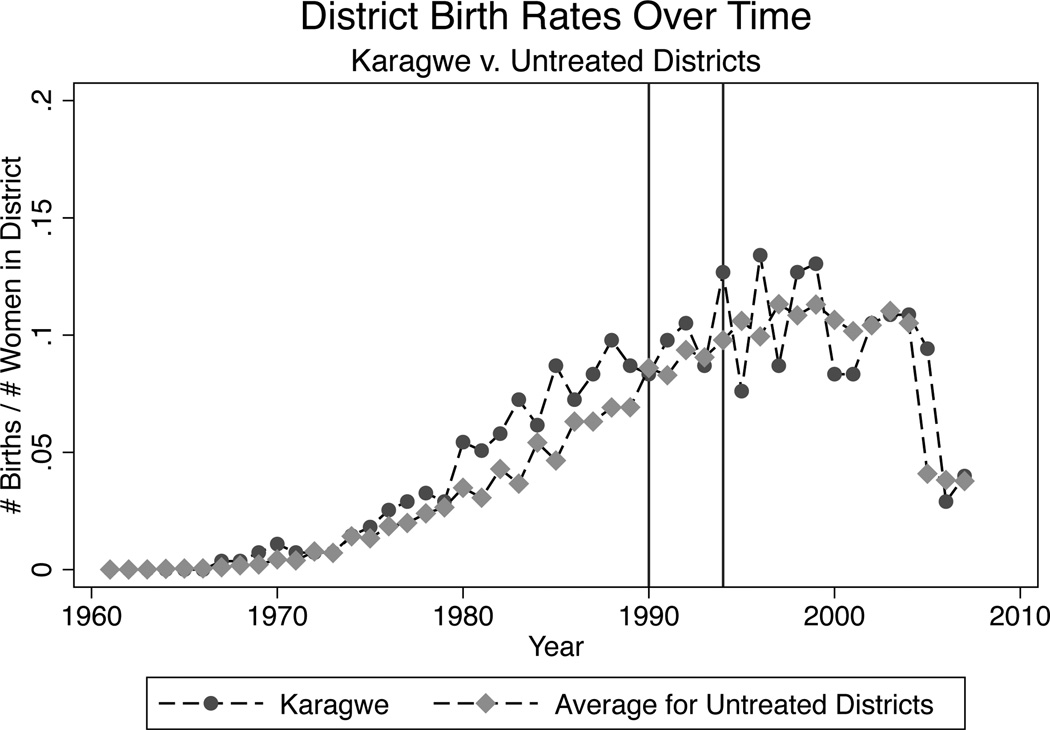
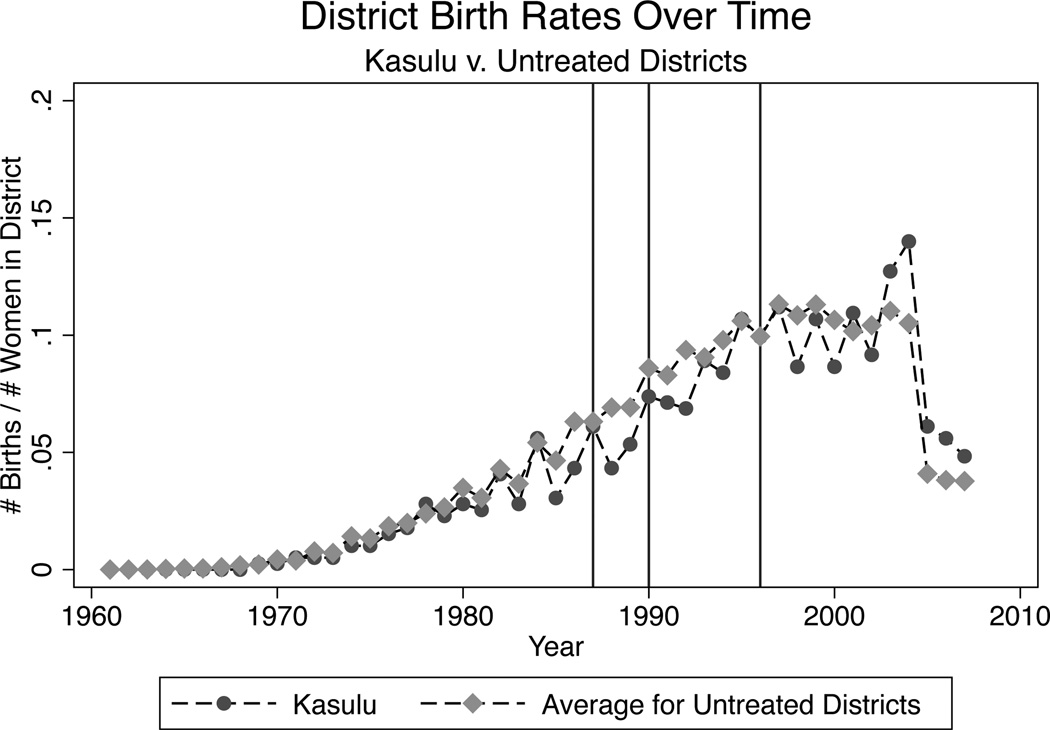
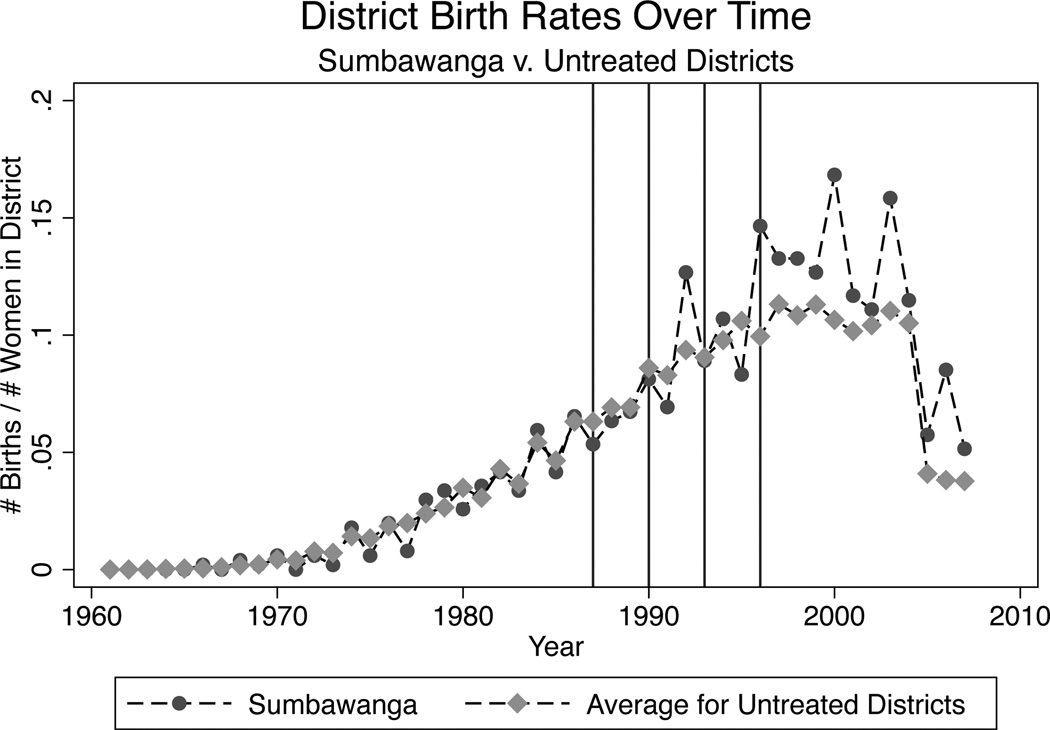
We examine the endogenous timing of births visually by plotting district level birth rates in programme districts by year against the average yearly birth rate for untreated districts. These plots are presented in Figures 1–5 for selected treatment districts. As mentioned above districts were visited anywhere from 1–5 times during the program. We have chosen to show an example district from each of these sets of districts which were visited 1, 2, 3, 4, or 5 times. In these figures, we have denoted programme years with red vertical lines. We see no structural breaks in the district birth rate trends during or just after programme years. Though some districts exhibit greater volatility in birth rates over time, no systematic pattern of peaks and troughs can be found.
FIGURE 1.
Birth Rate Trends
FIGURE 5.
Birth Rate Trends
To investigate empirically whether households’ fertility behaviors are affected by treatment, we reshaped the mother-level DHS data (appended across the 1999, 2004 and 2007 rounds) into a mother-by-year-level data set which expands the fertility histories of each mother into a panel of 5968 women spanning 47 years (the earliest birth reported in the data was in 1961). We restrict our analysis to the sample of years between 1986 and 2002 inclusive (the same birth year restriction used in the data). We are left with approximately 100,000 individual-year observations. Denote an indicator for a child birth for mother i in district j in year t as Bijt. Denote as a dummy which equals one k years after a programme year (t) in district j, for k ∈ {0, 1, 2, 3, 4}. We run the following specification relating births to programme years in intervention districts:
| (3) |
The above specification restricts attention to within-mother variation over time by employing mother-level fixed effects. We can thus determine whether programme roll-out has effects on fertility, and if so, with how much lag. The results of the estimation of this specification for k ∈ {0, 1, 2, 3, 4} are reported in Table 6. The five columns in panel A report results for the programme roll-out indicators as described above, while the four columns of panel B report results for specifications using cumulative indicators which span from the programme year to the kth year after. Across all of these specifications, we find extremely small estimates tightly bound around zero, indicating that programme roll-out does not have any discernable effects on mothers’ fertility patterns.
Table 6. Timing of Fertility.
Effects of IOC on Probability of Birth
| Panel A: Program and Subsequent Years | |||||
| Program Year |
1st Year After Program |
2nd Year After Program |
3rd Year After Program |
4th Year After Program |
|
| Birth in This Yr | −0.000950 (0.00295) |
−0.00142 (0.00319) |
−0.00112 (0.00326) |
0.00257 (0.00316) |
−0.00316 (0.00347) |
| Fixed Effects | Mother, Year | ||||
| Observations | 101456 | 101456 | 101456 | 101456 | 101456 |
| Mean of Dependent Variable |
0.0930 | 0.0930 | 0.0930 | 0.0930 | 0.0930 |
| Panel B: Program and Subsequent Years (Cumulative) | |||||
| Program Yr -> 1 Yr After |
Program Yr -> 2 Yrs After |
Program Yr -> 3 Yrs After |
Program Yr -> 4 Yrs After |
||
| Birth in This Yr | −0.00205 (0.00236) |
−0.00350 (0.00214) |
−0.00315 (0.00259) |
−0.00387 (0.00287) |
|
| Fixed Effects | Mother, Year | ||||
| Observations | 101456 | 101456 | 101456 | 101456 | |
| Mean of Dependent Variable |
0.0930 | 0.0930 | 0.0930 | 0.0930 | |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1), clustered at the level of DHS cluster (primary sampling unit). Sample is limited to 1986–2002 (5 years after the last wave of intervention roll-outs were completed).
Quantity and Spacing of Children
We now check whether the treatment probability affects the quantity and spacing of children. First, we regress the number of children born to a mother after a particular child on the treatment probability of that child. We employ the baseline restriction by including only those children born between 1986 and 2002 surveyed in intervention districts. We run various fixed effect models–specifically, district-level, household-level, and finally mother-level. The results are reported in the first panel of Table 7. The estimated coefficients, which are small and again tightly bound around zero, suggest that having a child who was highly exposed to treatment did not alter subsequent fertility decisions significantly.
Table 7. Quantity and Spacing of Births.
Effects of IOC on Quantity and Spacing of Births
| Panel A: No. of Children Born After Treated Child | |||
| IOC Treatment Exposure | 0.0393 (0.0437) |
0.0172 (0.0287) |
0.00823 (0.0209) |
| Fixed Effects | Disctrict | Household | Mother |
| Observations | 4048 | 4048 | 4048 |
| Mean of Dependent Variable | 1.761 | 1.761 | 1.761 |
| Panel B: Succeeding Birth Interval After Treated Child (Mos.) | |||
| IOC Treatment Exposure | −0.875 (0.631) |
0.132 (1.021) |
0.114 (1.022) |
| Fixed Effects | Disctrict | Household | Mother |
| Observations | 3046 | 3046 | 3046 |
| Mean of Dependent Variable | 34.85 | 34.85 | 34.85 |
| Panel C: Preceding Birth Interval Before Treated Child (Mos.) | |||
| IOC Treatment Exposure | 1.432 (1.278) |
1.519 (1.965) |
1.371 (2.063) |
| Fixed Effects | Disctrict | Household | Mother |
| Observations | 1448 | 1448 | 1448 |
| Mean of Dependent Variable | 35.79 | 35.79 | 35.79 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1), clustered at the level of DHS cluster (primary sampling unit). Treatment exposure calculated using month and year of birth, and years in which the program was rolled out in each district (see Table A1). Specifications also control for: district fixed effects; urban dummy; rainy season dummy; percent of household's salt that is iodized (0, 25, 50, 75, or 100); minimum and maximum sibling ages; dummies for median sibling age; household size (deciles); number of females in household (quintiles); gender-specific birth order dummies; dummies for number of younger and older siblings; dummies for mother's integer age; and dummies for mother's years of completed schooling. Sample includes children from the 1999, 2004, and 2007 waves combined.
We then explore, in an analogous fashion, the effects of treatment exposure on the spacing of preceding and succeeding births. We regressed succeeding and preceding birth interval on treatment exposure within district-, household-, and mother-level fixed effect specifications. The results are reported in the second and third panels of Table 7. The coefficients on treatment exposure are small compared to the mean interval between children (just under 35 months) and again tightly bound around zero.
Thus, overall we find little evidence that treatment exposure altered fertility patterns in any observable way. These findings, in tandem with the results reported earlier, suggest that inframarginal quality improvements can spur investment responses short of an adjustment along the quantity margin.
4.3 Results on Sibling Spillovers
Thus far we have focused on estimating the “own endowment effect,” that is, the impact of changing a child’s endowment on investments in that child. But investment decisions are not in general made one child at a time–parents often face hard choices regarding the allocation of resources among their children. Does changing the endowment of one child affect resource allocations to other children, and if so, are these spillovers beneficial or detrimental?
As described in section 3, we construct a sibling IOC exposure measure by adding up the treatment probabilities of each child’s siblings. We then regress vaccination and breastfeeding behavior on both own and sibling IOC exposure, in the same specification described previously. The results of this estimation are reported in Table 8. Across all investment measures, we find that 1) the magnitude and precision of the estimated effect of own IOC exposure does not change from the previous estimates in Table 2; and 2) sibling IOC exposure has significant effects on all investments save for breastfeeding duration, and this effect is consistently approximately half the magnitude of the own endowment effect. These results indicate that sibling spillovers, at least in this context, are positive: conditional on their own exposure, children whose siblings were exposed to iodine supplementation are more likely to receive necessary vaccinations.
Table 8. Intrahousehold Resource Allocations.
Effects of Own vs. Sibling IOC Treatment on Vaccinations and Breastfeeding Behavior
| Vaccinations | |||||
|---|---|---|---|---|---|
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
Breastfed for more than 6 mos. |
|
| Own IOC Treatment Exposure | 0.424*** (0.141) |
0.473*** (0.155) |
0.118** (0.0527) |
1.010*** (0.325) |
0.0920** (0.0385) |
| Siblings' IOC Treatment Exposure (Additive) |
0.228** (0.0933) |
0.207** (0.0979) |
0.0652* (0.0350) |
0.489** (0.201) |
0.0453 (0.0283) |
| 1(Female) | 0.102 (0.0655) |
0.127** (0.0615) |
0.0304 (0.0301) |
0.269* (0.142) |
0.0114 (0.0228) |
| 1(Age 1) | 0.857*** (0.180) |
0.856*** (0.190) |
0.655*** (0.0860) |
2.387*** (0.423) |
0.629*** (0.0637) |
| 1(Age 2) | 0.981*** (0.221) |
0.963*** (0.237) |
0.735*** (0.121) |
2.672*** (0.515) |
0.639*** (0.0685) |
| 1(Age 3) | 0.997*** (0.253) |
1.049*** (0.265) |
0.729*** (0.127) |
2.774*** (0.578) |
0.592*** (0.0755) |
| 1(Age 4) | 0.955*** (0.254) |
0.965*** (0.292) |
0.743*** (0.153) |
2.652*** (0.622) |
0.628*** (0.0786) |
| Observations | 456 | 456 | 454 | 454 | 453 |
| Mean of Dependent Variable | 2.645 | 2.629 | 0.756 | 6.026 | 0.872 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1). Stamdard errors are clustered at the district-age level. Sibling Treatment is the sum of treatment probabilities of the two older and two younger siblings. All specifications include dummies for age (integer years) and gender of the child as well as age (deciles) and education (five categorical levels of completion) of the mother. Controls also include a dummy for whether the household is located in an urban area and for whether the child was born during a rainy season, the household size and fixed effects for number of older and younger siblings of the child and number of female children in the household as well as the sum, max and min and dummies for the median of the ages of all children in the household. Finally, we include fixed effects for district and wave as well as for the child's place in a gender-specific birth order. The sample is restricted to households with at least 1 child under the age of 5 from the 1999 DHS, unless otherwise noted. All specifications run on the 1999 sample also include dummies for the percentage of households salt supply that is iodized (categorical in levels of 25 percentage points).
Almond, Edlund, and Palme (2009) address the core premise of this study regarding parental investment responses by comparing their main results with estimates obtained from sibling comparison specifications. They find that impacts of exposure to radioactive fallout from Chernobyl are stronger when estimated within families, comparing across sibling pairs in which one was exposed and the other not. They interpret these pattern as evidence that parents reinforced endowment differences with postnatal investments. This interpretation is of course consistent with our results. For the sake of comparison, we repeat their exercise to see if within sibling comparisons (using mother fixed effects) reflect similar increases. Of course, taken together, our own treatment and sibling treatment effect estimates indicate that within family comparisons might actually yield smaller impacts on investments. We report results from mother fixed effects specifications in Table A.8. Unfortunately, it appears that we do not have sufficient precision to glean much from this exercise. Point estimates are similar in magnitude to own treatment estimates reported in Table 2, but are no longer significant likely due to sibling exposure effects going in the same direction.
Table A.8.
Healthcare Investments in Infancy (Mother FE Specifications)
| Effects of IOC Treatment on Vaccinations and Breastfeeding Behavior | |||||
|---|---|---|---|---|---|
| Vaccinations | Breastfed for more than 6 mos. |
||||
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
||
| IOC Treatment Exposure | 0.405 (0.269) |
0.424 (0.328) |
0.0498 (0.108) |
0.878 (0.641) |
0.0534 (0.0819) |
| 1(Female) | −0.0216 (0.202) |
0.0101 (0.196) |
0.0280 (0.0829) |
0.0165 (0.426) |
−0.0130 (0.0807) |
| 1(Age 1) | 0.836** (0.348) |
0.862** (0.384) |
0.667*** (0.224) |
2.365*** (0.790) |
0.590*** (0.133) |
| 1(Age 2) | 0.872 (0.602) |
0.871 (0.665) |
0.858*** (0.269) |
2.601* (1.375) |
0.663*** (0.140) |
| 1(Age 3) | 0.577 (0.758) |
0.662 (0.755) |
0.663* (0.334) |
1.903 (1.643) |
0.490** (0.214) |
| 1(Age 4) | 0.643 (0.658) |
0.658 (0.800) |
0.697* (0.365) |
1.998 (1.519) |
0.578** (0.217) |
| Observations | 456 | 456 | 454 | 454 | 453 |
| Mean of Dependent Variable | 2.645 | 2.629 | 0.756 | 6.026 | 0.872 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1), clustered at the level of DHS cluster (primary sampling unit). Treatment exposure calculated using month and year of birth, and years in which the program was rolled out in each district (see Table A1). Specifications also control for: district fixed effects; urban dummy; rainy season dummy; percent of household's salt that is iodized (0, 25, 50, 75, or 100); minimum and maximum sibling ages; dummies for median sibling age; household size (deciles); number of females in household (quintiles); gender-specific birth order dummies; dummies for number of younger and older siblings; dummies for mother's integer age; and dummies for mother's years of completed schooling. Sample is restricted to households with at least 1 child < 5 years in 1999 DHS.
Next, we divide sibling IOC treatment exposure into the exposure of younger and older siblings to capture the potentially different resource reallocation patterns in response to shocks to the endowments of older or younger siblings. We include these two new variables in place of the composite sibling IOC measure described above. The results of this estimation are reported in Table 9. Across vaccination types, our findings are that 1) both older and younger siblings’ IOC exposure have significant effects on own investments; 2) the estimated magnitudes are always slightly larger (but not statistically) for older siblings’ exposure; and 3) breastfeeding duration does not respond significantly to either exposure measure. On the third point, regarding breastfeeding, we might expect that this investment does not respond to siblings’ exposure, given that contemporaneous resource reallocation is impossible for breastfeeding (except in the case of twins). However, dynamic reallocation of resources is possible, and in this case, we would only expect older sibling exposure to matter; indeed, we find that the coefficient on older sibling exposure is 4 to 5 times as large as the coefficient on younger sibling exposure, which is close to zero though imprecisely estimated.
Table 9. Health Investment Responses to Older and Younger Sibling Treatment.
Effects of IOC Treatment of Older and Younger Siblings on Investments
| Vaccinations | Breastfed for more than 6 mos. |
||||
|---|---|---|---|---|---|
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
||
| Own IOC Treatment Exposure | 0.424*** (0.141) |
0.473*** (0.155) |
0.118** (0.0524) |
1.010*** (0.325) |
0.0918** (0.0384) |
| Older Siblings' IOC Treatment Exposure (Additive) |
0.230** (0.105) |
0.209* (0.108) |
0.0733* (0.0368) |
0.498** (0.227) |
0.0515 (0.0338) |
| Younger Siblings' IOC Treatment Exposure (Additive) |
0.215** (0.105) |
0.197* (0.116) |
0.0256 (0.0590) |
0.444* (0.223) |
0.0149 (0.0366) |
| 1(Female) | 0.102 (0.0656) |
0.127** (0.0615) |
0.0297 (0.0303) |
0.268* (0.142) |
0.0110 (0.0232) |
| 1(Age 1) | 0.860*** (0.185) |
0.859*** (0.198) |
0.664*** (0.0901) |
2.397*** (0.436) |
0.635*** (0.0648) |
| 1(Age 2) | 0.986*** (0.235) |
0.966*** (0.255) |
0.749*** (0.127) |
2.688*** (0.547) |
0.650*** (0.0702) |
| 1(Age 3) | 1.003*** (0.273) |
1.054*** (0.286) |
0.748*** (0.134) |
2.796*** (0.616) |
0.607*** (0.0783) |
| 1(Age 4) | 0.963*** (0.282) |
0.971*** (0.320) |
0.769*** (0.166) |
2.681*** (0.677) |
0.648*** (0.0804) |
| Observations | 456 | 456 | 454 | 454 | 453 |
| Mean of Dependent Variable | 2.645 | 2.629 | 0.756 | 6.026 | 0.872 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1). Stamdard errors are clustered at the district-age level. Sibling Treatment variables are the sum of treatment probabilities of the two older and two younger siblings separately defined. All specifications include dummies for age (integer years) and gender of the child as well as age (deciles) and education (five categorical levels of completion) of the mother. Controls also include a dummy for whether the household is located in an urban area and for whether the child was born during a rainy season, the household size and fixed effects for number of older and younger siblings of the child and number of female children in the household as well as the sum, max and min and dummies for the median of the ages of all children in the household. Finally, we include fixed effects for district and wave as well as for the child's place in a gender-specific birth order. The sample is restricted to households with at least 1 child under the age of 5 from the 1999 DHS, unless otherwise noted. All specifications run on the 1999 sample also include dummies for the percentage of household's salt supply that is iodized (categorical in levels of 25 percentage points).
Finally, we might be concerned that even in the case of vaccinations, the opportunity to revisit the investment decisions for older untreated siblings after observing the endowment of younger treated siblings is minimal. That is, we might suspect that parents will not choose to vaccinate older siblings late if they believe vaccinations are less effective, and that any estimated impact of younger sibling treatments on older sibling vaccinations are evidence of lower cost of vaccination or even spurious relationships. Though the data show that children often receive vaccinations late, as shown in Table 10 and discussed below, we cannot know what drives this late vaccination and if it is attributable to IOC programme exposure. Accordingly, we run the specifications from Table 8 again using only the older sibling exposure from regressions reported in Table 9, excluding younger sibling exposure. These results are reported in Table A.10 and are nearly identical to those from both Tables 8 and 9. We interpret these results as evidence that sibling effects are not driven entirely by younger sibling exposure.
Table 10. Timing of Vaccinations.
1(Child received vaccination, but not by recommended age)
| Children Aged Under 5 in 1999 DHS | |||
|---|---|---|---|
| Recommended Age (WHO) | Mean | SD | |
| Vaccinations | |||
| Polio, dose 0 | 0 months | 0.324 | 0.469 |
| Polio, dose 1 | 6 months | 0.576 | 0.495 |
| Polio, dose 2 | 10 months | 0.725 | 0.447 |
| Polio, dose 3 | 14 months | 0.794 | 0.405 |
| DPT, dose 1 | 6 months | 0.589 | 0.493 |
| DPT, dose 2 | 10 months | 0.723 | 0.448 |
| DPT, dose 3 | 14 months | 0.797 | 0.403 |
| Measles | 9 months | 0.519 | 0.501 |
| BCG | 6 months | 0.209 | 0.407 |
4.3.1 Timing of vaccinations
Since our central measure of health investments is receipt of vaccinations, we must contend with the critique that vaccinations, unlike other types of health investments, are supposed to follow a schedule. For example, the WHO recommends that the first dose of DPT be administered at 6 months, the second dose at 10 months, and so on. While the timing of vaccinations poses little threat to the validity of the estimated effects of own treatment exposure, it may pose problems for the interpretation of the effects of sibling exposure. Specifically, suppose all vaccines were given according to the recommended timetable. Then, younger siblings’ treatment exposure should have no impact on vaccination decisions for older siblings, since those decisions would have preceded the birth of the younger siblings. Indeed, this assumption is the basis of identification strategies used in previous studies of intra-household allocations in developing countries (see, e.g., Dow, Philipson, and Sala-i-Martin (1999)). Thus if the timetable were always followed, and if we found an effect of sibling exposure, this would suggest that our interpretation of the results as the investment response of parents would be called into question.
There is, however, considerable evidence to the contrary. For the majority of children, vaccinations are not administered at the recommended ages in developing country contexts (Andrew Clark and Colin Sanderson 2009). As shown in Table 10, in our data, only the BCG vaccine is administered on time for the majority of children. Rates of delay are greater than one half for the rest of the recommended vaccinations, with proportion delayed ranging from 0.58 to 0.82. If children who did not receive vaccinations are included, these rates only increase. The evidence from other studies, as well as from our own data, thus suggest that vaccination decisions are plausibly made concurrently across siblings of varying ages.15
5 Model
In this section, to better interpret our results, we present a simple theoretical framework relating child endowments to intra-sibling allocations. The model generates predictions regarding parents’ investment responses to shifts in their children’s endowments of quality. The key insight of this model is that the pattern of investment responses to endowment shifts, which we have estimated in the data, contains information about the shapes of the production functions for child quality and the household’s utility function.
5.1 Setup
Consider a household with two children indexed i = 1, 2.16 Each child is born with an exogenously given endowment of quality ηi. The endowment combines with the amount parents choose to invest in each child, zi, to determine child-specific quality qi = q(zi, ηi). We assume that for each i, qi is increasing and concave in both its arguments. We make no restriction on the cross-partial, . When endowments and investments are complements in the production of child quality, this cross-partial will be positive; when they are substitutes, it will be negative.
Parents value their own consumption C and the quality of their children. We adopt a standard quasi-linear utility function, in which consumption is the numeraire good: U ≔ u(q1, q2) + C. We assume that the function u is increasing and concave in each of its arguments, but make no restriction on the cross-partial .17
The budget constraint, given income M and the price of quality investments pi, is p1z1+p2z2+C ≤ M.18 The household’s utility maximization problem can thus be written as maxz1,z2,C U subject to this budget constraint. The resulting three necessary first order conditions, corresponding to C, z1, and z2, respectively, are:
| (4) |
| (5) |
| (6) |
5.2 Investment responses to endowment changes
We now examine the effects of a shift in one child’s endowment on investments in quality for both children. These comparative statics generate predictions on the optimal intra-household re-allocation of parental investments in response to shifts in child-specific endowments.
Notice that since λ = 1 by the first order condition for C, equation 5 becomes , and equation 6 becomes .
Implicit differentiation of the first order condition for z1 with respect to η1 yields
| (7) |
Implicit differentiation of the first order condition for z2 with respect to η1 yields
| (8) |
The above equations relate the investment responses and to the extent of complementarity (or substitutability) in the utility function and the production function for quality. The estimated signs of these investment responses thus may contain information about the signs of these parameters of interest: u12 and .
Solving for u12 from equation 8, we get the following expression:
| (9) |
Here, . Note that the numerator of the above expression is increasing in , and the denominator is increasing in . Plugging this expression for u12 into equation 7, we arrive at the following expression for , the cross-partial of the quality production function:
| (10) |
Here, , and . Notice first that factors into the above expression only through β, and only the second-order (squared) term appears, implying that the sign of the cross-investment response does not contain information about the complementarity or substitutability of the production function.
On the other hand, as equation 10 shows, information on the sign of the cross-partial can be gleaned from the sign of . In particular, it is clear from equation 10 that the cross-partial is monotonically positively related to . Thus, for large enough positive values of , the cross-partial must be positive (i.e., endowments and investments must be complements), and for large negative values of , the cross-partial must be negative. In the intermediate range, the cross-partial is of indeterminate sign. Interestingly, since the size of determines the magnitude of β, if is large enough, the cross-partial may be negative (i.e., endowments and investments may be substitutes) even when is very positive.
5.3 Interpreting the results
In summary, the simple theory of intra-household allocations and endowments set forth above yields a set of equations that relates parents’ investment responses to two key parameters: inequality aversion in parents’ preferences (u12), and the complementarity (or substitutability) of endowments and investments in the child quality production function (). Based on the estimated signs of the investment responses, we can, in some cases, infer the signs of one or both of these parameters. We now return to equations 9 and 10 and assess what we can learn about the signs of u12 and from the estimates of and presented in section 4.
Overall, the positive sign and the (standardised) magnitudes of the coefficients on own and sibling treatment are remarkably similar across vaccinations and breastfeeding outcomes (albeit slightly smaller for siblings’ treatment exposure). Recall that the comparative statics equations in the model imply that . Since both and are positive, it is easy to see from this equation that u12 > 0. That is, our estimates of the investment responses to endowment shifts imply that parents are averse to inequality among their children.
On the other hand, recall equation 10, relating to the complementarity or substitutability of investments and endowments: , for positive coefficients α, β, γ. It is evident that this equation does not generate an unambiguous prediction without knowing the relative magnitudes of , and the other parameters of the model. Thus, using the estimated coefficients, we cannot infer whether investments and endowments are complementary or substitutable in the child quality production function.
6 Conclusion
The economically meaningful, long-run effects of early-life factors documented in recent studies have prompted a series of related questions. How do households respond to shifts in their children’s endowments? Do parents’ investment responses reinforce endowment shifts or compensate for them? Moreover, do reinforcing or compensatory investments come at the cost or to the benefit of otherwise unaffected siblings?
We answer these questions by exploiting variation induced by a large-scale iodine supplementation programme in Tanzania. We find that, at least in the context of iodine supplementation, parents reinforced endowment increases by making health investments in children who were exposed to the campaign while in utero. A variety of evidence is presented in favor of the interpretation that parents reacted to observed differences in their children’s endowments, and that indirect programme effects, if they existed, were not salient. We then present evidence that sibling spillovers in this case were positive: the siblings of treated children were also more likely to receive necessary vaccinations, and the magnitude of the spillover effect was about one-half the size of the effect on investments for the treated child.
If parents do indeed respond to shifts in children’s endowments, then it is natural to ask how much of the total (long-run) effect of improving early-life conditions is explained by these responses? In a recent review article, Bleakley (2010) invokes the Envelope Theorem to argue that, at least with regard to the direct effect, the answer should be very little. Drawing the analogy from his example of an investment, schooling, to ours, his argument states that parents’ investment responses contribute to the overall utility (or health) effects of endowment changes only because shifting the endowment changes the marginal returns to investment. By the Envelope Theorem, if investments are optimised, the direct effect of investment responses ( in our model) should be very small, because this effect only contributes to the overall effect on utility to the extent that investments affect utility, which, at the optimal level of investments, is necessarily 0.
If Bleakley’s Envelope Theorem critique is germane to the case of health investments, then perhaps the literature on early-life factors has focused too heavily thus far on estimating investment responses. Rather, as a corollary of the critique, more attention should be paid to verifying the existence and estimating the extent of complementarities between endowments and investments in the production of health.
On the other hand, we suggest that adapting Bleakley’s (2010) model to health investments necessitates two key extensions, each of which change the conclusions regarding the relevance of parents’ investment responses. First, parents may be uncertain about the returns to additional investment (particularly in the case of new or complicated health technologies). When the standard model is modified to incorporate this uncertainty, parents’ optimal allocations may be different from the full information optimum, because marginal benefits/costs are not fully known or are discovered over time via learning. If policy interventions can solve this information problem through incentives, then, given the distance from the full information optimum, we should expect a first-order contribution of parents’ investment responses on child health.
Second, the standard model does not address the Pigouvian nature of potential subsidy policies. For example, schooling subsidies may generate productivity complementarities (i.e., an additional year of schooling has larger returns if your peers are also more educated), generating larger private returns than in the case without spillovers. In a model with this sort of externality, a public education subsidy could effectively move the private schooling investment optimum, and thus, again, the direct (level) effect of investment responses would be salient.
As for the implications of our results on sibling spillovers, these results suggest that early childhood interventions targeting specific groups–e.g., children under five, school-aged children, girls, etc.–may have large spillovers onto untreated siblings via intra-household resource reallocations. In our context, we show that these spillovers are large and positive: both treated and untreated children benefited from the iodine supplementation intervention in Tanzania. The returns to early-childhood interventions may thus rely crucially on the way in which households reallocate resources among siblings. It is incumbent upon researchers and policymakers alike to measure the extent of these spillovers in order to accurately gauge the full impact of a wide variety of policies targeting children at early ages.
FIGURE 2.
Birth Rate Trends
FIGURE 3.
Birth Rate Trends
FIGURE 4.
Birth Rate Trends
A Additional Tables
A.1 Programme Years
Table A.1 presents the years in which the programme visited each district.
A.2 Treatment Probabilities
Table A.2 presents the calculated treatment probabilities by birth month and birth year of the child relative to the programme year in the child’s birth district.
A.3 Robustness to Alternate Treatment Definitions
We investigate the robustness of our results to alternate definitions of IOC treatment exposure. We use two treatment exposure indicators, one for treatment exposure greater than 0.75 (as is used in the summary statistics tables to compare raw means of outcomes for children with and without treatment), and one for full treatment exposure (i.e., treatment probability equals 1). The indicator based on the 0.75 cutoff is equivalent to two years of in utero IOC exposure, while the indicator based on the cutoff for full treatment is equivalent to one year of in utero IOC exposure.
We regress our main outcome measures on these alternate definitions of treatment exposure. The results are reported in Table A.3, Panels A and B. Panel A reports results for the 0.75 cutoff indicator, and Panel B reports results for the full treatment indicator. The results on IOC exposure are positive and significant in both panels, though the magnitudes of the coefficients are slightly attenuated compared to the main results presented in Table 2. This is perhaps unsurprising, given that we are 1) not using available variation in the treatment exposure measure, and 2) misclassifying “treated” and “untreated” children around the cutoffs.
Table A.3. Robustness to Alternate Treatment Definitions.
Effects of Varied Definitions of Treatment on Early-life Investments
| Panel A: Binary for Treatment Probability > 0.75 | |||||
| Vaccinations | Breastfed for more than 6 mos. |
||||
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
||
| IOC Treatment Exposure (Pr > 0.75) |
0.198** (0.0950) |
0.233** (0.110) |
0.0608 (0.0395) |
0.504** (0.233) |
0.0692*** (0.0253) |
| Observations | 456 | 456 | 454 | 454 | 453 |
| Mean of Dependent Variable | 2.645 | 2.629 | 0.756 | 6.026 | 0.872 |
| Panel B: Binary for Treatment Probability = 1 | |||||
| Vaccinations | Breastfed for more than 6 mos. |
||||
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
||
| IOC Treatment Exposure (Pr = 1) |
0.212** (0.0925) |
0.256*** (0.0830) |
0.0789 (0.0608) |
0.546** (0.211) |
0.0163 (0.0255) |
| Observations | 456 | 456 | 454 | 454 | 453 |
| Mean of Dependent Variable | 2.645 | 2.629 | 0.756 | 6.026 | 0.872 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1), clustered at the level of DHS cluster (primary sampling unit). Treatment exposure calculated using month and year of birth, and years in which the program was rolled out in each district (see Table A1). Specifications also control for: district fixed effects; urban dummy; rainy season dummy; percent of household's salt that is iodized (0, 25, 50, 75, or 100); minimum and maximum sibling ages; dummies for median sibling age; household size (deciles); number of females in household (quintiles); gender-specific birth order dummies; dummies for number of younger and older siblings; dummies for mother's integer age; and dummies for mother's years of completed schooling. Sample is restricted to households with at least 1 child < 5 years in 1999 DHS.
A.4 Robustness to Alternate Age Controls
Since the probability of IOC treatment exposure is largely determined by birth month and year of the child, we must carefully control for variations in age in order to isolate variation in programme exposure. In the primary analysis, we include fixed effects for integer age of the child so that we are the effects of treatment within a particular age. We might worry, however, that variations in the controls for age might affect the results considerably. In particular, we want to be careful to rule out the possibility that the pattern of results is driven largely by age rather than treatment exposure.
In order to check for this possibility, we explore the robustness of results to various sets of age controls. We replicate our analysis of receipt of vaccinations and breastfeeding using alternately no age controls, a smooth quadratic in age, and quarter of birth by integer age fixed effects. The results from these robustness checks are reported in Panels A–C, respectively, of Table A.4. We find that the general pattern of results is robust to various sets of age controls.
Table A.4. Robustness to Alternate Age Controls.
Effects of Treatment on Early-life Investments with Varied Age Controls
| Panel A: No Age Controls | |||||
| Vaccinations | Breastfed for more than 6 mos. |
||||
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
||
| Own Treatment Exposure | 0.492*** (0.153) |
0.544*** (0.163) |
0.191*** (0.0608) |
1.224*** (0.356) |
0.161*** (0.0538) |
| Observations | 456 | 456 | 454 | 454 | 453 |
| Mean of Dependent Variable | 2.645 | 2.629 | 0.756 | 6.026 | 0.872 |
| Panel B: Smooth Quadratic | |||||
| Vaccinations | Breastfed for more than 6 mos. |
||||
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
||
| Own Treatment Exposure | 0.372** (0.137) |
0.425*** (0.152) |
0.104* (0.0562) |
0.899*** (0.322) |
0.0842* (0.0484) |
| Observations | 456 | 456 | 454 | 454 | 453 |
| Mean of Dependent Variable | 2.645 | 2.629 | 0.756 | 6.026 | 0.872 |
| Panel C: Quarter of Birth × Integer Age | |||||
| Vaccinations | Breastfed for more than 6 mos. |
||||
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
||
| Own Treatment Exposure | 0.214* (0.122) |
0.257* (0.136) |
0.0550 (0.0554) |
0.523* (0.290) |
8.25e-05 (0.00943) |
| Observations | 456 | 456 | 454 | 454 | 453 |
| Mean of Dependent Variable | 2.645 | 2.629 | 2.629 | 6.026 | 0.872 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1), clustered at the level of DHS cluster (primary sampling unit). Treatment exposure calculated using month and year of birth, and years in which the program was rolled out in each district (see Table A1). Specifications also control for: district fixed effects; urban dummy; rainy season dummy; percent of household's salt that is iodized (0, 25, 50, 75, or 100); minimum and maximum sibling ages; dummies for median sibling age; household size (deciles); number of females in household (quintiles); gender-specific birth order dummies; dummies for number of younger and older siblings; dummies for mother's integer age; and dummies for mother's years of completed schooling. Sample is restricted to households with at least 1 child < 5 years in 1999 DHS.
A.5 Alternative Vaccination Results (Individual Doses)
Next, we provide some evidence that the results on vaccinations are robust to changes in the construction of vaccination counts as well as to the empirical model used. First, we disaggregate the count variables and estimate effects for each of the three DPT and polio vaccines separately. These results are presented in Table A.5. Linear probability models are estimated. The results clearly show that IOC treatment exposure remains a strong determinant of receipt of individual vaccinations. The magnitude of the treatment effect across all doses of DPT and polio is roughly the same.
Table A.5. Results by Individual Vaccination Dose (DPT and Polio).
Effects of IOC Treatment on Vaccinations
| Vaccinations | ||||||
|---|---|---|---|---|---|---|
| DPT 1 | DPT 2 | DPT 3 | Polio 1 | Polio 2 | Polio 3 | |
| IOC Treatment Exposure | 0.130** (0.0512) |
0.144*** (0.0523) |
0.152** (0.0594) |
0.0901** (0.0396) |
0.135** (0.0548) |
0.147** (0.0579) |
| 1(Female) | 0.0331 (0.0228) |
0.0479* (0.0270) |
0.0424* (0.0213) |
0.0301 (0.0221) |
0.0485* (0.0241) |
0.0199 (0.0332) |
| 1(Age 1) | 0.153** (0.0623) |
0.290*** (0.0671) |
0.417*** (0.0848) |
0.123* (0.0673) |
0.315*** (0.0634) |
0.423*** (0.0811) |
| 1(Age 2) | 0.196** (0.0766) |
0.304*** (0.0832) |
0.505*** (0.102) |
0.168** (0.0807) |
0.316*** (0.0777) |
0.542*** (0.101) |
| 1(Age 3) | 0.193** (0.0867) |
0.365*** (0.0935) |
0.536*** (0.117) |
0.146 (0.0889) |
0.338*** (0.0951) |
0.560*** (0.121) |
| 1(Age 4) | 0.160 (0.0992) |
0.325*** (0.104) |
0.555*** (0.137) |
0.150 (0.0949) |
0.332*** (0.0965) |
0.552*** (0.140) |
| Observations | 456 | 456 | 456 | 456 | 456 | 456 |
| Mean of Dependent Variable | 0.914 | 0.886 | 0.829 | 0.932 | 0.897 | 0.816 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1), clustered at the level of DHS cluster (primary sampling unit). Treatment exposure calculated using month and year of birth, and years in which the program was rolled out in each district (see Table A1). Specifications also control for: district fixed effects; urban dummy; rainy season dummy; percent of household's salt that is iodized (0, 25, 50, 75, or 100); minimum and maximum sibling ages; dummies for median sibling age; household size (deciles); number of females in household (quintiles); gender-specific birth order dummies; dummies for number of younger and older siblings; dummies for mother's integer age; and dummies for mother's years of completed schooling. Sample is restricted to households with at least 1 child < 5 years in 1999 DHS.
A.6 Alternative Vaccination Results (Count Regressions)
Second, we estimate count (negative binomial) models for the number of DPT, polio, and total vaccines received, rather than the linear probability model specified in the main results. The results are reported in Table A.6. The count model results are consistently precisely estimated and large, with imputed magnitudes (computed at the means of the dependent and independent variables) comparable to the linear probability effects.
Table A.6.
Effects of IOC Exposure on Vaccination Counts Effects of IOC Treatment on Vaccinations using Negative Binomial (Count) Models
| No. of polio doses | No. of DPT doses | No. of total vaccinations |
|
|---|---|---|---|
| IOC Treatment Exposure | 0.146*** (0.0504) |
0.173*** (0.0584) |
0.159*** (0.0536) |
| 1(Female) | 0.0353 (0.0245) |
0.0438* (0.0238) |
0.0415* (0.0243) |
| 1(Age 1) | 0.371*** (0.0763) |
0.385*** (0.0827) |
0.476*** (0.0820) |
| 1(Age 2) | 0.424*** (0.0891) |
0.434*** (0.0956) |
0.524*** (0.0936) |
| 1(Age 3) | 0.438*** (0.0998) |
0.475*** (0.105) |
0.546*** (0.103) |
| 1(Age 4) | 0.434*** (0.104) |
0.453*** (0.115) |
0.536*** (0.112) |
| Observations | 456 | 456 | 454 |
| Mean of Dependent Variable | 2.645 | 2.629 | 6.026 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1), clustered at the level of DHS cluster (primary sampling unit). Treatment exposure calculated using month and year of birth, and years in which the program was rolled out in each district (see Table A1). Specifications also control for: district fixed effects; urban dummy; rainy season dummy; percent of household's salt that is iodized (0, 25, 50, 75, or 100); minimum and maximum sibling ages; dummies for median sibling age; household size (deciles); number of females in household (quintiles); gender-specific birth order dummies; dummies for number of younger and older siblings; dummies for mother's integer age; and dummies for mother's years of completed schooling. Sample is restricted to households with at least 1 child < 5 years in 1999 DHS.
A.7 Sibling Spillover Results Using Sample of Only Multiple-child Households
Finally, we replicate the main results for own and siblings’ IOC treatment exposure using the sample of households with multiple children, since in the main results, we used all households, including those with only 1 child, imputing zeros for siblings’ IOC exposure in these cases. The results when the sample is restricted to multiple-child households are presented in Table A.7. We find the magnitudes of the effects on own and sibling exposure are slightly attenuated, though in most cases the coefficients are comparable to those in Table 8. Some of the precision of the estimates for sibling spillover effects is diminished when the sample is restricted, but the overall qualitative pattern remains the same.
Table A.7.
Results Using Only Sample of Households with Multiple Children Under 5
| Effects of IOC Treatment on Vaccinations and Breastfeeding Behavior | |||||
|---|---|---|---|---|---|
| Vaccinations | Breastfed for more than 6 mos. |
||||
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
||
| Own IOC Treatment Exposure | 0.303** (0.120) |
0.363** (0.134) |
0.0986** (0.0446) |
0.765*** (0.271) |
0.0767* (0.0408) |
| Siblings' IOC Treatment Exposure (Additive) |
0.195* (0.111) |
0.171 (0.122) |
0.0640 (0.0411) |
0.429* (0.252) |
0.0456 (0.0396) |
| 1(Female) | 0.107 (0.0813) |
0.140* (0.0767) |
0.0367 (0.0343) |
0.284 (0.174) |
0.00436 (0.0293) |
| 1(Age 1) | 0.816*** (0.190) |
0.811*** (0.205) |
0.633*** (0.0950) |
2.260*** (0.459) |
0.623*** (0.0640) |
| 1(Age 2) | 1.003*** (0.262) |
0.983*** (0.266) |
0.760*** (0.124) |
2.747*** (0.590) |
0.625*** (0.0729) |
| 1(Age 3) | 1.097*** (0.289) |
1.115*** (0.295) |
0.730*** (0.126) |
2.943*** (0.654) |
0.560*** (0.0717) |
| 1(Age 4) | 1.010*** (0.298) |
0.991*** (0.309) |
0.762*** (0.158) |
2.763*** (0.703) |
0.596*** (0.0813) |
| Observations | 374 | 374 | 374 | 374 | 371 |
| Mean of Dependent Variable | 2.642 | 2.634 | 0.765 | 6.040 | 0.876 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1), clustered at the level of DHS cluster (primary sampling unit). Treatment exposure calculated using month and year of birth, and years in which the program was rolled out in each district (see Table A1). Specifications also control for: district fixed effects; urban dummy; rainy season dummy; percent of household's salt that is iodized (0, 25, 50, 75, or 100); minimum and maximum sibling ages; dummies for median sibling age; household size (deciles); number of females in household (quintiles); gender-specific birth order dummies; dummies for number of younger and older siblings; dummies for mother's integer age; and dummies for mother's years of completed schooling. Sample is restricted to households with > 1 child who is < 5 years in 1999 DHS.
A.8 Mother Fixed Effects Estimates
For the sake of comparison with the literature, we repeat the exercise from Almond, Edlund, and Palme (2009) to see if within sibling comparisons (using mother fixed effects) reflect larger or smaller estimates of investment responses. Taken together, our positive own treatment and positive sibling treatment effect estimates indicate that within family comparisons might actually yield smaller impacts on investments. We report results from mother fixed effects specifications in Table A.8. Unfortunately, it appears that we do not have sufficient precision to glean much from this exercise. Point estimates are similar in magnitude to own treatment estimates reported in Table 2, but are no longer significant likely due to sibling exposure effects going in the same direction.
A.9 Robustness and Heterogeneity (Urban vs Rural Households)
We might be concerned, given the higher programme exposure in urban areas, that breastfeeding results are driven more by an emphasis on breastfeeding among urban mothers, particularly those delivering in formal sector facilities. We check for this in three ways and report the results in Table A.9: first, we report the correlations between formal sector delivery, breastfeeding, and the urban dummy (Panel A); next, we run the main results from Table 2 as well as the formal sector delivery results using only the rural subsample of households (Panel B); finally, we check for heterogeneous impacts of treatment exposure by urban (Panel C). Taken together, while the impact of treatment on breastfeeding appears to be strongest for urban mothers, this heterogeneity appears not to be driven by formal sector delivery as much as perhaps a higher opportunity cost of time for urban mothers. That is, treatment exposure does not predict formal sector delivery, even for urban mothers, and urban mothers appear to on average be less likely to breastfeed in the absence of treatment, and are simply more likely to respond to treatment in breastfeeding behavior.
Table A.9.
Robustness and Heterogeneity (Urban)
| Panel A: Correlations | |||
|---|---|---|---|
| Formal Sector Delivery |
Breastfed for more than 6 mos. |
Urban | |
| Formal Sector Delivery | 1 | ||
| Breastfed for more than 6 mos. | 0.0071 | 1 | |
| Urban | 0.2276 | −0.0564 | 1 |
| Panel B: Rural Only Sample | ||||||
|---|---|---|---|---|---|---|
| Vaccinations | Breastfed for more than 6 mos. |
Formal Sector Delivery |
||||
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
|||
| IOC Treatment Exposure | 0.398** (0.158) |
0.464** (0.177) |
0.108* (0.0599) |
0.967** (0.373) |
0.0687 (0.0433) |
0.0208 (0.0785) |
| 1(Female) | 0.102 (0.0742) |
0.129* (0.0728) |
0.0200 (0.0317) |
0.263 (0.164) |
0.00982 (0.0258) |
−0.0263 (0.0437) |
| 1(Age 1) | 0.916*** (0.188) |
0.957*** (0.187) |
0.651*** (0.0843) |
2.532*** (0.426) |
0.624*** (0.0662) |
0.0386 (0.103) |
| 1(Age 2) | 1.079*** (0.225) |
1.086*** (0.236) |
0.757*** (0.122) |
2.902*** (0.527) |
0.643*** (0.0713) |
−0.144 (0.117) |
| 1(Age 3) | 1.035*** (0.265) |
1.121*** (0.272) |
0.729*** (0.131) |
2.865*** (0.610) |
0.586*** (0.0851) |
−0.126 (0.153) |
| 1(Age 4) | 1.041*** (0.265) |
1.119*** (0.288) |
0.771*** (0.150) |
2.902*** (0.638) |
0.637*** (0.0835) |
−0.161 (0.188) |
| Observations | 417 | 417 | 416 | 416 | 414 | 417 |
| Mean of Dependent Variable | 2.626 | 2.612 | 0.752 | 5.988 | 0.874 | 0.415 |
| Panel C: Heterogeneity by Urban | ||||||
|---|---|---|---|---|---|---|
| Vaccinations | Breastfed for more than 6 mos. |
Formal Sector Delivery |
||||
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
|||
| IOC Treatment Exposure | 0.360** (0.145) |
0.434** (0.163) |
0.0992* (0.0570) |
0.891** (0.344) |
0.0657 (0.0410) |
0.0171 (0.0756) |
| IOC Treatment Exposure × Urban | 0.192 (0.233) |
−0.149 (0.263) |
0.0637 (0.0970) |
0.0896 (0.547) |
0.271*** (0.0992) |
0.211 (0.138) |
| 1(Urban) | 0.163 (0.188) |
0.187 (0.202) |
0.0193 (0.0748) |
0.355 (0.438) |
−0.177** (0.0764) |
0.247** (0.115) |
| 1(Female) | 0.103 (0.0665) |
0.128** (0.0618) |
0.0306 (0.0310) |
0.270* (0.145) |
0.0116 (0.0227) |
0.0116 (0.0227) |
| 1(Age 1) | 0.859*** (0.185) |
0.858*** (0.194) |
0.656*** (0.0872) |
2.392*** (0.433) |
0.629*** (0.0636) |
0.629*** (0.0636) |
| 1(Age 2) | 1.023*** (0.228) |
1.001*** (0.242) |
0.747*** (0.121) |
2.762*** (0.532) |
0.647*** (0.0684) |
0.647*** (0.0684) |
| 1(Age 3) | 1.040*** (0.270) |
1.088*** (0.278) |
0.741*** (0.128) |
2.867*** (0.614) |
0.601*** (0.0756) |
0.601*** (0.0756) |
| 1(Age 4) | 1.029*** (0.280) |
1.032*** (0.312) |
0.764*** (0.151) |
2.811*** (0.674) |
0.644*** (0.0774) |
0.644*** (0.0774) |
| Observations | 456 | 456 | 454 | 454 | 453 | 453 |
| Mean of Dependent Variable | 2.645 | 2.629 | 0.756 | 6.026 | 0.872 | 0.872 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1), clustered at the level of DHS cluster (primary sampling unit). Treatment exposure calculated using month and year of birth, and years in which the program was rolled out in each district (see Table A1). Specifications also control for: district fixed effects; urban dummy; rainy season dummy; percent of household' s salt that is iodized (0, 25, 50, 75, or 100); minimum and maximum sibling ages; dummies for median sibling age; household size (deciles); number of females in household (quintiles); gender-specific birth order dummies; dummies for number of younger and older siblings; dummies for mother' s integer age; and dummies for mother' s years of completed schooling. Sample is restricted to households with at least 1 child < 5 years in 1999 DHS.
A.10 Intrahousehold Resource Allocations (Older Siblings Only)
We reproduce the results from Table 8 using only older sibling exposure as calculated for regressions in Table 9 and exclude younger sibling exposure. These results are reported in Table A.10 and show that sibling treatment results are not driven entirely by younger sibling exposure, but rather are nearly identical when estimated using only older sibling treatment.
Table A.10. Intrahousehold Resource Allocations (Older Siblings Only).
Effects of Own vs. Sibling IOC Treatment on Vaccinations and Breastfeeding Behavior
| Vaccinations | Breastfed for more than 6 mos. |
||||
|---|---|---|---|---|---|
| No. of polio doses | No. of DPT doses | Measles | No. of total vaccinations |
||
| Own IOC Treatment Exposure | 0.413*** (0.139) |
0.463*** (0.153) |
0.117** (0.0527) |
0.987*** (0.322) |
0.0913** (0.0387) |
| Older Siblings’ IOC Treatment Exposure (Additive) |
0.218** (0.102) |
0.198* (0.105) |
0.0736* (0.0370) |
0.475** (0.223) |
0.0513 (0.0338) |
| 1(Female) | 0.101 (0.0654) |
0.126** (0.0615) |
0.0301 (0.0306) |
0.265* (0.143) |
0.0113 (0.0229) |
| 1(Age 1) | 0.892*** (0.183) |
0.888*** (0.194) |
0.665*** (0.0851) |
2.461*** (0.431) |
0.636*** (0.0635) |
| 1(Age 2) | 1.042*** (0.227) |
1.017*** (0.243) |
0.751*** (0.116) |
2.800*** (0.527) |
0.651*** (0.0666) |
| 1(Age 3) | 1.074*** (0.263) |
1.118*** (0.273) |
0.749*** (0.119) |
2.936*** (0.595) |
0.607*** (0.0740) |
| 1(Age 4) | 1.063*** (0.273) |
1.061*** (0.307) |
0.769*** (0.144) |
2.876*** (0.657) |
0.648*** (0.0747) |
| Observations | 456 | 456 | 454 | 454 | 453 |
| Mean of Dependent Variable | 2.645 | 2.629 | 0.756 | 6.026 | 0.872 |
Notes: Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1). Stamdard errors are clustered at the district-age level. Sibling Treatment is the sum of treatment probabilities of the two older and two younger siblings. All specifications include dummies for age (integer years) and gender of the child as well as age (deciles) and education (five categorical levels of completion) of the mother. Controls also include a dummy for whether the household is located in an urban area and for whether the child was born during a rainy season, the household size and fixed effects for number of older and younger siblings of the child and number of female children in the household as well as the sum, max and min and dummies for the median of the ages of all children in the household. Finally, we include fixed effects for district and wave as well as for the child's place in a gender-specific birth order. The sample is restricted to households with at least 1 child under the age of 5 from the 1999 DHS, unless otherwise noted. All specifications run on the 1999 sample also include dummies for the percentage of household's salt supply that is iodized (categorical in levels of 25 percentage points).
Footnotes
Many thanks to Doug Almond, Michael Boozer, A. V. Chari, Joe Doyle, James Fenske, Erica Field, Jason Fletcher, Omar Robles, Chris Udry, Atheen Venkataramani, and seminar participants at the NBER Children’s Meeting, PACDEV, Yale, Cornell, Wesleyan, and IFPRI for helpful comments and suggestions. We thank Chandresh Ladva for assistance with the map data. Adhvaryu gratefully acknowledges funding from the NIH/NICHD (5K01HD071949) and the Yale MacMillan Center Directors Award. All errors are our own. All necessary data sets and programmes to replicate results are available online.
For example, Jere Behrman and Mark Rosenzweig (2004) find a positive relationship between birth weight and adult height and schooling attainment in the US. Sandra Black, Paul Devereux, and Kjell Salvanes (2007) confirm these results using data from Norway, finding positive effects on IQ and earnings. Almond (2006) shows that in utero exposure to the 1918 influenza pandemic in the United States negatively affected completed educational attainment, income, socioeconomic status and adult health. Similarly, Almond, Lena Edlund, and Marten Palme (2009) find negative effects of prenatal exposure to radioactive fallout from Chernobyl on academic performance, but no effect on health outcomes. Erica Field, Omar Robles, and Maximo Torero (2009) find positive effects of in utero iodine supplementation on schooling attainment in Tanzania. David Cutler et al. (2010) show that cohorts who benefited in early life from a malaria eradication campaign in India had higher economic status as adults. Almond, Hilary Hoynes, and Diane Schanzenbach (2010) find large long-run effects of in utero and early childhood exposure to the Food Stamps Program. Baird et al. (2011) find that school-based de-worming can lead to gains in educational attainment, health and productivity in adulthood. Prashant Bharadwaj, Katrine Loken, and Christopher Neilson (2012) find that medical treatment for low birth weight infants positively affects test scores and grades in school. Sonia Bhalotra and Atheendar Venkataramani (2012) find large effects of pneumonia in infancy on education and socioeconomic status in adulthood for whites (but not blacks) in the United States.
Almond and Bhashkar Mazumder’s (2013) recent review article offers a nice summary of the emerging evidence in this area.
In the appendix, we replicate our main results using alternate definitions of treatment; the results are robust to these alternate definitions.
See, for example, Brandon Restrepo (2011), Richard Akresh et al. (2012), Anna Aizer and Flavio Cunha (2012), and Venkataramani (2012).
See Currie (2008) for a review of recent studies using sibling fixed effects estimators in the early life literature.
Given the continuous nature of treatment probability, in order to compare means across sub-samples of the population with differing exposure to the program, we must first choose some discrete cutoff in treatment probability. We have chosen a treatment probability of 0.75 as the cutoff because this roughly corresponds to the child being born in the 2 years after the programme year visited the district. We explore the robustness of our main results to the use of this binary (as well as a binary corresponding to a treatment probability of 1) in the Appendix.
We explore the robustness of our main results to alternate age controls. Results from these robustness checks are presented and discussed in the Appendix
We are very grateful to Erica Field and Omar Robles for their guidance in this process.
Unlike FRT, who use the Tanzania Household Budget Survey for the majority of analyses, we know the birth year and birth month of each child, so we need not generate a year-level measure of treatment probability using the weighting procedure (using seasonality of births) outlined in FRT. We instead use the raw treatment probabilities in the matrix shown in Appendix Table A.2.
Our results are qualitatively similar when we relax this restriction to include all siblings in the calculation of sibling treatment; however, magnitudes of these effects are decreasing in the size of the birth-order bandwidth, as expected under the notion that large age differences sever the joint nature of the allocation decision.
Rainy season dummy equals 1 if month of birth is March-May inclusive or October-December inclusive, 0 otherwise.
Within-gender birth order is birth order within gender categories among children within the household.
This finding is also in line with the medical evidence that iodine deficiency does not have clear negative consequences on physical health (Lindsay Allen and Stuart Gillespie 2001), but certainly affects cognitive ability. FRT show some evidence that health outcomes in their sample are not affected as well (see FRT, Table 6). In addition, FRT provide some convincing evidence from IOC programmatic details as well as their own empirical results, which we do not reproduce here, that indirect programme effects seem unlikely. In short, Peterson (2000) finds no evidence in the programme implementation reports that any additional health information or health services were administered to target populations during the IOC campaign rollout. Moreover, FRT show that the impact of in utero exposure on educational attainment does not change when restricting the treatment group to children born in programme years, which implies that the contribution of indirect effects of the programme (not related to iodine supplementation) is negligible.
Unfortunately, we do not have data on prenatal care and thus cannot test for effects on investments before birth.
Of course, as we increase the age gap across siblings, the likelihood that younger siblings’ treatment exposure affects vaccination decisions for older siblings naturally decreases. This fact further validates our use of birth order bandwidths when calculating sibling exposure, as detailed in subsection 2.
The model can easily generalise to an n-child household.
The cross-partial u12 determines the complementarity or substitutability of child quality in the utility function, or equivalently, the degree of parents’ aversion to inequality. Indeed, the cross partial can be mapped fully into the canonical Constant Elasticity of Substitution utility that explicitly defines a parameter (call it ρ) governing inequality aversion (see, e.g., Behrman et al. (1982), Conti et al. (2010), and Bharadwaj et al. 2013). It is easy to show that u12 > 0 if and only if ρ < 1, which is exactly the condition for inequality aversion in this class of models.
The price of the numeraire good C is normalised to 1.
References
- Aizer A, Cunha F. The Production of Child Human Capital: Endowments, Investments and Fertility. working paper. 2012 URL: http://www.econ.brown.edu/fac/anna_aizer/main_files/research_files/invest_nber_july27_2010.pdf. [Google Scholar]
- Akresh R, Bagby E, de Walque D, Kazianga H. Child Labor, Schooling, and Child Ability. working paper. 2012 URL: https://netfiles.uiuc.edu/akresh/www/Research/Akresh_ChildAbilitySchooling.pdf. [Google Scholar]
- Allen LH, Gillespie SR. What Works? A Review of the Efficacy and Effectiveness of Nutrition Interventions. Geneva and Manila: UN Sub-Committee on Nutrition and the Asian Development Bank; 2001. [Google Scholar]
- Almond D. Is the 1918 Influenza Pandemic Over? Long-term Effects of In Utero Influenza Exposure in the Post-1940 U.S. Population. Journal of Political Economy. 2006;1114(4):672–712. [Google Scholar]
- Almond D, Mazumder B. Fetal Origins and Parental Responses. Annual Review of Economics. 2013;5 [Google Scholar]
- Almond D, Hoynes H, Schanzenbach DW. Childhood Exposure to the Food Stamp Program: Long-run Health and Economic Outcomes. working paper. 2010 URL: http://www.econ.ucdavis.edu/faculty/hoynes/working_papers/almondhoynesschanzenbach-longrunfsp.pdf. [Google Scholar]
- Almond D, Currie J. Killing Me Softly: The Fetal Origins Hypothesis. Journal of Economic Perspectives. 2011;25(3):15372. doi: 10.1257/jep.25.3.153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almond D, Edlund L, Palme M. Chernobyl’s Subclinical Legacy: Prenatal Exposure to Radioactive Fallout and School Outcomes in Sweden. Quarterly Journal of Economics. 2009;124(4):1729–1772. [Google Scholar]
- Baird S, Hicks JH, Kremer M, Miguel E. Worms at Work: Long-run Impacts of Child Health Gains. working paper. 2011 doi: 10.1093/qje/qjw022. URL: http://elsa.berkeley.edu/~emiguel/pdfs/miguel_wormsatwork.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckwith L, Cohen SE, Hamilton CE. Maternal sensitivity during infancy and subsequent life events relate to attachment representation at early adulthood. Developmental Psychology. 1999;35(3):693. doi: 10.1037//0012-1649.35.3.693. [DOI] [PubMed] [Google Scholar]
- Behrman J, Rosenzweig M. Returns to Birthweight. Review of Economics and Statistics. 2004;86(2):586–601. [Google Scholar]
- Behrman JR, Pollak RA, Taubman P. Parental preferences and provision for progeny. The Journal of Political Economy. 1982:52–73. [Google Scholar]
- Bhalotra S, Venkataramani A. Shadows of the Captain of the Men of Death: Early Life Health Interventions, Human Capital Investments, and Institutions. Working paper. 2012 URL: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1940725. [Google Scholar]
- Bharadwaj P, Loken K, Neilson C. Early Life Health Interventions and Academic Achievement. The American Economic Review. 2012 forthcoming. [PubMed] [Google Scholar]
- Bharadwaj P, Eberhard J, Neilson C. Health at Birth, Parental Investments and Academic Outcomes. Working Paper. 2013 [Google Scholar]
- Black SE, Devereux PJ, Salvanes KG. From the Cradle to the Labor Market? The Effect of Birth Weight on Adult Outcomes. Quarterly Journal of Economics. 2007;122(1):409–439. [Google Scholar]
- Bleakley H. Health, Human Capital, and Development. Annual Reviews of Economics. 2010;2:283–310. doi: 10.1146/annurev.economics.102308.124436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brazelton TB. Neonatal Behavior Assessment Scale. 2nd edition. Philadelphia: JB Lippincott, Spastics International Medical Publications: 1984. [Google Scholar]
- Bullowa M. Before Speech: The Beginning of Interpersonal Communication. CUP Archive. 1979 ISBN: 052129522X, 9780521295222. [Google Scholar]
- Clark A, Sanderson C. Timing of children’s vaccinations in 45 low-income and middle-income countries: an analysis of survey data. The Lancet. 2009;373(9674):1543–1549. doi: 10.1016/S0140-6736(09)60317-2. [DOI] [PubMed] [Google Scholar]
- Conti G, Heckman J, Yi J, Zhang J. Early Health Shocks, Parental Responses, and Child Outcomes. working paper. 2011 [Google Scholar]
- Cutler D, Fung W, Kremer M, Singhal M, Vogl T. Early-life Malaria Exposure and Adult Outcomes: Evidence from Malaria Eradication in India. American Economic Journal: Applied Economics. 2010;2(2):72–94. [Google Scholar]
- Currie J. Healthy, wealthy, and wise: Socioeconomic status, poor health in childhood, and human capital development. National Bureau of Economic Research. 2008 No. w13987. [Google Scholar]
- Datar A, Kilburn MR, Loughran DS. Endowments and Parental Investments in Infancy and Early Childhood. Demography. 2010;47(1):145–162. doi: 10.1353/dem.0.0092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dow WH, Philipson TJ, Sala-i-Martin X. Longevity Complementarities under Competing Risks. American Economic Review. 1999;89(5):1358–1371. [Google Scholar]
- Field E, Robles O, Torero M. Iodine Deficiency and Schooling Attainment in Tanzania. American Economic Journal: Applied Economics. 2009;1(4):140–169. [Google Scholar]
- Laurberg P, Pedersen IB, Knudsen N, Ovesen L, Andersen S. Environmental Iodine Intake Affects the Type of Nonmalignant Thyroid Disease. Thyroid. 2001;11(5):457–469. doi: 10.1089/105072501300176417. [DOI] [PubMed] [Google Scholar]
- Meltzoff AN, Moore MK. Newborn infants imitate adult facial gestures. Child development. 1983:702–709. [PubMed] [Google Scholar]
- Meltzoff AN, Moore MK. Explaining facial imitation: A theoretical model. Early development and parenting. 1997;6(34):179–192. doi: 10.1002/(SICI)1099-0917(199709/12)6:3/4<179::AID-EDP157>3.0.CO;2-R. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitt MM, Rosenzweig MR, Hassan MdN. Productivity, Health, and Inequality in the Intrahousehold Distribution of Food in Low-Income Countries. The American Economic Review. 1990;80(5):1139–1156. [Google Scholar]
- Peterson S. PhD diss. Acta Universitatis Upsaliensis; 2000. Controlling Iodine Deficiency Disorders: Studies for Programme Management in Sub-Saharan Africa. [Google Scholar]
- Peterson S, Assey V, Forsberg BC, Greiner T, Kavishe FP, Mduma B, Rosling H, Sanga AB, Gebre-Medhin M. Coverage and Cost of Iodised Oil Capsule Distribution in Tanzania. Health Policy and Planning. 1999;14(4):390399. doi: 10.1093/heapol/14.4.390. [DOI] [PubMed] [Google Scholar]
- Restrepo B. Who Compensates and Who Reinforces? Parental Investment Responses to Child Endowment Shocks. working paper. 2011 [Google Scholar]
- Rosenzweig MR, Schultz TP. Estimating a Household Production Function: Heterogeneity, the Demand for Health Inputs, and Their Effects on Birth Weight. The Journal of Political Economy. 1983;91(5):723–746. [Google Scholar]
- Rosenzweig MR, Wolpin KI. Heterogeneity, Intrafamily Distribution, and Child Health. The Journal of Human Resources. 1988;23(4):437–461. [Google Scholar]
- Rosenzweig MR, Zhang J. Do Population Control Policies Induce More Human Capital Investment? Twins, Birth Weight and China’s“One-Child” Policy. The Review of Economic Studies. 2009;76(3):1149–1174. [Google Scholar]
- Susman-Stillman A, Kalkoske M, Egeland B, Waldman I. Infant temperament and maternal sensitivity as predictors of attachment security. Infant Behavior and Development. 1996;19(1):33–47. [Google Scholar]
- Van der Haar F, Kavishe P, Medhin MG. The Public Health Importance of IDD in Tanzania. Central African Journal of Medicine. 1988;34(3):6065. [PubMed] [Google Scholar]
- Venkataramani A. Early Life Exposure to Malaria and Cognition in Adulthood: Evidence from Mexico. Journal of Health Economics. 2012;31(5):767–780. doi: 10.1016/j.jhealeco.2012.06.003. [DOI] [PubMed] [Google Scholar]