SENCA: A Multilayered Codon Model to Study the Origins and Dynamics of Codon Usage

Abstract

Gene sequences are the target of evolution operating at different levels, including the nucleotide, codon, and amino acid levels. Disentangling the impact of those different levels on gene sequences requires developing a probabilistic model with three layers. Here we present SENCA (site evolution of nucleotides, codons, and amino acids), a codon substitution model that separately describes 1) nucleotide processes which apply on all sites of a sequence such as the mutational bias, 2) preferences between synonymous codons, and 3) preferences among amino acids. We argue that most synonymous substitutions are not neutral and that SENCA provides more accurate estimates of selection compared with more classical codon sequence models. We study the forces that drive the genomic content evolution, intraspecifically in the core genome of 21 prokaryotes and interspecifically for five Enterobacteria. We retrieve the existence of a universal mutational bias toward AT, and that taking into account selection on synonymous codon usage has consequences on the measurement of selection on nonsynonymous substitutions. We also confirm that codon usage bias is mostly driven by selection on preferred codons. We propose new summary statistics to measure the relative importance of the different evolutionary processes acting on sequences.

Introduction

Nucleotide substitutions that act on coding DNA sequences can be classified as either: 1) Synonymous substitutions, which cause no change in the encoded protein; or 2) nonsynonymous substitutions, which change the encoded protein sequence. Evolutionary studies thus aim to distinguish between these two kinds of substitutions (Miyata and Yasunaga 1980; Nei and Gojobori 1986). As the substitution type depends on its position within a codon, this led to the emergence of codon substitution models (Goldman and Yang 1994; Muse and Gaut 1994; Yang and Nielsen 1998; Pond and Muse 2005; Kosiol et al. 2007; Mayrose et al. 2007), taking the codon as the unit of evolution. Such models are currently used to estimate the strength of selection acting on coding sequences, usually assuming that synonymous substitutions are neutral. In addition, they can be used to model nonuniform frequencies of synonymous codons in real coding sequences.

Indeed, the usage of synonymous codons in genes and genomes is not random and shows for every organism a specific set of preferences (Grantham et al. 1980), called codon usage bias (CUB). In prokaryotes, codon preferences are stable enough within a genome to be a useful tool to detect, for example, recent horizontal transfer between genomes, based on differences in CUB (Karlin 2001). Furthermore, CUB intensity is variable within a genome, which helps to predict gene expression levels (Gouy and Gautier 1982; Sharp et al. 1986; Thomas et al. 1988; Agashe et al. 2013; Wallace et al. 2013; Gilchrist et al. 2015). Two explanations for the existence of CUB are usually proposed: Mutational bias (neutral or nonadaptative) or selective pressures to optimize translational efficiency or accuracy (Akashi and Eyre-Walker 1998; Hershberg and Petrov 2008; Sharp et al. 2010). Mutational biases can be due to either mutational processes (Sueoka 1988; Rocha et al. 2006; Hershberg and Petrov 2010; Hildebrand et al. 2010; Palidwor et al. 2010) or biased gene conversion (Duret 2002), whereas selective pressures act for coadapting codon usage and tRNA content in the cell (Gouy and Grantham 1980; Sharp and Li 1986; Bulmer 1987; Kanaya et al. 1999; Rocha 2004). These hypotheses explain the existence of CUB through evolutionary processes. However, CUB is usually studied on extant sequences, using statistics that do not consider its evolution, such as Codon adaptive index (CAI) (Sharp and Li 1986, 1987) or ENC (effective number of codons) (Wright 1990), which respectively, measure the similarity of a gene’s CUB relative to a reference gene set or to a uniform distribution. Some studies propose CUB measures that account for mutational bias (e.g., Knight et al. 2001; Supek et al. 2010; O’Neill et al. 2013), and the more widespread $ENC\prime$ by Novembre (2002). These descriptive statistics are insufficient to quantify the level of selection acting on CUB through time as they only take extant genomic nucleotide composition into account. Hence evolutionary models are needed to infer and quantify the processes acting on sequences, by gathering information from the phylogenetic signal.

By construction, usual codon models assume that CUB arises by neutral mechanisms. However, the existence of selection on synonymous codons may have strong consequences on these models (Spielman and Wilke 2015). McVean and Vieira (2001) built a codon model restricted to synonymous mutations that jointly use neutral rates of mutation, and a model of relative fitness between synonymous codons to derive codon substitution rates that involve codon-specific selection coefficients. This idea of relative fitness of codons has been first adapted in a broader phylogenetic context in Nielsen et al. (2007), to add selection on CUB to synonymous and nonsynonymous substitutions. Their modeling is more simple, because codons are either preferred or not-preferred, and all codons of the same category share the same fitness. A more realistic model was after proposed by Yang and Nielsen (model FMutSel in Yang and Nielsen [2008]), where each codon has its own fitness. However, in both models, the relative fitness between two codons is computed in the same way whether they encode for the same amino acid or not. But amino acids themselves have their own specific fitness, as their distribution is not uniform in proteins. In these models, the fitness of codons does not only consider CUB, but also amino acid preferences, which may blur the specific analysis of CUB. In Halpern and Bruno (1998), Rodrigue et al. (2010), and Tamuri et al. (2012), amino acid fitness is explicitly modeled in site-specific context as the main feature of selection in addition to a neutral mutation process on nucleotides.

Here, we extend the work of McVean and Vieira to synonymous and nonsynonymous substitutions in a model that disentangles the selective processes acting on synonymous codons and on amino acids, and considers explicitly the fitness of amino acids, as in the work of Halpern and Bruno. Specifically, we add a process of substitution between amino acids to the nucleotide and synonymous codon substitution process. We organize then the substitution processes of coding sequences in three layers: The nucleotide layer describes the neutral mutation process that every site undergoes, the amino acid layer describes how the nonsynonymous substitutions change the coded amino acids, and the codon layer describes how each codon is preferred among its synonymous codons. Our model name is SENCA for site evolution of nucleotides, codons, and amino acids and is implemented in Bio ++ (Guéguen et al. 2013).

SENCA allows us to explicitly estimate mutational processes, preferences on codon usage and on the usage of amino acids. Because of this organization, we can propose summary statistics, based on GC content and ENC, to measure the relative importance of mutational processes and selection on the evolution of codon usage. In this article, we show how SENCA disentangles qualitatively and quantitatively the effect of mutational processes and selection upon CUB and GC content. For this, we use SENCA in an homogeneous and nonstationary way, first on 21 groups of prokaryotes (Lassalle et al. 2015) that span a wide diversity of genomic GC content (between 27% and 65%), and then, at a deeper evolutionary scale, on five species of the Enterobacteria clade.

New Approaches

Theoretical Model

We modeled the evolution of codon sequences by specifying the substitution rate from sense codon $I=I_1{I}_2{I}_3$ to $J=J_1{J}_2{J}_3$, where I_k changed to J_k ($k\in [1;3]$). The instantaneous substitution rate from I to J is

$$q_{IJ}\propto \{\begin{array}{l}0\text{if}I\text{and}J\text{differ at two or three different positions},\\ m_{I_k{J}_k}g(x_I,x_J)\text{if}{I}_k\to J_k\text{is a synonymous mutation},\\ m_{I_k{J}_k}\omega g(x_I,x_J)\text{if}{I}_k\to J_k\text{is a nonsynonymous mutation},\end{array}$$ (1)

where $m_{I_k{J}_k}$ is the mutation parameter from nucleotide I_k to J_k; x_I (respectively x_J) is the overall preference of codon I (respectively J) and g is the part of the substitution rates due to fixation bias from the formula introduced in McVean and Vieira (2001) and Yang and Nielsen (2008), in a similar way as in Halpern and Bruno (1998):

$$g(x_I,x_J)=\{\begin{array}{c}\frac{-\log (\frac{x_I}{x_J})}{1-\frac{x_I}{x_J}}\text{if}{x}_I\ne x_J,\\ 1\text{if}{x}_I=x_J.\end{array}$$ (2)

We considered that g depends on the product of synonymous codon preference with the respective amino acid preference (if they code for different amino acids). Thus, we defined the overall preference of codon I as the product of the relative preference of the amino acid encoded by codon I, AA_I, over the other amino acids $\psi ({\text{AA}}_I)$; the relative preference of codon I over synonymous codons, ${\phi }_{{\text{AA}}_I}(I)$; and $d_{{\text{AA}}_I}$ the degeneracy of amino acid AA_I. Thus

$$x_I=\psi ({\text{AA}}_I)\times d_{{\text{AA}}_I}\times {\phi }_{{\text{AA}}_I}(I).$$ (3)

g ranges between 0 and $+\infty$. Interestingly, $\frac{g(x_J,x_I)}{g(x_I,x_J)}=\frac{x_I}{x_J}$ (see supplementary equation 1, Supplementary Material online), which means that, considering only preferences between codons, the ratio of substitution rates between two codons equals the ratio of their preferences.

SENCA is based on three substitution layers: Nucleotide (N), codon (C), and amino acid (A) layers. These layers act simultaneously as represented on figure 1.

Fig. 1.—

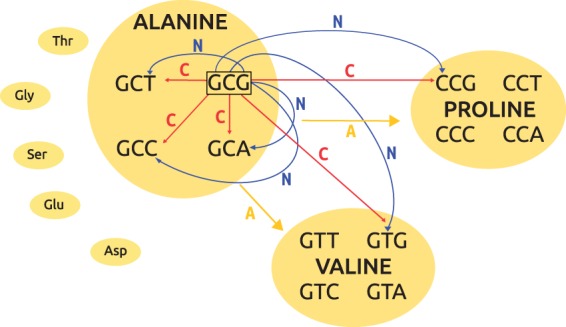
SENCA representation. Here is an example of construction of some—not all—instantaneous substitutions from sense codon GCG, that codes for Alanine, to other codons, for example, coding for Alanine, Valine, or Proline. In blue is the nucleotide (N) layer, in red the codon (C) layer, and in yellow the amino acids (A) layer. Arrows indicate which layer affects each substitution.

• The nucleotide layer N accounts for a neutral process of nucleotidic mutations, and is modeled through a classic nucleotide model (see http://biopp.univ-montp2.fr/manual/html/bppsuite/2.2.0/Nucleotide.html#Nucleotide for a list of available models). We can compute equilibrium frequencies of A,…,T nucleotides: ${\pi }_A^{\mathrm{☆}}$,…,${\pi }_T^{\mathrm{☆}}$ from the mutation parameter from nucleotide I_k to J_k, $m_{I_k{J}_k}$. The number of free parameters depends on the chosen model.

• The codon layer C accounts for the relative preferences between synonymous codons; let us denote ${\text{cod(AA}}_I)$ the set of synonymous codons translated into AA_I. The relative preference of codon I over synonymous codons is ${\phi }_{{\text{AA}}_I}(I)\in [0,1]$, and for each amino acid these preferences are normalized such that $\sum _{I\in {\text{cod(AA}}_I)}{\phi }_{{\text{AA}}_I}(I)=1$. This layer has 61 parameters and only $61-20=41$ free ones due to our intra amino acid normalization process.

• The amino acid layer A accounts for the preferences between amino acids in the case of nonsynonymous substitutions; in our case, we modeled it with a unique overall selection parameter on nonsynonymous substitutions (as is usually done in codon models), called ω, and a preference profile on amino acids. We then have 20 free parameters: ω represents the ratio of the nonsynonymous over synonymous substitution rates, and for any amino acid AA the relative preference of AA over the other amino acids is $\psi (\text{AA})$, and they are normalized such that $\sum _{\text{AA}\in \text{amino acids}}\psi (\text{AA})=1$.

After this parameterization, the generator q is normalized as usual, with one substitution per site per unit of time on the stationary distribution.

Hereafter we use the notation SENCA[layers] to indicate the “layers” that are considered under a particular set of assumptions. In the case of uniform codon usage (i.e., no CUB), the C layer follows a null hypothesis—we denote that assumption as SENCA[NA]—and ${\phi }_{A{A}_I}(I)=\frac{1}{d_{A{A}_I}}$. The preference of codon I is then the preference of its amino acid ${\psi }_{A{A}_I}$. In the case of no preference on the amino acids, the A layer follows a null hypothesis—denoted as SENCA[NC]—and $\psi (AA)=\frac{1}{20}$ for each amino acid AA. There the overall preference of codon I is proportional to $d_{A{A}_I}\times {\phi }_{A{A}_I}(I)$. One can notice that in the joint case of no preference of amino acids nor on codons—that is, null model, denoted SENCA[N]—the preferences of the 61 sense codons are equal (stop codons are not considered in the model).

Equilibrium Frequencies

From equation (1), when the nucleotidic model is reversible we can compute the equilibrium frequency of codon I, $f^{\mathrm{☆}}(I)$:

$$f^{\mathrm{☆}}(I)\propto \left(\underset{N\text{layer}}{\underbrace{{\displaystyle \prod _{k=1}^3{\pi }_{I_k}^{\mathrm{☆}}}}}\right)\times \left(\underset{C\text{layer}}{\underbrace{d_{A{A}_I}\times {\phi }_{A{A}_I}\left(I\right)}}\right)\times \left(\underset{A\text{layer}}{\underbrace{\psi \left(A{A}_I\right)}}\right).$$ (4)

This illustrates how processes induced by SENCA are separated into three layers N, C, and A. We computed partial equilibrium frequencies of codons that result from either N (i.e., model SENCA[N]), C (i.e., SENCA[C]), or A (i.e., SENCA[A]) layer only, by setting the other layers’ parameters to their null hypothesis value in equation (4). Under SENCA[N], amino acids and codons preferences are ignored and for each codon I equation (4) becomes $f_N^{\mathrm{☆}}(I)\propto {\displaystyle {\Pi }_{k=1}^3{\pi }_{I_k}^{\mathrm{☆}}}$. Under SENCA[C] equation (4) becomes $f_C^{\mathrm{☆}}(I)\propto {\phi }_{A{A}_I}(I)\times d_{A{A}_I}$, and under SENCA[A] it becomes $f_A^{\mathrm{☆}}(I)\propto \psi (A{A}_I)$. These partial equilibrium frequencies are useful for comparing evolutionary layers, but as they are deduced from extant sequences which have been applied simultaneously to all (N, C, and A) layers, they should always be interpreted together and not separately.

Summary Statistics

As SENCA has many free parameters, we developed three summary statistics to estimate the overall role played by each layers based on classical codon usage statistics: GC and GC3 composition, and ENC (Wright 1990). First, we deduced from equation (4) the GC equilibrium frequency for each layer, respectively, noted $G{C}_N^{\mathrm{☆}},G{C}_C^{\mathrm{☆}}$_, and $G{C}_A^{\mathrm{☆}}$ in order to estimate the influence of each layer on the equilibrium genome composition. Similarly, we estimated the equilibrium frequency at the third position within codons, denoted $GC{3}^{\mathrm{☆}}$ for each layer. Because the redundancy in the genetic code is greater at this position compared with others, GC3 is often used as a proxy for underlying mutational bias in prokaryotic genomes (Muto and Osawa 1987). As genomes with very different CUB can be similar in terms of $G{C}^{\mathrm{☆}}$ and $GC{3}^{\mathrm{☆}}$, we used the same approach by computing $EN{C}^{\mathrm{☆}}$ statistics for each layer.

We computed distance of genomic $G{C}^{\mathrm{☆}}$ content to a uniform usage of the 61 sense codons (i.e., 51.4% of GC, after removing the stop codons, which are AT-rich) as

$$dG{C}^{\mathrm{☆}}=G{C}^{\mathrm{☆}}-\mathrm{0.514.}$$ (5)

We also defined $dG{C}_N^{\mathrm{☆}},dG{C}_C^{\mathrm{☆}}$_, and $dG{C}_A^{\mathrm{☆}}$ as the distances to unbiased content for each layer.

We defined similar statistics for genomic $GC{3}^{\mathrm{☆}}$ content. A uniform usage of the 61 sense codons leads to $GC3=0.508$. Then

$$dGC{3}^{\mathrm{☆}}=GC{3}^{\mathrm{☆}}-\mathrm{0.508.}$$ (6)

Similarly, we defined $dGC{3}_N^{\mathrm{☆}},dGC{3}_C^{\mathrm{☆}}$_, and $dGC{3}_A^{\mathrm{☆}}$.

To study more specifically CUB, we computed ENC (Wright 1990) for observed sequences using codons frequencies. ENC is a measure of CUB as it goes from 20 (maximum bias) to 61 (no bias):

$$ENC={\displaystyle \sum _{R\in \text{ARC}}\frac{k_R^2}{{\displaystyle \sum _{\text{AA}\in R}\frac{1}{n_{\text{AA}}-1}}\left(\left(n_{\text{AA}}{\displaystyle \sum _{I\in \text{cod(AA})}{p}^2}(I)\right)-1\right)}}$$ (7)

with ARC the set of all degeneracy classes of amino acids, k_R the number of amino acids of such a class, n_AA the observed number of codons coding for AA, cod(AA) the set of codons of amino acid AA, p(I) the relative frequency of codon I among its synonymous.

We computed $EN{C}^{\mathrm{☆}}$, the effective number of codons on sequences at equilibrium of the model, by replacing in equation (7): $n_{\text{AA}}=L\times f^{\mathrm{☆}}(\text{AA})$ with L the length (in codons) of the data and $f^{\mathrm{☆}}(AA)$ the equilibrium frequency of amino acid AA and replacing $p(I)=\frac{f^{\mathrm{☆}}(I)}{\sum _{J\in \text{cod(AA)}}{f}^{\mathrm{☆}}(J)}$ the relative frequency of codon I at equilibrium. We also defined $EN{C}_{\text{layer}}^{\mathrm{☆}}$ induced by each layer, by computing ENC using partial codon equilibrium frequencies described previously: $n_{\text{AA}}{}_{\text{layer}}^{\mathrm{☆}}=L\times \sum _{I\in \text{cod(AA)}}{f}_{\text{layer}}^{\mathrm{☆}}(I)$ and $p_{\text{layer}}^{\mathrm{☆}}(I)=\frac{f_{\text{layer}}^{\mathrm{☆}}(I)}{\sum _{J\in \text{cod(AA)}}{f}_{\text{layer}}^{\mathrm{☆}}(J)}$ the relative equilibrium frequency of the codon I of this layer. For both N and C layers, $f_N^{\mathrm{☆}}(I)$ and $f_C^{\mathrm{☆}}(I)$ were computed as described in the section “Equilibrium Frequencies.”

From the $EN{C}^{\mathrm{☆}}$ estimates, we computed the distance from uniform usage (61) to the effective codon usage. We denoted $dEN{C}^{\mathrm{☆}}=61-EN{C}^{\mathrm{☆}}$, for any layer: $dEN{C}_{\text{layer}}^{\mathrm{☆}}=61-EN{C}_{\text{layer}}^{\mathrm{☆}}$.

Materials and Methods

Data and Model Implementation

Intraspecies Data Set

Our data set came from Lassalle et al. (2015), see table 1. We used coding DNA sequences from the core genomes of 20 bacterial pathogens and of one archeal group. These species were chosen because they encompass the diversity of genome composition among prokaryotes and that we could select nonrecombinant genes. We obtained between 6 and 35 strains per species. For each species, we built codonwise nucleotide alignments using seqinR package in R (Charif and Lobry 2007) to translate nucleotide sequences, ClustalW (Larkin et al. 2007) to align protein sequences, and PAL2NAL (Suyama et al. 2006) to retrieve nucleic alignments. Within a species, we sorted genes by increasing ENC values and concatenated them by groups of around 50 genes, to ensure we had enough data for precise parameter estimation. In total, we obtained 166 concatenates (from 1 to 16 per species, see table 1). Then, we computed a phylogenetic tree for each concatenate using CodonPhyML (Gil et al. 2013), with an Nearest Neighbor Interchange (NNI) tree topology search and the GY + W+K + F, F3x4 model. We selected one tree per species, as trees topologies were consistent within each species (see supplementary fig. S1 for topology, Supplementary Material online). We rooted our trees using TPMS (Bigot et al. 2013) and a reference species tree built with BIONJ (Gascuel 1997) from a distance matrix of the complete genomes of HOGENOM V6 database (Penel et al. 2009).

Table 1.

Summary of the Data Set Characteristics

Data Set	Taxon Name	No. of Strains	No. of Concatenates	Mean GC %	Median ENC
Clostridium	Clostridium botulinum	8	11	29.6	35.3
Campylo	Campylobacter jejunii	6	7	31.6	39.8
Francis	Francisella tularensis	8	7	33.8	41.6
Staph	Staphylococcus aureus	15	11	34.2	40.5
Sulfoa	Sulfolobus spp.	8	9	35.4	45.0
B_anthracis	Bacillus antharcis/aureus group	17	6	37.0	42.5
Listeria	Listeria spp.	8	6	38.8	47.6
Strep_pyo	Streptococcus pyogenes	12	7	39.6	48.5
Helico	Helicobacter pylori	14	2	40.4	46.6
Acineto	Acinetobacter spp.	6	10	40.8	43.7
Clamy_trach	Clamydia trachomatis	13	7	41.8	50.7
Strep_pneu	Streptococcus pneumoniae	13	7	42.0	48.8
Yersinia	Yersinia pestis	11	13	49.3	51.8
Escherichia	Escherichia coli	35	3	53.3	45.5
Salmo	Salmonella enterica	14	12	54.6	45.3
Neisseiria	Neisseiria meningitidis	8	4	55.3	43.8
Brucella	Brucella spp.	9	8	58.8	41.6
Bifido_longum	Bifidobacterium longum	6	7	61.9	38.2
Mycobacterium	Mycobacterium tuberculosis complex	7	1	66.1	41.5
Burk_ceno	Burkholderia cenocepacia complex	8	16	68.2	31.0
Burk_mal	Burkholderia mallei group	9	12	68.7	31.0

Note.—Data comes from Lassalle et al. (2015). On each line is indicated the species and the corresponding number of strains in the alignments, the number of concatenates, the mean observed GC content and the median observed ENC, each concatenate being approximately 50 genes long. Genes are from the core genome, at least 900 nt long and classified as nonrecombinant in Lassalle et al. (2015).

^aArcheal species of the data set.

Interspecies Data Set

We considered five enterobacteria that present an average GC content: Klebsiella pneumoniae 342 (KLEP3), Escherichia coli E24377A (ECO24), Citrobacter koseri ATCC BAA-895 (CITK8), Salmonella enterica subsp. enterica serovar Typhimurium str (SAENT1), and Escherichia fergusonii ATCC 35469 (ESCF3). These species present a similar GC content of 55% and the phylogenetic depth of the tree is such that we can perform our SENCA analysis in a homogenous context. Moreover, we chose this data set as it contains S. enterica and E. coli, two species present in the intraspecies data set. Indeed, we will compare the results of both data sets. From HOGENOM, we selected the 1,797 gene families containing these five species, and only kept gene families for which the topology correspond to the reference HOGENOM species tree (see supplementary fig. S2, Supplementary Material online) and for which there were neither duplications nor deletions. We obtained 222 HOGENOM families that were then aligned codonwise as previously described. We concatenated genes sorted by increasing ENC values into four concatenates of around 50 genes each.

Implementation

SENCA was implemented in Bio ++ (Guéguen et al. 2013) and likelihood optimized with bppml (Dutheil and Boussau 2008). For the N layer, under the hypothesis that the mutation process is strand symmetric and reversible, as, in our study, we are interested in broad tendencies in GC content at equilibrium, we used the T92 model (Tamura 1992) which depends on two free parameters, the equilibrium frequencies of the GC pairs ${\pi }_{CG}^{\mathrm{☆}}$ and κ which is the transition/transversion ratio. Additionally, to reduce computational complexity in the intraspecies analysis, we supposed that the A layer is stable within a species, that is, ${\psi }_{A{A}_I}$ stationary (which is more realistic than assuming stationary amino acids frequencies). This assumption is reasonable as we studied intraspecies evolution, with short tree depths. We relaxed this assumption in the interspecies analysis. We tested the informativeness of SENCA layers N, C, and A with likelihood ratio tests (LRT, see supplementary table S1, Supplementary Material online). In order to demonstrate the usefulness of our approach, we compared SENCA with the more classical YN98 + F61 codon model (Yang and Nielsen 1998), noted YN98 hereafter, in which synonymous substitutions are neutral, but where any CUB can be modeled, as each codon has its own equilibrium frequency. We performed nonstationary analyses using a homogeneous modeling for all models (numbers of parameters in supplementary table S1, Supplementary Material online). We compared SENCA and YN98 using Akaike information criterion (AIC) and Bayesian information criterion (BIC) (see supplementary table S1, Supplementary Material online). Please note that, if we use HKY85 (Hasegawa et al. 1985) model for the N layer and assume stationarity, then the fitness of codon I, noted F_I, presented in Yang and Nielsen (2008) is equal to $F_I=d_{A{A}_I}\times {\phi }_{A{A}_I}(I)\times \psi (A{A}_I)$.

Simulations

We performed simulation studies using bppseqgen sequences generator with SENCA model (Dutheil and Boussau 2008). We used a species trees with 13 leaves and median branch length $\approx 0.10$ (see supplementary fig. S3, Supplementary Material online) and simulated an alignment of 20,000 sites. Root was set equal to the global null hypothesis, that is, uniform codon usage, and we simulated with combinations of $G{C}_N^{*}$ at 0.3, 0.5 and 0.7, and $GC{3}_C^{*}$ at 0.3, 0.5 and 0.7. We tested different classical nucleotidic models for the N layer of SENCA: T92 (Tamura 1992), HKY85 (Hasegawa et al. 1985, as in FMutSel of Yang and Nielsen [2008]), GTR (Tavar 1986), SSR (Yap and Speed 2004), and L95 (Lobry 1995, the most general strand symmetric model). As there are many ways to set the parameters of the codon layer for a given $GC{3}_C^{*}$, we used the scenario that may be the most difficult to discriminate, where the amino acids of a same redundancy class share the same codon preferences and where for each amino acid all GC ending synonymous codons share uniformly this $GC{3}_C^{*}$ preference (and symmetrically for AT). The AA preferences of the A layer were chosen randomly, to be different from the root preferences which equals to $\frac{1}{20}$ for each amino acid. Hence, the A layer is not stationary (see supplementary material, Supplementary Material online, for the values). For each parametrization, we ran five replicates.

We also performed parametric bootstrap tests on Burkholderia cenocepacia complex, Campylobacter jejunii species (GC-rich and AT-rich, respectively) to check the variance of real estimates that considers particular codon bias. We performed 30 replicates for each concatenate.

Results

We studied 21 groups of prokaryotes that are diverse in terms of genomic content (GC content ranges from 29% to 68%). We showed two main results. First, SENCA better predicts genomic content and CUB than YN98 + F61. Second, SENCA parameterization is relevant to distinguish mutational effects from selection on codons, and to compare them. Finally, we studied a deeper Enterobacteria tree of five species to see how the different layer effects scale with the depth of the tree.

Model Identifiability and Validation

Simulations

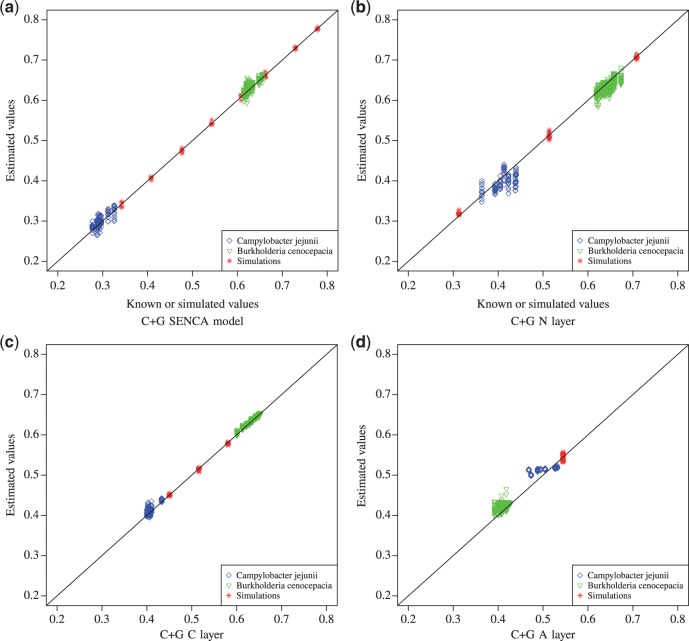
In theory, SENCA is identifiable (see supplementary material, Supplementary Material online, for demonstration), but we wanted to check its practical identifiability on our data. For this, we performed a simulation study and parametric bootstraps. Results are shown in figure 2, for controlled parameters (red dots) and for parametric bootstraps on C. jejunii (AT-rich species, blue dots) and B. cenocepacia complex (GC rich species, green dots). In both cases maximum-likelihood estimates from SENCA retrieved with good precision the values used for simulations, confirming the model identifiability. In particular, one concern may be that opposite effects from the nucleotidic and codon layers may be hard to grasp by SENCA. Here we see that SENCA retrieves the input parameters correctly, even in those difficult cases.

Fig. 2.—

Simulation results for each layer. x axis corresponds to the chosen values (red dots) or known values (green and blue dots) used to simulate data, y axis to the values estimated by maximum likelihood. Red dots correspond to simulations with GC_N and GC_C ranging from 0.3 to 0.7. Green and blue dots correspond to parametric bootstrap where parameter values taken from previous estimations are used to first simulate, then infer, the evolutionary processes, respectively, of Burkholderia cenocepacia complex and of Campylobacter jejunii.

We also tested a simulation study with N layer modeled by HKY85, SSR, GTR, or L95. We saw that using complex nucleotidic models, such as SSR, GTR or L95, reduced the practical identifiability of the model, and that HKY85 and T92 gave similar results justifying our usage of the T92 nucleotidic model. Results are shown in supplementary figure S4, Supplementary Material online.

Model Validation

We compared likelihoods of SENCA and YN98 models using AIC and BIC criteria (see supplementary table S1, Supplementary Material online). Using AIC, SENCA is better-fit than YN98 for 152 concatenates out of 166. Using BIC ($\Delta \text{BIC}>2$), SENCA is better-fit than YN98 in 121 concatenates. SENCA has fewer parameters to estimate than YN98: Both models approximately share the same number of total parameters, but in SENCA we can hypothesize the stationarity layer by layer, and doing it for the AA layer reduces the number of free parameters by 19. This possibility of tuning each layer in the model according to the biological signal under study is one of the most relevant features of SENCA. To check the importance of each layer, we also performed estimations by fixing one layer to its null hypothesis at a time: ${\text{SENCA}}_{[NC]},{\text{SENCA}}_{[NA]},{\text{SENCA}}_{[CA]}$. We computed LRT to validate the significance of our parametrization. Layers N, C, and A are always informative (P value < 0.05 after Bonferroni correction) except for the layer N of the enterobacteria study.

Comparison to YN98 + F61 Model

GC Content at Equilibrium

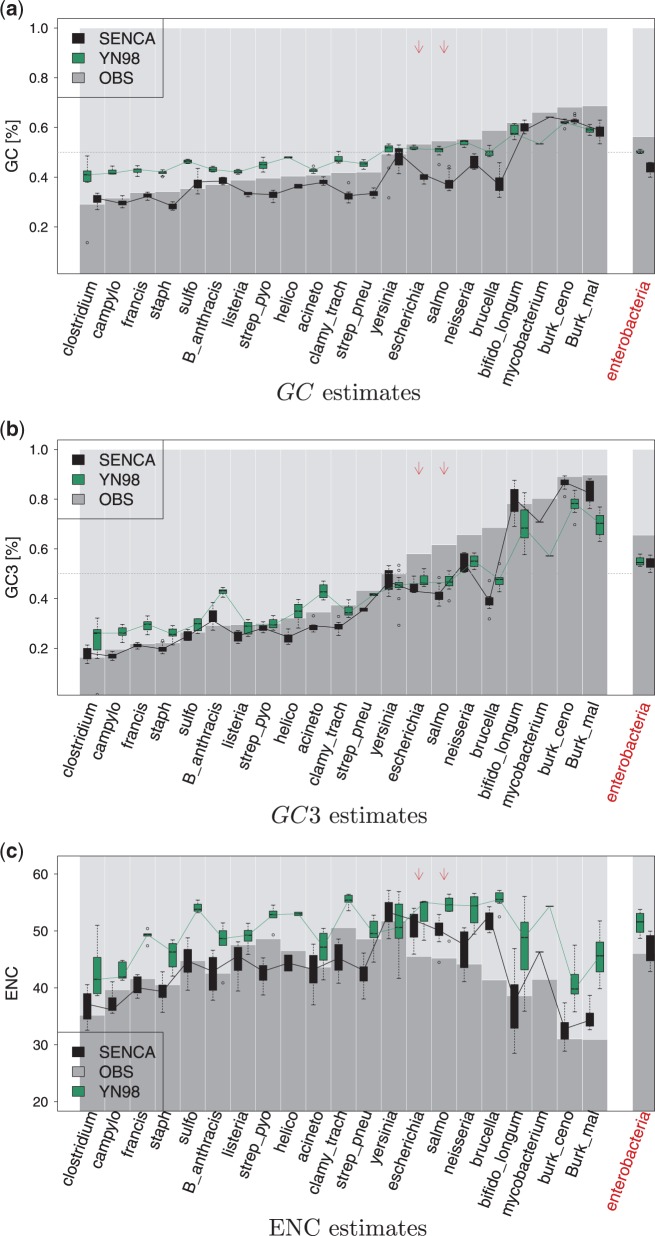
In figure 3, we compare the equilibrium $G{C}^{\mathrm{☆}}$ content of YN98 and SENCA with T92 model of the N layer (analyses using HKY85 are similar, results are not shown). For most of the species, global $G{C}^{\mathrm{☆}}$ estimates of SENCA are below GC_obs, indicating a global tendency toward AT enrichment at equilibrium. In particular, for all AT-rich species, $G{C}^{\mathrm{☆}}$ is close to 0.3, a value observed in some recent studies (Hershberg and Petrov 2010; Hildebrand et al. 2010) as the equilibrium of mutation forces. This overall tendency is not identified by YN98, whose estimates are often closer to a uniform GC content relative to SENCA estimates.

Fig. 3.—

GC, GC3 contents and ENC estimates at equilibrium from SENCA and YN98. Species are ordered by increasing GC content in (a) and (c), and by increasing GC3 in (b). Interspecific results are shown on the right. Gray bars represent observed GC in (a), observed GC3 in (b), and observed ENC in (c). Boxplots span the different concatenates within a species. Black stands for SENCA estimates, green for YN98 estimates. Arrows indicate Escherichia coli and Salmonella enterica.

As already observed in many species, in figure 3b, we found GC3 content more biased than GC content. Comparing equilibrium $GC{3}^{\mathrm{☆}}$ of both models, we see that SENCA estimates are often closer to the observed values than YN98, especially for AT-rich and GC-rich species, even though models are theoretically both able to retrieve such extreme GC3 biases. It suggests that explicitly taking into account the structure of the genetic code in the substitution process is an important modeling feature.

It is interesting to understand how these results depend on the evolutionary scale. In particular, intraspecific results for Escherichia and Salmonella can be compared with those of the interspecific study (fig. 3) which includes these species. For global GC content, results are quite similar between and inside species, with YN98 still closer to a uniform GC content relative to SENCA. For GC3, the equilibrium estimates both by SENCA and YN98 are higher than the intraspecific estimates, which reveals the difference between studies at inter- versus intraspecific scales, where synonymous mutations may still be polymorphic. We can see that the difference is more marked for SENCA, which we attribute to a better capacity to grasp the evolutionary signal at the third position in the intraspecific study.

Codon Usage Bias

We then explored CUB using ENC (Wright 1990). We computed equilibrium $EN{C}^{\mathrm{☆}}$ estimated by YN98 and by SENCA (see fig. 3c). As expected, ENC_obs is lower in AT-rich or GC-rich species: The higher the bias in genomic content, the higher the bias in codon usage. By comparison to ENC_obs, ${\text{ENC}}_{\text{YN}98}^{\mathrm{☆}}$ almost invariably shows lower CUB than the observed values, whereas ${\text{ENC}}_{\text{SENCA}}^{\mathrm{☆}}$ and ENC_obs are closer for all species. At the interspecific level, SENCA also predicts an equilibrium ENC closer to the observed one, whereas YN98 has higher values, matching what is seen on the intraspecific analysis of E. coli and S. enterica. Moreover, we can notice that $EN{C}^{\mathrm{☆}}$ of Enterobacteria is lower than of E. coli and S. enterica. This is explained because at the intraspecific scale, slightly deleterious mutations are expected to be still present whereas they must have been deleted at the interspecific scale. Those deleterious mutations increase the frequency of unpreferred codons and lead to an increase of $EN{C}^{\mathrm{☆}}$ values.

Effects on Selection Measure

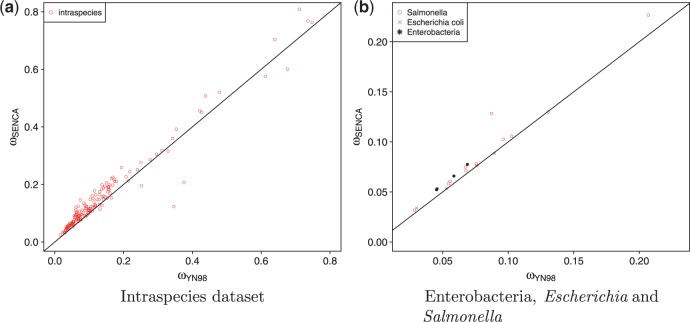
ω is used as an index for the strength of selection—the lower the value of ω, the stronger the purifying selection. ω is considered as the ratio between nonsynonymous substitutions and synonymous substitutions. In a context where some synonymous substitutions are slightly deleterious, they are less frequent than if considered as neutral substitutions, and SENCA will estimate higher ω than YN98. As shown in figure 4a, we indeed observe that ω values inferred with SENCA are significantly higher than with YN98 ($P<2\hspace{0.5em}{10}^{-16}$, unilateral paired Wilcoxon test). Moreover, these differences are even greater in the enterobacteria estimates of ω than in E. coli or S. enterica estimates (except for two concatenates of Salmonella), see figure 4b. Indeed, for enterobacteria, the median difference between ω estimates is 0.0075 (variance $5.8\hspace{0.5em}\times {10}^{-7}$) whereas for E. coli or S. enterica, the median is 0.0035 (variance $1.1\hspace{0.5em}\times {10}^{-4}$). In fact, in intraspecific studies, slightly deleterious mutations may not yet have been suppressed, and less difference is expected between neutral and synonymous substitutions than in interspecific studies.

Fig. 4.—

Estimates of ω from SENCA and YN98. The line represents ${\omega }_{\text{SENCA}}={\omega }_{\text{yn98}}$. Estimates of SENCA are significantly higher than those of YN98 (see main text). (a) represents the intraspecies data set and (b) represents in blue Escherichia coli, in red Salmonella enterica, and in black the concatenates from the interspecific data set. Each point is a concatenate.

This demonstrates that taking CUB into account for evolutionary studies is important as it can change the classical estimates of selection acting on genomic sequences.

SENCA: A Multilayered Model

GC Content at Equilibrium

As SENCA is a multilayered model, it is possible to examine the different layers separately. At first, we blocked one layer at a time, which leads to the loss of useful information (see LRT results; supplementary table S1, Supplementary Material online). Even though, in this case, the global $G{C}^{*}$ content is mostly reliable (see supplementary fig. S5, Supplementary Material online), the dynamics between layers are different and the CUB (through $EN{C}^{*}$; see supplementary fig. S5c, Supplementary Material online) is highly impacted if C (for average GC species) or A is fixed (for every species). This is explained as each layer refines the model, and it confirms the importance to examine the joint contribution of N, C, and A on $G{C}^{*}$ and $GC{3}^{*}$ estimates.

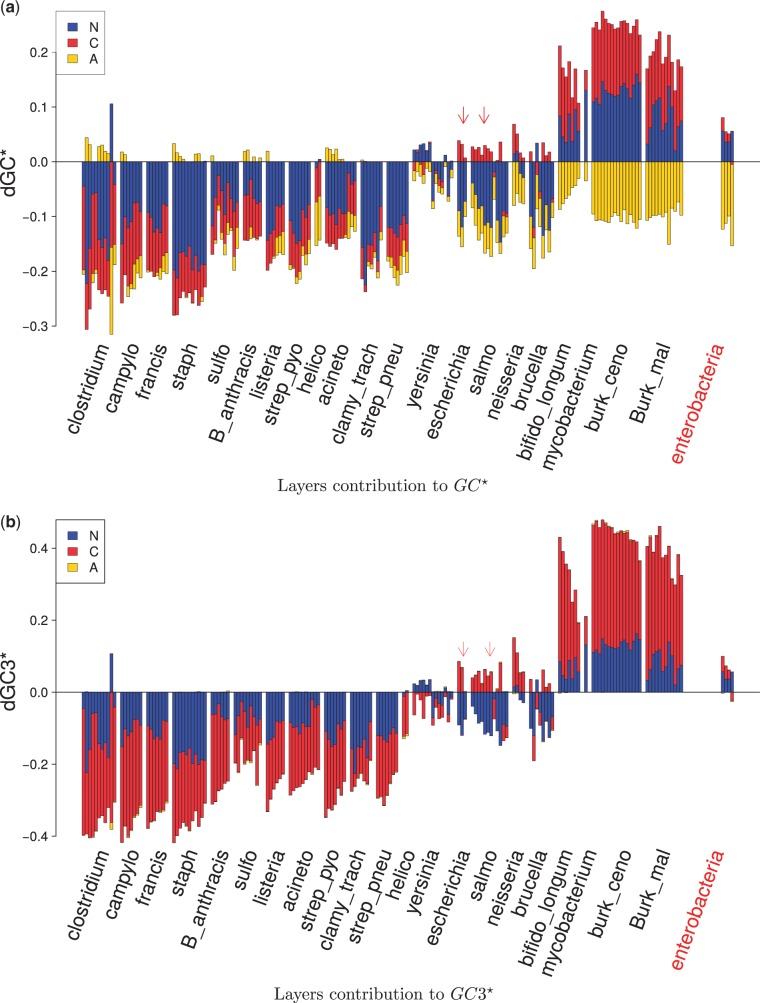
We looked at $dG{C}^{\mathrm{☆}}$, the distance between $G{C}^{\mathrm{☆}}$ and uniform composition (see eq. 5). We checked whether the effects of the different layers may be summed to explain the equilibrium GC content. Indeed the correlation between $dG{C}^{\mathrm{☆}}$ and the sum $dG{C}_A^{\mathrm{☆}}+dG{C}_C^{\mathrm{☆}}+dG{C}_N^{\mathrm{☆}}$ is highly significant ($R^2=0.996,P<{10}^{-16}$, see supplementary fig. S6a, Supplementary Material online), and the slope of the regression is 0.95 (intercept was fixed to 0). Therefore, $dG{C}^{\mathrm{☆}}$ estimates can be seen as different forces acting separately on the global $G{C}^{\mathrm{☆}}$ content. Thus, we looked at the contribution of N, C, and A layers on equilibrium GC content (fig. 5a). We observed that in most of the cases C and N layers influence GC in the same direction. This leads to a more biased $dG{C}^{\mathrm{☆}}$—that is, further from 0.514—than any layer taken independently. For AT-rich species, the N layer has negative $dG{C}^{\mathrm{☆}}$ values, whereas for GC-rich species ($>60\%$), $dG{C}_N^{\mathrm{☆}}$ is positive. The C layer follows the same pattern in a smoother way.

Fig. 5.—

Layers contribution to GC and GC3 contents at equilibrium from SENCA. Blue stands for $G{C}_N^{\mathrm{☆}}$, red for $G{C}_C^{\mathrm{☆}}$_, and yellow for $G{C}_A^{\mathrm{☆}}$. (a) represents the distances of N, C, and A to a uniform GC content ($dG{C}_{layer}^{\mathrm{☆}}=G{C}_{layer}^{\mathrm{☆}}-0.514$) and (b) the distances of N, C, and A to a uniform GC3 content ($dGC{3}_{layer}^{\mathrm{☆}}=GC{3}_{layer}^{\mathrm{☆}}-0.508$). Each bar represents one concatenate. Species are ordered by increasing observed GC in (a) in and observed GC3 in (b). Interspecific results are shown on the right. Arrows indicate Escherichia coli and Salmonella enterica.

Furthermore, we saw that similar $dG{C}^{\mathrm{☆}}$ can be due to very different $dG{C}_N^{\mathrm{☆}},dG{C}_C^{\mathrm{☆}}$_, and $dG{C}_A^{\mathrm{☆}}$. As an example, the species Clostridium botulinum, Staphylococcus aureus and Streptococcus pyogenes present similar $dG{C}^{\mathrm{☆}}$ values, approximately −0.2, but different layers effect, with the N layer dominating in St. aureus, or C and A layers having opposite effects in Cl. botulinum. This illustrates the ability of our multilayered model to explain the nucleotide composition of sequences.

Overall, we observed two large categories of intraspecific results. For all the species but the GC-rich ones and Yersinia pestis, the N layer has a negative effect on $dGC*$ and $dGC3*$. This makes sense in relation to the theory that mutations are universally biased toward AT (Hershberg and Petrov 2010; Hildebrand et al. 2010). For average GC species, selection may compensate for such a bias by being GC-driven. However, the behavior on GC-rich species is very different. This difference is not due to the model, as it is symmetric with GC, and the causes should be looked in the evolution process. The C layer contributes far more to GC in these species than in other ones. Both N and C layers are toward high GC, and the A layer is strongly in the opposite direction, all with equal strength, suggesting a complex process on content equilibrium.

Comparing the interspecific analysis with results from Escherichia and Salmonella is interesting as the decomposition in the interspecific analysis is different than the one of Escherichia and Salmonella species. In the interspecific data, mutations are fixed, which means that the N layer is concerned by substitutions, that is, mutations plus selection. These substitutions are GC-driven, and as in the intraspecific studies the mutations are toward AT, we can hypothesize that selection biased toward GC. At this evolution scale, preferences on amino acids have a strong impact toward AT, much stronger than in the intraspecific studies, with the exception of GC-rich species. This unexpected result is connected to previous hypotheses published as Lobry (1997). Indeed, the preference toward AT in the A layer is probably related to the chemical constraints of the bacterial proteome.

Finally, we studied $GC{3}^{\mathrm{☆}}$ (fig. 5b). The correlation between $dGC{3}^{\mathrm{☆}}$ and the sum $dGC{3}_A^{\mathrm{☆}}+dGC{3}_C^{\mathrm{☆}}+dGC{3}_N^{\mathrm{☆}}$ is highly significant ($R^2=0.997,P<{10}^{-16}$, see supplementary fig. S6b, Supplementary Material online) with a slope of 0.87 and an intercept fixed to 0. Globally, $dGC{3}^{\mathrm{☆}}$ is clearly driven by the C layer. Red barplots are predominant for every species but S. enterica. This is different from the behavior of $G{C}^{\mathrm{☆}}$ estimates but it is expected as most—but not all—of the C layer action should be seen in the third codon position. This is consistent with the classical observation that GC3 is more biased than GC12 (GC at the first and second codon positions) in prokaryote genomes (Muto and Osawa 1987). The N layer effect is weak, but not null at this position. By definition, it is equal to the global N effect which acts identically on all positions. Note that for $G{C}^{*}3$ there is nearly no impact from the A layer because of the degeneracy of the genetic code at this position.

Codon Usage Bias

We computed partial $EN{C}^{\mathrm{☆}}$, that is, ENC computed on codon partial equilibrium frequencies due to each layer separately, and compared this with $EN{C}^{\mathrm{☆}}$ and ENC_obs (see supplementary fig. S7, Supplementary Material online). Our main result is that $EN{C}^{\mathrm{☆}}$ is quite close to $EN{C}_C^{\mathrm{☆}}$ and that $EN{C}_N^{\mathrm{☆}}$ was very high (mean value is 58.4). This suggests that the C layer dominates the establishment of CUB at equilibrium, with a relatively small effect of the N layer. There are a few interesting exceptions: St. aureus, Chlamydia trachomatis, or, among GC-rich species, Burkholderia cenocepaia show a lower value of $EN{C}_N^{\mathrm{☆}}$, indicating a marked effect of the N layer on CUB. These effects need to be studied in context, that is, to be compared with $EN{C}^{\mathrm{☆}}$.

To quantify the effects of C and N layers on CUB at equilibrium, we defined dENC as the distance of ENC to 61 (no bias). In figure 6, we see that the C layer is predominant in the estimation of CUB for the 21 species: $dEN{C}_C^{\mathrm{☆}}>dEN{C}_N^{\mathrm{☆}}$. Similarly to our procedure for $dG{C}^{\mathrm{☆}},$ we checked whether $dEN{C}^{\mathrm{☆}}$ could be predicted from the layer estimates, by fitting $dEN{C}^{\mathrm{☆}}$ to $dEN{C}_N^{\mathrm{☆}}+dEN{C}_C^{\mathrm{☆}}$ with a linear regression model. The fit indicates that the intuitive idea of adding separate layer effects to estimates CUB at equilibrium works quite well ($R^2=0.964$ with $P<{10}^{-16}$, slope: 0.98 with an intercept fixed to 0, see supplementary fig. S8, Supplementary Material online). The slope of 0.9806 of the linear model indicates that the direct sum of $dEN{C}_N^{\mathrm{☆}}$ and $dEN{C}_C^{\mathrm{☆}}$ slightly overestimates $dEN{C}^{\mathrm{☆}}$ in these data. Moreover, we can see that this tendency varies with GC content, as the ratio $\frac{dEN{C}_C^{\mathrm{☆}}+dEN{C}_N^{\mathrm{☆}}}{dEN{C}^{\mathrm{☆}}}$ is mostly below 1 for GC-poor species, and above 1 for GC-rich species (see fig. 6).

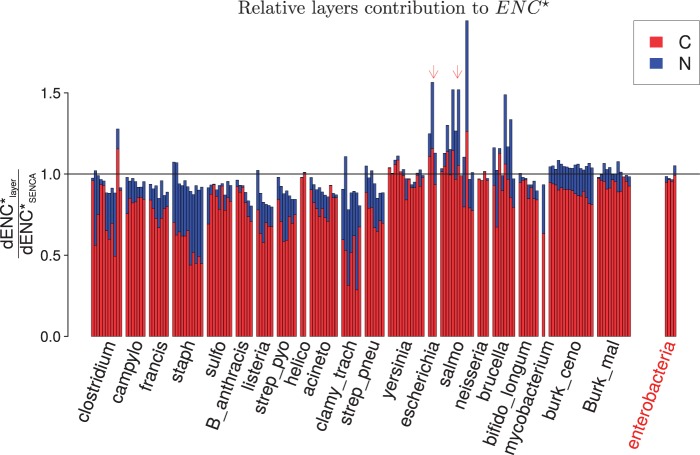
Fig. 6.—

Quantification of N and C layers’ effect on CUB. Blue represents $\frac{dEN{C}_N^{\mathrm{☆}}}{dEN{C}^{\mathrm{☆}}}$ and red $\frac{dEN{C}_C^{\mathrm{☆}}}{dEN{C}^{\mathrm{☆}}}$. Species are ordered by increasing observed GC content. Interspecific results are shown on the right. Arrows indicate Escherichia coli and Salmonella enterica.

As ENC is a statistic computed on multidimensional data, the sum of $dEN{C}^{\mathrm{☆}}$ for the C and N layers neglects the overlapping effects of these layers. By direct comparison, our model allows us to measure how N and C layers interact to influence the overall CUB, either positively or negatively. One clear example of negative interaction is Salmonella: In figure 5b, we see that $dGC{3}_N^{\mathrm{☆}}$ and $dGC{3}_C^{\mathrm{☆}}$ do not have the same sign for this species. Correspondingly, in figure 6, the sum $dEN{C}_C^{\mathrm{☆}}+dEN{C}_N^{\mathrm{☆}}$ overestimates $dEN{C}^{\mathrm{☆}}$, for all Salmonella concatenates but the three where the N and C layers agree on $GC{3}^{\mathrm{☆}}$, which means that N and C layers interact negatively, as expected. One can also see a pattern of “descending staircase” for the red bars in figure 6, for many species (in particular St. aureus and B. cenocepaia, respectively, for AT- or GC-rich examples). This is related to the data structuration, as genes were concatenated according to their observed ENC values, higher ENC (and then lower CUB) last. This pattern then indicates that for genes having a low level of observed CUB, SENCA finds the C layer effect to be less important than in genes with higher CUB.

Discussion

In sequence evolution, several biological processes act together at nucleotides, codons, and amino acids scales. In order to quantify the effects of mutation and selection at each of these scales, we developed an evolutionary model, SENCA, divided into three layers: nucleotide (N), codon (C), and amino acid (A). SENCA, by construction, is very flexible, and can be employed to tackle a variety of biological questions. As an example, we can set each layer to be stationary or not in function of the data. The decomposition of evolutionary signals in different layers allows for treating each layer separately; for example, by using specific amino acid substitution models for the A layer, or specific nucleotide substitution models for the N layer. Moreover, because the genetic code is explicit in this model, selection on CUB and on nonsynonymous substitutions can be studied simultaneously. This different modeling makes the most prominent difference with model FMutSel, where layers A and C are not distinguishable. Moreover, FMutSel is all stationary, which is a strong hypothesis (actually not supported by our data). Considering the model described in Nielsen et al. (2007), the authors assume that 1) CUB is only defined through an optimal codon per amino acid, 2) selection on CUB shows the same intensity for all amino acids, and 3) the set of optimal codons is known a priori. In this model, this unique fitness on all preferred codons neutralizes all preferences on amino acids (which is not supported by our data). Moreover, SENCA does not require the optimal codons to be known—which is particularly useful when using a nonhomogeneous codon layer where preferences may change over time. One additional feature of SENCA is that we can easily study the overall equilibrium of the model in a mixture of equilibrium from each layer, through summary statistics, such as $dG{C}_{\text{layer}}^{\mathrm{☆}},dGC{3}_{\text{layer}}^{\mathrm{☆}}$, and $dEN{C}_{\text{layer}}^{\mathrm{☆}}$. We have shown that these statistics can be manipulated intuitively, as the effects of all layers can be summed up almost linearly to give the global equilibrium. Moreover, these statistics all account for the phylogenetic signal, which was not considered in previous studies such as Novembre (2002), Supek et al. (2010), and O’Neill et al. (2013).

We performed a nonstationary analysis of the core genomes of 21 bacterial and archaeal species from Lassalle et al. (2015), and of five Enterobacteria. We estimated equilibrium frequencies using SENCA in comparison with similar estimates using classical codon model YN98 + F61. The main mechanistic difference between the two models is that SENCA considers explicitly the genetic code, and synonymous substitutions are a priori not neutral. Indeed, $EN{C}^{\mathrm{☆}}$ of YN98 is higher than $EN{C}^{\mathrm{☆}}$ of SENCA (fig. 3c), which challenges the assumption that synonymous substitutions are neutral. As expected, and in accordance with simulations in Spielman and Wilke (2015), we show that this assumption leads to a systematic bias in the estimation of the strength of selection acting on nonsynonymous substitutions. When synonymous substitutions have a selective cost, they are less frequent, leading to higher estimates of ω. These estimates are in most cases more accurate than those of YN98, as shown by maximum-likelihood comparisons with the AIC and BIC. On the other hand, it is possible that codon preferences change, in which case synonymous substitutions may be advantageous, and lead to lower estimates of ω. SENCA is then useful for detecting selective pressure on nonsynonymous substitutions, as it better estimates the cost of synonymous substitutions by distinguishing them from the background mutational bias (Lawrie et al. 2011).

Moreover, taking into account selection on CUB allows our model to better predict genome composition. This is unexpected, as in comparison with YN98 + F61 there is no additional composition specific feature in our modeling. First, our estimates of the evolutionary processes acting on genome composition in all these species are in agreement with the recent findings of Hershberg and Petrov (2008) and Hildebrand et al. (2010), as $G{C}_N^{\mathrm{☆}}$ is low, indicating a bias toward AT in the mutational process. Second, our model describes more accurately how GC3 is more biased than GC. Interestingly, although this higher variability of the third codon position is often hypothesized to come from mutational processes unrestricted by selection (as is the case in first and second positions of codons, e.g., Muto and Osawa 1987), SENCA explains most of this variability through selection on CUB. On the other hand, the influence of nucleotide processes is stronger when considering the global genome composition, as CUB has a much weaker impact on the first and second positions.

The SENCA approach allows us to draw conclusions with respect to the relative influence of selection and mutation on codon usage. In our analysis, multiple AT-rich pathogens have very similar $G{C}^{\mathrm{☆}}$ values, which are decomposed in different effects of each layer. We also show that the A layer effects is prominent in GC-rich species, with an amino acid composition depleting the genome in GC, whereas the A layer is quantitatively less important in AT-rich species. Finally, our results clearly indicate that CUB is driven by the C layer (fig. 6). These differences may arise from differences in host, population size or species evolutionary history (Losada et al. 2010).

Globally, our results on intraspecific data can be interpreted in the context of the current thinking that mutations are universally biased toward AT. For middle and low GC species, we observe a quite constant effect of the N layer with a partial equilibrium GC of 30%, in agreement with Hershberg and Petrov (2010) and Hildebrand et al. (2010). The C layer effect on $G{C}^{\mathrm{☆}}$, on the contrary, goes smoothly upwards with increasing observed GC content. Then, it appears that non-GC-rich species all share the same nucleotide processes, and their actual GC content depends on the level of selection on CUB.

A surprising result is the inversion of the N pattern for GC-rich species. One explanation could be the selection on CUB: In those species, there would be such a strong selection deleting AT-driven mutations, that the N layer would stand for substitutions, and not mutations, even though the data are intraspecific. Indeed, comparing Brucella and Bifidobacterium, two $GC$-rich species with close observed GC, we can see that their N layers are very different, and $EN{C}^{\mathrm{☆}}$ is much lower in Bifidobacterium, indicating a stronger selection on CUB. Another hypothesis is that nucleotidic processes in those species are more complex; in particular, one may think of GC-biased gene conversion, which may push the GC content of those genomes higher. A third hypothesis would be selection on GC content itself by the environment, an hypothesis hotly debated at the turn of the century (Galtier and Lobry 1997; Naya et al. 2002; Musto et al. 2006; Palmeira et al. 2006) and still driving research nowadays (Reichenberger et al. 2015)

Our interspecific analysis shows that, if the average results on genome composition are quite similar with those of the corresponding species studied intraspecifically (Salmonella) and Escherichia, the internal evolutionary dynamics can be quite different. This may be related to the evolutionary scale or the rate of fixation of mutations in the intraspecific data. These results emphasize the interest of decomposing the evolutionary signals in layers, as done by SENCA, to better test hypotheses on the evolution of those species.

One future SENCA development is to distinguish gBGC from other genomic signals. This would be particularly relevant for applications to metazoan, where gBGC acts as a spurious mode of positive selection, promoting the fixation of deleterious mutations (Ratnakumar et al. 2010) whereas selection on CUB might also be effective (Gingold et al. 2014). Concerning bacteria, which have been shown to also be subject to gBGC in recombining genes (Lassalle et al. 2015), application of SENCA is also in theory possible but much more difficult because the method would require the knowledge of several site-specific phylogenetic trees, which is hard to infer when between species recombination is strong. Eventually, likelihood inference will have to consider all these trees simultaneously.

Finally, flexibility of our model allows for an investigation of biological questions focused on each particular layer. With SENCA, rates of substitutions between amino acids are only based on a profile of 20 preferences. To be more realistic, an ongoing project is to use empirical matrices of preferences between amino acids, as done in models of protein evolution. But specific matrices will be needed, as in our case overall nucleotide biases are handled by the nucleotide layer and classical protein models already include them. Several methods to model site-specific amino acid fitness have been proposed previously (Halpern and Bruno 1998; Rodrigue et al. 2010; Tamuri et al. 2012), with similar formula for the selection, and it may be straightforward to adapt them on our modeling. However, the additional complexity may prevent the direct estimation of the whole process, and perhaps it will be necessary to estimate this site-specificity in a second step.

The codon layer accounts for the relative preferences between synonymous codons. We could compare these preferences to biological correlates such as tRNA content and gene expression. For example, are the most frequent tRNA in cells linked to codon preferences estimates? There is a known correlation between tRNA content and codon usage (e.g., Kanaya et al. 1999; Rocha 2004). Using SENCA, we could quantify if this correlation is only due to the C layer, or if CUB originating from N layer has an impact on this correlation. Moreover, nonhomogeneous modeling will permit us to analyze how and when CUB has evolved. This could be applied to cases of genome reduction caused by ecological changes, such as the marine cyanobacteria Prochlorococcus (Batut et al. 2014) or Mycobacterium leprae (Gómez-Valero et al. 2007).

Last but not least, the evolutionary estimation of CUB by SENCA could be used as a predictive factor instead of observed CUB in multiple applications. One potential application is the correlation between CUB and gene expression, and we hope that SENCA will provide a relevant estimator along these lines. Using techniques such as stochastic mapping (Minin and Suchard 2008; Romiguier et al. 2012), it is possible to infer heterogeneous ancestral patterns of evolution from an homogeneous model, and then to infer ancestral gene expression. As an extension of SENCA, we plan to parametrize site-specific selection on codon usage, and use mixtures of these site models to obtain site-specific and gene-specific estimates of the effect of selection on codon usage.

Supplementary Material

Supplementary equation, material, figures S1–S8, and table S1 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).