A Genome-Scale Investigation of How Sequence, Function, and Tree-Based Gene Properties Influence Phylogenetic Inference

Abstract

Molecular phylogenetic inference is inherently dependent on choices in both methodology and data. Many insightful studies have shown how choices in methodology, such as the model of sequence evolution or optimality criterion used, can strongly influence inference. In contrast, much less is known about the impact of choices in the properties of the data, typically genes, on phylogenetic inference. We investigated the relationships between 52 gene properties (24 sequence-based, 19 function-based, and 9 tree-based) with each other and with three measures of phylogenetic signal in two assembled data sets of 2,832 yeast and 2,002 mammalian genes. We found that most gene properties, such as evolutionary rate (measured through the percent average of pairwise identity across taxa) and total tree length, were highly correlated with each other. Similarly, several gene properties, such as gene alignment length, Guanine-Cytosine content, and the proportion of tree distance on internal branches divided by relative composition variability (treeness/RCV), were strongly correlated with phylogenetic signal. Analysis of partial correlations between gene properties and phylogenetic signal in which gene evolutionary rate and alignment length were simultaneously controlled, showed similar patterns of correlations, albeit weaker in strength. Examination of the relative importance of each gene property on phylogenetic signal identified gene alignment length, alongside with number of parsimony-informative sites and variable sites, as the most important predictors. Interestingly, the subsets of gene properties that optimally predicted phylogenetic signal differed considerably across our three phylogenetic measures and two data sets; however, gene alignment length and RCV were consistently included as predictors of all three phylogenetic measures in both yeasts and mammals. These results suggest that a handful of sequence-based gene properties are reliable predictors of phylogenetic signal and could be useful in guiding the choice of phylogenetic markers.

Introduction

An accurate evolutionary history is the first step toward understanding the evolution of genes, pathways, phenotypes, and lineages (e.g., Barraclough and Nee 2001; Clark et al. 2007; Parker et al. 2008; Tabach et al. 2013; Hahn and Nakhleh 2016). Nowadays, most inferences of evolutionary history stem from analyses of molecular sequence data, typically in the form of genes or, more precisely, in the form of nuclear protein-coding portions of gene sequences (e.g., Song et al. 2012; Salichos and Rokas 2013; Shen et al. 2013; Wickett et al. 2014; Hahn and Nakhleh 2016). As a result, errors in the inference of gene histories can greatly impact our understanding of evolutionary history.

Accurate inference of gene histories is inherently dependent on choices in both methodology (e.g., choices in optimality criterion or model of sequence evolution) and data (e.g., choices in which genes to use and which to exclude). Many insightful studies have shown how choices in methodology can strongly influence the reconstruction of gene histories. For example, choices in the program and algorithm used for multiple sequence alignment (Liu et al. 2009; Blackburne and Whelan 2013; Hossain et al. 2015), in the model of sequence evolution employed (Yang et al. 1994; Lemmon and Moriarty 2004; Luo et al. 2010; Hess and Goldman 2011), in the partitioning scheme used to account for substitution rate variation among sites (Nylander et al. 2004; Kainer and Lanfear 2015), in the tree space search strategy (Takahashi and Nei 2000; Lakner et al. 2008), or in the optimality criterion (Kolaczkowski and Thornton 2004; Philippe et al. 2005; Doyle et al. 2015), have all been shown capable of yielding different topologies when applied to the same data matrix.

In contrast, much less is known about how the choice in data, that is, usually, the choice of genes, influences phylogenetic inference. One notable contribution in this direction is the work of Townsend and coworkers on phylogenetic informativeness (Townsend 2007; López-Giráldez and Townsend 2011; López-Giráldez et al. 2013), which is estimated from the rate of evolution of a given gene (or any other given set of characters). However, this method is more geared toward predicting the gene’s power to optimally resolve particular internodes rather than examining the gene’s influence on the whole phylogeny.

It can be argued that there are three key types of properties for a gene used in phylogenetic inference; sequence-based properties that have to do with the gene’s nucleotide or amino acid sequence (e.g., Guanine-Cytosine [GC] content), function-based properties associated with its function in the cell or organism (e.g., cellular location or biological process), and tree-based properties that pertain to its gene tree (e.g., total branch length). Several studies have examined the effect of sequence- and tree-based properties, such as the number of variable sites (Rokas et al. 2003; Aguileta et al. 2008), gene alignment length (Rokas et al. 2003; Aguileta et al. 2008; Betancur et al. 2014), amount of missing data (Wiens and Morrill 2011; Roure et al. 2013), base composition (Collins et al. 2005; Betancur et al. 2013; Romiguier et al. 2013), evolutionary rate (Betancur et al. 2014; Xi et al. 2014; Doyle et al. 2015), phylogenetic information content (Dell’Ampio et al. 2014; Doyle et al. 2015), and the recovery of known bipartitions or topologies (Regier et al. 2010; Salichos and Rokas 2013; Capella-Gutierrez et al. 2014; Chen et al. 2015) on phylogenetic inference. However, these studies usually examine certain properties in isolation from other properties (Collins et al. 2005; Wiens and Morrill 2011; Romiguier et al. 2013; Capella-Gutierrez et al. 2014), they often involve small numbers of genes (Regier et al. 2010; Betancur et al. 2013; Roure et al. 2013), and do not include function-based properties of genes.

The goals of this study were 1) to examine the associations between sequence-based, gene function-based, and gene tree-based properties, 2) to assess standard and partial correlations between gene properties and phylogenetic signal, and 3) to identify the gene properties that best predict phylogenetic signal. To this end, we investigated 24 sequence-based, 19 gene function-based, and 9 gene tree-based properties (see table 1 for their full description) and three phylogenetic measures using genome-scale data from a highly diverged yeast lineage (2,832 genes from 12 taxa) as well as from the more recently diverged mammal lineage (2,002 genes from 24 mammalian genomes).

Table 1.

Information on the 52 Gene Properties Used in This Study

Property	Name	Description
Sequence-based	Aln_quality	Average of column confident scores (calculated using GUIDANCE2 from Landan and Graur [2008]; Sela et al. [2015])
	AlnLen	Alignment length
	AlnLen_nogaps	Alignment length after exclusion of all sites containing gaps
	CAM	Number of sites containing RGC-CAM substitutions (as defined by Rogozin et al. [2007]; Polzin and Rokas [2014])
	CAM_pct	Percentage of CAM substitutions
	Gap_pct_mean	Percent average of sites containing gaps across taxa
	Gap_pct_var	Variance of percentage of sites containing gaps across taxa
	GC_pct_mean	Percent average of GC content of all sites across taxa
	GC_pct_var	Variance of GC content percentage of all sites across taxa
	GC1_pct_mean	Percent average of GC content of first codon positions across taxa
	GC1_pct_var	Variance of GC content percentage of first codon positions across taxa
	GC2_pct_mean	Percent average of GC content of second codon positions across taxa
	GC2_pct_var	Variance of GC content percentage of second codon positions across taxa
	GC3_pct_mean	Percent average of GC content of third codon positions across taxa
	GC3_pct_var	Variance of GC content percentage of third codon positions across taxa
	nonCAM	Number of sites containing RGC_non-CAM substitutions (as defined by Rogozin et al. [2007]; Polzin and Rokas [2014])
	nonCAM_pct	Percentage of non-CAM substitutions
	PI_pct_mean	Percent average of pairwise identity across taxa
	PI_pct_var	Variance of percentage of pairwise identity across taxa
	PI_sites	Number of parsimony-informative sites
	PI_sites_pct	Percentage of parsimony-informative sites
	RCV	Relative nucleotide composition variability (as defined by Phillips and Penny [2003])
	Varsites	Number of variable sites
	Varsites_pct	Percentage of variable sites
Function-based	CAI	Codon adaptation index for a S. cerevisiae or H. sapiens gene (calculated using codonw 1.4.2 from Peden [1999])
	CBI	Codon bias index for a S. cerevisiae or H. sapiens gene (calculated using codonw 1.4.2 from Peden [1999])
	CC_regions	Number of coiled–coil regions for a S. cerevisiae or H. sapiens gene (identified by Paircoil2 from McDonnell et al. [2006])
	Cen_distance	The physical distance between gene and centromere divided by chromosome length for a S. cerevisiae or H. sapiens gene
Function-based	Exons	Number of exons in a S. cerevisiae or H. sapiens gene
	Gen_interactions	Number of genetic interactions for a S. cerevisiae or H. sapiens gene (calculated using the BioGRID database from Chatr-Aryamontri et al. [2015])
	Gene_expression	Number of mapped reads per kilobase for a given gene from one million mapped reads (calculated using 2-replicate RNA-Seq data of S. cerevisiae from Busby et al. [2011] or H. sapiens RNA-Seq data across 122 samples from Uhlén et al. [2015])
	GO_numbers	Number of Gene Ontology terms for a S. cerevisiae or H. sapiens gene
	InterPros	Number of unique domains for a S. cerevisiae or H. sapiens gene
	Paralogs	Number of paralogs of a S. cerevisiae or H. sapiens gene
	Phy_interactions	Number of physical interactions for a S. cerevisiae or H. sapiens gene (calculated using the BioGRID database from Chatr-Aryamontri et al. [2015])
	Prot2Tran	Number of protein isoforms divided by number of transcripts for a S. cerevisiae or H. sapiens gene
	Protein_abundance	Protein abundance levels for a S. cerevisiae or H. sapiens gene (calculated using the PaxDb database from [Wang et al. 2012])
	Proteins	Number of protein isoforms for a S. cerevisiae or H. sapiens gene
	Rel_distance	The physical position of a S. cerevisiae or H. sapiens gene divided by the length of the chromosome on which it resides
	Repeats	Number of repeat elements for a S. cerevisiae or H. sapiens gene (identified by RepeatMasker [http://www.repeatmasker.org/; last accessed on March 21, 2016])
	Syn_codons_fre	Frequency of synonymous codons for a S. cerevisiae or H. sapiens gene (calculated using codonw 1.4.2 from Peden [1999])
	TFs	Number of transcription factors targeting a given gene (calculated using the Yeastract database of S. cerevisiae from Teixeira et al. [2014] or the ITFP database of H. sapiens from Zheng et al. [2008])
	Transcripts	Number of transcripts for a S. cerevisiae or H. sapiens gene
Tree-based	Inter_len_mean	Average length of internal branches across the maximum likelihood tree of a given alignment
	Inter_len_var	Variance of lengths of internal branches across the maximum likelihood tree of a given alignment
	Leaf_len_mean	Average length of external branches across the maximum likelihood tree of a given alignment
	Leaf_len_var	Variance of lengths of external branches across the maximum likelihood tree of a given alignment
	Leaf2node_mean	Average of the sum of all branch lengths that are between the outgroup node and each ingroup node across the maximum likelihood tree of a given alignment
	Leaf2node_var	Variance of the sum of all branch lengths that are between the outgroup node and each ingroup node across the maximum likelihood tree of a given alignment
	Total_treelen	Sum of all branch lengths across the maximum likelihood tree of a given alignment
	Treeness	Proportion of sum of internal branch lengths over sum of all branch lengths across the maximum likelihood tree of a given alignment (as defined by Phillips and Penny [2003])
	Treeness/RCV	Treeness divided by RCV (as defined by Phillips and Penny [2003])

Materials and Methods

Data Set Acquisition

We sampled nuclear protein-coding genes from an anciently diverged yeast lineage (12 taxa) and from the more recently diverged mammal lineage (24 taxa) (see supplementary table S1, Supplementary Material online). For yeasts, we used the synteny and orthology information in the YGOB (version 7) database (Byrne and Wolfe 2005) to identify orthologous groups. For mammals, we used the human gene (annotation version GRCh38.p3) to retrieve one-to-one orthologous groups predicted by Ensembl BioMart (www.ensembl.org/biomart; last accessed on January 07, 2015). After discarding genes with missing data, we constructed two data sets of 2,832 yeast and 2,002 mammalian genes. Original alignments and resulting trees are available from Figshare at DOI: 10.6084/m9.figshare.1597710.

Phylogenetic Analysis

To obtain two distinct alignments (amino acid and nucleotide), which were used to estimate some sequence-based properties (e.g., GC content and number of sites containing RGC-CAM substitutions), we first aligned the amino acid sequences from each gene using the G-INS-i strategy for global homology implemented by the program MAFFT, version 7.164 (Katoh and Standley 2013), with the default gap opening penalty (–op = 1.53). Next, we used a custom Perl script to map the nucleotide sequences on the amino acid alignment and generate the codon-based nucleotide alignment.

Individual gene trees for the yeast data set were built using the amino acid sequence-based alignments and for the mammal data set using the codon-based alignments. For yeasts, the best-fitting model of amino acid evolution for each gene was selected using the Bayesian information criterion implemented in ProtTest 3.4 (Darriba et al. 2011). For mammals, the “GTRGAMMA” model was used to accommodate for nucleotide substitution. The unrooted maximum likelihood tree was reconstructed using RAxML (Stamatakis 2014). For each gene, we conducted 500 rapid bootstrapping replicates and the search for the best-scoring ML tree in one single run (-f a option).

For each lineage, the concatenation, coalescent-based, and extended majority-rule consensus (eMRC) phylogenies were reconstructed. The concatenation phylogeny was inferred using RAxML under an unpartitioned “PROTGAMMAIWAGF” model of amino acid substitution (yeasts) or an unpartitioned “GTRGAMMA” model of nucleotide substitution (mammals). To reconstruct the concatenation phylogeny, we first performed 20 separate ML searches to find the best-scoring ML tree, and then evaluated branch support for each internode in this best-scoring ML tree with 500 rapid bootstrapping replicates as implemented in RAxML. The coalescent-based phylogeny was estimated using ASTRAL (Mirarab, Reaz, et al. 2014). Briefly, individually estimated ML gene trees were used as input to generate the coalescent-based phylogeny. The robustness of this phylogeny was evaluated by 100 replicates, each of which consisted of individual gene trees each selected randomly from the set of 500 rapid bootstrapping trees available for each gene to estimate a new coalescent-based phylogeny. The eMRC phylogeny was summarized from individual estimated ML gene trees using the CONSENSE program in PHYLIP package (http://evolution.genetics.washington.edu/phylip.html; last accessed on March 21, 2016).

Calculation of the Three Phylogenetic Measures

To quantify the phylogenetic signal for each gene, we examined three commonly used phylogenetic measures of topological resolution or accuracy. The two measures of topological resolution examined were the average bootstrap support (ABS) and the relative gene tree certainty (TCA). The former corresponds to the average value of all bootstrap support values across the maximum likelihood tree of a given gene. The latter corresponds to the average of all internode certainty (ICA) values across the tree (Salichos and Rokas 2013; Salichos et al. 2014). Briefly, ICA calculates the degree of certainty for a given internode by considering the frequency of the bipartition defined by the internode in a given set of trees in conjunction with that of all conflicting bipartitions in the same underlying tree set (Salichos et al. 2014). The tree set used to quantify ICA and TCA was the 500 trees generated from bootstrapping. The measure of topological accuracy that we used was the normalized Robinson–Foulds tree distance (RFD) (Robinson and Foulds 1981), which corresponds to the topological distance between the estimated individual ML gene tree and the eMRC species phylogeny (the reference tree).

Although both ABS and TCA measure aspects of tree resolution in a set of bootstrap replicate trees, TCA focuses on the distribution of resolution by considering all most prevalent conflicting bipartitions rather than only the first most prevalent bipartition for each individual internode. For example, assume that a given internode has two prevalent bipartitions; one that is, supported by 60% of the bootstrap replicate trees and another that is, supposed by the remaining 40%. In such a case, the bootstrap support value for the internode would be 60 but the ICA value would be ∼0.03 (Salichos and Rokas 2013; Salichos et al. 2014). Finally, RFD measures topological accuracy and is distinct from the ABS and TCA measures.

Examination of Gene Properties

A total of 52 properties were examined for each gene in yeasts and mammals, which we classified into three categories—24 sequence-based, 19 function-based, and 9 tree-based properties (see table 1 for their full descriptions). For sequence-based properties, we used custom Perl scripts to calculate their corresponding values from a given gene alignment. The only exception was gene alignment quality, which was determined using the GUIDANCE2 software (Landan and Graur 2008; Sela et al. 2015). For function-based properties, we used Saccharomyces cerevisiae or Homo sapiens gene name in a given gene alignment as the query to retrieve their values (e.g., number of exons and protein isoforms) through Ensembl BioMart (www.ensembl.org/biomart; last accessed on February 17, 2015) and other curated databases such as PaxDb (Wang et al. 2012), BioGRID (Chatr-Aryamontri et al. 2015), Yeastract (Teixeira et al. 2014) and ITFP (Zheng et al. 2008). For tree-based properties, we used custom Perl scripts to estimate their values from the estimated ML gene tree.

Statistical Analysis

Standard Pearson’s correlations between the 52 gene properties as well as between the 52 gene properties and the three phylogenetic measures were analyzed using R 3.1.3 (Ihaka and Gentleman 1996). The analysis of partial correlations between the gene properties and the three phylogenetic measures was performed following (Drummond et al. 2006), in which gene alignment length and evolutionary rate were simultaneously controlled. To visualize the correlations between the 52 gene properties and the three phylogenetic measures, we converted their Pearson’s correlation coefficients (see supplementary tables S7 and S8, Supplementary Material online) to heat maps using HemI (Deng et al. 2014). The relative importance of each gene property to each of the three phylogenetic measures was determined using the function of the “calc.relimp” in the R package “relaimpo” (Groemping 2006). Finally, identification of the subset of gene properties that optimally models each of the three phylogenetic measures using the subset selection technique was implemented by the function of the “Regsubsets” in the R package “leaps” (Lumley 2009; James et al. 2013). All bar or dot plots were generated using the ggplot2 package (Wickham 2009) in R.

Results

Characteristics of the Two Data Sets

We assembled two complete (i.e., without any missing data) data sets of 2,832 genes from 12 yeast genomes and 2,002 genes from 24 mammalian genomes (see supplementary tables S1–S3, Supplementary Material online). The lengths of the yeast gene sequence alignments ranged between 57 and 5,070 amino acid sites (aa), with an average length of 609 aa, and the lengths of the mammalian gene sequence alignments ranged between 270 and 23,937 base pairs (bp), with an average length of 2,452 bp.

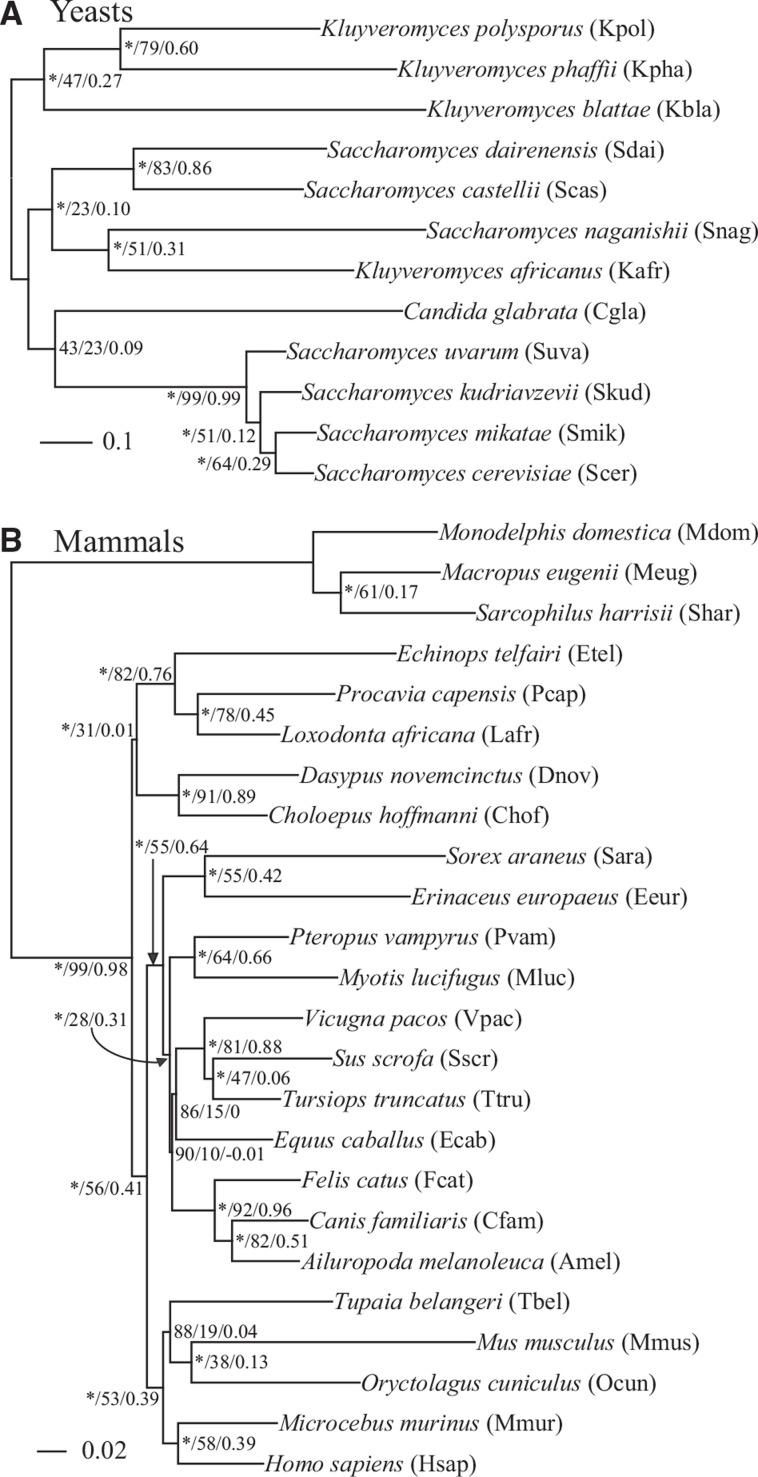
All internodes in both the yeast and the mammalian concatenation phylogenies received 100% BS values (see supplementary fig. S1, Supplementary Material online). Similarly, most internodes in coalescent-based phylogenies of yeasts and mammals also received 100% BS values (yeasts, 8 of 9 internodes; mammals, 19 of 21 internodes) (fig. 1), but the gene support frequency (GSF) and all TCA values of several internodes in the eMRC phylogenies were low (yeasts: average GSF = 57.8; average relative TCA = 0.40; mammals: average GSF = 56.9; average relative TCA = 0.43) (fig. 1). Moreover, the concatenation, coalescent-based, and eMRC phylogenies of yeasts were topologically identical; the coalescent-based and eMRC phylogenies of mammals were topologically identical but differed from the concatenation phylogeny (see fig. 1B and supplementary fig. S1B, Supplementary Material online). Interestingly, all three observed conflicts between the coalescent-based or eMRC phylogeny and the concatenation phylogeny (the root of the placental mammals, the placement of bats, and the placement of horses) were also observed in recent phylogenomic studies (see fig. 1B and supplementary fig. S1B, Supplementary Material online) (McCormack et al. 2012; Song et al. 2012; Morgan et al. 2013; Romiguier et al. 2013; Tsagkogeorga et al. 2013; Mirarab, Bayzid, et al. 2014). Conversely, a clade comprising tree shrews and Glires (Romiguier et al. 2013; Mirarab, Bayzid, et al. 2014), which was contradictory to the placement of tree shrews as sister to primates (McCormack et al. 2012; Song et al. 2012; Morgan et al. 2013), was consistently recovered in all of our concatenation, coalescent-based, and eMRC phylogenies of mammals (see fig. 1B and supplementary fig. S1B, Supplementary Material online). Because the mammalian topology supported by eMRC and coalescent-based approaches is more compatible with the topologies supported by previous phylogenomic studies, we used the eMRC topology rather than the concatenation topology as the reference phylogeny in measuring the topological incongruence between gene trees and the mammalian species phylogeny.

Fig. 1.—

The eMRC phylogenies inferred from 2,832 yeast genes (A) and 2,002 mammalian genes (B). Branch support values near internodes are indicated in order of bootstrap support values (* represents 100%) using ASTRAL (Mirarab, Reaz, et al. 2014), GSF, and ICA. The branch lengths were estimated on the eMRC topology, as implemented in RAxML (Stamatakis 2014) (-f e option). Note that the eMRC topology is identical to the ASTRAL topology.

We quantified the phylogenetic signal of each yeast and mammal gene tree in terms of its phylogenetic resolution (measured by the ABS), topological conflict (measured by the TCA, in the 500 trees generated from bootstrapping), and topological distance of the gene tree from the eMRC phylogeny (measured by the normalized RFD) (see supplementary fig. S2, Supplementary Material online). The distributions of yeast and mammalian genes were highly similar in all three of these measures (yeast averages: ABS = 63%, TCA = 0.38, and RFD = 0.42; mammal averages: ABS = 60%, TCA = 0.38, and RFD = 0.43) (see supplementary fig. S2, Supplementary Material online). Seventy five of the 2,832 yeast gene trees (2.65%) were topologically identical to the eMRC phylogeny, whereas none of the 2,002 mammalian gene trees showed the same topology as the eMRC phylogeny and only one gene tree was topologically identical to the concatenation phylogeny (see supplementary fig. S2C, Supplementary Material online).

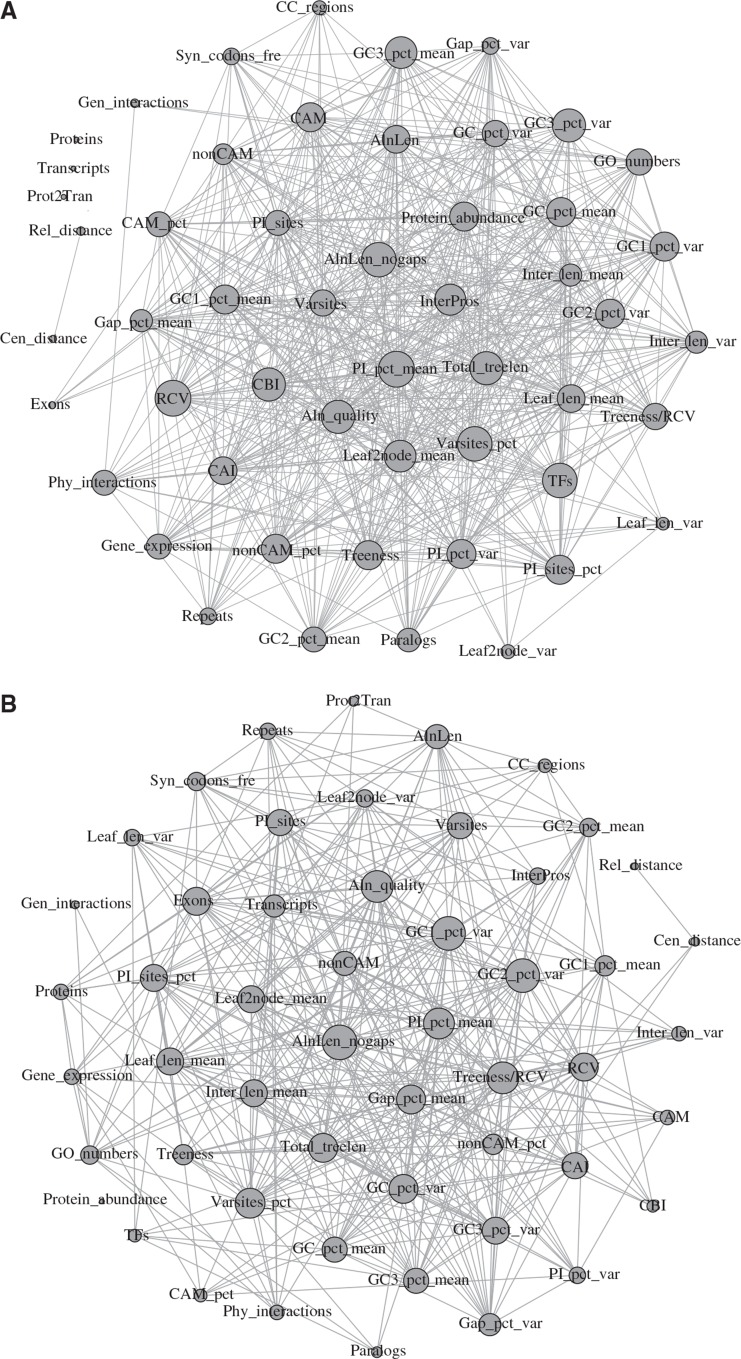
The Correlation Networks of Gene Properties

To examine and visualize the correlations between the 52 gene properties, we used their correlation coefficient r values (see supplementary tables S4 and S5, Supplementary Material online) to construct correlation networks of gene properties in yeasts and mammals (fig. 2). The network of gene properties in yeasts consisted of 49 nodes corresponding to the 49 gene properties measured in the yeast data set, and 1,305 edges corresponding to the 1,305 pairwise correlations between the 49 gene properties in which Pearson’s correlation coefficient r was equal or greater than 0.1 (fig. 2A). Three additional properties (Proteins: number of protein isoforms for a S. cerevisiae or H. sapiens gene, Transcripts: number of transcripts for a S. cerevisiae or H. sapiens gene, and Prot2Tran: number of protein isoforms divided by number of transcripts for a S. cerevisiae or H. sapiens gene) had standard deviations (SDs) of 0 and were uncorrelated with the remaining 49 properties. The network of gene properties in mammals consisted of 51 nodes and 827 edges (fig. 2B), when only considering edges where Pearson’s correlation coefficient r was equal or greater than 0.1 between the 52 gene properties (the correlation coefficient of one additional property, Protein abundance (measuring abundance levels for a S. cerevisiae or H. sapiens protein), to each of the other 51 properties was less than 0.1). Several gene properties exhibited high correlations with other gene properties, including but not limited to the percent average of pairwise identity across taxa (r ≥ 0.1 with 39/48 other yeast gene properties, average r = 0.41) and total tree length (r ≥ 0.1 with 24/50 other mammal gene properties, average r = 0.35) (supplementary table S6, Supplementary Material online). Overall, the most correlated gene properties (to other gene properties) were sequence-based and tree-based in both yeasts and mammals.

Fig. 2.—

The correlation networks of 52 gene properties in yeasts (A) and mammals (B). Networks were explored and visualized with the interactive platform Gephi 0.8.2 (Bastian et al. 2009). The size of each node (nodes are depicted by circles) is proportional to the number of connections (edges) where Pearson’s coefficient r was ≥ 0.1. The full descriptions of the 52 gene properties are given in table 1. Values for the Pearson’s coefficients and the correlation networks are provided in supplementary tables S4–S6, Supplementary Material online.

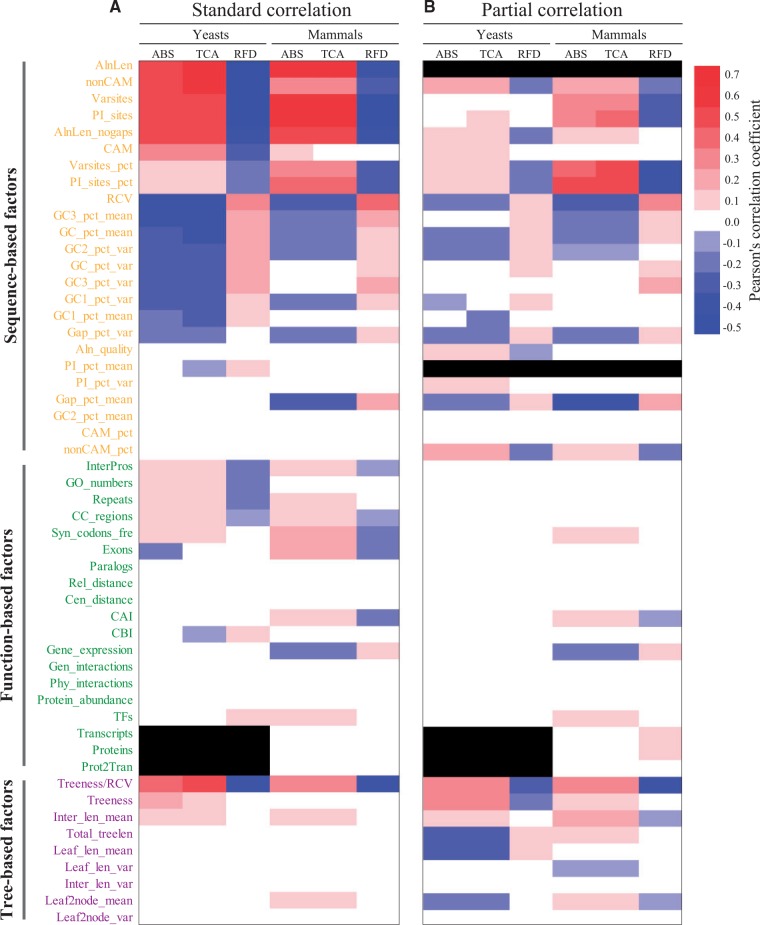
The Relationships Between Gene Properties and Measures of Phylogenetic Inference Using Standard and Partial Correlation Analysis

We first evaluated the standard correlations between 52 gene properties (24 sequence-based, 19 function-based, and 9 tree-based) and three phylogenetic measures (ABS, TCA, and RFD) for yeast and mammalian data sets, respectively. All the correlations where Pearson’s correlation coefficient r was equal or greater than 0.1 between the 52 gene properties and the three phylogenetic measures were statistically significant in yeasts and mammals (P value < 0.05; see supplementary table S7, Supplementary Material online).The proportions of such correlations (coefficient r ≥ 0.1, P value < 0.05) between the 52 gene properties and the three phylogenetic measures were similar in both lineages (yeasts, 77 of 156 correlations examined or 49.4%; mammals, 74 of 156 correlations examined or 47.4%). Sequence-based properties showed the highest proportion of correlations with the tree phylogenetic measures (yeasts, 52 of 72 correlations examined or 72.2%; mammals, 45 of 72 correlations examined or 62.5%), followed by tree-based properties (yeasts, 7 of 27 correlations examined, 25.9%; mammals, 7 of 27 correlations examined, 25.9%), and function-based properties (yeasts, 18 of 57 correlations examined, 31.6%; mammals, 22 of 57 correlations examined, 38.6%) (fig. 3A).

Fig. 3.—

Heat maps representing all correlations between 52 gene properties and three phylogenetic measures (ABS; TCA all, RFD, Normalized RFD in recovering the eMRC phylogeny) before (A) and after (B) simultaneously controlling for gene alignment length and evolutionary rate in yeast and mammalian data sets. Only correlations having Pearson’s coefficient values ≥ 0.1 and P values < 0.05 are displayed in the heat map. Black cells represent cases in which the SD of a gene property is zero. The full descriptions of the 52 gene properties are given in table 1. Detailed values for the Pearson’s coefficients are provided in supplementary tables S7 and S8, Supplementary Material online.

For both yeasts and mammals, 12 sequence-based properties (AlnLen: gene alignment length, nonCAM: number of sites containing RGC_non-CAM substitutions [i.e., substitutions between amino acids that can occur via a single nucleotide substitution], Varsites: number of variable sites, PI_sites: number of parsimony-informative sites, Varsites_pct: percentage of variable sites, PI_sites_pct: percentage of parsimony-informative sites, AlnLen_nogaps: gene alignment length after exclusion of all sites containing gaps, RCV: relative composition variability, GC3_pct_mean: percent average of GC content of third codon positions, GC_pct_mean: percent average of GC content of all sites across taxa, GC1_pct_var: variance of GC content percentage of first codon positions, and GC2_pct_var: variance of GC content percentage of second codon positions across taxa), two function-based properties (InterPros: number of protein domains and CC_regions: number of potential coiled-coil regions), and one tree-based property (Treeness/RCV: the proportion of tree distance on internal branches divided by RCV), were consistently correlated (Pearson’s correlation coefficient ≥ 0.1 and P < 0.0001) with the three phylogenetic measures (fig. 3A; see supplementary table S7, Supplementary Material online). Of these 15 gene properties, gene alignment length (AlnLen) was the property showing the highest correlations to the three phylogenetic measures in yeasts (AlnLen against ABS, r = 0.57; AlnLen against TCA, r = 0.61; AlnLen against RFD, r = −0.45; see supplementary table S7, Supplementary Material online). In mammals, the property with the highest correlations to three phylogenetic measures was the number of parsimony-informative sites (PI sites against ABS, r = 0.67; PI sites against TCA, r = 0.69; PI sites against RFD, r = −0.42; see supplementary table S7, Supplementary Material online). Gene alignment length was the third most correlated property, after the number of parsimony-informative sites (PI_sites) and the number of variable sites (Varsites); however, both properties were significantly correlated with gene alignment length (number of parsimony-informative sites: r = 0.90, P < 0.0001; number of variable sites: r = 0.93, P < 0.0001; see supplementary table S5, Supplementary Material online).

Since percent average of pairwise identity across taxa (PI_pct_mean, i.e., evolutionary rate) was broadly correlated with many of other gene properties in both yeasts and mammals (fig. 2) and alignment length (AlnLen) was strongly correlated with measures of phylogenetic inference (fig. 3A), we next examined the partial correlations between the remaining 50 gene properties and the three phylogenetic measures by simultaneously controlling for the effect of both percent average of pairwise identity across taxa and alignment length for yeast and mammalian data sets, respectively. The partial correlation analysis showed that 7 of 15 gene properties (all except gene alignment length, number and percentage of variable sites, gene alignment length after exclusion of all sites containing gaps, percent average of GC content of third codon positions across taxa, variance of GC content percentage of second codon positions across taxa, number of protein domains, and number of potential coiled-coil regions) originally identified in the standard correlation analysis maintained Pearson’s correlation coefficient r values ≥ 0.1 and P < 0.0001 (fig. 3B; see supplementary table S8, Supplementary Material online), albeit weaker in strength. Furthermore, three additional sequence-based properties (Gap_pct_mean: average of percentage of sites containing gaps across taxa, Gap_pct_var: variance of percentage of sites containing gaps across taxa, and nonCAM_pct: percentage of non-CAM substitutions) were consistently correlated with the three phylogenetic measures in yeasts and mammals (fig. 3B). Finally, these analyses showed that the correlations between function-based properties and the three phylogenetic measures were weakly reduced, whereas the correlations between tree-based properties and the three phylogenetic measures were substantially increased. Interestingly, two tree-based properties (Leaf2node_mean: average of all branch lengths that are between the outgroup node and each ingroup node across the maximum likelihood tree and Total_treelen: sum of all branch lengths across the maximum likelihood tree) were negatively correlated with two of the phylogenetic measures (ABS and TCA) in yeasts, but were positively correlated with the same two measures in mammals (fig. 3B).

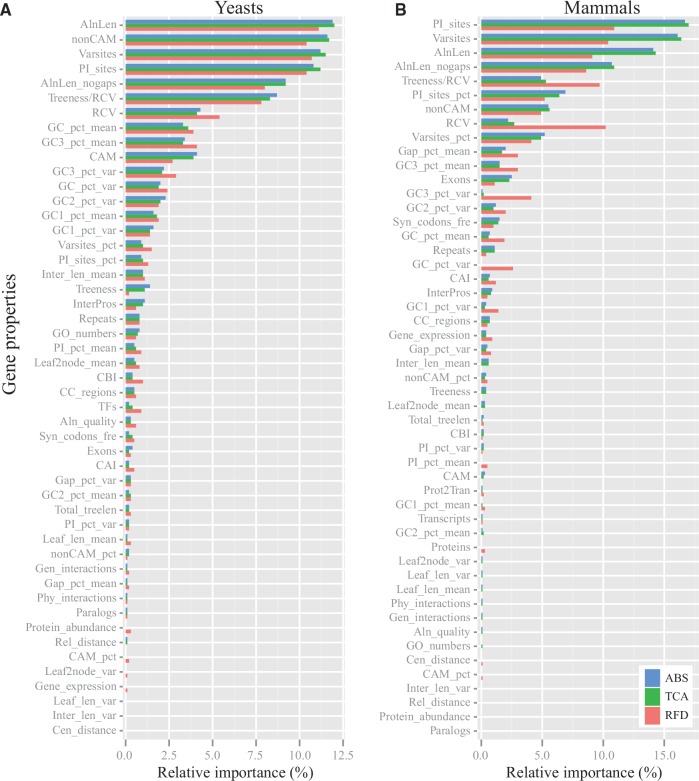
Identifying the Gene Properties That Best Predict Phylogenetic Signal

Finally, we sought to estimate the power of each gene property to predict phylogenetic signal as well as to identify the subset of gene properties that best models phylogenetic signal. Addressing both questions requires techniques that take into account the fact that most gene properties are highly intercorrelated (fig. 2).

To identify which gene property is the most important and to create their ranking with respect to phylogenetic signal, we used the relative importance technique (Groemping 2006). Briefly, relative importance creates a set of new independent variables that are the maximally related to the set of gene properties but which (unlike gene properties) are uncorrelated to each other. Because these new variables are not intercorrelated, they can be regressed onto measures of phylogenetic inference, and their R² values of the coefficients of determination can be used to rank variables according to their relative importance in predicting phylogenetic signal.

The relative importance of the different gene properties was very similar for all three phylogenetic measures (ABS, TCA, and RFD) in yeasts (fig. 4A) but not in mammals where it was similar for ABS and TCA but differed for RFD (fig. 4B). Overall, the relative importance values of sequence-based properties were higher than the values of tree-based and function-based ones in both yeasts and mammals (fig. 4; see supplementary table S9, Supplementary Material online). Specifically, seven gene properties (AlnLen: gene alignment length, Varsites: number of variable sites, PI_sites: number of parsimony-informative sites, non-CAM: number of sites containing RGC_non-CAM substitutions, AlnLen_nogaps: gene alignment length after exclusion of all sites containing gaps, RCV: relative composition variability, and Treeness/RCV: the proportion of tree distance on internal branches divided by RCV) were highly correlated with the three measures of phylogenetic inference in both yeasts and mammals (fig. 4). In addition, GC content of all sites across taxa (GC_pct_mean) and percent average of GC content of third codon positions across taxa (GC3_pct_mean) also highly contributed to phylogenetic signal in yeasts (fig. 4A) but not in mammals (fig. 4B). In contrast, the contributions of percentage of variable sites (PI_sites_pct), percent average of sites containing gaps across taxa (Gap_pct_mean), and number of exons (Exons) in mammals were significantly greater than those in yeasts, and were highly ranked.

Fig. 4.—

Relative importance of each of the gene properties to three phylogenetic measures in yeasts (A) and mammals (B). Full descriptions of the 52 gene properties are given in table 1. Note that three gene properties (Transcripts, Proteins, and Prot2Tran) whose SDs are zero, are not included in the analysis of yeast gene properties (A); similarly, the TFs gene property, which has a lot of missing data, is not included in the analysis of mammal gene properties (B). The exact values of relative importance of each gene property to each phylogenetic measure can be found in supplementary table S9, Supplementary Material online.

To identify the subset of gene properties that best models phylogenetic signal, we used the best subset selection technique (Lumley 2009; James et al. 2013). Briefly, we split our data into ten roughly equal sized bins (folds): nine bins were used as training data to identify the best regression model for a given number of predictors (i.e., gene properties) and a dependent variable (i.e., phylogenetic measure) while one bin was used as testing data. This process was repeated 10 times (each time using a different one of the 10 bins as testing data) and the mean squared error (MSE) of each model in predicting the testing data was calculated. The predictors from the model with the lowest MSE were considered the best subset of gene properties in predicting phylogenetic signal.

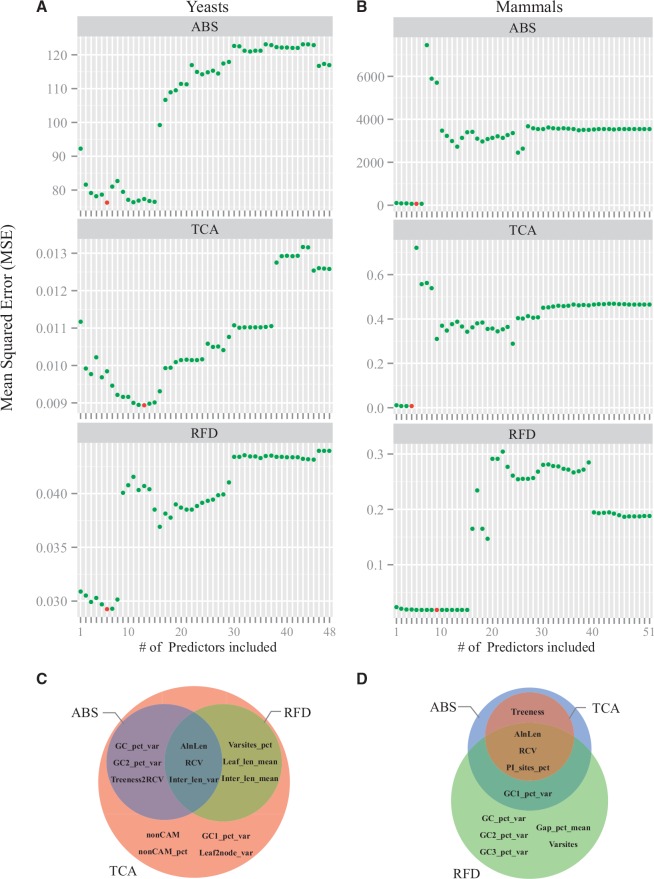
The subset selection technique identified three subsets containing 13 distinct gene property predictors of the three phylogenetic measures (ABS, TCA, and RFD) in yeasts (fig. 5C; the subset modeling ABS contained six predictor gene properties, the subset modeling TCA contained 13 predictors, and the subset modeling RFD contained six predictors) and 10 distinct ones in mammals (fig. 5D; the subset modeling ABS contained five predictor gene properties, the subset modeling TCA contained four predictors, and the subset modeling RFD contained nine predictors).

Fig. 5.—

The relative performance of optimal models comprised of varying numbers of gene property predictors in predicting the values of each of three phylogenetic measures in yeasts (left panel) and mammals (right panel). For a given number of gene property predictors and the training data, the best regression model was determined by the subset selection technique. For each given best regression model, its MSE in predicting the accuracy in the testing data was calculated in yeasts (A) and mammals (B). The model with the lowest MSE value in each analysis is indicated by the red dot and was considered the best subset selection. The identity and overlap of gene property predictors of the three different phylogenetic measures in the two data sets are summarized into Venn diagrams (C and D). Full descriptions of the 52 gene properties are given in table 1. Note that three predictors (Transcripts, Proteins, and Prot2Tran) whose SDs are zero, and the Treeness predictor, which is too collinear with other predictors, are not included in yeasts (A); similarly, the TFs predictor, which has much data missing, is not included in mammals (B). Detailed values from the analysis of subset selections in yeasts and mammals are provided in supplementary tables S10 and S11, Supplementary Material online.

Overall, gene property predictors identified by the subset selection technique were either sequence-based or tree-based (fig. 5; see supplementary tables S10 and S11, Supplementary Material online). Furthermore, gene property predictors included in subsets obtained from the yeast data were considerably different from those obtained from the mammal data; the same was true for gene property predictors included in subsets obtained for each phylogenetic measure (fig. 5; see supplementary tables S10 and S11, Supplementary Material online). Specifically, only two sequence-based gene properties (AlnLen: gene alignment lengthand RCV: relative composition variability) were consistently included as predictors of all three phylogenetic measures in both yeasts and mammals (fig. 5C and D). Additionally, one tree-based gene property (Inter_len_var: the variance of lengths of internal branches across the maximum likelihood tree) and one sequence-based property (PI_sites_pct: the percentage of number of parsimony-informative sites) were consistently recovered as predictors of all three phylogenetic measures in yeasts (fig. 5C; see supplementary table S10, Supplementary Material online) and mammals (fig. 5D; see supplementary table S11, Supplementary Material online), respectively. Finally, several other gene properties were identified as predictors of one or two of the three phylogenetic measures in either yeasts or mammals (fig. 5; see supplementary tables S10 and S11, Supplementary Material online).

Discussion

It has long been recognized that choosing “good” markers, typically genes, is a vital component of phylogenetic inference. In the last few years, high-throughput sequencing has greatly facilitated the development of variety of approaches for constructing phylogenomic data matrices, including whole genome sequencing (Jarvis et al. 2014; Neafsey et al. 2015) and transcriptome sequencing (Hittinger et al. 2010; Misof et al. 2014; Wickett et al. 2014), as well as more tailored approaches that specifically target hundreds or thousands of loci with specific characteristics (Faircloth et al. 2012; Lemmon et al. 2012). Irrespective of the approach chosen and the much larger amounts of data available for inference, identification of reliable gene properties that predict “good” markers is still a key aspect of molecular phylogenetic studies.

To address this question, we examined 52 properties obtained from 2,832 genes in 12 yeast taxa and 2,002 genes from 24 mammalian taxa and three measures of phylogenetic signal obtained from these yeast and mammalian gene trees. We found that most, but not all, gene properties were highly correlated with each other and with phylogenetic signal and identified a handful of sequence-based and tree-based gene properties as the best predictors of phylogenetic signal. These results bear on our understanding of the interrelationships among different gene properties as well as what general attributes of genes are most useful in the identification of “good” phylogenetic markers.

Function-Based Properties are not Useful Predictors of Phylogenetic Signal

In contrast to several sequence- and tree-based gene properties, none of 19 function-based properties consistently showed strong correlation or were reliable predictors of any of the three measures of phylogenetic signal (figs. 3–5). Although it is possible that their impact on phylogenetic signal may be truly weaker than that of sequence- and tree-based properties, the difference may also be explained by methodological disparities in examining the different types of gene properties. For example, all function-based properties were based on information from the gene of a single species (S. cerevisiae in the case of yeasts, or H. sapiens in the case of mammals), whereas sequence-based and tree-based properties were based on the entire gene alignment or on the resulting gene tree reconstructed from the gene alignment.

Evolutionary Rate, One of the Largest Hubs in the Correlation Network of Gene Properties, Is Not Predictive of Phylogenetic Signal

Evolutionary rate is arguably one of the most informative properties of a gene (Kimura 1968; Zhang and Yang 2015). Consistent with the previous studies (e.g., Wall et al. 2005; Drummond et al. 2006; Wei et al. 2014), we found that evolutionary rate (as measured by the percent average of pairwise identity across taxa or PI_pct_mean) was one of the largest hubs in the correlation networks of gene properties in both yeasts and mammals (fig. 2). However, we also found that evolutionary rate was not an important predictor of phylogenetic signal in the two data sets we examined (figs. 4 and 5). Understanding how a gene’s evolutionary rate influences phylogenetic inference has received considerable attention in recent years (Rokas et al. 2003; Aguileta et al. 2008; Jian et al. 2008; Regier et al. 2008; Zhang et al. 2012; Salichos and Rokas 2013; Betancur et al. 2014), with some (Jian et al. 2008; Regier et al. 2008; Zhang et al. 2012; Betancur et al. 2014), but not all (Rokas et al. 2003; Aguileta et al. 2008; Salichos and Rokas 2013), studies arguing that slowly evolving genes are more useful for reconstructing anciently diverged lineages than genes with other evolutionary rates. Thus, the effect of the evolutionary rate on phylogenetic signal may be dependent on the specifics of the diversification event under study (e.g., how ancient, how rapid, etc.) or may be better captured by some of the many gene properties it is correlated with (fig. 2; see supplementary table S6, Supplementary Material online).

Several Sequence- and Tree-Based Gene Properties are Good Predictors of Phylogenetic Signal

Our analyses identified several sequence-based and few tree-based properties that were predictive of phylogenetic signal (figs. 4 and 5). In general, sequence-based predictors of phylogenetic signal involved gene properties associated with gene sequence length (e.g., AlnLen: gene alignment length, Varsites: number of variable sites, PI_sites: parsimony-informative sites, nonCAM: number of sites containing RGC_non-CAM substitutions) or nucleotide composition (e.g., GC_pct_mean: GC content, and RCV: relative nucleotide composition variability), whereas tree-based predictors were associated with internode length (e.g., Treeness: proportion of sum of internal branch lengths over sum of all branch lengths, Leaf_len_mean: average length of external branches across the maximum likelihood tree of a given alignment).

Predictors associated with gene sequence length were by far the most influential on phylogenetic signal (figs. 4 and 5). Genes with longer sequence lengths tended to exhibit stronger phylogenetic signal, which has been shown to ameliorate incongruence in phylogenomic data matrices (Salichos and Rokas 2013). For example, the average alignment length of the 75 genes whose gene trees were topologically identical (RFD = 0) to the yeast eMRC phylogeny is more than 2-fold that of the remaining 2,757 genes whose gene trees topologically disagreed (RFD > 0) with the eMRC phylogeny (see supplementary table S2, Supplementary Material online). Interestingly, a recent binning approach in which genes with the same or weakly conflicting topologies were binned into a single “supergene” with longer length (Mirarab, Bayzid, et al. 2014) was shown to improve the accuracy of species tree methods.

The pervasive influence of gene sequence length on phylogenetic signal offers insights for understanding signal distribution in phylogenomic data matrices as well as suggestions for strengthening it. First, in phylogenomic data matrices that contain genes with wide variance in their alignment lengths it is the longest genes that will have the strongest phylogenetic signal; thus, if the objective is to obtain the phylogenetic history supported by the majority of genes, standardization of gene alignment lengths (or statistical standardization of their effects) is essential. Second, approaches that typically generate short gene fragments (e.g., the average length of successfully captured loci in recent vertebrate phylogenetic studies using target enrichment approaches ranged between 410 and 580 bp, (Crawford et al. 2012; Faircloth et al. 2013; Brandley et al. 2015; Peloso et al. 2016) will yield phylogenomic data matrices whose genes have weak phylogenetic signal. In such cases, resorting to approaches such as conditional binning into longer “supergenes” (Bayzid and Warnow 2013; Mirarab, Bayzid, et al. 2014) or optimizing protocols so that longer gene fragments can be obtained, will likely be advantageous.

The second influential set of predictors of phylogenetic signal included gene properties that capture nucleotide composition and its degree of homogeneity across taxa. Genes with lower compositional heterogeneity typically had stronger phylogenetic signal (figs. 4 and 5). For example, the average RCV of the 75 yeast gene trees that were topologically identical (RFD = 0) to the yeast eMRC phylogeny is about three quarters that of the remaining 2,757 yeast genes that topologically disagreed (RFD > 0) with the eMRC phylogeny (see supplementary table S2, Supplementary Material online). In general, models of sequence evolution assume that sequences are compositionally homogeneous, an assumption often violated in biological data sets, leading to systematic error and topological incongruence (e.g., Conant and Lewis 2001; Betancur et al. 2013; Pisani et al. 2015; Romiguier et al. 2016). Thus, selection of genes that show high compositional homogeneity or inference using models that take into account compositional heterogeneity is likely to be advantageous.

The final influential set of predictors of phylogenetic signal included gene properties associated with the internode length. Gene trees with longer internode lengths tended to yield stronger phylogenetic signal (figs. 4 and 5). For example, the mean internode branch length (Inter_len_mean) of the 75 yeast gene trees that were topologically identical (RFD = 0) to the yeast eMRC phylogeny is slightly higher than that of the remaining 2,757 yeast gene trees that topologically disagreed (RFD > 0) with the eMRC phylogeny (mean internode length in the 75 genes is 0.163 substitutions/site, whereas in the 2,757 genes is 0.145 substitutions/site; see supplementary table S2, Supplementary Material online). This finding is consistent with the previous work showing that shorter internode branches are associated with poor resolution and higher phylogenetic incongruence (Salichos and Rokas 2013).

In conclusion, from a “choices in data” phylogenetic perspective, our analyses of thousands of genes from yeasts and mammals suggest that “good markers” for phylogenetic inference are likely to be genes that are long in sequence, that show nucleotide composition homogeneity across the set of taxa examined, and that generate gene trees with long internodes. Although it is self-evident that the accuracy of phylogenetic inference is not solely dependent on the underlying data but also on many other biological (e.g., the tempo and mode of evolution of a particular lineage) and analytical (e.g., model of sequence evolution) factors, we believe that selection of markers based on their underlying gene properties will improve the accuracy of phylogenetic inference and reduce topological incongruence.

Supplementary Material

Supplementary tables S1–S11 and figures S1–S2 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).