Skip to main content
PMC home page
Genome Biology and Evolution logoLink to Genome Biology and Evolution
letter
. 2016 Aug 13;8(8):2624–2631. doi: 10.1093/gbe/evw198

Genomic Complexity Places Less Restrictions on the Evolution of Young Coexpression Networks than Protein–Protein Interactions

Wen Wei 1,2, Yan-Ting Jin 3,4, Meng-Ze Du 3,4, Ju Wang 2, Nini Rao 3,4, Feng-Biao Guo 3,4,*
PMCID: PMC5010916  PMID: 27521813

Abstract

The differences in evolutionary patterns of young protein–protein interactions (PPIs) among distinct species have long been a puzzle. However, based on our genome-wide analysis of available integrated experimental data, we confirm that young genes preferentially integrate into ancestral PPI networks, and that this manner is consistent in all of six model organisms with widely different levels of phenotypic complexity. We demonstrate that the level of restrictions placed on the evolution of biological networks declines with a decrease of phenotypic complexity. Compared with young PPI networks, new co-expression links have less evolutionary restrictions, so a young gene with a high possibility to be coexpressed other young genes relatively frequently emerges in the four simpler genomes among the six studied. However, it is not favorable for such young–young coexpression in terms of a young gene evolving into a coexpression hub, so the coexpression pattern could gradually decline. To explain this apparent contradiction, we suggest that young genes that are initially peripheral to networks are temporarily coexpressed with other young genes, driving functional evolution because of low selective pressure. However, as the expression levels of genes increase and they gradually develop a greater effect on fitness, young genes start to be coexpressed more with members of ancestral networks and less with other young genes. Our findings provide new insights into the evolution of biological networks.

Keywords: young gene, biological network, phenotypic complexity

Young Genes and the Evolution of Protein–Protein Interaction Networks

Gene contents and complexity roughly increases with increasing phenotypic complexity of an organism. The number of genes tends to evolve via gene gain or loss during long-term evolutionary processes (McLysaght et al. 2003; Hahn et al. 2007; Kettler et al. 2007; Chen et al. 2010). A gene is considered to be relatively young when its detectable orthologs are limited to very closely related species (Chen et al. 2013). Compared with ancestral genes, which are less likely to be lost, the fate of young genes is more uncertain because of their potentially unnecessary or redundant functions (Vishnoi et al. 2010; Chen et al. 2012). To avoid elimination over the course of evolution, young genes acquire necessary functions by rapid amino acid changes, followed by their adjustment of protein–protein interactions (PPIs) (Zhang et al. 2004; Ross et al. 2013).

The emergence of young genes provides important genetic novelties that could promote the evolution of PPI networks (Qin et al. 2003; Capra et al. 2010; Zhang et al. 2015). Proteins encoded by young genes integrate into and reshape ancestral PPI networks to develop corresponding biological roles, which has been confirmed in several individual young-gene studies (Matsuno et al. 2009; Chen et al. 2012; Weng et al. 2012). Using genome-wide data, a large number of young genes were found to have integrated into biological networks throughout human and mouse evolution (Zhang et al. 2015). However, it was observed in yeast that genes of similar age and origin preferentially interact with each other (Qin et al. 2003; Capra et al. 2010). Thus, in the case of yeast, protein products of young genes were more likely to interact with those of other young genes, but less likely to participate in ancestral PPI networks.

The differences in evolutionary patterns of PPI networks between mammals and simple living organisms (such as yeast) have long been a puzzle. The STRING database quantitatively integrates interaction data for a large number of organisms and includes data from other well-known interaction databases (Szklarczyk et al. 2015). To address this issue, we used the latest release of PPI data (version 10) to investigate the evolution of PPIs among six model organisms, listed here in decreasing order of phenotypic complexity: Homo sapiens (human), Mus musculus (mouse), Drosophila melanogaster (fruit fly), Caenorhabditis elegans (worm), Saccharomyces cerevisiae (yeast) and Escherichia coli. All integrated PPI data were in accordance with classic and robust power-law distributions of connectivity (see “Material and Methods” section).

Phylogenetic ages were determined using a method described by Wolf et al. (2009). First, we assigned reference genomes (see “Material and Methods” section; supplementary table S1, Supplementary Material online) into eight, seven, six, six, four and five phylogenetic branches for human, mouse, fruit fly, worm, yeast and E. coli, respectively, in accordance with taxonomic classifications and divergence times. Second, matching protein orthologs in the reference genomes were determined using the best reciprocal hit (RBH) from a BLASTP search. Finally, we assigned a gene to a certain branch if it matched at least half of the genomes in the branch, considering a genome of a constant size under a steady-state process of gene acquisition and loss (Wolf et al. 2009). Genes that could not be assigned to any branches were classified as the youngest one (branch 1).

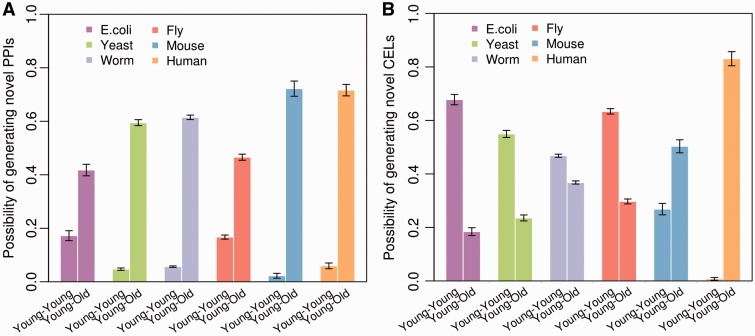
Large numbers of proteins encoded by young genes were found to interact with other ones with similar origins (Qin et al. 2003). In the current study, it was necessary to consider the variations in gene numbers among the age classes (supplementary table S1, Supplementary Material online) to avoid bias in the results. Thus, we used the proportion that the number of an observed interaction was greater than the number expected by chance to estimate the possibility that the interaction emerges. For each gene in the “branch 1”, we randomly picked its interacting genes in accordance with observed connectivity with 10,000 Monte Carlo simulations. The possibility of the birth of interactions involving “branch 1” genes significantly increases with increasing divergence times of the genes interacting with “branch 1” genes (E. coli, r = 0.241, P < 2.2 × 10 − 16; yeast, r = 0.457, P < 2.2 × 10 − 16; worm, r = 0.412, P < 2.2 × 10 − 16; fruit fly, r = 0.274, P < 2.2 × 10 − 16; mouse, r = 0.591, P < 2.2 × 10 − 16; human, r = 0.451, P < 2.2 × 10 − 16). This suggests that a protein product of younger gene prefer to interact with proteins encoded by older genes. To further confirm the preference for “young–old” PPIs, we identified young genes as those that had diverged fewer than 50 Ma, but old genes as those belonging to the oldest branch (marked in supplementary table S1, Supplementary Material online). All six PPI datasets show that the possibility of novel “young–young” interactions emerging is significantly lower than that of “young–old” interactions doing so (t-test: P < 2.2 × 10 − 16; fig. 1A), suggesting that the establishment of “young–old” PPIs could be an effective way to improve young gene fitness.

Fig. 1.—

Fig. 1.—

Open in a new tab

Comparison of the possibilities of “young–young” and “young–old” (A) PPIs and (B) CELs emerging in six organisms. The bars denote the mean possibilities for the “young–young” and “young–old” groups and the error bars show the SEM for each group. All “young–young” distributions are significantly different from “young–old” distributions (t-test: P < 2.2 × 10 − 16).

To estimate the robustness of these results, we randomly removed or added one or two reference species in accordance with phylogenetic relationships by 20 times in the process of human age estimation and then performed 10,000 Monte Carlo simulations as mentioned earlier. All 20 validations suggested that the possibility of “young–old” PPIs emerging was significantly higher (t-test: P < 2.2 × 10 − 16). The finding of a preference for “young–old” PPIs was also robust upon merging neighboring branches or separating a branch into several individuals according to divergence times. Changing the species in the phylogenetic tree did not affect our results. There is no single, optimal method to define the age of a gene. Young genes arise from not only de novo (orthologs) but also via duplication (paralogs). In this work, we simply used a straightforward and crude procedure to identify gene ages based on the absence and presence of orthologs in the genomes through phylogenetic branches. Here, another dataset on human gene age was retrieved from a study by Zhang et al. (2010). Owing to being based on more sophisticated genome alignment, rather than gene alignment, these data provided excellent estimates of the ages of new genes that originated from DNA-based duplication or RNA-based duplication, or arose from de novo. From the data of Zhang et al. (2010), we further confirmed that the possibility of novel PPIs emerging for genes from the youngest branch was significantly increased with increasing divergence times of the interacting genes (r = 0.386, P < 2.2 × 10 − 16). Thus, using the cruder method of identifying gene-based age does not change the results.

Fewer Restrictions on the Evolution of Young Co-expression Links

Both PPI and co-expression link (CEL) networks reflect biological communications, with the former being direct and physical, but the latter being functionally related; however, they are controlled by similar transcriptional regulatory systems. At present, we generally understand less about CELs than about PPIs. However, it has been found that young genes were significantly integrated into CELs associated with specific stages of fruit fly development (Liu et al. 2014). In our study, CELs were also independently investigated and their manner of evolution was compared with that of PPIs. All integrated CEL data met the criteria for classic and robust power-law distributions of connectivity, the same as the PPI data (see “Material and Methods” section).

Using 10,000 Monte Carlo simulations, we observed that the possibility of the emergence of a connection for the “branch 1” gene significantly and positively correlates the divergence times of the connected gene in both mouse (r = 0.302, P < 2.2 × 10 − 16) and human (r = 0.463, P < 2.2 × 10 − 16) in CEL networks, as well as in PPI networks. This suggests that the possibility of generating a novel CEL indeed increases with the age of the gene that is coexpressed with during mammalian evolution. However, this situation is reversed in the four simpler genomes (E. coli, r = −0.371, P < 2.2 × 10 − 16; yeast, r = −0.257, P < 2.2 × 10 − 16; worm, r = −0.198, P < 2.2 × 10 − 16; fly, r = −0.337, P < 2.2 × 10 − 16). Furthermore, we observed more “young–young” CELs than “young–old” among the genomes of E. coli, yeast, worm and fruit fly (t-test: P < 2.2 × 10 − 16; fig. 1B). Our results suggest that a young gene is more likely to be coexpressed with other young genes in the four simpler genomes.

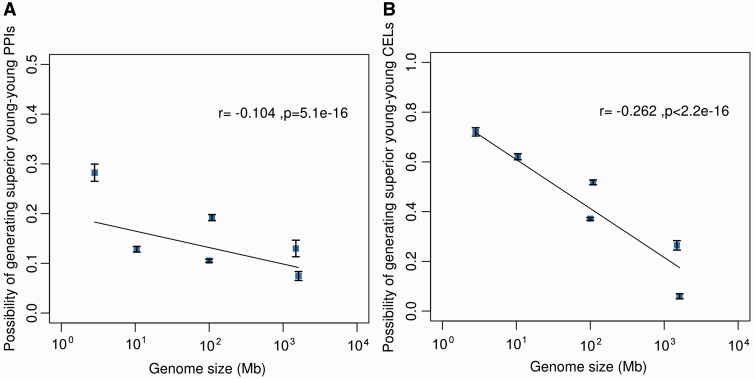
We then investigated the evolutionary restriction on the emergence of “young–young” CELs among six model organisms with widely different levels of phenotypic complexity. We used the proportion that the value of observed “young–young” divided by “young–old” connection counts was greater than expected by chance to estimate the possibility of emergence of superior “young–young” PPIs (CELs) from 10,000 Monte Carlo simulations. With each Monte Carlo repeat, we randomly picked the interacting genes for a young gene in accordance with observed connectivity. As shown in figure 2A and B, in either PPIs (r = −0.104, P = 5.1 × 10 − 16) or CELs (r = −0.262, P < 2.2 × 10 − 16), simpler genomes are more likely to gain “young–young” connections. We compared the possibility of generating superior “young–young” PPIs and CELs. Such possibilities for CELs are significantly higher than those for PPIs in E. coli (t-test: P < 2.2 × 10 − 16), yeast (P < 2.2 × 10 − 16), worm (P < 2.2 × 10 − 16), fruit fly (P < 2.2 × 10 − 16) and mouse (P = 1.4 × 10 − 7). However, there was no significant difference between human PPIs and CELs (P = 0.272). These results suggest that the restrictions placed on the evolution of networks decline with decreasing phenotypic complexity. Compared with young PPI networks, new CEL networks are under less stringent evolutionary restrictions, so in the four simpler genomes, young coexpression between pairs of young genes emerges more often.

Fig. 2.—

Fig. 2.—

Open in a new tab

Correlations of phenotypic complexity (genome size) and possibility of generating superior “young–young” (A) PPIs or (B) CELs among six organisms. The dots denote the mean possibilities for six organisms and the error bars show the SEM. The line indicates the significant regression correlation between genome sizes and possibilities.

More Young Coexpression, Less Evolutionary Restriction

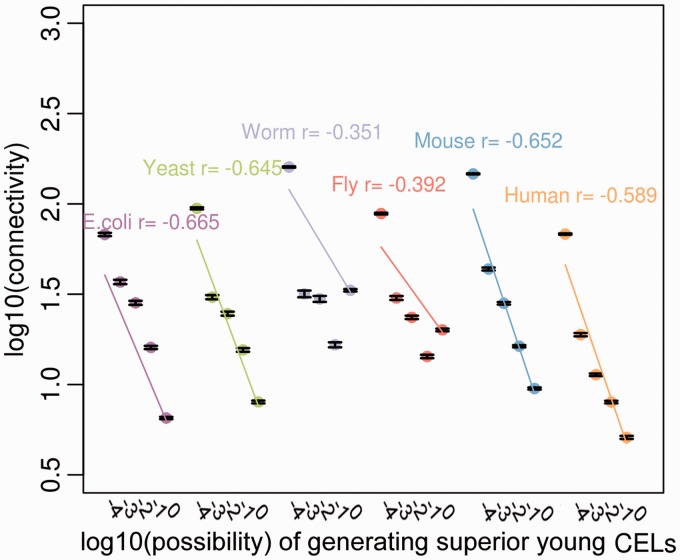
The young gene with a high possibility to be coexpressed other young genes relatively frequently emerges in the four simpler genomes. To further explain this issue, here we focused on investigating network features of all genes rather than the only young genes. We then investigated the coexpression connectivity of genes with such high possibility of emerging novel CELs. We denoted the young CEL as that a gene had coexpressed a young gene, whereas the old CEL as that a gene had coexpressed an old gene. To estimate the possibility that gain superior young CELs, we obtained the proportion for a gene that the observed value of young divided by old CEL counts was greater than expected by chance from 10,000 Monte Carlo simulations. With each Monte Carlo repeat, we randomly picked the interacting genes for an investigated gene in accordance with observed connectivity. The genes are classified into five groups with different orders of magnitude of such superior possibilities (−4, −3, −2, −1 and 0). Significant negative correlations were found between connectivity and the possibility scales (fig. 3; E. coli, r = −0.665, P < 2.2 × 10 − 16; yeast, r = −0.645, P < 2.2 × 10 − 16; worm, r = −0.351, P < 2.2 × 10 − 16; fruit fly, r = −0.392, P < 2.2 × 10 − 16; mouse, r = −0.652, P < 2.2 × 10 − 16; human, r = −0.589, P < 2.2 × 10 − 16). Young genes usually shows low connectivity (Zhang et al. 2015), however, the possibility that the gene with lower connectivity is coexpressed with other young genes rises. This could be suggestive of a gradual process of young genes evolving to become hubs as they show a decline in terms of the proportion of “young–young” patterns of coexpression.

Fig. 3.—

Fig. 3.—

Open in a new tab

Trends of gene connectivity and its possibility of generating superior young CELs among six organisms. The x-axis and y-axis represent log-transformed data. The genes are classified into five groups with different orders of magnitude of possibilities (−4, −3, −2, −1 and 0). The dots denote the mean log10-transformed connectivity of each possibility group and the error bars show the SEM. The lines indicate the significant regression correlation between log10-transformed connectivity and possibility scales (P < 2.2 × 10 − 16).

Young genes may have a reduced chance of becoming coexpression hubs if they have already developed a large number of “young–young” coexpressions. The interactions in “young–young” CELs could be unstable and thus would decline in the long term over the course of evolution, especially for E. coli, yeast, worm and fruit fly. However, if this were the case, why do these genes with low CEL network connectivity have such high young coexpression levels? One answer to this might be that this is a potential mechanism to improve the likelihood of survival during early evolution because young genes are gradually integrated into networks to form newer and less connected nodes (Zhang et al. 2015). High expression and strong essentiality are both considered to be critical features of topologically central genes. Next, to confirm this, the correlations between the possibility scales of gaining superior young CELs and critical features, focusing on the four simpler genomes among the six included in this study, were compared.

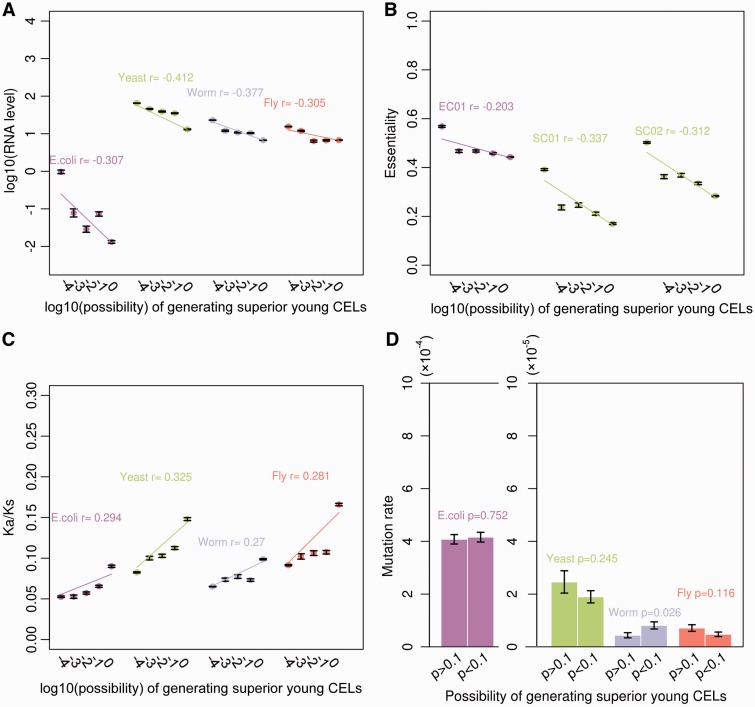
In this study, we assessed the RPKM or FPKM values (reads or fragments per kilobase per million mapped reads) from the RNA-seq data obtained from public data. Then, the RPKM/FPKM values were scaled by a log function to describe mRNA levels. Through comparative analysis of mRNA levels, a significant negative correlation between mRNA levels and the possibility scales of the emergence of superior young CELs was observed (fig. 4A; E. coli, r = −0.307, P < 2.2 × 10 − 16; yeast, r = −0.412, P < 2.2 × 10 − 16; worm, r = −0.377, P < 2.2 × 10 − 16; fruit fly, r = −0.305, P < 2.2 × 10 − 16). Meanwhile, a negative relationship between essentiality and young coexpression percentage was confirmed in three experimental knock-out datasets for the genomes of E. coli and yeast (fig. 4B; EC01, r = −0.203, P < 2.2 × 10 − 16; SC01, r = −0.337, P < 2.2 × 10 − 16; SC02, r = −0.312, P < 2.2 × 10 − 16). This could indirectly confirm that young genes are initially coexpressed with other young genes, temporarily, before they are integrated into core networks. However, as evolutionary time passes, the expression of genes increases and they have more of an effect on essentiality, and establish more interactions with older genes and networks.

Fig. 4.—

Fig. 4.—

Open in a new tab

Relationships between the possibility of genes generating superior young CELs and their (A) mRNA levels, (B) essentiality, (C) Ka/Ks and (D) mutation rates in four simpler genomes. In (A–C), the y-axis represents log10-transformed data and the genes are classified into five groups with different orders of magnitude of possibilities (−4, −3, −2, −1 and 0). The dots denote the mean of (A) log10-based R(F)PKM values, (B) essentiality and (C) Ka/Ks. The error bars show the SEM. The lines indicate the significant regression correlation (P < 2.2 × 10 − 16). In (D), the genes are classified into two groups (P > 0.1 and P < 0.1). The bars denote the mean mutation rates of each possibility group and the error bars show the SEM.

Mutations are the driving force of variation on which natural selection acts (Lynch 2010). The Ka/Ks ratios are usually used as a signature for selection. These selection signatures were computed by comparing the following genomes: C. elegans versus C. briggsae, D. melanogaster versus D. yakuba, S. cerevisiae versus S. mikatae and E. coli versus Salmonella typhimurium. Significant correlations of Ka/Ks ratios and the possibility scales of the emergence of superior young CELs indicated that the genes with a higher proportion of young coexpressions are rapidly evolving (fig. 3C; E. coli, r = 0.294, P < 2.2 × 10 − 16 yeast, r = 0.325, P < 2.2 × 10 − 16; worm, r = 0.270, P < 2.2 × 10 − 16; fruit fly, r = 0.281, P < 2.2 × 10 − 16). Next, we focused on an analysis of the impact of neutral mutations on young CEL evolution using integrated mutation accumulation (MA) experimental data. Here, we only classified the genes into two subgroups (one group with P > 0.1, the other with P < 0.1), to reduce the noise from abundant unmutated sites. As figure 4D shows, there was no significant mutation bias within coding regions between the two gene subgroups among E. coli (t-test, P = 0.752), yeast (P = 0.245) and fruit fly (P = 0.116); however, weak but significant bias was shown in worm (P = 0.026). These results imply that young genes gradually come under increasing selective pressure or decreasing evolutionary rates while they increase their rates of coexpression with older genes. This relationship holds regardless of the level of gene mutation.

Conclusions

In this work, we compared the evolutionary patterns between PPI and CEL networks among different genomes. Although similar patterns were obtained for all of the PPI networks, networks were found to be subjected to less evolutionary restrictions with decreasing phenotypic complexity. Compared with young PPI networks, the evolution of new CEL networks is less restricted, so that the evolutionary patterns change in CEL networks in simple organisms. In these simple organisms, young genes preferentially generate novel “young–young” CELs, but they tend to interact with ancestral links in PPI networks. These young genes are initially coexpressed with other young genes, which could be a way to drive functional evolution because of the low selective pressure that they are facing. Upon increasing their expression and having more of an effect on fitness, young genes develop more patterns of coexpression with core networks and fewer with young genes. However, “young–young” CELs are limited in human and mouse, possibly because of the phenotypic complexity of such higher animals. Such young networks could, however, have important phenotypic effects in brain development (Zhang et al. 2015). Our results indicate that the impact of evolutionary pressure on biological networks increases with increasing phenotypic complexity.

Material and Methods

Phylogenetic Ages

We downloaded completely sequenced eukaryotic genomes from Ensembl Genomes (http://www.ensembl.org/; V31) and bacterial/archaeal genomes from RefSeq (http://www.ncbi.nlm.nih.gov/refseq/). In accordance with NCBI taxonomic classifications and divergence times from publications listed in supplementary table S1, Supplementary Material online, we assigned the genomes into eight, seven, six, six and four phylogenetic branches for H. sapiens (Ensembl assembly version: GRCh38), M. musculus (GRCm38), D. melanogaster (BDGP6), C. elegans (WBcel235) and S. cerevisiae (R64), respectively. These branches indicated that the genes diverged from 0 to 1,296 Ma. Closely related genomes were removed in each branch and then we randomly chose at most 12 reference genomes, ensuring that the references were not closely related to each other in each branch (Langille et al. 2008). Finally, 35, 27, 39, 32 and 26 genomes were used for determination of the gene origins of human, mouse, fruit fly, worm and yeast, respectively (supplementary table S1, Supplementary Material online). However, 40, 235, 113, 69 and 86 randomly collected genomes from Archaea, Bacteria, Proteobacteria, Gammaproteobacteria and Enterobacteriaceae classes (supplementary table S1, Supplementary Material online), respectively, was used to determine the phylogenetic relationships of the bacterial species E. coli (RefSeq accession: NC_000913). This relationships suggested a longer evolutionary time scale (>4,000 Ma).

All raw homologous matches of H. sapiens, M. musculus, D. melanogaster, C. elegans and S. cerevisiae were obtained from Ensembl’s BioMart homology track. Then, we confirmed protein orthologs using the RBH from a BLASTP search with an E-value cut-off of 10 − 6 and 80% minimum alignable residues, based on an age-identifying method described by Wolf et al. (2009). In a similar way, all-against-all BLASTP was used for an ab initio search of homologs of E. coli genes (E-value < 10 − 6 and coverage > 80%).

Considering gene loss and gain events, the number of matched genomes required to assign a protein to a specific age class was determined as half the effective number of collected genomes in each branch (Wolf et al. 2009; Chen et al. 2012). The oldest age was adopted if a gene could be assigned to multiple branches. Additionally, if only one genome involved in a branch, we required genes to assign into this branch unless they also matched at least in one genome in the next younger branch. Genes that could not be assigned to any branches were classified as the youngest ones (branch 1).

CEL and PPI Data

We extracted the integrated CEL and PPI data from the STRING database (http://string-db.org/), which quantitatively integrates protein interaction data for a large number of organisms and includes data from other well-known interaction databases. Each interaction in the database was assigned a confidence score (0–1) corresponding to the probability of finding the interaction in experiments. Only interactions with itself were excluded from further analysis. The reconstructed network should be scale-free and in accordance with the power-law distribution of connectivity (Barabási 2009; Zhang et al. 2015). We found strong and significant negative log10-transformed relationships between connectivity and gene counts with corresponding connectivity in six reconstructed PPIs (r = −0.962 ± 0.029, P < 2.2 × 10 − 16) and six reconstructed CELs (r = −0.964 ± 0.009, P < 2.2 × 10 − 16), which indicated that the power-law distribution of connectivity was followed in all integrated scale-free CEL and PPI data (supplementary table S2, Supplementary Material online). To examine the robustness of the integrated network, we removed interactions using different quantile cut-offs and re-estimated the log10-transformed relationships. The correlation coefficients with high similarity suggest that power-law distributions were robust when data were removed using confidence score cut-offs (supplementary table S2, Supplementary Material online). However, the removal of interactions would be responsible for reducing the average connectivity; thus, we retained integrated networks in their entirety.

Expression Levels

E. coli RNA-seq data (of SRR794833, SRR794834, SRR794835, SRR794836, SRR794837 and SRR794838) were extracted from the Sequence Read Archive database (http://www.ncbi.nlm.nih.gov/sra). The reads were mapped to the corresponding reference genomes and RPKM values were estimated using Rockhopper (McClure et al. 2013). Previously assembled RNA-seq data of S. cerevisiae were used to estimate FPKM values (Nookaew et al. 2012). C. elegans and D. melanogaster RNA-seq data were downloaded from WormBase (http://www.wormbase.org/) and FlyBase (http://flybase.org/), respectively. We used average RPKM values for D. melanogaster and average FPKM values for C. elegans to assess transcript abundance.

Essentiality

We downloaded fitness data on E. coli and S. cerevisiae from the Integrated Fitness Information for Microbial Genes (IFIM; http://cefg.uestc.edu.cn/ifim) database (Wei and Ye et al. 2014). The S. cerevisiae datasets of SC01 and SC02 and E. coli of EC01 were estimated from experiments on single-gene deletion mutants. IFIM records the fitness upon the deletion of a gene, and we used these data (1 − deletion fitness) to estimate the essentiality effects.

Substitution Rates

Complete coding sequences of C. briggsae (release CB4), D. yakuba (release 1.04), S. mikatae (release 1.1) and S. typhimurium (NC_003197) were obtained from WormBase, FlyBase, the Saccharomyces Genome Database (http://www.yeastgenome.org/) and RefSeq, respectively. Orthologs of the coding sequences were identified by RBH from a BLASTP search with an E-value cut-off of 10 − 6, a minimum of 80% aligned residues, and 30% shared identity. We only retained orthologs for which the protein sequences matched their nucleotide sequences. Protein alignments were generated with ClustalW (Thompson et al. 1994) and then back-translated into nucleotide alignments based on their original nucleotide sequences. The numbers of substitutions per nonsynonymous site (Ka) and per synonymous site (Ks) were computed by PAML (Xu and Yang 2013).

Mutation Data

There are 33 sequenced MA datasets in the current version (v1.7) of the SMAL (http://cefg.uestc.edu.cn/smal) database (Wei and Ning et al. 2014). We integrated MA datasets: CELE1001/2/3/4 for C. elegans (598 mutated bases), DMEL1001/3/4 for D. melanogaster (936 mutated bases), SCER1001/2 for S. cerevisiae (298 mutated bases) and ECOL2001/2 for E. coli (1,857 mutated bases). The mutation rate of coding regions at each gene was estimated directly from MA lines.

Supplementary Material

Supplementary tables S1 and S2 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).

Supplementary Data
supp_8_8_2624__index.html (1KB, html)

Acknowledgments

This work was supported by the National Natural Science Foundation of China (grant numbers 31470068 and 31501063); Tianjin Natural Science Foundation of China (16JCQNJC09600); Sichuan Youth Science and Technology Foundation of China (2014JQ0051); Postdoctoral Science Foundation of China (2015M580211); Fundamental Research Funds for the Central Universities of China (ZYGX2015Z006 and ZYGX2015J144); and Sichuan Science and Technology Support Program (2015SZ0191).

Literature Cited

  1. Barabási AL. 2009. Scale-free networks: a decade and beyond. Science 325:412–413. [DOI] [PubMed] [Google Scholar]
  2. Capra JA, Pollard KS, Singh M. 2010. Novel genes exhibit distinct patterns of function acquisition and network integration. Genome Biol. 11:R127.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Chen SD, et al. 2012. Reshaping of global gene expression networks and sex-biased gene expression by integration of a young gene. Embo J. 31:2798–2809. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chen SD, Krinsky BH, Long MY. 2013. New genes as drivers of phenotypic evolution. Nat Rev Genet. 14:645–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chen SD, Zhang YE, Long MY. 2010. New genes in Drosophila quickly become essential. Science 330:1682–1685. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chen WH, Trachana K, Lercher MJ, Bork P. 2012. Younger genes are less likely to be essential than older genes, and guplicates are less likely to be essential than singletons of the same age. Mol Biol Evol. 29:1703–1706. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Hahn MW, Demuth JP, Han SG. 2007. Accelerated rate of gene gain and loss in primates. Genetics 177:1941–1949. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Kettler GC, et al. 2007. Patterns and implications of gene gain and loss in the evolution of Prochlorococcus. PLoS Genet. 3:2515–2528. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Langille MG, Hsiao WW, Brinkman FS. 2008. Evaluation of genomic island predictors using a comparative genomics approach. BMC Bioinformatics 9:329.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Liu HQ, Li Y, Irwin DM, Zhang YP, Wu DD. 2014. Integrative analysis of young genes, positively selected genes and lncRNAs in the development of Drosophila melanogaster. BMC Evol Biol. 14:241.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Lynch M. 2010. Evolution of the mutation rate. Trends Genet. 26:345–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Matsuno M, et al. 2009. Evolution of a novel phenolic pathway for pollen development. Science 325:1688–1692. [DOI] [PubMed] [Google Scholar]
  13. McClure R, et al. 2013. Computational analysis of bacterial RNA-Seq data. Nucleic Acids Res. 41:e140.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. McLysaght A, Baldi PF, Gaut BS. 2003. Extensive gene gain associated with adaptive evolution of poxviruses. Proc Natl Acad Sci U S A. 100:15655–15660. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Nookaew I, et al. 2012. A comprehensive comparison of RNA-Seq-based transcriptome analysis from reads to differential gene expression and cross-comparison with microarrays: a case study in Saccharomyces cerevisiae. Nucleic Acids Res. 40:10084–10097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Qin H, Lu HHS, Wu WB, Li WH. 2003. Evolution of the yeast protein interaction network. Proc Natl Acad Sci U S A. 100: 12820–12824. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Ross BD, et al. 2013. Stepwise evolution of essential centromere function in a Drosophila neogene. Science 340:1211–1214. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Szklarczyk D, et al. 2015. STRING v10: protein-protein interaction networks, integrated over the tree of life. Nucleic Acids Res. 43:D447–D452. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Thompson JD, Higgins DG, Gibson TJ. 1994. Clustal-W – improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 22:4673–4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Vishnoi A, Kryazhimskiy S, Bazykin GA, Hannenhalli S, Plotkin JB. 2010. Young proteins experience more variable selection pressures than old proteins. Genome Res. 20:1574–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Wei W, Ning LW, et al. 2014. SMAL: a resource of spontaneous mutation accumulation lines. Mol Biol Evol. 31:1302–1308. [DOI] [PubMed] [Google Scholar]
  22. Wei W, Ye YN, et al. 2014. IFIM: a database of integrated fitness information for microbial genes. Database bau052 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Weng JK, Li Y, Mo HP, Chapple C. 2012. Assembly of an evolutionarily new pathway for alpha-pyrone biosynthesis in Arabidopsis. Science 337:960–964. [DOI] [PubMed] [Google Scholar]
  24. Wolf YI, Novichkov PS, Karev GP, Koonin EV, Lipman DJ. 2009. The universal distribution of evolutionary rates of genes and distinct characteristics of eukaryotic genes of different apparent ages. Proc Natl Acad Sci U S A. 106:7273–7280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Xu B, Yang ZH. 2013. pamlX: a graphical user interface for PAML. Mol Biol Evol. 30:2723–2724. [DOI] [PubMed] [Google Scholar]
  26. Zhang JM, Dean AM, Brunet F, Long MY. 2004. Evolving protein functional diversity in new genes of Drosophila. Proc Natl Acad Sci U S A. 101:16246–16250. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Zhang WY, Landback P, Gschwend AR, Shen BR, Long MY. 2015. New genes drive the evolution of gene interaction networks in the human and mouse genomes. Genome Biol. 16:202.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Zhang YE, Vibranovski MD, Landback P, Marais GAB, Long M. 2010. Chromosomal redistribution of male-biased genes in mammalian evolution with two bursts of gene gain on the X chromosome. PLoS Biol. 8:e1000494.. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_8_8_2624__index.html (1KB, html)
supp_evw198_Table_S1.xls (115.5KB, xls)
supp_evw198_Table_S2.xls (30.5KB, xls)

Articles from Genome Biology and Evolution are provided here courtesy of Oxford University Press

RESOURCES