Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Sep 6;6:31921. doi: 10.1038/srep31921

Millimetre Wave with Rotational Orbital Angular Momentum

Chao Zhang 1,a, Lu Ma 1
PMCID: PMC5011649  PMID: 27596746

Abstract

Orbital angular momentum (OAM) has been widely studied in fibre and short-range communications. The implementation of millimetre waves with OAM is expected to increase the communication capacity. Most experiments demonstrate the distinction of OAM modes by receiving all of the energy in the surface vertical to the radiation axis in space. However, the reception of OAM is difficult in free space due to the non-zero beam angle and divergence of energy. The reception of OAM in the space domain in a manner similar to that in optical fibres (i.e., receiving all of the energy rings vertical to the radiation axis) is impractical, especially for long-distance transmission. Here, we fabricate a prototype of the antenna and demonstrate that rather than in the space domain, the OAM can be well received in the time domain via a single antenna by rotating the OAM wave at the transmitter, i.e., the radio wave with rotational OAM. The phase and frequency measured in the experiment reveal that for different OAM modes, the received signals act as a commonly used orthogonal frequency division multiplexing (OFDM) signal in the time domain. This phase rotation has promising prospects for use in the practical reception of different OAMs of millimetre waves in long-distance transmission.

Electro-magnetic (EM) waves have an angular momentum, which can be divided into a spin angular momentum and an orbital angular momentum (OAM) in paraxial beams1. The spin angular momentum is well known as the polarization that describes the intrinsic property of the spin characteristics of the EM rotational degrees of freedom2. In contrast, the OAM of the EM wave is an extrinsic property that describes the orbital characteristics of its rotational degrees of freedom, which has a helical transverse phase structure of exp(ilθ), where θ is the transverse azimuthal angle and l is an unbounded integer that indicates the OAM mode. Hence, the signals of an arbitrary OAM in a beam have the same carrier frequency, are mutually orthogonal, and propagate independently. This phenomenon can provide the benefits of transmission with a very high spectrum efficiency3.

Since its discovery in 1992 by Allen4, the optical vortex, i.e., light beams with helical phase fronts can carry OAM, has been widely studied in astronomy5, micromanipulation6, quantum state manipulation7,8, and other diverse applications9. Because optics and radio waves are basically EM waves, enlarging the range of OAM application in the free space propagated by radio wave is useful. The first radio OAM simulation was performed by B. Thidé in 2007, and the first real-world experiment was performed by Tamburini et al. in Venice in 201110,11. The experiment demonstrated that it is possible to simultaneously transmit and receive two incoherent radio waves encoded in two different OAM modes at the same frequency. Subsequently, several experiments on OAM at radio frequency have been conducted12,13,14. However, all of the simulations and experiments have revealed that the beam angle becomes larger with the increase in the OAM mode15. Even if convergent lenses are involved, the beam angle is definitely non-zero16. In an optical fibre, the problem of the beam angle increasing with the OAM mode shows less trouble due to the characteristic of the total internal reflection of fibre. Because all the OAMs should be received orthogonally, the entire energy of the fibre is received on the end face. Different OAMs with different coaxial rings are distributed on the end face17,18. Thus, different OAMs can be distinguished with different rings in the space domain. However, it is impractical for OAM radio waves to be propagated in free space. Without a boundary such as a fibre, the non-zero beam angle leads to an increasing radius of the required receiving energy ring in the intersection surface vertical to the radiation axis when the transmission distance increases. As a result, if we still want to utilize the traditional space domain reception method in a manner similar to that in the fibre, the aperture of the receiving antenna becomes extremely large, with the size increasing with the increasing beam angles, i.e., the OAM modes. This makes the reception of the OAM radio signals difficult in practice, especially for long-distance transmission19.

In this paper, to address the above reception problem of OAM millimetre waves, we propose to receive a portion of the signal in the time domain rather than receiving the whole energy in the space domain. Specifically, the idea is to rotate the OAM millimetre wave at the transmitter and receive it with a single antenna in a fixed location. Note that as revealed in our experiment, the rotation of the OAM wave in our scheme does not change the polarization. With the rotational OAM, a different OAM brings a different frequency shift in the receiving antenna, which finally maps different OAMs into different frequency shifts and obtains the orthogonal reception in the time domain. This approach will enable OAM millimetre wave signals to be applied in long-distance transmission. Note that in optical OAM transmission, similar rotational frequency shifts have been detected20,21 and analyzed22 with Laguerre-Gaussian (LG) beams. Moreover, for optical photons, the mathematical formulas are deduced from the relevant Schrodinger equations23. However, to our knowledge, the experiment and ascertainment of such rotational frequency shifts for millimetre waves have not been reported.

Results

Design method of a millimetre wave with a rotational OAM

The prototype experiment substantiates this significant assertion of our proposal. The conceptual transmission structure of the rotational OAM is illustrated in Fig. 1.

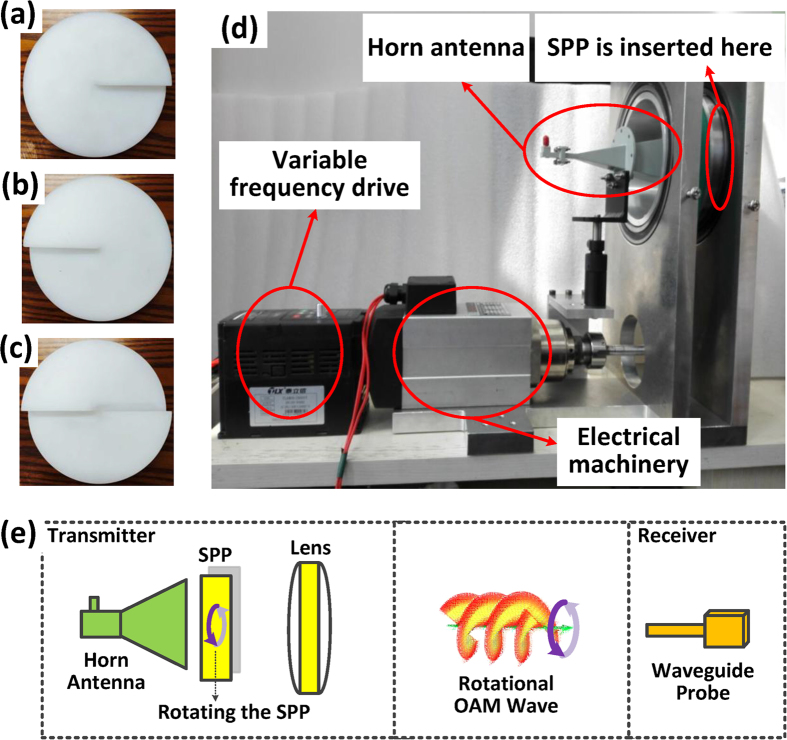
Figure 1. Transmission structure with a rotational OAM wave.

Figure 1

Open in a new tab

(a) Spiral phase plates with OAM l = −1. (b) Spiral phase plates with OAM mode l = +1. (c) Spiral phase plates with OAM mode l = +2. (d) The prototype of the transmitting antenna to generate the rotational OAM wave. (e) Schematic of the transmission with the rotational OAM wave.

Three spiral phase plates (SPPs) are considered in the experiments, as shown in Fig. 1a~c, i.e., mode −1, mode +1 and mode +2. The SPP is defined by its thickness, which varies azimuthally and results in the maximum thickness difference of Δh = lλ/(n −1) (n is the refractive index of the plate material, and λ is the wavelength of the EM wave)24. In the experiment, the thickness difference of the SPP is calculated as 16.4835 mm for a horn antenna with a centre frequency of 35 GHz and an antenna gain of 25 dB. These SPPs are used to generate EM waves with different OAMs. A prototype of the transmitting antenna to generate rotational OAM waves is fabricated as shown in Fig. 1d. Electrical machinery is used to rotate the SPP ahead of the horn antenna. The electric machinery is controlled by a variable-frequency drive for adjusting the rotational speed. Based on the rotational OAM wave, the transmission scheme is illustrated in Fig. 1e. In this scheme, an antenna is used to generate an OAM wave by putting an SPP ahead of a horn antenna. After generating the OAM wave, a rotation manipulation, which is achieved by rotating the SPP, is performed to rotate the wavefront of the OAM wave and thereby obtain the rotational OAM wave. Next, a lens is used to converge the radio beam and decrease the beam angle25,26. The SPP and the lens were fabricated with high density polyethylene (HDPE). At the receiving side, a single antenna located at the scope of the beam can be used to receive the signals.

Experiment 1: Phase measurements

Based on this rotation concept, the phase of the wave is measured in the microwave chamber. The experiment is illustrated in Fig. 2a and shown in Fig. 2b. The phase variations caused by rotating the OAM waves are measured in Fig. 2c. The data are obtained by unwrapping the corresponding measured periodic phase data (see Supplementary Information). A vector network analyser (VNA) set in the state of frequency sweep is used in experiment to record the phase data. The frequency is fixed at 35 GHz. The bandwidth and the number of measurement points are set as 100 Hz and 5000, respectively. The probe is fixed in the location of (x, y, z) = (30,0,300) mm, with the centre of the SPP as the origin. The rotational speed of the SPP is set as 0.3 (r/s). From Fig. 2c, we can observe the following:

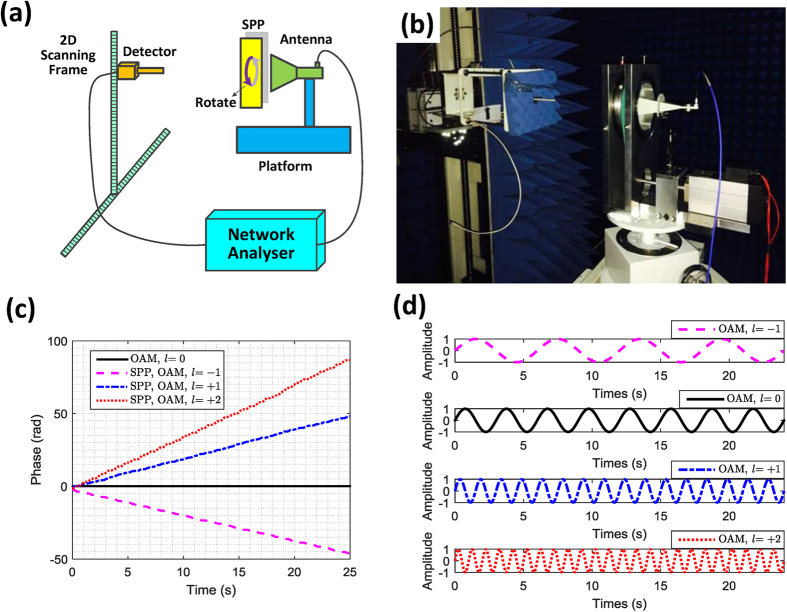
Figure 2. Phase measurements of the rotational OAM waves.

Figure 2

Open in a new tab

(a) Schematic illustration of the phase measurements experiment. (b) Picture of the experiment scenario. (c) The received phases of the rotational OAM wave with different OAM modes. (d) Illustration of the received orthogonal signals generated by the rotational OAM waves.

(1) With a fixed rotational speed, the direction of the phase variation caused by the two OAM waves with opposite modes is opposite, e.g., the blue line of mode +1 and the pink line of mode −1;

(2) With a fixed rotational speed, the frequency of the phase variation increases with the increasing OAM mode in equal proportion, e.g., the red line of mode +2 and the blue line of mode +1.

From this experiment, when rotating the phase of the OAM wave at the transmitter, it can be clearly deduced that a continuous phase mask will be added on the received signal for a fixed point on the receiver. The continuous variation of the phase, seen in Fig. 2c, corresponds to a sinusoidal signal modulated on the radio wave. This will cause a frequency shift in the radio wave at the receiver. Specifically, two OAM waves with opposite modes will result in opposite frequency shifts. With the same rotation speed, these frequency shifts caused by different OAM will be orthogonal to each other. This property is shown in Fig. 2d, where we add these three phase masks of Fig. 2c onto a sinusoidal signal with a period of 3 s. It can be seen that this manipulation results in three orthogonal sinusoidal signals with different periods of 6 s, 1.5 s and 1 s. For comparison, the reference signal of the OAM mode l = 0 with a period of 3 s is also plotted. Such effects will be further verified in the following experiment.

Experiment 2: Frequency measurements

The experimental platform is illustrated in Fig. 3a. The rotational OAM wave is generated by a horn antenna with a phase plate rotated by electrical machinery at the aperture. Two types of phase plates fabricated by HDPE are observed, i.e., SPP and step plate. The structures of the SPPs are the same as with experiment 1, and the structures of the step plates are shown in Fig. 3b. The phase profiles of these two types of phase plates detected in the microwave chamber are shown in Fig. 3c. At the receiver, a rectangular waveguide probe fabricated on a tripod is used to receive the signal and feed it to a spectrum analyser for frequency observation. The frequency and the amplitude are set as 35 GHz and 10 dBm, respectively, for the signal generator. The centre frequency and the frequency span are set as 35 GHz and 500 Hz, respectively, for the spectrum analyser.

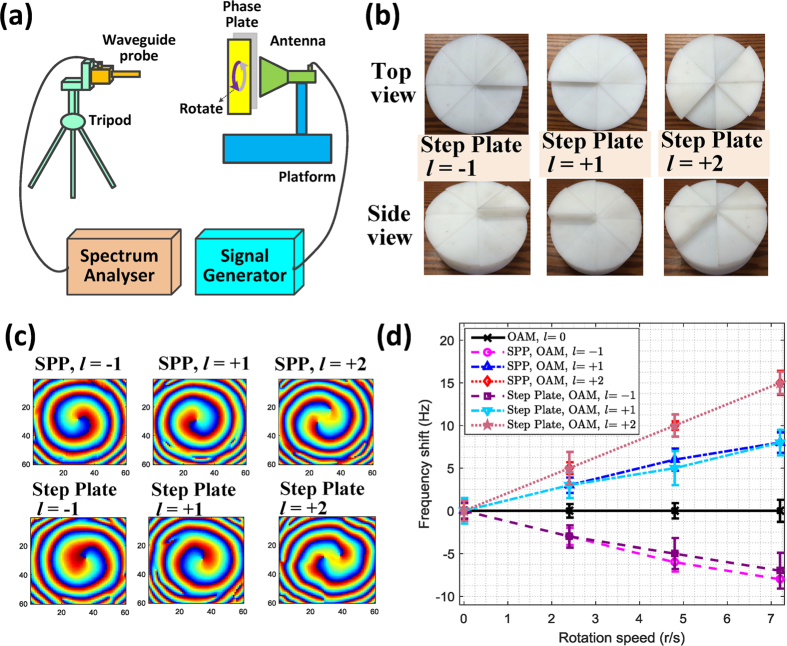
Figure 3. Frequency measurements of the rotational OAM waves.

Figure 3

Open in a new tab

(a) Schematic illustration of the frequency measurements experiment. (b) Step plates used in the experiments. (c) Phase profiles detected for two types of plates with different OAM modes. (d) The received frequency shifts of the rotational OAM wave with different OAM modes.

For a traditional radio wave, no frequency shift will occur at the receiving side when a plane wave is incident perpendicular to the rotational plane plate at the transmitting side, but for the radio wave with an OAM, the wavefront corkscrews along the propagation axis. When rotating the OAM wave, a frequency shift will occur. From Fig. 3d, we can observe the following:

(1) With the same rotational speed, the frequency shifts generated by the two OAM waves with an opposite mode are equal and opposite in direction, e.g., the blue line of mode +1 and the pink line of mode −1;

(2) With the same rotational speed, with the increasing of the OAM mode, the frequency shift will increase with equal proportion, e.g., the red line of mode +2 and the blue line of mode +1;

(3) For a specific OAM wave, the frequency shift increases with the rotational speed of the SPP;

(4) The step plate can generate OAM waves, and the same frequency shift can be observed when rotating the step plate;

(5) The frequency shift is caused by the rotational OAM wave rather than changes in the frequency of the transmitted radio wave. This shift is similar to the Doppler effect of the radio wave in the linear movement.

Compared with experiment 1, the consistency between the frequency shift effects in Fig. 3d and the phase variation in Fig. 2c can be revealed: the slope of the phase variation curve shown in Fig. 2c is indeed the frequency shift shown in Fig. 3d. According to the experiments, with the same rotation speed at the transmitter, a series of orthogonal frequencies can be received for the different transmitting OAM modes. This process is similar to an orthogonal frequency division multiplexing (OFDM) transmission scheme27. The difference is that no orthogonal carrier frequencies need to be generated, either for the transmitter or the receiver in the rotational OAM scheme, and the orthogonal frequencies are equivalent to the utilization of rotating different OAM modes.

Experiment 3: Polarization measurements

To verify that the frequency shift is caused by OAM rotation instead of the polarization rotation, the received polarization is measured. The experiment structure is illustrated in Fig. 4a. All configurations are the same as those used in experiment 1. The transmitting polarization direction is vertical (denoted as 0°), as shown in Fig. 4a. The polarization direction of the waveguide probe at the receiver is also vertical. To detect whether the received polarization is changed via rotational SPP, the waveguide probe is rotated to two additional directions, i.e., 45° and 90°. Three SPPs with OAM modes −1, +1 and +2, at a rotation speed of 2.4 (r/s), are measured as shown in Fig. 4b. At each polarization direction, 5000 points are measured and averaged. The maximal amplitude is found for the 0° polarization direction, which is the transmitting polarization direction; i.e., the polarization does not change with OAM rotation. If the polarization direction does change with the rotation of the SPP, due to symmetry, the amplitudes of 45° and 90° directions should be almost the same value as the amplitude of the 0° direction.

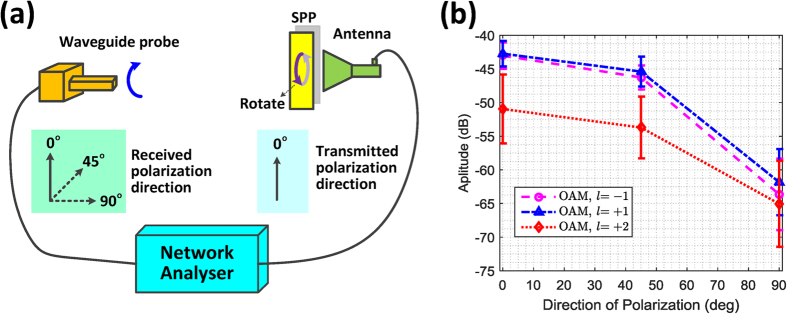
Figure 4. Polarization measurements of the rotational OAM waves.

Figure 4

Open in a new tab

(a) Schematic illustration of the experiment. (b) Polarization measurements at different received polarization directions.

Due to the system noise, there are measurement errors indicated by the error bars on Fig. 4b. We can find that the errors at the 90° direction are greater than those at 0° and 45° directions. This is because the received signal energy is minimal at the 90° direction, and the system noise dominates the error in this case. Moreover, since the divergence angle of the OAM wave increases with the OAM mode, the detected signal strength of OAM mode +2 is less than those of OAM mode +1 and −1 for a fixed detection point at the receiving side. Then, the errors of OAM mode +2 are greater than those of mode +1 and −1.

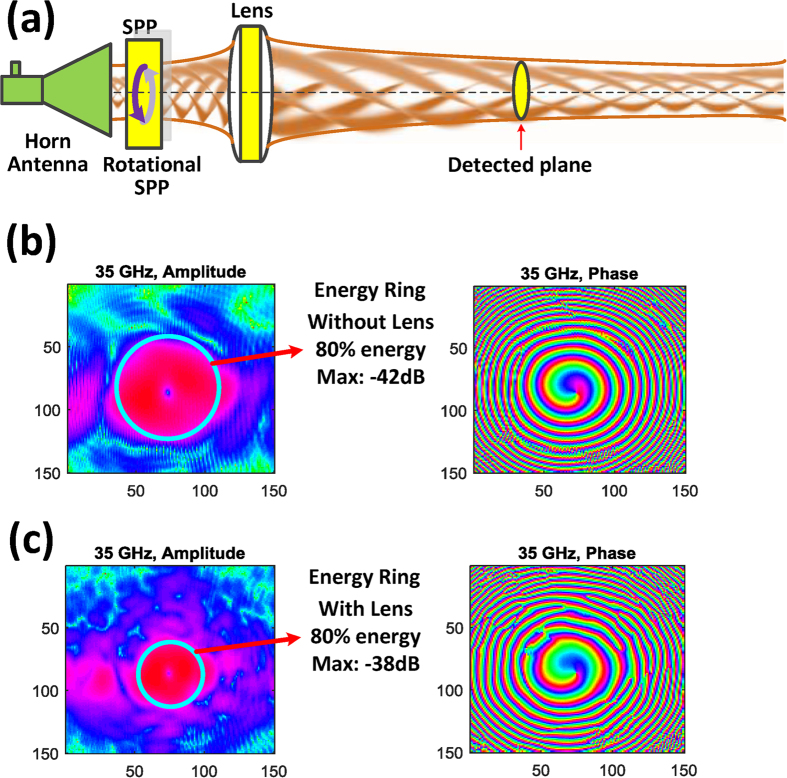
Experiment 4: Energy convergence

Because the radius of the energy ring of the OAM millimetre wave will diverge with the increase in the propagation distance, lens modules can be used to properly reduce the size of the beam. As shown in Fig. 5a, the focal length of the biconvex lens used in the experiment is set as 500 mm. Consider the beam angle after SPP: if the equivalent radio wave source is placed on the left focus, then the radio wave after the lens will be converged at infinity. Here, for simplicity, we set the equivalent source front of the left focus; in this case, the millimetre wave converges over a finite distance in the right side of lens. Comparing Fig. 5b,c, it can be seen that the energy of the OAM wave can indeed be converged by the lens. This observation is true for all OAM modes. Thus, for long-distance transmission with different OAM modes, the lens can be used to properly reduce the size of the beam energy at the transmitter, and a common antenna located in the beam can be used for signal reception.

Figure 5. Measurements with a lens to focus the beam energy.

Figure 5

Open in a new tab

(a) Schematic illustration of the focusing system. (b) The measured energy and phase without a lens. (c) The measured energy and phase with a lens.

The proposed method of rotating the radio wave with OAM leads to the concept of receiving the OAM signal in the time domain instead of the space domain. This concept is a promising method for long-distance communication. This proposed method does not require that the entire energy ring be received in the intersection surface vertical to the radiation axis, as is the case in optical fibre OAM transmission. In the proposed method, only a portion of the energy ring must be obtained; i.e., a common antenna such as a dipole antenna or a horn antenna can be used at the receiver to receive the signal. Furthermore, such rotational OAM radio waves can be expected to be applied in many fields, such as near-Earth and deep-space communications28,29,30, navigation and astronomy31,32, radar detection and imaging33,34. Large aperture antennas and arrays, such as Cassegrain antennas, parabolic antennas and even phased-array antennas, can be used.

Discussion

In our experiments, the method is realized by rotating an SPP mechanically. However, the method can also be implemented using a fixed antenna array, such as a phased-array antenna. In this case, for a specific OAM mode, the phase difference among the antennae will rotate azimuthally around the array. At the transmitter, assume that there are 8 elements equally spaced on the circular array and marked from 1 to 8. The phases, i.e., 0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315°, will be fed into the elements marked from 1 to 8, respectively. When performing phase rotation, the phase feed into each element will vary azimuthally around the array. Take element 1 and 2 as examples. Phase 0° and phase 45° will be fed into elements 1 and 2, respectively, when they are stationary. When phase rotation is performed, phase 0° will be fed into element 2, and phase 315° will be fed into element 1. The rest of the elements can be treated in the same manner. In this case, with the rotation method on the feed phase, a phase mask will be added on the transmitted signal for each OAM mode. The detailed scheme can be further developed.

Methods

To observe how the rotation manipulation will affect the OAM wave, we first measured the phase pattern of the radiation field for the SPP at 8 different azimuth angles, i.e., 0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315°. Three SPPs with OAM modes of −1, +1 and +2 are measured in the experiment. Using these data, we find that for a fixed point of the phase pattern, the frequency of phase variation differs with the OAM mode. This result inspired us to hypothesize that when rotating the SPP, the phases detected by a fixed point at the phase pattern will vary continuously and periodically. Moreover, the varying frequency will be different for different OAM modes. Thus, we used electrical machine to rotate the SPP and set the vector network analyser to the state of frequency sweep. The frequency was fixed at 35 GHz, the bandwidth was set at 100 Hz and the number of measurement points was set as 5000. In this case, the phase variation curves with different OAM modes were plotted, as shown in Fig. 2c. These curves revealed that when rotating the SPP, a phase mask will be generated. This inspired us to consider whether such consecutive phase masks would affect the radio frequency. Thus, in this context, we conducted an experiment to measure the received frequency, as shown in Fig. 3a and the measurements were plotted, as shown in Fig. 3d. Further, to verify that the frequency shift is caused by the OAM rotation instead of the polarization rotation, the received polarization direction was measured, as shown in Fig. 4.

In our experiments, the machining precision of the mechanical structure with numerically-controlled machine tool is 0.1 mm. We established the simulation with the corresponding errors added on the coordinates of the transmitting antenna and found that these errors had almost no effect on the measured phases and frequency shifts. Moreover, to verify whether mechanical vibrations will affect the proposed millimetre wave transmission and receiving, the acceleration of vibration were measured using tri-axis accelerometers of model 356A16 manufactured by PCB Piezotronics Inc. (see the sensors deployment in Supplementary Information). The calculated effective values of vibrations were no more than 0.1 mm in all the three directions. This revealed that the mechanical and other vibrations had hardly effect on the measured phases and frequency shifts.

Additional Information

How to cite this article: Zhang, C. and Ma, L. Millimetre Wave with Rotational Orbital Angular Momentum. Sci. Rep. 6, 31921; doi: 10.1038/srep31921 (2016).

Supplementary Material

Supplementary Information
srep31921-s1.pdf (749.6KB, pdf)

Acknowledgments

We thank the National Key Lab of Microwaves and Digital Communications in Dept. of Elec. Engr., Tsinghua Univ., for providing the experimental instruments and the microwave anechoic chamber. This research is sponsored by China Innovation Fund for Aerospace Science and Technology, China PLA Fund, as well as Tsinghua University Initiative Scientific Research Program.

Footnotes

Author Contributions Prof. C.Z. proposed the concept and conducted the experiment. Mr. L.M. proved the concept with designing and carrying out the detailed experiments. All authors performed the theoretical, numerical analyses and analyzed the experimental data. All authors contributed to writing and finalizing the paper.

References

  1. Poynting J. H. The wave motion of a revolving shaft, and a suggestion as to the angular momentum in a beam of circularly polarized light. Pro. R. Soc. Lond. A 82, 560–567 (1909). [Google Scholar]
  2. Beth R. Mechanical detection and measurement of the angular momentum of light. Phys. Rev. 50, 115–125 (1936). [Google Scholar]
  3. Wang J. et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nature Photonics 6, 488–496 (2012). [Google Scholar]
  4. Allen L., Beijerbergen M. W., Spreeuw R. J. C. & Woerdan J. P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian modes. Phys. Rev. A 45, 8185–8190 (1992). [DOI] [PubMed] [Google Scholar]
  5. Foo G. et al. Optical vortex coronagraph. Opt. Lett. 30, 3308–3310 (2005). [DOI] [PubMed] [Google Scholar]
  6. Grier D. G. A revolution in optical manipulation. Nature 424, 810 (2003). [DOI] [PubMed] [Google Scholar]
  7. Mair A., Vaziri A., Weihs G. & Zeilinger A. Entanglement of the orbital angular momentum states of photons. Nature 412, 313 (2001). [DOI] [PubMed] [Google Scholar]
  8. Andersen M. F. et al. Quantized rotation of atoms from photons with orbital angular momentum. Phys. Rev. Lett. 97, 170406 (2006). [DOI] [PubMed] [Google Scholar]
  9. Franke-Arnold S., Allen L. & Padgett M. Advances in optical angular momentum. Laser Photon. Rev. 2, 299–313 (2008). [Google Scholar]
  10. Thidé B. et al. Utilization of photon orbital angular momentum in the low-frequency radio domain. Phys. Rev. Lett. 99, 087701 (2007). [DOI] [PubMed] [Google Scholar]
  11. Tamburini F. et al. Encoding many channels on the same frequency through radio vorticity: first experimental test. New J. Phys. 14, 033001 (2012). [Google Scholar]
  12. Cheng L., Hong W. & Hao Z.-C. Generation of electromagnetic waves with arbitrary orbital angular momentum modes. Scientific Reports 4, 4814 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Yan Y. et al. High-capacity millimetre-wave communications with orbital angular momentum multiplexing. Nature Comm. 5, 4876 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hui X. et al. Multiplexed millimeter wave communication with dual orbital angular momentum (OAM) mode antennas. Scientific Reports 5, 10148 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Oldoni M., Spinello F., Mari E. et al. Space-division demultiplexing in orbital-angular-momentum-based MIMO radio systems. IEEE Trans. Antennas Propag. 63, 4582–4587 (2015). [Google Scholar]
  16. Dorn R., Quabis S. & Leuchs G. Sharper focus for a radially polarized light beam. Phys. Rev. Lett. 91, 233901 (2003). [DOI] [PubMed] [Google Scholar]
  17. Dashti P. Z., Alhassen F. & Lee H. P. Observation of orbital angular momentum transfer between acoustic and optical vortices in optical fiber. Phys. Rev. Lett. 96, 043604 (2006). [DOI] [PubMed] [Google Scholar]
  18. Shuhui L. et al. Controllable all-fiber orbital angular momentum mode converter. Opt. Lett. 40, 4376–4379 (2015). [DOI] [PubMed] [Google Scholar]
  19. Mohammadi S. M. et al. Orbital angular momentum in radio - a system study. IEEE Trans. Antennas Propag. 58, 565–572 (2010). [Google Scholar]
  20. Basistiy I. V. et al. Manifestation of the rotational Doppler effect by use of an off-axis optical vortex beam. Optics Lett. 28, 1185–1187 (2003). [DOI] [PubMed] [Google Scholar]
  21. Vasnetsov M. V. et al. Observation of the orbital angular momentum spectrum of a light beam. Optics Lett. 28, 2285–2287 (2004). [DOI] [PubMed] [Google Scholar]
  22. Anzolin G. et al. Method to measure off-axis displacements based on the analysis of the intensity distribution of a vortex beam. Phys. Rev. A 79, 1039–1044 (2009). [Google Scholar]
  23. Andrews David, L. & Babiker M. The Angular Momentum of Light. Cambridge University Press, 115–125 (2012). [Google Scholar]
  24. Turnbull G. A. et al. The generation of free-space Laguerre-Gaussian modes at millimetre-wave frequencies by use of a spiral phaseplate. Optics Comm. 127, 183–188 (1996). [Google Scholar]
  25. Kun H. et al. Vector-vortex Bessel–Gauss beams and their tightly focusing properties. Optics Lett. 36, 888–890 (2011). [DOI] [PubMed] [Google Scholar]
  26. Youngworth K. & Brown T. Focusing of high numerical aperture cylindrical-vector beams. Opt. Ex. 7, 77–87 (2000). [DOI] [PubMed] [Google Scholar]
  27. Wong C. Y. et al. Multiuser OFDM with adaptive subcarrier, bit, and power allocation. IEEE J. Sel. Areas Commun. 17, 1747–1758 (1999). [Google Scholar]
  28. Djordjevic I. B. Deep-space and near-Earth optical communications by coded orbital angular momentum (OAM) modulation. Opt. Ex. 19, 14277–14289 (2011). [DOI] [PubMed] [Google Scholar]
  29. Wang X. et al. Potential of vortex beams with orbital angular momentum modulation for deep-space optical communication. Opt. Eng. 53, 056107 (2014). [Google Scholar]
  30. Djordjevic A. I. B. Orbital angular momentum (OAM) based LDPC-coded deep-space optical communication. SPIE LASE 7923, 792306 (2011). [Google Scholar]
  31. Elias N. M. Photon orbital angular momentum in astronomy. Astron. Astrophys. 492, 883–992 (2008). [Google Scholar]
  32. Uribe-Patarroyo N. et al. Detecting photons with orbital angular momentum in extended astronomical objects: application to solar observations. Astron. Astrophys. 526, 202–207 (2011). [Google Scholar]
  33. Oesch D. W., Sanchez D. J. & Matson C. L. The aggregate behavior of branch points - measuring the number and velocity of atmospheric turbulence layers. Opt. Ex. 18, 22377 (2010). [DOI] [PubMed] [Google Scholar]
  34. Lavery M. P. J. et al. Detection of a spinning object using light’s orbital angular momentum. Science 341, 537–540 (2013). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep31921-s1.pdf (749.6KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES