Abstract
Numerical simulations of mantle convection with a viscoplastic rheology usually display mobile, episodic or stagnant lid regimes. In this study, we report a new convective regime in which a ridge can form without destabilizing the surrounding lithosphere or forming subduction zones. Using simulations in 2‐D spherical annulus geometry, we show that a depth‐dependent yield stress is sufficient to reach this ridge only regime. This regime occurs when the friction coefficient is close to the critical value between mobile lid and stagnant lid regimes. Maps of convective regime as a function of the parameters friction coefficients and depth dependence of viscosity are provided for both basal heating and mixed heating situations. The ridge only regime appears for both pure basal heating and mixed heating mode. For basal heating, this regime can occur for all vertical viscosity contrasts, while for mixed heating, a highly viscous deep mantle is required.
Keywords: convection regime, ridge only, viscoplastic, depth dependent, yield stress
Key Points
Stable ridges can appear in the lithosphere without generating subduction zones
A depth‐dependent yield stress is necessary to obtain stable ridges
This “ridge only” regime can be found between stagnant and mobile lid regimes
1. Introduction
The terrestrial planets and the satellites of the solar system display a large variety of enigmatic large‐scale surface features [Schubert et al., 2001]. Numerical simulations of thermal convection have shown that planets form a thick undeformable lithosphere called a “stagnant lid” when a strongly temperature‐dependent viscosity is used [Solomatov, 1995], as indicated by experimental data [Kohlstedt, 2007]. It has been demonstrated that the consideration of plasticity is sufficient to obtain models in which the lithosphere can deform and potentially form plates as we observe on Earth, due to the high stress typically reached in the cold surface regions [Moresi and Solomatov, 1998; Trompert and Hansen, 1998; Tackley, 2000a; Stein et al., 2004]. The term “mobile lid” is often used to describe a simulation in which the lithosphere deforms and resurfaces, independent whether this occurs continuously or not. Different surface expressions of mobile lid regimes can be found, and two major regimes have been documented. First, in the “plate‐like” regime, the lithosphere is continuously recycled back into the mantle. Second, in the “episodic” regime, the lithospheric stresses are sufficient to break the lid only when it is very thick and parts or the whole lithosphere can suddenly resurface [Moresi and Solomatov, 1998; Stein et al., 2004]. Up to now, only stagnant, plate‐like and episodic regimes were reported for viscoplastic simulations.
Yet the global behavior of the mantle and lithosphere of convecting bodies such as the resurfacing of Venus [Fowler and O'Brien, 1996, 2003; Noack et al., 2012; Rozel, 2012; Armann and Tackley, 2012] or plate tectonics on Earth [Tackley, 2000a, 2000b; Bercovici et al., 2000; Ogawa, 2003; Stein et al., 2004] cannot always be fully reproduced. A long list of potentially crucial mechanisms that should be considered in studies of thermomechanical convection can be compiled: melting [Korenaga, 2009], water circulation [Hirth and Kohlstedt, 2003; Kohlstedt, 2007], viscoelastoplasticity of the lithosphere [Burov, 2007], shear heating [Bercovici and Karato, 2003; Burg and Schmalholz, 2008; Thielmann and Kaus, 2012], nonlinear rheologies [Christensen, 1983; Bercovici, 1995], damage [Bercovici et al., 2001; Ricard and Bercovici, 2009], generation of geochemical reservoirs [Tackley, 2007], the presence of continental crust [Rolf and Tackley, 2011], etc. Incorporating all these complexities in numerical simulations is challenging [Zhong et al., 2007]. Also, complex simulations make it difficult to identify the dominant mechanism involved. Therefore, we explore here the space of convective regimes using a simple model considering only depth‐dependent plastic yielding. We show that a convection state, which we term “ridge only” (RO), first observed by Tackley [2000a] in 3‐D Cartesian geometry using a depth‐dependent yield stress, can develop for a considerable range of parameters.
2. Setup
We assume a 2‐D spherical annulus geometry [Hernlund and Tackley, 2008]. The Prandtl number is considered to be infinite [e.g., Schubert et al., 2001], and the convecting material is assumed to be incompressible under the Boussinesq approximation. The dimensionless equations of conservation of momentum, mass, and energy are [e.g., Schubert et al., 2001]
| (1) |
| (2) |
| (3) |
where τ is the deviatoric stress tensor, P is the pressure, R a b is the bottom Rayleigh number, T is the temperature (between 0 and 1), z is the downward pointing unit vector, v is the velocity of the fluid, t is time, and H is the internal radiogenic heating rate.
The bottom Rayleigh number is defined as
| (4) |
where α is the thermal expansivity, ρ the density, g the gravity, ΔT the temperature contrast, h the depth of the computational domain, κ the thermal diffusivity, and η ref is a reference viscosity.
Since we solve dimensionless equations, manipulating several dimensional parameters can result in the same Rayleigh number. This enables the activity of the RO regime on various types of planetary objects to be studied. The bottom Rayleigh number used in this study is 5·107, and for mixed heated cases we use a dimensionless internal heat production rate of H = 10.
The viscosity is both temperature and depth dependent:
| (5) |
where is the dimensionless depth (from 0 to 1) and V is a dimensionless activation volume. The dimensionless activation energy is set to 41.4465 to generate 9 orders of magnitude of viscosity contrast (for an activation volume equal to zero). Lower and upper viscosity cutoffs allow for a total viscosity contrast of 24 orders of magnitude. Yet the definition of the rheology (equation (7)) is such that the viscosity cutoffs are never reached. The core size is set to 1.5 times the mantle thickness. Basally and mixed heating cases are tested for various activation volumes and various values of the friction coefficient f, which represents the depth dependence of the yield stress τ y:
| (6) |
where z is the dimensional depth. When the stress is below τ y, deformation is fully ductile. When stresses are too high, τ y is used to decrease the viscosity, such that the effective stress is equal to the yield stress. The effective viscosity becomes
| (7) |
where is the strain rate. This formulation ensures a smooth transition from ductile to brittle deformation.
The conservation equations (1)–(3) are solved using a finite volume formalism on a staggered grid [Harlow and Welch, 1965], using the convection code StagYY [Tackley, 1993, 2008]. The grid is refined in radial direction in the top and bottom boundary layers. A grid of 64 times 512 nodes in radial and angular direction has been found to provide a satisfactory resolution throughout the whole set of simulations. For the present calculations, the direct solver UMFPACK is used [Davis, 2004] and is accessed using the PETSc toolkit [Balay et al., 2012] (http://www.mcs.anl.gov/petsc) to obtain velocity, pressure, and temperature fields. The temperature equation is solved using the fully implicit Crank‐Nicolson method. Twenty‐eight simulations were performed assuming basal heating only, and 75 simulations considered mixed heating (both basal and internal heating). Additional simulations in 2‐D Cartesian geometry are provided in the supporting information. Since history‐dependent convective regimes have been reported in previous studies [Weller and Lenardic, 2012], we provide the initial temperature field in the supporting information. All our simulations started with a top thermal boundary layer, an internal temperature equal to the core temperature, and some white noise.
3. Results
In both sets of simulations—basally heated and mixed heated—we observe either the mobile lid, RO, or stagnant lid regimes, depending on the vertical viscosity contrast induced by the activation volume of the rheology and on the friction coefficient. The RO regime always appears at the boundary between stagnant lid and mobile lid regimes, where the presence of the episodic regime was reported previously [Moresi and Solomatov, 1998; Stein et al., 2004].
Figure 1 depicts two examples of the RO regime, obtained in a basally heated case (above the dashed line, using V = 3.4012 and f = 0.14) and in a mixed heated simulation (below the dashed line, using V = 18.4207 and f = 0.4). Green arrows point at the respective ridge. Snapshots in Figures 1a–1d show the temperature, viscosity, root‐mean‐square velocity, and stress fields for the basally heated simulation. Figures 1e and 1f display the temperature and viscosity fields in the mixed heated case only. Plots of the second invariant of the 2‐D strain rate fields are provided for both cases in the supporting information. We depict an example for both heating situations since they represent two different kinds of RO regime (see the discussion for details).
Figure 1.
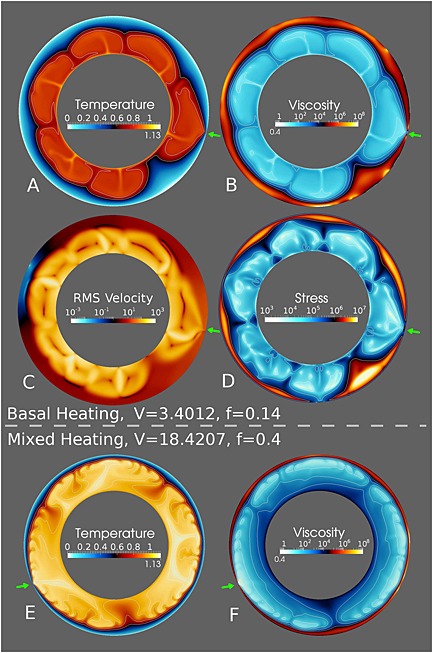
(a–d) Dimensionless temperature, viscosity, velocity, and stress fields obtained in the simulation using the parameters: V = 3.4012 and f = 0.14, in the 2‐D spherical annulus geometry with basal heating. (e and f) Dimensionless temperature and viscosity fields in a mixed heating case using V = 18.4207 and f = 0.4. Green arrows point at the ridges. See section 3 for a detailed description.
To our knowledge, this specific regime, which does not result in the formation of subduction zones and lithosphere resurfacing, was previously reported only by Tackley [2000a], where its dynamics were compared to the sluggish lid regime [Solomatov, 1995]. In both basally and mixed heated cases, RO is present when the convective degree reaches sufficient stability, although convection does not necessarily have to be stationary. Thus, this regime can appear after a certain global equilibration time, usually when the internal temperature of the convecting domain is about to stabilize or is actually stable. Figure 1 indicates that the basal heating case converged to degree 6 and that the mixed heating case displays a degree 3. Figure 1 shows that under these conditions the gathering downwellings tend to be viscous enough to connect the sloping bottom of the lithosphere to the very viscous deep interior (see the dark areas in Figures 1d and 1f). Apart from the existence of the ridge structure itself, the RO regime is very similar to the stagnant lid regime, with moderate internal stresses and higher stresses in the lithosphere. Figures 1a and 1e show that large upwellings generate very localized ridges, without yielding the top boundary layers of the two corresponding convection cells, as it usually happens in the mobile lid regime. Figure 1c reveals that the ridge generates a weak velocity field in the surrounding lithosphere, with velocities 10 times slower than the internal velocities (yellow) throughout the entire lid (see blue, black, and red areas). This corresponds to a compressional horizontal stress field which instantaneously follows the location of the ridge wherever it appears. The deformation of the lithosphere surrounding the ridge is limited, and the lithosphere remains stable. Finally, although Figure 1b depicts a very thick and viscous downwelling next to the ridge, Figures 1e and 1f show that such a structure is not necessary to obtain the RO regime. The RO regime appears in certain cases long after the stabilization of the stagnant lid regime, when several plumes happen to gather and are sufficiently strong to pierce through the lithosphere.
Figure 2 depicts the top Nusselt numbers of five simulations using identical activation volume (V = 3.4012), but different friction coefficients (ranging from 0.1 to 0.2), all purely basally heated. Plots of both a RO and a mobile lid case (showing episodic resurfacing) are also shown in the same figure, for moments in time displaying strong variations of the top Nusselt number (Figures 2a to 2e). Horizontal profiles for both the surface velocity and the Nusselt number are provided in the supporting information. In the mixed heated simulations, all bottom Nusselt numbers of RO and stagnant lid cases are between −1 and 2. The top Nusselt numbers are between 10 and 13. These simulations can be considered fully internally heated to first order since the basal heat flux is significantly smaller than the surface heat flux.
Figure 2.
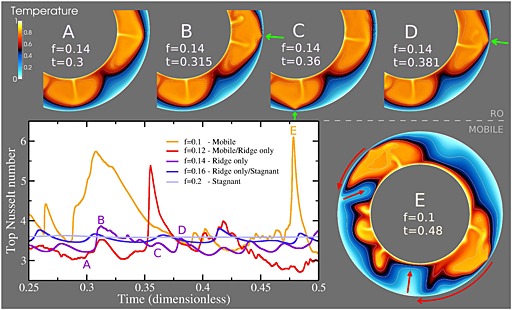
(a–d) Temperature time series displaying an oscillating ridge for a model in RO regime. Green arrows point at the ridge structure. (e) An example of a resurfacing event for a model in the mobile lid regime (see red arrows). (bottom left) Top Nusselt numbers obtained for cases assuming basal heating using V = 3.4012. The temperature fields (see Figures 2a–2e) correspond to important times in the Nusselt number plot.
Figure 2 (bottom left) shows that the top Nusselt number for RO and stagnant lid regimes are comparable, although variations of 20% can be observed for the RO regime (comparing blue, light blue, and violet curves). The local increase of heat flux above the ridge is very high, due to the temperature gradient at the ridge (see supporting information). The temperature fields in Figures 2a to 2d show that the position of the ridge alternates between preferential sites (see green arrows), causing the Nusselt number oscillations of the purple curve. The simultaneous presence of two ridges has only been observed in mixed heating simulations, when considering the largest vertical viscosity contrast. This always occurs for cases on the convective regime map close to the border of the mobile lid regime. On the other hand, for RO cases close to the stagnant lid regime, the single ridge remains stationary. However, close to the mobile lid regime the ridge position alternates remarkably quickly between preferential sites. For comparison, the orange and red curves show the top Nusselt numbers for simulations in which resurfacing events occur.
Figure 2e illustrates the resurfacing events observed for the episodic regime (see the red circular arrows) and the associated broad downwellings dragging the destabilized lithosphere into the deep mantle (red arrows inside the domain). This shows that the mobile lid regime can assume very exotic forms, distinct from the classical plate tectonics regime. The top right part of the spherical annulus seems to be temporarily in a diffusive state, while three new plumes appear at the bottom left. This coexistence of low and high convective activities is due to both the absence of radiogenic heating and the depth dependence of the rheology, as reported, for example, in Christensen [1983]. Figures 2b–2e clearly show that the main difference between RO and mobile lid regimes is the lack of horizontal mobility of the lithosphere, while the internal activity is comparable.
Figure 3 shows the convective regimes obtained for all simulations, for both (top) basally heated and (bottom) mixed heated conditions. The vertical viscosity contrast plotted on the y axis represents the viscosity contrast caused by the activation volume V only (the temperature dependence is excluded here):
| (8) |
Figure 3.
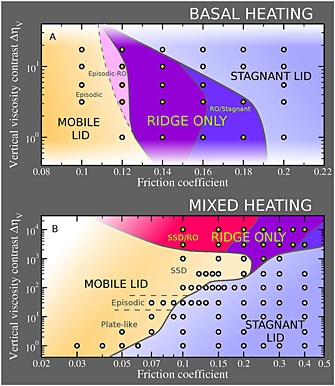
Convective regimes obtained at statistical equilibrium for (top) basally heated and (bottom) mixed heated simulations. Black circles represent the simulations (circles filled green represent the RO regime). The background colors depict in more detail the regime boundaries obtained: orange and pink represent mobile lid, light blue represents stagnant lid, and darker colors stand for RO/mobile lid (red), RO regime (purple), and stagnant/RO regime (blue). White blending is used to emphasize the lack of data in certain areas. “SSD” stands for “Slow Stationary Downwellings” (see text).
For basally heated cases the RO regime is always obtained at the boundary between stagnant and mobile lid regimes. For mixed heated cases, the RO regime is absent when small vertical viscosity contrasts are applied, but it occurs for a wide range of parameters in cases where a large vertical viscosity contrast is prescribed. As expected, the stagnant lid regime was always observed when considering large friction coefficients.
Figure 3 displays a large variety of convective states in the mobile and RO regimes. In basally heated cases, the plate‐like behavior was never observed because of the low internal temperature and plates being too thick and viscous. Thus, only the episodic regime displayed in Figure 2 can be reached (yellow area in Figure 3, top). The pink area in Figure 3 (top) represents simulations in which the RO regime was observed, but resurfacing events can occur at locations far from the ridge and therefore have no direct link to the already present ridges. We classify this state as being part of the mobile lid regime since resurfacing events occur but ridges without related subduction zones were observed. In mixed heating cases (Figure 3, bottom), plate‐like behavior was observed at low‐viscosity contrasts and the episodic regime was reached in the simulations considering a vertical viscosity contrast of 30. Vertical viscosity contrasts larger than 30 always lead to a state showing slow stationary downwellings (labeled “SSD” in Figure 3) that stabilize convection, which can no longer be considered to be episodic (see supporting information for a description).
The red area (SSD/RO) in Figure 3 represents simulations in which large and slow downwellings are stabilized but one or several RO features occur. The purple areas in both panels of Figure 3 represent the simulations in which the RO regime is fully stationary and no resurfacing events occur at equilibrium. The deep blue regions stands for simulations in which stagnant lid and RO regimes alternate through time. The two regimes are successively active because of changes in the convection degree in the internal region. The RO regime is the equilibrium state of a given degree, but the appearance of an additional convection cell, which reduces the stress state in the lithosphere, brings the regime back to stagnant lid regime. Yet the additional cell is no longer stable in the stagnant lid and disappears again. This allows the largest cells to pierce through the lithosphere and to reestablish the RO regime.
4. Discussion
For the basally heated cases our results show that an increasing vertical viscosity contrast results in a transition from the RO to the stagnant lid regime (see Figure 3a). However, this is not the case for mixed heating cases (see Figure 3b), where the RO regime can also occur for the largest vertical viscosity contrast considered in our study. This difference in behavior is caused by the higher temperatures that can be observed in the latter case (compare Figures 1a and 1e), enabling the formation of sufficiently strong plumes able to penetrate the lid locally. This difference in internal temperature between basally and mixed heating cases also explains why we only investigated Δη V = 20 in the first situation and up to Δη V = 104 in the latter case. For basally heated simulations, a nonnegligible activation volume results in a large viscosity at the base of the mantle forming a thick bottom boundary layer, which tends to insulate the mantle from the core, thus decreasing its temperature. In mixed heated cases, internal heating prevents the mantle from reaching such low temperatures. In basally heated cases the effective Rayleigh numbers typically range between 5·105 (at large vertical viscosity contrast) and 7·106 (at small vertical viscosity contrast). In mixed heating cases, the effective Rayleigh number varies between 5·105 and 108. As discussed in the previous section the lithosphere is stable in the RO regime without occurrence of resurfacing events. Therefore, the thickness of the lithosphere in these models is only limited by the presence of plumes at nearly stationary locations eroding the bottom of the lid.
For both heating scenarios studied here the RO regime can only occur when the lower mantle is viscous enough to prevent the lithosphere from yielding. When we consider a locally thicker region of lithospheric material (see, e.g., Figure 1), its sinking into the mantle can be treated as a Rayleigh‐Taylor instability. Since the growth rate of such an instability is dependent on both the viscosity of the underlying mantle and of the lithosphere itself [Turcotte and Schubert, 2014], a high viscosity in both regions will result in negligible growth rates, thus effectively holding the thickened lithosphere in place. In basally heated cases, the viscosity is large enough to achieve this state, even without any vertical viscosity contrast, due to the low internal temperature (Figures 1a and 1b). In mixed heated cases, it seems that the vertical viscosity contrast helps to halt potential instabilities that could result in lithosphere resurfacing events, even if the internal temperature is high (Figures 1e and 1f).
Thus, the RO regime can be expected in convecting bodies at relatively low Rayleigh number when internal heating is absent, as it might be the case, for example, in icy satellites. In rocky planets or satellites that have significant internal heating, our models show that a large vertical viscosity contrast (of more than a factor 100) is needed to reach this state. Whether or not large internal vertical viscosity contrasts are to be expected in large exoplanets is still under debate [Karato, 2011; Stein et al., 2011; Stamenković et al., 2012; Tackley et al., 2013]. Since vertical internal viscosity contrasts of at least 2 orders of magnitude are nowadays considered to be required to model the Earth [C̆íz̆ková et al., 2012], one could expect the RO regime to be at least active in Earth‐ or Venus‐sized planets, when their internal cooling brings them close to the transition between plate tectonics to stagnant lid.
Additional complexities such as melting, neglected in this study, might change this result and drive the convecting body toward the episodic regime, as it occurred in the case of Venus [Johnson and Richards, 2003]. Furthermore, the RO regime has only been observed using depth‐dependent yielding. Additional studies are required to characterize under what conditions the episodic regime or the ridge‐only regime can be expected to occur in between mobile lid and stagnant lid regimes.
5. Conclusion
A singular convective state called the “ridge‐only” regime, in which one or two ridges can form in an otherwise stagnant lid, is shown to exist in the regime diagram between stagnant and mobile lid regimes, when we consider a viscoplastic rheology with a yield stress proportional to depth. We show that the lid does not deform significantly when such a ridge appears. We observe that single ridges can oscillate between preferential sites but rarely coexist with a second one, with the exception of mixed heating cases considering a large vertical viscosity contrast. Two regime maps are provided for basally and mixed heating situations. The new convection regime presented in this paper can be expected to occur in Earth‐sized (or larger) planets or in icy satellites.
Supporting information
Table S1
Readme
Text S1, Captions of Table S1 and Movie S1, and Figures S1–S4
Movie S1
Acknowledgments
The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007‐2013) / ERC Grant Agreement 320639 project iGEO. All data used to produce the results of this article are provided in the supporting information. For more information, feel free to contact the corresponding author using the email address provided in this article. The author thank the two anonymous reviewers for their very helpful feedback.
The Editor thanks two anonymous reviewers for their assistance in evaluating this paper.
Rozel, A. , Golabek G. J., Näf R., and Tackley P. J. (2015), Formation of ridges in a stable lithosphere in mantle convection models with a viscoplastic rheology. Geophys. Res. Lett., 42, 4770–4777. doi: 10.1002/2015GL063483.
The copyright line for this article was changed on 7 JAN 2016 after original online publication.
References
- Armann, M. , and Tackley P. (2012), Simulating the thermochemical magmatic and tectonic evolution of Venus's mantle and lithosphere: Two‐dimensional models, J. Geophys. Res., 117, E12003, doi:10.1029/2012JE004231. [Google Scholar]
- Balay, S. , Brown J., Buschelman K., Eijkhout V., Gropp D. K. W., Knepley M., McInnes L. C., Smith B., and Zhang H. (2012), PETSc users manual, Tech. Rep. ANL‐95/11 ‐ Revision 2.1.5. Argonne Natl. Lab., Lemont, Ill. [Google Scholar]
- Bercovici, D. (1995), A source‐sink model of the generation of plate tectonics from non‐Newtonian mantle flow, J. Geophys. Res., 100, 2013–2030. [Google Scholar]
- Bercovici, D. , and Karato S. (2003), Theoretical analysis of shear localization in the lithosphere, in Reviews in Mineralogy and Geochemistry: Plastic Deformation of Minerals and Rocks, vol. 51, edited by Karato S. and Wenk H., chap. 13, pp. 387–420, Mineral. Soc. Am. and Geochem. Soc, Washington, D. C. [Google Scholar]
- Bercovici, D. , Ricard Y., and Richards M. (2000), The relation between mantle dynamics and plate tectonics: A primer, in History and Dynamics of Global Plate Motions, Geophys. Monogr. Ser., vol. 121, edited by Richards M. A., Gordon R., and van der Hilst R., pp. 5–46, AGU, Washington, D. C. [Google Scholar]
- Bercovici, D. , Ricard Y., and Schubert G. (2001), A two‐phase model of compaction and damage: 3. Applications to shear localization and plate boundary formation, J. Geophys. Res., 106(B5), 8925–8940. [Google Scholar]
- Burg, J.‐P. , and Schmalholz S. (2008), Viscous heating allows thrusting to overcome crustal‐scale buckling: Numerical investigation with application to the Himalayan syntaxes, Earth Planet. Sci. Lett., 274(1–2), 189–203, doi:10.1016/j.epsl.2008.07.022. [Google Scholar]
- Burov, E. (2007), Plate rheology and mechanics, in Treatise on Geophysics, edited by Schubert G., pp. 99–151, Elsevier, Amsterdam., doi:10.1016/B978-044452748-6.00102-4 [Google Scholar]
- Christensen, U. (1983), Convection in a variable‐viscosity fluid: Newtonian versus power‐law rheology, Earth Planet. Sci. Lett., 64, 153–162. [Google Scholar]
- C̆ízková, H. , van den Berg A., Spakman W., and Matyska C. (2012), The viscosity of Earth's lower mantle inferred from sinking speed of subducted lithosphere, Phys. Earth Planet. Inter., 200–201, 56–62, doi:10.1016/j.pepi.2012.02.010. [Google Scholar]
- Davis, T. (2004), Algorithm 832: UMFPACK, an unsymmetric‐pattern multifrontal method, ACM Trans. Math. Software, 30(2), 196–199. [Google Scholar]
- Fowler, A. , and O'Brien S. (1996), A mechanism for episodic subduction on Venus, J. Geophys. Res., 101, 4755–4763. [Google Scholar]
- Fowler, A. , and O'Brien S. (2003), Lithospheric failure on Venus, Proc. R. Soc. A, 459, 2663–2704. [Google Scholar]
- Harlow, F. , and Welch J. (1965), Numerical calculation of time‐dependent viscous incompressible flow of fluid with a free surface, Phys. Fluids, 8, 2182. [Google Scholar]
- Hernlund, J. W. , and Tackley P. J. (2008), Modeling mantle convection in the spherical annulus, Phys. Earth Planet. Inter., 171(1–4), 48–54, doi:10.1016/j.pepi.2008.07.037. [Google Scholar]
- Hirth, G. , and Kohlstedt D. (2003), Rheology of the upper mantle and the mantle wedge: A view from the experimentalists, in Subduction Factory Monograph, vol. 138, edited by Eiler J., pp. 83–105, AGU, Washington, D. C. [Google Scholar]
- Johnson, C. , and Richards M. (2003), A conceptual model for the relationship between coronae and large‐scale mantle dynamics on Venus, J. Geophys. Res., 108(E6), 5058, doi:10.1029/2002JE001962. [Google Scholar]
- Karato, S. (2011), Rheological structure of the mantle of a super‐Earth: Some insights from mineral physics, Icarus, 212(1), 14–23. [Google Scholar]
- Kohlstedt, D. (2007), Properties of rocks and minerals—Constitutive equations, rheological behavior, and viscosity of rocks, in Treatise on Geophysics, vol. 2, edited by Kohlstedt D., pp. 389–417, Elsevier, Amsterdam. [Google Scholar]
- Korenaga, J. (2009), Scaling of stagnant‐lid convection with Arrhenius rheology and the effects of mantle melting, Geophys. J. Int., 179, 154–170, doi:10.1111/j.1365-246X.2009.04272.x. [Google Scholar]
- Moresi, L. , and Solomatov V. (1998), Mantle convection with a brittle lithosphere: Thoughts on the global tectonic style of the Earth and Venus, Geophys. J., 133, 669–682. [Google Scholar]
- Noack, L. , Breuer D., and Spohn T. (2012), Coupling the atmosphere with interior dynamics: Implications for the resurfacing of Venus, Icarus, 217(2), 484–498. [Google Scholar]
- Ogawa, M. (2003), Plate‐like regime of a numerically modeled thermal convection in a fluid with temperature‐, pressure‐, and stress‐history‐dependent viscosity, J. Geophys. Res., 108(B2), 2067, doi:10.1029/2000JB000069. [Google Scholar]
- Ricard, Y. , and Bercovici D. (2009), A continuum theory of grain size evolution and damage, J. Geophys. Res., 114, B01204, doi:10.1029/2007JB005491. [Google Scholar]
- Rolf, T. , and Tackley P. (2011), Focussing of stress by continents in 3D spherical mantle convection with self‐consistent plate tectonics, Geophys. Res. Lett., 38, L18301, doi:10.1029/2011GL048677. [Google Scholar]
- Rozel, A. (2012), Impact of grain size on the convection of terrestrial planets, Geochem. Geophys. Geosyst., 13, Q10020, doi:10.1029/2012GC004282. [Google Scholar]
- Schubert, G. , Turcotte D., and Olson P. (2001), Mantle Convection in the Earth and Planets, Cambridge Univ. Press, Cambridge, U. K. [Google Scholar]
- Solomatov, V. S. (1995), Scaling of temperature‐ and stress‐dependent viscosity convection, Phys. Fluids, 7, 266–274. [Google Scholar]
- Stamenković, V. , Noack L., Breuer D., and Spohn T. (2012), The influence of pressure‐dependent viscosity on the thermal evolution of super‐Earths, Astrophys. J., 748(1), 41. [Google Scholar]
- Stein, C. , Schmalzl J., and Hansen U. (2004), The effect of rheological parameters on plate behaviour in a self‐consistent model of mantle convection, Phys. Earth Planet. Inter., 142, 225–255. [Google Scholar]
- Stein, C. , Finnenkötter A., Lowman J., and Hansen U. (2011), The pressure‐weakening effect in super‐Earths: Consequences of a decrease in lower mantle viscosity on surface dynamics, Geophys. Res. Lett., 38, L21201, doi:10.1029/2011GL049341. [Google Scholar]
- Tackley, P. (1993), Effects of strongly temperature‐dependent viscosity on time‐dependent, 3‐dimensional models of mantle convection, Geophys. Res. Lett., 20(20), 2187–2190. [Google Scholar]
- Tackley, P. (2007), Mantle geochemical geodynamics, in Treatise on Geophysics, vol. 7, edited by Tackley P., pp. 437–505, Elsevier, Amsterdam. [Google Scholar]
- Tackley, P. , Ammann M., Brodholt J., Dobson D., and Valencia D. (2013), Mantle dynamics in super‐Earths: Post‐perovskite rheology and self‐regulation of viscosity, Icarus, 225, 50–61. [Google Scholar]
- Tackley, P. J. (2000a), Self‐consistent generation of tectonic plates in time‐dependent, three‐dimensional mantle convection simulations. Part 1: Pseudoplastic yielding, Geochem. Geophys. Geosyst., 1, 1021, doi:10.1029/2000GC000036. [Google Scholar]
- Tackley, P. J. (2000b), Self‐consistent generation of tectonic plates in time‐dependent, three‐dimensional mantle convection simulations: Part 2. Strain weakening and asthenosphere, Geochem. Geophys. Geosyst., 1, 1026, doi:10.1029/2000GC000043. [Google Scholar]
- Tackley, P. J. (2008), Modelling compressible mantle convection with large viscosity contrasts in a three‐dimensional spherical shell using the yin‐yang grid, Phys. Earth Planet. Inter., 171(1–4), 7–18, doi:10.1016/j.pepi.2008.08.005. [Google Scholar]
- Thielmann, M. , and Kaus B. J. (2012), Shear heating induced lithospheric‐scale localization: Does it result in subduction?, Earth Plan. Sci. Lett., 359–360, 1–13. [Google Scholar]
- Trompert, R. , and Hansen U. (1998), On the Rayleigh number dependence of convection with a strongly temperature‐dependent viscosity, Phys. Fluids, 10, 351–360. [Google Scholar]
- Turcotte, D. , and Schubert G. (2014), Geodynamics, 3rd ed., 636 pp., Cambridge Univ. Press, Cambridge, U. K. [Google Scholar]
- Weller, M. , and Lenardic A. (2012), Hysteresis in mantle convection: Plate tectonics systems, Geophys. Res. Lett., 39, L10202, doi:10.1029/2012GL051232. [Google Scholar]
- Zhong, S. , Yuen D., and Moresi L. (2007), Numerical methods for mantle convection, in Treatise on Geophysics, edited by Schubert G., pp. 227–252, Elsevier, Amsterdam., doi:10.1016/B978-044452748-6.00118-8 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1
Readme
Text S1, Captions of Table S1 and Movie S1, and Figures S1–S4
Movie S1


