Abstract
An analysis of diabatic heating and moistening processes from 12 to 36 h lead time forecasts from 12 Global Circulation Models are presented as part of the “Vertical structure and physical processes of the Madden‐Julian Oscillation (MJO)” project. A lead time of 12–36 h is chosen to constrain the large‐scale dynamics and thermodynamics to be close to observations while avoiding being too close to the initial spin‐up of the models as they adjust to being driven from the Years of Tropical Convection (YOTC) analysis. A comparison of the vertical velocity and rainfall with the observations and YOTC analysis suggests that the phases of convection associated with the MJO are constrained in most models at this lead time although the rainfall in the suppressed phase is typically overestimated. Although the large‐scale dynamics is reasonably constrained, moistening and heating profiles have large intermodel spread. In particular, there are large spreads in convective heating and moistening at midlevels during the transition to active convection. Radiative heating and cloud parameters have the largest relative spread across models at upper levels during the active phase. A detailed analysis of time step behavior shows that some models show strong intermittency in rainfall and differences in the precipitation and dynamics relationship between models. The wealth of model outputs archived during this project is a very valuable resource for model developers beyond the study of the MJO. In addition, the findings of this study can inform the design of process model experiments, and inform the priorities for field experiments and future observing systems.
Keywords: diabatic processes, Madden‐Julian Oscillation, modeling, convection, Year of Tropical convection, uncertainties
Key Points
Uncertainties in modeling convection in GCMs are highlighted
Radiation and clouds is a key driver of some of the model uncertainties
Convection dynamics link is key to time step intermittency of convection
1. Introduction
The Madden‐Julian Oscillation (MJO), being the dominant component of the tropical subseasonal variability spectrum [Madden and Julian, 1971] influences the global climate and weather systems (see reviews by Lau and Waliser [2011] and Zhang, [2005]). It also represents the major source of predictability at subseasonal time scales. Despite its critical importance in the global climate system, the fundamental physics of the MJO remains elusive. The roles of various diabatic heating processes for the MJO have been suggested based on general circulation model (GCM) studies, including shallow convective heating [e.g., Benedict and Randall, 2009; Li et al., 2009], stratiform heating [e.g., Fu and Wang, 2009; Seo and Wang, 2010], and radiative heating and cloud‐radiative interactions [Lee et al., 2001; Kim et al., 2011; Chikira, 2014]. A transition in the vertical heating structure during MJO evolution, namely, from shallow, to deep, and then to stratiform, was reported based on observations from Tropical Ocean–Global Atmosphere Coupled Ocean‐Atmosphere Response Experiment (TOGA‐COARE) Webster and Lukas [1992]; Lin et al. [2004]; Kiladis et al. [2005]. From recent reanalysis data sets, a transition from a shallow to deep heating structure during the MJO evolution is also clearly evident over both the eastern equatorial Indian Ocean and western Pacific [e.g., Jiang et al., 2011; Ling and Zhang, 2011; Zhang et al., 2010]. The critical roles of diabatic heating associated with vertically tilted propagating mesoscale systems and synoptic scale waves associated with the MJO, forexample, through upscale convective momentum transport and multicloud effects were discussed in Moncrieff [2004]; Majda and Stechmann [2009]; Khouider et al. [2011]; Miyakawa et al. [2012].
The ability of current generation GCMs to simulate and predict the MJO is strongly influenced by the performance of their physical parametrization schemes and therefore MJO is often seen as a useful test bed for their evaluation. Motivated by this, the “Vertical structure and physical processes of the MJO” Global‐Model Evaluation Project has been organized and supported by the World Climate Research Programme (WCRP)/The World Weather Research Programme (WWRP) The Observing System Research and Predictability Experiment (THORPEX) and the Years of Tropical Convection (YoTC) [Waliser et al., 2012; Moncrieff et al., 2012] MJO Task Force (at the time of this study, the MJO Task Force was under the collective auspices of the WCRP‐WWRP/THORPEX and the YoTC. It is currently under the auspices of the Working Group on Numerical Experimentation—WGNE) and the Global Atmospheric Systems Studies (GASS) panel of the Global Energy and Water Cycle Experiment (GEWEX) [Petch et al., 2011]. The project aims to improve understanding of the role that convection, cloud, radiative, and dynamic processes play in the development and evolution of the MJO in order to achieve better fidelity in our global prediction models.
There are three components to this multimodel intercomparison project which are described in Petch et al. [2011]. More information on the project and links to data access are available on the project website (https://earthsystemcog.org/projects/gass-yotc-mip/). This paper describes results from the short‐term hindcasts (referred to as component 2 in Petch et al. [2011]). It focuses on providing highly detailed and comprehensive (e.g., every model grid point and time step) diagnostics related to the diabatic heating and moistening processes from a series of 48 h hindcasts during two MJO events within the YoTC period. These are the successive MJO events during boreal winter 2009–2010 (i.e., YoTC events E and F). The 20 year climate simulations (component 1; see the companion paper Jiang et al. [2015]) provide a characterization of the models' intrinsic capabilities at representing MJO variability. Component 3 (see the companion paper Klingaman et al. [2015a]) links the models' MJO performance to their simulated diabatic processes and the results of the three components are summarized in Klingaman et al. [2015b]. This experimental framework is designed in such a way that it attempts to take advantage of the known links between biases seen in short‐range forecasts through to the long‐term climate simulations [Boyle et al., 2008; Martin et al., 2010].
The role of convective parametrizations in the simulation of tropical convection have been previously studied under the GASS framework [Phillips et al., 2004; Xie et al., 2012]. For example, simulation of suppressed and transition phases of convection were studied by Woolnough et al. [2010]. They examine the role of convective processes in moistening the atmosphere during suppressed and transition phases of MJO using cloud‐resolving model (CRM) simulations and single‐column models (SCMs). The framework in which climate models are initialized from identical global analysis data for short‐range weather forecasts has been previously used by GASS for the evaluation of convective parametrization [e.g., Petch et al., 2007; Willett et al., 2008; Ma et al., 2013] and cloud properties [Lin et al., 2012] and for the diagnosis of initial climate model errors (Transpose‐AMIP) [Williams et al., 2013; Ma et al., 2014]. This study involves a similar approach, but with a greater focus on the vertical structure during different phases of the MJO using a large number of GCMs.
This paper provides an overview of the experimental framework of the short‐range component of the MJO diabatic process model intercomparison project. The results of this intercomparison aims to provide a benchmark for centers involved in model development to work on their models' various parametrization schemes. The project has archived large amounts of data from this experiment, and we expect several more specific studies from those involved in the project and the model development community at large. Section 2 describes experimental design. Section 3 describes the growth of model biases over the first 48 h of the forecast, and section 4 shows heating and moistening tendencies from the parametrizations in the models involved. Section 5 highlights some features associated with the physical processes on the model time step, and a summary is provided in section 6.
2. Experiment Design
Two strong MJO events occurred between October 2009 and February 2010 and are named as YoTC MJO cases E and F (Figure 1). The specific dates used in this experiment for initializing the models are 20 October 2009 to 10 November 2009 for case E and 20 December 2009 to 10 January 2010 for case F [Waliser et al., 2012]. The experiments are composed of 22 forecasts of 48 h lead time for each MJO case. All models have been initialized at 00Z on all the days given above from the European Centre for Medium‐Range Weather Forecasts (ECMWF) operational analysis during the YoTC period (May 2008 to April 2010; hereafter referred to as the ERA YoTC analysis) with some modifications to the initial conditions as required by each model. SST and sea ice from the YoTC analysis are used as lower boundary forcing. This ensures consistency with other fields in the initial conditions.
Figure 1.
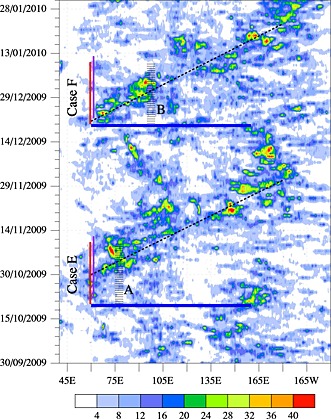
Hovmoller plot of TRMM 3B42 daily rainfall averaged between 10°S and 10°N to show the YoTC MJO cases E and F. Dotted black lines mark the approximate phase propagation. Blue horizontal line marks the longitudinal extend of the requested data domain from models. Red vertical line shows the range of consecutive days on which models are initialized for the two MJO cases. The range of days at the end of each 48 h forecast is marked in purple line. Hatched regions indicate the longitude extent of two 5°x5° domains marked A (75°–80°E, 0°–5°N) and B (95°–100°E, 10°S‐5°S) used to characterize the evolution of convection from a suppressed state to convective state.
Table 1 lists the models and their temporal and spatial resolutions. While all models are run as global configurations (except Pacific Northwest National Laboratory (PNNL)‐Weather Research and Forecasting (WRF)), only the data over equatorial Indian Ocean‐West Pacific (60°–160°E, 10°S–10°N) are archived. All the prognostic variables, cloud variables, fluxes and tendencies of heat, moisture and momentum from different parametrization schemes are archived at every time step and model level (detailed information on the experiment description and variables are available at the project website). Unlike in the other two components of the project [Klingaman et al., 2015a; Jiang et al., 2015], model data at native horizontal and vertical grid are archived in order to identify grid‐scale features in model behavior.
Table 1.
Details of Models Used in This Studya
| Horizontal Resolution | Vertical | |||||
|---|---|---|---|---|---|---|
| Model Name | Abbreviation | Institution | Time Step | (Longitude × Latittude) | Levels | Reference |
| Community Atmospheric Model | CAM5 | NCARb, USA | 30 min | 1.25 × 0.9 | 30 | Neale et al. [2010] |
| Canadian Coupled Model | CanCM4 | CCCMAc, Canada | 60 min | 2.8 × 2.8 | 35 | Merryfield et al. [2013] |
| CNRM Atmospheric Model | CNRM‐AM | CNRMd, France | 30 min | 1.4 × 1.4 | 31 | Voldoire et al. [2013] |
| European Community Model | ECEarth3 | SMHIe, Sweden | 45 min | 0.7 × 0.7 | 91 | Hazeleger et al. [2012] |
| Goddard Earth Observing | GEOS5 | GMAO‐NASA f, | 20 min | 0.625 × 0.5 | 72 | Rienecker et al. [2008] |
| System | USA | |||||
| Goddard Institute for Space | GISS‐E2 | GISS g, USA | 30 min | 2.5 × 2 | 40 | Schmidt et al. [2014] |
| Studies GCM | ||||||
| Integrated Forecast System | IFS | ECMWF h, UK | 60 min | 1.125 × 1.125 | 62 | Bechtold et al. [2008] |
| Met Office Unified Model | MetUM‐GA3 | Met Office, UK | 12 min | 0.5625 × 0.375 | 85 | Walters et al. [2011] |
| Model for Interdisciplinary | MIROC5 | AORI i, Japan | 30 min | 1.4 × 1.4 | 40 | Watanabe et al. [2010] |
| Research on Climate | ||||||
| MRI Atmospheric GCM | MRI‐AGCM3 | MRI j, Japan | 30 min | 1.125 × 1.125 | 48 | Yukimoto et al. [2012] |
| The Weather Research | PNNL‐WRF | PNNL k, USA | 12 min | 0.25 × 0.25 | 27 | Shamarock et al. [2008] |
| and Forecasting Model | ||||||
| Super‐Parameterized CAM | SPCAM3 | U. Washington, USA | 60 min | 2.8 × 2.8 | 30 | Khairoutdinov et al. [2008] |
Their time step, horizontal, and vertical resolution and the relevant reference are given.
National Center for Atmospheric Research.
Canadian Centre for Climate Modelling and Analysis.
Centre National de Recherches Météorologiques‐ Météo France.
Swedish Meteorological and Hydrological Institute.
Global Modeling and Assimilation Office‐NASA.
NASA Goddard Institute for Space Studies.
European Centre for Medium Range Weather Forecasts.
Atmosphere and Ocean Research Institute, The University of Tokyo.
Meteorological Research Institute.
Pacific Northwest National Laboratory.
CanCM4 (Table 1) is the only atmosphere‐ocean coupled model that participated in these short hindcasts. It uses the Canadian Atmospheric Model, [CanAM4; von Salzen et al., 2013]) and the Canadian Ocean Model [CanOM4; Arora et al., 2011]. Due to the coupled nature of this model, in order to maintain atmospheric ocean balance at the early stages of the forecasts, it uses initial conditions from analyses produced by assimilating 6‐hourly ECMWF‐Interim reanalysis (ERA‐Interim) [Dee et al., 2011] atmospheric temperature, horizontal winds and specific humidity into CanAM4. Since this procedure is different from other models initialization some of the initial model error calculations may not be consistent. This must be acknowledged in interpreting some of the biases of CanCM4 presented in the study. PNNL‐WRF [Shamarock et al., 2008], is a regional tropical channel model with midlatitude boundaries forced with ERA‐Interim reanalysis run at 0.25°×0.25° resolution. Only a limited set of variables from this model are included in this study. SPCAM3 implements a two‐dimensional cloud resolving model (the System for Atmospheric Modelling SAM, [Khairoutdinov and Randall, 2001]) inside a relatively coarser T42 (2.8°×2.8°) grid.
A 5°×5° domain is chosen as the focus of our analysis (75°–80°E, 0°–5°N for case E and 95°–100°E, 10°S–5°S for case F). This is chosen to be large enough to include information from the lower resolution models (Table 1) (e.g., SPCAM3 and CanCM4) and capture the evolution of the MJO while small enough to isolate the convectively active and suppressed regions. The longitudinal extent of these boxes are marked in Figure 1. Model vertical profiles are converted to a common pressure coordinate determined by the average pressure variations during each forecast at model levels. All temporal means used in this analysis are derived from the time step data. Model precipitation is compared with the TRMM 3B42 3‐hourly rainfall data [Kummerow et al., 2000]. Temperature, humidity, and winds are taken from the ERA YoTC analysis for evaluation of model biases. Other variables such as cloud properties, mass flux, heat, and moisture tendencies are obtained from the short (3–24 h) forecasts using the ECMWF model used to generate the analysis. These variables are linked to somewhat better constrained dynamics than the models used for the experiments but are still strongly a function of the parametrizations in the ECMWF model. They are thus treated as an additional piece of information rather than the truth. Quality controlled model outputs from all three experiments are archived at Earth System Grid (https://earthsystemcog.org/projects/gass-yotc-mip/) and are available for download. All data analysis and visualization in this study are done using NCAR Command Language [2014].
3. Short‐Term Model Biases and Spread
All models (other than CanCM4) are initialized using the ERA YoTC analysis. It is expected that the large‐scale dynamics of the model within the first 48 h is constrained by the analysis—which remains our best estimate of the state of the real atmosphere. It is important to acknowledge that the ERA YoTC analysis is influenced by the underpinning ECMWF Integrated Forecasting System (IFS) model used to generate it, and this may provide an initial shock to the models compared to being initialized by their own analysis (where available). Figure 2 shows the evolution of precipitation at every time step averaged over 75°–80°E, 0°–5°N as a function of forecast lead time for all the 22 forecasts for MJO case E. The corresponding rainfall verification from TRMM is also shown as the black line. The model spread appears to be larger than the diurnal variability from the TRMM data associated with this period and domain. MetUM‐GA3 shows spikes in the initial few time steps but is well adjusted in about 10 h into the forecasts. IFS and ECEarth3 are newer versions of the ECMWF model used to generate the YoTC analysis. Therefore, these models also take a few hours to spin‐up. Models such as MRI‐AGCM3 and CAM5 start with little or no rain and require time for spinning up to produce a stable mean state. This figure suggest that 12–36 h is also a good forecast period to avoid spin‐up issues while remaining as close to analysis as possible for all models. This finding is consistent with the TOGA‐COARE modeling study using a similar methodology [Willett et al., 2008].
Figure 2.
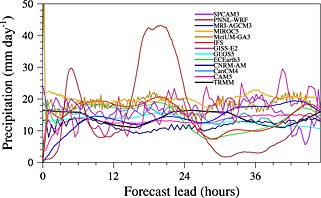
Time step evolution of domain (75°–80°E, 0°–5°N) averaged precipitation as a function of forecast lead time for all the 22 forecasts for MJO case E. 48 h evolution of TRMM rainfall from each of the model initialization date are also shown as solid black line.
A time series of 12–36 h accumulated precipitation is constructed over the 5°×5° boxes mentioned above for the two MJO cases from TRMM and models. Figure 3 shows the time series of precipitation and highlights the different phases of convection. The dates corresponding to these phases are marked as shading in Figures 3a and 3b. In this study these phases are referred to as “suppressed,” “transition,” and “convective” phases. Most models show good skill in capturing the general transition from a suppressed to convective phase. However, there are large differences in the precipitation amounts between models when compared to TRMM observations. It is worth acknowledging that TRMM has difficulties measuring rain from shallow convective clouds and there is a possibility of underestimation of low rainfall (∼10 mm d−1) values [Chen et al., 2013]. Compared to TRMM, all models produce more rain in the suppressed phase, which is a known problem in GCMs [e.g., Stephens et al., 2010; Xavier, 2012]. SPCAM3 and MIROC5 are consistently wetter by about 50–60% during the convective phase for both MJO cases. Compared to case E, the observed rainfall transition in case F is more gradual with significant amount of rain in the transition phase and models represent this transition better (Figure 3b).
Figure 3.
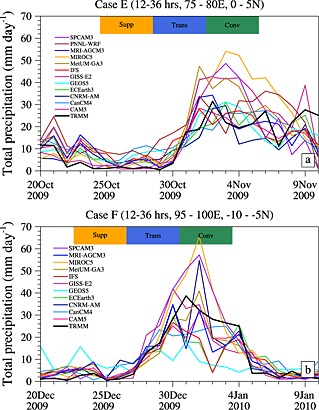
Time series of 12–36 h accumulated precipitation from models over 75°–80°E, 0°–5°N for MJO case E and 90°–95°E, 10°S–5°S for case F. Corresponding TRMM observations are shown as black line. Three phases of the convection in both panels are marked as suppressed, transition, and convective depending on the observed rainfall amounts.
3.1. Evolution of Large‐Scale Dynamics
The evolution of large‐scale dynamics in the forecasts are analyzed for the three phases described in Figure 3. The multimodel mean and standard deviation of zonal winds (u) during the different convective phases are shown in Figure 4 for three 24 h lead time windows. The zonal winds in the models are reasonably close to the analysis (Figure 4), and with little intermodel spread at short lead times when the feedback from convection remains relatively weak. A similar plot for large‐scale pressure vertical velocity (ω) is shown in Figure 5. The models are close to each other, both in suppressed and transition phases, within the first 48 h. In the first 24 h the multimodel mean lies close to the YoTC analysis even though there are intermodel differences, especially during the convective phase. The variations of ω at longer forecast lead time (days 5, 7, and 12) are obtained from the component 3 of the experiments [Klingaman et al., 2015a], and are shown in Figures 5d–5f. Here the three phases defined in Figure 3 are used as target periods at these lead times. The spread is larger in the convective phase at day 5 and the multimodel mean starts to drift from the analysis. By days 7 and 12, model spread grows much larger and the phases become indistinguishable meaning there is little correspondence of the models with the corresponding analysis at longer leads (e.g., Figure 5e). For MJO case E, a convective phase emerges about 10 days after a suppressed phase (Figure 3a). Models when initialized from a suppressed phase often fail to generate convective signals beyond short lead times. Several MJO forecast skill studies [Waliser et al., 2003; Goswami and Xavier, 2003] show that models have better skills when initialized from a convective state than from a suppressed phase. Figure 5 also demonstrates that the initialization from the analysis provides reasonable constraint on the large‐scale dynamics within the first 2 days of the forecasts and hence justifies the use of 12–36 h as a useful time window to study the evolution of model errors that are due to physical parametrizations.
Figure 4.
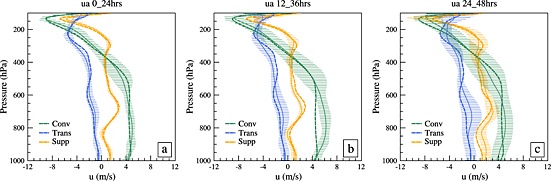
Multimodel mean (solid lines) and standard deviation (whiskers) of zonal winds during (a) 0–24 h, (b) 12–36 h, and (c) 24–48 h into the forecasts.
Figure 5.
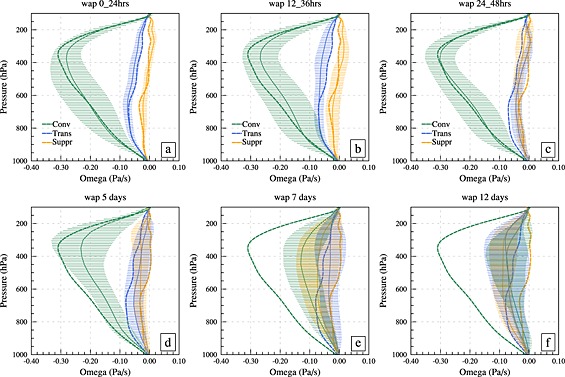
Multimodel mean (solid lines) and standard deviation (whiskers) of ω during (a) 0–24 h, (b) 12–36 h, and (c) 24–48 h into the forecasts. d, e and f are similar plots for day 5, day 7, and day 12 leads from Component 3 of the experiments [Klingaman et al., 2015a], respectively. The corresponding analysis values are plotted as thick dashed line. Each color indicates different phases of the convection. Corresponding phases of the two MJO cases are combined in this figure.
3.2. Temperature and Humidity Biases
Temperature and humidity in the models vary due to numerous interactions between processes such as radiation, convection, boundary layer(BL), and precipitation with the large‐scale environment. It has been shown that some key tropical biases affect model performance at times scales ranging from a few days to several decades [Boyle et al., 2008; Martin et al., 2010]. Figure 6 shows the mean temperature (T), specific humidity (q), and relative humidity (RH) biases at the 12–36 h time window with respect to corresponding YoTC analysis. All forecasts of the two MJO cases are combined to construct the biases here. The multimodel mean bias is shown as thick black line. There is a general tendency for models to have a warm bias in the lowest 100 hPa but little or no systematic bias above that up to 500 hPa. Above 500 hPa (which is roughly the freezing level), there is a mean cold bias with strong contributions from MetUM‐GA3 and GISS‐E2. Vertical profiles of q show mean wet bias near the surface related to the warmer BL, and a mean dry bias (with large intermodel differences) at midlevels (refers to 800–600 hPa here), with MIROC5 model having relatively larger dry bias at 12–36 h near 800 hPa (Figure 6b). The combined effects of T and q are reflected in the RH biases (Figure 6c) with most models having smaller RH at lower and midlevels compared to the ERA YoTC analysis and generally higher RH at upper levels with larger intermodel difference, likely due to the cold biases at upper levels (Figure 6a). These RH biases are consistent with the behavior of CMIP3 and CMIP5 models for much larger regions diagnosed using composite profiles of RH based on precipitation intensity [e.g., Thayer‐Calder and Randall, 2009; Xavier, 2012; Kim et al., 2014]. The near‐surface warm bias, the upper troposphere cold bias and the humidity biases do not show much dependency on the phase of convection (not shown). The vertically integrated temperature and humidity biases are reasonably small compared to those in long‐term climate simulations [John and Soden, 2007].
Figure 6.
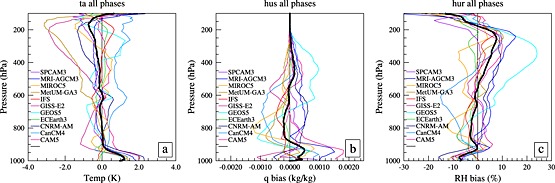
The 12–36‐hourly biases of T, q, and RH with respect to YoTC analysis for all MJO phases based on both MJO cases. The thick black line is the multimodel mean bias.
Many of the MJO theories suggest a direct relationship between precipitation and total column moisture [e.g., Raymond, 2000] that is supported by observations [Bretherton et al., 2004; Kikuchi and Takayabu, 2004; Thayer‐Calder and Randall, 2009]. Recent studies show that increased moisture sensitivity to convection often results in improved MJO simulations [Hirons et al., 2013; Kim et al., 2014]. These studies suggest that tropospheric moisture control on convection is critical for simulating the interaction between the convective heating and the large‐scale wave forcing associated with the MJO. The observed development of MJO convection follows from an accumulation of moisture in the BL due to frictional convergence or modest evaporative fluxes. This promotes shallow cumuli and cumulus congestus which warms and moistens the lower troposphere to midtroposphere [e.g., Bladé and Hartmann, 1993; Hu and Randall, 1994; Benedict and Randall, 2007]. This moist region helps maintain buoyancy for ascending air parcels and feeds back for further convection development [Grabowski, 2003]. The heating and moistening processes during the MJO phase transition are examined in the next section.
4. Diabatic Processes During MJO Phases
In this section we focus on the tendencies of the parametrization schemes at 12–36 h when the dynamics is reasonably well constrained. All models provide profiles of tendencies of temperature (dT/dt) and moisture (dq/dt) from the different parametrization schemes such as convection, BL, microphysics, diffusion, radiation (for dT/dt) etc. at every time step. For each model the number of terms contributing to the total budget varies but they are grouped into the above categories. Figure 7 shows the budget of dT/dt and dq/dt due to convection scheme (dq/dt conv), dynamics (dq/dt dyn) and BL, microphysics, and diffusive terms combined (dq/dt BMD). The multimodel means are plotted as solid lines with the intermodel range as whiskers. The tendencies from ERA YoTC forecasts are also given as dotted lines. Individual model behaviors are not discussed here because it would become too complex for an overview paper. However, we would expect individual centers to look into the details of their models using general findings as a baseline.
Figure 7.
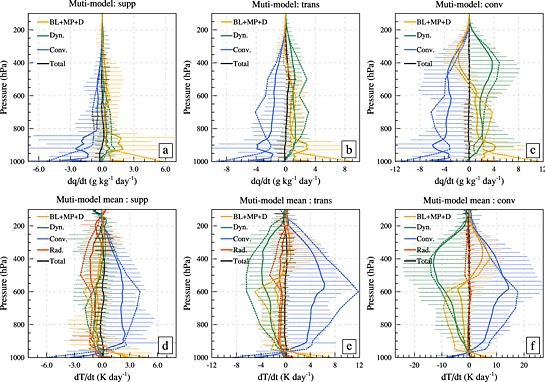
Tendencies of specific humidity (a–c) due to convection, dynamics, and BL, microphysics, and diffusion combined during the 12–36 h forecasts. (d–f) The heating tendencies due to radiation, convection, dynamics, and BL, microphysics, and diffusion combined (BL + MP + D). Total tendencies are also shown. Multimodel means are plotted as solid lines and the range of model values (unlike the standard deviation in Figures 4 and 5 to span the full range of model behaviors) as whiskers. The tendencies from the ERA YoTC analysis is also plotted as dotted lines. Tendencies for suppressed (Figures 7a and 7d), transition (Figures 7b and 7e) and convective phases (Figures 7c and 7f) are shown. Please note the change of scale between panels.
During the suppressed phase, moistening in the BL (dq/dt BMD, Figure 7a, orange lines) is nearly compensated by the removal of moisture at low levels by convection (dq/dt conv, Figure 7a, blue lines), but both these processes show large spread among models. The enhancement of boundary layer moisture is important for MJO development [Hsu and Li, 2012]. ERA YoTC data show a bimodal vertical structure of moisture tendencies due to convection with peaks in the boundary layer (due to shallow convection) and at midlevels. This vertical structure is different in models across all MJO phases and does not agree with the YoTC forecasts.
The contribution of microphysics terms and diffusion are nearly zero in the BL and hence the dq/dt BMD (orange lines) represent tendencies predominantly due to BL schemes only at low levels. Likewise, at middle and upper levels the contribution to this term is due to condensation, freezing, evaporation of rain, and melting of ice. These increased convective (drying) tendencies in the BL (Figure 7a) may be linked to the warmer surface temperature bias promoting increased shallow convection in most models (Figure 6a). The heating structure, despite large intermodel spread, shows weaker (compared to other phases) heating due to convection up to midlevels (Figure 7d, blue lines). At upper levels total radiative cooling (Figure 7d, red lines) are important.
During the transition phase, the dominant balance is between moistening due to dynamical lifting (Figure 7b, green lines) and convective drying (Figure 7b, blue lines). Compared to the suppressed phase, there is increased moistening (Figure 7b) due to evaporation and moisture convergence in the BL with convective drying balancing this moistening. While acknowledging the influence of IFS physics on the YoTC analysis, we note that no model matches the midlevel convective tendencies and the related dynamics tendencies. Below the freezing level (around 600 hPa) convective heating (blue line) is nearly balanced by the adiabatic cooling due to vertical motion (green line) as well as the microphysical processes (orange line) including evaporation of large scale precipitation (Figures 7d–7f). Contribution from microphysical processes are larger in the transition phase compared to the suppressed (Figures 7d and 7e). At the upper levels during the convective phase (Figure 7f), the large‐scale cooling due to vertical ascent (green lines) is nearly balanced by the combined effect of convective heating as well as the heating due to large‐scale precipitation. This effect is also seen in the moisture tendencies during the convective phase (Figure 7c). The convective heating tendencies (Figure 7f) show large spread around 600–500 hPa possibly due to uncertainties in the representation of mass fluxes in the models at these levels (Figure 9). There are large contributions to heating and moistening balanced by drying in the active phase (Figure 7f). Figure 8 shows the total physics tendencies of moisture and heating for the three phases. This figure highlights the large spread in the contributing tendency terms across models although the multimodel mean has a reasonable correspondence with the ERA YoTC data. Large disagreements are seen at midlevels for the transition phase (blue lines).
Figure 9.
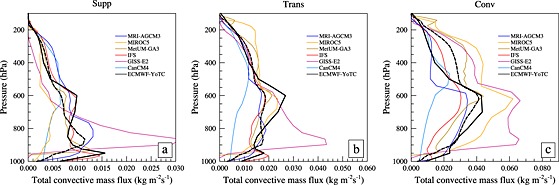
The 12–36‐hourly total mass flux for the (a) suppressed, (b) transition, and (c) convective MJO phases. The dashed black line is the multimodel mean and the continuous black line is the YoTC data. Please note the change of scale between panels.
Figure 8.
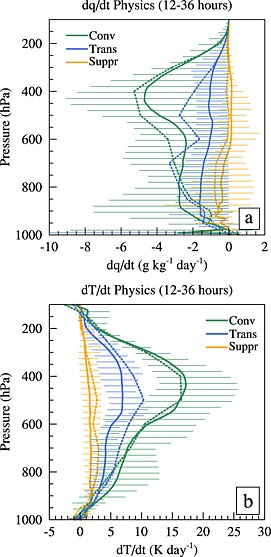
Tendencies due to all the physics terms combined (convection, BL, microphysics, and diffusion) during the 12–36 h forecasts for the three convective phases for (a) moisture and (b) temperature. Intermodel spread is shown as whiskers around the multimodel mean (solid lines). The tendencies from the ERA YoTC analysis are shown as dotted lines.
Observational evidence [e.g., Kikuchi and Takayabu, 2004] suggests the presence of shallow cumuli confined in the trade inversion layer during the transition phases. During this phase, a mix of shallow cumuli, cumulus congestus, and some deep clouds drive the deepening of a moist layer. In the ERA YoTC data there is indication of convection with a midheavy heat and moisture tendency profile (blue dotted line in Figures 7b and 7e) but less so in the models. This is also true for the convective phase where there is a greater mismatch between multimodel mean tendency due to convection schemes and the corresponding ERA YoTC tendencies at midlevels. The total convective mass flux profiles (Figures 9a and 9b) also highlight these intermodel differences in all three phases, especially in representing the mass flux at midlevels. Mitovski et al. [2010] show that the models and reanalyses do not fully represent the features of midlevel congestus well. The differences in midlevel convective tendencies seen here also highlight this common bias in the models.
The radiative cooling at upper levels during the suppressed period (red lines in Figure 7d) is generally weaker in the models compared to the ERA YoTC tendencies. A weaker radiative cooling during the suppressed phase would mean an underestimation of the destabilizing effects due to radiative feedback and thus weaker convection in the subsequent phases. This may be a contributing factor to the weaker convective heating and moistening during the transition and convective phases (Figures 7b, 7e, 7c, and 7f). During the convective phase the temperature tendencies due to nonradiative physics nearly compensates the dynamics with a relatively smaller contribution from radiation (Figure 7f). Cooling due to large‐scale ascent, evaporation of rain and melting of ice (as seen from the BL + MP + D term, given that BL and diffusion terms are nearly zero at midlevels) have opposing effects on the convective heating (Figure 7f) below 600 hPa. Above this level there is increased contribution (compared to other phases) from the microphysics terms such as stratiform heating and freezing (Figure 7f).
Figure 10a shows the behavior of radiative heating separately for the convective phase. It shows that models have similar profiles up to around 600 hPa above which models have large spread and hardly agree on the sign. Breaking down into the longwave and shortwave components (Figures 10b and 10c) shows lesser spread for the shortwave heating compared to the longwave heating.
Figure 10.
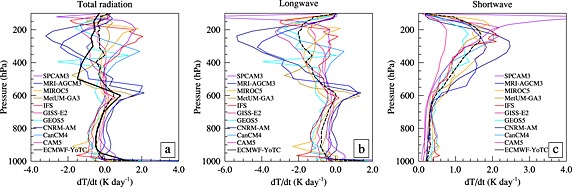
The 12–36‐hourly average profiles of heating tendency due to (a) total radiation (dT/dt rad) and the contribution from (b) longwave and (c) shortwave radiation tendencies during convective phase. The dashed black line is the multimodel mean and the continuous black line is the YoTC data. Only the total tendency is available in the ERA YoTC data set and is plotted in Figure 10a).
The importance of radiative heating associated with water vapor and clouds on the global climate system cannot be overstated. Feedbacks associated with clouds remain the largest source of uncertainty in climate models [Stocker et al., 2013]. For realistic representation of tropical circulation and cloud feedbacks, it is critical that the models produce cloud and radiative heating rate profiles with realistic horizontal, vertical, and diurnal variability [McFarlane et al., 2007]. The column energy budget and the distribution of radiative heating within the column depend on total cloud amount, optical properties of cloud layers, and the vertical distribution of clouds [Stephens and Webster, 1981]. Clear‐sky radiative heating tendencies (not shown) show a high level of consistency between models confirming the key role of cloud distribution and properties in contributing to the uncertainties in radiative heating. Total cloud fraction, cloud liquid, and cloud ice (available from 7 models) are shown in Figure 11 for the convective phase. All models represent the increase of cloud fraction above the freezing level during the convective phase. Nearly half of the models have a bimodal vertical cloud fraction profile with peaks above freezing level as well as in the BL. High cloud layers occur frequently from 200 to 100 hPa in most models (Figure 11a). Most notable though is that the spread between the model cloud fractions are large, for example, at around 500 hPa, where the cloud fraction ranges between 20 and 80% for different models. When this is combined with uncertainties in the cloud water at lower and midlevels (Figure 11b) and cloud ice at upper levels (Figure 11c), it introduces large spread in the radiative heating. In addition, it may be possible that the uncertainties in temperature and RH profiles at upper levels (Figures 6a and 6c) also contribute to the spread in radiative heating profiles.
Figure 11.
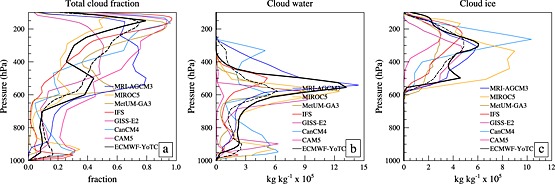
The 12–36‐hourly profiles of (a) total cloud fraction, (b) cloud water, and (c) cloud ice for the convective phase. The dashed black line is the multimodel mean and the continuous black line is the YoTC data.
5. Time Step Intermittency
Figure 2 highlighted that some models (e.g., MetUM‐GA3) have strong intermittency of rainfall variying from heavy to light rain when going from one time step to the next. To analyze this further, Figure 12a shows the root‐mean‐squared (RMS) difference between consecutive time steps of rainfall averaged over the region 75°–80°E, 0°–5°N for each of the 22 forecasts during MJO case E. Area averaging is done to extract the spatially coherent time step behavior and to reduce spatial inconsistencies resulting from different model grid resolutions (RMS differences computed at every grid point and then area averaging shows similar behavior and hence are not shown here). For some models (e.g., MetUM‐GA3 and GISS‐E2), the variations of rainfall between time steps are as much as half of the total 12–36 h rainfall (Figure 3a) in the convective phase of the MJO, even after area averaging over a reasonably large region. In MetUM‐GA3 (which has a time step of 12 min), there is indication of “on and off” behavior of convection scheme between time steps. This measure of time step intermittency is the largest during the convective phase for all models.
Figure 12.
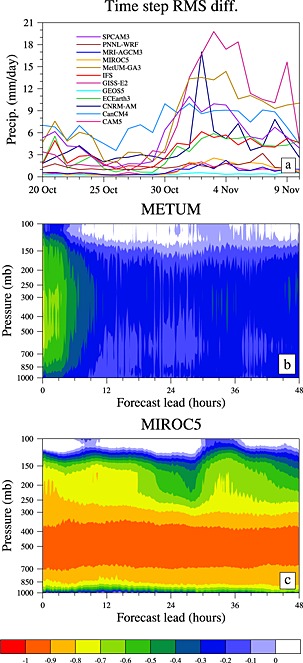
(a) RMS difference between consecutive time steps of rainfall averaged over 75°–80°E, 0°–5°N for MJO case E. The pattern correlations between rainfall and ω at all vertical levels over 50°–90°E, 10°S–10°N (a convective region) at every model time step initialized on 3 November 2009 are shown to highlight the contrasting behaviors of models with (b) strong (MetUM) and (c) weak (MIROC5) time step intermittency of rainfall.
Figures 12b and 12c examine this in a bit more detail by attempting to link the time step changes in rainfall to the large‐scale dynamics. Two models with contrasting time step variations (MetUM‐GA3 for large time step intermittency and MIROC5 with little variations between time steps) are chosen. Figures 12b and 12c show the spatial pattern correlation values of rainfall and ω at every model level over a sufficiently large convecting region 50–90°E, 10°S–10°N. This diagnostic is done for the forecast initialized on 3 November 2009 (a convectively active period for the region). For MetUM‐GA3 there is a significant negative correlation throughout the troposphere at the beginning of the forecasts (up to about 6 h lead time) suggesting that the spatial patterns of convection and ω are reasonably related to each other. It may be noticeable from Figure 2 that MetUM‐GA3 has relatively less time step intermittency in the first few hours. This initial time window (0–6 h) is when the large‐scale dynamics and convection have the strongest influence from the observation, and the stronger correlation seen at the beginning of the forecasts may be a manifestation of the observational constraints due to initialization. In about 6 h this relation weakens and there is no significant correlation between convection and dynamics further into the forecasts. The MIROC5 model, on the contrary, shows strong correlation throughout the troposphere during the entire forecast span.
This is an indication that models behave quite differently in their links between deep convection the large‐scale dynamics at the time step level. For MetUM‐GA3 this link is weak, often with precipitation at any one time step unrelated to the large‐scale dynamics. From this short preliminary analysis it is unclear whether the time step intermittency seen in some models has any significant effect on their diabatic tendencies averaged over several time steps. Time step intermittency and the convection‐dynamics relationship is nevertheless an important question that requires more focused studies.
6. Summary and Conclusions
This paper presents results from one of the three components of a GASS‐YoTC project on the vertical structure and diabatic processes of the MJO. This component evaluates the diabatic processes and growth of model errors at lead times when the model dynamics is constrained by observations. The results included in the paper and data available online are designed to provide a benchmark case for the model development communities focused on improving representation of tropical convection and the MJO. Thermodynamic tendencies and diabatic processes from participating models have been captured with the highest temporal and spatial resolution of any GASS global modeling project.
Twelve models have participated in this experiment and each has simulated daily 48 h hindcasts during two strong MJO cases from 20 October 2009 to 10 November 2009 and from 20 December 2009 to 10 January 2010. All models (except CanCM4 and PNNL‐WRF; see section 2) were initialized with the ERA YoTC analysis, run at their native resolution and provided diagnostics from every time step and every grid point for a key region of the tropics (60°–160°E, 10°S–10°N).
The modeling framework used here (short lead time hindcasts) aims to constrain the large‐scale dynamics and thermodynamics to be as close to observed as possible to evaluate the early stages of error growth in the model and differences in model physics tendencies in a dynamically constrained system. The ERA YoTC analysis is chosen as the best possible constraint on the system, although we must acknowledge the influence of the IFS model in this product. Evaluation of results showed that, as was seen in Willett et al. [2008], a 12–36 h lead time was the best balance for remaining constrained by the analysis but avoiding initial spin‐up issues from using a nonnative analysis. It was also shown that the growth of dynamic and thermodynamic biases was not dependent on the local MJO state. It is, however, acknowledged that the initial model drift can be quite regionally structured, and hence, some of the lessons learned in this analysis may not be completely representative of other convecting zones.
Evaluation of the thermodynamic properties in the of the models showed a fairly large spread in the upper tropospheric temperature biases (±2 K) as well as midlevel humidity biases (±1 g kg−1), although the multimodel mean showed little systematic bias. In terms of the large‐scale dynamics, the vertical velocities for suppressed, transition, and active phases of the MJO were nicely constrained and different from each other at a 12–36 h lead time. Analysis of longer lead time data from the 20 day hindcast component of this experiment showed that this was not true by 7 or 12 days lead time where there was little separation between the phases.
Detailed analysis of the diabatic heating and moisture tendencies highlighted that there remain large differences in the response of physical parametrizations in different models even when the dynamics is relatively well constrained. Results from the companion paper [Klingaman et al., 2015a] suggest little variation in the heating and moistening profiles with lead time which means that these large differences are likely to persist through many days. One particular feature of the diabatic processes that stood out was the large intermodel differences and differences from the ERA YoTC moisture tendencies at lower and midlevels (Figure 8a) during the transition phase. Reducing these uncertainties and biases in midlevel moistening may be a key to improving MJO simulation in models across time scales. This relationship between diabatic moistening and the MJO fidelity in the 20 day forecasts and the climate simulations is highlighted in the synthesis paper [Klingaman et al., 2015b]. Unlike in these experiments, skill of 2 day hindcasts at 12–36 h is generally high for all models and a clear separation of model performance based on such a metric computed over a limited range of start dates and cases proves to be difficult [see Klingaman et al., 2015b, section 3].
Radiative heating during the convective phase, which, although not the largest diabatic term, had by far the largest relative spread across models. Indeed, models could not agree on the sign of the total radiative heating at many heights. This was linked to a wide spread in cloud fraction as well as liquid and ice contents in the clouds and was most notable during the most active phase of the MJO. This highlights that the representation of clouds and radiation in global models remains poor and still needs a strong focus from the model develop community, particularly those developing convection schemes which are perhaps most strongly influencing the cloud water and fraction in such a convective region.
Another model feature highlighted by this work, and worthy of further study, is the strong intermittency in rainfall from one time step to another seen in some models but not in other models. Results here show clearly that some models link precipitation at the time step much more closely to large‐scale dynamics than others. While truth is hard to come by for such an issue the signal is strong and this project has a wealth of model data available to consider this issue further.
The purpose of this paper has been to provide a basic reference and summary of the 2 day hindcast component of the GASS‐YoTC project on the vertical structure and diabatic processes of the MJO. It has merely scratched the surface of a vast resource which is available to the model development community. This resource should be a very valuable tool in evaluating their modeling systems with a level of detail which can allow them to understand and improve the behavior of their physical parametrization schemes. Quality‐controlled model data from all three experiments are archived at Earth System Grid (https://earthsystemcog.org/projects/gass-yotc-mip/) and are available for download.
Acknowledgments
The GASS‐YoTC Vertical Structure and Physical Processes Multi‐model Experiment was supported by the World Climate Research Program and World Weather Research Program and organized by the GEWEX Global Atmospheric System Studies (GASS) subproject and the YoTC/WGNE MJO Task Force. IT support and data services hosted by the NASA Jet Propulsion Laboratory. P. Xavier and J. Petch are supported by the Joint DECC/Defra Met Office Hadley Centre Climate Programme (GA01101). Support for D. Waliser was provided by the U.S. National Science Foundation (NSF) and the NASA Modeling, Analysis and Prediction (MAP) program with his research carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. X. Jiang acknowledges support by NSF Climate and Large‐Scale Dynamics Program under award AGS‐1228302 and NOAA MAPP program under award NA12OAR4310075. Support for N. Klingaman and S. Woolnough was provided by the National Centre for Atmospheric Science, a Natural Environment Research Council collaborative center. T. Miyakawa acknowledges the MIROC team (for developing the model), M. Watanabe (for supervising the simulations), N. Hirota and T. Hashino (for their support in data processing), and the Earth simulator (for computation). S. Hagos acknowledges support from the Office of Biological and Environmental Research of the U.S. Department of Energy as part of the Atmospheric Systems Research Program. D. Kim appreciates the NASA/GISS modeling group, especially M. Kelley, M.‐S. Yao, and A. Del Genio for their invaluable and unlimited support. D. Kim was supported by the NASA grant NNX13AM18G and the Korea Meteorological Administration Research and Development Program under grant CATER 2013‐3142. NCAR is sponsored by the U.S. National Science Foundation. M. Pritchard was supported by a NOAA CGC postdoctoral fellowship; he thanks M. Khairoutdinov for developing and making SPCAM3 available through the Center for Multiscale Modeling of Atmospheric Processes, a NSF Science and Technology Center managed by Colorado State University under Cooperative agreement ATM‐0425247. Computing resources for SPCAM3 simulations were provided courtesy of the Extreme Science and Engineering Discovery Environment, supported by NSF grant OCI‐1053575 under allocation TG‐ATM120034. We acknowledge the insightful comments from C. Zhang and three anonymous reviewers which helped improve the manuscript. M. Webb and A. Bodas‐Salcedo are acknowledged for providing information on cloud radiative heating. Quality‐controlled model data from all three experiments are archived at Earth System Grid (https://earthsystemcog.org/projects/gass-yotc-mip/) and are available for download.
Xavier, P. K. , et al. (2015), Vertical structure and physical processes of the Madden‐Julian Oscillation: Biases and uncertainties at short range, J. Geophys. Res. Atmos., 120, 4749–4763. doi:10.1002/2014JD022718.
This article is a companion to Klingaman et al. [2015a] doi:10.1002/2014JD022374; Klingaman et al. [2015b] doi:10.1002/2015JD023196; and Jiang et al. [2015] doi:10.1002/2014JD022375. doi:10.1002/2014JD022718.
The copyright line for this article was changed on 22 JUL 2015 after original online publication.
References
- Arora, V. , Scinocca J., Boer G., Christian J., Denman K., Flato G., Kharin V., Lee W., and Merryfield W. (2011), Carbon emission limits required to satisfy future representative concentration pathways of greenhouse gases, Geophys. Res. Lett., 38, L05805, doi:10.1029/2010GL046270. [Google Scholar]
- Bechtold, P. , Köhler M., Jung T., Doblas‐Reyes F., Leutbecher M., Rodwell M. J., Vitart F., and Balsamo G. (2008), Advances in simulating atmospheric variability with the ECMWF model: From synoptic to decadal time‐scales, Q. J. R. Meteorol. Soc., 134(634), 1337–1351. [Google Scholar]
- Benedict, J. J. , and Randall D. A. (2007), Observed characteristics of the MJO relative to maximum rainfall, J. Atmos. Sci., 64(7), 2332–2354. [Google Scholar]
- Benedict, J. J. , and Randall D. A. (2009), Structure of the Madden–Julian Oscillation in the superparameterized CAM, J. Atmos. Sci., 66(11), 3277–3296. [Google Scholar]
- Bladé, I. , and Hartmann D. L. (1993), Tropical intraseasonal oscillations in a simple nonlinear model, J. Atmos. Sci., 50, 2922–2939. [Google Scholar]
- Boyle, J. , Klein S., Zhang G., Xie S., and Wei X. (2008), Climate model forecast experiments for TOGA COARE, Mon. Weather Rev., 136(3), 808–832. [Google Scholar]
- Bretherton, C. S. , Peters M. E., and Back L. E. (2004), Relationships between water vapor path and precipitation over the tropical oceans, J. Clim., 17(7), 1517–1528. [Google Scholar]
- Chen, Y. , Ebert E. E., Walsh K. J., and Davidson N. E. (2013), Evaluation of TRMM 3B42 precipitation estimates of tropical cyclone rainfall using PACRAIN data, J. Geophys. Res. Atmos., 118, 2184–2196, doi:10.1002/jgrd.50250. [Google Scholar]
- Chikira, M. (2014), Eastward‐propagating intraseasonal oscillation represented by Chikira–Sugiyama cumulus parameterization. Part II: Understanding moisture variation under weak temperature gradient balance, J. Atmos. Sci., 71(2), 615–639. [Google Scholar]
- Dee, D. , et al. (2011), The ERA‐Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. R. Meteorol. Soc., 137(656), 553–597. [Google Scholar]
- Fu, X. , and Wang B. (2009), Critical roles of the stratiform rainfall in sustaining the Madden–Julian oscillation: GCM experiments, J. Clim., 22(14), 3939–3959. [Google Scholar]
- Goswami, B. N. , and Xavier P. K. (2003), Potential predictability and extended range prediction of Indian summer monsoon breaks, Geophys. Res. Lett., 30(18), 1966, doi:10.1029/2003GL017810. [Google Scholar]
- Grabowski, W. W. (2003), MJO‐like coherent structures: Sensitivity simulations using the Cloud‐Resolving Convection Parameterization (CRCP), J. Atmos. Sci., 60, 847–864. [Google Scholar]
- Hazeleger, W. , et al. (2012), EC‐Earth V2. 2: Description and validation of a new seamless earth system prediction model, Clim. Dyn., 39(11), 2611–2629. [Google Scholar]
- Hirons, L. , Inness P., Vitart F., and Bechtold P. (2013), Understanding advances in the simulation of intraseasonal variability in the ECMWF model. Part II: The application of process‐based diagnostics, Q. J. R. Meteorol. Soc., 139(675), 1427–1444. [Google Scholar]
- Hsu, P.‐c. , and Li T. (2012), Role of the boundary layer moisture asymmetry in causing the eastward propagation of the Madden‐Julian Oscillation*, J. Clim., 25(14), 4914–4931. [Google Scholar]
- Hu, Q. , and Randall D. A. (1994), Low‐frequency oscillations in radiative‐convective systems, J. Atmos. Sci., 51(8), 1089–1099. [Google Scholar]
- Jiang, X. , Waliser D. E., Olson W. S., Tao W.‐K., L'Ecuyer T. S., Li K.‐F., Yung Y. L., Shige S., Lang S., and Takayabu Y. N. (2011), Vertical diabatic heating structure of the MJO: Intercomparison between recent reanalyses and TRMM estimates, Mon. Weather Rev., 139(10), 3208–3223. [Google Scholar]
- Jiang, X. , et al. (2015), Vertical structure and physical processes of the Madden‐Julian Oscillation: Exploring key model physics in climate simulations, J. Geophys. Res. Atmos., 120, doi:10.1002/2014JD022375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- John, V. , and Soden B. (2007), Temperature and humidity biases in global climate models and their impact on climate feedbacks, Geophys. Res. Lett., 34, L18704, doi:10.1029/2007GL030429. [Google Scholar]
- Khairoutdinov, M. , DeMott C., and Randall D. (2008), Evaluation of the simulated interannual and subseasonal variability in an AMIP‐style simulation using the CSU multiscale modeling framework, J. Clim., 21(3), 413–431. [Google Scholar]
- Khairoutdinov, M. F. , and Randall D. A. (2001), A cloud resolving model as a cloud parameterization in the NCAR community climate system model: Preliminary results, Geophys. Res. Lett., 28(18), 3617–3620. [Google Scholar]
- Khouider, B. , St‐Cyr A., Majda A. J., and Tribbia J. (2011), The MJO and convectively coupled waves in a coarse‐resolution GCM with a simple multicloud parameterization, J. Atmos. Sci., 68(2), 240–264. [Google Scholar]
- Kikuchi, K. , and Takayabu Y. N. (2004), The development of organized convection associated with the MJO during TOGA COARE IOP: Trimodal characteristics, Geophys. Res. Lett., 31, L10101, doi:10.1029/2004GL019601. [Google Scholar]
- Kiladis, G. N. , Straub K. H., and Haertel P. T. (2005), Zonal and vertical structure of the Madden–Julian oscillation, J. Atmos. Sci., 62(8), 2790–2809. [Google Scholar]
- Kim, D. , Sobel A. H., and Kang I.‐S. (2011), A mechanism denial study on the Madden‐Julian Oscillation, J. Adv. Model. Earth Syst., 3, M12007, doi:10.1029/2011MS000081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, D. , et al. (2014), Process‐oriented MJO simulation diagnostic: Moisture sensitivity of simulated convection, J. Clim., 27, 5379–5395. [Google Scholar]
- Klingaman, N. P. , et al. (2015a), Vertical structure and physical processes of the Madden‐Julian oscillation: Linking hindcast fidelity to simulated diabatic heating and moistening, J. Geophys. Res. Atmos., 120, doi:10.1002/2014JD022374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klingaman, N. P. , Jiang X., Xavier P. K., Petch J., Waliser D., and Woolnough S. J. (2015b), Vertical structure and physical processes of the Madden‐Julian Oscillation: Synthesis and summary, J. Geophys. Res. Atmos., 120, doi:10.1002/2015JD023196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kummerow, C. , et al. (2000), The status of the Tropical Rainfall Measuring Mission (TRMM) after two years in orbit, J. Appl. Meteorol., 39(12), 1965–1982. [Google Scholar]
- Lau, W. K. M. , and Waliser D. E. (2011), Intraseasonal Variability of the Atmosphere‐Ocean Climate System, 2nd ed., 613 pp., Springer, Heidelberg, Germany. [Google Scholar]
- Lee, M.‐I. , Kang I.‐S., Kim J.‐K., and Mapes B. E. (2001), Influence of cloud‐radiation interaction on simulating tropical intraseasonal oscillation with an atmospheric general circulation model, J. Geophys. Res., 106(D13), 14,219–14,233. [Google Scholar]
- Li, C. , Jia X., Ling J., Zhou W., and Zhang C. (2009), Sensitivity of MJO simulations to diabatic heating profiles, Clim. Dyn., 32(2–3), 167–187. [Google Scholar]
- Lin, J. , Mapes B., Zhang M., and Newman M. (2004), Stratiform precipitation, vertical heating profiles, and the Madden–Julian oscillation, J. Atmos. Sci., 61(3), 296–309. [Google Scholar]
- Lin, Y. , et al. (2012), TWP‐ICE global atmospheric model intercomparison: Convection responsiveness and resolution impact, J. Geophys. Res., 117, D09111, doi:10.1029/2011JD017018. [Google Scholar]
- Ling, J. , and Zhang C. (2011), Structural evolution in heating profiles of the MJO in global reanalyses and TRMM retrievals, J. Clim., 24(3), 825–842. [Google Scholar]
- Ma, H.‐Y. , Xie S., Boyle J., Klein S., and Zhang Y. (2013), Metrics and diagnostics for precipitation‐related processes in climate model short‐range hindcasts, J. Clim., 26(5), 1516–1534. [Google Scholar]
- Ma, H.‐Y. , et al. (2014), On the correspondence between mean forecast errors and climate errors in CMIP5 models, J. Clim., 27(4), 1781–1798. [Google Scholar]
- Madden, R. A. , and Julian P. R. (1971), Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific, J. Atmos. Sci., 28(5), 702–708. [Google Scholar]
- Majda, A. J. , and Stechmann S. N. (2009), A simple dynamical model with features of convective momentum transport, J. Atmos. Sci., 66(2), 373–392. [Google Scholar]
- Martin, G. , Milton S., Senior C., Brooks M., Ineson S., Reichler T., and Kim J. (2010), Analysis and reduction of systematic errors through a seamless approach to modeling weather and climate, J. Clim., 23(22), 5933–5957. [Google Scholar]
- McFarlane, S. A. , Mather J. H., and Ackerman T. P. (2007), Analysis of tropical radiative heating profiles: A comparison of models and observations, J. Geophys. Res., 112, D14218, doi:10.1029/2006JD008290. [Google Scholar]
- Merryfield, W. J. , Lee W.‐S., Boer G. J., Kharin V. V., Scinocca J. F., Flato G. M., Ajayamohan R., Fyfe J. C., Tang Y., and Polavarapu S. (2013), The Canadian seasonal to interannual prediction system. Part I: Models and initialization, Mon. Weather Rev., 141(8), 2910–2945. [Google Scholar]
- Mitovski, T. , Folkins I., Von Salzen K., and Sigmond M. (2010), Temperature, relative humidity, and divergence response to high rainfall events in the tropics: Observations and models, J. Clim., 23(13), 3613–3625. [Google Scholar]
- Miyakawa, T. , Takayabu Y. N., Nasuno T., Miura H., Satoh M., and Moncrieff M. W. (2012), Convective momentum transport by rainbands within a Madden‐Julian Oscillation in a global nonhydrostatic model with explicit deep convective processes. Part I: Methodology and general results, J. Atmos. Sci., 69(4), 1317–1338. [Google Scholar]
- Moncrieff, M. W. (2004), Analytic representation of the large‐scale organization of tropical convection, J. Atmo. Sci., 61(13), 1521–1538. [Google Scholar]
- Moncrieff, M. W. , Waliser D. E., Miller M. J., Shapiro M. A., Asrar G. R., and Caughey J. (2012), Multiscale convective organization and the yotc virtual global field campaign, Bull. Am. Meteorol. Soc., 93(8), 1171–1187. [Google Scholar]
- NCAR Command Language (2014), The NCAR Command Language (version 6.2.1) [software], UCAR/NCAR/CISL/VETS, Boulder, Colo., doi:10.5065/D6WD3XH5. [Google Scholar]
- Neale, R. B. et al. (2010), Description of the NCAR community atmosphere model (CAM 5.0), NCAR Tech. Note NCAR/TN‐486+ STR, Natl. Cent. for Atmos. Res., Boulder, Colo.
- Petch, J. , Willett M., Wong R., and Woolnough S. (2007), Modelling suppressed and active convection. Comparing a numerical weather prediction, cloud‐resolving and single‐column model, Q. J. R. Meteorol. Soc., 133(626), 1087–1100. [Google Scholar]
- Petch, J. , Waliser D., Jiang X., Xavier P., and Woolnough S. (2011), A global model intercomparison of the physical processes associated with the Madden–Julian oscillation, GEWEX News, 21, 3–5. [Google Scholar]
- Phillips, T. J. , Potter G. L., Williamson D. L., Cederwall R. T., Boyle J. S., Fiorino M., Hnilo J. J., Olson J. G., Xie S., and Yio J. J. (2004), Evaluating parameterizations in general circulation models: Climate simulation meets weather prediction, Bull. Am. Meteorol. Soc., 85(12), 1903–1915. [Google Scholar]
- Raymond, D. J. (2000), Thermodynamic control of tropical rainfall, Q. J. R. Meteorol. Soc., 126(564), 889–898. [Google Scholar]
- Rienecker, M. M. , et al. (2008), The GEOS‐5 data assimilation system—Documentation of versions 5.0.1, 5.1.0, and 5.2.0, in Technical Report Series on Global Modeling and Data Assimilation, vol. 27, edited by Suarez M. J., pp. 1–118, NASA, Washington, D. C. [Google Scholar]
- Schmidt, G. A. , et al. (2014), Configuration and assessment of the GISS ModelE2 contributions to the CMIP5 archive, J. Adv. Model. Earth Syst., 6, 141–184, doi:10.1002/2013MS000265. [Google Scholar]
- Seo, K.‐H. , and Wang W. (2010), The Madden‐Julian Oscillation simulated in the NCEP Climate forecast system model: The importance of stratiform heating, J. Clim., 23(18), 4770–4793. [Google Scholar]
- Shamarock, W. , Klemp J., Dudhia J., Gill D., Barker D., Duda M., Huang X., Wang W., and Powers J. (2008), A description of the advanced research WRF version 3, NCAR Tech. Note NCAR/TN/u2013475, Natl. Cent. for Atmos. Res., Boulder, Colo.
- Stephens, G. L. , and Webster P. J. (1981), Clouds and climate: Sensitivity of simple systems, J. Atmos. Sci., 38(2), 235–247. [Google Scholar]
- Stephens, G. L. , L'Ecuyer T., Forbes R., Gettlemen A., Golaz J.‐C., Bodas‐Salcedo A., Suzuki K., Gabriel P., and Haynes J. (2010), Dreary state of precipitation in global models, J. Geophys. Res., 115, D24211, doi:10.1029/2010JD014532. [Google Scholar]
- Stocker, T. F. , Qin D., Plattner G.‐K., Tignor M., Allen S. K., Boschung J., Nauels A., Xia Y., Bex V., and Midgley P. M. (2013), Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 1535 pp., Cambridge Univ. Press, Cambridge, U. K., and New York. [Google Scholar]
- Thayer‐Calder, K. , and Randall D. A. (2009), The role of convective moistening in the Madden‐Julian Oscillation, J. Atmos. Sci., 66(11), 3297–3312. [Google Scholar]
- Voldoire, A. , et al. (2013), The CNRM‐CM5. 1 global climate model: Description and basic evaluation, Clim. Dyn., 40(9–10), 2091–2121. [Google Scholar]
- von Salzen, K. , et al. (2013), The Canadian fourth generation atmospheric global climate model (CanAM4). Part I: Representation of physical processes, Atmos. Ocean, 51(1), 104–125. [Google Scholar]
- Waliser, D. E. , Lau K. M., Stern W., and Jones C. (2003), Potential predictability of the Madden‐Julian Oscillation, Bull. Am. Meteorol. Soc., 84, 33–50. [Google Scholar]
- Waliser, D. E. , et al. (2012), The year of tropical convection (May 2008‐April 2010): Climate variability and weather highlights, Bull. Am. Meteorol. Soc., 93(8), 1189–1218. [Google Scholar]
- Walters, D. , et al. (2011), The Met Office Unified Model global atmosphere 3.0/3.1 and JULES global land 3.0/3.1 configurations, Geosci. Model Dev. Discuss., 4(2), 919–941. [Google Scholar]
- Watanabe, M. , et al. (2010), Improved climate simulation by MIROC5: Mean states, variability, and climate sensitivity, J. Clim., 23(23), 6312–6335. [Google Scholar]
- Webster, P. J. , and Lukas R. (1992), TOGA COARE: The coupled ocean‐atmosphere response experiment, Bull. Am. Meteorol. Soc., 73(9), 1377–1416. [Google Scholar]
- Willett, M. , Bechtold P., Williamson D., Petch J., Milton S., and Woolnough S. (2008), Modelling suppressed and active convection: Comparisons between three global atmospheric models, Q. J. R. Meteorol. Soc., 134(636), 1881–1896. [Google Scholar]
- Williams, K. , Bodas‐Salcedo A., Deque M., Fermepin S., Medeiros B., Watanabe M., Jakob C., Klein S., Senior C., and Williamson D. (2013), The transpose‐AMIP II experiment and its application to the understanding of Southern Ocean cloud biases in climate models, J. Clim., 26(10), 3258–3274. [Google Scholar]
- Woolnough, S. J. , et al. (2010), Modelling convective processes during the suppressed phase of a Madden‐Julian Oscillation: Comparing single‐column models with cloud‐resolving models, Q. J. R. Meteorol. Soc., 136(647), 333–353. [Google Scholar]
- Xavier, P. K. (2012), Intraseasonal convective moistening in CMIP3 Models, J. Clim., 25(8), 2569–2577. [Google Scholar]
- Xie, S. , Ma H.‐Y., Boyle J. S., Klein S. A., and Zhang Y. (2012), On the correspondence between short‐and long‐time‐scale systematic errors in CAM4/CAM5 for the year of tropical convection, J. Clim., 25(22), 7937–7955. [Google Scholar]
- Yukimoto, S. , et al. (2012), A new global climate model of the Meteorological Research Institute: MRI‐CGCM3‐model description and basic performance–, J. Meteorol. Soc. Jpn., 90, 23–64. [Google Scholar]
- Zhang, C. (2005), Madden‐Julian Oscillation, Rev. Geophys., 43, RG2003, doi:10.1029/2004RG000158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, C. , Ling J., Hagos S., Tao W.‐K., Lang S., Takayabu Y. N., Shige S., Katsumata M., Olson W. S., and L”Ecuyer T. (2010), MJO signals in latent heating: Results from TRMM retrievals, J. Atmos. Sci., 67(11), 3488–3508. [Google Scholar]


