A Genealogical Look at Shared Ancestry on the X Chromosome

Abstract

Close relatives can share large segments of their genome identical by descent (IBD) that can be identified in genome-wide polymorphism data sets. There are a range of methods to use these IBD segments to identify relatives and estimate their relationship. These methods have focused on sharing on the autosomes, as they provide a rich source of information about genealogical relationships. We hope to learn additional information about recent ancestry through shared IBD segments on the X chromosome, but currently lack the theoretical framework to use this information fully. Here, we fill this gap by developing probability distributions for the number and length of X chromosome segments shared IBD between an individual and an ancestor k generations back, as well as between half- and full-cousin relationships. Due to the inheritance pattern of the X and the fact that X homologous recombination occurs only in females (outside of the pseudoautosomal regions), the number of females along a genealogical lineage is a key quantity for understanding the number and length of the IBD segments shared among relatives. When inferring relationships among individuals, the number of female ancestors along a genealogical lineage will often be unknown. Therefore, our IBD segment length and number distributions marginalize over this unknown number of recombinational meioses through a distribution of recombinational meioses we derive. By using Bayes’ theorem to invert these distributions, we can estimate the number of female ancestors between two relatives, giving us details about the genealogical relations between individuals not possible with autosomal data alone.

CLOSE relatives are expected to share large contiguous segments of their genome due to the limited number of crossovers per chromosome each generation (Fisher et al. 1949, 1954; Donnelly 1983). These large identical by descent (IBD) segments shared among close relatives leave a conspicuous footprint in population genomic data, and identifying and understanding this sharing is key to many applications in biology (Thompson 2013). For example, in human genetics, evidence of recent shared ancestry is an integral part of detecting cryptic relatedness in genome-wide association studies (Gusev et al. 2009), discovering misspecified relationships in pedigrees (Sun et al. 2002), inferring pairwise relationships (Epstein et al. 2000; Glaubitz et al. 2003; Huff et al. 2011), and localizing disease traits in pedigrees (Thomas et al. 2008). In forensics, recent ancestry is crucial both for accounting for population-level relatedness (Balding and Nichols 1994) and in familial DNA database searches (Belin et al. 1997; Sjerps and Kloosterman 1999). Additionally, recent ancestry detection methods have a range of applications in anthropology and ancient DNA to understand the familial relationships among sets of individuals (Keyser-Tracqui et al. 2003; Haak et al. 2008; Baca et al. 2012; Fu et al. 2015). In population genomics, recent ancestry has been used to learn about recent migrations and other demographic events (Palamara et al. 2012; Ralph and Coop 2013). An understanding of recent ancestry also plays a large role in understanding recently admixed populations, where individuals draw ancestry from multiple distinct populations (Pool and Nielsen 2009; Gravel 2012; Liang and Nielsen 2014). Finally, relative finding through recent genetic ancestry is increasingly a key feature of direct-to-consumer personal genomics products and an important source of information for genealogists (Royal et al. 2010; Durand et al. 2014).

Approaches to infer recent ancestry among humans have often used only the autosomes, as the recombining autosomes offer more opportunity to detect a range of relationships than the Y chromosome, mitochondria, or X chromosome. However, the nature of X chromosome inheritance means that it can clarify details of the relationships among individuals and be informative about sex-specific demography and admixture histories in ways that autosomes cannot (Ramachandran et al. 2004, 2008; Pool and Nielsen 2007; Bustamante and Ramachandran 2009; Bryc et al. 2010; Goldberg and Rosenberg 2015; Rosenberg 2016; Shringarpure et al. 2016).

In this article, we look at the inheritance of chromosomal segments on the X chromosome among closely related individuals. Our genetic ancestry models are structured around biparental genealogies back in time, an approach used by many previous authors (e.g., Donnelly 1983; Chang 1999; Rohde et al. 2004; Barton and Etheridge 2011). If we ignore pedigree collapse, the genealogy of a present-day individual encodes all biparental relationships back in time; e.g., the two parents, four grandparents, eight great-grandparents, $2^k$ ${\text{great}}^{k-2}$ grandparents, and in general the $2^k$ ancestors k generations back; and we refer to these individuals as one’s genealogical ancestors. Note that throughout this article, kth generation ancestors refers to the ancestors within generation k, not the total number of ancestors from generations 1 to k. A genealogical ancestor of a present-day individual is said to also be a genetic ancestor if the present-day individual shares genetic material by descent from this ancestor. We refer to these segments of shared genetic material as being identical by descent, and in doing so we ignore the possibility of mutation in the limited number of generations separating our individuals. Throughout this article, we ignore the pseudoautosomal region(s) (PAR) of the X chromosome, which undergoes crossing over with the Y chromosome in males (Koller and Darlington 1934) to ensure proper disjunction in meiosis I (Hassold et al. 1991). We also ignore gene conversion that is known to occur on the X (Rosser et al. 2009).

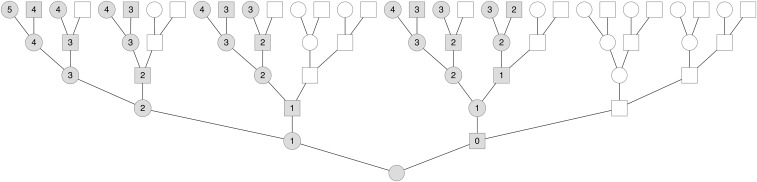
Here, we are concerned with inheritance through the X genealogy embedded inside an individual’s genealogy, which includes only the subset of one’s genealogical ancestors who could have possibly contributed to one’s non-PAR X chromosome. We refer to the individuals in this X genealogy as X ancestors. Since males receive an X only from their mothers, a male’s father cannot be an X ancestor. Consequently, a male’s father and all of his ancestors are excluded from the X genealogy (Figure 1). Therefore, females are overrepresented in the X genealogy, and as we go back in one’s genealogy, the fraction of individuals who are possible X ancestors shrinks. This property means that genetic relationships differ on the X compared to the autosomes, a fact that changes the calculation of kinship coefficients on the X (Pinto et al. 2011, 2012) and also has interesting implications for kin-selection models involving the X chromosome (Rice et al. 2008; Fox et al. 2009).

Figure 1.

A genealogy back five generations with the embedded X genealogy. Males are depicted as squares and females as circles. Individuals in the X genealogy are shaded while unshaded individuals are ancestors that are not X ancestors. Each X ancestor is labeled with the number of recombinational meioses to the present-day female.

In the Autosomal Ancestry section (and in the Appendix) we review models of autosomal identity by descent among relatives, on which we base our models of X genetic ancestry. Then, in the X Ancestry section we look at X genealogies, as their properties affect the transmission of X genetic material from X ancestors to a present-day individual. We develop simple approximations to the probability distributions of the number and length of X chromosome segments that will be shared IBD between a present-day female and one of her X ancestors a known number of generations back. These models provide a set of results for the X chromosome equivalent to those already known for the autosomes (Donnelly 1983; Thomas et al. 1994). Then, in the Shared X Ancestry section, we look at shared X ancestry—when two present-day cousins share an X ancestor a known number of generations back. We calculate the probabilities that genealogical half and full cousins are also connected through their X genealogy and thus can potentially share genetic material on their X. We then extend our models of IBD segment length and number to segments shared between half and full cousins. Finally, in the Inference section we show that shared X genetic ancestry contains additional information (compared to genetic autosomal ancestry) for inferring relationships among individuals and explore the limits of this information.

Autosomal Ancestry

To facilitate comparison with our X chromosome results, we first briefly review analogous autosomal segment number and segment length distributions (Donnelly 1983; Thomas et al. 1994; Huff et al. 2011). Throughout this article, we assume that one’s genealogical ancestors k generations back are distinct (e.g., there is no inbreeding); i.e., there is no pedigree collapse due to inbreeding (see Appendix for a model of how this assumption breaks down with increasing k). Thus, an individual has $2^k$ distinct genealogical ancestors. Assuming no selection and fair meiosis, a present-day individual’s autosomal genetic material is spread across these $2^k$ ancestors with equal probability, having been transmitted to the present-day individual solely through recombination and segregation.

We model the process of crossing over during meiosis as a continuous-time Markov process along the chromosome, as in Thomas et al. (1994) and Huff et al. (2011) and described by Donnelly (1983). In doing so we assume no crossover interference, such that in each generation b recombinational breakpoints occur as a Poisson process running with a uniform rate equal to the total length of the genetic map (in morgans), ν. Within a single chromosome, b breaks create a mosaic of $b+1$ alternating maternal and paternal segments. This alternation between maternal and paternal haplotypes creates long-run dependency between segments (Liang and Nielsen 2014). We ignore these dependencies in our analytic models by assuming that each chromosomal segment survives segregation independently with probability 1/2 per generation. For d independent meioses separating two individuals, we imagine the Poisson recombination process running at rate $\nu d,$ and for a segment to be shared IBD between the two ancestors it must survive $1/2^d$ segregations. Consequently, the expected number of segments shared IBD between two individuals d meioses apart in a genome with c chromosomes is approximated as (Thomas et al. 1994)

$$\mathbb{E}\left[N\right]=\frac{1}{2^d}\left(\nu d+c\right).$$ (1)

Intuitively, we can understand the $1/2^d$ factor as the coefficient of kinship [or path coefficient (Wright 1922, 1934)] of two individuals d meioses apart, which gives the probability that two alleles are shared IBD between these two individuals. Then, the expected number of IBD segments $\mathbb{E}\left[N\right]$ can be thought of as the average number of alleles shared between two individuals in a genome with $\nu d\mathrm{+}c$ loci total. Under this approximation, recombination increases the number of independent loci linearly each generation (by a factor of the total genetic length). A fraction $1/2^d$ of parental alleles at these loci survive the d meioses to be IBD with the present-day individual.

By convention, we count the number of contiguous IBD segments N in the present-day individual, not the number of contiguous segments in the ancestor. For example, an individual will share exactly one block per chromosome with each parent if we count the contiguous segments in the offspring, even though these segments may be spread across the parent’s two homologs. This convention, which we use throughout the article, is identical to counting the number of IBD segments that occur in $d-1$ meioses rather than d meioses. This convention affects only models of segments shared IBD between an individual and one of its ancestors; neither the distribution of segment lengths nor the distributions for segment number shared IBD between cousins are affected by this convention.

The distribution of IBD segments between a present-day individual and an ancestor

Given that a present-day individual and an ancestor in the kth generation are separated by k meioses, the number of IBD segments can be modeled with what we call the Poisson-binomial approximation. Over $d=k$ meioses, $B=b\mathrm{\sim Pois}\left(\nu k\right)$ recombinational breakpoints fall on c independently assorting chromosomes, creating $b+c$ segments. Ignoring long-range dependencies, we assume all of these $b+c$ segments have an independent chance of surviving the k segregations to the present-day individual, and thus the probability that n segments survive given $b+c$ trials is binomially distributed with probability $1/2^k.$ Marginalizing over the unobserved number of recombinational breakpoints b and replacing k with $k-1$ to follow the convention described above,

$$P\left(N=n|k\right)={\displaystyle \sum _{b=0}^{\mathrm{\infty }}\mathrm{Bin}\left(N=n|l=b+c,p=1/2^{k-1}\right)}\times \mathrm{Pois}\left(B=b|\lambda =\nu \left(k-1\right)\right).$$ (2)

The expected value of the Poisson-binomial model is given by Equation 1 with $d=k-1$ and this model is similar to those of Donnelly (1983) and Thomas et al. (1994). We can further approximate this by assuming that we have a Poisson total number of segments with mean $\left(c+\nu \left(k-1\right)\right)$ and these segments are shared with probability $1/2^{k-1}$ as in Huff et al. (2011). This gives us a thinned Poisson distribution of shared segments:

$$\begin{array}{c}P\left(N=n|k,\nu ,c\right)=\mathrm{Pois}\left(N=n|\lambda =\left(c+\nu \left(k-1\right)\right)/2^{k-1}\right)\\ =\frac{{\left(\left(c+\nu \left(k-1\right)\right)/2^{k-1}\right)}^n{e}^{-\left(c+\nu \left(k-1\right)\right)/2^{k-1}}}{n\mathrm{!}}.\end{array}$$ (3)

This thinned Poisson model also has an expectation given by Equation 1 but compared to the Poisson-binomial model has a larger variance than the true process. This overdispersion occurs because modeling the number of segments created after b breakpoints involves incorporating the initial number of chromosomes into the Poisson rate. However, this initial number of chromosomes is actually fixed, which the Poisson-binomial model captures but the Poisson-thinning model does not [i.e., one generation back such that $k=1,$ the thinning model treats the number of segments shared IBD with one’s parents as $\mathit{N}\mathrm{\sim Pois}\left(c\right)$ rather than c]. See the Appendix for a further comparison of these two models. A more formal description of this approximation as a continuous-time Markov process is given in Thomas et al. (1994). In the Appendix, we describe similar results for the number of autosomal segments shared between cousins and the length distributions of autosomal segments.

We use similar models to these in modeling the length and number of X chromosome segments shared been relatives. However, the nature of X genealogies (which we cover in the next section) requires we adjust these models. Specifically, while one always has k recombinational meioses between an autosomal ancestor in the kth generation, the number of recombinational meioses varies across the lineages to an X ancestor with the number of females in a lineage, since X homologous recombination occurs only in females (Figure 1). This varying number of recombinational meioses across lineages leads to a varying-rate Poisson recombination process, with the rate depending on the specific lineage to the X ancestor. After we take a closer look at X genealogies in the next section, we adapt the models above to handle the varying-rate Poisson process needed to model IBD segments in X genealogies.

X Ancestry

Number of genealogical X ancestors

While a present-day individual can potentially inherit autosomal segments from any of its $2^k$ genealogical ancestors k generations back, only a fraction of these individuals can possibly share segments on the X chromosome. In contrast to biparental genealogies, males have only one genealogical X ancestor—their mothers—if we ignore the PAR. This constraint (which we refer to throughout as the no two adjacent males condition) shapes both the number of X ancestors and the number of females along an X lineage. For example, consider a present-day female’s X ancestors one generation back: Both her father and mother contribute X chromosome material. Two generations back, she has three X genealogical ancestors: Her father inherits an X only from her paternal grandmother, while her mother can inherit X material from either parent. Continuing this process, this individual has five X ancestors three generations back and eight ancestors four generations back (Figure 1).

In general, a present-day female’s X genealogical ancestors are growing as a Fibonacci series (Laughlin 1920; Basin 1963), such that k generations back she has ${\mathrm{ℱ}}_{k+2}$ X genealogical ancestors, where ${\mathrm{ℱ}}_k$ is the kth Fibonacci number [where k is 0 indexed and the series begins $F_0=0,F_1=1,\mathrm{\dots };$ Online Encyclopedia of Integer Sequences reference A000045 (Sloane 2010)]. We can demonstrate that one’s number of X genealogical ancestors ($n_k$) grows as a Fibonacci series by encoding the X inheritance rules for the number of males and females ($m_k$ and $f_k,$ respectively) in the kth generation as a set of recurrence relations:

$f_k=n_{k-1}$	Every individual receives an X chromosome from his/her mother
$m_k=f_{k-1}$	Every female receives an X chromosome from her father
$n_k=f_k+m_k$

Rearranging these recurrence equations gives us $n_k=n_{k-1}+n_{k-2},$ which is the Fibonacci recurrence. Starting with a female in the $k=0$ generation, we have initial values $n_0=1$ and $n_1=2,$ which gives us the Fibonacci numbers offset by two, ${\mathrm{ℱ}}_{k+2}.$ For a present-day male, his number of X ancestors is ${\mathrm{ℱ}}_{k+1},$ i.e., offset by one to count the number of X ancestors his mother has. To simplify our expressions, we assume throughout this article that all-present day individuals are female since a simple offset can be made to handle males.

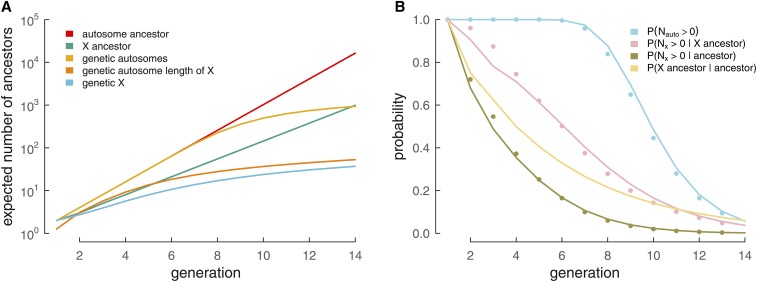
In Figure 2A we show the increase in the number of X genealogical and genetic ancestors (green and light blue) and compare these to the growth of all of one’s genealogical ancestors and autosomal genetic ancestors. The closed-form solution for the kth Fibonacci number is given by Binet’s formula $\left({\mathrm{ℱ}}_n=\left({\left(1+\sqrt{5}\right)}^n-{\left(1-\sqrt{5}\right)}^n\right)/\left(2^n\sqrt{5}\right)\right),$ which shows that the Fibonacci sequence grows at an exponential rate slower than $2^k.$

Figure 2.

How the number of genetic and genealogical ancestors and probabilities of sharing genetic material vary back through the generations for different cases. (A) Each line represents a present-day female’s expected number of ancestors (y-axis) in the kth generation (x-axis; where $k=1$ is the parental generation), for a variety of cases. The present-day female’s number of genealogical ancestors in the kth generation is in red, and the expected number of these ancestors that contribute any autosome genetic material is in yellow. Likewise, the present-day female’s number of genealogical X ancestors is in green, and the expected number of these ancestors that contribute any X genetic material is in blue. For comparison, the number of genetic ancestors of an autosome of length equal to the X is included (orange). (B) The probability of genealogical and genetic ancestry (y-axis) from an arbitrary ancestor in the kth generation (x-axis). $P\left(N_{\mathrm{auto}}>0\right)$ is derived from equation (The distribution of IBD segments between a present-day individual and an ancestor), $P\left(N_{\mathrm{X}}>0|\text{X}\hspace{0.17em}\text{ancestor}\right)$ from Equation 8, $P\left(N_{\mathrm{X}}>0|\text{ancestor}\right)$ from Equations 8 and 4, and $P\left(\text{X}\hspace{0.17em}\text{ancestor}|\text{ancestor}\right)$ from Equation 4. Circles show simulated results.

Consequently, the fraction of ancestors who can contribute to the X chromosome declines with k. Given that a female has ${\mathrm{ℱ}}_{k+2}$ X ancestors and $2^k$ genealogical distinct ancestors, her proportion of X ancestors is

$$P\left(\text{X}\hspace{0.17em}\text{ancestor}|\text{ancestor}\right)=\frac{{\mathrm{ℱ}}_{k+2}}{2^k}.$$ (4)

This fraction can also be interpreted as the probability that a randomly chosen genealogical ancestor k generations ago is also an X genealogical ancestor. We show this probability as a function of generations into the past in Figure 2B (yellow line).

From our recurrence equations we can see that a present-day female’s ${\mathrm{ℱ}}_{k+2}$ ancestors in the k^th generation are composed of ${\mathrm{ℱ}}_{k+1}$ females and ${\mathrm{ℱ}}_k$ males. Likewise for a present-day male, his ${\mathrm{ℱ}}_{k+1}$ ancestors in the kth generation are composed of ${\mathrm{ℱ}}_k$ females and ${\mathrm{ℱ}}_{k-1}$ males. We use these results when calculating the probability of a shared X ancestor.

Ancestry simulations

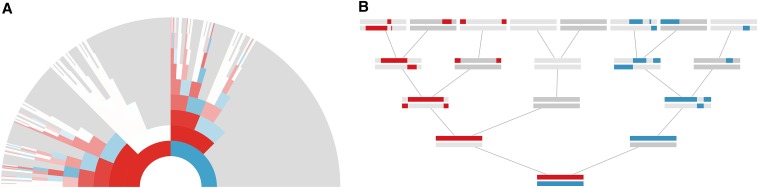
In the next sections, we use stochastic simulations to verify the analytic approximations we derive; here we briefly describe the simulation methods. We have written an X genealogy simulation procedure (source code available in 6 Supplemental Material, File S1 and at https://github.com/vsbuffalo/x-ancestry/), using C (Kernighan 1978), Python (Rossum, 1995), and analyzed the data using R (R Core Team 2015; Ram and Wickham 2015; Wickham 2009; Wickham 2016b; Wickham and Francois 2015). We simulate a female’s X chromosome genetic ancestry back through her X genealogy. Figure 3 visualizes the X genetic ancestors of one simulated example X genealogy back nine generations to illustrate this process. Each simulation begins with two present-day female X chromosomes, one of which is passed to her mother and one to her father. Segments transmitted to a male ancestor are simply passed directly back to his mother (without recombination). For segments passed to a female ancestor, we place a Poisson number of recombination breakpoints (with mean ν) on the X chromosome and the segment is broken where it overlaps these recombination events. The first segment along the chromosome is randomly drawn to have been inherited from either her mother or her father, and we alternate this choice for subsequent segments. This procedure repeats until the target generation back to k is reached. The segments in the k-generation ancestors are then summarized as either counts (number of IBD segments per individual) or lengths. These simulations are necessarily approximate as they ignore crossover interference. However, unlike our analytic approximations, our simulation procedure maintains long-run dependencies created during recombination, allowing us to see the extent to which assuming independent segment survival adversely affects our analytic results.

Figure 3.

Graphical representations of an example X chromosome genealogy. (A) Simulated X genealogy of a present-day female, back nine generations. Each arc is an ancestor, with female ancestors colored red and male ancestors colored blue. The transparency of each arc reflects the genetic contribution of this ancestor to the present-day female. White arcs correspond X genealogical ancestors that share no genetic material with the present-day female, and gray arcs are genealogical ancestors that are not X ancestors. (B) The X segments of the simulation in A, back five generations. The maternal X lineage’s segments are colored red, and the paternal X segments are colored blue. A male ancestor’s sex chromosomes are colored dark gray (and include the Y) and a female ancestor’s sex chromosomes are colored light gray.

The number of recombinational meioses along an unknown X lineage

If we pick an ancestor at random k generations ago, the probability that they are an X genealogical ancestor is given by Equation 4. We can now extend this logic and ask the following: Having randomly sampled an X genealogical ancestor, how many recombinational meioses (i.e., females) lie in the lineage between a present-day individual and this ancestor? Since IBD segment number and length distributions are parameterized by a rate proportional to the number of recombination events, this quantity is essential to our further derivations. Specifically, if there is uncertainty about the particular lineage between a present-day female and one of her X ancestors k generations back (such that all of the ${\mathrm{ℱ}}_{k+2}$ lineages to an X ancestor are equally probable), the number of females (thus, recombinational meioses) that occur is a random variable R. By the no two adjacent males condition, the possible number of females R is constrained; R has a lower bound of $\lfloor k/2\rfloor ,$ which corresponds to male–female alternation each generation to an ancestor in the kth generation. Similarly, the upper bound of R is k, since it is possible every individual along one X lineage is a female. Noting that an X genealogy extending back k generations enumerates every possible way to arrange r females such that none of the $k-r$ males are adjacent, we find that the number of ways of arranging r such females this way is

$$\left(\begin{array}{c}r+1\\ k-r\end{array}\right).$$ (5)

For some readers, it may be useful to visualize the relationship between the numbers of recombinational meioses across the generations, using Pascal’s triangle (Figure 4). The sequence of recombinational meioses is related to a known integer sequence; see Online Encyclopedia of Integer Sequences reference A030528 (Sloane 2010) for a description of this sequence and its other applications.

Figure 4.

The number of individuals (black numbers) with r recombinational meioses (each diagonal, labeled at base of triangle) for a generation k (each row). This encodes the number of recombinational meioses as the binomial coefficient $\left(\begin{array}{c}r+1\\ k-r\end{array}\right).$ Each value is further decomposed into the number of recombinational meioses from the female (red value, upper left) and male (blue value, upper right) lineages. Each black value is calculated by adding the black number to the left in the row above (the number of recombinational meioses from the maternal side) and the black number two rows directly above (the number of recombinational meioses from the paternal side). The sum of each row (fixed k) is a Fibonacci number and the values in the diagonal corresponding to a fixed value of r are binomial coefficients. Reading from the top left side to the bottom right corner, Pascal’s triangle is contained in the red, blue, and black numbers.

If we pick an X genealogical ancestor at random k generations ago, the probability that there are r female meioses along the lineage leading to this ancestor is

$$P_R\left(R=r|k\right)=\frac{\left(\begin{array}{c}r+1\\ k-r\end{array}\right)}{{\mathrm{ℱ}}_{k+2}}.$$ (6)

In the Appendix, we derive a generating function for the number of recombinational meioses. We can use this generating function to obtain properties of this distribution such as the expected number of recombinational meioses. We can show that the expected number of recombinational meioses converges rapidly to $\mathbb{E}\left[R\right]\approx \left(\varphi /\sqrt{5}\right)\hspace{0.17em}k$ with increasing k, where φ is the golden ratio, $\left(1+\sqrt{5}\right)/2.$

The distribution of number of segments shared with an X ancestor

Using the distribution of recombinational meioses derived in the last section, we now derive a distribution for the number of IBD segments shared between a present-day individual and an X ancestor in the kth generation. For clarity, we first derive the number of IBD segments counted in the parents (i.e., not following the convention described in the Autosomal Ancestry section), but we can adjust this simply by replacing k with $k-1.$

First, we calculate the probability of a present-day individual sharing $N=n$ IBD segments with an X genealogical ancestor k generations in the past, where it is known that there are $R=r$ females (and thus recombinational meioses) along the lineage to this ancestor. This probability uses the Poisson-binomial model described in Equation 2.

$$P\left(N=n|r,k,\nu \right)={\displaystyle \sum _{b=0}^{\mathrm{\infty }}\mathrm{Bin}\left(N=n|l=b+1,p=1/2^r\right)}\times \mathrm{Pois}\left(B=b|\lambda =\nu r\right).$$ (7)

Note that once we have conditioned on the number of recombinational meioses r, the lineages to an X ancestor are interchangeable; the specific X lineage affects recombination (and thus the IBD number and length distributions) only through the number of recombinational meioses along the lineage.

If we consider an X genealogical ancestor k generations back, this individual could be any of the present-day female’s ${\mathrm{ℱ}}_{k+2}$ X ancestors. Since the particular lineage to this ancestor is unknown, we marginalize over all possible numbers of recombinational meioses that could occur:

$$\begin{array}{c}P\left(N=n|k,\nu \right)={\displaystyle \sum _{r=\lfloor k/2\rfloor }^k{\displaystyle \sum _{b=0}^{\mathrm{\infty }}\mathrm{Bin}\left(N=n|l=b+1,p=1/2^r\right)}}\times \hspace{0.17em}\mathrm{Pois}\left(B=b|\lambda =\nu r\right)\hspace{0.17em}\frac{\left(\begin{array}{c}r+1\\ k-r\end{array}\right)}{{\mathrm{ℱ}}_{k+2}}\\ ={\displaystyle \sum _{r=\lfloor k/2\rfloor }^k{\displaystyle \sum _{b=0}^{\mathrm{\infty }}\left(\begin{array}{c}b+1\\ n\end{array}\right)1/2^{rn}{\left(1-1/2^r\right)}^{b-n+1}}}\times \frac{{\left(\nu r\right)}^b{e}^{-\nu r}}{b\mathrm{!}}\frac{\left(\begin{array}{c}r+1\\ k-r\end{array}\right)}{{\mathrm{ℱ}}_{k+2}}.\end{array}$$

For the distribution of number of IBD segments counted in the offspring, we substitute $k-1$ for k:

$$P\left(N=n|k,\nu \right)={\displaystyle \sum _{r=\lfloor \left(k-1\right)/2\rfloor }^{k-1}{\displaystyle \sum _{b=0}^{\mathrm{\infty }}\mathrm{Bin}\left(n|l=b+1,p=1/2^r\right)}}\mathrm{\times Pois}\left(B=b|\lambda =\nu r\right)\times \frac{\left(\begin{array}{c}r+1\\ k-r-1\end{array}\right)}{{\mathrm{ℱ}}_{k+1}}.$$ (8)

In this formulation, if $k=1,$ $r=0.$ In this case, the lack of recombinational meioses implies $b=0,$ such that a present-day female shares $n=1$ X chromosomes with each of her two parents in the $k=1$ generation with certainty. These segment number distributions are visualized in Figure 5 (light blue lines) alongside simulated results (gray circles).

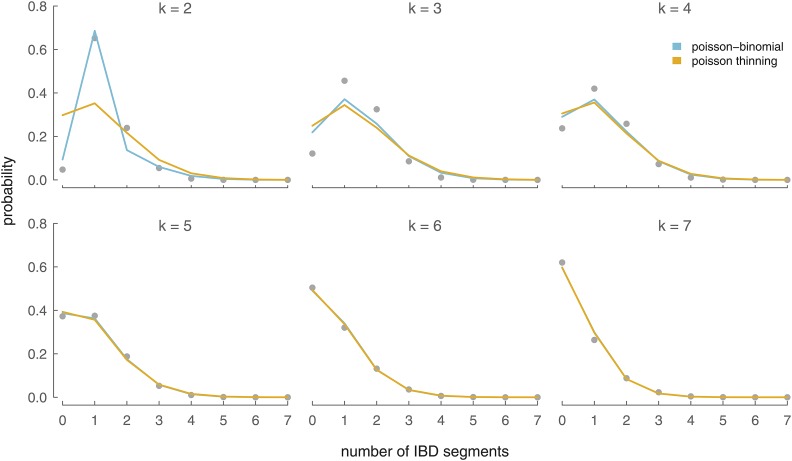
Figure 5.

The Poisson thinning (yellow lines) and Poisson-binomial (blue lines) analytic distributions of IBD segment number between an X ancestor in the kth generation (each panel) and a present-day female. Simulation results averaged over 5000 simulations are the gray circles.

We can use our Equation 8 to obtain $P\left(N>0\right),$ the probability that a genealogical X ancestor k generations ago is a genetic ancestor. This probability over $k\in \left\{1,2,\dots ,14\right\}$ generations is shown in Figure 2B. For comparison, Figure 2B also includes the probability of a genealogical ancestor in the kth generation being an autosomal genetic ancestor and the probability of being a genetic X ancestor unconditional on being an X genealogical ancestor.

We have also assessed the Poisson-thinning approach to modeling X IBD segment number. As with the Poisson-binomial model, we marginalize over R,

$$P\left(N=n|k,\nu \right)={\displaystyle \sum _{r=r_M}^{k-1}\mathrm{Pois}\left(B=b|\lambda =\left(1+\nu r\right)/2^r\right)}\times \frac{\left(\begin{array}{c}r+1\\ k-r-1\end{array}\right)}{{\mathrm{ℱ}}_{k+1}},$$ (9)

where $r_M=\lfloor \left(k-1\right)/2\rfloor .$

In Figure 5 we have compared the Poisson-binomial and Poisson-thinning approximations for the number of IBD segments (counted in the offspring) shared between an X ancestor in the kth generation and a present-day female. Overall, the analytic approximations are close to the simulation results, with the Poisson-binomial model a closer approximation for small k and both models’ accuracy improving quickly with increasing k. For a single chromosome (like the X), the Poisson-thinning model offers a notable worse fit than it does for the autosomes due to overdispersion (see Appendix for details). Throughout this article, we use the more accurate Poisson-binomial model rather than this Poisson-thinning model. If only X ancestry more than three generations back is of interest, the Poisson-thinning approach may be used without much loss of accuracy.

The distribution of IBD segment lengths with an X ancestor

The distribution of IBD segment lengths between a present-day female and an unknown X genealogical ancestor in the kth generation is similar to the autosomal length distribution described in the Appendix (Equation A2). However, with uncertainty about the particular lineage to the X ancestor, the number of recombinational meioses can vary between $\lfloor k/2\rfloor \le r\le k;$ we marginalize over the unknown number of recombinational meioses, using the distribution Equation 6. Our length density function is

$$p\left(U=u|k\right)={\displaystyle \sum _{r=\lfloor k/2\rfloor }^{k}r{e}^{-ru}\frac{\left(\begin{array}{c}r+1\\ k-r\end{array}\right)}{{\mathrm{ℱ}}_{k+2}}}.$$ (10)

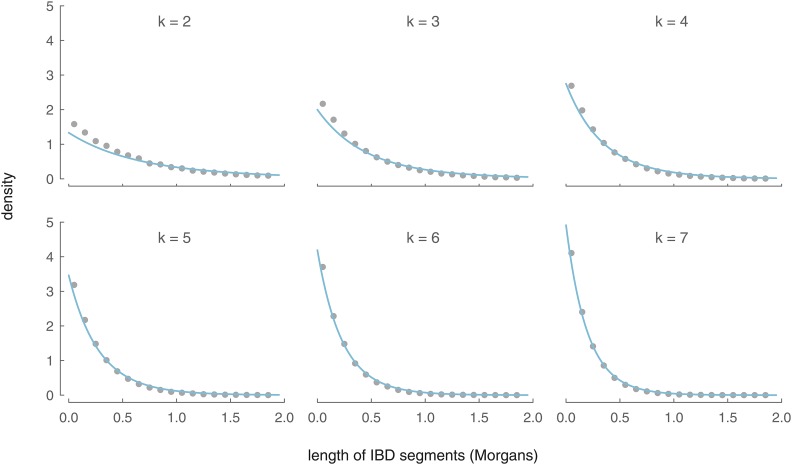
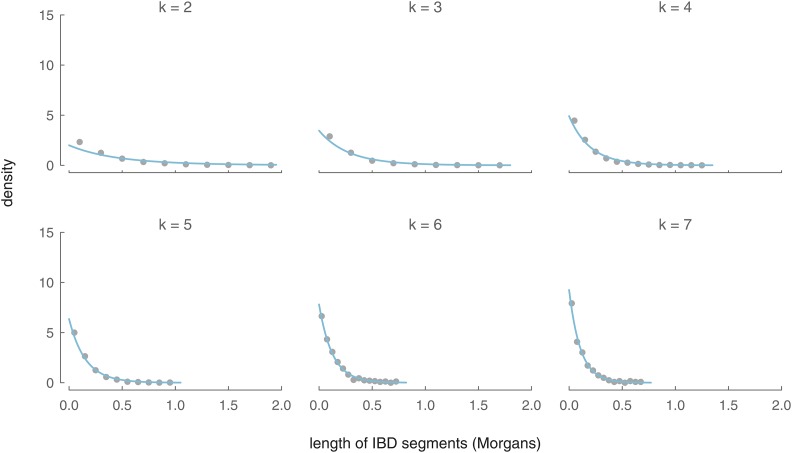
In Figure 6, we compare our analytic length density to an empirical density of X segment lengths calculated from 5000 simulations. As with our IBD segment number distributions, our analytic model is close to the simulated data’s empirical density and converges rapidly with increasing k.

Figure 6.

The analytic distributions of IBD segment length between an ancestor in the kth generation (for $k\in \left\{2,\dots ,7\right\}$) and a present-day female (blue lines) and the binned average over 5000 simulations (gray circles).

Note that both the IBD segment length and number distributions marginalize over an unobserved number of recombinational meioses (R) that occur along the lineage between individuals. As the IBD segments shared between two individuals is a function of the number breakpoints B, and thus recombinational meioses, the length and number distributions $P\left(N=n\right)$ and $p\left(U=u\right)$ (which separately marginalize over both R and B) are not independent of one another.

Shared X Ancestry

Because only a fraction of one’s genealogical ancestors are X ancestors (and this fraction rapidly decreases with k; see Equation 4), two individuals sharing X segments IBD from a recent ancestor considerably narrows the possible ancestors they could share. In this section, we describe the probability that a genealogical ancestor is an X ancestor and the distributions for IBD segment number and length across full- and half-cousin relationships. For simplicity we concentrate on the case where the cousins share a genealogical ancestor k generations ago in both of their pedigrees; i.e., the individuals are $k-1$-degree cousins. The formulas could be generalized to ancestors of unequal generational depths (e.g., second cousins once removed) but we do not pursue this here.

Probability of a shared X ancestor

Two individuals share their first common genealogical ancestor in the kth generation if one of an individual’s $2^k$ ancestors is also one of the other individual’s ancestors k generations back. Given this shared ancestor, we can calculate the probability that this single ancestor is also an X genealogical ancestor. Since this shared ancestor must be of the same sex in each of the two present-day individuals’ genealogies, we condition on the ancestor’s sex (with probability $1/2$ each) and then calculate the probability that this individual is also an X ancestor (with the same sex). Let us define $N_{\mathrm{♀}}$ and $N_{\mathrm{♂}}$ as the number of genealogical female and male ancestors and $N_{\mathrm{♀}}^{\mathrm{X}}$ and $N_{\mathrm{♂}}^{\mathrm{X}}$ as the number of X female and male ancestors of a present-day individual in the kth generation. Then

$$\begin{array}{l}P\left(\text{shared}\hspace{0.17em}\text{X}\hspace{0.17em}\text{ancestor}|\text{shared}\hspace{0.17em}\text{ancestor}\hspace{0.17em}k\hspace{0.17em}\text{generations}\right)\\ =\frac{N_{\mathrm{♀}}}{2^k}{\left(\frac{N_{\mathrm{♀}}^{\mathrm{X}}}{N_{\mathrm{♀}}}\right)}^2+\frac{N_{\mathrm{♂}}}{2^k}{\left(\frac{N_{\mathrm{♂}}^{\mathrm{X}}}{N_{\mathrm{♂}}}\right)}^2\\ =\frac{1}{2}{\left(\frac{{\mathrm{ℱ}}_{k+1}}{2^{k-1}}\right)}^2+\frac{1}{2}{\left(\frac{{\mathrm{ℱ}}_k}{2^{k-1}}\right)}^2.\end{array}$$ (11)

Thus, the probability that a shared genealogical ancestor is also a shared X ancestor is decreasing at an exponential rate. By the eighth generation, a shared genealogical ancestor has a <5% chance of being a shared X ancestor of both present-day individuals.

The sex of shared ancestor

Unlike genealogical ancestors—which are equally composed of males and females—recent X genealogical ancestors are predominantly female. Since a present-day female has ${\mathrm{ℱ}}_{k+1}$ female ancestors and ${\mathrm{ℱ}}_k$ male ancestors k generations ago, the ratio of female to male X genealogical ancestors converges to the golden ratio $\varphi =\left(1+\sqrt{5}\right)/2$ (Simson 1753):

$$\underset{k\to \mathrm{\infty }}{\lim }\frac{{\mathrm{ℱ}}_{k+1}}{{\mathrm{ℱ}}_k}=\mathit{\varphi }\mathit{.}$$ (12)

In modeling the IBD segment number and length distributions between present-day individuals, the sex of the shared ancestor k generations ago affects the genetic ancestry process in two ways. First, a female shared ancestor allows the two present-day individuals to share segments on either of her two X chromosomes while descendants of a male shared ancestor share IBD segments only through his single X chromosome. Second, the no two adjacent males condition implies a male shared X genealogical ancestor constrains the X genealogy such that the present-day X descendants are related through his two daughters. Given that the ratio of female to male X ancestors is skewed, our later distributions require an expression for the probability that a shared X ancestor in the kth generation is female, which we work through in this section.

As in Equation 11, an ancestor shared in the kth generation of two present-day individuals’ genealogies must have the same sex in each genealogy. Assuming both present-day cousins are females, in each genealogy there are ${\mathrm{ℱ}}_k$ possible male ancestors and ${\mathrm{ℱ}}_{k+1}$ female ancestors that could be shared. Across each present-day female’s genealogies there are ${\left({\mathrm{ℱ}}_k\right)}^2$ possible male ancestor combinations and ${\left({\mathrm{ℱ}}_{k+1}\right)}^2$ possible female ancestor combinations. Thus, if we let ${\mathrm{♀}}_{\mathrm{X}}$ and ${\mathrm{♂}}_{\mathrm{X}}$ denote that the sex of the shared ancestor is female and male, respectively, the probability of a female shared ancestor is

$$P\left({\mathrm{♀}}_{\mathrm{X}}\right)=\frac{{\left({\mathrm{ℱ}}_{k+1}\right)}^2}{{\left({\mathrm{ℱ}}_k\right)}^2+{\left({\mathrm{ℱ}}_{k+1}\right)}^2}.$$ (13)

The probability that the shared ancestor is male is simply $1-P\left({\mathrm{♀}}_{\mathrm{X}}\right).$ One curiosity is that as $k\to \mathrm{\infty },$ $P\left({\mathrm{♀}}_{\mathrm{X}}\right)\to \varphi /\sqrt{5}=\left(5+\sqrt{5}\right)/10\approx 0.7236,$ where ϕ is the golden ratio.

Partnered shared ancestors

Thus far, we have looked at only two present-day individuals sharing a single X ancestor k generations back. In monogamous populations, most shared ancestry is likely to descend from two ancestors; we call such relationships partnered shared ancestors. In this section, we look at full cousins descending from two shared genealogical ancestors that may also be X ancestors. Two full cousins could (1) both descend from two X ancestors such that they are X full cousins; (2) share only one X ancestor, such that they are X half cousins; or (3) share no X ancestry. We calculate the probabilities associated with each of these events here.

Two individuals are full cousins if the ${\text{great}}^{k-2}$ grandfather and the ${\text{great}}^{k-2}$ grandmother in one individual’s genealogy are in the other individual’s genealogy. For these two full cousins to be X full cousins, this couple must also be a couple in both individuals’ X genealogies. In every X genealogy, the number of couples in generation k is the number of females in generation $k-1,$ as every female has two X ancestors in the prior generation (while males have only one). Thus, the probability two female $k-1$-degree full cousins are also X full cousins is

$$P\left(\text{X}\hspace{0.17em}\text{full cousins}|\text{full cousins}\right)={\left(\frac{{\mathrm{ℱ}}_k}{2^{k-1}}\right)}^2.$$ (14)

Now, we consider the event that two genealogical full cousins are X half cousins. Being X half cousins implies that the partnered couple these full cousins descend from includes a single ancestor that is in the X genealogies of both full cousins. This single X ancestor must be a female, as a male X ancestor’s female partner must also be an X ancestor (since mothers must pass an X). For a female to be an X ancestor but not her partner, one or both of her offspring must be male. Either of these events occurs with probability

$$P\left(\text{X}\hspace{0.17em}\text{half cousins}|\text{full cousins}\right)=\frac{{\mathrm{ℱ}}_{k-1}^2+2{\mathrm{ℱ}}_{k-1}{\mathrm{ℱ}}_k}{2^{2\left(k-1\right)}}.$$ (15)

The distribution of recombinational meioses between two X half cousins

To find distributions for the number and lengths of IBD segments shared between two half cousins on the X chromosome, we first need to find the distribution for the number of females between two half cousins with a shared ancestor in the kth generation. We refer to the individuals connecting the two cousins as a genealogical chain. As we will see in the next section, the number of IBD X segments shared between half cousins depends on the sex of the shared ancestor; thus, we also derive distributions in this section for the number of recombinational meioses along a genealogical chain, conditioning on the sex of the shared ancestor. As earlier, our models assume two present-day female cousins but are easily extended to male cousins.

First, there are $2k-1$ ancestral individuals separating two present-day female $\left(k-1\right)\mathrm{th}$-degree cousins. These X ancestors in the genealogical chain connecting the two present-day female cousins follow the no two adjacent male condition; thus the distribution of females follows the approach used in Equation 6 with k replaced with $2k-1,$

$$P_H\left(R=r|k\right)=\frac{\left(\begin{array}{c}r+1\\ 2k-r-1\end{array}\right)}{{\mathrm{ℱ}}_{2k+1}},$$ (16)

where the H (for half cousin) subscript differentiates this equation from Equation 6, and k is the generation of the shared ancestor. Similar to Equation 6, r is bounded such that $r_{H,M}\le r\le 2k-1,$ where $r_{H,M}=\lfloor \left(2k-1\right)/2\rfloor .$

Now, we derive the probability of $R=r$ females conditional on the shared ancestor being female, ${\mathrm{♀}}_{\mathrm{X}}.$ This conditional distribution differs from Equation 16 since it eliminates all genealogical chains with a male shared ancestor. We find the distribution of recombinational meioses conditional on a female shared ancestor by placing the other $R^{\prime }=r^{\prime }$ females (the prime denotes we do not count the shared female ancestor here) along the two lineages of $k-1$ individuals from the shared female ancestor down to the present-day female cousins. These $R^{\prime }=r^{\prime }$ females can be placed in both lineages by positioning s females in the first lineage and $r^{\prime }-s$ females in the second lineage, where s follows the constraint $\lfloor \left(k-1\right)/2\rfloor \le s\le k-1.$ Our Equation 6 models the probability of an X genealogical chain having r females in k generations; here, we use this distribution to find the probabilities of s females in $k-1$ generations in one lineage and $r^{\prime }-s$ females in $k-1$ generations in the other lineage. As the number of females in each lineage is independent, we take the product of these probabilities and sum over all possible s; this is the discrete convolution of the number of females in two lineages $k-1$ generations long. Finally, we account for the shared female ancestor, by the transform $R=R^{\prime }+1=r:$

$$P_H\left(R=r|{\mathrm{♀}}_{\mathrm{X}},k\right)={\displaystyle \sum _{s=\lfloor \left(k-1\right)/2\rfloor }^{k-1}\frac{\left(\begin{array}{c}s+1\\ k-s-1\end{array}\right)\left(\begin{array}{c}r-s\\ k+s-r\end{array}\right)}{{\left({\mathrm{ℱ}}_{k+1}\right)}^2}}.$$ (17)

In general, this convolution approach allows us to find the distribution of females in a genealogical chain under various constraints and can easily be extended to the case of a shared male X ancestor (with necessarily two daughters).

Finally, note that we have modeled the number of females in a genealogical chain of $2k-1$ individuals. Thus far in our models, the number of females has equaled the number of recombinational meioses. However, when considering the number of recombinational meioses between half cousins, two recombinational meioses occur if the shared ancestor is a female (as she produced two independent gametes she transmits to her two offspring). Thus, for a single shared X ancestor, the number of recombinational meioses ρ is

$$\rho =\{\begin{array}{ll}r+1\hfill & \text{if}\hspace{0.17em}{\mathrm{♀}}_{\mathrm{X}}\hfill \\ r\hfill & \text{if}\hspace{0.17em}{\mathrm{♂}}_{\mathrm{X}},\hfill \end{array}$$ (18)

which we use when parameterizing the rate of recombination in our IBD segment number distributions. Furthermore, since a shared female ancestor has two X haplotypes that present-day cousins could share segments IBD through, the binomial probability $1/2^{\rho }$ is doubled. Further constraints are needed to handle full cousins; we discuss these below.

Half cousins

In this section we calculate the distribution of IBD X segments shared between two present-day female X half cousins with a shared ancestor in the kth generation. We imagine we do not know any details about the lineages to this shared ancestor or the sex of the shared ancestor, so we marginalize over both. Thus, the probability of two $\left(k-1\right)\mathrm{th}$-degree X half cousins sharing $N=n$ segments is

$$\begin{array}{r}P\left(N=n|k\right)={\displaystyle \sum _{r=r_{H,M}}^{2k-1}{P}_H\left(R=r|k\right)\times [P\left(N=n|{\mathrm{♀}}_{\mathrm{X}},R=r\right)P\left({\mathrm{♀}}_{\mathrm{X}}|R=r\right)+}\\ \hspace{0.17em}P\left(N=n|{\mathrm{♂}}_{\mathrm{X}},R=r\right)P\left({\mathrm{♂}}_{\mathrm{X}}|R=r\right)].\end{array}$$ (19)

As discussed in the previous section, the total number of recombinational meioses along the genealogical chain between half cousins depends on the unobserved sex of the shared ancestor (i.e., Equation 18). Likewise, the binomial probability also depends on the shared ancestor’s sex. Accounting for these adjustments, the probabilities $P\left(N=n|{\mathrm{♀}}_{\mathrm{X}},R=r\right)$ and $P\left(N=n|{\mathrm{♂}}_{\mathrm{X}},R=r\right)$ are

$$P\left(N=n|{\mathrm{♀}}_{\mathrm{X}},R=r\right)={\displaystyle \sum _{b=0}^{\mathrm{\infty }}\mathrm{Pois}\left(B=b|\lambda =\left(r+1\right)\nu \right)}\times \mathrm{Bin}\left(N=n|l=b+1,p=1/2^r\right)$$ (20a)

$$P\left(N=n|{\mathrm{♂}}_{\mathrm{X}},R=r\right)={\displaystyle \sum _{b=0}^{\mathrm{\infty }}\mathrm{Pois}\left(B=b|\lambda =r\nu \right)}\times \mathrm{Bin}\left(N=n|l=b+1,p=1/2^r\right).$$ (20b)

Since the sex of the shared ancestor depends on the number of females in the genealogical chain between the two cousins (e.g., if $r=2k-1,$ the shared ancestor is a female with certainty), we require an expression for the probability of the shared ancestor being male or female given $R=r.$ Using Bayes’ theorem, we can invert the conditional probability $P\left(R=r|{\mathrm{♀}}_{\mathrm{X}}\right)$ to find that the probability that a shared X ancestor is female conditioned on R females in the genealogical chain is

$$P_H\left({\mathrm{♀}}_{\mathrm{X}}|R=r,k\right)=\frac{{\mathrm{ℱ}}_{2k-1}}{\left(\begin{array}{c}r+1\\ 2k-r-1\end{array}\right)\left({\left({\mathrm{ℱ}}_{k+1}\right)}^2+{\left({\mathrm{ℱ}}_k\right)}^2\right)}\times {\displaystyle \sum _{s=\lfloor \left(k-1\right)/2\rfloor }^{k-1}\left(\begin{array}{c}s+1\\ k-s+1\end{array}\right)\left(\begin{array}{c}r-s\\ k+s-r\end{array}\right)}$$ (21)

and $P\left({\mathrm{♂}}_{\mathrm{X}}|R=r\right)$ can be found as the complement of this probability.

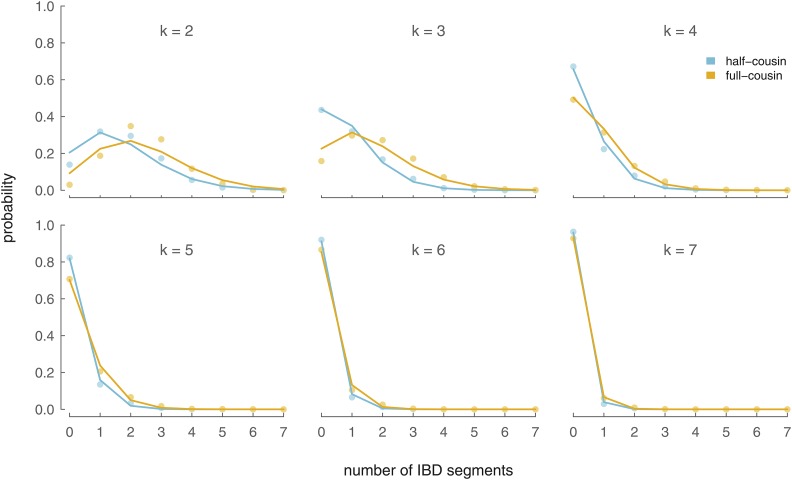
Inserting Equations 20a, 20b, and 21 into Equation 19 gives us an expression for the distribution of IBD segment numbers between two half cousins with a shared ancestor k generations ago. Figure 7 compares the analytic model in equation (half cousins) with the IBD segments shared between half cousins over 5000 simulated pairs of X genealogies.

Figure 7.

Distributions of X IBD segment number for X half cousins (blue) and X full cousins (yellow). Lines show the analytic approximations [Equations 19 and 23 and blue and yellow circles show the probabilities for X half cousins and X full cousins averaged over 5000 simulations.

The density function for IBD segment lengths between X cousins (either half or full cousins; length distributions are affected only by the number of recombinations in the genealogical chain) is Equation 10 but marginalized over the number of recombinational meioses between two cousins (Equation 16) rather than the number of recombinational meioses between a present-day individual and a shared ancestor. Simulations show the length density closely matches simulation results (see Figure A2 in the Appendix).

Full cousins

Full-cousin relationships allow descendants to share IBD autosomal segments from their shared maternal ancestor, their shared paternal ancestral, or both. In contrast, since males pass an X chromosome only to daughters, only full-sibling relationships in which both offspring are female (due to the no two adjacent males condition) are capable of leaving X genealogical descendants. We derive a distribution for the number of IBD segments shared between $\left(k-1\right)\mathrm{th}$-degree full X cousins by conditioning on this familial relationship and marginalizing over the unobserved number of females from the two full-sibling daughters to the present-day female full cousins.

First, we find the number of females [including the two full-sibling daughters in the $\left(k-1\right)\mathrm{th}$ generation] in the genealogical chain between the two X full cousins (omitting the shared male and female ancestors, which we account for separately). Like Equation 17, this is a discrete convolution,

$$P_F\left(R=r,k\right)={\displaystyle \sum _{s=\lfloor \left(k-2\right)/2\rfloor }^{k-2}\frac{\left(\begin{array}{c}s+1\\ k-s-2\end{array}\right)\left(\begin{array}{c}r-s-1\\ k-r+s\end{array}\right)}{{\left({\mathrm{ℱ}}_k\right)}^2}},$$ (22)

where the F subscript indicates this equation is for full cousins. This probability is valid for $r_{F,M}+2\le r\le 2k-2$ and is 0 elsewhere, where $r_{F,M}=2\lfloor \left(k-2\right)/2\rfloor +2.$ For $N=n$ segments to be shared between two X full cousins, z segments can be shared via the maternal shared X ancestor (where $0\le z\le n$) and $n-z$ segments can be shared through the paternal shared X ancestor. We marginalize over all possible values of z, giving us another discrete convolution,

$$P\left(N=n|R=r\right)={\displaystyle \sum _{r=r_{F,M}}^{2k-2}{\displaystyle \sum _{z=0}^{n}P\left(N=z|{\mathrm{♀}}_{\mathrm{X}}\right)}}\times P\left(N=n-z|{\mathrm{♂}}_{\mathrm{X}}\right)P_F\left(R=r\right),$$ (23)

where

$$P\left(N=n|{\mathrm{♀}}_{\mathrm{X}},R=r\right)={\displaystyle \sum _{b=0}^{\mathrm{\infty }}\mathrm{Bin}\left(N=n|l=b+1,p=1/2^{r+1}\right)}\times \mathrm{Pois}\left(B=b|\lambda =\nu \left(r+2\right)\right)$$ (24)

$$P\left(N=n|{\mathrm{♂}}_{\mathrm{X}},R=r\right)={\displaystyle \sum _{b=0}^{\mathrm{\infty }}\mathrm{Bin}\left(N=n|l=b+1,p=1/2^r\right)}\times \mathrm{Pois}\left(B=b|\lambda =\nu r\right)$$ (25)

are the probabilities of sharing n segments through the shared female and male X ancestors, respectively. For the female shared ancestor, we account for two additional recombinational meioses (one for each of the two gametes she passes to her two daughters) and the fact she can share segments through either of her X chromosomes (hence, why the binomial probability is $1/2^{r+1}$). We compare our analytic X full-cousin IBD segment number results to 5000 genealogical simulations in Figure 7.

Inference

With our IBD X segment distributions, we now turn to how these can be used to infer details about recent X ancestry. In practice, inferring the number of generations back to a common ancestor (k) is best accomplished through the signature of recent ancestry from the 22 autosomes, rather than through the short X chromosome. A number of methods are available for the task of estimating k through autosomal IBD segments (Huff et al. 2011; Henn et al. 2012; Durand et al. 2014). Therefore, we concentrate on questions about the extra information that the X provides conditional on k being known with certainty.

Here, we focus on two separate questions: (1) What is the probability of being an X genealogical ancestor given that no IBD segments are observed? And (2) can we infer details about the X genealogical chain between two half cousins? These questions address how informative the number of segments shared between cousins is about the precise relationship of cousins. We assume that segments of X chromosome IBD come only from the kth generation and not from deeper relationships or from false positives. In practice, inference from the X IBD segments would have to incorporate both of these complications, and as such our results represent best-case scenarios.

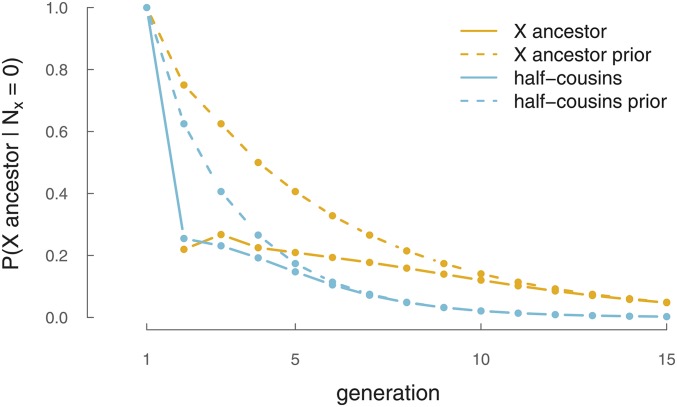
It is possible that k generations back, an individual is a genealogical X ancestor but shares no X genetic material with a present-day descendant. To what extent is the lack of sharing on the X chromosome with an ancestor informative about our relationship to them? Similarly, how does the lack of sharing of the X chromosome between $\left(k-1\right)\text{th}$ cousins change our views as to their relationship? To get at these issues, we can use our analytic approximations to calculate the probability that one is an X ancestor given that no segments are observed, $P\left(\text{X}\hspace{0.17em}\text{ancestor}|N=0\right):$

$$P\left(\text{X}\hspace{0.17em}\text{ancestor}|N=0\right)=\frac{P(\text{X}\hspace{0.17em}\text{ancestor}P\left(N=0|\text{X}\hspace{0.17em}\text{ancestor}\right)}{P\left(N=0|\text{X}\hspace{0.17em}\text{ancestor}\right)P\left(\text{X}\hspace{0.17em}\text{ancestor}\right)+P\left(\text{not}\hspace{0.17em}\text{X}\hspace{0.17em}\text{ancestor}\right)}.$$ (26)

Here, $P\left(N=0|\text{X}\hspace{0.17em}\text{ancestor}\right)$ is given by Equation 8 and $P\left(\text{X}\hspace{0.17em}\text{ancestor}\right)$ is given by Equation 4. This function is shown in Figure 8 (yellow lines). We can derive an analogous expression for the probability of two female half cousins sharing an X ancestor but not having any X segments IBD by replacing $P\left(\text{X}\hspace{0.17em}\text{ancestor}|N=0\right)$ with Equation 19 and replacing $P\left(\text{X}\hspace{0.17em}\text{ancestor}\right)$ with $P\left(\text{shared}\hspace{0.17em}\text{X}\hspace{0.17em}\text{ancestor}\right),$ which is given by Equation 11 and plotted in Figure 8 (blue lines). We also plot the prior distributions to show the answer if no information about the X chromosome was observed. In both cases, observing zero shared segments on the X chromosome makes it more likely that a shared ancestor was not a shared X ancestor. This additional information is strongest—compared to the prior—for close relationships ($k<5$), where segments on the X are likely to be shared if the ancestor was an X genealogical ancestor.

Figure 8.

The probability of X ancestry given no shared X genetic material. Yellow solid line shows the probability an individual in the kth generation (x-axis) is an X ancestor to a present-day female, given it shares no X genetic material with her. Blue solid line shows the probability that two half cousins share an X ancestor in the kth generation, given they share no X genetic material between them. Dashed lines indicate the prior probabilities.

Additionally, X IBD segments carry information about genealogical details that are not possible, considering autosome IBD segments alone. While IBD autosome segments leave a signature of recent ancestry between two individuals, the uniformity of recombinational meioses across every lineage to the shared ancestor leaves no signal of which genealogical chain connects two present-day cousins. In contrast, since the number of females varies along X lineages and affects the number of recombination events, the number and length of X segments carry information about which genealogical chain connects two cousins. Information about the genealogical chain between cousins is summarized by the number of female ancestors between two cousins, R, and constrains the possible X genealogical chains between these two cousins by varying amounts dependent on R and k.

Our approach to inference is through the posterior distribution of R given an observed number of IBD segments N and conditioning on k. We calculate this posterior conditional on the cousins sharing an X ancestor; we do this to separate it from the question of whether a pair share an X ancestor (derived in Equation 26). Our posterior probability is given by Bayes’ theorem

$$P\left(R|N=n,k\right)=\frac{P\left(N=n|R\right)P\left(R\right)}{P\left(N=n\right)},$$ (27)

where the prior $P\left(R\right)$ is readily calculable through Equation 16 and $P\left(N=n\right)$ is given by Equation 19. The data likelihood $P\left(N=n|R\right)$ is given by Equation 7.

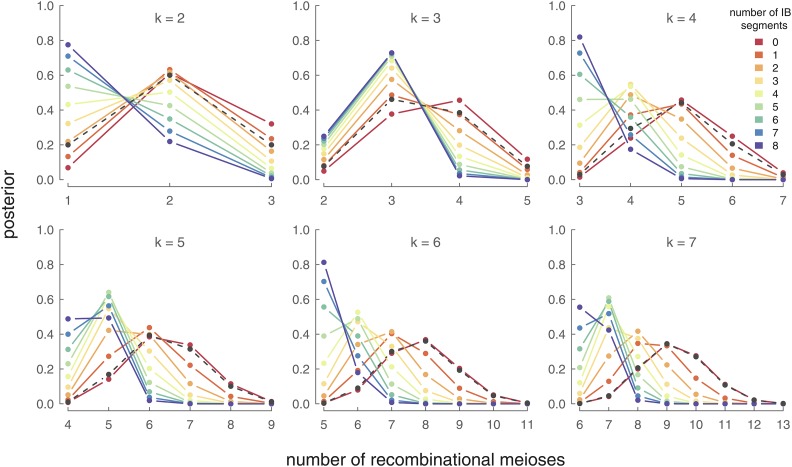
In Figure 9, we show the posterior distributions over the number of recombinational meioses, given an observed number of IBD segments between two females known to be X half cousins. Again, these posterior distributions condition on knowing how many generations have occurred since the shared ancestor, k. With an increasing number of generations to the shared ancestor, fewer segments survive to be IBD between the present-day cousins. Consequently, observing IBD segments increases the likelihood of fewer females (and thus fewer recombinational meioses) between the cousins. For example, for $k=6,$ observing (the admittedly unlikely) six or more IBD segments leads to a posterior mode over the smallest possible number of females in the genealogical chain $[\lfloor \left(2k-1\right)/2\rfloor =5;$ Figure 9$]$. Similarly, observing between three and five segments places the posterior mode over six females in the genealogical chain. For $k>4,$ seeing zero segments provides little information over the prior about the relationship between the cousins, as sharing zero segments is the norm. In each case, a posterior distribution over the number of females in a genealogical chain can greatly reduce the number of likely genealogical configurations. For example, observing $n=3$ shared X segments between half cousins $k=4$ generations back first restricts their shared ancestor to be one of the 34 possible shared X ancestors (of the total 128 possible shared ancestors). Furthermore, these three shared X segments, combined with our posterior distribution over recombinational meioses, lead to a maximum a posteriori estimate of $\widehat{R}=4$ females along the genealogical chain connecting the half cousins. Only 10 genealogical chains connecting these cousins contain four females, and thus the likely relationship of these cousins is considerably narrowed from the original 128 possible relationships. Therefore, sharing genetic segments on the X can provide considerable information about genealogical relationships.

Figure 9.

Posterior probability distribution $P\left(R=r|N=n,k\right)$ for different generations (each panel) and the observed number of IBD segments (each colored line). The prior distribution of recombinational meioses given k is indicated by a black dashed line.

Data availability

All simulated data used to create figures is present in Supplemental Material, File S1. Additionally, all simulation and analysis code to produce the figures is also available in File S1 and on the Github repository available at: https://github.com/vsbuffalo/x-ancestry/.

Discussion

Detecting and inferring the nature of recent ancestry is important for a range of applications and the nature of such relationships is often of inherent interest. As the sample sizes of population genomic data sets increase, so will the probability of sampling individuals that share recent ancestry. In particular, the very large data sets being developed in human genetics will necessitate taking a genealogical view of recent relatedness. Our methods extend existing methods for the autosomes by accounting for the special inheritance pattern of the X. Specifically, recent ancestry on the X differs from the autosomes since males inherit an X only from their mothers, and fathers pass an unrecombined (ignoring the PAR) X to their daughters. Consequently, the number of recombinational meioses, which determine the length and number of IBD segments, varies across the X genealogy. Since in most cases the number of females between two individuals in a genealogical chain is often unknown, we derive a distribution for recombinational meioses (Equation 6).

We also derive distributions for the length and number of IBD X segments by marginalizing over the unknown number of recombinational meioses that can occur between two individuals connected through a genealogical chain. In both cases, we condition on knowing k (the generations back to a shared ancestor), which can be inferred from the autosomes (Huff et al. 2011). Our models for IBD segment number and length use a Poisson-binomial approximation to the recombination process, which matches simulation results closely.

The genomic information about the genealogical relationship between pairs of individuals is inherently limited (due to the small number of segments shared and the stochasticity of the process); thus making full use of all shared segments on all chromosomes will be key to better inference. Our results here not only allow X IBD segments to be used to model recent ancestry, but also in fact provide qualitatively different information about genealogical ancestry than autosomal data alone. This additional information occurs through two avenues. First, sharing IBD segments on the X immediately reduces the potential genealogical ancestors two individuals share, since one’s X ancestors are only a fraction of their possible genealogical ancestors (i.e., ${\mathrm{ℱ}}_{k+2}/2^k$ in the case of a present-day female). Second, the varying number of females in an X genealogy across lineages combined with the fact that recombinational meioses occur only in females to some extent leave a lineage-specific signature of ancestry.

Unfortunately, the X chromosome is short, such that the chance of any signal of recent ancestry on the X decays rather quickly. However, growing sample sizes will increase both the detection of the pairwise relatedness and cases of relatedness between multiple individuals. In these large data sets, overlapping pairwise relationships (e.g., a present-day individual that shares X segments with two distinct other individuals) could be quite informative about the particular ancestors that individuals share.

Our results should also be of use in understanding patterns of admixture on the X chromosome. In particular, our results about the posterior information from the number and length of X segments shared with a genealogical ancestor can help us understand what can be learned from the presence (or absence) of segments of particular ancestry on the X chromosome. For example, if one observed long segments of a particular ancestry on one’s X chromosome, our results could be used to aid the identification of which parts of one’s family tree this ancestry has been inherited from. These genetic genealogical inferences can provide informative details in genealogy reconstruction where historical genealogical information is missing or uncertain. While this information for an individual decays somewhat quickly after a small number of generations, models of X chromosome segment ancestry will be useful at the population level for understanding sex-biased admixture (Bryc et al. 2010; Goldberg and Rosenberg 2015; Shringarpure et al. 2016).

Appendix

Convergence of the Thinned Poisson Process to the Poisson-Binomial Model

We compared the Poisson-thinning approximation and the Poisson-binomial models. We can show using the law of total expectation that the Poisson-binomial and Poisson models have the same expected value:

$$\mathbb{E}\left[N\right]={\displaystyle \sum _{b=0}^{\mathrm{\infty }}\mathbb{E}\left[N|B=b\right]P\left(B=b\right)}$$

$$\mathbb{E}\left[N\right]=\frac{1}{2^d}\left({\displaystyle \sum _{b=0}^{\mathrm{\infty }}b\mathrm{Pois}\left(B=b\right)+c{\displaystyle \sum _{b=0}^{\mathrm{\infty }}\mathrm{Pois}\left(B=b\right)}}\right)$$

$$\mathbb{E}\left[N\right]=\frac{1}{2^d}\left(\nu d+c\right).$$

This is the same expected value as the thinned Poisson process with rate $\left(\nu d+c\right)/2^d.$ However, the Poisson-thinning and Poisson-binomial models differ in their variance. Using Eve’s law, we can show the Poisson-binomial model has variance

$$\text{V}\left[N\right]={\mathbb{E}}_B\left[\text{V}\left[N|B\right]\right]+{\text{V}}_B\left[\mathbb{E}\left[N|B\right]\right]$$

$$\text{V}\left[N\right]=\frac{dv+1}{2^d}-\frac{1}{2^{2d}}.$$

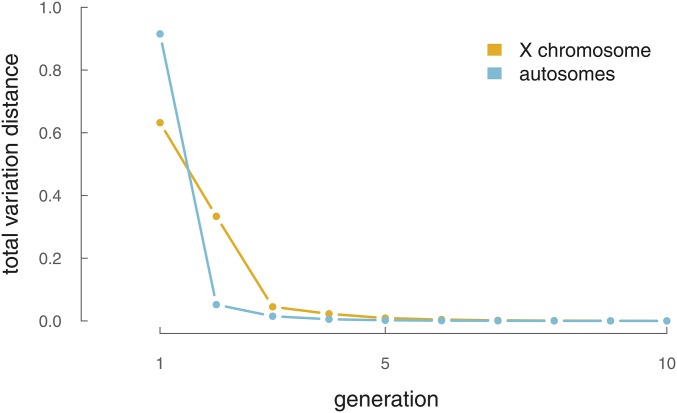
This differs from the thinned Poisson process variance by the term $1/2^{2d},$ which grows smaller with increasing d. Finally, we numerically show these two distributions [here, we label the two distributions for k generations ${\mu }_k\left(x\right)$ and ${\nu }_k\left(x\right),$ where x is the number of segments] converge quickly in total variational distance [$d_{\mathrm{TV}}\left({\mu }_k,{\nu }_k\right)=1/2{\displaystyle {\sum }_{n=0}^{\mathrm{\infty }}\left|{\mu }_k\left(n\right)-{\nu }_k\left(n\right)\right|}$] as k increases, in Figure A1.

Additional Autosomal Segment Distributions

The distribution of IBD segments between cousins

Similar to the distribution of autosomal segments between a present-day individual and an ancestor (The distribution of IBD segments between a present-day individual and an ancestor section), we can derive the distribution for the number of IBD segments shared between two half cousins with an ancestor in the kth generation. Two half cousins are separated by $2k$ meioses, and thus the distribution for the number of segments is

$$P\left(N=n|k,\nu ,c\right)=\mathrm{Pois}\left(N=n|\lambda =\left(c+2k\nu \right)/2^{2k-1}\right).$$ (A1)

Since either of the shared ancestor’s haplotypes can be shared IBD between the two cousins, the Poisson process rate is doubled. Full cousins can share segments via either of their two shared ancestors, leading the distribution to be

$$P\left(N=n|k,\nu ,c\right)=\mathrm{Pois}\left(N=n|\lambda =\left(c+2k\nu \right)/2^{2k-2}\right).$$

The distribution of autosome segment lengths

In addition to the number of IBD segments, the length of segments is also informative about ancestry (e.g., Palamara et al. 2012). As we model crossing over as a Poisson process, a 1-M region will experience on average d recombination events over d meioses. Therefore, the probability density of segment lengths shared IBD between two individuals d meioses apart is exponential with rate d:

$$p\left(U=u|d\right)=d{e}^{-du}.$$ (A2)

Equations A2 and A1 specify a model of the number and lengths of segments shared between various degree relatives. Various authors have used these types of results to derive likelihood-based models for classifying the genealogical relationship between pairs of individuals, using autosome IBD data (Huff et al. 2011; Henn et al. 2012; Durand et al. 2014).

Generating function for recombinational meioses

We also develop a generating function $g\left(x,k\right)$ that encodes the number of recombinational meioses in the kth generation as the coefficient for the term $x^k.$ This generating function can also be used in approximations and finding moments of the distribution $p_k\left(r\right).$

An expansion of the generating function below encodes the number of lineages with r females in a genealogical chain k generations long ($n_{k,r}$) as the coefficient of the term $x^k,$

$$g\left(x,k\right)=\frac{1}{2^{k+1}\sqrt{x}\sqrt{x+4}}\left[x\left({\left(R^{+}\right)}^k-{\left(R^{-}\right)}^k\right)+\sqrt{x}\sqrt{x+4}\left({\left(R^{-}\right)}^k+{\left(R^{+}\right)}^k\right)+-2{\left(R^{-}\right)}^k+2{\left(R^{+}\right)}^k\right],$$

where

$$R^{-}=x-\sqrt{x}\sqrt{x+4}$$

$$R^{+}=x+\sqrt{x}\sqrt{x+4}.$$

Proof. We begin by stating some recurrences that occur from the inheritance pattern of X ancestry:

$$n_{k,r}=m_{k,r}+f_{k,r}$$ (A3a)

$$m_{k,r}=f_{k-1,r}$$ (A3b)

$$f_{k,r}=f_{k-1,r-1}+m_{k-1,r-1}.$$ (A3c)

Starting from Equation A3a:

$$n_{k,r}=m_{k,r}+f_{k,r}$$

$$n_{k,r}=f_{k-1,r}+f_{k,r}$$

$$n_{k,r}=f_{k-1,r}+f_{k-1,r-1}+m_{k-1,r-1}$$

$$n_{k,r}=f_{k-1,r}+n_{k-1,r-1}$$

$$n_{k,r}=f_{k-2,r-1}+m_{k-2,r-1}+n_{k-1,r-1}.$$

Finally, substituting Equation A3a again gives us the desired recurrence relation for $n_{k,r}:$

$$n_{k,r}=n_{k-2,r-1}+n_{k-1,r-1}.$$ (A4)

We can now use generating functions (Wilf 2013) to tackle this recurrence. Define

$$A_k\left(x\right)={\displaystyle \sum _{r\ge 0}{n}_{k,r}{x}^r}.$$

Then, multiply both sides of (A4) by $x^r$ and sum over r. On the right-hand side:

$$={\displaystyle \sum _{r\ge 0}{n}_{k-2,r-1}{x}^r+{\displaystyle \sum _{r\ge 0}{n}_{k-1,r-1}{x}^r}}.$$

Note that $n_{k,r}=0$ if $r<0.$ Multiplying and dividing the second term by x yields

$$x\left(n_{k-1,0}x+n_{k-1,1}{x}^2+n_{k-1,2}{x}^3+\mathrm{\dots }\right)/x=x{A}_{k-1}\left(x\right).$$

An identical derivation works for the first term. We find

$$A_k\left(x\right)=x{A}_{k-1}\left(x\right)+x{A}_{k-2}\left(x\right).$$

This generating function is in the form of another recurrence. We can solve this recurrence (i.e., with Mathematica) with the initial conditions below [which can be derived from (A3a) and its initial conditions],

$$1.\hspace{0.17em}{A}_0\left(x\right)=1$$

$$2.\hspace{0.17em}{A}_1\left(x\right)=1+x$$

to find a solution with these initial conditions, giving us our desired generating function $g\left(x,k\right).$

∎

We can see that our generating function works via an expansion and verify the coefficients match known numbers of recombinational meioses for some k. For example, let us expand $g\left(x,k\right)$ at $k=5,$

$$x^2+6x^3+5x^4+x^5,$$

which matches the $n_{k,r}$ values found via computational calculation.

Half Cousins IBD Length Distribution Simulation Results

Figure A2 show the concordance between our cousin IBD segment length analytic distributions and the binned average (1.98-cM bin intervals) of 5000 simulations.

An Approximation of X Pedigree Collapse

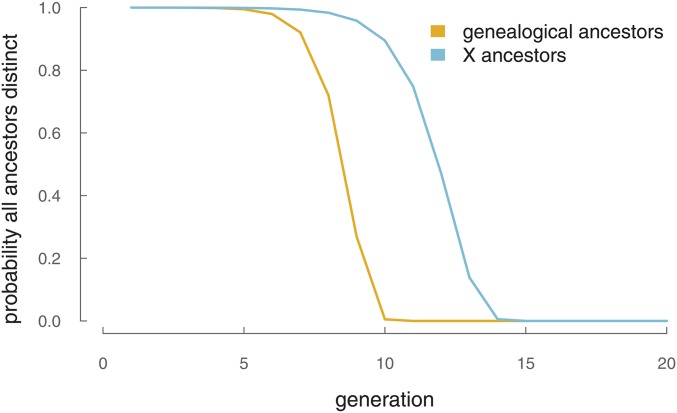
Since our models of recent X ancestry omit the possibility of pedigree collapse, it is worthwhile to see when this assumption breaks down. To see how pedigree collapse becomes an increasing problem farther generations back, we look at the probability that all of a single individual’s ${\mathrm{ℱ}}_{k+2}$ X ancestors, when sampled from a population of N individuals with replacement, are distinct. We treat generations as discrete and nonoverlapping and look at the probability that all ${\mathrm{ℱ}}_{k+2}$ are distinct individuals as a function of how many generations we go back. This problem is similar to the celebrated birthday problem, but with two rooms of participants: one room of females and another of males. Assuming random mating, each generation, one’s X ancestors must be randomly selected with replacement from a population of N individuals. For all ancestors to be distinct, all ${\mathrm{ℱ}}_k$ male ancestors selected from a pool of $N/2$ and ${\mathrm{ℱ}}_{k+1}$ female ancestors selected from a pool of $N/2$ must be unique:

$$\begin{array}{c}P\left(\text{X}\hspace{0.17em}\text{ancestors}\hspace{0.17em}\text{all}\hspace{0.17em}\text{distinct}\right)=P\left(\text{male}\hspace{0.17em}\text{X}\hspace{0.17em}\text{ancestors}\hspace{0.17em}\text{unique}\right)\\ \times \hspace{0.17em}P\left(\text{female}\hspace{0.17em}\text{X}\hspace{0.17em}\text{ancestors}\hspace{0.17em}\text{unique}\right)\\ ={\displaystyle \prod _{i=1}^{{\mathrm{ℱ}}_k}\left(1-\frac{2i}{N}\right){\displaystyle \prod _{j=1}^{{\mathrm{ℱ}}_{k+1}}\left(1-\frac{2j}{N}\right)}}.\end{array}$$

This probability as a function of k is plotted in Figure A3. For X ancestors, the probability that at least two individuals are nondistinct becomes a significant problem only after ∼12 generations. Note that this is a very conservative account of how pedigree collapse could affect our calculations; even if two ancestors were to be nondistinct, this is unlikely to affect our calculations greatly. For pedigree collapse to affect our IBD segment models, an individual has to both be a genealogical ancestor and a genetic ancestor of the present-day individual; pedigree collapse has no genetic effect if nondistinct individuals are not genetic ancestors.

For other pedigree collapse-related quantities (e.g., What is the average number of distinct ancestors k generations back?), see Wachter et al. (1979) approximations, which use Feller’s (1950) occupancy models.

Figure A1.

The total variation distance between the Poisson-thinning and the Poisson-binomial model for IBD segment number for X segments (yellow) and the autosomal segments (blue).

Figure A2.

The analytic distributions of IBD segment length (blue lines) between two present-day female half cousins with a shared ancestor in the kth generation (each panel) and the binned average over 5000 simulations (gray circles).

Figure A3.

The probability that all genealogical and X ancestors are distinct in a population of $\mathit{N}\mathrm{=}100\mathrm{,}000.$