Simulation of Various Randomization Strategies for a Clinical Trial in Sickle Cell Disease

Abstract

Objective

To use numerical simulation to evaluate various randomization strategies for a clinical trial in Sickle Cell Disease (SCD).

Methods

The IMPROVE trial^* is a randomized, controlled, feasibility study of inhaled mometasone for individuals with SCD who do not have asthma. The target sample size is 45 patients and one goal is to limit imbalance with respect to two important covariates 1) hydroxyurea use and 2) historical emergency department utilization. We compared three methods of patient allocation (simple randomization, block randomization, biased-coin adaptive randomization) using numerical simulation (10,000 trials). The primary outcome measure was the proportion of simulated trials with numerically apparent differences in the two covariates: hydroxyurea use (binary) and emergency department utilization (three level ordinal).

Results

Overall, only 1.6% of simulated trials had any covariate comparison with p<0.3 across groups for simple randomization, and 0% for both the block and adaptive randomization. In trials where the total sample size was 45 patients, the block randomization strategy achieved the greatest balance because participants were deterministically assigned to the treatment arm that balanced covariates. The adaptive strategy achieved similar results without deterministic treatment assignments even when trials included only 45 patients.

Discussion

Adaptive clinical trial designs have potential to mitigate some of the challenges that have hampered SCD trials. In small exploratory trials, even non-statistically significant differences in important covariates can threaten interpretability and external validity.

Conclusion

Adaptive randomization performed similarly to block randomization offers advantages including better allocation concealment and less ability for investigators to predict the next assignment.

Introduction

SCD is an inherited disorder of hemoglobin that affects approximately 100,000 Americans.¹ In individuals who suffer from the disease, a complex state of hemolysis, inflammation, vascular damage and cell adhesion manifests disease-related pathology in all organs but the most common manifestation is the vaso-occlusive painful episode. Healthcare expenditures for acute care utilization in SCD have reached $1.5 billion per year.^2,3

Despite the staggering costs of SCD, hydroxyurea remains the only FDA approved medication to treat the disease. While the molecular pathophysiology of SCD is well understood, efforts to develop new therapies have been fraught with failure.⁴ In SCD, where disease prevalence can hamper recruitment, trial design inefficiencies become a critical barrier to progress.^5-8

Adaptive clinical trial designs have potential to mitigate some of the challenges that have hampered SCD trials in the past and one aspect of adaptive trial design that has potential to increase efficiency of small, early-phase trials is adaptive covariate balanced randomization. Small clinical trials are challenging as a general rule, and particularly challenging in SCD. As such, even small, non-statistically significant differences in important covariates can potentially threaten the interpretability and external validity of small sample size exploratory trials. While randomization should generally balance covariates, the risk of a numerically meaningful imbalance increases with a small sample size.^9,10 For example, within a trial of 40 patients if one treatment arm has 60% patients with hydroxyurea use and the other has 20%, this difference is important to those interpreting the results, but may not be statistically significant. The risk of such imbalances is best quantified using numerical simulation.^11,12 As such, the planners of the trial can compare various methods of patient allocation (simple randomization, block randomization or adaptive randomization) using simulations over several important situations. In the current investigation, our aim was to compare the risk of significant covariate imbalance using three potential randomization strategies within a 45 patient SCD trial.

Methods

Clinical problem

The detailed methods and rationale for the Inhaled Mometasone to Promote Reduction in Vaso-occlusive Events (IMPROVE) trial have been previously described elsewhere (https://clinicaltrials.gov/ct2/show/NCT02061202). Briefly, the IMPROVE trial is a randomized, controlled, feasibility study of inhaled mometasone for individuals with SCD who do not have asthma (1K23 HL119351 01). The trial was conceived in response to data that, in individuals with SCD who do not have asthma, wheezing is common and is associated with increased rates of pain and death.^13-16

Trial design and needs

The proposed trial is a pilot randomized controlled trial of inhaled corticosteroids for patients with sickle cell disease. This is a double blinded, placebo-controlled trial with a primary objective of establishing feasibility and collecting preliminary measurements on important biomarkers. The intended maximum N for this trial is 45, with 2:1 allocation between active treatment and placebo. Two important prognostic baseline covariates are intended to be balanced using adaptive randomization: hydroxyurea use (prevalence about 60%), and ED utilization (categorical low, medium and high with 40% each in the low and medium categories and 20% in the high category.) Exact balance on the 2:1 allocation was determined a priori to be of lower importance than maintaining balance on the clinical covariates.

Potential approaches to balancing covariates

The simplest approach would be individual level randomization with a biased coin (33.3% probability of placebo) while ignoring covariates. A more typical approach would be block randomization (where patients are randomized in groups of 3, with each group having 1 of its members selected at random to receive placebo.). This approach raises concerns about allocation concealment and does not address covariate balance. A more sophisticated approach would use stratified, block randomization, where each of the 6 possible combinations of covariates would be issued blocks of size 3, with the member receiving placebo randomly determined within each. This approach also has the potential for the investigators to predict, or know the next subject allocation. (For example, if the first subject in the block is assigned placebo, the next two will receive active treatment.) Finally, an innovative approach is to use adaptive randomization, where the probability of receiving active treatment or placebo is never deterministic, and the bias of the coin is adjusted with the goal of maintaining balance on the covariates, along with relative closeness to the 33.3% placebo ratio. For the IMPROVE trial, an additional important goal was demonstrating the feasibility of using a real-time, continuously updating program to provide treatment assignments to the study team.

Description of adaptive approach

There are two key variables that we aim to balance: use of hydroxyurea and frequency of ED visits. Hydroxyurea is dichotomized by whether the patient is currently taking the medicine. ED use is split into three groups: subjects with <5 ED, 5-10, or 11-15 ED visits in the previous 12 months. Therefore there are 6 subsets of covariate combinations, and we aim to produce an algorithm that measures the imbalance between placebo and treatment within each subgroup.

The procedure works as follows. The first two trial patients are randomized with 1/3 probability to placebo and 2/3 to the treatment without any adjustment for covariates. For patients 3-45, when a patient is randomized, it is first determined which subset the patient belongs to. Then, the algorithm calculates the imbalance will be larger or smaller if the next patient is assigned to treatment or placebo. For each subject assigned to placebo, the imbalance matrix for that type has 1 added to it; for each subject assigned to treatment, the imbalance matrix has 0.5 subtracted from it. Therefore, within each covariate type, balance will be achieved by assigning 1 subject to placebo and 2 to treatment. When calculating imbalances across groups at the end of the simulated trials the actual proportions were used. The 3 levels of ED utilization were described with binary indicator variables for high and moderate utilization, and hydroxyurea use For example, if 45% of placebo patients received hydroxyurea, and 60% of treatment patients received hydroxyurea that would be summarized by an imbalance of −15%, the difference in proportions subtracting treatment from placebo. Negative differences indicate imbalance towards treatment (i.e more hydroxyurea use in the treatment group relative to placebo) and positive differences indicate imbalance towards placebo.

The randomization vector is set as follows based on the current imbalance for that covariate type.

$$imbalance=v=p^{e^{(imbalanc{e}_{placebo}+imbalanc{e}_{treatment})}}$$

In this equation p = 1/3 (the desired placebo proportion), and the sum of the proposed imbalance if the next patient is assigned to placebo and the proposed imbalance if the next patient is assigned to treatment. The term e represents Euler's constant. The use of the exponential in this case allows zero imbalance situations to remain at the baseline randomization probability of 1/3. In addition, the exponential function produces a positive value below 1 for negative imbalances, and a positive value greater than 1 for positive imbalances and therefore adjusts the randomization probability appropriately, while never reaching a randomization probability for treatment of either zero or one (as we wish to avoid deterministic assignments.) If already at balance (1 for placebo and −1 for treatment), the sum will be zero and the randomization vector will remain at 1/3. If the sum imbalance is negative (too many patients within this covariate type on treatment) the equation will bias the vector towards assigning the next patient to placebo; if sum imbalance is positive, the vector will bias towards assigning the next patient to treatment.

As an example, if one patient has previously been randomized to treatment in group six (on hydroxyurea, high ED utilization) the imbalance matrix will be at −0.5 for that group. The proposed imbalance if the next patient is randomized to placebo will be 0.5 (adding one), and it will be −1 (subtracting 0.5) if the next patient is randomized to treatment.

$$0.51={0.33333}^{e^{({0.5}_{placebo}+-1_{treatment})}}$$

After the proposed vector is calculated, the algorithm determines whether the overall trial placebo proportion is deviating outside the desired range from 0.23 to 0.43. This is to ensure that the trial does not deviate too far from 1:2 randomization. If this condition is met, the algorithm overrides the previous proposed vector using this equation.

$$imbalance=v=p^{\left(\frac{P_{current}}{p}\right)}$$

Again, p represents the desired placebo proportion of 1/3 and p_current is the overall proportion of patients assigned to placebo within the trial so far. It is important to note that this will still not result in deterministic assignments, and will either decrease or increase the probability of placebo assignments to bring the overall trial placebo proportion into the 0.23 to 0.43 range. When enforcing this range, the algorithm will ignore covariate imbalance. As an example, if the current proportion of placebo is 0.5 (above the upper threshold of 0.43), then the randomization vector is calculated as follows

$$imbalance=v={0.3333}^{\left(\frac{0.5}{0.3333}\right)}=0.1924$$

An extreme yet unlikely example is the case of all subjects receiving placebo. The probability of placebo assignment in this case would be 0.037.

Comparisons

We compared this using simulation to simple randomization (using a binomial distribution with 0.333 placebo probability) and block randomization (using 3 patient blocks for each of 6 combinations) and simulated 10000 trials using R statistical package software. We first present the results of a single example simulated trial to further illustrate the algorithm procedure, and summarize the differences between the treatment and placebo groups.

Imbalances were calculated at the end of each trial and summarized as a difference in proportions, subtracting the treatment group from the placebo group. The overall imbalance was calculated as the sum of imbalance on hydroxyurea plus the sum of the average imbalance on moderate ED utilization and high ED utilization (this calculation was conducted such that imbalance on one covariate in favor of placebo would tend to be counteracted by imbalance on another covariate in favor of treatment). We also calculated Absolute Sum Imbalance, where the absolute value of the imbalances arrived at by subtracting the treatment group proportions from the placebo group proportions were used.

Sensitivity analysis: We expected that with increasing sample size, the adaptive randomization approach would be exceedingly similar to the block randomization. We repeated the simulations using a total trial sample size of 450, again with 2:1 allocation of treatment to placebo.

Results

The progress and treatment allocation decisions of the single example trial are presented in table 1. Note the randomization vector calculated for patient 45 of 0.51 and is the same as the example provided in the methods of the imbalance matrix starting at −0.5 for that subset. In this example trial, the rule for having too high a proportion of placebo patients triggered for patients three through seven. Good numerical balance was achieved between the groups for all levels of the covariates and no statistically significant differences were observed (Table 2).

Table 1.

Example Trial and Status of Imbalance and Proposed Randomization Vectors with Treatment Assignments

Patient Number	Hydroxyurea	ED Utilization	Placebo Proportion Prior to Randomization	Hydroxyurea Imbalance	Moderate ED Imbalance	High ED Imbalance	Overall Weighted Imbalance	Randomization Vector (Probability of placebo)	Assignment
1	Taking	Moderate	0*	0	0	0	0	0.33*	Treatment
2	Not Taking	High	0*	−1.00	−1.00	1.00	−1.00	0.33*	Placebo
3	Taking	Low	0.50	−0.50	−1.00	0.50	−0.75	0.19	Placebo
4	Taking	Moderate	0.67	−0.50	−1.00	0.50	−0.75	0.11	Treatment
5	Taking	Moderate	0.50	−0.33	−0.67	0.33	−0.50	0.19	Placebo
6	Taking	Moderate	0.60	−0.33	−0.67	0.33	−0.50	0.14	Treatment
7	Not Taking	Moderate	0.50	−0.08	−0.67	0.33	−0.25	0.19	Treatment
8	Not Taking	High	0.43	0.07	−0.47	0.13	−0.10	>0.01	Treatment
9	Taking	High	0.38	0	−0.33	0	−0.17	0.16	Treatment
10	Not Taking	Moderate	0.33	0.10	−0.38	0.05	−0.07	0.51	Treatment
11	Not Taking	Moderate	0.30	0.17	−0.42	0.08	0	0.78	Treatment
12	Not Taking	Moderate	0.27	0	−0.25	0	−0.13	0.91	Placebo
13	Taking	Low	0.33	−0.06	−0.17	0.03	−0.13	>0.01	Treatment
14	Taking	High	0.31	0.04	−0.27	0.18	0	0.51	Placebo
15	Not Taking	Moderate	0.36	0.10	−0.30	0.20	0.05	0.51	Treatment
16	Not Taking	Low	0.33	0.15	−0.24	0.22	0.14	0.16	Treatment
17	Taking	Moderate	0.31	0.21	−0.14	0.15	0.22	0.51	Placebo
18	Not Taking	Low	0.35	0.12	−0.21	0.10	0.06	0.51	Placebo
19	Taking	Moderate	0.39	0.07	−0.24	0.12	0.01	0.01	Treatment
20	Taking	Moderate	0.37	0.03	−0.26	0.13	−0.03	0.33	Treatment
21	Taking	High	0.35	0	−0.21	0.07	−0.07	0.01	Treatment
22	Taking	Low	0.33	−0.03	−0.17	0.09	−0.07	0.33	Treatment
23	Taking	Low	0.32	−0.05	−0.13	0.10	−0.07	0.33	Treatment
24	Not Taking	Low	0.30	−0.02	−0.10	0.11	−0.01	0.01	Treatment
25	Taking	Moderate	0.29	0.04	−0.03	0.07	0.06	0.33	Placebo
26	Taking	Moderate	0.32	0.01	−0.06	0.08	0.03	0.01	Treatment
27	Taking	Moderate	0.31	0.06	0	0.06	0.08	0.33	Placebo
28	Taking	Moderate	0.33	0.04	−0.02	0.06	0.06	>0.01	Treatment
29	Not Taking	Moderate	0.32	−0.03	0.02	0.04	0	0.78	Placebo
30	Not Taking	High	0.34	0	0.05	0	0.03	0.33	Treatment
31	Not Taking	High	0.33	−0.05	0	0.07	−0.02	0.33	Placebo
32	Taking	Low	0.35	−0.07	0.02	0.08	−0.02	0.51	Treatment
33	Taking	Low	0.34	−0.04	−0.02	0.06	−0.02	0.78	Placebo
34	Taking	Moderate	0.36	−0.05	−0.05	0.07	−0.04	0.33	Treatment
35	Taking	Low	0.35	−0.07	−0.02	0.08	−0.04	0.33	Treatment
36	Not Taking	High	0.34	−0.04	0	0.04	−0.02	>0.01	Treatment
37	Not Taking	Moderate	0.33	−0.09	0.04	0.02	−0.06	0.16	Placebo
38	Not Taking	Moderate	0.35	−0.06	0.02	0.03	−0.04	>0.01	Treatment
39	Taking	Moderate	0.34	−0.08	0	0.04	−0.06	0.16	Treatment
40	Taking	Low	0.33	−0.09	0.02	0.05	−0.06	0.51	Treatment
41	Taking	High	0.33	−0.10	0.04	0.02	−0.08	0.16	Treatment
42	Taking	Low	0.32	−0.12	0.06	0.02	−0.08	0.78	Treatment
43	Taking	Low	0.31	−0.08	0.02	0.01	−0.07	0.91	Placebo
44	Taking	Low	0.33	−0.06	−0.02	−0.01	−0.07	0.51	Placebo
45	Taking	High	0.34	−0.07	0	−0.03	−0.08	0.51	Treatment

The progress and treatment allocation decisions of the single example trial. Weighted overall imbalance is the sum of the hydroxyurea imbalance and one half times the sum of the moderate and high ED imbalances.

^*The first two patients are enrolled with a 1/3 probability of placebo.

Table 2.

Baseline characteristics of sample trial

	Treatment N=30		Placebo N=15		P - values
	N	Proportion	N	Proportion	Fisher's	Chi Square
Hydroxyurea	20	0.67	9	0.60	0.746	0.913
ED Utilization
Low	9	0.30	5	0.33	1	0.958
Medium	14	0.47	7	0.47
High	7	0.23	3	0.20

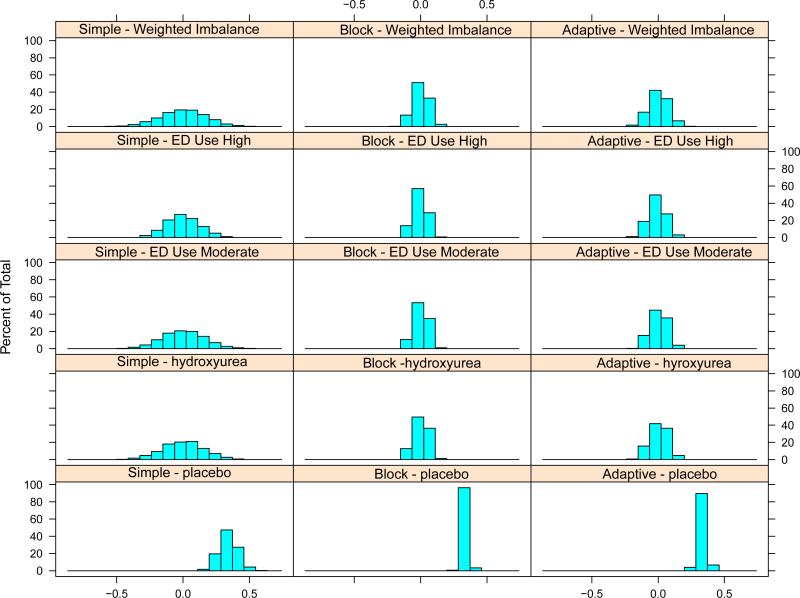
Overall, only 1.6% of simulated trials had any covariate comparison with p<0.3 on Fisher's exact test across groups for simple randomization, and 0% for both the block and adaptive randomization. Figure 1 shows trial performance across the three methods. Tables 3 and 4 summarize the magnitude of imbalances and the probability of observing imbalances measured using the two methods (sum or sum of absolute values). In trials where the total sample size was 45 patients, as expected, the block randomization strategy achieved the greatest balance because participants were deterministically assigned to the treatment arm that balanced covariates. The adaptive strategy was able to achieve similar results without deterministic treatment assignments even when trials included only 45 patients.

Figure 1. Performance of the three methods.

Histograms depict the final imbalance states of simulated trials of 45 participants. A total of 10,000 sets of virtual patients were generated, and each of the three trial algorithms were applied to each set. For the top four rows, the positive portion of the histogram represents trials with imbalances (and their magnitude) with a higher proportion of that covariate for the placebo group. The bottom row depicts the distribution of final placebo proportion from the various methods.

Table 3.

Proportion of Simulated Trials with Different Levels of Imbalance

Type	2%	5%	10%	20%	50%
Simple	0.417	0.350	0.295	0.229	0.117
Block	0.121	0.101	0.088	0.069	0.036
Adaptive	0.167	0.139	0.117	0.088	0.046

Simulated trial imbalance proportion from the various methods. Overall imbalance is the sum of the differences in proportions for each covariate between treatment and placebo. As an example, 50% of trials with simple randomization had an overall end of trial imbalance of 0.117 or greater.

Table 4.

Simulation Quantiles for Overall End of Trial Absolute Sum Imbalances

Type	50%	75%	90%	95%	97.50%	99%
Simple	0.171	0.251	0.333	0.389	0.439	0.492
Block	0.055	0.083	0.104	0.119	0.133	0.150
Adaptive	0.068	0.103	0.137	0.161	0.180	0.207

This method used the absolute value of all of the imbalances. For the simple randomization case, 50% of trials had sum imbalance of 0.171 or more, and 2.5% of simulated trials had sum imbalances of 0.439 or more.

Results of sensitivity analysis

We expected that with increasing sample size, the adaptive randomization approach would be exceedingly similar to the block randomization. We repeated the simulations using trial sample sizes of 100, 200, 300 and 450, again with 2:1 allocation of treatment to placebo. At a sample size of 450, there was nearly complete balance on all covariates and the adaptive randomization algorithm appeared nearly identical on the histograms and quantiles (see supplement).

Discussion

A 2011 report by the Institute of Medicine identified innovative trial design strategies including Bayesian adaptive methodologies as a key tool to accelerate research and development in rare diseases.¹⁷ Here we report, to our knowledge, the first use of adaptive covariate balancing randomization and the first use of simulation to inform study design in a clinical trial for SCD. R code for this algorithm is provided as a supplement to facilitate use of this technique by other SCD investigators.

The simulations presented demonstrated that an adaptive covariate balanced randomization strategy achieves similar balance to a traditional block randomization with several benefits including improved masking of investigators and avoiding deterministic treatment assignments. Based on these simulations we chose an adaptive randomization strategy for the IMPROVE trial. One potential critique of adaptive trials is that they add substantial logistical burden that may outweigh any increase in trial efficiency. Our group designed a simple user interface within the software program R coupled with a file sharing system. Investigators are able to monitor and maintain the randomization algorithm from off-site and research coordinators have randomized 25 participants to date without difficulty. The file sharing site does not collect any protected health information, and all changes made are logged and older versions of files can be easily recovered and restored if a subject is randomized in error. While simulation was used here to inform the choice of randomization strategy, it can be used for almost any aspect of trial design to concretely describe the probability of success under various design strategies.

The current study has several important limitations. We report the results of a numerical simulation study as opposed to the conduct of a completed trial. Operational and logistical issues impact real clinical trials, and not simulated ones. The performance of adaptive trial designs can be simulated under a variety of operational stressors such as slow recruitment; in the current investigation our design was focused only on adapting to baseline covariates and as such simulating scenarios of operational stress did not seem to be helpful. We did not introduce correlations between the covariate types, whereas in practice it is plausible that ED utilization and hydroxyurea use have a relationship. In addition, there are several important covariates known to affect SCD outcomes (gender, fetal hemoglobin, age etc.) which we chose not to balance on. With increasing numbers of covariates, adaptive balancing provides diminishing returns (while the overall imbalance score can be minimized, between-group differences for some covariates become inevitable) thus investigators are still forced to choose only a few covariates upon which to balance in a small trial.

An adaptive randomization approach to balancing two categorical covariates along with keeping the treatment to placebo ratio close to 2:1 performed nearly as well as block randomization and offers several potential advantages including better allocation concealment and less ability for the investigator to predict the next assignment. For the purposes of this simulation we had a goal of 2:1 allocation to drug and placebo and chose an acceptable range of 0.23 – 0.43 before the coin became biased. The allocation scheme and acceptable deviation range can be modified based on the needs of the trial where larger or smaller deviations from the allocation goal are acceptable. Statistically significant imbalances on the covariates are unlikely within a 45 patient trial, however this method ensures good numerical balance and less likelihood of imbalances that may compromise the external validity and clinical interpretation of the trial. Based upon the results of these simulations, we chose an adaptive randomization algorithm for the IMPROVE trial. Simulation may be used for all aspects of trial design to avoid pitfalls and increase efficiency especially for studies in rare diseases such as SCD.