Prediction of accrual closure date in multi-center clinical trials with discrete-time Poisson process models

Abstract

In a phase III multi-center cancer clinical trial or large public health studies, sample size is predetermined to achieve desired power and study participants are enrolled from tens or hundreds of participating institutions. As the accrual is closing to the target size, the coordinating data center needs to project the accrual closure date based on the observed accrual pattern and notify the participating sites several weeks in advance. In the past, projections were simply based on some crude assessment and conservative measures were incorporated in order to achieve the target accrual size. This approach often resulted in excessive accrual size and subsequently unnecessary financial burden on the study sponsors. Here we proposed a discrete-time Poisson process-based method to estimate the accrual rate at time of projection and subsequently the trial closure date. To ensure that target size would be reached with high confidence, we also proposed a conservative method for the closure date projection. The proposed method was illustrated through the analysis of the accrual data of NSABP trial B-38. The results showed that application of proposed method could help to save considerable amount of expenditure in patient management without compromising the accrual goal in multi-center clinical trials.

1. INTRODUCTION

The spending on clinical trials is enormous and ever increasing though patient care costs for clinical trials are not appreciably higher than costs for patients not enrolled in trials. The average cost of a phase III clinical trial could potentially exceed $20,000 per patient. There could be many reasons for the higher spending on the clinical trials. Some are necessary costs which are hard to avoid, such as costs on patient registration, treatment, subsequent health management, and data collection. Certain costs, such as those due to extra enrollment beyond the target sample size, may be lessened. In a multi-center phase III trial, the sample size is pre-determined in order to achieve sufficient power for its primary hypothesis. Participants are often recruited from tens or hundreds of clinical sites such as hospitals, community clinics and cancer centers over time. Because of the complexity of recruiting process, it is almost impossible for the coordinating center, especially of cancer clinical trials, to determine a cut-off date on accrual in advance and eventually reach the target sample size exactly. It has been the usual practice to choose an accrual closure date so that reaching the target sample size can be guaranteed though this often leads to extra and sometimes excessive accruals. Extra accruals up to a certain degree are helpful because they would fill in for participants who later on withdraw consent or lose to follow up. However, excessively extra accrual would increase unnecessary financial burden on the coordinating centers and their sponsors.

In 2004, a phase III trial B-38 was designed by the National Surgical Adjuvant Breast and Bowel Project (NSABP) to compare the treatment efficacy of three adjuvant chemotherapy regimens for node-positive breast cancer patients. The accrual size of 4,800 was pre-determined in order to achieve sufficient power for the primary hypothesis that the investigative arm, dose-dense doxorubicin and cyclophosphamide (AC) followed by paclitaxel plus gemcitabine, improved the disease-free survival over the other two arms, docetaxel plus AC, and dose-dense AC followed by paclitaxel alone, respectively. Patients were accrued from hundreds of participating institutions or sites over time. The protocol was opened on October 1, 2004, and the first patient entered this trial on November 3, 2004. As the cumulative accrual was closing to the target sample size, on March 20, 2007, the coordinating data center needed to project an accrual closure date for this trial based on past accrual pattern and notify participating sites several weeks in advance. Such an early notice was necessary because it took 2-4 weeks for the sites to screen a patient for the eligibility criteria and work up the patient with medical scans such as multi-gated acquisition (MUGA) scan and magnetic resonance imaging (MRI) during the process. At that time, May 3 of 2007 was determined as the closure date. This prediction was based on the average daily accrual during the 3-month period before March 20, 2007, an assumption that this average accrual rate would be maintained in the future, and a conservative measure via adding three days to make sure that the target sample size would be reached. Eventually 4894 patients were randomized in this trial with following this crude method.

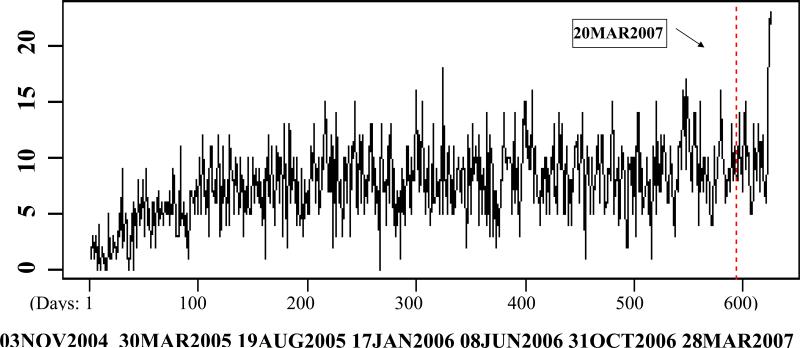
Figure 1 shows the daily accrual in B-38 over time. The horizontal axis displays the number of days from November 3 of 2004 on when the first patient was randomized and the vertical axis shows the daily accruals. Weekends and holidays are not included because accruals were not performed in those days. Several interesting phenomena were observed. At first, the accrual rate increased steadily during the first 4 or 5 months. This reflects that it took time for the participating institutions to fulfill regulatory requirements and start recruiting patients for a trial. Subsequently, the accrual pattern became relatively stable after March of 2005. Finally, during the last five days of the accrual period prior to the designated closure date, the daily accrual increased to about twice of the average daily accrual prior to that period. This accrual pattern has been observed in other several other NSABP trials. Accrual data from B-38 supplied an excellent opportunity for us to study the prediction of the trial closure dates.

Figure 1.

Daily accrual in the NSABP B-38 trial.

Time aspects of accrual are pertinent to the modeling of the clinical trial accrual process. First, in a typical multi-center phase III trial, hundreds of participating institutions recruit hundreds or thousands of patients during a 2-4 year period. Consequently, the chance to recruit one or more patients during a short period such as a day would be small for any single institution. Second, in general the patient accruals during disjoint time intervals are independent from each other. These properties lead to an observation that the accrual process approximately follows a continuous-time Poisson process, often simply mentioned as Poisson process. ¹

Senn (1998) considered modeling the accrual process as a homogeneous Poisson process with a constant rate. With time points for past accruals as the observed data, this constant rate can be estimated.² Based on the theory of Poisson processes, the time to reach the target accrual would follow a Gamma distribution with parameters depending on the accrual rate and the number of further accruals. Gajewski et al. (2008) considered the corresponding Bayesian approach to predict the time to completion of target accrual.³ After deriving the posterior distribution of the accrual rate based on past accrual data, values of this rate are drawn from this posterior distribution. Then an empirical distribution of the time to accrual completion can be simulated through Gamma distributions with parameters depending on the number of additional patients needed to complete accrual and those drawn values of accrual rate. Another extension assumes that accrual from each participating site follows a homogeneous Poisson process but the accrual rates from these sites follow a Gamma distribution.⁴

While this type of modeling is useful, it is not always appropriate for the real-world situation. In many occasions only the daily accrual counts instead of the exact accrual time are available. Furthermore, in many clinical trials the accrual rate increases dramatically during the last few days before the predicted accrual closure date because participating clinical institutions strive to enroll as many patients as possible before enrollment to the trial is closed. More flexible methods are needed under such circumstances.

2. PREDICTION OF ACCRUAL CLOSURE

2.1 A flexible model for patient accrual

We propose a flexible discrete-time Poisson process-based method to model patient accrual and predict the accrual closure date. Consider a multi-center trial where the daily accrual of the coordinating center is denoted by {x(t), t=1, 2,...}, t is the number of days from the initiation of study. Assume that the patient's arrival follows a discrete-time Poisson process and the daily accrual rates are {λ(t)=E[x(t)], t=1,2,...}. Denote the cumulative accrual at time t by N(t), i.e.,

$$N\left(t\right)=\sum _{k=1}^{t}x\left(k\right).$$

Assume that accrual needs a period of time to start at t₀ and increase until reaching full potential at a later time t₁. Then the accrual becomes stable for a substantial period. When the cumulative accrual is close to the target size N, say at time t₂>t₁, the coordinating center needs to assess the observed accrual data up to t₂, denoted as D(t₂)={x(1), x(2), ..., x(t₂)}, and predict a future date as the trial closure date. As mentioned before, the accrual during the final few days was often much faster than the average. We propose the following Poisson process model for the daily accrual rate λ(t) :

$$\lambda \left(t\right)=\{\begin{array}{cc}0,\hfill & \text{when}t\le t_0\hfill \\ {\lambda }_1\left(t\right),\hfill & \text{when}{t}_0<t\le t_1\hfill \\ \mu ,\hfill & \text{when}{t}_1<t\le t_3-\Delta \hfill \\ \varphi \mu ,\hfill & \text{when}t>t_3-\Delta \hfill \end{array}\phantom{\}}$$ (1)

where t₃ is the predicted closure date and Δ is the length of the short period with high accrual rate before t₃. The accrual rate during [t₀+1,t₁] is usually not of interest and is not specified here because the focus is the projection of accrual closure date. If the initiation of participating institutions follows a homogeneous Poisson process before t₁, then the intensity rate λ(t) during [t₀+1,t₁] is a linear function of t. In practice, time point t₀ usually refers to the day before the first accrual. Time point t₁ represents the time when all sites start actively enrolling patients and is usually unknown. Estimation of t₁ by an ad-hoc method and a change-point analysis will be discussed in Section 3. Time point t₂ is the time point when the coordinating center needs to predict the future closure date. The constants Δ and ϕ>1 could be speculated from accrual patterns of past trials that are similar to the current trial in terms of patient characteristics and treatment regimen. When such clinical trials are not available, an alternative is to conduct sensitivity analysis under various plausible values of Δ and ϕ.

Denote T as the day when the cumulative accrual exceeds the target sample size N. Because the primary concern is to predict T rather than accurately modeling λ(t) during the whole accrual process, we propose to use the accrual data in [t₁+1,t₂] to estimate the accrual rate at t₂ and predict T under the assumed model (1). Time t₁ is tentatively assumed known and its determination will be discussed in Section 3.

2.2. Inference based on past accrual pattern

Based on model (1), {x(t₁+1),x(t₁+2),...,x(t₂)} is an independent identically distributed Poisson sequence with a common mean μ. The maximum likelihood estimator (MLE) of μ is:

$$\widehat{\mu }=\frac{\sum _{t=t_1+1}^{t_2}x\left(t\right)}{t_2-t_1}$$

The standard error of $\widehat{\mu }$ is

$$\mathrm{se}\left(\widehat{\mu }\right)=\frac{{\left\{\sum _{t=t_1+1}^{t_2}x\left(t\right)\right\}}^{\frac{1}{2}}}{t_2-t_1}$$

2.3. Estimation of ϕ from a past trial

Once a clinical institution learns the projected date of accrual closure, they expedite their accrual effort to enroll as many patients as possible before the closure date. This leads to a higher than usual accrual rate during the last few days. This phenomenon was manifested in B-38 (Figure 1) where the accrual rate during the last five days doubled the previously observed accrual rate. Assume the length of this fast accrual period, Δ, is known. Based on the similar completed accrual data from a past multi-center trial carried out by the same coordinating center, an estimate of ϕ can be obtained from maximizing the following likelihood function:

$$L(\mu ,\varphi )=\left\{\prod _{t=t_1+1}^{t_3-\Delta }\exp (-\mu ){\mu }^{x\left(t\right)}\right\}\left\{\prod _{t=t_3-\Delta +1}^{t_3}\exp (-\varphi \mu ){\left(\varphi \mu \right)}^{x\left(t\right)}\right\}$$

Then the MLE of ϕ is:

$$\widehat{\varphi }=\frac{(t_3-\Delta -t_1)\sum _{t=t_3-\Delta +1}^{t_3}x\left(t\right)}{\Delta \sum _{t=t_1+1}^{t_3-\Delta }x\left(t\right)}$$

However, when such a similar clinical trial does not exist, one could perform a sensitivity analysis by predicting the accrual closure date under plausible choices of Δ and ϕ. The sensitivity analysis will be briefly described in the Discussion.

2.4. Determination of accrual closure date

Assume that N is the target accrual size and the accrual after occasion t₂ follows (1) with t₁<t₂<t₃-Δ, two methods are proposed here to determine the accrual closure date. The first method uses E(T) and the second method uses a more conservative date t_α=min{t: pr[T< t]≥ 1-α}, for a pre-determined small value α>0. The choices of α may be 0.05, 0.1, or a larger number in (0, 0.5), depending on how conservative the investigator would like to be.

Let W=T-t₂ denote the additional accrual time, after t₂, needed to reach the target sample size. From T=min{t:N(t)≥ N}, we have

$$\begin{array}{cc}\hfill E\left[W\right]& =\sum _{k=0}^{\infty }pr[W>k]=\sum _{k=0}^{\infty }pr[T-t_2>k]\hfill \\ \hfill & =\mathrm{pr}[T-t_2>0]+\sum _{k=1}^{\infty }pr[T>t_2+k]\hfill \\ \hfill & =1+\sum _{k=1}^{\infty }pr[N(t_2+k)<N]\hfill \\ \hfill & =1+\sum _{k=1}^{\infty }pr[N(t_2+k)-N\left(t_2\right)<N-N\left(t_2\right)]\hfill \\ \hfill & =1+\sum _{k=1}^{\infty }\sum _{j=0}^{N-N\left(t_2\right)-1}pr[N(t_2+k)-N\left(t_2\right)=j]\hfill \\ \hfill & =1+\sum _{k=1}^{\infty }\sum _{j=0}^{N-N\left(t_2\right)-1}\frac{e^{-{\mu }_k}{\mu }_k^j}{j!},\hfill \end{array}$$

where,

$${\mu }_k=E[N(t_2+k)-N\left(t_2\right)]=\{\begin{array}{cc}(k-\Delta )\mu +\Delta \varphi \mu ,\hfill & \text{if}\mathrm{k}>\Delta \hfill \\ k\varphi \mu ,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$

Because the total accrual N(t₂) at t₂ must be less than N, pr[T-t₂>0]=1. From Ê(T) = Ê(W) + t₂, E(T) can be estimated with μ substituted by $\widehat{\mu }$.

The standard error of ${\widehat{E}\left(T\right)\mid }_{\mu =\widehat{\mu }}$ can be estimated by the Delta method as $\mid {\mathrm{h}}^{\prime }\left(\widehat{\mu }\right)\mid \mathrm{se}\left(\widehat{\mu }\right)$, where the function h(μ)=E(T).

For any given t>t₂, let

$$\begin{array}{cc}\hfill 1-\alpha & \le pr(T\le t)=pr[N\left(t\right)\ge N]\hfill \\ \hfill & =pr[N\left(t\right)-N\left(t_2\right)\ge N-N\left(t_2\right)]\hfill \\ \hfill & =1-pr[N\left(t\right)-N\left(t_2\right)<N-N\left(t_2\right)]\hfill \\ \hfill & =1-\sum _{k=0}^{N-N\left(t_2\right)-1}pr[N\left(t\right)-N\left(t_2\right)=k]\hfill \end{array}$$ (2)

Then t_α would be the smallest t that satisfies (2). Because of (1),

$$N\left(t\right)-N\left(t_2\right)=\sum _{s=t_2+1}^{t-\Delta }x\left(s\right)+\sum _{s=t-\Delta +1}^{t}x\left(s\right)$$ (3)

follows a Poisson distribution with mean {(t – Δ – t₂) + Δϕ}μ.

With μ estimated based on observed accrual data D(t₂) the estimator $\widehat{\mu }$ can be used in the above formula to derive t_α. Its variability can be obtained by the bootstrap method.

2.5. Prediction of total number of accrual given a closure date t₃

After the closure date t₃ is determined, from (3), a natural estimator of the final accrual size N(t₃) would be

$$\widehat{N}\left(t_3\right)=N\left(t_2\right)+\{(t_3-\Delta -t_2)+\Delta \varphi \}\widehat{\mu }.$$

The standard deviation associated with the estimated total accrual can be estimated by

$${\left[\{(t_3-\Delta -t_2)+\Delta \varphi \}\widehat{\mu }\right]}^{\frac{1}{2}}.$$

3. DETERMINATION OF t₁

In the previous section, the estimation of accrual rate at time t₂ is based on the assumption that accrual data from [t₁+1,t₂] follow a homogeneous discrete-time Poisson process and t₁ is assumed known. In practice, t₁ is usually unknown and needs to be determined from the accrual data. A heuristic approach is to choose t₁ based on model diagnostic measures such as the goodness-of-fit statistic for the Poisson sequence {x(t₁+1), x(t₁+2), ..., x(t₂)}:

$$G^2=2\sum _{t=t_1+1}^{t_2}x\left(t\right)\{\log x\left(t\right)-\log \widehat{\mu }\}.$$

G² approximately follows a Chi-square distribution with a degree of freedom (t₂-t₁-1) if the accrual process in [t₁+1, t₂] is homogeneous.

An alternative model diagnostic measure that can be used is the ratio between the sample mean and sample variance of the accrual data in [t₁+1, t₂]. This ratio should be close to 1 under the same assumption. For all t in [t₀, t₂], we can obtain the corresponding p-values for the goodness-of-fit test from the analysis of accrual data between t and t₂, and the ratios between the sample means and sample variances. Then choose a t that is related to a large p-value and a ratio close to 1 as t₁.

Because the choice of t₁ is for estimation of the accrual rate at t₂, one may only consider accrual data starting from a t₀* in [t₀, t₂] such that the accrual in [t₀*, t₂] is relatively stable and apply a change point analysis to find out whether there is a change point for λ(t) within [t₀*, t₂]. Change point analysis is a method to find one or more locations where a parameter of a statistical model changes its value. Such analyses have been applied to data collected from the fields of finance, econometrics, software development, and medicine. ^5-10 Akman and Raftery (1986) studied the change point problem in a continuous time Poisson process. ¹¹ Hinkley (1970) discussed the maximum likelihood method for estimating a change point in a sequence of random variables and the likelihood ratio test statistic. ⁹ Testing the existence of one or more change points in the means, of a sequence of independent Poisson-distributed random variables, was investigated by Henderson and Matthews (1993) and the general approaches for change point problems were discussed in Bhattacharya (1994). ^7,12

For a pre-determined t₀*, consider the sequence of independent Poisson random variables {y_k=x(t₀*+k), k=1,2, ..., n=t₂- t₀*} with means E[y_k]=μ_k. If these y_k 's are generated from a homogeneous Poisson process, then μ_k 's are equivalent. However, if the corresponding Poisson process is non-homogeneous, μ_k 's would change with k. Assuming that μ_k's change only once, that is, μ₁=μ₂=...= μ_τ≠ μ_τ+1=...= μ_n, where τ is the change point. The likelihood function is

$$\begin{array}{cc}\hfill L({\eta }_1,{\eta }_2,\tau )& =\prod _{i=1}^{\tau }f(y_i;{\eta }_1)\prod _{i=\tau +1}^{n}f(y_i;{\eta }_2)\hfill \\ \hfill & =\prod _{i=1}^{\tau }\frac{e^{-{\eta }_1}{{\eta }_1}^{y_i}}{y_i!}\prod _{i=\tau +1}^n\frac{e^{-{\eta }_2}{{\eta }_2}^{y_i}}{y_i!}\hfill \end{array}$$

With τ fixed, the MLEs for (η_1, η₂) are $({\widehat{\eta }}_{1\tau },{\widehat{\eta }}_{2\tau })=({\sum }_{i=1}^{\tau }{y}_i∕\tau ,{\sum }_{i=\tau +1}^n{y}_i∕(n-\tau ))$.

Therefore the logarithm of the profile likelihood of τ is

$$l_{pl}\left(\tau \right)\propto \{\log \left(\sum _{i=1}^{\tau }{y}_i\right)-\log \tau \}\sum _{i=1}^{\tau }{y}_i-\{\log \left(\sum _{i=\tau +1}^n{y}_i\right)-\log (n-\tau )\}\sum _{i=\tau +1}^n{y}_i$$

The MLE of τ is $\widehat{\tau }=\arg {\max }_{1\le \tau \le n-1}{l}_{pl}\left(\tau \right)$. One of the regularity conditions for the maximum likelihood method for data with change point is that τ /n converges to a constant, as the sample size n→∞.

Under the circumstance that the likelihood function l_pl(τ) has multiple modes, the MLE is often chosen as the one that is not close to either end of the period. Subsequently, it is of interest to test whether $\tau =\widehat{\tau }$ is truly a change point. The likelihood ratio test for the following hypothesis testing: H₀ : μ₁ = μ₂ = ... = μ_n against H_A : μ₁ = μ₂ = ... = μ_τ ≠ μ_τ+1 = ... = μ_n, with $\tau =\widehat{\tau }$, is:

$$\begin{array}{cc}\hfill LRT& =\left\{\prod _{i=1}^{\widehat{\tau }}\frac{e^{-{\stackrel{‒}{y}}_{\widehat{\tau }}}{{\stackrel{‒}{y}}_{\widehat{\tau }}}^{y_i}}{y_i!}\prod _{i=\widehat{\tau }+1}^n\frac{e^{-{{\stackrel{‒}{y}}_{n-\widehat{\tau }}}^{\prime }}{{\stackrel{‒}{y}}_{n-\widehat{\tau }}}^{\prime y_i}}{y_i!}\right\}∕\prod _{i=1}^n\frac{e^{-\stackrel{‒}{y}}{\stackrel{‒}{y}}^{y_i}}{y_i!}\hfill \\ \hfill & ={{\stackrel{‒}{y}}_{\widehat{\tau }}}^{\widehat{\tau }{\stackrel{‒}{y}}_{\widehat{\tau }}}{{\stackrel{‒}{y}}_{n-\widehat{\tau }}}^{\prime (n-\widehat{\tau }){{\stackrel{‒}{y}}_{n-\widehat{\tau }}}^{\prime }}∕{\stackrel{‒}{y}}^{n\stackrel{‒}{y}}\hfill \end{array}$$

where ${\stackrel{‒}{y}}_{\widehat{\tau }}={\sum }_{i=1}^{\widehat{\tau }}{y}_i∕\widehat{\tau },{{\stackrel{‒}{y}}_{n-\widehat{\tau }}}^{\prime }={\sum }_{i=\widehat{\tau }+1}^n{y}_i∕(n-\widehat{\tau })$, and $\stackrel{‒}{y}={\sum }_{i=1}^n{y}_i∕n$.

When n→∞, 2log(LRT) approximately follows the χ² distribution with one degree of freedom under the null.

4. APPLICATION TO THE NSABP TRIAL B-38

To illustrate the proposed method, we considered the accrual data of the motivating study, the NSABP B-38 trial. Its target sample size was 4800 and 172 sites contributed patients on this study. The first patient was enrolled on November 3, 2004. On March 20, 2007, 4465 patients had been randomized and the NSABP Biostatistical Center needed to make a projection on the trial closure date. A crude mechanism was used to predict T based on the average daily accrual during the 3-month period before March 20, 2007. Then, 3 more days were added and the accrual closure date was determined as May 3, 2007. At the end of the designated closure date, a total of 4894 patients were randomized in B-38 resulting in the accrual of about 100 more patients than necessary and several millions of dollars extra in treatment and follow-up expenses.

Here we applied the proposed method to determine t₁ in (1), estimated the accrual rate on t₂ or March 20, 2007, and subsequently predicted the accrual closure date based on accrual data up to March 20, 2007.

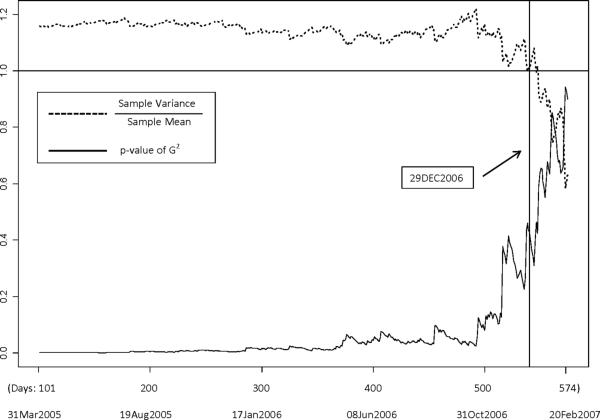
With t varying from March 7, 2005 and February 20, 2007, we considered the fit of a Poisson model for the assumed identically and independently distributed sequence {x(t+1), x(t+2), ..., x(t₂)}. The p-values of the goodness-of-fit statistic G² and the ratio between the sample variances and sample means are plotted in Figure 2.

Figure 2.

Plots of the goodness-of-fit p-values and the ratios between the sample variances and sample means of Poisson sequences against potential locations of the change point.

This figure shows that the ratio of sample variance to mean is relatively close to 1 and the p-value of G² is relatively large around the end of 2006. After all, an ad-hoc estimate of t₁ is December 29, 2006 with a ratio of 1.01 and p-value at 0.429 for the goodness-of-fit test.

Because our focus was to estimate the accrual rate at t₂, we were only concerned with the last change point in accrual rate prior to t₂. In the change point analysis, we considered the sequence of daily accrual counts between July 15, 2005 and March 20, 2007. The maximum likelihood estimate of the single change point happened to be December 29, 2006 as well. The test statistic for whether December 29, 2006 was truly a change point or not had value 2log(LRT)=6.83 (p<0.001).

These results implied that December 29, 2006 was an appropriate choice of t₁. Subsequently the estimate of the daily accrual rate between t₁ and t₂ was $\widehat{\mu }=9.8$ and $\widehat{\varphi }=2.24$. The predicted closure date by using E(T) yielded a predicted date at April 19, 2007. The corresponding predicted accumulative accrual was 4809 with a standard deviation at 16.3. The predicted closure date by using the 95 percentile of T, t_0.05, yielded a predicted date at April 23, 2007. This implies that had we chosen April 23, 2007 as the trial closure date, we would have about 95% confidence that the accrual target would be achieved. The corresponding predicted accumulative accrual was 4829 with a standard deviation at 16.9.

As an empirical comparison, we also considered hypothetical scenarios when any day, from April 18 of 2007 to May 3 of 2007, had been chosen as the accrual closure date. The calendar dates and corresponding days from November 3 of 2004 are displayed in the first two columns of Table 1. For each hypothetically chosen closure date t₃, we calculated the actual cumulative accrual up to day t₃-5 plus the actual accruals during the last week (from April 27 to May 3 of 2007). These numbers reflected the empirical total accruals had any of those dates been chosen as the closure date and are presented in the last column of Table 1. The results suggest that had we applied our method and chosen April 23, 2007 as the closure date, we would have enrolled about 75 less patients than using May 3, 2007 as the accrual closure date. The savings in patient management would exceed 1.5 million dollars.

Table 1.

Potential choices of the accrual closure dates and the corresponding empirical accrual sizes

Calendar Dates	Days from initiation of accrual (t3)	Observed cumulative accrual by t3-5 plus observed accrual during the fast accruing final week
April 18, 2007	615	4793
April 19, 2007*	616	4802
April 20, 2007	617	4811
April 23, 2007**	618	4819
April 24, 2007	619	4832
April 25, 2007	620	4842
April 26, 2007	621	4849
April 27, 2007	622	4860
April 30, 2007	623	4872
May 1, 2007	624	4881
May 2, 2007	625	4888
May 3, 2007	626	4894

^*Predicted accrual closure date using E(T)

^**Predicted accrual closure date using t_0.05

5. DISCUSSION

Patient accrual in multi-center clinical trials approximately follows a Poisson process because each institution has little chance to enroll a patient during a single day and accruals over time are generally independent. In the NSABP B-38 accrual data, the correlogram analysis, as described in the textbook by Diggle (1990), was performed and the results showed very little serial correlation if any. ¹³

A few continuous-time Poisson process-based methods have been developed for predicting trial closure time but they required the actual times of day when each patient is enrolled. ^2-4 In most multi-center clinical trials when counts by daily accrual are available and ad-hoc methods are usually applied to determine the trial closure date. To ensure that the target sample size is reached, some conservative measures are implemented. This type of approach is crude and usually leads to unnecessarily excessive accrual. Here we proposed a flexible discrete-time Poisson process-based method to model the overall accrual process and provided straightforward estimates of the mean and quantiles of the date when accrual would exceed the target size. The proposed method relies on an accurate estimate of current accrual rate and assumption on the future accrual pattern. Because the accrual pattern can be irregular in the beginning and we are not really concerned with accrual rates during that period, we look for a critical date when the accrual follows a homogeneous discrete-time Poisson process afterwards. Goodness-of-fit measures and change point analysis were both considered to determine an appropriate choice of this critical date. In the application on the B-38 accrual date, these two approaches actually resulted in the same critical date.

To predict the date when accrual would exceed the target size in B-38, we assumed that accrual had followed a homogeneous discrete-time Poisson process till the last few fast accrual days prior to the closure date where the accrual would exceed. The length of this fast accrual period Δ and the accrual inflation factor ϕ could either be obtained or estimated from past similar trials on similar patient population. In similar trials as B-38 where Δ and ϕ are totally unknown, one can perform sensitivity analysis to present the projected closure dates under plausible choices of Δ and ϕ. For the B-38 application, the projected closure dates by using the 95 percentile were 623, 622, 620 and 617 days after initiation of accrual for ϕ =1, 1.5, 2, and 2.5, respectively. Based on the analysis of the B-38 data, the closure date identified would have been 10 days sooner than that was actually selected and the over-accrual would have been reduced by 80% from 94 to only 19 patients.

In practice, some investigators may opt to choose the change point t₁ as the date when a large percentage of the participating sites started putting patients in the trial. In the NSABP B-38 study, 75% of the 172 eventual participating sites had enrolled patients on July 18, 2005; 90% had enrolled patients on December 29, 2005; and 95% had enrolled patients on May 8, 2006. By choosing these dates as the change point t₁ and the acceleration rate ϕ as 2, the projected closure dates by using the 95 percentile are 623, 622 and 621, respectively. Based on the empirical data presented in Table 1, the over-accrual would vary from 72 to 49. This phenomenon reflects that even though the most majority of the sites had started enrolling patients but it would take a few more months for them to reach their regular accrual capacity. The change-point analysis provided a more accurate assessment of the point when the patient accrual reached a stable rate late phase.at its