Defining and estimating causal direct and indirect effects when setting the mediator to specific values is not feasible

Abstract

Natural direct and indirect effects decompose the effect of a treatment into the part that is mediated by a covariate (the mediator) and the part that is not. Their definitions rely on the concept of outcomes under treatment with the mediator “set” to its value without treatment. Typically, the mechanism through which the mediator is set to this value is left unspecified, and in many applications it may be challenging to fix the mediator to particular values for each unit or patient. Moreover, how one sets the mediator may affect the distribution of the outcome. This article introduces “organic” direct and indirect effects, which can be defined and estimated without relying on setting the mediator to specific values. Organic direct and indirect effects can be applied for example to estimate how much of the effect of some treatments for HIV/AIDS on mother-to-child transmission of HIV infection is mediated by the effect of the treatment on the HIV viral load in the blood of the mother.

1. Introduction

Researchers are often interested in investigating the mechanisms behind effective treatments or exposures. The topic of which part of the effect of a treatment is “mediated” by a covariate is of particular importance. The mediated part of a treatment effect is due to treatment induced changes in a “mediator” covariate M. This is the so-called indirect effect; as opposed to the so-called direct effect, not mediated by covariate M. Mediation analysis has gained much prominence in methodological and empirical research in recent years. Mediation analysis is particularly popular in the health sciences, like medicine, epidemiology and psychology. In April 2016, [1] has over 58.000 citations in Google Scholar, many of them after 2010. Therefore, clarifying the assumptions required for mediation analysis is paramount.

A recent literature has provided a rigorous theoretical framework for the definition and estimation of causal direct and indirect effects, see e.g. [2, 3, 4, 5, 6, 7, 8]. In this literature, the controlled direct effect is the effect of a treatment had the mediator for each patient or unit (from now on, patient) been set to a pre-determined value. The natural direct effect is the effect of a treatment had the mediator been set to the value that it would have taken without treatment. Thus, the natural direct effect for a particular patient can be represented by Y_1,M0 − Y₀: the difference between the patient’s outcome Y_1,M0 under treatment had the mediator been set to the value M₀ it would have taken without treatment and the patient’s outcome Y₀ without treatment. Notice that the mediator is kept constant at M₀, so this is the natural direct effect not mediated by M. Similarly, the natural indirect effect can be represented by Y₁ − Y_1,M0, where Y₁ is the outcome under treatment. It has been argued that to study the causal mechanisms by which particular treatments are effective, natural direct and indirect effects are more relevant than controlled direct effects ([3, 6]). [3] also notes that controlled indirect effects are not defined.

As seen from the definition of natural direct and indirect effects, one needs “cross-worlds” quantities in order to define natural direct and indirect effects. In particular, Y_1,M0 is the outcome under treatment but with the mediator set to the value, M₀, it would have taken without treatment. In practice, it may be rare that mediators take the same value with treatment, M₁, as without treatment, M₀. Even if this happened for specific patients, it would be impossible to identify those patients. Under treatment, the value of the mediator without treatment is usually not observed, so it is unclear to which value the mediator should be set for any particular patient in order to obtain Y_1,M0. In addition, identification of natural direct and indirect effects relies on assumptions about the outcomes Y_a,m of a patient under all combinations of the treatment and the mediator ([3, 4, 6, 5, 8]). This is a problem in many practical applications: setting the mediator to particular values is often not feasible if the mediator is not a treatment itself. If setting the mediator to a particular value m is not feasible, the interpretation of the Y_a,m is unclear. However, the common approaches to causal mediation analysis all rely on the existence of all Y_a,m ([7]).

To overcome these problems, this article proposes instead to base mediation analysis on newly defined “organic” interventions (I) on the mediator. Organic interventions I cause the mediator to have a specific distribution: the distribution of the mediator without treatment, given pre-treatment common causes of mediator and outcome. An organic intervention could be an additional treatment that affects the distribution of the mediator. Theorem 4.4 shows that organic direct and indirect effects are often generalizations of natural direct and indirect effects and the direct and indirect effects introduced in [9]. Like the current article, [10] considers interventions on the mediator, but does not condition on common causes C of mediator and outcome, unless the interest is in effects conditional on C or in effects when C is manipulated. [2], [3], and, for organic interventions, Section 4 argue that ignoring C can produce invalid estimators. Also Section 5 on uniqueness of organic direct and indirect effects requires that C is taken into account.

Most of the causal inference literature on mediation has adopted the so-called cross-worlds assumption, an assumption involving the joint distribution of counterfactuals under different values of the treatment ([3, 4, 6, 5, 8]). An issue with this assumption is that it can never be tested or imposed by design, not even in a clinical trial where the treatment and the mediator can both be set to any desired value by the experimenter. In contrast, whether “setting the mediator” is an organic intervention can be tested in such a clinical trial.

The theory in this article turns out to lead to the same numerical results as introduced by other authors, [1] and, more recently, e.g. [3, 4, 5, 6, 9, 11]. This article thus provides an interpretation of existing numerical results when the mediator cannot be set.

This article is organized as follows. Section 2 introduces the setting and notation. Section 3 reviews natural direct and indirect effects. Section 4 introduces organic interventions and organic direct and indirect effects. Section 5 shows that organic direct and indirect effects do not depend on the choice of organic intervention, nor on the choice of pre-treatment common causes of mediator and outcome, provided those are “complete”. Section 6 provides an identification result for organic direct and indirect effects when treatment is randomized. Section 7 provides an identification result for organic direct and indirect effects for observational studies. The usefulness of organic direct and indirect effects as opposed to natural direct and indirect effects is illustrated in three examples: 1. the smoking and low birth weight paradox, see Web-appendix B, 2. the effect of AZT, a drug used for the treatment of HIV, on mother-to-child transmission of HIV infection, and 3. the effect of antidepressants on depressive symptoms. How much of the effect of AZT is mediated by the HIV viral load, the amount of HIV virus in the blood of the mother, is investigated in Section 8. How much of the effect of antidepressants on depressive symptoms is not mediated by the participants’ expectations is investigated in Section 9. Section 10 concludes this article with a discussion. Proofs can be found in Appendix A.

2. Setting and notation

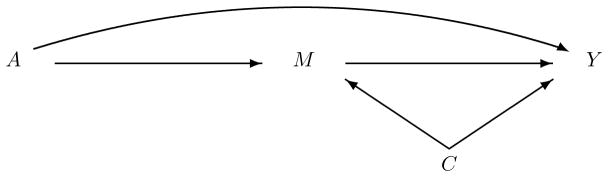
For ease of exposition, I first consider randomized treatments. Section 7 extends the analysis to non-randomized treatments. For each patient, observables include the following quantities. A is the randomized treatment, which is 1 for the treated and 0 for the untreated. C are pre-treatment common causes of the mediator and the outcome. As noted by [2], [3], and others, these variables C have to be taken into account in order to identify the natural direct and indirect effect, even if the treatment is randomized. As will become clear later, pre-treatment common causes C also have to be taken into account to identify the organic direct and indirect effect. Like most of the literature on mediation, this article assumes that there are no post-treatment common causes of the mediator and the outcome. M is the observed value of the mediator. Y is the observed outcome. Y₀ is the (counterfactual) outcome without treatment, and Y₁ is the (counterfactual) outcome under treatment. Obviously, for each patient either Y₁ or Y₀ is observed, but not both. Similarly, M₀ is the mediator without treatment, and M₁ is the mediator under treatment. I assume that C is observed first, then A, then M, and then Y. The Directed Acyclic Graph (DAG) of Figure 1 describes the set-up. In all of this article, it is assumed that observations and counterfactuals for the different patients are independent and identically distributed.

Figure 1.

DAG summarizing the data.

Because treatment A is randomized, the pre-treatment covariate C is not a cause of A in the DAG.

3. Natural direct and indirect effects: an overview

Natural direct and indirect effects, introduced in [2] and [3], are based on the outcome Y_1,M0 under treatment with the mediator set to the value it would have taken without treatment, M₀. The natural direct effect is defined as Y_1,M0 − Y₀. The natural direct effect is not affected by changes in the value of the mediator induced by the treatment, because for both Y_1,M0 and Y₀ the mediator is equal to M₀. The natural indirect effect is defined as Y₁ − Y_1,M0. This is the mediated part: the only difference between these quantities is the change in the value of the mediator, M₁ versus M₀.

To identify natural direct and indirect effects, previous authors (e.g. [2, 3, 4, 5, 6, 8]) assume the existence of counterfactual outcomes under all possible combinations of the treatment and the mediator, Y_a,m. In the words of [7], there has to be “reasonable agreement” as to what is the “closest possible world” in which the mediator has a specific value, a value which is different from the one that was observed. There are cases where reasonable agreement may exist. For example, [3] describes a setting where the mediator is a treatment, aspirin, in which case the mediator could be set to specific values. However, in many practical situations the mediator of interest is not a treatment, and there is no known way in which one can set the mediator to a specific value. Then, the quantities Y_1,M0 and Y_a,m are not clearly defined. [12] provide a nice example: “There are many competing ways to assign (hypothetically) a body mass index of 25 kg/m² to an individual, and each of them may have a different causal effect on the outcome”.

The cross-worlds or mediator-randomization assumption that is generally used to identify natural direct and indirect effects states that

$$Y_{a^{\prime },m}⫫M_a\mid C=c,A=a.$$ (1)

In words: for a patient with treatment A = a and pre-treatment covariates C, the mediator under treatment a (M_a), should be independent of the outcome under any other treatment-mediator combination (Y_a′,m, the outcome under treatment a′ had the mediator been set to m). Identification of natural direct and indirect effects thus involves assumptions about the joint distribution of cross-worlds quantities, quantities under treatments a and a′. Suppose for now that the Y_a′,m are all well-defined: there is reasonable agreement about how to set the mediator to a specific value. Then (1) is similar to the classical assumption of no unmeasured confounding in causal inference (e.g., [13]). To understand (1), notice that “nature” determines the values of the mediators M_a and the outcomes Y_a′,m, based on C and possibly other factors. Equation (1) thus states that given C, the Y_a′,m do not help to predict M_a; or, nature did not have more information on the potential outcomes Y_a′,m to determine the value of the mediator M_a than recorded in C. In other words, all common causes of mediator and outcome have to be recorded in C. Then, under a consistency assumption,

$$E(Y_{1,M_0})={\int }_{(c,m)}E[Y\mid M=m,C=c,A=1]f_{M\mid C=c,A=0}(m)f_C(c)dmdc;$$ (2)

the “mediation formula”, see e.g. [3, 4, 5, 6].

Under certain conditions (strong parametric assumptions, linear models and no exposure-mediator interaction), the estimators for the natural direct and indirect effects resulting from (2) are the same as the estimators in [1], the founding article on direct and indirect effects (see e.g. [14]). The causal inference literature on natural direct and indirect effects thus generalizes the approach of [1] and adds a causal interpretation to their estimators.

4. Definitions of organic intervention and organic direct and indirect effects

This section defines organic direct and indirect effects. Analogously to natural direct and indirect effects, this article focuses on interventions I that cause the mediator under treatment A = 1 and intervention I, M_1,I=1, to have the same distribution as M₀, given the pre-treatment common causes C of mediator and outcome. However, for individual patients, M_1,I=1 does not need to be exactly the value the mediator would have had without treatment, M₀. This is a considerable relaxation, especially because this distribution can be estimated from the observed data (provided C has been measured), while individual values of M₀ are not observed under treatment. Hence, it is possible to imagine an intervention that leads to this distribution. I term this type of interventions organic because they depend on the entire distribution of M₀, the mediator without treatment, rather than on individual values of M₀. Write Y_1,I=1 for the outcome under treatment A = 1 and intervention I. Then,

Definition 4.1 (Organic intervention)

An intervention I is an organic intervention with respect to C if

$$M_{1,I=1}\mid C=c~M_0\mid C=c$$ (3)

$$Y_{1,I=1}\mid M_{1,I=1}=m,C=c~Y_1\mid M_1=m,C=c,$$ (4)

both hold, where ~ indicates having the same distribution.

Equation (3) says that I “holds the mediator at its distribution under no treatment”: given C, there is no difference in the distribution of the mediator under treatment A = 1 combined with intervention I and the distribution of the mediator under no treatment A = 0. Equation (3) fixes the distribution of the mediator rather than setting the mediator to its value under no treatment. In particular, the mediator under intervention I does not need to depend deterministically on M₀ or M₁. Furthermore, instead of the cross-worlds assumption of equation (1), I assume equation (4). Equation (4) intuitively states that I “has no direct effect on the outcome”: for patients with pre-treatment common causes of mediator and outcome fixed at C = c, the prognosis of patients under treatment “with mediator M_1,I=1 being equal to m under intervention I” is the same as the prognosis of patients under treatment “with mediator M₁ being equal to m without I”. In other words, given C, treated patients with mediator equal to m without intervention I (M₁ = m) are representative of treated patients with M_1,I=1 = m under intervention I. Equation (4) could be relaxed by assuming instead that E [Y_1,I=1 | M_1,I=1 = m, C = c] = E [Y₁ | M₁ = m, C = c]. If the intervention I on the mediator has a direct effect on the outcome, equation (4) fails to hold. Equation (4) is related to the assumption of “partial exchangeability” in [2] and can be discussed with subject matter experts (Web-appendix E may also help).

Example 4.2

A = 1 could be a blood pressure lowering medicine, M blood pressure, and Y the occurrence of a heart attack. To investigate whether A = 1 also has a direct effect on heart attacks, one could do mediation analysis. Suppose that $M_0={\alpha }_0^{(0)}+{\alpha }_{1}C+e_0$, and $M_1={\alpha }_0^{(1)}+{\alpha }_{1}C+e_1$, and suppose that e₀ ~ e₁, e₀ and e₁ are random error terms in ℝ independent of C, and ${\alpha }_0^{(0)},{\alpha }_0^{(1)}$, α₁ ∈ ℝ. Thus, treatment A = 1 shifts the distribution of the blood pressure by ${\alpha }_0^{(1)}-{\alpha }_0^{(0)}$ without changing its shape. Suppose an intervention I leads to $M_{1,I=1}={\alpha }_0^{(2)}+{\alpha }_{1}C+e_{1,I=1}$. Then, I satisfies equation (3) if 1. ${\alpha }_0^{(2)}={\alpha }_0^{(0)}$ (that is, I = 1 shifts the distribution of the blood pressure, in the treated, by ${\alpha }_0^{(0)}-{\alpha }_0^{(1)}$ and 2. e_1,I=1 ~ e₀ is independent of C (that is, I shifts the distribution of the blood pressure, in the treated, without changing its shape). Then, M_1,I=1 ~ M₀, leading to (3). Intervention I could for example be salt in a (possibly random) dosage depending on C. The effect of salt on heart attacks is believed to be through its effect on blood pressure (see for example the CDC website, http://www.cdc.gov/vitalsigns/Sodium/index.html), making equation (4) and thus Definition 4.1 plausible for this intervention. For natural direct and indirect effects, one would need to be able to shift the distribution of M by ${\alpha }_0^{(0)}-{\alpha }_0^{(1)}$ without changing its shape, but additionally set e_1,I=1 = e₀, resulting in M_1,I=1 = M₀. For the direct and indirect effects introduced in [9], one would randomize e_1,I=1 ~ e₀ independent of C, and then need to set the mediator to $M_{1,I=1}={\alpha }_0^{(0)}+{\alpha }_{1}C+e_{1,I=1}$. [9] avoid the use of counterfactuals altogether using graphical models. Of the three interventions above, obviously, e_1,I=1 = e₀ places the strongest restriction. It is related to the assumption of rank preservation sometimes made in the causal inference literature. Rank preservation also implies that two patients with the same observed data have the same counterfactual data.

In this example, one could replace the fully parametric models by M₀ = g(C, e₀) and M₁ = g(C, e₁) + β, with g some function of C and elements in ℝ. Then, I needs to shift the distribution of M₁ given C by −β. Or, one could have M₀ = g(C, e₀) and M₁ = g(C, e₁) + β₀ + β₁C, where now I needs to shift the distribution of M₁ given C by −β₀ −β₁C.

If a pre-treatment common cause C̃ of mediator and outcome has not been observed, equation (4) without C̃ is unlikely to hold. The reason is that the predictive value of the mediator having a specific value under intervention I is likely not the same as the predictive value of the mediator having a specific value without intervention. The mediator M₁ under treatment is predicted by the common cause C̃. However, if C̃ is not included, under intervention I the mediator M_1,I=1 is not necessarily predicted by C̃. Thus, the mediator M₁ carries information on the common cause C̃, but the mediator under intervention I, M_1,I=1, may not. Even if M_1,I=1 carries information on C̃, then the information on C̃ from M_1,I=1 = m may be different than the information on C̃ from M₁ = m, because M_1,I=1 and M₁ have a different distribution. As a consequence, the prognosis under treatment of patients with M₁ = m is different from the prognosis under treatment of patients with M_1,I=1 = m, violating equation (4). Web-appendix B describes a detailed example of the consequences of ignoring a pre-treatment common cause C̃ of mediator and outcome.

When there is a post-treatment common cause C′ of the mediator and the outcome, equation (4) is also unlikely to hold. Assuming that the intervention I does not affect C′, the reason is the same as for unobserved pre-treatment common causes. If the intervention I also changes C′, basing mediation analysis on I results in estimating the effect mediated by the combination (C′, M).

If an intervention I satisfying equation (3) is feasible, which can be tested, equation (4) or its relaxation could be tested as well, by comparing the distribution of Y_1,I=1 given (M_1,I=1, C) to the distribution of Y₁ given (M₁, C). In order to test this, an experiment must be carried out with three arms: “do not treat”, “treat”, and “treat combined with intervention I”. This is in contrast with the existing literature on natural direct and indirect effects, the assumptions of which can never be tested because they involve the joint distribution of counterfactuals under different treatments, which can never be jointly observed.

Now the organic direct and indirect effect of a treatment on the outcome can be defined:

Definition 4.3 (Organic direct and indirect effect)

Consider an organic intervention I. The organic direct effect of a treatment A based on I is E(Y_1,I=1) − E(Y₀). The organic indirect effect of a treatment A based on I is E(Y₁) − E(Y_1,I=1).

Because the treatment is the same for both Y₁ and Y_1,I=1, E(Y₁) − E(Y_1,I=1) is the organic indirect effect, or mediated part of the effect. It is the effect of the organic intervention on the mediator, I, under A = 1. If the distribution of the mediator does not depend on A, I could be “no intervention on M”, and the organic indirect effect is 0. The organic indirect effect is also 0 if the intervention I on the mediator does not affect the outcome. Because the mediator has the same distribution for both Y_1,I=1 and Y₀, E(Y_1,I=1) − E(Y₀) is the organic direct effect. The direct effect is the effect of treatment combined with an organic intervention I as compared to no treatment. Very loosely, the direct effect is the effect of a treatment that 1. has the same direct effect as treatment A = 1: the dependence of Y_1,I=1 on the covariates C and on the mediator is the same as that of Y₁, but 2. has no indirect effect through the mediator (see equation (3)). Notice that E(Y₁) − E(Y₀) = (E(Y₁) − E(Y_1,I=1)) + (E(Y_1,I=1) − E(Y₀)). Thus, like for natural direct and indirect effects, organic direct and indirect effects add up to the total effect of a treatment. Organic direct and indirect effects often generalize natural direct and indirect effects:

Theorem 4.4

Under equation (1), natural direct and indirect effects, if the mediator under treatment can be set to its value without treatment, and the direct and indirect effects defined in [9], if the mediator can be set to any specific value, are special cases of organic direct and indirect effects.

The proof of Theorem 4.4 can be found in Appendix A.

5. Uniqueness of organic direct and indirect effects

Definition 4.3 of organic direct and indirect effects depends on the organic intervention I and on the choice of baseline common causes of mediator and outcome C. Although the definitions of natural direct and indirect effects also depend on the intervention (the mediator is “set” to a specific value), this has not usually been made explicit. I argued that C has to include all common causes of mediator and outcome for equation (4) to be plausible, and thus for an intervention I to be organic. This section formalizes the notion of common causes of mediator and outcome, and proves that the organic direct and indirect effects do not depend on (a) for given C, the choice of organic intervention I or (b) on the choice of common causes C of mediator and outcome, even if more than one set of common causes exists.

Define a common cause of mediator and outcome given C as follows:

Definition 5.1 (common cause)

X is not a common cause of mediator and outcome given C if either equation (5) or equation (6) holds:

$$X⫫M_0\mid C\text{and}X⫫M_1\mid C$$ (5)

$$X⫫Y_1\mid M_1,C.$$ (6)

That is, X is not a common cause if, given C, either X does not predict the mediator, or, given the mediator, X does not predict the outcome. In graphical language: X is not a common cause of mediator and outcome if in a DAG that has C, X, M, and Y, there either is no arrow from X to M, or there is no direct arrow from X to Y. This definition is in line with, for example, [15]. If (all given C) X predicts the mediator and, given the mediator, X predicts the outcome, it is a common cause of mediator and outcome, and usually needs to be included in C for equation (4) to hold with C (see the discussion below Definition 4.1). The following theorem is proved in Appendix A:

Theorem 5.2

For given C, the organic direct and indirect effect do not depend on the choice of organic intervention I with respect to C. Furthermore, if C and C̃ are different sets of common causes of mediator and outcome, C is not a common cause of mediator and outcome given C̃, and C̃ is not a common cause of mediator and outcome given C, then the organic direct and indirect effect do not depend on whether the intervention is organic with respect to C or organic with respect to C̃.

Thus, if we restrict ourselves to interventions that are organic with respect to “complete” common causes C (given C, any other pre-treatment covariate X is not a common cause), organic direct and indirect effects are unique, and one can speak of “the” organic direct and indirect effect.

6. Identifiability and estimation of organic direct and indirect effects

When the treatment A is randomized, E(Y₁) and E(Y₀) can simply be estimated by the averages of Y₁ and Y₀ among patients receiving treatment and not receiving treatment, respectively. Therefore, in order to estimate the organic direct and indirect effects of a randomized treatment, this section focuses on estimating the expectation of Y_1,I=1. The following theorem is the main result of this article:

Theorem 6.1 (Organic direct and indirect effects: the mediation formula for randomized experiments)

Under randomized treatment and Definition of organic interventions 4.1, the following holds for an intervention I that is organic with respect to C:

$$E(Y_{1,I=1})={\int }_{(c,m)}E[Y\mid M=m,C=c,A=1]f_{M\mid C=c,A=0}(m)f_C(c)dmdc.$$

Notice that to estimate E (Y_1,I=1), only the distribution of M under A = 0 and of Y under A = 1 are needed. Thus, Theorem 6.1 can be used both in the absence and in the presence of treatment-mediator interaction (where the expectation of Y depends on M differently with or without treatment). Theorem 6.1 provides the same mediation formula as the previous literature (see Section 3). This formula depends on observable quantities only, and can be estimated using standard models. The contribution of the current article is to show that the definition and thus the interpretation of direct and indirect effects, as well as the conditions under which estimators for these effects are meaningful, can be considerably relaxed.

7. Estimating organic direct and indirect effects in observational studies

So-far, treatment was randomized. This section extends the identification to non-randomized treatments A. As before, A is treatment, which is 1 for the treated and 0 for the untreated. I adopt the usual consistency assumption (see e.g. [13]) relating the observed to the counterfactual data:

Assumption 7.1 (Consistency)

If A = 1, M = M₁ and Y = Y₁. If A = 0, M = M₀ and Y = Y₀.

For observational data, I allow that there exist baseline covariates Z (beyond the common causes of mediator and outcome, C) that need to be included in the analysis in order to eliminate confounding:

Assumption 7.2 (No Unmeasured Confounding)

$$A⫫(Y_1,M_1)\mid C,Z\text{and}A⫫Y_0\mid C,Z\text{and}A⫫M_0\mid C,Z.$$

Thus, given the measured pre-treatment covariates C and Z, treatment should not depend on the prognosis of the patients with or without treatment. For Assumption 7.2 to hold, it is sufficient that (C, Z) includes all the common causes of the treatment, the mediator, and the outcome. This is a particular representation of the usual assumption of no unmeasured confounding in causal inference (see e.g. [13]). Assumption 7.2 cannot be tested statistically. Subject matter experts have to indicate whether they believe that enough pre-treatment patient characteristics have been observed in order for Assumption 7.2 to be plausible.

Under Assumption 7.2, the expectation of Y₁ and Y₀ can be estimated using marginal structural models, the G-computation formula, or structural nested models. Thus, I focus on the expectation of Y_1,I=1. Section 4 argued that in order for an intervention to be organic with respect to C, C usually has to include all common causes of mediator and outcome. Therefore, if an extra Z was necessary for Assumption 7.2 of no unmeasured confounding to hold, I will assume that given C, Z is not a common cause of mediator and outcome, as defined in Definition 5.1. Then,

Theorem 7.3 (Organic direct and indirect effects: the mediation formula for observational studies)

Assume No Unmeasured Confounding Assumption 7.2, Consistency Assumption 7.1, intervention I is organic with respect to C as in Definition 4.1, and given C, Z is not a common cause of mediator and outcome as in Definition 5.1. Then

$$E(Y_{1,I=1})={\int }_{(c,z,m)}E[Y\mid M=m,C=c,Z=z,A=1]f_{M\mid C=c,Z=z,A=0}(m)f_{C,Z}(c,z)dmd(c,z).$$

The proof is in Appendix A. The resulting organic direct and indirect effects are similar to Theorem 6.1, in terms of observable quantities only, and can be estimated using standard methods.

8. Application: Mother-to-child transmission of HIV/AIDS

HIV infection can be transmitted from an HIV positive mother to her infant in utero, during birth, and by breast feeding. The rate of HIV transmission can be lowered by avoiding breast feeding, as well as by treatments such as antiretroviral treatment (ART) and zidovudine (AZT). ART and AZT lower the amount of HIV virus, the HIV viral load, in the blood of the mother. [16] describe that the effect of AZT on mother-to-child transmission of HIV infection is surprisingly large, given the limited effect of AZT on the HIV viral load in the blood of the mother. They estimated that less than 20% of the effect of AZT on mother-to-child transmission is due to the effect of AZT on the mother’s HIV viral load, but their analysis was not based on current causal notions of direct and indirect effects.

This section describes how one could investigate how much of the effect of AZT on mother-to-child transmission is mediated by the effect of AZT on the HIV viral load in the blood of the mother (from now on, the HIV viral load). I argue that the organic direct and indirect effects defined in this article are well-defined and identified in this situation, whereas natural direct and indirect effect are undefined.

Suppose one would like to investigate the likely effect on mother-to-child transmission of a potential new treatment that has the same effect on HIV viral load as AZT but no direct effect on the child’s HIV status. Potentially, a low dosage of ART not containing AZT could be such treatment. (There are several types of ART, some of which contain AZT and some of which do not.) Let I be an intervention that, without AZT treatment, causes the distribution of HIV viral load to be the same as under AZT treatment; I represents the potential new treatment. Here, in contrast to most of the literature on mediation analysis, which focuses on the effect of an intervention on the mediator under treatment, interest focuses on the effect of an intervention on the mediator under no treatment. In order to directly apply the method described in this article, we therefore re-code A = 0 if a person was treated with AZT, and A = 1 if a person was not treated with AZT. In the case of a linear model without treatment-mediator interaction, $E[Y\mid M=m,A=a,C=c]={\beta }_0+{\beta }_{1}m+{\beta }_{2}a+{\beta }_3^{\top }c$ (no term β₄am), both approaches lead to the same direct effect, β₂, and therefore also to the same indirect effect. In general, both approaches can lead to different results. [6] and Web-appendix C discuss when each definition is most useful; this depends on the context of the investigation.

In this example, one would expect that if AZT has a direct effect on mother-to-child transmission, a mother’s adherence to AZT treatment is a post-treatment common cause of both HIV viral load M and mother-to-child transmission Y, because both M and Y will be reduced under better adherence. Thus, one seems to need the post-treatment covariate “adherence”, ad, in C. However, equation (4) seems reasonable without compliance: if all pre-treatment common causes are in C, so adherence is not a proxy for other confounders, ad⫫(Y₁, M₁)|C (recall 1 indicates no treatment in this section). If adherence is not an issue for I, ad⫫(Y_1,I=1, M_1,I=1|C. And if it is: because I does not have a direct effect on mother-to-child transmission, Y_1,I=1⫫ad|M_1,I=1, C. Thus, if equation (4) holds with ad in the conditioning event and all pre-treatment common causes are in C, equation (4) will also hold without ad.

For ease of exposition, suppose that AZT treatment is randomized (the approach can be generalized to observational studies as in Section 7). I now illustrate how to use the identification result of Section 6 to estimate the indirect effect of AZT on mother-to-child transmission. Suppose that $M_1~M_0+{\beta }_1+{\beta }_3^{\top }C\mid C$ holds for M equal to log HIV viral load. Suppose in addition that the probability of mother-to-child transmission without treatment follows a logistic regression model of the form $\text{logit}(Y=1\mid M=m,C=c,A=1)={\theta }_0+{\theta }_1^{\top }M+{\theta }_2^{\top }C$. Notice that one only needs such a model for mother-to-child transmission under A = 1 (no treatment in this case). Then, by Web-appendix D, it follows that

$$E(Y_{1,I=1})=E[1/(1+exp(-{\theta }_0-{\theta }_1(M-{\beta }_1-{\beta }_3^{\top }C)-{\theta }_2^{\top }C))\mid A=1].$$ (7)

This expression can be estimated as indicated in Web-appendix D. This leads to an estimator for the indirect effect that does not use data on the outcomes of treated mothers (it does depend on the mediator values of treated mothers).

In contrast to the organic direct and indirect effects, the natural direct and indirect effects are undefined in this application. They involve Y_1,M0, whether or not a newborn is infected without AZT but with the HIV viral load of the mother set to the value it would have had under AZT (A = 0 here). How one could set the mediator to the value under AZT is unclear. One can imagine treatments, for example low-dose ART, that have the same effect on HIV viral load as AZT, as needed for organic direct and indirect effects. However, it is unlikely that such a treatment would, for all mothers, set the HIV viral load to the exact same value it would have had under AZT. If AZT were a combination of substances, some combination of a substance that affects HIV viral load and another substance that might directly affect mother-to-child transmission, one could imagine setting the HIV viral load to involve only the substance that affected HIV viral load. However, like many treatments, AZT is just one substance. I therefore conclude that for a treatment like AZT, the organic direct and indirect effects are more natural than their natural counterparts.

9. The effect of antidepressants on depressive symptoms not mediated by participants’ expectations

[17] describe a meta-analysis of the effects of antidepressants when an “active” placebo is used instead of a standard placebo. The active placebo, in this case atropine, was designed to mimic the side effects of the active drugs, so patients and the persons rating the patients’ symptoms could not guess whether a patient was on an active drug based on the observed side effects. The underlying idea was that if patients and raters could guess that a patient was on an active drug, they would have favorable expectations about the outcome, depressive symptoms, leading to an overestimation of the benefits of the active drug.

It is interesting to explore how this experimental design with active placebos relates to mediation analysis. When estimating the effect of antidepressants, the object of interest is often the direct effect of the active components in the antidepressants, not mediated by patients’ and raters’ expectations. If the effect of active placebo on side effects is the same as the effect of active treatment on side effects, the effect of the active placebo can be interpreted as the indirect effect, mediated by the unblinding/participants’ expectations due to side effects.

In the notation of this article, side effects are denoted by M, the outcome, depressive symptoms, by Y, “no treatment” or “standard placebo” by 1, the active drug by 0, and the active placebo by I = 1. The meta-analysis in [17] estimated Y₀−Y_1,I=1: the effect of active treatment compared to active placebo. This is the organic direct effect of the treatment as defined in Definition 4.1, if (1) the distribution of side effects due to active placebo is the same as the distribution of side effects due to active treatment, given pre-treatment covariates C (equation (3)), and if (2) given the observed side effects in patients not on active treatment, whether these side effects occurred by atropine (I = 1) or by nature (I = 0) did not affect the measured depressive symptoms of the patients (equation (4)).

[17] estimated a considerably smaller effect of active treatments versus active placebo than the estimated effect of active treatments versus standard placebo. This result suggests that part of the beneficial effect of the antidepressants could be mediated by their side effects, which may affect participants’ expectations and, therefore, the measured depressive symptoms.

[17] did not consider new generation antidepressants such as SSRIs, because after their introduction it was considered unethical to carry out experiments with active placebos in patients with depressive symptoms.

In Section 7 and in earlier sections, I consider organic interventions under active treatment labeled A = 1. In this section, like in Section 8 (mother-to-child-transmission of the HIV virus), the active treatment is labeled A = 0 and “no treatment” is labeled A = 1. This change in the labels is motivated by the nature of the quantities of clinical interest in the examples of this section and Section 8. In this section, the quantities of interest are the difference between active placebo and standard placebo (that is, the effect of the organic intervention I = 1 under no active drug) and the difference between the active drug and the active placebo (that is, the remaining effect of the antidepressants above and beyond that of the active placebo).

10. Discussion

This article shows that, in contrast to the assumptions behind natural direct and indirect effects, cross-worlds quantities and setting the mediator are not always necessary to define causal direct and indirect effects. This leads to newly defined organic direct and indirect effects. Furthermore, this article proves that, in contrast to natural direct and indirect effects, identification of organic direct and indirect effects does not rely on the existence of counterfactual outcomes under all combinations of the treatment and the mediator. For identifiability of organic direct and indirect effects, a distributional assumption linking the distribution of the outcome under an organic intervention to the data replaces the cross-worlds assumption which identifies natural direct and indirect effects. This article focuses on organic interventions I, which cause the distribution of the mediator given C to be the same as M₀, rather than setting the mediator value to M₀, as in natural direct and indirect effects. In applications in the health or social sciences, like epidemiology, or psychology, one often wants to consider which part of the effect of a treatment is mediated through some covariate or trait. For example, one may want to investigate how much of the effect of antiretroviral treatment, ART, on AIDS-defining events and death is mediated by the CD4 count. In this example, it is easier to envision an intervention that causes the CD4 count to have a particular distribution rather than setting the CD4 count to a specific value for each patient. However, if interventions on the mediator are inconceivable, both natural and organic direct and indirect effects are undefined.

I have shown that the proposed organic direct and indirect effects are identified by the same expressions as developed previously in the literature for natural direct and indirect effects. The contribution of this article is to show that these mediation formulas hold in substantially more generality. As a consequence, estimators based on the mediation formulas have a broader causal interpretation than previously shown. The new definitions introduced in this article are easy to interpret and can therefore be easily discussed with subject matter experts. For an intervention I to be organic it has to be that, given pre-treatment characteristics C, the outcome under treatment “for a patient with M₁ = m under treatment” is representative of the outcome under treatment “if the organic intervention I caused M_1,I=1 = m”. This can be interpreted as that, under treatment, the organic intervention has no direct effect on the outcome.

An organic intervention I is a considerable relaxation of M_1,I=1 = M₀. Still, it may be difficult to find an organic intervention. Notice, however, that if there is an intervention Ĩ such that equation (4) holds, then in some cases it may be possible to construct an organic intervention I by adapting the dosage of Ĩ as a function of C (deterministically or randomly) in a way such that equation (3) holds. If there is interest in figuring out what might be the benefit of an intervention with only a direct or only an indirect effect, if such an intervention would be developed in a lab, organic direct and indirect effects are of interest. In any case, being able to actually carry out organic interventions is not necessary to identify and estimate organic direct and indirect effects. Rather, organic interventions can be employed as thought experiments useful to frame the analysis and define the parameters of interest.

Natural direct and indirect effects are defined at the individual level as well as the population level, whereas organic direct and indirect effects are defined only at the population level. This reflects that an organic intervention does not set the mediator to a pre-specified value for each patient.

In related work, the appendix of [18] considers interventions that cause the mediator to have the same distribution as without treatment, conditional on C. However, for identification [18] still assumes existence of all Y_a,m and Y_a,m⫫M | A, C, L, where L is a post-treatment common cause of mediator and outcome. This is problematic if one cannot set the mediator to particular values.

Following the previous literature, this article studies interventions that do not affect pre-treatment common causes of mediators and outcomes. For example, inherited risk factors are thought to be common causes of low birth weight and infant mortality. For equation (4) to be plausible, such common causes of mediators and outcomes have to be taken into account. The consequences of ignoring common causes are illustrated in Web-appendix B for the direct effect of smoking on infant mortality, not mediated by low birth weight. The importance of observing common causes was also noted in e.g. [5].

[7] argue that the natural direct effect, which they call pure direct effect, “is non-manipulable relative to A, M and Y in the sense that, in the absence of assumptions, the pure direct effect does not correspond to a contrast between treatment regimes of any randomized experiment performed via interventions on A, M and Y.” Organic direct and indirect effects are not subject to that caveat. If there exists an organic intervention I (not necessarily M_1,I=1 = M₀), then the organic direct and indirect effect induced by I are identified from the experiments “do not treat”, “treat”, and “treat under intervention I.” Both conditions for I to be organic can be tested on the basis of these experiments, and the organic direct and indirect effects do not depend on the choice of organic intervention I (Section 5).

Under an agnostic model, which does not assume the existence of counterfactual outcomes, the natural direct and indirect effects are obviously not defined: they are based on the cross-worlds counterfactuals Y_1,M0. In contrast, if an organic intervention I exists, the organic direct and indirect effects could have been equivalently defined without counterfactual outcomes, because they can be defined on the basis of interventions; see Web-appendix F for details.

In future work, I will show that in contrast to natural direct and indirect effects, organic direct and indirect effects can be extended to provide an identification result for the case where there are post-treatment mediator-outcome confounders. This will provide another alternative to the three quantities described in [19].

The methodology in this article could also be applied to the study of the effects of future treatments based on prior data. Consider, for example, the effect of a future treatment to lower immune activation (M in the notation of this article) in HIV positive patients. Suppose that this future treatment is aimed to eventually prevent clinical events (Y). Assume that under the future treatment, patients would have a specific distribution of immune activation M₁, and the future treatment has no direct effect on the outcome Y : conditional on a set of covariates C, the prognosis of patients under the future treatment, Y₁, is the same as the prognosis Y of patients with the same immune activation in the observed data (compare with (4)). Then the mean outcome under the future treatment can be estimated using a sample counterpart of

$$E(Y_1)={\int }_{(c,m)}E[Y\mid M=m,C=c]f_{M_1\mid C=c}(m)f_C(c)dmdc.$$

The proof follows the same lines as the proof of Theorem 6.1, but the interpretation is different because the future treatment does not necessarily cause immune activation to have the same distribution as some existing treatment A. Of course, since the identifying assumption of equation (4) cannot be verified without experimental data of the future treatment, an experiment with the future treatment would be necessary to confirm this result. This last formula also provides a mathematical underpinning of the application in [20], who estimate the controlled direct effect of an intervention when “only a portion of the population’s mediator is altered”.

To conclude, this article introduces organic direct and indirect effects and provides identification and estimators for these effects. The assumptions are weaker than for natural direct and indirect effects.

A. Appendix: Proofs

Proof of Theorem 4.4

(4.3) is trivial for M_1,I=1 = M₀. (4.3) also follows immediately if M_1,I=1 is a random draw of M₀ given C. Furthermore, it is easy to see that for M_1,I=1 = M₀, and if all Y_a,m are well-defined, then cross-worlds Assumption (3.1) implies equation (4.4): for M_1,I=1 = M₀, equation (4.4) states Y_1,m | M₀ = m, C = c ~ Y_1,m | M₁ = m, C = c, and under equation (3.1) for randomized treatment A, Y_1,m depends, for given C, neither on M₀ nor on M₁. For M_1,I=1 a random draw, equation (4.4) states Y_1,m | M_1,I=1 = m, C = c ~ Y_1,m | M₁ = m, C = c, and under equation (3.1) for randomized treatment A, Y_1,m depends, for given C, not on any mediators.

Proof of Theorem 5.2

First, let I be an intervention that is organic with respect to C. Then

$$\begin{array}{l}E(Y_{1,I=1})=E(E[Y_{1,I=1}\mid M_{1,I=1},C])\\ ={\int }_{(c,m)}E[Y_{1,I=1}\mid M_{1,I=1}=m,C=c]f_{M_{1,I=1}\mid C=c}(m)dm{f}_C(c)dc\\ ={\int }_{(c,m)}E[Y_1\mid M_1=m,C=c]f_{M_0\mid C=c}(m)dm{f}_C(c)dc.\end{array}$$ (8)

In this proof, the first two equalities follow from the definition of conditional expectation. The third equality follows from Definition 4.1, (4.3) and (4.4). Thus, the choice of I does not influence the direct and indirect effect, as long as it is organic with respect to C.

Next, let I^C be an intervention that is organic with respect to C and I^C̃ and intervention that is organic with respect to C̃. I assumed that C is not a common cause of mediator and outcome given C̃, and C̃ is not a common cause of mediator and outcome given C; hence there are 4 different cases, with either (5.5) or (5.6) holding for C and C̃, respectively. I will show that under any of the 4 different cases,

$$E\left(Y_1^{I^{\stackrel{\sim }{C}}}\right)={\int }_{(\stackrel{\sim }{c},m,c)}E[Y_1\mid M_1=m,\stackrel{\sim }{C}=\stackrel{\sim }{c},C=c]f_{M_0\mid \stackrel{\sim }{C}=\stackrel{\sim }{c},C=c}(m)f_{\stackrel{\sim }{C},C}(\stackrel{\sim }{c},c)dcdmd\stackrel{\sim }{c}.$$

Since the conditions and the result are symmetric in C, C̃, it follows that also

$$E\left(Y_1^{I^C}\right)={\int }_{(\stackrel{\sim }{c},m,c)}E[Y_1\mid M_1=m,\stackrel{\sim }{C}=\stackrel{\sim }{c},C=c]f_{M_0\mid \stackrel{\sim }{C}=\stackrel{\sim }{c},C=c}(m)f_{\stackrel{\sim }{C},C}(\stackrel{\sim }{c},c)dcdmd\stackrel{\sim }{c}.$$

But then, $E\left(Y_1^{I^{\stackrel{\sim }{C}}}\right)=E\left(Y_1^{I^C}\right)$.

Suppose first that C⫫M₀ | C̃ and C⫫M₁ | C̃. Then

$$\begin{array}{l}E\left(Y_1^{I^{\stackrel{\sim }{C}}}\right)={\int }_{(\stackrel{\sim }{c},m)}E[Y_1\mid M_1=m,\stackrel{\sim }{C}=\stackrel{\sim }{c}]f_{M_0\mid \stackrel{\sim }{C}=\stackrel{\sim }{c}}(m)f_{\stackrel{\sim }{C}}(\stackrel{\sim }{c})dmd\stackrel{\sim }{c}\\ ={\int }_{(\stackrel{\sim }{c},m,c)}E[Y_1\mid M_1=m,\stackrel{\sim }{C}=\stackrel{\sim }{c},C=c]f_{C\mid M_1=m,\stackrel{\sim }{C}=\stackrel{\sim }{c}}(c)dc{f}_{M_0\mid \stackrel{\sim }{C}=\stackrel{\sim }{c}}(m)f_{\stackrel{\sim }{C}}(\stackrel{\sim }{c})dmd\stackrel{\sim }{c}\\ ={\int }_{(\stackrel{\sim }{c},m,c)}E[Y_1\mid M_1=m,\stackrel{\sim }{C}=\stackrel{\sim }{c},C=c]f_{C\mid \stackrel{\sim }{C}=\stackrel{\sim }{c}}(c)f_{M_0\mid \stackrel{\sim }{C}=\stackrel{\sim }{c},C=c}(m)f_{\stackrel{\sim }{C}}(\stackrel{\sim }{c})dcdmd\stackrel{\sim }{c}\\ ={\int }_{(\stackrel{\sim }{c},m,c)}E[Y_1\mid M_1=m,\stackrel{\sim }{C}=\stackrel{\sim }{c},C=c]f_{M_0\mid \stackrel{\sim }{C}=\stackrel{\sim }{c},C=c}(m)f_{\stackrel{\sim }{C},C}(\stackrel{\sim }{c},c)dcdmd\stackrel{\sim }{c}.\end{array}$$

The first line follows from equation (8). The second line conditions on C. In the third line I changed the order of integration and used C⫫M₀ | C̃ and C⫫M₁ | C̃.

Alternatively, suppose that C⫫Y₁|M₁, C̃. Then,

$$\begin{array}{l}E\left(Y_1^{I^{\stackrel{\sim }{C}}}\right)={\int }_{(\stackrel{\sim }{c},m)}E[Y_1\mid M_1=m,\stackrel{\sim }{C}=\stackrel{\sim }{c}]f_{M_0\mid \stackrel{\sim }{C}=\stackrel{\sim }{c}}(m)f_{\stackrel{\sim }{C}}(\stackrel{\sim }{c})dmd\stackrel{\sim }{c}\\ ={\int }_{(\stackrel{\sim }{c},m)}E[Y_1\mid M_1=m,\stackrel{\sim }{C}=\stackrel{\sim }{c}]{\int }_c{f}_{M_0\mid \stackrel{\sim }{C}=\stackrel{\sim }{c},C=c}(m)f_{C\mid \stackrel{\sim }{C}=\stackrel{\sim }{c}}(c)dc{f}_{\stackrel{\sim }{C}}(\stackrel{\sim }{c})dmd\stackrel{\sim }{c}\\ ={\int }_{(\stackrel{\sim }{c},m),c}E[Y_1\mid M_1=m,\stackrel{\sim }{C}=\stackrel{\sim }{c}]f_{M_0\mid \stackrel{\sim }{C}=\stackrel{\sim }{c},C=c}(m)f_{C\mid \stackrel{\sim }{C}=\stackrel{\sim }{c}}(c)f_{\stackrel{\sim }{C},c}(\stackrel{\sim }{c},c)dcdmd\stackrel{\sim }{c}\\ ={\int }_{(\stackrel{\sim }{c},m),c}E[Y_1\mid M_1=m,\stackrel{\sim }{C}=\stackrel{\sim }{c},C=c]f_{M_0\mid \stackrel{\sim }{C}=\stackrel{\sim }{c},C=c}(m)f_{\stackrel{\sim }{C},c}(\stackrel{\sim }{c},c)dcdmd\stackrel{\sim }{c}.\end{array}$$

The first line follows from equation (8). The second line conditions on C. The last line follows from C⫫Y₁ | M₁, C̃.

Proof of Theorem 6.1

$$\begin{array}{l}E(Y_{1,I=1})={\int }_{(c,m)}E[Y_1\mid M_1=m,C=c]f_{M_0\mid C=c}(m)dm{f}_C(c)dc\\ ={\int }_{(c,m)}E[Y_1\mid M_1=m,C=c,A=1]f_{M_0\mid C=c,A=0}(m)dm{f}_C(c)dc\\ ={\int }_{(c,m)}E[Y\mid M=m,C=c,A=1]f_{M\mid C=c,A=0}(m)f_C(c)dmdc.\end{array}$$

The first equality follows from equation (8). The second equality follows from the fact that treatment was randomized; this implies that

$$A⫫(Y_1,M_1)\mid C\text{and}A⫫M_0\mid C.$$

The last equality follows from the randomization.

Proof of Theorem 7.3

Theorem 7.3 assumed that either equation (5.5) or equation (5.6) holds for Z. Suppose first that equation (5.5) holds for Z. Then

$$\begin{array}{l}E(Y_{1,I=1})={\int }_{(c,m)}E[Y_1\mid M_1=m,C=c]f_{M_0\mid C=c}(m)dm{f}_C(c)dc\\ ={\int }_{(c,m)}{\int }_{z}E[Y_1\mid M_1=m,Z=z,C=c]f_{Z\mid M_1=m,C=c}(z)dz{f}_{M_0\mid C=c}(m)f_C(c)dmdc\\ ={\int }_{(c,z,m)}E[Y_1\mid M_1=m,Z=z,C=c,A=1]f_{Z\mid C=c}(z)f_{M_0\mid Z=z,C=c}(m)f_C(c)dzdmdc\\ ={\int }_{(c,z,m)}E[Y_1\mid M_1=m,Z=z,C=c,A=1]f_{M_0\mid Z=z,C=c,A=0}(m)f_{C,Z}(c,z)dzdmdc\\ ={\int }_{(c,z,m)}E[Y\mid M=m,Z=z,C=c,A=1]f_{M\mid Z=z,C=c,A=0}(m)f_{C,Z}(c,z)dmdzdc.\end{array}$$

The first line follows from equation (8). The second line conditions on Z. The third line uses (5.5), for both M₀ and M₁, Assumption 7.2, and changes the order of integration. The fourth line follows from Assumption 7.2. The last line follows from Assumption 7.1.

Next, suppose that equation (5.6) holds for Z.

$$\begin{array}{l}E(Y_{1,I=1})={\int }_{(c,m)}E[Y_1\mid M_1=m,C=c]f_{M_0\mid C=c}(m)dm{f}_C(c)dc\\ ={\int }_{(c,m)}E[Y_1\mid M_1=m,C=c]{\int }_z{f}_{M_0\mid Z=z,C=c}(m)f_{Z\mid C=c}(z)dzdm{f}_C(c)dc\\ ={\int }_{(c,z,m)}E[Y_1\mid M_1=m,Z=z,C=c]f_{M_0\mid Z=z,C=c}(m)f_{Z,C}(z,c)dmdzdc\\ ={\int }_{(c,z,m)}E[Y_1\mid M_1=m,Z=z,C=c,A=1]f_{M_0\mid Z=z,C=c,A=0}(m)f_{Z,C}(z,c)dmdzdc\\ ={\int }_{(c,z,m)}E[Y\mid M=m,Z=z,C=c,A=1]f_{M\mid Z=z,C=c,A=0}(m)f_{Z,C}(z,c)dmdzdc.\end{array}$$

The first line follows from equation (8). The second line follows by conditioning on Z. The third line follows from (5.6) and changing the order of integration. The fourth line follows from Assumption 7.2. The fifth line follows from Assumption 7.1.