Spatially dense morphometrics of craniofacial sexual dimorphism in 1‐year‐olds

Abstract

Recent advances in the field of geometric morphometrics allow for powerful statistical hypothesis testing for effects of biological and environmental variables on anatomical shape. This study used partial least‐squares regression (PLSR) and the recently developed bootstrapped response‐based imputation modelling (BRIM) algorithm to test for sexual dimorphism in the craniofacial shape of 1‐year‐old humans. We observed a recession of the forehead in boys relative to girls, and differences in the nose, consistent with adult dimorphism. Results also suggest that the degree to which individuals express dimorphic traits is continuous throughout the population. This is also seen in adult dimorphism but in 1‐year‐olds the amount of overlap between groups is much higher, indicating the strength of dimorphism between sexes is lower. Our results demonstrate early sexual dimorphism that is not attributable to the influx of sex hormones at puberty. This highlights the need to look at very early ontogeny for the origins of sexual dimorphism. We suggest that future work look at potential mediating effects of this early dimorphism on the later impact of puberty. The subtle shape differences we have detected, may also be applied to sexing fossilised crania. A common artefact in 3D images of faces of young children is that they often have their mouths open to varying degrees, introducing variability in the data unrelated to anatomy. We describe two PLSR‐based methods of correcting this. These methods may facilitate surgical planning and assessment of young children based on 3D images.

Introduction

Sexual dimorphism refers to the characteristic morphological differences between males and females. Sexual dimorphism of faces has been confirmed in adults (Hennessy et al. 2005; Claes et al. 2011, 2014; Velemínská et al. 2012; Tanikawa et al. 2016). The developmental, evolutionary and biological bases for sexual dimorphism are of considerable interest to anthropologists and biologists. It is widely supposed that dimorphic traits emerge only with the onset of puberty, where increased testosterone triggers a masculinisation of males’ faces (Enlow & Hans, 1996; Verdonck et al. 1999). There is evidence for independent effects of both adult hormone levels and those experienced in utero on adult facial shape (Penton‐Voak & Chen, 2004; Fink et al. 2005; Schaefer et al. 2005). It has been proposed that uterine hormone levels organise the underlying ‘architecture’ of the face, which is then activated at puberty (Neave et al. 2003). Such early differences in facial architecture should be detectable very early in life if sufficiently sensitive methods are employed. Although dimorphism in the size of the neurocranium has been demonstrated in infants and in utero (Joffe et al. 2005; Bulygina et al. 2006) the presence of adult patterns of shape dimorphism has, to the best of our knowledge, only been demonstrated in adolescents, down to approximately age 11 (Ferrario et al. 2003; Bulygina et al. 2006; Koudelová et al. 2015).

Many previous studies of sexual dimorphism have employed univariate comparisons of selected inter‐landmark measurements (Kondo et al. 1999; Joffe et al. 2005; Tanikawa et al. 2016). However, any fewer than all pairwise distances between all pairs of landmarks, fail to capture the full spatial arrangement and geometrical relationships between landmarks (Dryden & Mardia, 1998). Geometric morphometrics (Rohlf & Marcus, 1993; Adams et al. 2004; Mitteroecker & Gunz, 2009) comprises techniques for the analysis of entire landmark configurations. These capture the spatial arrangement between all landmarks by using landmark locations themselves as the fundamental unit of analysis. Previous such studies of children have derived conclusions from visual inspections of the differences between average male and female configurations (Ferrario et al. 2003; Bulygina et al. 2006) and not from statistical hypothesis testing. They have also used a relatively limited representation of the surface defined by anatomical (and some pseudo‐anatomical) landmarks. This precludes analysis of the surface where these are not present. Finally they have not controlled for the effect of allometry. Within morphometrics, allometry refers to shape changes that accompany changes in size (Klingenberg, 1996). Males’ heads are larger than females’ heads, meaning that a general allometric effect may confound the true pattern of shape differences attributable to sex (Rosas & Bastir, 2002).

Surface registration algorithms (Andresen & Nielsen, 2001; Hutton et al. 2003a; Claes, 2007; Claes et al. 2012b) allow the automatic mapping of spatially dense configurations of landmarks from a template shape to every instance in a population. In combination with geometric morphometric techniques, this defines spatially dense morphometrics which can be used to analyse the entire geometry of the surface under study (Andresen et al. 2000; Hutton et al. 2001, 2003a,b; Hammond et al. 2004; Hennessy et al. 2005; Claes, 2007; Cox‐Brinkman et al. 2007; Hammond, 2007; Claes et al. 2011, 2012a,b,c, 2014).

Here we use partial least‐squares regression (PLSR; De Jong, 1993; Wold et al. 2001) coupled with a permutation‐based framework for significance testing (Kennedy, 1995; Anderson & Legendre, 1999, p. 278) to test for sexual dimorphism in 1‐year‐old boys and girls, improving on earlier comparisons of average shapes. We analysed the entirety of the craniofacial complex, whereas previous studies of this age‐group have only analysed the face and the anterior neurocranium (Bulygina et al. 2006), or a single measure of head‐circumference (Joffe et al. 2005). We also use the Bootstrapped Response‐based Imputation Modeling (BRIM; Claes et al. 2014) algorithm to test for sexual dimorphism and determine whether dimorphic traits are distributed continuously in the population, and the degree of overlap in morphology of males and females. Extensions of PLSR were used to correct a problem observed in the sample, of variable mouth openness due to limited co‐operation of the young children.

Method

Sample

To test for sexual dimorphism in a homogeneous 1‐year‐old population, 473 infants were imaged at the age of 1 year (M = 363.47, SD = 8.83 days old). One child's sex was not recorded and was excluded from the analyses of sexual dimorphism, although they were included in the sample used to assess the mouth closing techniques. The final sample with known sex thus contained 248 boys and 224 girls. These were a subsample of the Asking Questions about Alcohol (AQUA; Muggli et al. 2014) cohort. The mothers were a cross‐section of a low‐risk pregnancy population recruited during their first visit to an antenatal clinic. Data about lifestyle and biological factors that may affect craniofacial shape were collected, with a focus on maternal alcohol consumption. Analyses were conducted to determine whether the effect of sex reported here was independent of these factors (Supporting Data S1.2). In all included cases, parent‐reported ethnicity was either ‘white’ or of European extraction.

Image acquisition and pre‐processing

The outer surface of the facial soft‐tissue was encoded as a three‐dimensional (3D) image. In a 3D image, faces are represented as a ‘mesh’. This comprises a cloud of points (vertices) in three dimensions and a triangulation of neighbouring vertices that defines the outer surface of the face.

Images were collected at the Royal Children's Hospital, Melbourne, Australia, using the 3dMD 7‐pod system (3dMD corporation, Atlanta, GA, USA). This captures a full 360° image of the head including the face and cranium. Images were taken with a tight‐fitting stocking placed over the cranial vault, so as to capture its shape, unobscured by hair, which was pressed very tightly against the scalp.

To establish anatomical correspondence across the sample of images, spatially dense configurations of quasi‐landmarks were automatically indicated on each 3D image via a non‐rigid registration (Snyders et al. 2014 for technical details, Claes et al. 2012b for a non‐technical description). This is essentially a spatially dense, automatic extension of the process of manually indicating anatomical landmarks on a subject or specimen. Quasi‐landmarks are defined as the vertices of a template mesh (e.g. an average 1‐year‐old face). Each point may or may not have a well‐defined biological meaning (hence quasi‐), but together they provide a representation of the entire surface.

Although differing patterns of asymmetry in males and females may be of interest (Claes et al. 2012c), in this work we concentrate on the symmetric component of shape variation. Asymmetry was removed by superimposing a reflected copy of the face onto the original and taking the mean of the two faces as a symmetrical version of that face (Claes et al. 2011).

Generalised Procrustes analysis

To isolate differences in the scans due to anatomical variability from those differences due to the location, rotation and size of the images, all scans were co‐aligned to the sample mean via generalised Procrustes analysis (GPA; Gower, 1975). GPA iteratively estimates the mean (the Procrustes mean) configuration of the sample, with which all faces are subsequently aligned. Standard GPA is sensitive to gross, localised form differences such as the ‘Pinocchio’ effect (Zelditch et al. 2004) and so robust Procrustes superimposition was used (Claes et al. 2012a). To remove differences in size, all faces were scaled to the mean size of all faces in the sample. Although it is more usual to scale all faces to unit centroid size (see below), the mean size of the sample was used to keep the regression coefficients in millimetre units, as the magnitude of shape differences may be of interest to clinicians. It was empirically verified that this had no effect on the statistical inferences drawn here (data not shown). As a measure of size we use centroid size:

$$\sqrt{\sum _{i=1}^k{d_i}^2}$$

where d _i is the distance of the i _th quasi‐landmark from the centroid (mean) of the landmark configuration.

The co‐ordinates of the Procrustes mean configuration were subtracted from each face to define the Procrustes residuals. The Procrustes residuals of the entire sample (P) can be represented as a matrix:

$$P=\left[\begin{array}{ccc}{1}_{x_1},1_{y_1},1_{z_1}& \cdots & 1_{x_k},1_{y_k},1_{z_k}\\ ⋮& \ddots & ⋮\\ j_{x_1},j_{y_1},j_{z_1}& \cdots & j_{x_k},j_{y_k},j_{z_k}\end{array}\right]$$

The elements of P code the deviation of each point from the Procrustes mean configuration. Each row contains the k quasi‐landmarks, which together define the shape of a particular face. There are j number of faces. The geometric interpretation of this matrix is as a point‐cloud in k × 3 dimensional space, with the Procrustes mean at the centre. Each face is a single point within this space.

Partial least‐squares regression

Partial least‐squares regression was used to characterise the effects of sex and size on shape. PLSR was accomplished by the SIMPLS method (De Jong, 1993). PLSR models the association between one or more predictor variables and one or more response variables. In this case the matrix of Procrustes residuals (defining facial shape) constituted the matrix of response variables. Procrustes residuals are highly correlated, and there are more Procrustes residuals than observations in our sample. In such situations PLSR is preferable to ordinary least‐squares regression (Wold et al. 1984; Shrimpton et al. 2014).

Geometrically PLSR defines the vector through the point‐cloud that best captures the covariance between predictor/s (e.g. sex) and facial shape. The effects of sex and centroid size on shape were separated by including both as predictors in the regression model. This forces each regression path to model different variability, thus isolating their independent effects on shape. The vector of elementwise products of size and shape was also included as a predictor to model the interaction between the two variables.

The permutation‐based significance testing protocol described in Claes et al. (2014) was used to determine the significance both of the overall effect of each variable on facial morphology and of the effect on each individual quasi‐landmark. All significance tests were based on 1000 permutations.

Bootstrapped response‐based imputation modeling

The algorithm BRIM (Claes et al. 2014) was also used to characterise the effects of sex on shape, and to determine whether dimorphic features are distributed continuously in the population. The core principle in BRIM, with reference to the current problem, is that the categories ‘Male’ and ‘Female’ are imprecise; it is likely that they do not capture the full range of maleness/femaleness. Some people have very masculine or feminine faces, and some appear more androgynous. BRIM iteratively extracts the regression vector (using PLSR) that best characterises the effect of the predictor on the response variables and derives an RIP (response‐based imputed predictor) value for each face, which indicates that face's position along this regression vector. Thus, the dichotomous variable (male/female) is transformed into a continuous variable that represents each face's masculinity–femininity. The algorithm consists of two nested loops, which are described in Supporting Data S1.1, Video S1, Video S2 and elsewhere (Claes et al. 2014). This imputation can be ‘conditioned’ by including other variables in the model. We conditioned this analysis with centroid size and the interaction term (described earlier), to ensure the regression path and RIPs were independent of these effects.

The hypothesis test for BRIM is an anova test of mean difference in the RIP variables, with sex as the independent variable. This tests for a difference in the groups’ position along the regression vector. Significance is determined using an empirically estimated F‐distribution (Supporting Data S1.1). The regression vector extracted can be visualised by regressing Procrustes residuals onto shape and using the methods of visualisation described below.

Correction of mouth openness

Non‐anatomical variation in the images, due to mouth openness, was removed by defining a variable to represent the degree of mouth openness for each face. As a preliminary step, all faces were rated by the first author (H.M.) on a continuous scale from 0 through to 3, indicating how open the mouth was.

Partial least‐squares regression defines the direction in the point‐cloud that captures the covariance between the variable and the shape. When more than one variable is included as a predictor, it defines a direction for each variable. Each direction will be orthogonal to the other and thus statistically independent; two regression vectors cannot account for the same variability. Including a variable that will account for the irrelevant variability, such as ratings of mouth openness, is one method of removing the irrelevant variability. It follows that the residuals of the model with mouth openness as a predictor constitute corrected versions of each face. This corrected face could be explicitly constructed by adding its corresponding residuals to the Procrustes mean configuration (which was subtracted during GPA).

A limitation of the above method is that the accuracy of the correction of an individual face is determined entirely by the rating it was initially given and the overall consistency of the ratings across the sample. The accuracy of the correction can be controlled by allowing an operator manually to adjust the degree of the correction. The regression coefficients are a vector of weights on each Procrustes residuals (the vector of ms below). These weights constitute a transformation that can be applied to the face, manually to open or close the mouth. The degree to which the mouth is opened or closed is determined by adjusting t while observing its effect on the facial image. Specifically, a transformed version of a particular face is calculated by:

$$\left[\begin{array}{c}{f}_{x_1}^{\prime }\\ f_{y_1}^{\prime }\\ f_{z_1}^{\prime }\\ ⋮\\ f_{x_k}^{\prime }\\ f_{y_k}^{\prime }\\ f_{z_k}^{\prime }\end{array}\right]=\left[\begin{array}{c}{f}_{x_1}\\ f_{y_1}\\ f_{z_1}\\ ⋮\\ f_{x_k}\\ f_{y_k}\\ f_{z_k}\end{array}\right]+t\ast \left[\begin{array}{c}{m}_{x_1}\\ m_{y_1}\\ m_{z_1}\\ ⋮\\ m_{x_k}\\ m_{y_k}\\ m_{z_k}\end{array}\right]$$

where the vector of fs contains the original landmark locations of the face, and f′ is the corrected location. A primitive graphical user interface was built which enabled the operator (H.M.) to adjust t interactively, using a slider, while visualising the results. t was adjusted until the mouth was judged closed and then the corrected image was saved.

Visualising regression effects

The effects of variables on face shape can be illustrated using false‐colour maps. These are the Procrustes mean shape colour‐indexed according to some value of interest. Regression coefficients define a set of weights on each quasi‐landmark. Together they define how much and the direction in which the landmark is displaced per unit of the predictor. Imagine an arrow at each landmark. The values of interest represented in the heat maps are: (1) the ‘Effect’ (magnitude), i.e. the length of the arrow at each point, or the magnitude of the effect in the lateral, vertical and depth direction; (2) the proportion of the variance at each quasi‐landmark explained (partial R ²) by the predictor; and (3) the significance of the effect at each quasi‐landmark.

Another way to visualise the effect is to apply the transformation to the Procrustes mean face as described above for correcting the scans of individual faces, to create a morph or shape transformation. It is most sensible to construct morphs within the actual range of the predictor, but extrapolating beyond this can help to elucidate a small effect, even if it results in morphs that are anatomically implausible.

Results

Mouth correction

Figure 1 displays false‐colour maps of the regression of Procrustes residuals onto mouth openness. Figure 2 illustrates the estimated transformation with morphs constructed within the actual range of mouth openness ratings (t = 0, t = 3) and extrapolated beyond it (t = −3, t = 6). The estimated transformation is a good approximation of the action of opening or closing the mouth. The variability present in the sample before and after each correction was investigated using principal components analysis (Supporting Data S1.3). Results indicated that the variability due to variation in mouth openness was removed by both corrections.

Figure 1.

The regression of Procrustes residuals onto ratings of mouth openness. Shows the effect magnitude (effect) and the effect decomposed into lateral, vertical and depth directions. In ‘lateral’, red indicates (viewers) right‐directed displacement, blue indicates left‐directed displacement. In ‘vertical’, red indicates superior displacement, blue indicates inferior displacement. In ‘depth’, blue indicates posterior displacement and red indicates anterior displacement. The units of the colour‐bars for these images are mm. Partial R ² indicates the amount of variability in the location of each quasi‐landmark that is explained by mouth openness. P < 0.05 indicates the areas where partial R ² was significant.

Figure 2.

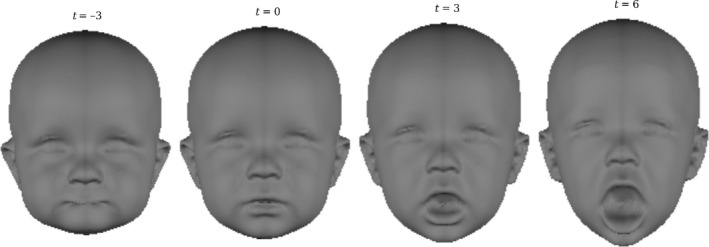
The transformation estimated by the regression onto mouth openness ratings. Morphs were constructed by varying the value of t. 0 and 3 represent the limits of the variation that is actually present in the population. −3 and 6 are exaggerations of the effect.

The sexual dimorphism analysis was performed on data corrected using each method of mouth correction and without any correction (Supporting Data S1.4). No difference was observed in the outcome of the analysis between the methods. In particular there was no difference in the dimorphism in the lower face where the mouth openness would have been expected to have more effect. For simplicity the analyses on the uncorrected sample are reported below.

Sexual dimorphism of size and shape

The global (centroid) size of males’ (M = 21 120.70, SD = 501.16) heads were significantly larger than females’ (M = 20 624.26, SD = 479.08) heads (F = 119.90, P < 0.001, η² = 0.203) (Fig. 3.

Figure 3.

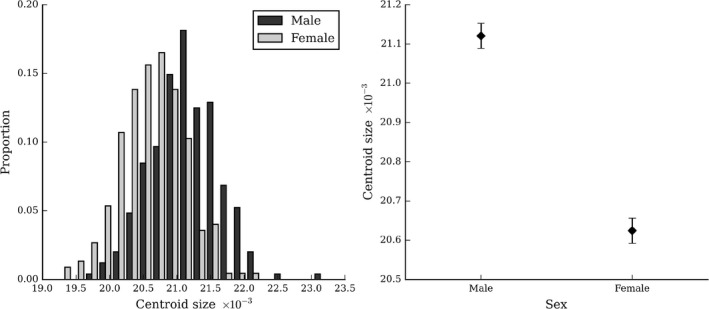
Sex differences in head size. Shows the distributions (left) and means (right) of head centroid size of males and females. Error bars indicate the standard error of the mean.

There was no interaction between the effects of sex and size (P = 0.449), indicating that their effects on shape can be considered independently. Overall the effect of sex was significant (partial R ² = 0.008, P = 0.002). The strongest difference in the facial appearance is around the forehead, where sex accounts for up to 4% of the total variance, but there are also differences in the vault shape (Figs 4 and 5). The forehead in females protrudes by approximately 1 mm relative to males, and as a consequence the naso‐frontal angle is more acute. The nose is narrower and smaller in females than in males. Female cheeks are more prominent in the area lateral to the nasolabial crease. The effect around the ears indicates that females’ lower earlobes tend to point inwards whereas the males’ earlobes point more outwards.

Figure 4.

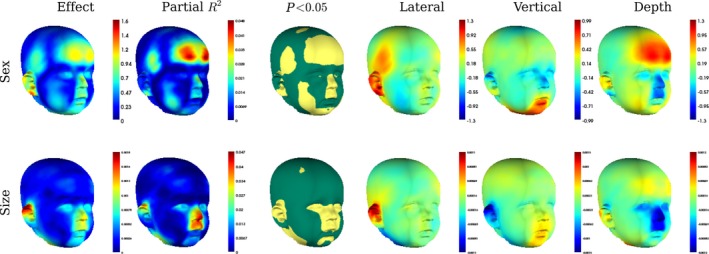
The regression of Procrustes residuals onto sex and centroid size, including an interaction in the model. Shows the overall magnitude of the predicted vertex displacements (Effect) and the magnitude of the predicted displacements in the lateral, vertical and depth directions, from males to females. They are colour‐indexed to mm displacement, per unit of the predictor. The proportion of variance that the predictor variable predicts at each individual vertex is shown in partial R ² and the significance of the effect on each landmark (yellow regions are significant at α = 0.05).

Figure 5.

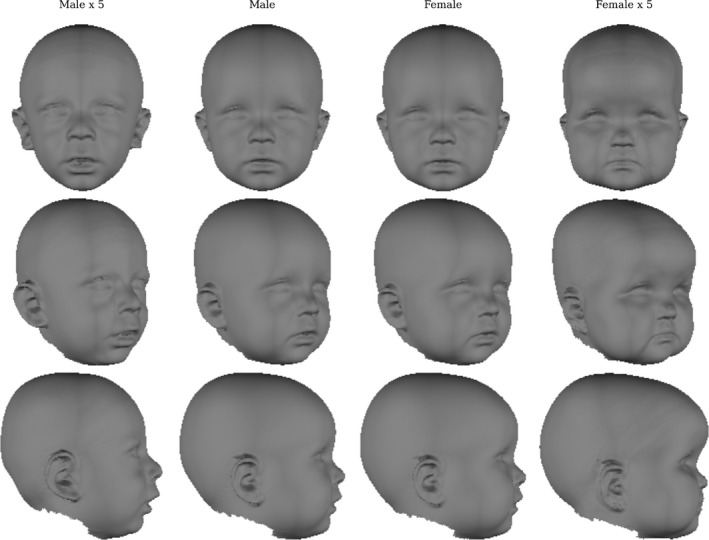
Effect of sex on face shape. The centre two columns show the typical male (t = 1) and typical female (t = 2) faces predicted by the model. The outer columns show the difference between these two typical faces magnified five times (t = −4, t = 7).

The effect of size was also significant (partial R ² = 0.008, P < 0.001). The effect is concentrated in the nasal region and on the upper lip and consists primarily of a superior and posterior displacements of these landmarks as centroid size increases. The upper portion of the ears appear to point out more in larger children. Not surprisingly, faces that are larger, also appear to have greater general fat deposition (Figs 4 and 6).

Figure 6.

Effect of head centroid size on head shape. This shows the face predicted by the regression model with centroid size = ±6 SD.

Bootstrapped response‐based imputation modeling

The distribution and means of RIP values are shown in Fig. 7 and the extracted regression vector is shown in Fig. 8. The females (M = 1.51, SD = 0.09) tend to have higher RIP values than males (M = 1.43, SD = 0.09; F = 72.03, P < 0.001, η² = 0.133). This indicates that males and females differ in their mean position along the extracted regression path; higher values correspond to increased femininity of the face. There is also overlap between the male and female groups. This indicates that there is a continuum of masculinity–femininity in 1‐year‐olds. Similar effects, to those observed in the PLSR analysis, are evident around the cranial vault and nose. The effect on the ears disappeared, the effect on the cheeks is reduced.

Figure 7.

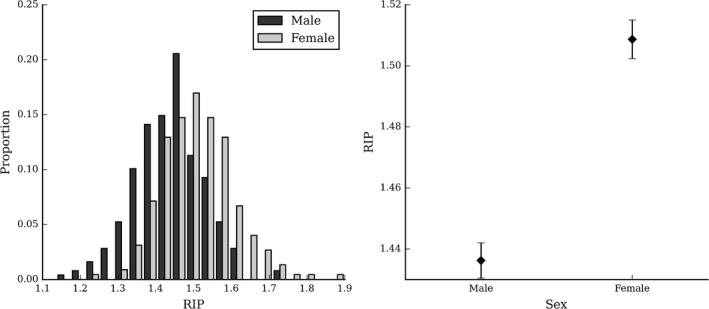
Imputed masculinity–femininity. This shows the distribution (left) and mean (right) of the RIP values for males and females. Error bars indicate the standard error of the mean.

Figure 8.

Regression of Procrustes residuals onto RIP variables. This shows the regression path best characterising the difference between males and females estimated by the BRIM algorithm.

To provide a more comprehensive picture of the overlap between males and females, we plotted centroid size against RIP scores (Fig. 9). This represents the difference between the groups in a size‐and‐shape space, where the multivariate shape is compressed into a single dimension.

Figure 9.

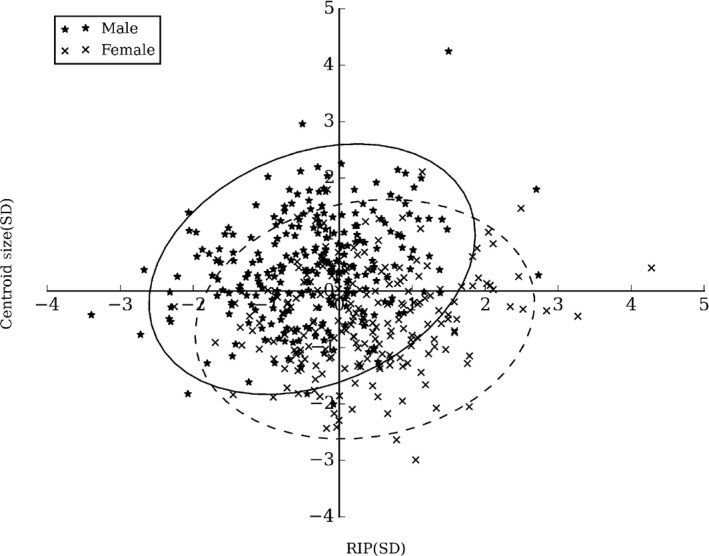
RIP scores and centroid size for males and females. The 95% confidence ellipses for males (solid line) and females (dotted line) are also shown.

Discussion

This study investigated sexual dimorphism in the craniofacial morphology of a sample of 1‐year‐old humans. We used partial least‐squares regression and BRIM, coupled with a spatially dense representation of the soft‐tissue anatomy, to test for statistically significant differences in the shape of the entire craniofacial complex. We also included centroid size in the regression, allowing us to separate the effects of size and sex on shape.

We observed that global size of the face and cranial vault was larger in males than females. Partial least‐squares regression showed an effect of sex the shape of the forehead, with the girls’ foreheads protruding more forwards than the boys’. Females’ noses were also smaller and narrower than males. This effect on the forehead and nose may signal a relatively smaller basicranium in females. A smaller basicranium could make both the forehead relatively more bulbous as well as narrowing the maxilla and nasal passages. There was also an effect on the cheeks, possibly corresponding to greater fat deposition on the cheeks in girls. Interestingly also, the lower ear‐lobes of girls have a tendency to point inwards more than those of boys.

Bootstrapped Response‐Based Imputation Modeling extracted a similar, though not identical, vector of sexual dimorphism in the sample, identifying the differences in the forehead and nose as those that best differentiated the groups. A recession of the forehead in males, relative to females is a classic dimorphic feature, which has been identified consistently in adults (Rosas & Bastir, 2002; Hennessy et al. 2005; Claes et al. 2014). The presence of this trait has previously only been documented in adolescents as young as 11 (Ferrario et al. 2003) and 12 (Koudelová et al. 2015). In adults the forehead slopes backwards in both males and females but is more recessed for males. In 1‐year‐olds the forehead generally protrudes forwards in both sexes but is relatively less protruding in males. To the best of our knowledge this is the first study to document shape dimorphism in this adult direction in such a young sample. Curiously, Bulygina et al. (2006), in a longitudinal study of lateral radiographs, observed the opposite dimorphism in younger children (0.5 through to 8 years), that is the male forehead protruded more than the female, with the trend reverting into the clearly adult pattern at puberty (their Fig. 7). Their sample size was very small (14 for each sex) and did not apply significance tests to their analysis of shape, and so sampling error in that study may explain the different results.

The differences in the shape of the nose is also quite consistent with differences observed in adult soft‐tissue studies (Hennessy et al. 2005; Claes et al. 2014). Koudelová et al. (2015) observed differences in the nose emerging at 14 years (their Fig. 2) but not earlier. Such differences were not investigated by Bulygina et al. (2006) study of hard tissue landmarks and were not observed by Ferrario et al. (2003), possibly due to the sparse landmark configurations used to represent the shape of the face.

The distributions for RIP values of each sex overlap in adults (Fig. 4B of Claes et al. 2014) as we have reported here for 1‐year‐olds. This indicates that the features identified are distributed continuously within each sample, i.e. there is a continuum of masculinity–femininity in facial shape within 1‐year‐olds, as there is in adults. The distributions for 1‐year‐olds overlap much more than in adults, suggesting that more 1‐year‐olds than adults occupy an androgynous middle region of the continuum. Comparison of the distributions of RIP values of sex for different ages may add an interesting new dimension to the study of the ontogeny of sexual dimorphism.

The observed effect of sex was independent of the effect of size on shape. There was also a significant effect of size, or allometry, which was independent of the effect of sex. Our allometric effect consisted primarily of superior and posterior displacement of the landmarks around the nose and upper lip as centroid size increases. Furthermore, the upper portion of the ears point out and there appears to be greater general fat deposition as centroid size increases. No strong claims can be made regarding whether this effect is consistent with adults, as the effects are seen on regions with deep soft‐tissue. The only similar analyses of adults have been performed on skulls (Rosas & Bastir, 2002) or have not separated the effects of allometry and sex, making comparison of these findings difficult.

It is generally assumed that an increase in testosterone around puberty triggers a masculinisation of male faces, leading to dimorphism between the sexes (Enlow & Hans, 1996; Verdonck et al. 1999). It is well‐established that serum testosterone is related to facial masculinity in adults (Penton‐Voak & Chen, 2004; Schaefer et al. 2005). Our results demonstrate that some dimorphic traits are present in a subtler form at 1 year of age, long prior to this pubertal increase in serum testosterone. This may represent the effect of the sex hormone levels in the uterine environment on the early configuration of the face, hypothesised by Neave et al. (2003). The difference may also be attributable to inherited sex‐linked facial characteristics, and not directly to uterine hormone levels. In either case these differences should be present in newborns. Future work should make use of the powerful methods employed here to test also for shape differences in newborns, and explicitly investigate the effect of the uterine hormone environment.

This work quantifies an early sexual dimorphism that is not attributable to the influx of sex hormones at puberty. It may be of interest in future to investigate the relationship between this early dimorphism and the later impact of puberty. For example, how dimorphic a face is prior to puberty may or may not mediate the magnitude or direction of the changes that occur at puberty (e.g. faces that are already masculine may experience a more profound masculinisation at puberty).

Different developmental mechanisms may lead to sexual dimorphism (Shea, 1986). Studies of hominids, including humans, support the notion that adult sexual dimorphism is in part due to ontogenetic scaling (that is, that adult females resemble more juvenile males) and in part due to divergence in growth trajectories (O'Higgins & Collard, 2002; Schaefer et al. 2004; Cobb & O'Higgins, 2007). The ontogenetic scaling component of adult sexual dimorphism can be explained by differences in the time taken to mature, with males continuing to grow along the same trajectory for a longer time, or by differences in the rate of maturation, with males progressing faster along a common growth trajectory, for a similar length of time. Shea (1983) terms these mechanisms time and rate hypermorphosis, respectively. It is possible that different mechanisms operate differently at different times in ontogeny. For example, Cobb & O'Higgins (2007) argued that, in apes, sexual dimorphism prior to puberty was a product of ontogenetic scaling, but subsequent sexual dimorphism was produced by a deviation of male and female growth trajectories. Within our sample of a single juvenile ontogenetic stage, it is not possible to determine the developmental mechanisms that produced the dimorphism, but our study does demonstrate the need for future work looking very early in ontogeny, to develop a full understanding of the development of dimorphic characteristics.

In anthropology a common problem is determining the sex of fossilised crania (Franklin et al. 2005; Deshmukh & Devershi, 2006; Abdel Fatah et al. 2014). This is particularly difficult for pre‐adolescent remains (Molleson et al. 1998). Our results demonstrate that there are shape differences in the crania that distinguish the sexes very early in ontogeny. Shape may be more useful than size for sexing juveniles where the age, and therefore expected size, of the crania is unknown.

Cranial sexing is usually achieved using a univariate or multivariate approach. The univariate approach treats a particular trait (e.g. bizygomatic breadth) as a binary classifier. That is, an appropriate threshold is determined, and observations on one side are considered male and those on the other are considered female. A multivariate approach defines a discriminant function in which values on multiple traits can be used to determine the sex of an observation (Deshmukh & Devershi, 2006 for a comparison of the two approaches). The former is limited in that any particular trait is unlikely to serve as an optimal classifier. The latter is limited in that a decision must be made regarding which traits are important and which are not. Furthermore, the common method of linear discriminant‐function analysis is sensitive to the number of traits included in the model and collinearity between traits. A PLSR‐based approach may, therefore, be desirable.

A PLS regression vector through shape–space constitutes a single dimension that captures the variability in all traits (landmarks) that is most strongly associated with the predictor (sex). RIPs, being projections onto this vector, can be interpreted as a univariate ‘compression’ of this multivariate variability. We suggest that RIPs can be used as a univariate binary classifier, keeping the simplicity of the univariate approach, while capturing the important multivariate shape information. We report classification accuracy using RIPs and describe a method of building and assessing a classification model in Supporting Data S1.5. On the current data, the model performs above chance. We suggest that future work can investigate this issue more thoroughly using 3D hard‐tissue representations derived from 3D images of skeletons, or CT of living subjects, and examine classification accuracy on juveniles of different ages.

This sample was collected as part of a larger study on the effects of alcohol intake during pregnancy (Muggli et al. 2014). This study recruited mothers during normal, low‐risk pregnancy to monitor the effects of typical levels of alcohol intake on a range of outcomes including face shape. As such the sample represents a typical cross‐section of 1‐year‐olds and the effect of alcohol consumption was expected to be unrelated to the effect of sex. To confirm this, the analysis was repeated on a subsample of mothers who did not drink at all while pregnant (Supporting Data S1.5). The effect on the forehead was present, although the effects on other regions were not statistically significant. This is most likely due to the substantially reduced sample size and statistical power in that analysis. We cannot exclude the possibility that the effects on other regions are specific to mothers who drank some alcohol during pregnancy.

Instantaneous image capture by 3D stereo‐photogrammetry reduces the requirement for prolonged co‐operation that often hampers the collection of anthropometric measurements in children, such as those used in the planning and assessment of craniofacial surgery. Even with this, a residual problem remains in images of young children such that a neutral facial pose is difficult to ensure. This can greatly affect the accuracy of such measurements (Hermann et al. 2016). Stereo‐photogrammetry, coupled with a mouth‐correction protocol, may therefore greatly facilitate the collection of such measurements on this otherwise difficult population.

We suggest correcting mouth openness by including it as a covariate in a PLSR model, or using PLSR to define a transformation that can be applied manually to the face. Inspection of the residual variability after treating the data with either approach (Supporting Data S1.3), suggests that both successfully remove the variability due to mouth openness, and both are probably quite adequate for a PLSR‐based analysis. For applications where the accuracy of the correction at the level of an individual is important, such as anthropometry for surgical planning, manual correction is likely preferable.

To the best of our knowledge, this is the first study to demonstrate the presence of sexual dimorphism, consistent with adult patterns, in a sample of 1‐year‐olds. We quantify a sexual dimorphism that is not attributable to the influx of sex hormones at puberty. This may represent the effect of uterine hormone levels or inherited sex‐linked facial characteristics. We highlight the need to look very early in ontogeny for the beginnings of sexual dimorphism and suggest future studies investigate potential mediating effects of early dimorphism on the impact of puberty. Furthermore, the study illustrates the power of spatially dense morphometrics to detect subtle differences in the shape of anatomical structures, which may be applied to the problem of sexing fossilised crania. We also illustrate the application of PLSR‐based techniques to correct non‐standard poses in 3D images, which may facilitate surgical planning and assessment from 3D images of this age group.

Author contributions

H.M. conducted the analyses reported here, developed the manual mouth‐closing procedure, assembled the first draft of the manuscript and incorporated the suggestions of co‐authors. T.P. offered extensive suggestions for revision of the manuscript. I.S. conducted preliminary analyses on the data and first identified the presence of sexual dimorphism. P.C. oversaw the implementation and application of the analyses, and provided extensive comments on the manuscript. J.H. and E.M. oversaw the collection of the images in the AQUA study and contributed to manuscript content.

Conflict of interest

The authors declare they have no conflicts of interest.

Supporting information

Video S1. BRIM Inner Loop.

Video S2. BRIM outer loop.

Supporting Data S1. Supplementary methods and analysis.