Abstract
Objectives
There is no consensus on whether studies with no observed events in the treatment and control arms, the so-called both-armed zero-event studies, should be included in a meta-analysis of randomised controlled trials (RCTs). Current analytic approaches handled them differently depending on the choice of effect measures and authors' discretion. Our objective is to evaluate the impact of including or excluding both-armed zero-event (BA0E) studies in meta-analysis of RCTs with rare outcome events through a simulation study.
Method
We simulated 2500 data sets for different scenarios varying the parameters of baseline event rate, treatment effect and number of patients in each trial, and between-study variance. We evaluated the performance of commonly used pooling methods in classical meta-analysis—namely, Peto, Mantel-Haenszel with fixed-effects and random-effects models, and inverse variance method with fixed-effects and random-effects models—using bias, root mean square error, length of 95% CI and coverage.
Results
The overall performance of the approaches of including or excluding BA0E studies in meta-analysis varied according to the magnitude of true treatment effect. Including BA0E studies introduced very little bias, decreased mean square error, narrowed the 95% CI and increased the coverage when no true treatment effect existed. However, when a true treatment effect existed, the estimates from the approach of excluding BA0E studies led to smaller bias than including them. Among all evaluated methods, the Peto method excluding BA0E studies gave the least biased results when a true treatment effect existed.
Conclusions
We recommend including BA0E studies when treatment effects are unlikely, but excluding them when there is a decisive treatment effect. Providing results of including and excluding BA0E studies to assess the robustness of the pooled estimated effect is a sensible way to communicate the results of a meta-analysis when the treatment effects are unclear.
Keywords: both-armed zero-event, meta-analysis, rare event outcome, simulation
Strengths and limitations of this study.
A simulation study thoroughly investigated the impacts of including or excluding both-armed zero-event studies in meta-analyses by comparing all commonly used pooling methods.
The simulation parameters were chosen according to the characteristics of meta-analyses in the Cochrane Database of Systematic Reviews to closely reflect the reality.
Our results not only confirmed the findings from the previous empirical studies but also added more details on how including or excluding both-armed zero-event may affect the estimates of meta-analyses differently depending on the magnitude of true treatment effects.
Only OR was investigated through simulations; thus, the findings from this study may not be able to be fully extended to other effect measures such as relative risk or absolute risk difference.
Background
Systematic review with meta-analysis has become an important research tool for the health research literature which synthesises evidence from individually conducted studies that assess the same outcomes on the same topic. The PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) Statement1 adopted the definition used by Cochrane Group2 which defines systematic review as a review of a clearly formulated question that uses systematic and explicit methods to identify, select and critically appraise relevant research, and to collect and analyse data from the studies that are included in the review. Meta-analysis refers to the use of statistical techniques in a systematic review to integrate the results of included studies. Therefore, the results of meta-analyses from randomised controlled trials (RCTs) are considered to be the best quantitative clinical evidence in the literature.3 4 Studies included in a systematic review are selected rigorously according to predefined exclusion and inclusion criteria. Thus, all identified studies in a systematic review with available data should be included in the meta-analysis. However, there is no consensus among researchers whether this principle should be fully applied and how to apply to the meta-analyses using dichotomous outcomes.
This research focuses on the RCTs with dichotomous outcomes, that is, the participants do or do not experience the defined event. The total number of observed events in such a RCT is likely influenced by the event rate, sample size and study period. When the event rate is low, the sample size is small and the study period is short, it is possible that no outcome event is observed in the RCT although the probability of the event happening is not zero. A study with no outcome event observed in either treatment or control arms is called a zero-event study. An extreme case of the zero-event study is both-armed zero-event (BA0E) study, which is defined as a study in which no event is observed in treatment and control arms, and is also known as a double-zero-event or zero-total-event study.
When rare adverse events or rare diseases are used as the study outcomes, it is not an uncommon phenomenon that no outcome events are observed at the end of the study. In the USA, a rare adverse event is defined as 1 per 1000 patients.5 In the European Union, a rare disease is defined as 1 per 2000 people.6 To obtain a representative number of outcomes for a rare event study, a large number of patients are needed. However, very often, RCTs are either not designed primarily to investigate adverse events or do not have the resources to recruit the sample size required for such events. A published review of the Cochrane Database of systematic reviews showed that the median sample size for dichotomous outcomes was 102 (IQR of 50–243).7 Therefore, when the primary outcome in a meta-analysis is a rare event, zero-event studies could be among the qualified studies. Warren et al8 conducted a systematic review of meta-analyses published between 1994 and 2006 where rare events were a primary outcome. Among 166 meta-analyses, 65 (39%) included zero-event studies, and 41 (25%) included BA0E studies. Among the 41 meta-analyses with BA0E studies, 19 meta-analyses (46%) included them in the primary or sensitivity analyses, 18 (44%) excluded them and 4 (10%) were unclear. This review also found that continuity correction was the most used approach to incorporate zero-event studies, and 0.5 was the common choice of the correction factor. Of the 15 reviews in which continuity correction had been clearly used, 14 (93%) of them used 0.5 as the correction factor.
For single-armed zero-event studies, there is consensus on their inclusion in meta-analyses. Bradburn et al9 reported a simulation study comparing commonly used methods of handling zero-event studies in meta-analyses. This provides a good guideline for the subsequent meta-analyses. However, when BA0E studies were present in systematic reviews, the practice of handling varies.8 10
There are two major reasons why BA0E are handled variably in meta-analyses. First, the statistical methods and software such as RevMan (The Cochrane Collaboration. RevMan 5.1 User Guide. 2011) Stata's metan module11 and Comprehensive Meta-analysis (Altman D, Duval S, Lipsey M, et al. Comprehensive Meta Analysis Version 3.0) handle BA0E studies differ according to the choice of effect measures. BA0E studies are included in the pooled results when risk difference is used, but automatically excluded by all statistical software used for meta-analysis when OR or relative risk (RR) is used. Second, there is no guideline for handling BA0E studies in meta-analyses due to the lack of empirical evidence or simulation studies. Among the very limited published articles, which examined various approaches of dealing with BA0E studies using empirical data, the results were ambiguous. In 2007, Friedrich et al empirically compared the statistical methods of handling BA0E studies in meta-analysis and recommended that BA0E studies should be included in all analyses. They concluded that including BA0E studies could narrow the CI and increase the precision of the pooled estimates.12 In 2008, Dahabreh and Economopoulos13 conducted a sensitivity analysis to re-evaluate the treatment effect of rosiglitazone and found that including BA0E studies changed the pooled OR of myocardial infarction (MI) between treatment and control groups from significant to not significant statistically. Although the above empirical studies showed us that including BA0E studies could affect the results of meta-analyses, the impact may not be beneficial towards the truth in all scenarios. In addition to the above empirical studies, two recently published simulation studies argued that incorporating BA0E studies using Poisson random-effects model14 or a relatively complicated β-binomial regression15 could generate unbiased estimates for meta-analyses. However, these two recommended statistical models may not be a practical approach for non-statisticians who use the standard pooling methods to conduct meta-analyses.
Since number of events observed in studies using dichotomous outcomes is determined by event rates and number of subjects, zero-events are more likely to occur with the conditions of extremely low event rates or small sample sizes even though the event rates are different between two study groups. In the intuitive way, the arithmetical difference between two study groups with no observed events is null. Therefore, we hypothesise that the inclusion of BA0E studies in meta-analysis affects the pooled estimates of treatment effects in different ways, depending on the presence or absence of a true treatment effect. In the absence of a true treatment effect, that is, similar event rates in both arms, the inclusion of BA0E studies narrows the CI of the pooled estimate of treatment effect. When a true treatment effect exists, the inclusion of BA0E studies adds bias to the magnitude of the pooled estimate, leading to the underestimation of the treatment effect.
To test the hypotheses, we conducted a simulation study to evaluate the impact of excluding and including BA0E studies in meta-analysis under two circumstances—the presence and absence of a true treatment effect. Although it is not difficult to statistically deduce that the bias brought by including BA0E studies is affected by the factors such as (1) low event rate, (2) large treatment effect and (3) small sample size, stimulation is still needed to quantifying the magnitude of the bias. Our investigation focused on comparing the standard statistical pooling methods adopted by the commonly used software such as RevMan and Stata V.13.1 for meta-analysing aggregated data. We hope our study can provide some practical guidance to the researchers in this area.
Methods
OR and RR are the most commonly used effect measures for assessing the treatment effect for dichotomous outcomes in meta-analyses. The results of these two effect measures are similar when the event probability is <20%.16 17 Since the event rates used in our simulation study were much lower, we chose OR as the effect measure to engage the Peto method in our investigation. Bradburn et al9 have shown that the Peto method was a better choice for rare event meta-analyses for dichotomous outcomes when studies with zero-events in one but not both arms were included.
Simulation scenarios
The simulation scenarios in our study were chosen based on a combination of several simulation parameters. Three types of parameters were used in this simulation study: fixed (a single value was assigned to a certain parameter), varied (multiple values were assigned to a certain parameter) and derived (the value of a certain parameter was calculated according to a statistical formula). We believed that some parameters had more impact on the simulation results than others. We chose fixed values for the low impact parameters (unlikely to influence the simulation results) across all simulation scenarios, and let the values of those high impact parameters (more likely to influence the simulation results) vary in certain ranges. The parameter values were drawn from the published literature (table 1).
Table 1.
Simulation parameter setup
| Parameter | Assigned values | Rationale | Reference |
|---|---|---|---|
| OR | 0.2, 0.5, 0.8, 1, 1.25, 2, 5 | No treatment effect, small to medium, large and extremely large treatment effects | 18 |
| Control group event probability (p) | 0.001, 0.005, 0.01 | 1 in 2000 rare diseases in EU; 1 in 1000 rare adverse events | 6 19 |
| Number of studies in each meta-analysis (m) | 5 | Median=3; IQR: 2–6; <1% >29 | 7 |
| Number of patients in each individual study (n) | 50, 100, 250 | Median=102; IQR 50–243 | 7 |
| Between-study SD | 0.1, 0.5, 1 | Small, moderate, large | 18 |
| Ratio of group size (r) | 1:1 | 78% trials had equal group ratio | 20 |
The derived parameters were calculated by the input parameters according to a statistical formula. For the fixed parameters, we tested the following values. The numbers of studies (m) in each meta-analysis was set at 5. The review published in 2011 reported that the median (IQR) of the numbers of studies included in the meta-analysis in the Cochrane Database was 3 with IQR from 2 to 6.7 For the treatment and control arm ratio (r), we only considered 1:1 allocation. A review paper has shown that 78% of clinical trials were conducted with equal patient allocation strategies.20 To reduce the number of simulation scenarios, we deliberately chose to use the same number of patients across all studies in each meta-analysis.
For the following parameters, we chose to input multiple values instead of constants. The control arm event probabilities (p) investigated in this simulation were 0.001, 0.005 and 0.01. They are chosen according to the varying definitions of rare events.5 6 The treatment effects measured as OR were set as no effect (OR=1), small to medium sized (OR=0.8; OR=1.25), moderately large (OR=0.5; OR=2) and extremely large (OR=0.2; OR=5), where OR<1 indicates lower event rates in treatment arms and OR>1 indicates higher event rates in treatment arms.18 The numbers of patients (n) in each individual study included were 50, 100 and 250 based on the same review mentioned above,7 which revealed that the median (Q1, Q3) of the sample size in each individual study was 102 (100, 243). We also considered the potential impact of between-study variance in our simulation design. We set the between-study SD as 0.1, 0.5 and 1, which represented little, moderate and large between-study variance.18 The between-study variation was applied at the level of ORs, that is, the treatment effect.
In this simulation study, the treatment arm event probabilities were calculated through the control arm event probabilities and treatment effects (OR).
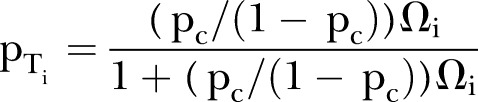 |
where pT=treatment arm probability, pc=control arm probability, Ω=OR, i=1, 2, …, study.
Number of simulations
We simulated 2500 data sets for each scenario to ensure the accuracy of our simulation results.21
Analysis methods
Five pooling procedures were used to meta-analyse each simulated data set. They were Peto, Mantel-Haenszel with fixed-effects and random-effects models, and inverse variance (IV) method with fixed-effects and random-effects models.2
Methods for including both-armed zero-events
To implement the above five pooled methods to incorporate studies with BA0E in meta-analysis, a continuity correction factor was added to each of the four cells of the 2×2 table for a BA0E study, that is, event in the treatment arm, non-event in the treatment arm, event in the control arm and non-event the in control arm. Continuity corrects were also used to incorporate single-armed zero-event studies for all methods except Peto's. We chose to use the constant continuity factor 0.5. It is common and plausible choice when the group ratio is balanced between treatment and control arms.22
Evaluating simulation performance
Four measures were used to assess the performance of this simulation study21 (table 2): (1) percentage bias, which is calculated as the percentage of the difference between the average of the estimated value of the treatment effect and the true value of the treatment effect (absolute bias) over the true value of the treatment effect; (2) root mean square error (RMSE), which measures the average distance of estimated treatment effects from the parameter value; (3) the average length of 95% CIs is also used to compare the precisions between pooling methods; and (4) coverage, which measures the percentage of the true treatment effects included in the available 95% CIs over all generated data sets. The RMSE and average 95% CI length were reported the log OR scale. The performances of the simulation were compared across the five pooling methods used for the approaches of including and excluding BA0E studies in the meta-analyses.
Table 2.
Measures for evaluating simulation performance
| Criteria | Formula |
|---|---|
| Percentage bias ((δ/β)%) |
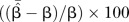 , where , where 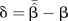
|
| RMSE | 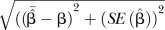 |
| Average width of 95% CI |
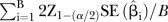 , for i=1, 2 ,…, B, where B=the number of meta-analyses conducted using simulated data sets , for i=1, 2 ,…, B, where B=the number of meta-analyses conducted using simulated data sets |
| Coverage of 95% CI | Percentage of times the 95% CI of 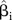 include β, for i=1, 2 ,…, M, where M=the number of meta-analyses conducted using simulated data sets include β, for i=1, 2 ,…, M, where M=the number of meta-analyses conducted using simulated data sets |
β, true value of estimate of interest—log OR; 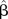 , estimate of β—estimates of log OR;
, estimate of β—estimates of log OR; 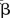 , mean of
, mean of 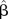 (log OR) in the simulation;
(log OR) in the simulation;
δ, absolute bias—the difference between the mean of the estimates of log OR and log OR; 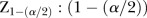 , quantile of the standard normal distribution; RMSE, root mean square error.
, quantile of the standard normal distribution; RMSE, root mean square error.
We also reported the inclusiveness of the approach of excluding BA0E studies in meta-analysis, which reported the percentage of number of studies included in the pooling process.
Since the focus of our investigation was whether and when including BA0E studies would introduce bias to the pooled estimates of the treatment effect in meta-analyses, we evaluated the simulation performance regarding the bias in different scenarios by varying the values of the treatment effect, control arm probability, number of patient and between-study variance. Other simulation performance measures (RMSE, average width of 95% CI and coverage of 95% CI) were evaluated on a common simulation scenario to minimise the required amount of work.
Statistical software and program
The data sets for each simulation scenario are generated using R V.2.15.2 (The R Foundation for Statistical Computing; simulation code of data generating is attached as online supplementary appendix 1). The meta-analyses were conducted using Stata (College Station, Texas, USA). The estimates summarising the overall performance of this simulation were also calculated using Stata.
bmjopen-2015-010983supp_appendices.pdf (214.9KB, pdf)
Results
In this study, we reported 13 simulation scenarios based on the input values of the simulation parameters (treatment effect, control arm probability, number of patients and between-study variance). Among all simulated meta-analysis data sets, 31.5% (minimum=21%; maximum=40%) of them were BA0E studies.
Including BA0E studies
Our simulation results supported our hypothesis that when there is no true treatment effect (OR=1), the approach of including BA0E studies in meta-analyses had the best overall performance regardless of the choice of pooling methods, which gave the smallest bias (<0.1%; table 3 and see online supplementary appendix 2) and RMSE (figure 1 and see online supplementary appendix 3a), and narrowest 95% CI (figure 2 and see online supplementary appendix 3b). However, when there was a true treatment effect, this approach gave the larger bias compared to the alternative approach of excluding BA0E studies. The magnitude of the bias increased with an increase in the treatment effect in the direction of underestimating the treatment effects by pulling the point estimates towards the null hypothesis (OR=1). Compared to the approach of excluding BA0E studies, the results obtained by including BA0E studies had smaller or similar RMSEs when the treatment effects were from none (OR=1) to moderately large (OR=0.5); but when the treatment effect was extremely large (OR=0.2), the approach of including BA0E studies led to the larger RMSEs compared to its alternative approach (figure 1 and see online supplementary appendix 3a). For the width of 95% CI, the approach of including BA0E studies constantly produced narrowed 95% CIs comparing to the approach of excluding BA0E studies (figure 2 and see online supplementary appendix 3b). The coverage of this approach was very high, from 100% to 95% (see online supplementary appendix 3c) regardless of the changes of the treatment effects. We also found that the bias of the pooled estimates increased with decreasing control arm probability (table 4) and number of patients (table 5) and increasing between-study variance (table 6).
Table 3.
Impact of the treatment effect changes on bias
| Number of studies=5 | Number of patients=100 |
Group ratio=1 |
Control arm probability=0.001 |
Number of simulated data sets=2500 |
Between-study SD=0.5 |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Excluding BA0E studies |
Including BA0E studies |
|||||||||||||||
| Positive treatment effect |
No treatment effect |
Positive treatment effect |
||||||||||||||
| OR=1.25 |
OR=2 |
OR=5 |
OR=1 |
OR=1 |
OR=1.25 |
OR=2 |
OR=5 |
|||||||||
| Methods | 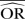 |
%bias | 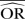 |
%bias | 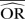 |
%bias | 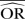 |
%bias | 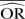 |
% bias | 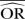 |
%bias | 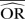 |
%bias | 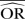 |
%bias |
| IV random effects | 1.11 | −12.6 | 1.45 | −37.9 | 2.28 | −119.3 | 1.01 | 0.8 | 1.00 | <0.1 | 1.03 | −21.4 | 1.13 | −77.0 | 1.56 | −220.5 |
| IV fixed effects | 1.11 | −12.6 | 1.46 | −37.0 | 2.28 | −119.3 | 1.01 | 0.7 | 1.00 | <0.1 | 1.03 | −21.4 | 1.15 | −73.9 | 1.56 | −220.5 |
| M-H random effects | 1.11 | −12.5 | 1.45 | −37.9 | 2.28 | −119.3 | 1.01 | 0.8 | 1.00 | <0.1 | 1.03 | −21.4 | 1.13 | −77.0 | 1.56 | −220.5 |
| M-H fixed effects | 1.11 | −12.6 | 1.46 | −37.0 | 2.30 | −117.4 | 1.01 | 0.8 | 1.00 | <0.1 | 1.03 | −21.4 | 1.15 | −73.9 | 1.62 | −208.6 |
| Peto | 1.19 | −5.0 | 1.87 | −7.0 | 3.68 | −35.9 | 1.01 | 1.4 | 1.00 | <0.1 | 1.04 | −20.2 | 1.19 | −68.1 | 1.92 | −160.4 |
| Negative treatment effect | No treatment effect | Negative treatment effect | ||||||||||||||
| Excluding BA0E studies | Including BA0E studies | |||||||||||||||
| OR=0.8 | OR=0.5 | OR=0.2 | OR=0.8 | OR=0.5 | OR=0.2 | |||||||||||
 |
%bias |  |
%bias |  |
%bias | 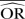 |
%bias | 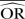 |
%bias | 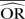 |
%bias | |||||
| IV random effects | 0.88 | −9.9 | 0.70 | −40.6 | 0.47 | −133.1 | 0.99 | −23.2 | 0.97 | −93.0 | 0.94 | −370.7 | ||||
| IV fixed effects | 0.88 | −9.9 | 0.70 | −40.6 | 0.47 | −133.1 | 0.98 | −23.0 | 0.96 | −92.3 | 0.93 | −367.4 | ||||
| M-H random effects | 0.88 | −9.9 | 0.70 | −40.6 | 0.47 | −133.1 | 0.99 | −23.2 | 0.97 | −93.0 | 0.94 | −370.7 | ||||
| M-H fixed effects | 0.88 | −9.9 | 0.70 | −40.6 | 0.47 | −133.1 | 0.98 | −23.0 | 0.96 | −92.3 | 0.93 | −367.4 | ||||
| Peto | 0.80 | 0.2 | 0.54 | −7.8 | 0.26 | −30.6 | 0.95 | −22.6 | 0.90 | −90.6 | 0.92 | −360.9 | ||||
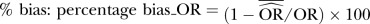 , when OR <1.
, when OR <1. 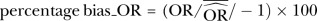 , when OR≥1. Negative (−) bias indicates underestimating of treatment effect; positive bias indicates overestimating of treatment effect.
, when OR≥1. Negative (−) bias indicates underestimating of treatment effect; positive bias indicates overestimating of treatment effect.
BA0E, both-armed zero-event; IV, inverse variance; M-H, Mantel-Haenszel.
Figure 1.
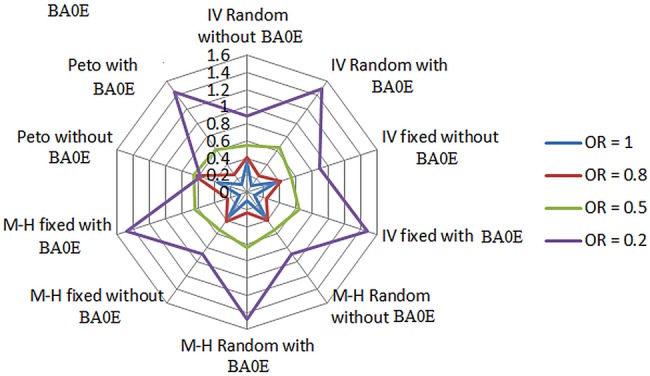
Comparing root mean square error (RMSE). BA0E, both-armed zero-event; IV, inverse variance; M-H, Mantel-Haenszel; RMSE, root mean square error.
Figure 2.
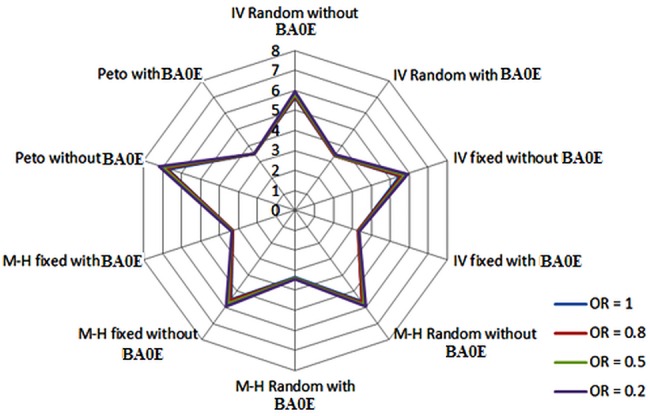
Comparing width of 95% confidence interval (CI). BA0E, both-armed zero-event; IV, inverse variance; M-H, Mantel-Haenszel.
Table 4.
Impact of the control arm probability changes on bias
| Number of studies=5 | Number of patients = 100 |
Group ratio=1 |
OR=0.5 |
Number of simulated data sets=2500 | Between-study SD=0.5 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Excluding BA0E studies |
Including BA0E studies |
|||||||||||
| pc=0.001 |
pc=0.005 |
pc=0.01 |
pc=0.001 |
pc=0.005 |
pc=0.01 |
|||||||
| Methods | 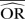 |
%bias | 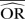 |
%bias | 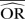 |
%bias | 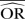 |
%bias | 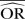 |
%bias | 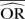 |
%bias |
| IV random effects | 0.70 | −40.6 | 0.68 | −35.1 | 0.64 | −28.5 | 0.97 | −93.0 | 0.85 | −70.8 | 0.76 | −51.3 |
| IV fixed effects | 0.70 | −40.6 | 0.67 | −34.9 | 0.64 | −27.3 | 0.96 | −92.3 | 0.84 | −68.5 | 0.74 | −48.0 |
| M-H random effects | 0.70 | −40.6 | 0.68 | −35.1 | 0.64 | −28.5 | 0.97 | −93.0 | 0.85 | −70.7 | 0.76 | −51.3 |
| M-H fixed effects | 0.70 | −40.6 | 0.67 | −34.9 | 0.64 | −27.3 | 0.96 | −92.3 | 0.84 | −68.5 | 0.74 | −48.0 |
| Peto | 0.54 | −7.8 | 0.52 | −4.6 | 0.51 | −1.1 | 0.90 | −90.6 | 0.80 | −59.5 | 0.67 | −33.2 |
BA0E, both-armed zero-event; IV, inverse variance; pc, control arm probability; M-H, Mantel-Haenszel.
Table 5.
Impact of the number of patient changes in each individual study on bias
| Number of studies=5 | Control group probability=0.001 |
Group ratio=1 |
OR=0.5 |
Number of simulated data sets=2500 | Between-study SD=0.5 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Excluding BA0E studies |
Including BA0E studies |
|||||||||||
| n=50 |
n=100 |
n=250 |
n=50 |
n=100 |
n=250 |
|||||||
| Methods | 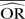 |
%bias | 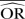 |
%bias | 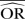 |
%bias | 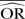 |
%bias | 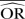 |
%bias | 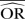 |
%bias |
| IV random effects | 0.73 | −45.7 | 0.70 | −40.6 | 0.68 | −36.5 | 0.98 | −96.8 | 0.97 | −70.7 | 0.93 | −86.0 |
| IV fixed effects | 0.73 | −45.8 | 0.70 | −40.6 | 0.68 | −36.3 | 0.98 | −96.5 | 0.96 | −68.5 | 0.92 | −84.5 |
| M-H random effects | 0.73 | −45.7 | 0.70 | −40.6 | 0.68 | −36.5 | 0.98 | −96.8 | 0.97 | −70.7 | 0.93 | −86.0 |
| M-H fixed effects | 0.73 | −45.8 | 0.70 | −40.6 | 0.68 | −36.3 | 0.98 | −96.5 | 0.96 | −68.5 | 0.92 | −84.5 |
| Peto | 0.58 | −15.2 | 0.54 | −7.8 | 0.51 | −2.4 | 0.98 | −95.8 | 0.95 | −59.5 | 0.90 | −80.7 |
BA0E, both-armed zero-event; IV, inverse variance; M-H, Mantel-Haenszel.
Table 6.
Impact of the between-study variance changes on bias
| Number of studies=5 | Control group probability=0.001 |
Group ratio=1 |
OR=0.5 |
Number of simulated data sets=2500 | Number of patients per arm=100 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Excluding BA0E studies |
Including BA0E studies |
|||||||||||
| SD=0.1 |
SD=0.5 |
SD=1 |
SD=0.1 |
SD=0.5 |
SD=1 |
|||||||
| Methods | 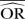 |
%bias | 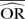 |
%bias | 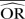 |
%bias | 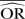 |
%bias | 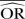 |
%bias | 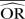 |
%bias |
| IV random effects | 0.68 | −35.3 | 0.70 | −40.6 | 0.88 | −76.7 | 0.96 | −92.5 | 0.97 | −93.0 | 0.99 | −97.3 |
| IV fixed effects | 0.68 | −35.3 | 0.70 | −40.6 | 0.88 | −76.7 | 0.96 | −91.6 | 0.96 | −92.3 | 0.99 | −97.0 |
| M-H random effects | 0.68 | −35.3 | 0.70 | −40.6 | 0.88 | −76.7 | 0.96 | −92.5 | 0.97 | −93.0 | 0.99 | −97.3 |
| M-H fixed effects | 0.68 | −35.3 | 0.70 | −40.6 | 0.88 | −76.7 | 0.96 | −91.6 | 0.96 | −92.3 | 0.99 | −97.0 |
| Peto | 0.50 | −0.9 | 0.54 | −7.8 | 0.80 | −60.5 | 0.95 | −89.9 | 0.90 | −90.6 | 0.98 | −96.4 |
BA0E, both-armed zero-event; IV, inverse variance; M-H, Mantel-Haenszel.
Excluding BA0E studies
Similarly, excluding BA0E studies for meta-analyses introduced little bias on the pooled estimates (0.7–1.4%) when there was no true treatment effect (table 3 and see online supplementary appendix 1). When a true treatment effect existed, the pooled estimates obtained using this approach yielded smaller bias compared to including BA0E studies. Again the magnitude of bias increased in the direction towards underestimating the treatment effects with a decrease in the control arm probability (table 4) and number of patients (table 5) and an increase in between-study variance (table 6). Besides the results of RMSE and width of 95% CI already mentioned in comparing to the approach of including BA0E studies, we noticed that the coverage was influenced by the changes of the treatment effects. With the increasing of the treatment effect from none to extremely large (ORs=1, 0.8, 0.5, 0.2), the coverage decreased sizeably (nearly 100%, 96%, 91% and 84%) (see online supplementary appendix 3c).
Peto method excluding BA0E studies
Among all five pooling methods, the Peto method excluding BA0E studies produced lowest bias across all simulation scenarios. When the treatment effect and between-study variance were from none (OR=1; SD=0.1) to moderately large (OR=2, OR=0.5; SD=0.5), with the reasonable number of patients in each study (>100), Peto method excluding BA0E studies generated the relatively reliable estimates of the pooled treatment effect (percentage bias<−8%). However, when the treatment effect and between-study variance were extremely large (OR=5, OR=0.2; SD=1) and number of patients in each study was small (<50), the bias of the estimates from this approach increased dramatically towards underestimating the treatment effects (tables 3–6 and see online supplementary appendix 2).
Summary
Our simulation study verified that when there was no true treatment effect (OR=1), the approach of including BA0E studies consistently outperformed the approach of excluding BA0E studies across all five pooling methods by providing nearly unbiased results. However, whenever a true treatment effect was present, the results from the approach of including BA0E studies introduced larger bias comparing to the approach of excluding them in the direction of underestimating the true treatment effect. Among all evaluated pooling methods for these two approaches, Peto methods excluding BA0E studies produced the least biased estimates when the true treatment effect existed.
Discussion
This simulation study investigated the impact of including or excluding BA0E studies in meta-analyses for rare event outcomes when OR is used as the effect measure for pooled estimates of dichotomous outcomes. We found that including BA0E studies provided more accurate overall pooled estimates than excluding them when there was no true treatment effect. However, when there was a true treatment effect, the results from both approaches underestimated the true treatment effect, and including BA0E studies increased bias further in the direction of underestimating treatment effects. Among the pooling methods, Peto's method with exclusion of BA0E studies provided the pooled OR considerably closer to the true treatment effect for small to moderate treatment effects under the condition of small to moderate between-study variance and relatively large sample size.
Our simulation study confirmed the empirical findings obtained by Friedrich et al.12 They recommended including BA0E studies in all meta-analyses for the benefits of providing conservative point estimates and increasing the study integrity. However, the ‘conservative’ estimate is a double-edged sword. In the sense of drawing the estimates towards null hypothesis, although underestimating benefit may delay or deny patient's access to a new treatment23 when evaluating the beneficial treatment effect for a new drug, with the patient safety as physician's priority concern, the conservative result might be the safer choice. With many uncertainties unchecked, quickly shifting from the standard care to a new treatment based on the findings from a small study (even it is a meta-analysis) can be a dangerous move. Some studies have showed that the treatment effect tends to be overestimates when the trials were underpowered.24 25 On the other hand, when the result of a meta-analysis is regarding the safety measures such as serious adverse event, the conservative result means underestimating the harm, which could lead to expose patients to unnecessary danger.26 Therefore, depending on the purpose of the systematic review (evaluating benefits or harms), including BA0E studies in meta-analysis could have different implications.
This simulation study confirmed that among all five commonly used pooling methods, only the Peto method without inclusion of BA0E studies produces a pooled OR approaching the true treatment effect when sample size is relatively large. This finding is consistent with the simulation study conducted by Bradburn et al,9 which evaluated performances of the common methods used to meta-analyse the sparse data for binary outcomes. Compared to Peto method, the other pooling methods even without including BA0E studies still produced biased results by underestimating the treatment effects, that is, pulling the pooled estimates towards null hypothesis. This phenomenon could be due to the extremely low event rates used in our simulation, but this assumption needs to be confirmed in future studies. In addition to Bradburn's findings, our simulation study also shows that compared to the random-effects model (IV or H-M), the Peto method as a fixed-effect model gave the least biased estimates when the between-study variance is from small to moderate. The reason for the Peto method outperforming the random-effects model is that as Sweeting et al22 has shown in their simulation study, the heterogeneity was difficult to estimate for the rare event data. Therefore, the benefit of using random-effect model does not overcome the bias introduced by the IV or H-M method, which were proven by the simulation study conducted by Bradburn et al.9
This simulation study clearly showed that including both-armed (and even single armed) zero-event studies in meta-analysis could severely underestimate the treatment effects for beneficial and harmful events. However, when the treatment effect is evaluating harmful outcomes, underestimating treatment effect may lead to more serious consequence such as compromising patients' safety in seeking new treatment. In reality, it is not easy or sometimes even impossible to know whether a true treatment effect exists or not. Therefore, a comprehensive approach of a series of sensitivity analyses needs to be conducted when performing systematic reviews that include zero-event studies. An example could be used is Dahabreh and Economopoulos13 who re-analysed the cardiovascular events in randomised trials of rosiglitazone. Although, the results showed that including BA0E studies turned the pooled odds of MI from statistically significant to not significant. Their conclusion that rosiglitazone increased MI was made after assessing the consistency of results from different methods. The above example demonstrates that when meta-analyses are conducted to evaluate rare events, it is difficult to get a concordant result. To assist readers to make their own informative decision about the results of a meta-analysis, its methods should be communicated in full transparency. In addition to reporting the result following the PRISMA guideline,1 the eligible studies with zero-event and the methods used to deal with zero-event studies need to be clearly described. We believe that an extension of the PRISMA guideline on how to report meta-analyses on rare event outcomes with zero-event studies needs to be developed to include a section of reporting the methods used to deal with zero-event studies and impact on the overall estimates of meta-analyses.
Although we chose the values of simulation parameters from literature review, we realise that the results of our simulation study cannot be generalised to all situations in meta-analysis. To reduce the simulation scenarios to a manageable level, we used fixed values for some parameters. We only considered the balanced group ratio between treatment and control arms, but only 22% of RCTs used unbalanced design among previous in a recent review.20 Within each simulated meta-analysis data set, we fixed the number of studies to five, each with the same number of patients. This approach might be oversimplified. Although we chose to investigate OR using common pooling methods, we believe that our findings can be applied to RR under similar condition for the estimates of OR and RR are similar when event rates are <0.2.16 17 For the continuity correction approach to incorporate zero-event studies, we only used 0.5 as continuity correction factor, which works well when the trial arms are balanced, but will increase the bias when there is a big difference on the numbers of patients between two arms and the treatment effect are large.22
The commonly used meta-analysis pooling methods we discussed in this simulation are based on parameter estimation, which requires the use of continuity correction to include zero-events. Some likelihood maximisation-based statistical models such as Poisson regression and β-binomial regression can incorporate both-armed or single-armed zero-events without continuity correction and supposedly generates an unbiased estimate of RR. The simulation from Spittal et al14 showed that random-effects Poisson regression outperformed the standard pooling methods when meta-analysing the incidence rate ratio for zero-events data. We ran the random-effects model Poisson regression on our stimulated data, and there was a convergence issue. The reason could be that there were a large proportion of zero-event (either in one arm or in both arms) studies presented in a relatively smaller number of studies in each meta-analysis due to extremely low event rate. This convergence problem may not be a problem for meta-analyses with larger number of studies. Another recently published simulation by Kuss15 recommended the use of β-binomial regression to incorporate both-armed and single-armed zero-event studies in meta-analyses. Since this model requires further programming on parameterisation to obtain the OR as the effect measures, it is not a practical choice for non-statisticians. Similar to random-effect Poisson regression and β-binomial regression, Bayesian approach using none-informative prior as an alternative of the classical statistical models can incorporate both-armed and single-armed zero-event studies without continuity correction, but it requires some programming work. Therefore, although the above full statistical models may have the advantage of incorporating BA0E in meta-analyses, the requirement of some special knowledge or skills creates the barriers for non-statistician users. We feel that before any new meta-analysis specialised and easy ready-to-use full statistical models developed, RevMan and Stata's metan module will remain as the most commonly used tools in conducting meta-analyses. With the lack of the capacity to conduct any advanced statistical model, how to deal with BA0E studies in meta-analyses may still present a challenge for researchers who use these standard meta-analysis packages. Therefore, based on our simulation results, we developed some general strategies to deal with BA0E studies using the standard meta-analysis methods for rare event outcomes (table 7).
Table 7.
Strategies in dealing with BA0E studies
| Approaches | Scenarios |
|---|---|
| Including BA0E studies |
|
| Excluding BA0E studies with Peto method |
|
BA0E, both-armed zero-event.
Conclusion
To conclude, we recommend including BA0E studies in meta-analysis using OR as effect measure in the following three scenarios: (1) when treatment effects are unlikely to present, (2) having strong rational for seeking the most conservative estimates on treatment effect when evaluating beneficial outcomes and (3) magnitudes of the treatment effects unclear when evaluating beneficial outcomes for new treatments. We recommend excluding BA0E studies in conjunction of Peto method in the following two scenarios: (1) when treatment effects are likely to present and (2) when evaluating harmful outcomes such as mortality, mobility or adverse events. When the above recommendations cannot apply, it is important to present the results of meta-analyses using approaches of including and excluding BA0E studies so that the readers can make their informed interpretation within the clinical content.
Footnotes
Contributors: JC, EP, JKM and LT designed the study. JC wrote the simulation programme, conducted the statistical analysis and drafted the manuscript. JC, EP, AI and LT provided input on statistical concept. JKM and AI provided the clinical expertise. All authors revised the manuscript for important clinical and statistical contents and approved the final manuscript.
Funding: This research received no specific grant from any funding agency in the public, commercial or not-for-profit sectors.
Competing interests: None declared.
Provenance and peer review: Not commissioned; externally peer reviewed.
References
- 1.Moher D, Liberati A, Tetzlaff J et al. Preferred reporting items for systematic reviews and meta-analyses: the PRISMA statement. Phys Ther 2009;89:873–80. 10.1136/bmj.b2535 [DOI] [PubMed] [Google Scholar]
- 2.Cochrane Group. Cochrane handbook: meta-analysis of dichotomous outcomes. http://handbook.cochrane.org/chapter_9/9_4_4_meta_analysis_of_dichotomous_outcomes.htm
- 3.Evans D. Hierarchy of evidence: a framework for ranking evidence evaluating healthcare interventions. J Clin Nurs 2003;12:77–84. 10.1046/j.1365-2702.2003.00662.x [DOI] [PubMed] [Google Scholar]
- 4.Cook DJ, Mulrow CD, Haynes RB. Systematic reviews: synthesis of best evidence for clinical decisions. Ann Intern Med 1997;126:376–80. 10.7326/0003-4819-126-5-199703010-00006 [DOI] [PubMed] [Google Scholar]
- 5.Marodin G, Goldim JR. Confusions and ambiguities in the classification of adverse events in the clinical research. Rev Esc Enferm USP 2009;43:690–6. 10.1590/S0080-62342009000300027 [DOI] [PubMed] [Google Scholar]
- 6. Drazen JM, Rainey J, Begg H, et al. Adverse Drug Event Reporting: The Roles of Consumers and Health-care Professionals: Workshop Summary (2007). Washington D.C.: The National Academies Press, 2007.
- 7.Davey J, Turner RM, Clarke MJ et al. Characteristics of meta-analyses and their component studies in the Cochrane Database of Systematic Reviews: a cross-sectional, descriptive analysis. BMC Med Res Methodol 2011;11:160 10.1186/1471-2288-11-160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Warren FC, Abrams KR, Golder S et al. Systematic review of methods used in meta-analyses where a primary outcome is an adverse or unintended event. BMC Med Res Methodol 2012;12:64 10.1186/1471-2288-12-64 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bradburn MJ, Deeks JJ, Berlin JA et al. Much ado about nothing: a comparison of the performance of meta-analytical methods with rare events. Stat Med 2007;26:53–77. 10.1002/sim.2528 [DOI] [PubMed] [Google Scholar]
- 10.Keus F, Wetterslev J, Gluud C et al. Robustness assessments are needed to reduce bias in meta-analyses that include zero-event randomized trials. Am J Gastroenterol 2009;104:546–51. 10.1038/ajg.2008.22 [DOI] [PubMed] [Google Scholar]
- 11.Harris RJ, Bradburn MJ, Deeks JJ et al. Metan: fixed- and random-effects meta-analysis. Stata J 2008;8:3–28. [Google Scholar]
- 12.Friedrich JO, Adhikari NKJ, Beyene J. Inclusion of zero total event trials in meta-analyses maintains analytic consistency and incorporates all available data. BMC Med Res Methodol 2007;7:5 10.1186/1471-2288-7-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dahabreh IJ, Economopoulos K. Meta-analysis of rare events: an update and sensitivity analysis of cardiovascular events in randomized trials of rosiglitazone. Clin Trials 2008;5:116–20. 10.1177/1740774508090212 [DOI] [PubMed] [Google Scholar]
- 14.Spittal MJ, Pirkis J, Gurrin LC. Meta-analysis of incidence rate data in the presence of zero events. BMC Med Res Methodol 2015;15:42 10.1186/s12874-015-0031-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kuss O. Statistical methods for meta-analyses including information from studies without any events-add nothing to nothing and succeed nevertheless. Stat Med 2015;34:1097–116. 10.1002/sim.6383 [DOI] [PubMed] [Google Scholar]
- 16.Grimes DA, Schulz KF. Making sense of odds and odds ratios. Obstet Gynecol 2008;111:423–6. 10.1097/01.AOG.0000297304.32187.5d [DOI] [PubMed] [Google Scholar]
- 17.Egger M, Smith GD, Phillips AN. Meta-analysis: principles and procedures. BMJ 1997;315:1533–7. 10.1136/bmj.315.7121.1533 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cohen J. Statistical power analysis for the behavioral sciences. 2nd edn Hillsdale: (NJ: ): Erlbaum, 1988. [Google Scholar]
- 19.EURORDIS. Rare Disease: Understanding This Public Health Priority. Paris, France: European Organisation for Rare Disease, Nov 2005.
- 20.Dumville JC, Hahn S, Miles JNV et al. The use of unequal randomisation ratios in clinical trials: a review. Contemp Clin Trials 2006;27:1–12. 10.1016/j.cct.2005.08.003 [DOI] [PubMed] [Google Scholar]
- 21.Burton A, Altman D, Royston P et al. The design of simulation studies in medical statistics. Stat Med 2006;25:4279–92. 10.1002/sim.2673 [DOI] [PubMed] [Google Scholar]
- 22.Sweeting MJ, Sutton AJ, Lambert PC. What to add to nothing? Use and avoidance of continuity corrections in meta-analysis of sparse data. Stat Med 2004;23:1351–75. 10.1002/sim.1761 [DOI] [PubMed] [Google Scholar]
- 23.Hayward RA, Kent DM, Vijan S et al. Reporting clinical trial results to inform providers, payers, and consumers. Health Aff (Millwood) 2005;24:1571–81. 10.1377/hlthaff.24.6.1571 [DOI] [PubMed] [Google Scholar]
- 24.Nüesch E, Trelle S, Reichenbach S et al. Small study effects in meta-analyses of osteoarthritis trials: meta-epidemiological study. BMJ 2010;341:c3515 10.1136/bmj.c3515 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang Z, Xu X, Ni H. Small studies may overestimate the effect sizes in critical care meta-analyses: a meta-epidemiological study. Crit Care 2013;17:R2 10.1186/cc11919 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Miller DB, Humphries KH. A new way to evaluate randomized controlled trials? New approach does more harm than good. BCMJ 2005;47:241–4. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
bmjopen-2015-010983supp_appendices.pdf (214.9KB, pdf)


