Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Sep 7;6:32625. doi: 10.1038/srep32625

Newtype single-layer magnetic semiconductor in transition-metal dichalcogenides VX2 (X = S, Se and Te)

Huei-Ru Fuh 1, Ching-Ray Chang 1, Yin-Kuo Wang 2, Richard F L Evans 3, Roy W Chantrell 3, Horng-Tay Jeng 4,5,a
PMCID: PMC5013522  PMID: 27601195

Abstract

We present a newtype 2-dimensional (2D) magnetic semiconductor based on transition-metal dichalcogenides VX2 (X = S, Se and Te) via first-principles calculations. The obtained indirect band gaps of monolayer VS2, VSe2, and VTe2 given from the generalized gradient approximation (GGA) are respectively 0.05, 0.22, and 0.20 eV, all with integer magnetic moments of 1.0 μB. The GGA plus on-site Coulomb interaction U (GGA + U) enhances the exchange splittings and raises the energy gap up to 0.38~0.65 eV. By adopting the GW approximation, we obtain converged G0W0 gaps of 1.3, 1.2, and 0.7 eV for VS2, VSe2, and VTe2 monolayers, respectively. They agree very well with our calculated HSE gaps of 1.1, 1.2, and 0.6 eV, respectively. The gap sizes as well as the metal-insulator transitions are tunable by applying the in-plane strain and/or changing the number of stacking layers. The Monte Carlo simulations illustrate very high Curie-temperatures of 292, 472, and 553 K for VS2, VSe2, and VTe2 monolayers, respectively. They are nearly or well beyond the room temperature. Combining the semiconducting energy gap, the 100% spin polarized valence and conduction bands, the room temperature TC, and the in-plane magnetic anisotropy together in a single layer VX2, this newtype 2D magnetic semiconductor shows great potential in future spintronics.

The semiconductor-based spintronics has attracted worldwide attention in recent years because of the allowable spin current transport without the presence of a net charge current, which could avoid problems arising from capacitances and Joule heating1. For example, the spin pumping2 or the spin Seebeck effect3,4 have successfully created pure spin currents by using the thermal gradients across a ferromagnetic layer. In many cases, it involves Y5Fe3O12 (YIG) as the magnetic insulator and Pt as the spin current detector5,6, in which the spin current is transformed into an observable transverse voltage by the inverse spin Hall effect7,8. A new type of magnetoresistance (MR) in a Pt-YIG hybrid structure has been discovered5,9 and used in transforming magnetic data and memory storage10,11,12,13,14.

The next generation spintronic devices can base on room temperature ferromagnetic semiconductors or heterostructures combining ferromagnetic metals with non-magnetic semiconductors. Nevertheless searching for semiconducting materials with strong ferromagnetism and higher TC is extremely difficult due to the conflicting requirements in the crystal and electronic structures of semiconductors and ferromagnets12. To date all the discovered ferromagnetic semiconductors exhibit magnetic order below room temperature, e.g., EuO (TC = 77 K15), BiMnO3 (TC = 100 K16), La2NiMnO6 (TC = 280 K17), and diluted magnetic semiconductor (DMS) such as the prototypical system (Ga, Mn)As and the newly reported (Ba1−xKx)(Zn1−yMny)2As2 (TC = 185 K, 180 K18). The only exception is the ferrimagnetic insulator Y3Fe5O12 (YIG) with a very high TC = 550 K19 far beyond room temperature. This is the reason why most of the spintronics related works rely on YIG. Meanwhile all of the know magnetic semiconductors belong to 3-dimensional bulk materials.

Two-dimensional materials such as graphene, boron nitride, and transition metal dichalcogenides (TMDs)20,21,22 with the single-layer thickness less than 1 nm have attracted tremendous attention in recent years. Because of the more than 40 different families23,24,25,26 and the rich electronic properties that can create extensive applications, the TMD has become a rapidly growing research field in the past few years. Representative TMDs such as MoS2, MoSe2, WS2, and WSe2 in the monolayer (ML) form are identified as direct-band-gap semiconductors. With the time reversal symmetry preserved, giant spin splittings of 148–456 meV resulting from missing inversion symmetry and existing spin-orbit coupling20,27,28 could be of high potential in spintronics. However, it is still a challenge to coordinate the TMDs into nanoelectronics29,30. Therefore, developing a new type 2D TMD with exotic electronic properties is imperative.

Very recently, a new 2D TMD, few layer Vanadium disulfide (VS2), has been synthesized experimentally31,32. The intrinsic ferromagnetism and potential applications attract particular interests31,33,34. The magnetic moments and magnetic coupling strength of the ultrathin VS2 nanosheets could be tuned by the isotropic strain34. The ferromagnetism provides a new opportunity to fabricate ferromagnetic 2D TMDs without introducing magnetic transition metal atoms or tensile strains34. The synthesis procedures are flexible for other VX2 such as VSe2 and VTe2 monolayers. Besides the bulk VX225, recent phonon dispersion calculations also reveal that monolayer VX2 are stable24.

In this work, we systematically investigate the electronic structures of monolayer and multilayer VX2 (X = S, Se and Te) in the 2H-phase based on the generalized gradient approximation (GGA) within the density function theory (DFT). We demonstrate that H-VX2 monolayers exhibit indirect semiconducting energy gaps with intrinsic ferromagnetism and in-plane magnetic anisotropy, achieving an exceptional 2-D magnetic semiconductor group. The magnitude of the band gap and even the metal-insulator transition (MIT) are tunable by applying the in-plane strain and/or changing the number of stacking layers. The GGA plus on-site Coulomb interaction (GGA + U) scheme, the GW approximation, as well as the HSE functional have been adopted to account for the strong correlation effect in transition-metal ions and for the well-known underestimation of the semiconducting band gaps. The Curie temperatures (TC) estimated by Monte Carlo simulations are close to or well beyond the room temperature, which makes this TMD family of high potential in real applications.

Computational Details

The electronic structure calculations of bulk and monolayer VX2 are performed using the projector augmented wave (PAW) method with the Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation (GGA)35 as implemented in the VASP package36,37. The energy cutoff of 400 eV is used for the plane-wave basis expansion with the total energy convergence criteria of 1 × 10−5 eV per unit cell. Gamma-centered k-grids 16 × 16 × 1 were sampled over the 2D Brillouin Zone. Optimized monolayer structures are obtained with the residual force and stress less than 0.01 eV/Å and 1.0 kBar, respectively. For few layered 2H-VX2 calculations, the van der Waals corrections (vdW-DF)38 are adopted to optimized the lattice structural parameters and bondlengths. With vdW correction, the intra-layer bond lengths are hardly changed, while the inter-layer bondlengths are significantly reduced, confirming that the interactions between VX2 layers of weak and non-local vdW type force. The on-site Coulomb energy U = 2 eV and J = 0.87 eV for V 3d electrons39 are taken into account for the electron-electron correlation effects of the localized V-3d orbitals in the GGA + U40 calculations. To correct the underestimated semiconducting band gaps, the GW formalism within a many-body quasiparticle framework is utilized to amend errors in the one-electron Kohn-Sham eigenvalues41,42. The Green’s function G0 and the screened potential W0 in the GW approach (G0W0) based on GGA and GGA + U ground states43 is adopted and henceforth denoted by GW for simplicity. The number of conduction bands nc,max = 591 is sufficient to clearly resolve the peak structure of the imaginary part of the dielectric function. Similar to refs 44 and 45, the convergences of G0W0 energy gaps of VX2 monolayers upon the k-point mesh and the vacuum thickness have been carefully examined with the k-point mesh ranging from 12 × 12 × 1 to 30 × 30 × 1 and the vacuum thickness ranging from 15 Å up to 70 Å and then extrapolated to the infinite vacuum thickness limit. To go beyond the standard GGA approach, calculations based on the HSE46 functional have also been performed for comparison with the converged G0W0 energy gaps.

Results and Discussion

VX2 monolayer structure

The bulk VX2 (X = S, Se, and Te) can be formed in two common TMD structures: 2H (D3h) and 1T (D3d) polymorphs25,31,33. The 2H-TMDs contain two hexagonal monolayers in the unit cell with an AbA stacking sequence in each layer that the V ion is sandwiched by two X ions as shown in Fig. 1. The 1T unit cell consists of only one trigonal monolayer with an AbC stacking sequence in the monolayer. The bulk and multilayer VS2 in the 2H and 1T structures have been synthesized in recently years33,47,48,49,50. However, the bulk VSe2 and VTe2 and multilayer VSe2 can only be synthesized in the 1T structure to date51,52,53,54. The 1T-VX2 (X = S, Se, and Te) monolayer series is metallic with higher formation energies than the 2H-VX233, therefore they are not considered in this work.

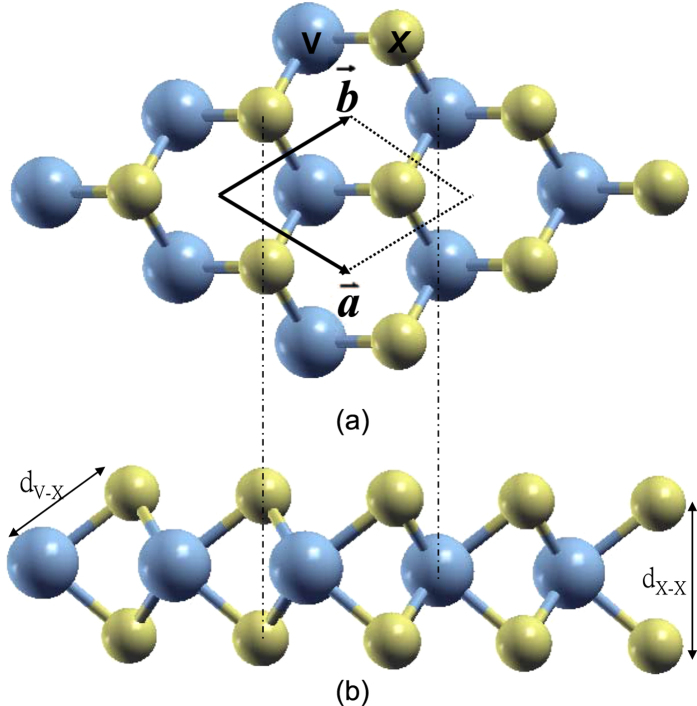
Figure 1. The 1H lattice structure of the monolayer VX2 (X = S, Se, and Te).

Figure 1

Open in a new tab

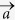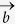(a,b) are the top and side views, respectively. Inline graphic and Inline graphic are the primitive lattice vectors of the 2D hexagonal unit cell.

Figure 1 shows the 1H lattice structure of the monolayer VX2. Each V ion is surrounded by six neighboring X ions, while each X ion has three neighboring V ions. The V ions occupy the center of a trigonal prism spanned by the X ions (point group PInline graphicM2 (D3h)). The structural parameters of monolayer VX2 are determined by the geometry optimization as shown in Table 1. The calculated lattice constant of VS2 and VSe2 are 3.173 and 3.325 Å, respectively, being in excellent agreement with previously calculated results34. The V-X bondlength, the interlayer distance between the two X layers and between the V and X layers also agree well with previous studies34. The geometrically optimized VTe2 monolayer has the largest structural parameters because of the larger atomic radius among the three materials.

Table 1. Optimized lattice constant a, V-X bondlength dV−X, interlayer distance between two X layers dX−X and between V and X layers ΔV−X of monolayer VX2 (X = S, Se, and Te).

(Å) a a(Theo.) dV−X dX−X ΔV−X
VS2 3.173 3.17434 2.362 2.982 1.491
VSe2 3.325 3.33134 2.501 3.205 1.602
VTe2 3.587 – 2.715 3.510 1.755
Open in a new tab

Ferromagnetism and magnetic anisotropy

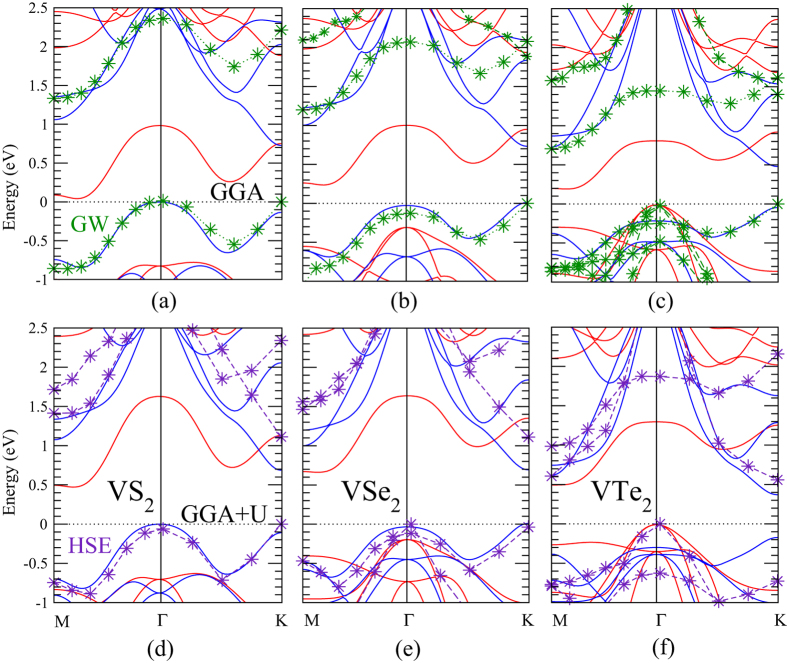
The spin-polarized band structures of monolayer VX2 along the high symmetry lines are shown in Fig. 2. The upper and lower panels show GGA and GGA + U results, respectively. The GGA calculations show spin polarized bands around the Fermi level (EF) with indirect band gaps of 0.05~0.22 eV originated from the exchange splitting of the V-dz2 bands, and integer magnetic moments of 1.0 μB/f.u. for all the three cases. These results lead to the desirable 2D ferromagnetic semiconducting ground state. To examine the possible antiferromagnetism (AFM), we have adopted the 2 × 2 × 1 supercell for the stripe type AFM arrangement. The calculated total energies demonstrate the ferromagnetic (FM) ground state for all the three VX2 monolayers, being consistent with previous studies34,55,56.

Figure 2. Spin-polarized band structures of VX2 monolayers without (upper panels) and with (lower panels) the on-site Coulomb energy (GGA + U) U = 2.0 eV and J = 0.87 eV for V 3d orbitals.

Figure 2

Open in a new tab

The blue and red lines denote the spin up and down channels, respectively. The EF (dotted horizontal line) is set at 0 eV. The GW/HSE highest valence and lowest conduction bands are denoted by green/purple star symbols in the upper/lower panels.

The Stoner criterion has been successfully applied to predict the magnetism of different compounds57. If the Stoner criterion58 ID(EF) ≥ 1 is satisfied, then the compound is ferromagnetic in nature at T = 0, where D(EF) is the density of states (DOS) at EF and I is the Stoner parameter measuring the strength of the exchange correlation. Here we adopt this criterion to examine the observed magnetism of VX2. Given from previous first principles calculations, the Stoner parameter I for the V atom is 0.859. Non-magnetic calculations show large D(EF) values of 3.7, 4.4, 5.4 states per eV per atom for VS2, VSe2, and VTe2, respectively. The high DOS at the Fermi level thus cause the Stoner instability, leading to the exchange splits and the intrinsic 2D ferromagnetic ordering.

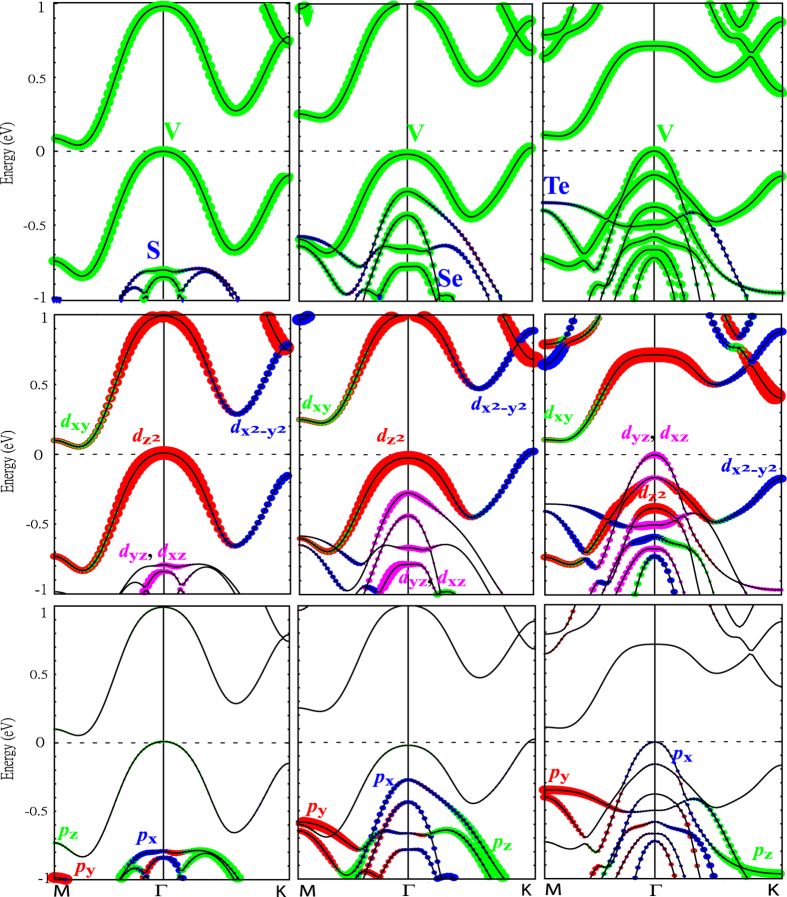
The atom and orbital decomposed band structures of VX2 monolayers from GGA calculations with the spin-orbit coupling (SOC) included self-consistently are shown in Fig. 3. Due to the weak SOC in 3d element V, the overall band structures are more or less the same as the non-spin-orbit counterparts shown in Fig. 2. The atom-decomposed band structures in the upper panels show that the V ion predominates the top most spin up valence band and the lowest spin down conduction band around the EF, while the X ion contributes only slightly to these bands, indicating the 2D ferromagnetism originates mainly from the V ions rather than from the X ions. The d-orbital-decomposed band structures of V ions are depicted in the middle panels of Fig. 3. For VS2 monolayer, the V-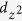Inline graphic orbital predominates the valence band maximum (VBM) at Γ and the conduction band minimum (CBM) around M are mainly the 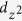Inline graphic and dxy hybridized states. While for VSe2, the V-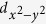Inline graphic electrons dominate the VBM at K and the CBM around M are mainly the 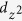Inline graphic and dxy mixed states. As for the VTe2 case, the VBM at Γ is replaced by the V-dyz and dxz hybridized bands arising from lower energies with the CBM around M being the 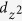Inline graphic and dxy hybridized states. The bottom panels of Fig. 3 illustrate the orbital contributions from the X ions. All the S, Se and Te ions play insignificant roles in the bands near the Fermi level. The above results demonstrate that these ~100% spin polarized bands around EF in VX2 monolayer stem mainly from the the V-3d local moments, being consistent with previous reports32. This new 2D ferromagnetic semiconducting material not only provides controllable spin current applications but also regards the spin filter devices by tuning the Fermi level appropriately. Note that the band structures of VX2 are unlike the MoS2 ones. In the latter case, giant spin splittings of 148–456 meV, resulting from the stronger spin-orbit coupling in 4d orbitals and the missing inversion symmetry26, can be found around the K-points with spin bands degenerate elsewhere, reserving the global time reversal symmetry in MoS2.

Figure 3. Atom and orbital decomposed band structures of VS2 (left hand side panels), VSe2 (middle panels), and VTe2 (right hand side panels) from GGA with spin-orbit coupling (SOC) included self-consistently.

Figure 3

Open in a new tab

The upper panels are the atom-decomposed band structures with the green and blue colors denote the components from V and X ions, respectively. The middle panels and bottom panels are the orbital decomposed band structures for V and X ions, respectively. The colors represent the contributions from different orbitals as indicated in the figures.

Table 2 shows the calculated magnetocrystalline anisotropy energies (MAE) of the VX2 monolayers in the optimized structures. MAE, the total energy difference between two magnetization directions, serves as a measure of the magnetic easy-axis of a material. The total energy calculations are performed with the spin-orbit coupling included self-consistently over the 20 × 20 × 1 k-mesh in the 2D Brillouin Zone under the energy convergence criteria of 10−8 eV. The out-of-plane MAE is the energy difference between the perpendicular [001] and parallel [100] magnetization directions defined as E[100]-E[001]. While the in-plane MAE, defined as E[100]-E[010], is the energy difference between two in-plane magnetization directions [100] and [010]. The out-of-plane MAE of VS2, VSe2, and VTe2 are −0.21, −0.60, and −1.78 meV/f.u., respectively. These negative out-of-plane MAEs indicate the in-plane magnetic anisotropy (in-plane easy axis of magnetization) for all the three VX2 monolayers, yielding the BKT magnetic transition in the 2D XY model for future spintronic applications. As for the in-plane MAEs, the calculated E[100]-E[010] values are 2 order of magnitude smaller and play insignificant roles only.

Table 2. Calculated magnetic anisotropy energies of the VX2 monolayers.

  VS2 VSe2 VTe2
E[100]-E[001] (meV) −0.21 −0.60 −1.78
E[100]-E[010] (μeV) −3 −7 −8
Open in a new tab

Band gap properties

The calculated energy gaps from GGA, GGA + SO, GGA + U, GGA + U + SO (U = 2, J = 0.87 eV), GW, as well as HSE for geometrically optimized VX2 (X = S, Se, and Te) monolayers are all listed in Table 3 for a systematical comparison. In the GGA scheme, the calculated indirect band gaps are 0.046, 0.225, and 0.201 eV for VS2, VSe2, and VTe2 MLs, respectively. As shown in Fig. 2, the CBM of VS2 is close to the M-point along the Γ-M direction and the VBM is located at the Γ-point. The overall band dispersion of VSe2 is similar to the VS2 one. The only difference is that the VBM goes to the K-point. The band structures of VTe2 are different from the previous ones in two aspects: Firstly, the VBM moves back to the Γ-point due to the rising dxz-dyz hybridized band from lower energies (Fig. 3). Secondly, this emergent top valence band is of the same spin as the bottom conduction band, resulting in the band gap between the same spin polarized bands (Fig. 2). This is very different from the energy gaps between opposite spin channels in VS2 and VSe2 (Fig. 2).

Table 3. Calculated energy gaps from GGA, GGA + SO, GGA + U, GGA + U + SO with U = 2, J = 0.87 eV, GW, and HSE for geometrically optimized VX2 (X = S, Se, and Te) monolayers.

(eV) GGA GGA + SO GGA + U GGA + U + SO GW HSE
VS2 0.046 0.044 0.473 0.473 1.334 1.110
VSe2 0.225 0.251 0.651 0.684 1.200 1.150
VTe2 0.201 0.149 0.379 0.282 0.705 0.560
Open in a new tab

To examine the importance of the spin-orbit interaction on the exchange splitting gaps, we have done calculations with the spin-orbit coupling (SOC) included self-consistently. As expected for 3d transition-metal ions that the weak SOC plays insignificant roles, the overall electronic and magnetic properties remain more or less the same. The only noticeable change is in the VTe2 band structures (Fig. 3), in which the degeneracy of the highest valence bands at Γ is lifted and the band energy at K is lowered by the SOC, as compared with the non-spin-orbit counterparts in Fig. 2. The enhanced SOC effect in these V-3d bands is induced by Te with stronger SOC in its 5p orbitals. Hence the energy gaps of VS2, VSe2, and VTe2 change slightly to 0.044, 0.251, and 0.149 eV, respectively, as shown in Table 3.

To take into consideration the strong electron correlations in the relatively localized 3d orbitals, we perform GGA + U band structure calculations as shown in the lower panels of Fig. 2. The on-site Coulomb repulsion U of 2 eV enhances the exchange splitting and gives rise to larger energy gaps of 0.473, 0.651, and 0.379 eV for VS2, VSe2, and VTe2, respectively, as listed in Table 3. Besides the significantly raised exchange gaps, the CBM and VBM locations of VS2 and VSe2 remain the same as those from GGA. However for the VTe2 case, the CBM from GGA + U locates at the K-point rather than around the M-point given by GGA. Finally the combined SOC and on-site Coulomb repulsion U effect slightly changes the GGA + U energy gaps as listed in Table 3. The broadest energy gap obtained from standard DFT (GGA and GGA + U) calculations is 0.684 eV of VSe2, which is adequately large for real applications.

As mentioned above, the on-site Coulomb repulsion U of 2 eV used in this work is given from a previous theoretical estimation for V atoms39. Since the U value of the same element in different materials also depends on the ionicity and the composition of the embedded compound, the precise value of U in VX2 is actually unknown. Because of the uncertainty of the U value, we therefore consider the GW correction which would give the most reliable band gaps in semiconducting materials. To compare with the standard GGA band structures, the GW approximation corrected band energies with carefully examined convergence upon vacuum thickness and number of k-points are denoted by green star symbols in the upper panels of Fig. 2. For simplicity we only depict the highest valence states and lowest conduction states with the top most GW valence band energies aligned at Ef. The GW corrected VBM and CBM of VS2 are located at Γ- and M-point, respectively. While for VSe2 and VTe2, the VBM and CBM are located at K- and M-point, respectively. The GW corrected band gaps are raised to 1.334, 1.200, and 0.705 eV for VS2, VSe2, and VTe2 monolayers, respectively, as shown in Table 3. To go beyond the standard GGA and GGA + U approach, we also adopt the HSE functional to calculate the band structures of VX2 monolayers as denoted by purple star symbols in the lower panels of Fig. 2 (only bands closest to Ef are depicted). The resultant HSE energy gaps of 1.110 eV, 1.150 eV, and 0.560 eV for VS2, VSe2, and VTe2 monolayers, respectively, are also listed in Table 3. As can be seen, the HSE energy gaps agree very well with the converged G0W0 results at the infinite vacuum thickness limit.

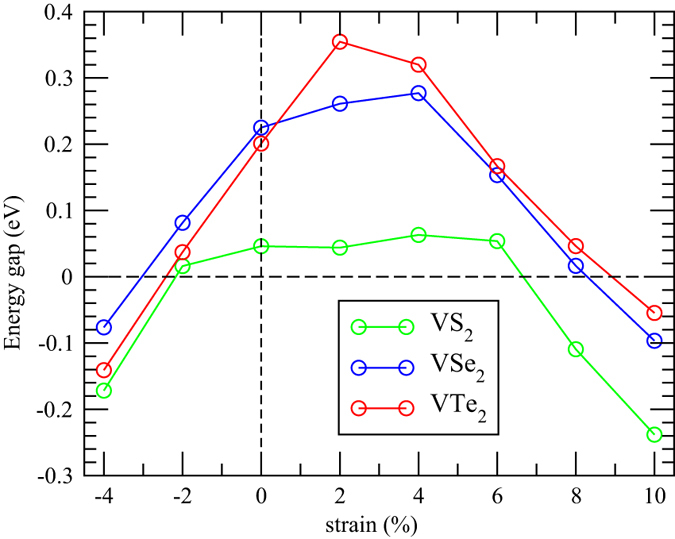
The GGA energy gap of VX2 monolayer as a function of the strain from −4% up to 10% is shown in Fig. 4. For VS2, the energy gap remains more or less the same below 6% strain, and then turns into the gapless metallic state. While for the other two cases, the energy gap increases below 4% and then decreases to a negative value (corresponding to the band overlap value) above 8% strain. In all cases the tensile strain affects the gap size significantly and eventually induces the metal-insulator transition (MIT) as shown in Fig. 4. This is because that the unoccupied dz2 band at the K-point shifts downward below the EF at high tensile strains due to the reduced Coulomb repulsion, and finally closes the energy gaps of the VX2 monolayers. We note that VTe2(VSe2) reaches the maximum energy gap of 0.36(0.28) eV under 2(4)% tensile strain. This strain-induced exchange gap enhancement implies a higher Curie temperature than the strain free one. On the other hand, due to the increased Coulomb repulsions and enhanced band dispersions of these dz2 bands under compressive strains, the energy gaps are therefore suppressed and achieve another MIT under negative strains around −2%, as can be seen in Fig. 4.

Figure 4. The GGA energy gap of the VX2 monolayer as a function of the strain.

Figure 4

Open in a new tab

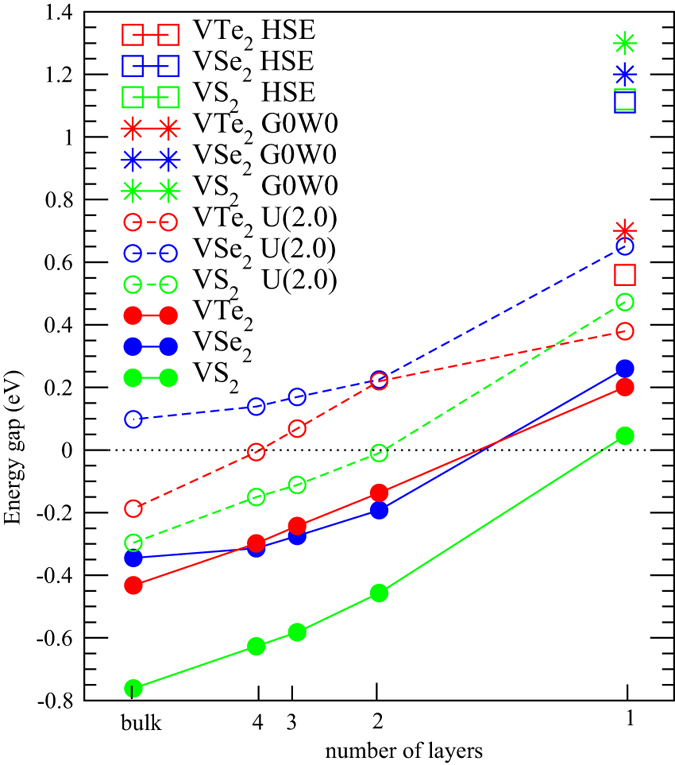
So far we have demonstrated various effects on the energy gaps of the VX2 monolayers. Below we discuss the dependence of the energy gaps on the thickness of VX2 multilayers. The gap values given from GGA, GGA + U, GW, as well as HSE calculations are summarized in Fig. 5. First of all we would like to emphasize that all kinds of calculations performed in this work demonstrate an exchange splitting energy gap for all the three VX2 monolayers, strongly supporting that the VX2 families in the monolayer form are indeed 2D ferromagnetic semiconductors. While increasing the number of layers would enhance the interlayer interactions and band dispersions, and hence significantly suppress the energy gap. For the bilayer systems, all the GGA gaps are closed while the GGA + U still gives gaps of ~0.23 eV for VSe2 and VTe2. As for the trilayer and thicker systems, the GGA + U gap size decreases further. At the bulk limit, only VSe2 exhibits a gap of about 0.1 eV from GGA + U, while no energy gap can be found for VS2 and VTe2. In comparison with the consistent semiconducting ground state for VX2 monolayers and the diverse results for bilayer and thicker layers, one may conclude that the ferromagnetic semiconducting phase exists only in the monolayer VX2 systems. Any thicker VX2 multilayers would cause the instability of the ferromagnetic semiconducting phase and result in the metallic phase, giving rise to the metal-insulator transition (MIT) upon layer thicknesses. Note that the experimental synthesis of monolayer VX2 is not yet reported, while multilayer VX2 has been demonstrated as a ferromagnetic metal experimentally32.

Figure 5. The energy gap of VX2 from GGA, GGA + U, GW, and HSE as a function of the number of layers.

Figure 5

Open in a new tab

Exchange interaction parameters and Curie temperature

To find the magnetic ground state of the VX2 monolayers, we considered three possible magnetic configurations within the 2 × 2 × 1 supercell including the ferromagnetic (FM), antiferromagnetic (AFM), and collinear antiferromagnetic (COL) spin arrangements as depicted in the upper panels of Fig. 6. The corresponding total energies of the three cases provide the estimation of the exchange interaction parameters between the nearest-neighbor (NN) couplings J1 and the next-NN (NNN) couplings J260,61 as illustrated in the lower panels of Fig. 6. To evaluate the exchange coupling, we consider the calculated total energy of the VX2 monolayer based on GGA-PBE functional as the sum of the NN spin-spin interactions in terms of the spin Heisenberg model,

Figure 6. Upper panels: Schematic view of the three magnetic configurations: the ferromagnetic EFM, antiferromagnetic EAF, and collinear antiferromagnetic Ecol spin arrangements.

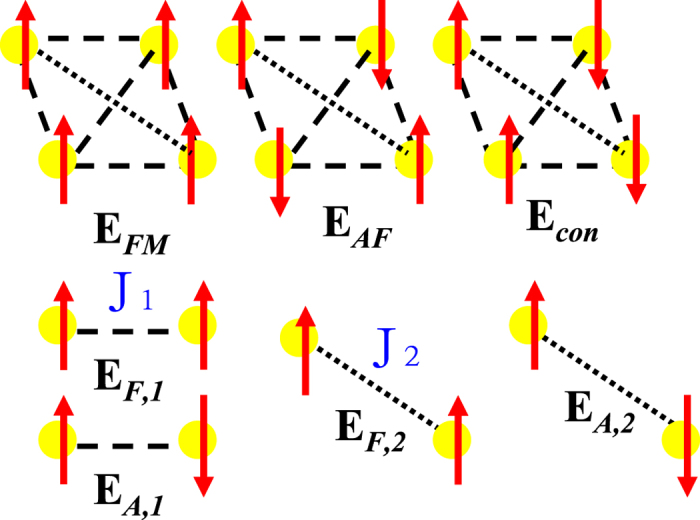
Figure 6

Open in a new tab

Lower panels: Schematic plot of the exchange parameters J1 and J2, magnetic bond energies EF1 and EA1 between the nearest V-V moments, and EF2 and EA2 between the next-nearest V-V moments.

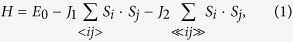graphic file with name srep32625-m7.jpg

where <ij> and ≪ij≫ are respectively the summation over the NN and NNN V site i and site j, and Si (Sj) is the unit vector representing the direction of the local magnetic moment at site i(j). J > 0 is assumed for the FM interaction, and J < 0 is assumed for the AFM interaction. The constant E0 contains all spin-independent interactions.

To determine the values of J1 and J2, one needs to evaluate the energy difference between a pair of nearest V-V moments in parallel (EF1) and antiparallel (EA1) alignments,

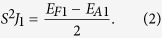graphic file with name srep32625-m8.jpg

The EF1 is not necessary to be equal to −EA1 since the energy of the reference state may not be located exactly at the middle of the energy between the EF1 and EA1. Meanwhile S2J2 also evaluates the energy difference between a pair of the next-nearest V-V moments in parallel (EF2) and antiparallel (EA2) arrangements,

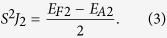graphic file with name srep32625-m9.jpg

The total energies of the ferromagnetic (EFM), antiferromagnetic (EAF), and collinear antiferromagnetic (Ecol) states with respect to the nonmagnetic state (ENM) can be expressed by the following equations:

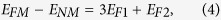graphic file with name srep32625-m10.jpg
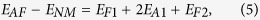graphic file with name srep32625-m11.jpg
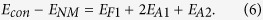graphic file with name srep32625-m12.jpg

By solving the above equations with calculated total energies of the related spin states, we obtain the exchange interaction parameters J1 and J2 for VX2 monolayers as listed in Table 4. As shown the ferromagnetic interactions between two NN V spins are very strong, especially in VSe2 and VTe2. The exchange coupling parameter J1 = 38.8(44.3) meV of VSe2(VTe2) is about twice larger compared with 23.8 meV of VS2. On the other hand, the negative J2 values of VX2 show the antiferromagnetic coupling between two next-nearest-neighboring V spins with the values being 2~3 order of magnitude smaller than the NN couplings. Thus summation over all the J1 and J2 would give rise to the ferromagnetic ground state in the 2D VX2 monolayers.

Table 4. Calculated exchange interaction parameters J1 and J2 and the Curie temperatures of VS2, VSe2, and VTe2 monolayers.

  VS2 VSe2 VTe2
J1 (meV) 23.8 38.8 44.3
J2 (meV) −0.05 −0.002 −0.001
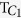Inline graphic (K) 138 223 225
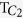Inline graphic (K) 369 600 686
β 0.423 0.393 0.374
TC (K) 292 472 553
Open in a new tab

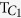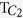Inline graphic and Inline graphic are estimated from the standard mean field expressions. TC is calculated from the Monte Carlo simulations with β the critical exponent.

With the exchange interaction parameter J available, the Curie temperature (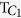Inline graphic) can then be estimated by J/kB as listed in Table 4. The ferromagnetic exchange coupling of VS2 monolayer gives rise to the 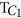Inline graphic of 138 K. This is reasonably close to the experimental observations that the ultrathin VS2 nanosheets with the averaged thickness of ~8 nm shows clear low-temperature ferromagnetism with TC = 72 K, while the Tc is decreased to 10 K for VS2 nanoflowers with the average thickness of ~150 nm62. Our calculations also show the suppressed ferromagnetic couplings and decreasing TC upon increasing the number of layers. The calculated TC of the bilayer VS2 is 124 K which is less than the 138 K of VS2 monolayer. More importantly, the TC of VSe2 and VTe2 monolayers are respectively 223 K and 225 K, which are much closer to the room temperature. It is noted previously that the exchange gaps of VSe2 and VTe2 can be enhanced by tensile strains, which implies stronger exchange interaction parameters and hence higher Curie temperatures than the strain free ones. As a result, the Tc could be even closer to the room temperature by appropriate manipulations.

For comparison, we also estimate the Curie temperature (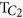Inline graphic) via a simplified method63, 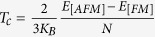Inline graphic, where N is the number of magnetic ions in the unit cell. The Curie temperature 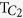Inline graphic estimated from the calculated total energy differences between the AFM and FM phases of VX2 monolayers are listed in Table 4. As shown the TC values of VX2 monolayers obtained in this way are much higher than the previous ones: all the estimated Inline graphic are above the room temperature. Particularly the Curie temperatures of VSe2 and VTe2 monolayers could be over 600 K.

To accurately calculate the Curie temperature beyond the simple mean field estimations (Inline graphic and Inline graphic), we have adopted the Monte Carlo simulations for the magnetizations as functions of the temperature. With the calculated exchange parameters J1 and J2, we simulate the Curie temperature of the monolayer system based on the Monte Carlo metropolis simulations using the VAMPIRE software package64,65. The simulated system for all materials consists of a platelet with 11172 spins with a hexagonal crystal structure. The spins are initialized along the [100] crystal direction and thermalized for 10000 equilibrium steps followed by 50000 averaging steps to calculate the thermal equilibrium magnetization at each temperature. The Monte Carlo simulations use the Hinzke-Nowak combinational algorithm66 for fast relaxation to thermal equilibrium. The simulated temperature dependent magnetization for VSe2, VS2 and VTe2 are shown in Fig. 7.

Figure 7. Monte Carlo simulation for the magnetization as functions of the temperature.

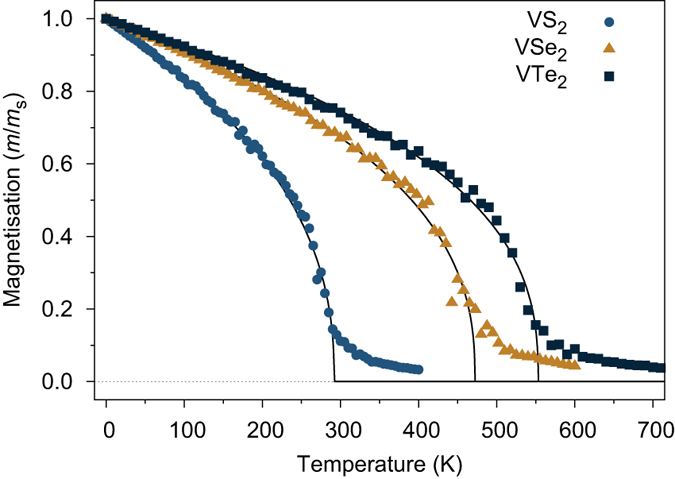
Figure 7

Open in a new tab

The temperature dependent magnetization is fitted using the Curie-Bloch equation in the classical limit67

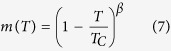graphic file with name srep32625-m21.jpg

where T is the temperature, TC is the Curie temperature and β ~ 0.36 is the critical exponent. The fitted Curie temperatures TC are summarized in Table 4. The Monte Carlo simulations predict TC values of 291 K, 472 K, and 553 K for VSe2, VS2 and VTe2 monolayer, respectively. All of them are close to or higher than the room temperature, which demonstrates excellent evidence for room temperature 2D magnetic semiconductors of VX2 monolayers. In comparison with previous estimations on the TC values from the standard mean field expression, the Monte Carlo results are in general slightly higher than the 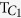Inline graphic68 while lower then 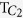Inline graphic69,70 estimated from the mean field expressions.

Conclusions

We present theoretical investigations on a new type 2D ferromagnetic semiconductor: VX2 (X = S, Se and Te) monolayer based on GGA, GGA + U, GW, as well as HSE calculations. The standard GGA scheme gives indirect exchange energy gaps of 0.046, 0.225, and 0.201 eV for VS2, VSe2, and VTe2 monolayers, respectively, with integer magnetic moment of 1 μB/f.u. for all the three cases. The 100% spin polarized bands around EF are mainly from the 3d local moments in the V ions. The weak spin-orbit interaction in V 3d electrons plays insignificant roles in the energy gaps. The MAE calculations show that the easy axes are parallel to the layers for all the three cases. The on-site Coulomb interaction U = 2 eV enhances the energy gaps by about 0.4 eV. The GW approximation corrected band gaps are 1.3, 1.2, and 0.7 eV for VS2, VSe2, and VTe2 monolayers, respectively. They agree very well with the HSE energy gaps of 1.1, 1.2, and 0.6 eV, respectively. The gap size and even the metal-insulator transitions are tunable via controlling the ambient parameters such as changing the number of layers and/or applying the strain. The theoretical evaluation on the exchange coupling constants reveals the dominant ferromagnetic coupling. Moreover our Monte Carlo simulations illustrate very high Curie temperatures of 292, 472, and 553 K for VS2, VSe2, and VTe2 monolayers, respectively. They are nearly or well beyond the room temperature. Our study demonstrates the great potential of the VX2 monolayers in spintronics and invites further experimental investigations on these ultrathin newtype room temperature 2D ferromagnetic semiconductors.

Additional Information

How to cite this article: Fuh, H.-R. et al. Newtype single-layer magnetic semiconductor in transition-metaldichalcogenides VX2 (X= S, Se and Te). Sci. Rep. 6, 32625; doi: 10.1038/srep32625 (2016).

Acknowledgments

The authors thank Peng-Jen Chen and Ke-Chuan Weng for fruitful discussions. H.R.Fuh thanks the computer and information networking center in National Taiwan University, Taiwan for the computational support. C.R.Chang acknowledges the financial support from the MOST, Taiwan under the Grant Numbers MOST 104-2112-M002-007-MY3 and MOEA 102-EC-17-A-01-S1-219. Y.K.Wang thanks Chun-Yen Chang for the financial support received from the Science Education Center. H.T.Jeng acknowledges the supports from NCTS, Ministry of Science and Technology, Academia Sinica, and National Tsing Hua University, Taiwan.

Footnotes

Author Contributions H.-R.F. performed the calculations, did the analysis, and prepared the manuscript. C.-R.C. and Y.-K.W. examined the calculations and the analysis. R.F.L.E. and R.W.C. performed the Monte Carlo TC simulations. H.-T.J. conceived and supervised the project. All authors reviewed the manuscript.

References

  1. Montoya E., Heinrich B. & Girt E. Quantum Well State Induced Oscillation of Pure Spin Currents in Fe/Au/Pd(001) Systems. Phys. Rev. Lett. 113, 136601 (2014). [DOI] [PubMed] [Google Scholar]
  2. Heinrich B. et al. Spin Pumping at the Magnetic Insulator (YIG)/Normal Metal (Au) Interfaces. Phys. Rev. Lett. 107, 066604 (2011). [DOI] [PubMed] [Google Scholar]
  3. Uchida K. I. et al. Observation of longitudinal spin-Seebeck effect in magnetic insulators, Appl. Phys. Lett. 97, 172505 (2010). [Google Scholar]
  4. Jaworski C. M. et al. Observation of the spin-Seebeck effect in a ferromagnetic semiconductor, Nature Mat. 9, 898 (2010). [DOI] [PubMed] [Google Scholar]
  5. Miao B. H., Huang S. Y., Qu D. & Chien C. L. Physical Origins of the New Magnetoresistance in Pt-YIG, Phys. Rev. Lett. 112, 236601 (2014). [DOI] [PubMed] [Google Scholar]
  6. Hahn C. et al., Comparative measurements of inverse spin Hall effects and magnetoresistance in YIG/Pt and YIG/Ta, Phys. Rev. B 87, 174417 (2013). [Google Scholar]
  7. Flipse J. et al. Observation of the spin Peltier effect for magnetic insulators. Phys. Rev. Lett. 112, 236601 (2014). [DOI] [PubMed] [Google Scholar]
  8. Hoffmann A. Spin Hall Effects in Metals. IEEE Trans. Magn. 49, 5172 (2013). [Google Scholar]
  9. Huang S. Y. et al. Comparative measurements of inverse spin Hall effects and magnetoresistance in YIG/Pt and YIG/Ta. Phys. Rev. Lett. 109, 107204 (2012).23005323 [Google Scholar]
  10. Chappert C., Fert A. & van Dau F. N. The emergence of spin electronics in data storage. Nature Mater. 6, 813–823 (2007). [DOI] [PubMed] [Google Scholar]
  11. Fert A. Nobel lecture: Origin, development, and future of spintronics. Rev. Mod. Phys. 80, 1517–1530 (2008). [DOI] [PubMed] [Google Scholar]
  12. Wolf S. A. et al. Spintronics: A Spin-Based Electronics Vision for the Future. Science. 294, 1488–1495 (2001). [DOI] [PubMed] [Google Scholar]
  13. Moodera J. S., Hao X., Gibson G. A. & Meservey R. Electron-Spin Polarization in Tunnel Junctions in Zero Applied Field with Ferromagnetic EuS Barriers. Phys. Rev. Lett. 61, 637 (1988). [DOI] [PubMed] [Google Scholar]
  14. Leclair P. et al. Large magnetoresistance using hybrid spin filter devices. Appl. Phys. Lett. 80, 625–627 (2002). [Google Scholar]
  15. Matthias B. T., Bozorth R. M. & Van Vleck J. H. Ferromagentic interaction in EuO. Phys. Rev. Lett. 7, 160 (1961). [Google Scholar]
  16. Kimura T. et al. Magnetocapacitance effect in multiferroic BiMnO3. Phys. Rev. B, 67, 180401 (2003). [Google Scholar]
  17. Rogado N. S., Li J., Sleight A. W. & Subramanian M. A. Magnetocapacitance and magnetoresistance near room temperature in a ferromagnetic semiconductor: La2NiMnO6, Advance Materials. 17, 2225–2227 (2005).
  18. Zhao K. et al. New diluted ferromagnetic semiconductor with Curie temperature up to 180 K and isostructural to the ‘122’ iron-based superconductors. Nature Communications. 4, 1442 (2013). [DOI] [PubMed] [Google Scholar]
  19. Hansen P., Witter K. & Tolksdorf W. Magnetic and magneto-optic properties of lead- and bismuth-substituted yttrium iron garnet films. Phys. Rev. B 27, 6608–6625 (1983). [DOI] [PubMed] [Google Scholar]
  20. Radisavljevic B., Radenovic A., Brivio J., Giacometti V. & Kis A. Single-Layer MoS2 Transistors. Nat. Nanotechnol. 6, 147–150 (2011). [DOI] [PubMed] [Google Scholar]
  21. Ma Y. D. et al. First-Principles Study of the Graphene@MoSe2 Heterobilayers. J. Phys. Chem. C. 115, 20237–20241 (2011). [Google Scholar]
  22. Splendiani A. et al. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 10, 1271–1275 (2010). [DOI] [PubMed] [Google Scholar]
  23. Marseglia E. A. Transition Metal Dichalcogenides and Their Intercalates. Int. Rev. Phys. Chem. 3, 177–216 (1983). [Google Scholar]
  24. Ataca C., Sahin H. & Ciraci S. Stable, Single-Layer MX2 Transition-Metal Oxides and Dichalcogenides in a Honeycomb-Like Structure. J. Phys. Chem. C. 116, 8983–8999 (2012). [Google Scholar]
  25. Chhowalla M. et al. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nature Chemistry. 5, 263–275 (2013). [DOI] [PubMed] [Google Scholar]
  26. Coleman J. N. et al. Two-Dimensional Nanosheets Producedby Liquid Exfoliation of Layered Materials. Science. 331, 568–571 (2011). [DOI] [PubMed] [Google Scholar]
  27. Zhu Z. Y., Cheng Y. C. & Schwingenschl U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B, 84, 153402 (2011). [Google Scholar]
  28. Kuc A., Zibouche N. & Heine T. Influence of quantum confinement on the electronic structure of the transition metal sulfide TS2. Phys. Rev. B 83, 245213 (2011). [Google Scholar]
  29. Xiao D., Liu G. B., Feng W. X., Xu X. D. & Yao W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett. 108, 196802 (2010). [DOI] [PubMed] [Google Scholar]
  30. Wang Q. H., Kalantar-Zadeh K., Kis A., Coleman J. N. & Strano M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012). [DOI] [PubMed] [Google Scholar]
  31. Feng J. et al. Metallic Few-Layered VS2 Ultrathin Nanosheets: High Two-Dimensional Conductivity for In-Plane Supercapacitors. J. Am. Chem. Soc. 133, 17832–17838 (2011). [DOI] [PubMed] [Google Scholar]
  32. Gao D. Q. et al. Ferromagnetism in ultrathin VS2 nanosheets. J. Mater. Chem. C. 1, 5909 (2013). [Google Scholar]
  33. Zhang H., Liu L. M. & Lau W. M. Dimension-dependent phase transition and magnetic properties of VS2. J. Mater. Chem. A. 11, 10821–10828 (2013). [Google Scholar]
  34. Ma Y. D. et al. Evidence of the Existence of Magnetism in Pristine VX2 Monolayers (X = S, Se) and Their Strain-Induced Tunable Magnetic Properties. Acs. Nano. 6, 1695–1701 (2012). [DOI] [PubMed] [Google Scholar]
  35. Perdew J. P., Burke K. & Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 477, 3865 (1996). [DOI] [PubMed] [Google Scholar]
  36. Blochl P. E. Projector augmented-wave method. Phys. Rev. B. 50, 17953 (1994); Kresse G., Joubert D., From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 59, 1758 (1999). [DOI] [PubMed] [Google Scholar]
  37. Kresse G. & Hafner J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B. 48, 13115 (1993). [DOI] [PubMed] [Google Scholar]
  38. Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comp. Chem. 27, 1787 (2006). [DOI] [PubMed] [Google Scholar]
  39. Solovyev I. V., Dederichs P. H. & Anisimov V. I. Corrected atomic limit in the local-density approximation and the electronic structure of d impurities in Rb. Phys. Rev. B 50, 16861 (1994). [DOI] [PubMed] [Google Scholar]
  40. Liechtenstein A. I., Anisimov V. I. & Zaane J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 52, R5467 (1995). [DOI] [PubMed] [Google Scholar]
  41. Shishkin M. & Kresse G. Implementation and performance of the frequency-dependent GW method within the PAW framework. Phys. Rev. B 74, 035101 (2006). [Google Scholar]
  42. Shishkin M. & Kresse G. Self-consistent GW calculations for semiconductors and insulators. Phys. Rev. B 75, 235102 (2007). [DOI] [PubMed] [Google Scholar]
  43. Onida G., Reining L. & Rubio A. Electronic excitations: density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 74, 601 (2002). [Google Scholar]
  44. Komsa H. P. & Krasheninnikov A. V. Effects of confinement and environment on the electronic structure and exciton binding energy of MoS2 from first principles. Phys. Rev. B 86, 241201(R) (2012). [Google Scholar]
  45. Hüser F., Olsen T. & Thygesen K. S. How dielectric screening in two-dimensional crystals affects the convergence of excited-state calculations: Monolayer MoS2, Phys. Rev. B 88, 245309 (2013). [Google Scholar]
  46. Heyd J., Scuseria G. E. & Ernzerhof M. J. Chem. Phys. 118, 8207 (2003), ibid 124, 219906 (2006). [Google Scholar]
  47. Feng J. et al. Giant moisture responsiveness of VS2 ultrathin nanosheets for novel touchless positioning interface. Adv. Mater. 24, 1969 (2012). [DOI] [PubMed] [Google Scholar]
  48. Dungey K. E., Curtis M. D. & Penner-Hahn J. E. Structural Characterization and Thermal Stability of MoS2 Intercalation Compounds. Chem. Mater. 10, 2152 (1998). [Google Scholar]
  49. Alexiev V., Prins R. & Weber T. Ab initio study of MoS2 and Li adsorbed on the (1010) face of MoS2. Phys. Chem. Chem. Phys. 2, 1815 (2000). [Google Scholar]
  50. Eda G. et al. Coherent Atomic and Electronic Heterostructures of Single-Layer MoS2. ACS Nano. 6, 7311 (2012). [DOI] [PubMed] [Google Scholar]
  51. Boscher N. D., Blackman C. S., Carmalt C. J., Parkin I. P. & Prieto A. G. Atmospheric pressure chemical vapour deposition of vanadium diselenide thin films. Appl. Surf. Sci. 253, 6041–6046 (2007). [Google Scholar]
  52. Guzman R., Lavela P., Morales J. & Tirado J. L. VSe2−ySy electrodes in lithium and lithium-ion cells. J. Appl. Electrochem. 27, 1207 (1997). [Google Scholar]
  53. Thompson A. H., Scanlon J. C. & Symon C. R. The Electrochemical Reaction of Li with Vse2 and Implications on the Ionicity of Intercalation Compounds. Solid State Ionics 1, 47 (1980). [Google Scholar]
  54. Vinokurov A. A., Tyurin A. V., Emelina A. L., Gavrichev K. S. & Zlomanov V. P. Thermodynamic properties of VTe2. Inorganic Materials. 45, 480–485 (2009). [Google Scholar]
  55. Abdul Wasey A. H. M., Chakrabarty S. & Das G. P. Quantum size effects in layered VX2 (X = S, Se) materials: Manifestation of metal to semimetal or semiconductor transition. Journal of Applied Physics. 117, 064313 (2015). [Google Scholar]
  56. Zhuang H. L. & Hennig R. G. Stability and magnetism of strongly correlated single-layer VS2. Phys. Rev. B 93, 054429 (2016). [Google Scholar]
  57. Fang C. M., Koster R. S., Li W. F. & Van Huis M. A. Predicted stability, structures, and magnetism of 3d transition metal nitrides: the M4N phases. RSC Adv. 4, 7885 (2014). [Google Scholar]
  58. Stoner E. C. Proc. R. Soc. London, Ser. A. Collective Electron Ferromagnetism. II. Energy and Specific Heat. 169, 339 (1939). [Google Scholar]
  59. Gunnarsson O. Band model for magnetism of transition metals in the spin-density-functional formalism. J. Phys. F: Metal Phys. 7, 4 (1976). [Google Scholar]
  60. Sato K., Dederics P. H. & Katayama-Yoshida H. Curie temperatures of III-V diluted magnetic semiconductors calculated from first principles. Europhys. Lett. 61, 403–408 (2003). [Google Scholar]
  61. Ma F., Lu Z. Y. & Xiang T. Arsenic-bridged antiferromagnetic superexchange interactions in LaFeAsO. Phys. Rev. B 78, 224517 (2008). [Google Scholar]
  62. Zhong M. Z. et al. Ferromagnetismin VS2 nanostructures:Nanoflowersversus ultrathinnanosheets. Materials Letters 124, 282 (2014). [Google Scholar]
  63. Hynninen T., Raebiger H., von Boehm J. & Ayuela A. High Curie temperatures in (Ga, Mn) N from Mn clustering. Appl. Phys. Lett. 88, 122501 (2006). [Google Scholar]
  64. Evans R. F. L. et al. Atomistic spin model simulations of magnetic nanomaterials. J. Phys. Condens. Matter 26, 103202 (2014). [DOI] [PubMed] [Google Scholar]
  65. Evans R. F. L. VAMPIRE software package version 4.0, York, UK. URL http://vampire.york.ac.uk (2016).
  66. Hinzke D. & Nowak U. Monte Carlo simulation of magnetization switching in a Heisenberg model for small ferromagnetic particles. Comput. Phys. Commun. 121–122, 334 (1999). [Google Scholar]
  67. Evans R. F. L., Atxitia U. & Chantrell R. W. Quantitative simulation of temperature-dependent magnetization dynamics and equilibrium properties of elemental ferromagnets Phys. Rev. B 91, 144425 (2015). [Google Scholar]
  68. Hynninen T., Raebiger H., von Boehm J. & Ayuela A. High Curie temperatures in (Ga, Mn) N from Mn clustering. Appl. Phys. Lett. 88, 122501 (2006). [Google Scholar]
  69. Garanin D. A. Self-consistent Gaussian approximation for classical spin systems: Thermodynamics. Phys. Rev. B 53, 11593 (1996). [DOI] [PubMed] [Google Scholar]
  70. Muthuselvam I. P. et al. Magnetic Orderings in Li2Cu(WO4)2 with Tungstate-Bridged Quasi-1D Spin-1/2 Chains 54. Inorg. Chem. 54, 43034309 (2015). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES