Skip to main content
PMC home page
Acta Crystallographica Section D: Structural Biology logoLink to Acta Crystallographica Section D: Structural Biology
. 2016 Aug 31;72(Pt 9):1062–1072. doi: 10.1107/S2059798316012225

Improved ligand geometries in crystallographic refinement using AFITT in PHENIX

Pawel A Janowski a,b, Nigel W Moriarty c, Brian P Kelley d, David A Case a,b, Darrin M York a,b, Paul D Adams c,e, Gregory L Warren f,*
PMCID: PMC5013598  PMID: 27599738

A method for the more accurate refinement of small molecules and ligands in biomolecular structures is provided. Improved ligand geometry is obtained via an all-atom molecular-mechanics force field.

Keywords: macromolecular refinement, ligands, geometry restraints, PHENIX, AFITT

Abstract

Modern crystal structure refinement programs rely on geometry restraints to overcome the challenge of a low data-to-parameter ratio. While the classical Engh and Huber restraints work well for standard amino-acid residues, the chemical complexity of small-molecule ligands presents a particular challenge. Most current approaches either limit ligand restraints to those that can be readily described in the Crystallographic Information File (CIF) format, thus sacrificing chemical flexibility and energetic accuracy, or they employ protocols that substantially lengthen the refinement time, potentially hindering rapid automated refinement workflows. PHENIX–AFITT refinement uses a full molecular-mechanics force field for user-selected small-molecule ligands during refinement, eliminating the potentially difficult problem of finding or generating high-quality geometry restraints. It is fully integrated with a standard refinement protocol and requires practically no additional steps from the user, making it ideal for high-throughput workflows. PHENIX–AFITT refinements also handle multiple ligands in a single model, alternate conformations and covalently bound ligands. Here, the results of combining AFITT and the PHENIX software suite on a data set of 189 protein–ligand PDB structures are presented. Refinements using PHENIX–AFITT significantly reduce ligand conformational energy and lead to improved geometries without detriment to the fit to the experimental data. For the data presented, PHENIX–AFITT refinements result in more chemically accurate models for small-molecule ligands.

1. Introduction  

Structural knowledge is fundamental to our understanding of biomolecular function in drug-discovery and drug-optimization efforts. X-ray crystallography remains the pre-eminent method for obtaining detailed structural information about molecules. Continued advances in data collection and processing, model building and structure refinement have gone a long way towards making crystallography a semi-automated, reliable technique for high-throughput structural biology. In the course of crystallographic structure solution, the process of refinement is used to optimize the atomic coordinates against the experimental data. However, because of the low data-to-parameter ratio in a typical experiment, additional a priori knowledge must be introduced into the optimization algorithm to make reliable model generation tractable. Usually, this additional knowledge is in the form of stereochemical restraints for bond lengths and angles and steric exclusions as well as additional restraints for dihedrals, chirality and other geometry restraints.

For standard biomolecular residues (proteins and nucleic acids), most modern refinement programs base these restraints on the so-called Engh and Huber restraints developed in 1991 (Engh & Huber, 1991 ▸) from a survey of small-molecule crystal structures and with later corrections added in 1996 for nucleic acids (Parkinson et al., 1996 ▸) and in 2001 (Engh & Huber, 2001 ▸) for amino-acid residues. Engh and Huber restraints function reasonably well for standard residues, but even in this case deficiencies have been exemplified (Davis et al., 2003 ▸; Moriarty et al., 2014 ▸; Priestle, 2003 ▸; Touw & Vriend, 2010 ▸). On the other hand, modeling of small-molecular ligands presents a particular challenge owing to their more complex chemistry, conformations and energetics. Thus, small-molecule ligands can be inaccurately modeled by the standard set of restraints (Davis et al., 2003 ▸; Kleywegt et al., 2003 ▸; Kleywegt & Jones, 1998 ▸; Moriarty et al., 2014 ▸; Priestle, 2003 ▸; Touw & Vriend, 2010 ▸). In fact, recent studies suggest that as many as 60% of the structures deposited in the Protein Data Bank (PDB; Berman et al., 2000 ▸, 2003 ▸) may contain questionable ligand conformations (Liebeschuetz et al., 2012 ▸; Pozharski et al., 2013 ▸).

Significant effort has been placed into developing tools for the accurate generation of ligand restraints in crystallographic models. Some (Davis et al., 2003 ▸; Lebedev et al., 2012 ▸; Moriarty et al., 2009 ▸; Schüttelkopf & van Aalten, 2004 ▸; Smart et al., 2012 ▸; Wlodek et al., 2006 ▸) employ sophisticated approaches to derive the same type of stereochemical restraints as those used by Engh and Huber for standard residues. In other words, these restraints must conform to the standard Crystallographic Information File (CIF) restraint dictionary format provided to the restraint program (Brown & McMahon, 2002 ▸; Hall et al., 1991 ▸, Vagin et al., 2004 ▸). Other approaches focus on more accurate ligand representation through the use of more elaborate protocols using force fields, semi-empirical or quantum methods.

The former approaches suffer from a potentially too simplistic representation of the ligand by using the restraint categories found in the standard restraint CIF format that insufficiently models or wholly ignores energetic effects such as electrostatics and dispersion forces. The latter approaches are often complicated to use, requiring multiple additional steps from the user. They are therefore difficult to integrate into an automated workflow and the speed requirements of many modern-day high-throughput laboratories such as those involved in pharmaceutical drug discovery (Borbulevych et al., 2016 ▸; Borbulevych, Plumley et al., 2014 ▸).

We present a more accurate but efficient structural modeling of small molecules in the refinement process using the combined power of two crystallographic applications. PHENIX (Adams et al., 2010 ▸) is the widely popular suite of software for integrated crystallography that includes the phenix.refine (Afonine et al., 2012 ▸) application for refinement; AFITT (v.2.4.0.4; http://www.eyesopen.com/afitt; Wlodek et al., 2006 ▸) is OpenEye’s package for automated ligand placement in real-space density. AFITT models ligand conformation and stereochemistry with the well regarded Merck Molecular Mechanics Force Field (MMFF; Halgren, 1996a ▸,b ▸,c ▸,d ▸, 1999 ▸; Halgren & Nachbar, 1996 ▸), but until now has written MMFF-derived restraints to the standard CIF format restraint files, sometimes to the detriment of the ligand conformation. By seamlessly integrating AFITT with PHENIX, the user gains the powerful advantage of a full molecular-mechanics representation of the ligand while being able to maintain the same efficient refinement workflow. Furthermore, alternating steps of standard macromolecular refinement followed by highly accurate ligand refinement is no longer necessary as both sets of restraints are applied simultaneously.

Here, we provide a comparison of refinements on a test set of 189 ligands and 304 ligand instances. We have chosen to only compare refinement using AFITT-derived CIF restraint dictionaries versus obtaining the ligand geometry gradients in refinement directly from AFITT (PHENIX–AFITT). Thus, our comparison is not complicated by differences in potential functions and target values for the methods used by various other ligand restraint-file generation and modeling methods (Borbulevych, Moriarty et al., 2014 ▸; Borbulevych, Plumley, et al., 2014 ▸; Davis et al., 2003 ▸; Fu et al., 2011 ▸; Lebedev et al., 2012 ▸; Moriarty et al., 2009 ▸; Schüttelkopf & van Aalten, 2004 ▸; Smart et al., 2010 ▸, 2012 ▸; Yu et al., 2005 ▸). Instead, differences hinge only on the improvement gained by representing the ligand with the full molecular-mechanics force field during the course of refinement. PHENIX–AFITT refinements yield the expected improved lower-energy small-molecule structures while maintaining the same degree of agreement with experiment. Thus, a PHENIX–AFITT refinement provides the user with a fully integrated ligand refinement that ensures accurate modeling of ligand conformation and chemistry. The implementation of AFITT in PHENIX is versatile, easy to use and powerful. Refinements can include different types of ligands and multiple instances of each ligand type. Support for ligands with full or partial alternate conformations is fully integrated, as is refinement of ligands covalently bound to the macromolecule.

2. Methods  

Phenix.refine (Afonine et al., 2012 ▸) optimizes a crystal structure via a series of repeated cycles. During each cycle a series of parameters of the user’s choosing are optimized. These usually include the atomic coordinates and the isotropic atomic displacement parameters, but can also include, for example, translation–libration–screw parameters, bulk-solvent scaling and anisotropic atomic displacement parameters. Each optimization is conducted by minimizing a residual function of the model against the experimental data using a maximum-likelihood approach.

AFITT (Wlodek et al., 2006 ▸) is a package developed by OpenEye Scientific Software for small-molecule real-space fitting in biomolecular crystallography. It uses a combination of a real-space electron-density shape-matching algorithm and a molecular-mechanics force field to fit small ligands into density while maintaining accurate chemical geometry. AFITT uses an ‘adiabatic’ method to find the best relative weight between these two components. It can be run without a solvent model or using either the Sheffield (Grant et al., 2007 ▸) or the Poisson–Boltzmann scheme (Grant et al., 2001 ▸) to model solvation effects. AFITT uses the Merck Molecular Mechanics Force Field (MMFF94; Halgren, 1996a ▸,b ▸,c ▸,d ▸, 1999 ▸; Halgren & Nachbar, 1996 ▸). This force field was designed to reproduce ab initio accuracy in a broad range of chemical functionality and has been shown to produce satisfactory results with the small molecules typically encountered in biomolecular crystallography (Fu et al., 2011 ▸; Gundertofte et al., 1996 ▸; Halgren, 1999 ▸).

In the case of reciprocal-space atomic coordinate refinement, the PHENIX refinement target function has the form

2.

where E X-ray is the residual of the structure factors, E geometry is the residual owing to the Engh and Huber restraints (Engh & Huber, 1991 ▸, 2001 ▸) and w is a weighting factor. If a ligand is present, the E geometry term can further be divided,

2.

where E ligand_bonded represents the so-called bonded terms in the geometry restraints that include bonds, angles, torsion angles, chiral and planar restraints. E ligand_nonbonded represents the nonbonded terms that in the case of Engh and Huber are the atomic steric overlap restraints. For the AFITT-generated CIF restraints the bond and angle target values are the MMFF94 target values. The torsion-angle values are taken from the ligand conformation and periodicity assigned by analysis of the MMFF94 functional for each torsion. On the other hand, during the PHENIX–AFITT refinement introduced here, the last term in (3) is replaced by a residual calculated by AFITT,

2.

The implementation in PHENIX combines the phenix.refine refinement scheme and optimization algorithm while using AFITT to obtain the E ligand_bonded part of the residual. The AFITT E ligand_bonded gradient consists of stretch, stretch–bend, bend, torsion, out-of-plane, van der Waals and Coulomb terms. The AFITT gradient is applied only to ligands specified by the user. The current implementation does not take into account protein–ligand interaction terms other than steric overlap. It is important to note that there are no equivalent terms in the geometry restraint CIF file method for attractive van der Waals (present in the van der Waals term ) or electrostatics (present in the Coulomb term).

A PHENIX–AFITT refinement is invoked with phenix.refine mymodel.pdb mymodel.mtz myligand.cif use_afitt=True afitt.ligand_file=myligand.cif afitt.ligand_names=BCL.

This implementation automatically searches for all instances of the ligand specified by the user (bacteriochlorophyll A in the example above) and uses AFITT to calculate the geometry gradients for these instances. More than one type of ligand can be included. The required restraints CIF dictionary file specifies the required atom type and bond topology for AFITT, but not the actual restraint force constants, which are calculated internally by AFITT. This implementation also accounts for alternate conformations of ligand atoms and ligands covalently bound to the macromolecule. A heuristically determined weight, based on R free and ligand energy, of 10 is placed on the E AFITT ligand_bonded term by default, but the user also has the option of modifying this weight. Additionally, there is a simple command-line tool to quickly obtain MMFF ligand energies from a given PDB coordinate file.

The root-mean-square deviation (r.m.s.d.) values reported were calculated using OpenEye’s r.m.s.d. (OERMSD) method found in OEChem (v.2015.October; http://www.eyesopen.com/oechem-tk). All r.m.s.d. values were calculated for heavy atoms only, with no ligand overlay, and accounting for automorphisms, which is a form of chemical symmetry that takes into account the atoms in the ligand that can be relabelled without changing the chemical structure of the ligand, e.g. carboxylate O atoms are equivalent. The Python script used to calculate the values (rmsd.py) is included along with all of the other data for download at http://www.phenix-online.org/phenix_data/Phenix_AFITT/.

3. Results  

Testing of the implementation of AFITT in PHENIX was performed using a set of 189 protein–ligand PDB structures taken from the Iridium data set (Warren et al., 2012 ▸). This set contains a chemically varied and largely drug-like set of ligands. While this data set is an annotated and curated set, we have chosen to use structures that were annotated as not being highly reliable. Some structures contained multiple small molecules and/or multiple instances, resulting in 304 small-molecule instances in total. Because many of the structures lacked reflection test sets (to calculate R free; Brünger, 1993 ▸), a new test set of reflections was assigned and each model was refined using phenix.refine with the default strategy for ten macrocycles to remove ‘memory’ of the original test set. Next, each structure was refined for a further five macrocycles using the default strategy and with the ligand modeled either using an AFITT-derived CIF dictionary file (hereafter referred to as ‘AFITT–CIF’ refinement) or with the new PHENIX–AFITT implementation. This focused strategy, as opposed to comparing results with another non-AFITT ligand-restraint tool, allowed rigorous testing of the benefits of implementing ligand optimization in the way advocated here; that is, by applying a full molecular-mechanics treatment of the ligand but in a manner fully integrated with the refinement optimizer.

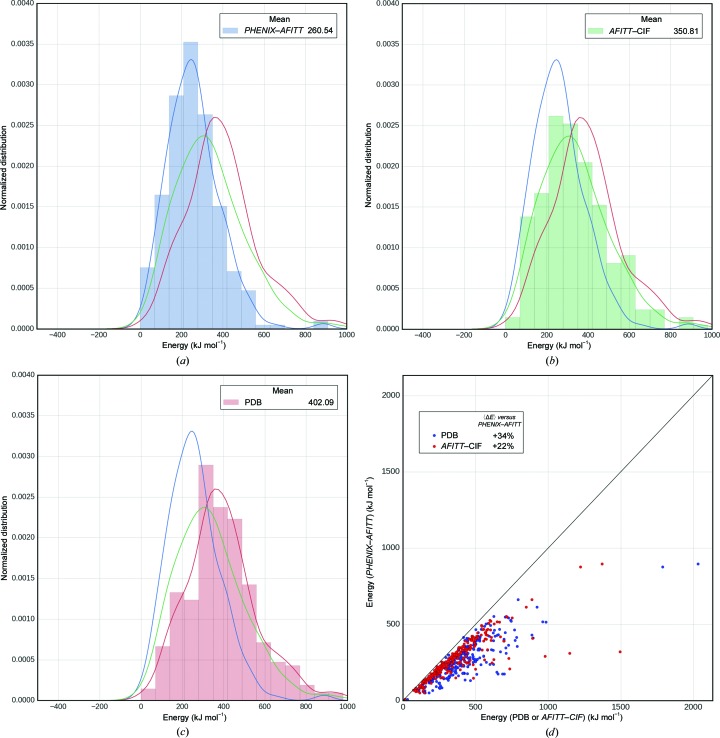
The PHENIX–AFITT method is expected to produce ligand conformations with lower MMFF94 ligand energies as MMFF94 is part of the target function. PHENIX–AFITT refinement produces ligand models with significantly lower ligand energies, both compared with the original deposited coordinates and with refinement using an MMFF-based CIF restraints file (Fig. 1 ▸). For our test set, the mean post-refinement ligand energy was 402.1 ± 210.1 kJ mol−1 for the set of deposited structures, 350.8 ± 199.9 kJ mol−1 for the AFITT–CIF refined structures and 260.5 ± 128.4 kJ mol−1 for the PHENIX–AFITT refined structures. This signifies an average reduction of ligand conformational energies of 34% versus the deposited conformation in the PDB and 22% versus refinement using MMFF-derived CIF restraint dictionaries. Fig. 1 ▸(d) shows scatter plots of the PHENIX–AFITT refined ligand energies versus either the deposited PDB or AFITT–CIF refined energies on a per-model basis. It is apparent that PHENIX–AFITT refinement results on average in models with a significant and in most cases a substantial reduction of ligand conformational energy. Statistical significance was measured using a dependent paired t-test (rel t-test; Student, 1908 ▸) and a two-sample distribution Kolmogorov–Smirnov test (ks_2samp; Kolmogorov, 1933 ▸; Pearson & Hartley, 1972 ▸; Smirnov, 1948 ▸). The Cohen d (Cohen, 1988 ▸) was used to test whether the difference of the means was substantial. For PDB-deposited versus PHENIX–AFITT the rel t-test p was 10−57, the ks_2samp p was 10−25 and the Cohen d was 0.81 or large. Thus, when comparing the MMFF energy of ligand conformations from PHENIX–AFITT refinements and deposited structures, PHENIX–AFITT generates both significantly and substantially lower energy conformations. For PHENIX–AFITT versus AFITT–CIF the rel t-test p was 10−33, the ks_2samp p was 10−9 and the Cohen d was 0.54 or moderate. While PHENIX–AFITT generates significantly lower energy conformations versus AFITT–CIF, the difference is only moderate in size. Last, the greatest energy reduction using AFITT in PHENIX (the distance below the identity line) tends to occur in the ligands with highest starting energies. In other words, the higher the initial conformational energy the more a PHENIX–AFITT refinement is able to reduce it.

Figure 1.

Figure 1

Open in a new tab

Ligand conformational energies from PDB-deposited models, AFITT–CIF refinement and PHENIX–AFITT refinement. (a, b, c) Histograms for PHENIX–AFITT (a), AFITT–CIF (b) and PDB-deposited (c) energies with kernel density estimates (KDE) of the distributions for the full set of test ligand energies. Means of each set of ligand conformation energies are shown in the legend. (d) A scatter plot comparing the conformation energy of each ligand obtained from a PHENIX–AFITT refinement against either the deposited PDB model (blue dots) or the models after refinement with an MMFF-derived CIF dictionary file (red dots). The mean percentage reduction in energy from using the PHENIX–AFITT protocol is 34% versus the PDB conformations and 22% versus AFITT–CIF.

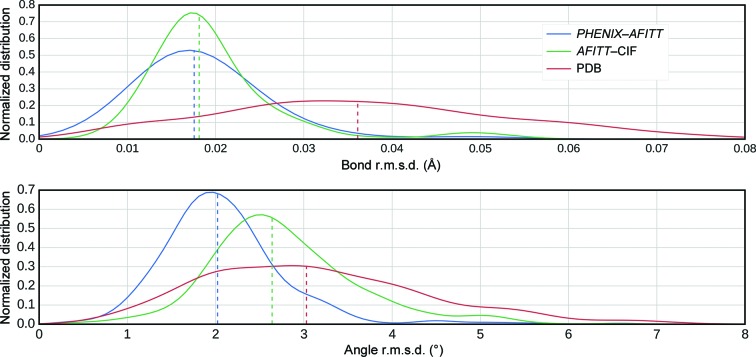
To further validate refinement quality, the Mogul software (Bruno et al., 2004 ▸) was used to assess the post-refinement ligand geometries. Mogul is a knowledge-based library derived from experimental small-molecule crystal geometries in the Cambridge Structural Database (CSD; Allen, 2002 ▸). Mogul (Bruno et al., 2004 ▸) has been shown to be an excellent independent evaluator of computationally derived geometries. The results (Fig. 2 ▸) show that both the PHENIX–AFITT refined and the AFITT–CIF refined geometries are significantly better than those found in the PDB and that PHENIX–AFITT geometries are better than AFITT–CIF geometries. The respective mean r.m.s.d. scores for bonds were 0.036 ± 0.017 Å for the deposited PDB set, 0.019 ± 0.007 Å for AFITT–CIF and 0.018 ± 0.016 Å for the PHENIX–AFITT protocol. For bond lengths, using a two-sample z-test, both PHENIX–AFITT and AFITT–CIF have significantly lower deviations from the CSD, with p = 0.0005 and p = 0.0009, respectively. The difference is substantial in both cases as measured by the Cohen d, where d = 1.6 (large) for deposited versus AFITT–CIF and d = 1.1 (large) for deposited versus PHENIX–AFITT. There is no statistically significant difference in the means between PHENIX–AFITT and AFITT–CIF as measured by the two-sample z-test (p = 0.39) and the Cohen d of 0.08 (trivial). However, if difference in the distribution is tested using ks_2samp there is a statistically significant difference in the distributions (p = 10−6) and this difference is visualized in the top panel of Fig. 2 ▸, where there is a large shoulder towards lower deviation for the PHENIX–AFITT curve. For angles, the respective mean difference was 3.11 ± 1.25° for the deposited PDB set, 2.77 ± 0.84° for AFITT–CIF and 2.09 ± 0.72° using PHENIX–AFITT. This is a statistically significant and in most cases substantial reduction in deviation, with z-test p values of p = 10−13 (Cohen d = 0.4 or moderate) for deposited versus AFITT–CIF, z-test p = 10−100 (Cohen d = 1.1 or large) for deposited versus PHENIX–AFITT and z-test p = 10−122 (Cohen d = 0.9 or large and ks_2samp p = 10−98) for AFITT–CIF versus PHENIX–AFITT. These data clearly show that PHENIX–AFITT refinements generate models with not only reduced conformational energies, as assessed by the MMFF force field, but more accurate bonds and angles when compared with small-molecule crystal geometries.

Figure 2.

Figure 2

Open in a new tab

Mogul validation of the PDB-deposited, AFITT–CIF refined and PHENIX–AFITT refined ligand conformations. The top panel shows the bond r.m.s.d. distribution in Å and the bottom panel shows the angle r.m.s.d. distribution in degrees. R.m.s.d. is relative to the Mogul library of ‘ideal’ bonds and angles.

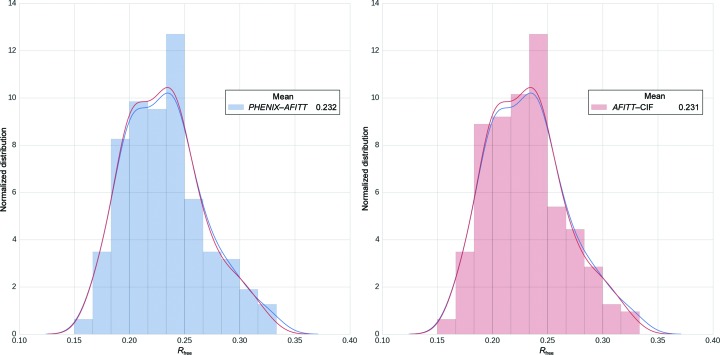
While significantly reducing ligand energies, PHENIX–AFITT refinements did not result in poorer agreement with experimental data both at the global and at the individual ligand-residue level. No differences in global fit measures such as R free were expected. The mean R free of the structures refined with AFITT–CIF was 0.231 ± 0.035, while for those refined with the PHENIX–AFITT protocol the mean R free was 0.232 ± 0.036 (Fig. 3 ▸). A pairwise comparison of PHENIX–AFITT and AFITT–CIF refinements yields a mean difference in R free between the two methods of 0.0012, which is a statistically significant difference as measured by a rel t-test p of 10−9, but is not significant or substantial as measured by a ks_2samp p of 0.995 or a Cohen d of 0.03 or trivial. Thus, on average AFITT–CIF results in a slightly lower R free, but this difference is very small (0.0012 on average). We found only one case with an R free difference greater than 0.01. This was the case of PDB entry 1ctr, which resulted in a ΔR free of 0.025. However, the starting model for PDB entry 1ctr is problematic in itself with 32% rotamer outliers, a clashscore of 50 and a MolProbity (Chen et al., 2010 ▸) score of 4.07. In addition, all low-resolution data beyond 6 Å are missing in the deposited structure factors. Thus, one might expect to see large R-factor fluctuations upon refinement using even slightly different protocols in this case.

Figure 3.

Figure 3

Open in a new tab

R free distributions and histograms after refining the test set using either AFITT–CIF (right) or the PHENIX–AFITT (left) protocol. Means of each distribution are shown in the legend.

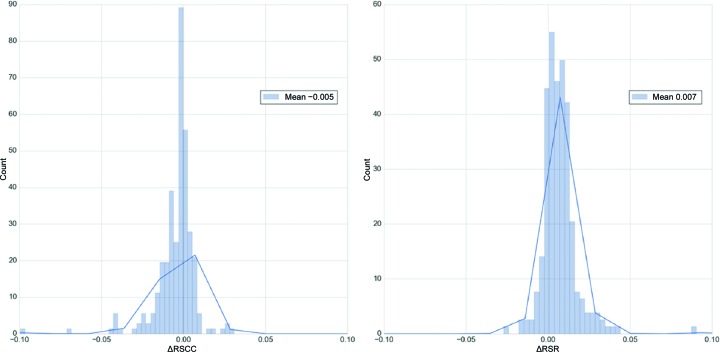
Ligand local fit to electron density was measured using the real-space correlation coefficient (RSCC) and real-space R factor (RSR) (Jones et al., 1991 ▸) calculated using the in-house program DCC (Yang et al., 2016 ▸) kindly provided by Huanwang Yang from the Protein Data Bank. The mean RSCC for AFITT–CIF was 0.944 ± 0.040 and that for PHENIX–AFITT was 0.939 ± 0.047. The mean RSCC pairwise difference was −0.005 (see Fig. 4 ▸), which is a statistically significant difference as measured by a rel t-test (p = 10−8), but not significant or substantial as measured by ks_2samp (p = 0.53) and a Cohen d of 0.12 or trivial. The mean RSR for AFITT–CIF was 0.125 ± 0.050 and that for PHENIX–AFITT was 0.132 ± 0.055. The mean pairwise difference of 0.007 (see Fig. 4 ▸) was again a statistically significant difference as measured by the rel t-test p of 10−17 but was not significant or substantial as measured by the ks_2samp p of 0.11 and a Cohen d of 0.14 or trivial. Thus, PHENIX–AFITT generates conformations with significantly lower conformational strain energy but with an equivalent fit to the data. However, the consistent slightly poorer numerical fits of the PHENIX–AFITT models might be an indication that the heuristic used to assess the default of weight of 10 placed on the E AFITT ligand_bonded gradient needs to be reassessed and a slightly lower default weight chosen.

Figure 4.

Figure 4

Open in a new tab

The difference distribution of the ligand RSCC (left) and RSR (right) for the AFITT–CIFF versus PHENIX–AFITT models. The mean difference for each distribution is shown in the legend.

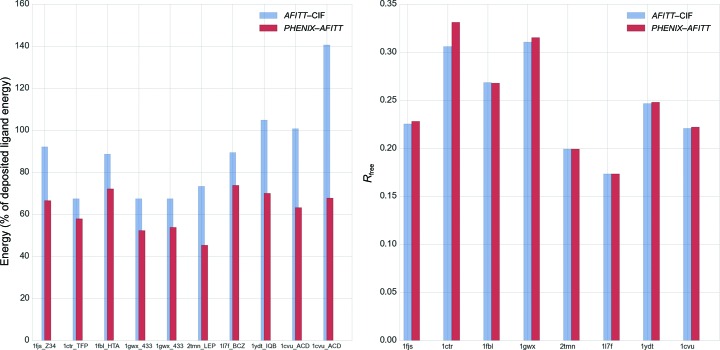
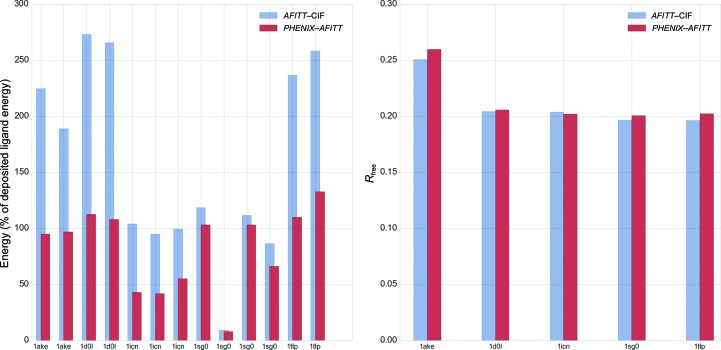
Fig. 5 ▸ shows a more detailed comparison of eight randomly selected structures from the test set with a total of ten ligands. As can be seen, PHENIX–AFITT refinement leads to significantly lower energies in all cases. In a few cases (for example the second ACD instance in PDB entry 1cvu) AFITT–CIF restraints lead to ligand energies that are much higher than even the deposited coordinates, while using AFITT directly in PHENIX gives the expected lower energies. At the same time, a comparison of R free, RSCC and RSR for the ligand shows that the fit to experimental data remains essentially the same between the two refinements. The structure with the highest R free difference in the entire data set, PDB entry 1ctr discussed previously, was included in the panel. PHENIX–AFITT can also handle ligands with alternate conformations. Fig. 6 ▸ shows a similar comparison of energies and R free factors for five PDB structures containing multiple ligands with alternate conformations. Analysis of these data for AFITT–CIF is complicated by the fact that only two of the deposited ligand conformations were modeled with alternate conformations (PDB entry 1ake copy 1 and 1icn). However, the conclusions for the PHENIX–AFITT models are similar in that these models have similar or substantially lower energy.

Figure 5.

Figure 5

Open in a new tab

Comparison of eight randomly selected PDB structures. The left panel shows energies obtained with AFITT–CIF refined and PHENIX–AFITT refined ligand restraints as a percentage of the deposited ligand energy. Labels provide the PDB code followed by the three-letter code for the ligand. Some PDB structures have more than one instance of a ligand. The right panel shows the R free obtained after refinement with Engh and Huber or AFITT geometry restraints on the ligands.

Figure 6.

Figure 6

Open in a new tab

Comparison of five PDB structures containing ligand instances with alternate conformations. It is important to note that only for PDB entries 1ake and 1icn were the deposited ligand conformations modeled as alternate conformations. All labels and statistics are as in Fig. 4 ▸.

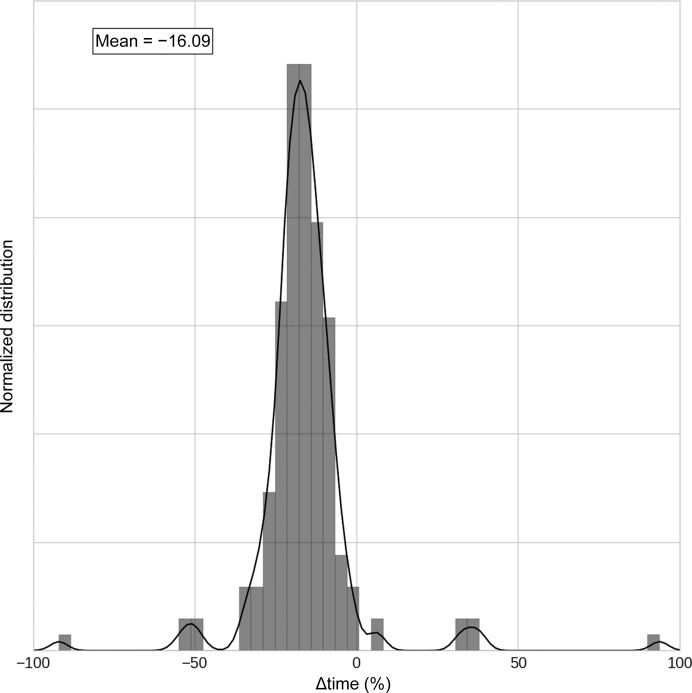
Structure refinement with the PHENIX–AFITT protocol is somewhat slower than refinement with a previously prepared CIF dictionary file. Fig. 7 ▸ presents a histogram of runtime differences between AFITT–CIF and PHENIX–AFITT refinement as a percentage of the AFITT–CIF runtime. In general, a PHENIX–AFITT refinement is slower by an average of 16% compared with the same refinement using a dictionary file with Engh and Huber-style restraints. Subsequent analysis has shown that most of the computational cost comes from a license check that is being performed for each gradient calculation. In addition, there were five structures with refinement times that were more than twice as slow as with the traditional algorithm: 1q41 (2235%), 1sq5 (1141%), 1q1g (440%), 1hq2 (219%) and 1dd7 (110%). There is no clear pattern as to why the refinement time for these structures was longer. The ligands range in size from molecular weights of 195 to 480 with from zero to nine rotatable bonds. For 1q1g and 1sq5 there are multiple copies of the ligand (six and four, respectively) but 1q41 with the longest refinement time has only two copies and zero rotatable bonds. The cause of the increase in refinement time is still under investigation. These five outliers have been omitted from the plot.

Figure 7.

Figure 7

Open in a new tab

Difference in run time between traditional Engh and Huber and PHENIX–AFITT refinement as a percentage of the Engh and Huber refinement run time. Positive numbers indicate that the PHENIX–AFITT refinement is faster and negative numbers that the PHENIX Engh and Huber refinement is faster. Five outliers (PDB entries 1q41, 1sq5, 1q1g, 1hq2 and 1dd7) have been omitted from the plot.

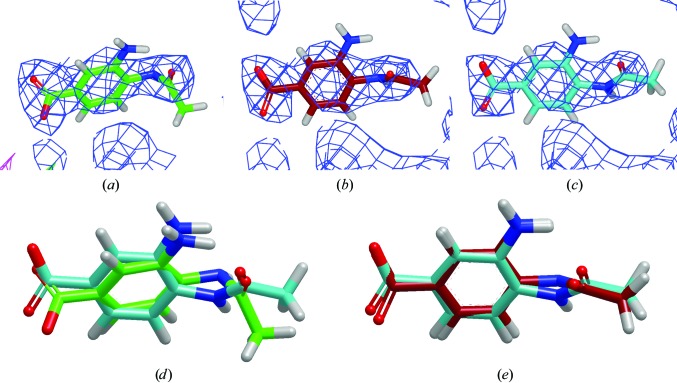
The data presented until now have been aggregate data showing that PHENIX–AFITT reduces conformational energy on average while improving small-molecule geometry. This section will present two examples of the maximum change or difference in the coordinates observed for this data set. The coordinate differences between the AFITT–CIF and PHENIX–AFITT conformations were less than 0.3 Å for all but 22 cases out of the 304 in this data set. An example of one of the larger differences is shown in Fig. 8 ▸ for PDB entry 1ive. Both copies of this ligand have a root-mean-square deviation (r.m.s.d.) that is only slightly greater than 0.3 Å between the AFITT–CIF and PHENIX–AFITT conformations, but the difference in energy is greater than 40 kJ mol−1. Very small coordinate changes have a profound effect on the conformational energy of the ligand. There are no examples in this data set where the r.m.s.d. difference in the coordinates for the AFITT–CIF and PHENIX–AFITT conformations is greater than 0.4 Å, yet the difference in energy was almost always large (>10 kJ mol−1). The second example of PDB entry 4cox, shown in Fig. 9 ▸, highlights another difference in performance between AFITT–CIF and PHENIX–AFITT. All of the refinements in this study used the same starting coordinates: the deposited coordinates for the ligand. If both methods were equivalent they should produce similar results with a similar amount of variability. As illustrated in Fig. 9 ▸, this was not the case. AFITT–CIF refinements had a much larger variability in the energy, as measured by standard deviation, for the conformations generated for 4cox and 21 other cases (data not shown) where the number of copies of the ligand was greater than or equal to three. This result is particularly troubling. Even though the same CIF restraints file was used for the coordinates, it appears that AFITT–CIF refinements exhibit chaotic-like behavior (Feher & Williams, 2012a ▸,b ▸), where small changes in the coordinates result in large changes in energy, versus PHENIX–AFITT refinements. An alternative explanation is that the PHENIX–AFITT refinement method has a larger radius of convergence.

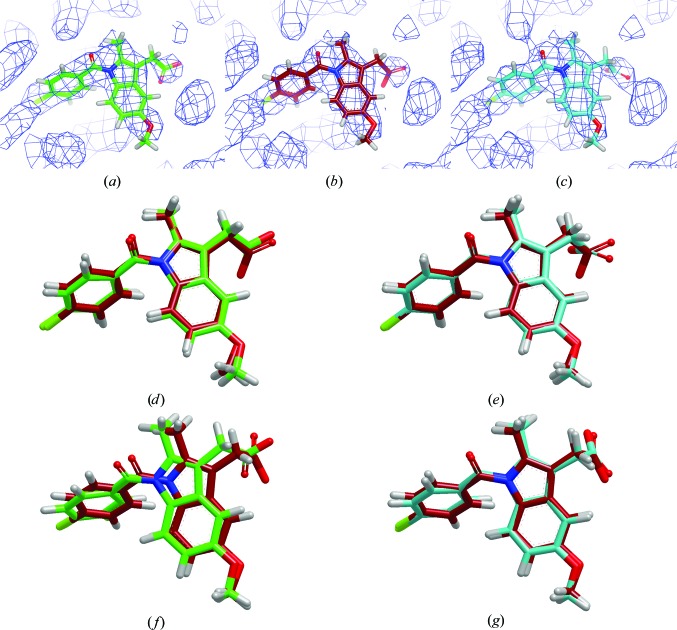
Figure 8.

Figure 8

Open in a new tab

A depiction of the conformations of the second copy of the ligand from PDB entry 1ive. (a), (b) and (c) show the deposited (C atoms colored green), AFITT–CIF (C atoms coloured red) and PHENIX–AFITT (C atoms colored turquoise) conformations, respectively. The density shown is σA-weighted 2F o − F c density contoured at 1σ and the difference map was contoured at 3σ. (d) shows the deposited and PHENIX–AFITT conformations using the previously described color scheme, where the r.ms.d. is 0.81 Å and the energy difference is 134 kJ mol−1. (e) shows an overlay of the AFITT–CIF and PHENIX–AFITT conformations. The r.m.s.d. is 0.31 Å and the energy difference is 41.6 kJ mol−1. There are no examples in this data set where the r.m.s.d. between the AFITT–CIF and PHENIX–AFITT conformations exceeds 0.4 Å, yet the energy difference between the two conformations was almost always large (>10 kJ mol−1).

Figure 9.

Figure 9

Open in a new tab

A depiction of the conformations of the first copy of the ligand from PDB entry 4cox. (a), (b) and (c) show the deposited (C atoms colored green), AFITT–CIF (C atoms colored red) and PHENIX–AFITT (C atoms colored turquoise) conformations, respectively. The density shown is σA-weighted 2F o − F c density contoured at 1σ. No difference density was observed when the density was contoured at 3σ. There are a total of four copies of the ligand in this deposition. (d) and (e) show the overlay for the first copy between the deposited and AFITT–CIF and between the AFITT–CIF and PHENIX–AFITT conformations, respectively, using the previously described coloring scheme. The r.m.s.d. between the deposited and the AFITT–CIF conformation was 0.24 Å, whereas the difference between the AFITT–CIF and PHENIX–AFITT conformations was 0.38 Å. In this case the AFITT–CIF refinement was unable to find the low-energy conformation generated by the PHENIX–AFITT refinement, as shown by the r.m.s.d. and the difference energies of 1.57 kJ mol−1 for the deposited versus AFITT–CIF and 119 kJ mol−1 for the deposited versus PHENIX–AFITT conformation. (f, g) Copy 4 presents a different result. The AFITT–CIF and PHENIX–AFITT methods both find a lower energy conformation where the r.m.s.d. for the deposited versus AFITT–CIF and deposited versus PHENIX–AFITT was 0.7 Å, but the r.m.s.d. for the AFITT–CIF and PHENIX–AFITT conformations was only 0.20 Å. The energy differences were 31.2 kJ mol−1 for deposited versus AFITT–CIF and 117 kJ mol−1 for deposited versus PHENIX–AFITT. An interesting observation from this example is that the PHENIX–AFITT method appears to be more consistent at finding low-energy conformations (the standard deviation across the four samples was 4.08 kJ mol−1), whereas the AFITT–CIF method was not as consistent (standard deviation of 19.6 kJ mol−1).

4. Discussion  

The PHENIX–AFITT protocol is a new tool that decreases ligand conformational energy versus the geometry restraints typically used in modern refinement programs. By implementing an interface to AFITT into PHENIX refinement, a more accurate set of geometric chemical gradients are made available, leading to a significant reduction in ligand conformational energies and a significant improvement in ligand geometries. This is accomplished without detriment to the fit of the model to experimental data and with only a modest increase in refinement time. AFITT is fully integrated with phenix.refine, is easy to use and automatically handles multiple ligands, alternate conformations and covalent linkage. A user’s guide is available online in the PHENIX documentation under the heading ‘Structure Refinement and Restraint Generation’.

The PHENIX–AFITT protocol not only improves on the deposited PDB ligand geometries but also on those obtained with refinements using a CIF-format restraints file derived from the same MMFF force field that AFITT uses. This is noteworthy because it underscores that improved refinement results are not solely the result of using better or more consistent dictionary file target values but also of how the force field is implemented within the refinement target function. Most target functions in use today only allow representation of bond, angle, simplified dihedral and atomic overlap penalty terms. Thus, a crystal structure refinement restraints representation of the geometry parameters of a ligand necessarily constrains the force field into a more primitive representation versus what is present in MMFF. For example, nonbonded interactions (electrostatics and van der Waals forces) are no longer accurately represented in the restraints format. This study cannot and does not prove that CIF-style restraints contain methodological flaws when attempting to accurately describe small-molecule ligand geometry. However, the fact that the Mogul validation results show a statistically significant decrease for PHENIX–AFITT versus AFITT–CIF models in angle deviations in contrast to bond lengths is consistent with this interpretation: angles are more susceptible to the nonbonded interactions more appropriately modeled by force-field terms than bonds. While not part of the current study, it is suspected that more complex components of conformation such as torsion angles and non­bonded inter­actions are unlikely to be adequately described under the current paradigm. More importantly, this study has shown that the use of a high-quality small-molecule force field eliminates the need, in a large part, for the user to be either an expert in writing and/or the need to be concerned about the quality of the parameters present in the small-molecule CIF dictionary. Unfortunately, CIF-like restraints dictionaries are in widespread use today because they represent the same geometry restraints function as has been found to function well with protein residues. While PDB_Redo (Cereto-Massagué et al., 2013 ▸) has shown that improvements to the quality of the model can be made, we have shown that there is a limit, when using restraint dictionaries, to how much of an improvement can be made to ligand conformation energy and geometry. As a move is made to obtain more accurate models, it is our hope that refinement target functions will more often be implemented according to the paradigm presented here (Borbulevych, Plumley et al., 2014 ▸; Smart et al., 2010 ▸, 2014 ▸) so as to more accurately represent the complex conformational space of small-molecule ligands.

Acknowledgments

The authors would like to acknowledge the funding provided by the OpenEye Scientific Software Summer Intern Program, which supported, in part, the work performed by PAJ. PHENIX was supported by the NIH (Project 1P01 GM063210), the Phenix Industrial Consortium and in part by the US Department of Energy under Contract No. DE-AC02-05CH11231. For those interested in accessing the data described in this paper, all of the data are available for download at the following link: http://www.phenix-online.org/phenix_data/Phenix_AFITT/. AFITT is software provided by OpenEye Scientific Software and can be obtained and used by academic users through a no-cost academic license at http://www.eyesopen.com/academic. Lastly, the authors would like to thank the editor and reviewers. Their dedication and excellent suggestions were vital and the work presented here was improved by their input.

References

  1. Adams, P. D. et al. (2010). Acta Cryst. D66, 213–221.
  2. Afonine, P. V., Grosse-Kunstleve, R. W., Echols, N., Headd, J. J., Moriarty, N. W., Mustyakimov, M., Terwilliger, T. C., Urzhumtsev, A., Zwart, P. H. & Adams, P. D. (2012). Acta Cryst. D68, 352–367. [DOI] [PMC free article] [PubMed]
  3. Allen, F. H. (2002). Acta Cryst. B58, 380–388. [DOI] [PubMed]
  4. Berman, H., Henrick, K. & Nakamura, H. (2003). Nature Struct. Biol. 10, 980. [DOI] [PubMed]
  5. Berman, H. M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T. N., Weissig, H., Shindyalov, I. N. & Bourne, P. E. (2000). Nucleic Acids Res. 28, 235–242. [DOI] [PMC free article] [PubMed]
  6. Borbulevych, O., Martin, R. I., Tickle, I. J. & Westerhoff, L. M. (2016). Acta Cryst. D72, 586–598. [DOI] [PMC free article] [PubMed]
  7. Borbulevych, O. Y., Moriarty, N. W., Adams, P. D. & Westerhoff, L. M. (2014). Comput. Crystallogr. Newsl. 5, 26–30.
  8. Borbulevych, O. Y., Plumley, J. A., Martin, R. I., Merz, K. M. & Westerhoff, L. M. (2014). Acta Cryst. D70, 1233–1247. [DOI] [PMC free article] [PubMed]
  9. Brown, I. D. & McMahon, B. (2002). Acta Cryst. B58, 317–324. [DOI] [PubMed]
  10. Brünger, A. T. (1993). Acta Cryst. D49, 24–36. [DOI] [PubMed]
  11. Bruno, I. J., Cole, J. C., Kessler, M., Luo, J., Motherwell, W. S., Purkis, L. H., Smith, B. R., Taylor, R., Cooper, R. I., Harris, S. E. & Orpen, A. G. (2004). J. Chem. Inf. Comput. Sci. 44, 2133–2144. [DOI] [PubMed]
  12. Cereto-Massagué, A., Ojeda, M. J., Joosten, R. P., Valls, C., Mulero, M., Salvado, M. J., Arola-Arnal, A., Arola, L., Garcia-Vallvé, S. & Pujadas, G. (2013). J. Cheminform. 5, 36. [DOI] [PMC free article] [PubMed]
  13. Chen, V. B., Arendall, W. B. III, Headd, J. J., Keedy, D. A., Immormino, R. M., Kapral, G. J., Murray, L. W., Richardson, J. S. & Richardson, D. C. (2010). Acta Cryst. D66, 12–21. [DOI] [PMC free article] [PubMed]
  14. Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences. Mahwah: Lawrence Erlbaum Associates.
  15. Davis, A. M., Teague, S. J. & Kleywegt, G. J. (2003). Angew. Chem. Int. Ed. 42, 2718–2736. [DOI] [PubMed]
  16. Engh, R. A. & Huber, R. (1991). Acta Cryst. A47, 392–400.
  17. Engh, R. A. & Huber, R. (2001). International Tables for Crystallo­graphy, Vol. F, edited by M. G. Rossmann & E. Arnold, pp. 382–392. Dordrecht: Kluwer Academic Publishers.
  18. Feher, M. & Williams, C. I. (2012a). J. Chem. Inf. Model. 52, 724–738. [DOI] [PubMed]
  19. Feher, M. & Williams, C. I. (2012b). J. Chem. Inf. Model. 52, 3200–3212. [DOI] [PubMed]
  20. Fu, Z., Li, X. & Merz, K. M. (2011). J. Comput. Chem. 32, 2587–2597. [DOI] [PubMed]
  21. Grant, J. A., Pickup, B. T. & Nicholls, A. (2001). J. Comput. Chem. 22, 608–640.
  22. Grant, J. A., Pickup, B. T., Sykes, M. J., Kitchen, C. A. & Nicholls, A. (2007). Chem. Phys. Lett. 441, 163–166. [DOI] [PubMed]
  23. Gundertofte, K., Liljefors, T., Norrby, P. & Pettersson, I. (1996). J. Comput. Chem. 17, 429–449.
  24. Halgren, T. A. (1996a). J. Comput. Chem. 17, 490–519.
  25. Halgren, T. A. (1996b). J. Comput. Chem. 17, 520–552.
  26. Halgren, T. A. (1996c). J. Comput. Chem. 17, 553–586.
  27. Halgren, T. A. (1996d). J. Comput. Chem. 17, 616–641.
  28. Halgren, T. A. (1999). J. Comput. Chem. 20, 730–748. [DOI] [PubMed]
  29. Halgren, T. A. & Nachbar, R. B. (1996). J. Comput. Chem. 17, 587–615.
  30. Hall, S. R., Allen, F. H. & Brown, I. D. (1991). Acta Cryst. A47, 655–685.
  31. Jones, T. A., Zou, J.-Y., Cowan, S. W. & Kjeldgaard, M. (1991). Acta Cryst. A47, 110–119. [DOI] [PubMed]
  32. Kleywegt, G. J., Henrick, K., Dodson, E. J. & van Aalten, D. M. F. (2003). Structure, 11, 1051–1059. [DOI] [PubMed]
  33. Kleywegt, G. J. & Jones, T. A. (1998). Acta Cryst. D54, 1119–1131. [DOI] [PubMed]
  34. Kolmogorov, A. N. (1933). Grundbegriffe der Wahrscheinlichkeitsrechnung. Berlin: Springer.
  35. Lebedev, A. A., Young, P., Isupov, M. N., Moroz, O. V., Vagin, A. A. & Murshudov, G. N. (2012). Acta Cryst. D68, 431–440. [DOI] [PMC free article] [PubMed]
  36. Liebeschuetz, J., Hennemann, J., Olsson, T. & Groom, C. R. (2012). J. Comput. Aided Mol. Des. 26, 169–183. [DOI] [PMC free article] [PubMed]
  37. Moriarty, N. W., Grosse-Kunstleve, R. W. & Adams, P. D. (2009). Acta Cryst. D65, 1074–1080. [DOI] [PMC free article] [PubMed]
  38. Moriarty, N. W., Tronrud, D. E., Adams, P. D. & Karplus, P. A. (2014). FEBS J. 281, 4061–4071. [DOI] [PMC free article] [PubMed]
  39. Parkinson, G., Vojtechovsky, J., Clowney, L., Brünger, A. T. & Berman, H. M. (1996). Acta Cryst. D52, 57–64. [DOI] [PubMed]
  40. Pearson, E. & Hartley, H. (1972). Biometrika Tables for Statisticians, pp. 117–123. Cambridge University Press.
  41. Pozharski, E., Weichenberger, C. X. & Rupp, B. (2013). Acta Cryst. D69, 150–167. [DOI] [PubMed]
  42. Priestle, J. P. (2003). J. Appl. Cryst. 36, 34–42.
  43. Schüttelkopf, A. W. & van Aalten, D. M. F. (2004). Acta Cryst. D60, 1355–1363. [DOI] [PubMed]
  44. Smart, O., Womack, T., Sharff, A., Flensburg, C., Keller, P., Paciorek, W., Vonrhein, C. & Bricogne, G. (2010). AutobusterLigandQM. http://www.globalphasing.com/buster/wiki/index.cgi?AutobusterLigandQM.
  45. Smart, O., Womack, T., Sharff, A., Flensburg, C., Keller, P., Paciorek, W., Vonrhein, C. & Bricogne, G. (2012). Grade v.1.2.1. Global Phasing Ltd, Cambridge, England.
  46. Smart, O. S., Womack, T. O., Sharff, A., Flensburg, C., Keller, P., Paciorek, W., Vonrhein, C. & Bricogne, G. (2014). AutobusterLigandForcefield. http://www.globalphasing.com/buster/wiki/index.cgi?AutobusterLigandForcefield.
  47. Smirnov, N. (1948). Ann. Math. Stat. 19, 279–281.
  48. Student (1908). Biometrika, 6, 1–25.
  49. Touw, W. G. & Vriend, G. (2010). Acta Cryst. D66, 1341–1350. [DOI] [PMC free article] [PubMed]
  50. Vagin, A. A., Steiner, R. A., Lebedev, A. A., Potterton, L., McNicholas, S., Long, F. & Murshudov, G. N. (2004). Acta Cryst. D60, 2184–2195. [DOI] [PubMed]
  51. Warren, G. L., Do, T. D., Kelley, B. P., Nicholls, A. & Warren, S. D. (2012). Drug Discov. Today, 17, 1270–1281. [DOI] [PubMed]
  52. Wlodek, S., Skillman, A. G. & Nicholls, A. (2006). Acta Cryst. D62, 741–749. [DOI] [PubMed]
  53. Yang, H., Peisach, E., Westbrook, J. D., Young, J., Berman, H. M. & Burley, S. K. (2016). J. Appl. Cryst. 49, 1081–1084. [DOI] [PMC free article] [PubMed]
  54. Yu, N., Yennawar, H. P. & Merz, K. M. (2005). Acta Cryst. D61, 322–332. [DOI] [PubMed]

Articles from Acta Crystallographica. Section D, Structural Biology are provided here courtesy of International Union of Crystallography

RESOURCES